Güç serisini çevrimiçi olarak genişletin. Kuvvet serileri, yakınsaklıkları, fonksiyonların kuvvet serilerine genişletilmesi

Fonksiyonel seriler arasında en önemli yeri kuvvet serileri almaktadır.

Kuvvet serisi bir seridir

terimleri artan negatif olmayan tamsayı kuvvetlerine göre düzenlenmiş kuvvet fonksiyonlarıdır X, A C 0 , C 1 , C 2 , C n - sabit değerler. Sayılar C 1 , C 2 , C n - seri terimlerin katsayıları, C 0 - ücretsiz üye. Kuvvet serisinin terimleri sayı doğrusunun tamamında tanımlanır.

Konsepti tanıyalım kuvvet serilerinin yakınsaklık alanları. Bu bir değişkenin değer kümesidir X, bunun için seri yakınsaktır. Kuvvet serileri oldukça basit bir yakınsama bölgesine sahiptir. Gerçek değişken değerleri için X yakınsama bölgesi ya bir noktadan oluşur ya da belirli bir aralıktır (yakınsama aralığı) ya da tüm eksenle çakışır Öküz .

Değerleri güç serisine yerleştirirken X= 0 bir sayı serisiyle sonuçlanacaktır

C 0 +0+0+...+0+... ,

hangi birleşir.

Bu nedenle ne zaman X= 0 herhangi bir kuvvet serisi yakınsar ve bu nedenle, yakınsama alanı boş küme olamaz. Tüm kuvvet serilerinin yakınsaklık bölgesinin yapısı aynıdır. Aşağıdaki teorem kullanılarak belirlenebilir.

Teorem 1 (Abel teoremi). Bir kuvvet serisi belirli bir değerde yakınsarsa X = X 0, sıfırdan farklıysa, yakınsar ve dahası, |'nin tüm değerleri için kesinlikle yakınsar. X| < |X 0 |

. Lütfen unutmayın: hem “X sıfırdır” başlangıç değeri hem de başlangıç değeriyle karşılaştırılan herhangi bir “X” değeri, işaret dikkate alınmaksızın modulo olarak alınır. Sonuçlar. Eğer kuvvet serisi ıraksar X = X bir değerde X| > |X 1 | .

1 ise |'nin tüm değerleri için ıraksar X Daha önce öğrendiğimiz gibi, herhangi bir kuvvet serisi şu değerde yakınsar: X= 0. Yalnızca şu durumlarda yakınsayan kuvvet serileri vardır: = 0 ve diğer değerler için ıraksak X X = X. Bu durumu göz önünde bulundurmadan, kuvvet serilerinin bir değerde yakınsadığını varsayıyoruz. X 0 |, |X 0, sıfırdan farklı. O halde Abel teoremine göre ]-| aralığının her noktasında yakınsar.

0 |[ (sol ve sağ sınırları, güç serisinin yakınlaştığı x değerleri olan, sırasıyla eksi işareti ve artı işaretiyle alınan bir aralık), kökene göre simetrik. X = X 1, o halde, Abel teoreminin sonucuna göre, [-| doğru parçasının dışındaki tüm noktalarda ıraksar. X 1 |, |X 1 |] . Herhangi bir kuvvet serisi için orijine göre simetrik bir aralık vardır. yakınsama aralığı, serinin yakınlaştığı her noktada, sınırlarda yakınlaşabilir veya uzaklaşabilir ve mutlaka aynı anda olması gerekmez ve segmentin dışında seri ıraksar. Sayı R kuvvet serisinin yakınsaklık yarıçapı denir.

Özel durumlarda kuvvet serilerinin yakınsama aralığı bir noktaya kadar yozlaşabilir (bu durumda seri ancak X= 0 ve öyle kabul edilir R= 0) veya sayı doğrusunun tamamını temsil eder (bu durumda seri sayı doğrusu üzerindeki tüm noktalarda yakınsar ve öyle olduğu varsayılır).

Dolayısıyla bir kuvvet serisinin yakınsaklık bölgesinin belirlenmesi, onun yakınsaklığının belirlenmesinden ibarettir. yakınsama yarıçapı R ve yakınsama aralığı sınırlarında ('da) serinin yakınsaklığının incelenmesi.

Teorem 2. Belirli bir seriden başlayarak bir güç serisinin tüm katsayıları sıfırdan farklıysa, yakınsama yarıçapı, ortak terimlerin katsayılarının mutlak değerleri oranındaki limite eşittir. onu takip eden dizi, yani

Örnek 1. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. Burada

Formül (28)'i kullanarak bu serinin yakınsama yarıçapını buluruz:

Yakınsaklık aralığının uçlarındaki serilerin yakınsaklığını inceleyelim. Örnek 13 bu serinin şu noktada yakınsadığını göstermektedir: X= 1 ve ıraksar X= -1. Sonuç olarak, yakınsama bölgesi yarı aralıktır.

Örnek 2. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. Serinin katsayıları pozitiftir ve

Bu oranın limitini bulalım. kuvvet serilerinin yakınsama yarıçapı:

Serinin aralığın sonlarındaki yakınsaklığını inceleyelim. Değerlerin değiştirilmesi X= -1/5 ve X= 1/5 bu satırda şunu verir:

Bu serilerden ilki yakınsar (bkz. Örnek 5). Ancak o zaman “Mutlak yakınsaklık” bölümündeki teorem gereği ikinci seri de yakınsar ve yakınsaklığının bölgesi segmenttir.

Örnek 3. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. Burada

Formül (28)'i kullanarak serinin yakınsaklık yarıçapını buluruz:

değerleri için serinin yakınsaklığını inceleyelim. Bunları bu seride yerine koyarsak sırasıyla şunu elde ederiz:

Her iki seri de ıraksaktır çünkü yakınsama için gerekli koşul sağlanmamıştır (ortak terimleri sıfıra yönelmemektedir). Yani yakınsama aralığının her iki ucunda da bu seri ıraksar ve yakınsaklık bölgesi aralıktır.

Örnek 5. Kuvvet serisinin yakınsaklık bölgesini bulun

Çözüm. İlişkiyi nerede buluyoruz ve :

Formül (28)'e göre, bu serinin yakınsama yarıçapı

yani seri yalnızca şu durumlarda yakınsar X= 0 ve diğer değerler için ıraksar = 0 ve diğer değerler için ıraksak.

Örnekler, yakınsama aralığının sonlarında serinin farklı davrandığını göstermektedir. Örnek 1'de seri yakınsaklık aralığının bir ucunda yakınsar, diğer ucunda ıraksar; örnek 2'de her iki uçta da yakınsar, örnek 3'te her iki uçta da ıraksar.

Bir güç serisinin yakınsama yarıçapı formülü, seri terimlerinin belirli bir noktadan başlayarak tüm katsayılarının sıfırdan farklı olduğu varsayımıyla elde edilir. Bu nedenle formül (28)'in kullanımına yalnızca bu durumlarda izin verilir. Bu koşul ihlal edilirse, güç serisinin yakınsama yarıçapı d'Alembert testi kullanılarak aranmalı veya değişken değiştirilerek seri, belirtilen koşulun karşılandığı bir forma dönüştürülmelidir.

Örnek 6. Kuvvet serisinin yakınsaklık aralığını bulun

Çözüm. Bu seri tek dereceli terimler içermiyor = 0 ve diğer değerler için ıraksak. Bu nedenle diziyi ayarlayarak dönüştürüyoruz. Sonra diziyi alıyoruz

formül (28)'i uygulayabileceğimiz yakınsama yarıçapını bulmak için. a olduğundan bu serinin yakınsaklık yarıçapı

Dolayısıyla elde ettiğimiz eşitlikten bu seri aralıkta yakınsar.

Güç serilerinin toplamı. Güç serilerinin farklılaşması ve entegrasyonu

Güç serisi için izin ver

yakınsama yarıçapı R> 0, yani bu seri aralıkta yakınsar.

Daha sonra her değer = 0 ve diğer değerler için ıraksak yakınsama aralığından serinin belirli bir toplamına karşılık gelir. Bu nedenle güç serilerinin toplamı şuna bağlıdır: = 0 ve diğer değerler için ıraksak yakınsama aralığında. Şununla belirtmek F(X), eşitliği yazabiliriz

bunu her noktadaki serinin toplamı anlamında anlamak = 0 ve diğer değerler için ıraksak yakınsama aralığından fonksiyonun değerine eşittir F(X) Bu noktada. Aynı anlamda kuvvet serisinin (29) fonksiyona yakınsadığını söyleyeceğiz. F(X) yakınsama aralığında.

Yakınsama aralığının dışında eşitliğin (30) hiçbir anlamı yoktur.

Örnek 7. Kuvvet serilerinin toplamını bulun

Çözüm. Bu geometrik bir seridir A= 1, bir Q= X. Bu nedenle toplamı bir fonksiyondur . Bir seri eğer yakınsar ve onun yakınsama aralığıdır. Bu nedenle eşitlik

işlev yalnızca değerler için geçerlidir, ancak işlev tüm değerler için tanımlanmış = 0 ve diğer değerler için ıraksak, hariç = 0 ve diğer değerler için ıraksak= 1.

Güç serilerinin toplamının olduğu kanıtlanabilir. F(X) yakınsama aralığındaki herhangi bir aralıkta, özellikle serinin yakınsama aralığındaki herhangi bir noktada sürekli ve türevlenebilirdir.

Kuvvet serilerinin terim terim türevi ve integrali ile ilgili teoremleri sunalım.

Teorem 1. Yakınsama aralığındaki kuvvet serileri (30), sınırsız sayıda terimden terime farklılaşabilir ve elde edilen kuvvet serileri, orijinal seri ile aynı yakınsama yarıçapına sahiptir ve bunların toplamları sırasıyla eşittir.

Teorem 2. Kuvvet serisi (30), 0 ile terim aralığında sınırsız sayıda terim terim integre edilebilir. = 0 ve diğer değerler için ıraksak, if , ve ortaya çıkan kuvvet serileri orijinal seriyle aynı yakınsaklık yarıçapına sahiptir ve toplamları buna uygun olarak eşittir

Fonksiyonların kuvvet serilerine genişletilmesi

Fonksiyon verilsin F(X), bunun bir kuvvet serisine genişletilmesi gerekiyor, yani. (30) formunda temsil edilir:

Görev katsayıları belirlemektir. sıra (30). Bunu yapmak için eşitliği (30) terimden terime ayırarak tutarlı bir şekilde şunu buluruz:

……………………………………………….. (31)

(30) ve (31) eşitliklerini varsayarsak = 0 ve diğer değerler için ıraksak= 0, buluruz

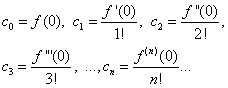
Bulunan ifadeleri eşitlik (30) ile değiştirerek şunu elde ederiz:

(32)

Bazı temel fonksiyonların Maclaurin serisi açılımını bulalım.

Örnek 8. Fonksiyonu Maclaurin serisinde genişletin

Çözüm. Bu fonksiyonun türevleri fonksiyonun kendisiyle çakışmaktadır:

Bu nedenle ne zaman = 0 ve diğer değerler için ıraksak= 0 elimizde

Bu değerleri formül (32)'ye değiştirerek istenen genişlemeyi elde ederiz:

(33)

Bu seri tüm sayı doğrusu üzerinde (yakınsaklık yarıçapı) yakınsar.

16.1. Taylor ve Maclaurin serilerinde temel fonksiyonların genişletilmesi

Bir küme üzerinde keyfi bir fonksiyonun tanımlandığını gösterelim.
, noktanın yakınında
birçok türevi vardır ve bir kuvvet serisinin toplamıdır:

o zaman bu serinin katsayılarını bulabilirsiniz.

Bir kuvvet serisinde yerine koyalım
. Daha sonra
.

Fonksiyonun ilk türevini bulalım
:

Şu tarihte:
:
.

İkinci türev için şunu elde ederiz:

Şu tarihte:
:
.

Bu prosedüre devam etmek N bir kez elde ettiğimizde:
.

Böylece şu formda bir kuvvet serisi elde ettik:

buna denir Taylor'ın yanında fonksiyon için
noktanın yakınında
.

Taylor serisinin özel bir durumu Maclaurin serisi en
:

Taylor (Maclaurin) serisinin geri kalanı ana serinin atılmasıyla elde edilir. N ilk üyeler ve şu şekilde gösterilir:
. Daha sonra fonksiyon
toplam olarak yazılabilir N serinin ilk üyeleri
ve geri kalanı
:,

Geriye kalan kısım genellikle
farklı formüllerle ifade edilir.

Bunlardan biri Lagrange formundadır:

, Nerede
.
.

Pratikte Maclaurin serisinin daha sık kullanıldığını unutmayın. Bu nedenle fonksiyonu yazmak için
kuvvet serisi toplamı şeklinde gereklidir:

1) Maclaurin (Taylor) serisinin katsayılarını bulun;

2) ortaya çıkan kuvvet serisinin yakınsaklık bölgesini bulun;

3) bu serinin fonksiyona yakınsak olduğunu kanıtlayın
.

Teorem 1 (Maclaurin serisinin yakınsaması için gerekli ve yeterli koşul). Serinin yakınsaklık yarıçapı olsun
. Bu serinin aralıkta yakınsaması için
işlev görmek
Koşulun gerçekleşmesi için gerekli ve yeterlidir:
belirtilen aralıkta.

Teorem 2. Bir fonksiyonun herhangi bir mertebeden türevleri varsa
belli bir aralıkta
mutlak değer olarak aynı sayıyla sınırlı M yani
, o zaman bu aralıkta fonksiyon
Maclaurin serisine genişletilebilir.

Örnek 1. Nokta etrafında Taylor serisini genişletin
işlev.

Çözüm.

,
;

.......................................................................................................................................

,
;

Yakınsama bölgesi
.

Örnek 2. Bir işlevi genişlet bir nokta etrafındaki Taylor serisinde
.

Çözüm:

Fonksiyonun değerini ve türevlerini bulun
.

,
;

...........……………………………

,
.

Bu değerleri sıralayalım. Şunu elde ederiz:

veya
.

Bu serinin yakınsaklık bölgesini bulalım. D'Alembert testine göre bir seri şu durumda yakınsar:

Bu nedenle herhangi bir kişi için bu limit 1'den küçüktür ve bu nedenle serinin yakınsaklık aralığı şöyle olacaktır:
.

Temel temel fonksiyonların Maclaurin serisi açılımının birkaç örneğini ele alalım. Maclaurin serisini hatırlayın:

aralıkta yakınsar
işlev görmek
.

Bir fonksiyonu bir seriye genişletmek için aşağıdakilerin gerekli olduğunu unutmayın:

a) bu fonksiyon için Maclaurin serisinin katsayılarını bulun;

b) ortaya çıkan serinin yakınsama yarıçapını hesaplayın;

c) Ortaya çıkan serinin fonksiyona yakınsak olduğunu kanıtlayın
.

Örnek 3. Fonksiyonu düşünün
.

Çözüm.

Fonksiyonun değerini ve türevlerini hesaplayalım.
.

O halde serinin sayısal katsayıları şu şekildedir:

herkes için N. Bulunan katsayıları Maclaurin serisine koyalım ve şunu elde edelim:

Ortaya çıkan serinin yakınsaklık yarıçapını bulalım:

Bu nedenle seri aralıkta yakınsar
.

Bu seri fonksiyona yakınsar herhangi bir değer için , çünkü herhangi bir aralıkta
işlev ve mutlak değerli türevlerinin sayısı sınırlıdır .

Örnek 4. İşlevi düşünün
.

Çözüm.

Eşit mertebeden türevlerin olduğunu görmek kolaydır
ve türevler tek sıralıdır. Bulunan katsayıları Maclaurin serisine koyalım ve açılımı elde edelim:

Bu serinin yakınsaklık aralığını bulalım. D'Alembert'in işaretine göre:

herkes için . Bu nedenle seri aralıkta yakınsar
.

Bu seri fonksiyona yakınsar
Çünkü tüm türevleri birlikle sınırlıdır.

Örnek 5.
.

Çözüm.

Fonksiyonun değerini ve türevlerini bulalım.
:

Böylece bu serinin katsayıları:
Ve
, buradan:

Önceki satıra benzer şekilde yakınsama alanı
. Seri fonksiyona yakınsar
Çünkü tüm türevleri birlikle sınırlıdır.

Lütfen işlevin
Tek kuvvetlerde tek ve seri açılım, fonksiyon
– çift ve çift kuvvetlerde bir seriye genişleme.

Örnek 6. Binom serisi:
.

Çözüm.

Fonksiyonun değerini ve türevlerini bulalım.
:

Bundan şunu görmek mümkündür:

Bu katsayı değerlerini Maclaurin serisine koyalım ve bu fonksiyonun bir kuvvet serisine genişletilmesini elde edelim:

Bu serinin yakınsaklık yarıçapını bulalım:

Bu nedenle seri aralıkta yakınsar
. Sınırlayıcı noktalarda
Ve
üsse bağlı olarak bir seri yakınsak olabilir veya olmayabilir
.

İncelenen seriler aralıkta yakınsaktır
işlev görmek
yani serinin toplamı
en
.

Örnek 7. Fonksiyonu Maclaurin serisine genişletelim
.

Çözüm.

Bu fonksiyonu bir seriye genişletmek için binom serisini kullanırız.
. Şunu elde ederiz:

Kuvvet serisinin özelliğine dayanarak (bir kuvvet serisi yakınsaklık bölgesinde entegre edilebilir), bu serinin sol ve sağ taraflarının integralini buluruz:

Bu serinin yakınsaklık alanını bulalım:
,

yani bu serinin yakınsaklık alanı aralıktır
.

Serinin aralığın uçlarındaki yakınsaklığını belirleyelim. Şu tarihte:
. Bu seri uyumlu bir seridir, yani ıraksamaktadır. Şu tarihte:
.

ortak terimli bir sayı serisi elde ederiz
.

Seri Leibniz kriterine göre yakınsaktır. Dolayısıyla bu serinin yakınsaklık bölgesi aralıktır.

16.2. Güç serilerinin yaklaşık hesaplamalarda uygulanması N Yaklaşık hesaplamalarda kuvvet serileri son derece önemli bir rol oynamaktadır. Onların yardımıyla, örneğin olasılık teorisi ve matematiksel istatistik gibi çeşitli bilgi alanlarında kullanılan trigonometrik fonksiyon tabloları, logaritma tabloları, diğer fonksiyonların değer tabloları derlenmiştir. Ek olarak, fonksiyonların kuvvet serilerine genişletilmesi teorik çalışmaları açısından faydalıdır. Yaklaşık hesaplamalarda kuvvet serilerini kullanırken asıl sorun, bir serinin toplamını ilk serinin toplamı ile değiştirirken hatayı tahmin etme meselesidir.

üyeler.

İki durumu ele alalım:

fonksiyon, işaret dönüşümlü bir seriye genişletilir;

fonksiyon bir dizi sabit işarete genişletilir.

Alternatif serileri kullanarak hesaplama
Fonksiyona izin ver alternatif kuvvet serisine genişletildi. Daha sonra bu fonksiyonu belirli bir değer için hesaplarken N Leibniz kriterini uygulayabileceğimiz bir sayı serisi elde ederiz. Bu kritere göre bir serinin toplamı ilk serinin toplamı ile değiştirilirse
.