Let's start by explaining what four-dimensional space is.
This is a one-dimensional space, that is, simply the OX axis. Any point on it is characterized by one coordinate.

Now let's draw the OY axis perpendicular to the OX axis. So we get a two-dimensional space, that is, the XOY plane. Any point on it is characterized by two coordinates - abscissa and ordinate.

Let's draw the OZ axis perpendicular to the OX and OY axes. The result is a three-dimensional space in which any point has an abscissa, ordinate and applicate.

It is logical that the fourth axis, OQ, should be perpendicular to the OX, OY and OZ axes at the same time. But we cannot accurately construct such an axis, and therefore we can only try to imagine it. Every point in four-dimensional space has four coordinates: x, y, z and q.
Now let's see how the four-dimensional cube appeared.

The picture shows a figure in one-dimensional space - a line.

If you make a parallel translation of this line along the OY axis, and then connect the corresponding ends of the two resulting lines, you will get a square.

Similarly, if you make a parallel translation of the square along the OZ axis and connect the corresponding vertices, you will get a cube.

And if we make a parallel translation of the cube along the OQ axis and connect the vertices of these two cubes, then we will get a four-dimensional cube. By the way, it's called tesseract.
To draw a cube on a plane, you need it project. Visually it looks like this: 
Let's imagine that it is hanging in the air above the surface wireframe model cube, that is, as if “made of wire,” and above it is a light bulb. If you turn on the light bulb, trace the shadow of the cube with a pencil, and then turn off the light bulb, a projection of the cube will be depicted on the surface.
Let's move on to something a little more complex. Look again at the drawing with the light bulb: as you can see, all the rays converge at one point. It is called vanishing point and is used to build perspective projection(and it can also be parallel, when all the rays are parallel to each other. The result is that the sensation of volume is not created, but it is lighter, and moreover, if the vanishing point is quite far removed from the projected object, then the difference between these two projections is little noticeable). To project a given point onto a given plane using a vanishing point, you need to draw a straight line through the vanishing point and the given point, and then find the intersection point of the resulting straight line and the plane. And in order to project a more complex figure, say, a cube, you need to project each of its vertices, and then connect the corresponding points. It should be noted that algorithm for projecting space onto subspace can be generalized to the case of 4D->3D, not just 3D->2D.
As I said, we can't imagine exactly what the OQ axis looks like, just like the tesseract. But we can get a limited idea of it if we project it onto a volume and then draw it on a computer screen!
Now let's talk about the tesseract projection.

On the left is the projection of the cube onto the plane, and on the right is the tesseract onto the volume. They are quite similar: the projection of a cube looks like two squares, small and large, one inside the other, and whose corresponding vertices are connected by lines. And the projection of the tesseract looks like two cubes, small and large, one inside the other, and whose corresponding vertices are connected. But we have all seen the cube, and we can say with confidence that both the small square and the large one, and the four trapezoids above, below, to the right and left of the small square, are actually squares, and they are equal. And the tesseract has the same thing. And a large cube, and a small cube, and six truncated pyramids on the sides of a small cube - these are all cubes, and they are equal.
My program can not only draw the projection of a tesseract onto a volume, but also rotate it. Let's look at how this is done.
First, I'll tell you what it is rotation parallel to the plane.
Imagine that the cube rotates around the OZ axis. Then each of its vertices describes a circle around the OZ axis. 
A circle is a flat figure. And the planes of each of these circles are parallel to each other, and in this case parallel to the XOY plane. That is, we can talk not only about rotation around the OZ axis, but also about rotation parallel to the XOY plane. As we see, for points that rotate parallel to the XOY axis, only the abscissa and ordinate change, while the applicate remains unchanged. And, in fact, we we can talk about rotation around a straight line only when we are dealing with three-dimensional space. In two-dimensional space everything rotates around a point, in four-dimensional space everything rotates around a plane, in five-dimensional space we talk about rotation around a volume. And if we can imagine rotation around a point, then rotation around a plane and volume is something unthinkable. And if we talk about rotation parallel to the plane, then in any n-dimensional space a point can rotate parallel to the plane.
Many of you have probably heard of the rotation matrix. Multiplying the point by it, we get a point rotated parallel to the plane by an angle phi. For two-dimensional space it looks like this: 
How to multiply: x of a point rotated by an angle phi = cosine of the angle phi*ix of the original point minus sine of the angle phi*ig of the original point;
ig of a point rotated by an angle phi = sine of the angle phi * ix of the original point plus cosine of the angle phi * ig of the original point.
Xa`=cosф*Xa - sinф*Ya
Ya`=sinф*Xa + cosф*Ya
, where Xa and Ya are the abscissa and ordinate of the point to be rotated, Xa` and Ya` are the abscissa and ordinate of the already rotated point
For three-dimensional space, this matrix is generalized as follows: 
Rotation parallel to the XOY plane. As you can see, the Z coordinate does not change, but only X and Y change
Xa`=cosф*Xa - sinф*Ya + Za*0
Ya`=sinф*Xa +cosф*Ya + Za*0
Za`=Xa*0 + Ya*0 + Za*1 (essentially, Za`=Za)

Rotation parallel to the XOZ plane. Nothing new,
Xa`=cosф*Xa + Ya*0 - sinф*Za
Ya`=Xa*0 + Ya*1 + Za*0 (essentially, Ya`=Ya)
Za`=sinф*Xa + Ya*0 + cosф*Za

And the third matrix.
Xa`=Xa*1 + Ya*0 + Za*0 (essentially, Xa`=Xa)
Ya`=Xa*0 + cosф*Ya - sinф*Za
Za`=Xa*0 + sinф*Ya + cosф*Za
And for the fourth dimension they look like this: 
I think you already understand what to multiply by, so I won’t go into detail again. But I note that it does the same thing as a matrix for rotation parallel to a plane in three-dimensional space! Both of them change only the ordinate and the applicate, and do not touch the other coordinates, so it can be used in the three-dimensional case, simply not paying attention to the fourth coordinate.
But with the projection formula, not everything is so simple. No matter how many forums I read, none of the projection methods worked for me. The parallel one was not suitable for me, since the projection would not look three-dimensional. In some projection formulas, to find a point you need to solve a system of equations (and I don’t know how to teach a computer to solve them), others I simply didn’t understand... In general, I decided to come up with my own way. For this purpose, consider the 2D->1D projection.

pov means "Point of view", ptp means "Point to project" (the point to be projected), and ptp` is the desired point on the OX axis.
Angles povptpB and ptpptp`A are equal as corresponding (the dotted line is parallel to the OX axis, the straight line povptp is a secant).
The x of the point ptp` is equal to the x of the point ptp minus the length of the segment ptp`A. This segment can be found from the triangle ptpptp`A: ptp`A = ptpA/tangent of angle ptpptp`A. We can find this tangent from the triangle povptpB: tangent ptpptp`A = (Ypov-Yptp)(Xpov-Xptp).
Answer: Xptp`=Xptp-Yptp/tangent of angle ptpptp`A.
I did not describe this algorithm in detail here, since there are a lot of special cases when the formula changes somewhat. If anyone is interested, look at the source code of the program, everything is described there in the comments.
In order to project a point in three-dimensional space onto a plane, we simply consider two planes - XOZ and YOZ, and solve this problem for each of them. In the case of four-dimensional space, it is necessary to consider three planes: XOQ, YOQ and ZOQ.
And finally, about the program. It works like this: initialize sixteen vertices of the tesseract -> depending on the commands entered by the user, rotate it -> project it onto the volume -> depending on the commands entered by the user, rotate its projection -> project onto the plane -> draw.
I wrote the projections and rotations myself. They work according to the formulas I just described. The OpenGL library draws lines and also handles color mixing. And the coordinates of the tesseract vertices are calculated in this way:
Coordinates of the vertices of a line centered at the origin and length 2 - (1) and (-1);
- " - " - square - " - " - and with an edge of length 2:
(1; 1), (-1; 1), (1; -1) and (-1; -1);
- " - " - cube - " - " -:
(1; 1; 1), (-1; 1; 1), (1; -1; 1), (-1; -1; 1), (1; 1; -1), (-1; 1; -1), (1; -1; -1), (-1; -1; -1);
As you can see, a square is one line above the OY axis and one line below the OY axis; a cube is one square in front of the XOY plane, and one behind it; The tesseract is one cube on the other side of the XOYZ volume, and one on this side. But it is much easier to perceive this alternation of ones and minus ones if they are written in a column
1; 1; 1
-1; 1; 1
1; -1; 1
-1; -1; 1
1; 1; -1
-1; 1; -1
1; -1; -1
-1; -1; -1
In the first column, one and minus one alternate. In the second column, first there are two pluses, then two minuses. In the third - four plus ones, and then four minus ones. These were the vertices of the cube. The tesseract has twice as many of them, and therefore it was necessary to write a loop to declare them, otherwise it is very easy to get confused.
My program can also draw anaglyph. Happy owners of 3D glasses can observe a stereoscopic image. There is nothing tricky about drawing a picture; you simply draw two projections onto the plane, for the right and left eyes. But the program becomes much more visual and interesting, and most importantly, it gives a better idea of the four-dimensional world.
Less significant functions are the illumination of one of the edges in red so that turns can be better seen, as well as minor conveniences - regulation of the coordinates of the “eye” points, increasing and decreasing the turning speed.
Archive with the program, source code and instructions for use.
Bakalyar Maria
Methods for introducing the concept of a four-dimensional cube (tesseract), its structure and some properties are studied. The question of what three-dimensional objects are obtained when a four-dimensional cube is intersected by hyperplanes parallel to its three-dimensional faces, as well as hyperplanes perpendicular to its main diagonal is addressed. The apparatus of multidimensional analytical geometry used for research is considered.
Download:
Preview:
Introduction……………………………………………………………………………….2
Main part……………………………………………………………..4
Conclusions………….. ………………………………………………………..12
References………………………………………………………..13
Introduction
Four-dimensional space has long attracted the attention of both professional mathematicians and people far from studying this science. Interest in the fourth dimension may be due to the assumption that our three-dimensional world is “immersed” in four-dimensional space, just as a plane is “immersed” in three-dimensional space, a straight line is “immersed” in a plane, and a point is in a straight line. In addition, four-dimensional space plays an important role in the modern theory of relativity (the so-called space-time or Minkowski space), and can also be considered as a special casedimensional Euclidean space (with).
A four-dimensional cube (tesseract) is an object in four-dimensional space that has the maximum possible dimension (just as an ordinary cube is an object in three-dimensional space). Note that it is also of direct interest, namely, it can appear in optimization problems of linear programming (as an area in which the minimum or maximum of a linear function of four variables is found), and is also used in digital microelectronics (when programming the operation of an electronic watch display). In addition, the very process of studying a four-dimensional cube contributes to the development of spatial thinking and imagination.
Consequently, the study of the structure and specific properties of a four-dimensional cube is quite relevant. It is worth noting that in terms of structure, the four-dimensional cube has been studied quite well. Of much greater interest is the nature of its sections by various hyperplanes. Thus, the main goal of this work is to study the structure of the tesseract, as well as to clarify the question of what three-dimensional objects will be obtained if a four-dimensional cube is dissected by hyperplanes parallel to one of its three-dimensional faces, or by hyperplanes perpendicular to its main diagonal. A hyperplane in four-dimensional space will be called a three-dimensional subspace. We can say that a straight line on a plane is a one-dimensional hyperplane, a plane in three-dimensional space is a two-dimensional hyperplane.
The goal determined the objectives of the study:
1) Study the basic facts of multidimensional analytical geometry;
2) Study the features of constructing cubes of dimensions from 0 to 3;
3) Study the structure of a four-dimensional cube;
4) Analytically and geometrically describe a four-dimensional cube;
5) Make models of developments and central projections of three-dimensional and four-dimensional cubes.
6) Using the apparatus of multidimensional analytical geometry, describe three-dimensional objects resulting from the intersection of a four-dimensional cube with hyperplanes parallel to one of its three-dimensional faces, or hyperplanes perpendicular to its main diagonal.
The information obtained in this way will allow us to better understand the structure of the tesseract, as well as to identify deep analogies in the structure and properties of cubes of different dimensions.
Main part
First, we describe the mathematical apparatus that we will use during this study.
1) Vector coordinates: if, That
2) Equation of a hyperplane with a normal vector looks like Here
3) Planes and are parallel if and only if
4) The distance between two points is determined as follows: if, That
5) Condition for orthogonality of vectors:
First of all, let's find out how to describe a four-dimensional cube. This can be done in two ways - geometric and analytical.
If we talk about the geometric method of specifying, then it is advisable to trace the process of constructing cubes, starting from zero dimension. A cube of zero dimension is a point (note, by the way, that a point can also play the role of a ball of zero dimension). Next, we introduce the first dimension (the x-axis) and on the corresponding axis we mark two points (two zero-dimensional cubes) located at a distance of 1 from each other. The result is a segment - a one-dimensional cube. Let us immediately note a characteristic feature: The boundary (ends) of a one-dimensional cube (segment) are two zero-dimensional cubes (two points). Next, we introduce the second dimension (ordinate axis) and on the planeLet's construct two one-dimensional cubes (two segments), the ends of which are at a distance of 1 from each other (in fact, one of the segments is an orthogonal projection of the other). By connecting the corresponding ends of the segments, we obtain a square - a two-dimensional cube. Again, note that the boundary of a two-dimensional cube (square) is four one-dimensional cubes (four segments). Finally, we introduce the third dimension (applicate axis) and construct in spacetwo squares in such a way that one of them is an orthogonal projection of the other (the corresponding vertices of the squares are at a distance of 1 from each other). Let's connect the corresponding vertices with segments - we get a three-dimensional cube. We see that the boundary of a three-dimensional cube is six two-dimensional cubes (six squares). The described constructions allow us to identify the following pattern: at each stepthe dimensional cube “moves, leaving a trace” ine measurement at a distance of 1, while the direction of movement is perpendicular to the cube. It is the formal continuation of this process that allows us to arrive at the concept of a four-dimensional cube. Namely, we will force the three-dimensional cube to move in the direction of the fourth dimension (perpendicular to the cube) by a distance of 1. Acting similarly to the previous one, that is, by connecting the corresponding vertices of the cubes, we will obtain a four-dimensional cube. It should be noted that geometrically such a construction in our space is impossible (since it is three-dimensional), but here we do not encounter any contradictions from a logical point of view. Now let's move on to the analytical description of a four-dimensional cube. It is also obtained formally, using analogy. So, the analytical specification of a zero-dimensional unit cube has the form:
The analytical task of a one-dimensional unit cube has the form:
The analytical task of a two-dimensional unit cube has the form:
The analytical task of a three-dimensional unit cube has the form:
Now it is very easy to give an analytical representation of a four-dimensional cube, namely:
As we see, in both the geometric and analytical methods of defining a four-dimensional cube, the method of analogies was used.
Now, using the apparatus of analytical geometry, we will find out what the structure of a four-dimensional cube is. First, let's find out what elements it includes. Here again we can use an analogy (to put forward a hypothesis). The boundaries of a one-dimensional cube are points (zero-dimensional cubes), of a two-dimensional cube - segments (one-dimensional cubes), of a three-dimensional cube - squares (two-dimensional faces). It can be assumed that the boundaries of the tesseract are three-dimensional cubes. In order to prove this, let us clarify what is meant by vertices, edges and faces. The vertices of a cube are its corner points. That is, the coordinates of the vertices can be zeros or ones. Thus, a connection is revealed between the dimension of the cube and the number of its vertices. Let us apply the combinatorial product rule - since the vertexmeasured cube has exactlycoordinates, each of which is equal to zero or one (independent of all others), then in total there ispeaks Thus, for any vertex all coordinates are fixed and can be equal to or . If we fix all the coordinates (putting each of them equal or , regardless of the others), except one, we obtain straight lines containing the edges of the cube. Similar to the previous one, you can count that there are exactlythings. And if we now fix all the coordinates (putting each of them equal or , independently of the others), except for some two, we obtain planes containing two-dimensional faces of the cube. Using the rule of combinatorics, we find that there are exactlythings. Next, similarly - fixing all the coordinates (putting each of them equal or , regardless of the others), except for some three, we obtain hyperplanes containing three-dimensional faces of the cube. Using the same rule, we calculate their number - exactlyetc. This will be sufficient for our research. Let us apply the results obtained to the structure of a four-dimensional cube, namely, in all the derived formulas we put. Therefore, a four-dimensional cube has: 16 vertices, 32 edges, 24 two-dimensional faces, and 8 three-dimensional faces. For clarity, let us define analytically all its elements.
Vertices of a four-dimensional cube:
Edges of a four-dimensional cube ():
Two-dimensional faces of a four-dimensional cube (similar restrictions):
Three-dimensional faces of a four-dimensional cube (similar restrictions):
Now that the structure of a four-dimensional cube and the methods for defining it have been described in sufficient detail, let us proceed to the implementation of the main goal - to clarify the nature of the various sections of the cube. Let's start with the elementary case when the sections of a cube are parallel to one of its three-dimensional faces. For example, consider its sections with hyperplanes parallel to the faceFrom analytical geometry it is known that any such section will be given by the equationLet us define the corresponding sections analytically:
As we can see, we have obtained an analytical specification for a three-dimensional unit cube lying in a hyperplane
To establish an analogy, let us write the section of a three-dimensional cube by a plane We get:
This is a square lying in a plane. The analogy is obvious.
Sections of a four-dimensional cube by hyperplanesgive completely similar results. These will also be single three-dimensional cubes lying in hyperplanes respectively.
Now let's consider sections of a four-dimensional cube with hyperplanes perpendicular to its main diagonal. First, let's solve this problem for a three-dimensional cube. Using the above-described method of defining a unit three-dimensional cube, he concludes that as the main diagonal one can take, for example, a segment with ends And . This means that the vector of the main diagonal will have coordinates. Therefore, the equation of any plane perpendicular to the main diagonal will be:
Let's determine the limits of parameter change. Because , then, adding these inequalities term by term, we get:
Or .
If , then (due to restrictions). Likewise - if, That . So, when and when the cutting plane and the cube have exactly one common point ( And respectively). Now let's note the following. If(again due to variable limitations). The corresponding planes intersect three faces at once, because, otherwise, the cutting plane would be parallel to one of them, which does not take place according to the condition. If, then the plane intersects all faces of the cube. If, then the plane intersects the faces. Let us present the corresponding calculations.
Let Then the planecrosses the line in a straight line, and . The edge, moreover. Edge the plane intersects in a straight line, and
Let Then the planecrosses the line:
edge in a straight line, and .
edge in a straight line, and .
edge in a straight line, and .
edge in a straight line, and .
edge in a straight line, and .
edge in a straight line, and .
This time we get six segments that have sequentially common ends:
Let Then the planecrosses the line in a straight line, and . Edge the plane intersects in a straight line, and . Edge the plane intersects in a straight line, and . That is, we get three segments that have pairwise common ends:Thus, for the specified parameter valuesthe plane will intersect the cube along a regular triangle with vertices
So, here is a comprehensive description of the plane figures obtained when a cube is intersected by a plane perpendicular to its main diagonal. The main idea was as follows. It is necessary to understand which faces the plane intersects, along which sets it intersects them, and how these sets are related to each other. For example, if it turned out that the plane intersects exactly three faces along segments that have pairwise common ends, then the section is an equilateral triangle (which is proven by directly calculating the lengths of the segments), the vertices of which are these ends of the segments.
Using the same apparatus and the same idea of studying sections, the following facts can be deduced in a completely analogous way:
1) The vector of one of the main diagonals of a four-dimensional unit cube has the coordinates
2) Any hyperplane perpendicular to the main diagonal of a four-dimensional cube can be written in the form.
3) In the equation of a secant hyperplane, the parametercan vary from 0 to 4;
4) When and a secant hyperplane and a four-dimensional cube have one common point ( And respectively);
5) When the cross section will produce a regular tetrahedron;
6) When in cross-section the result will be an octahedron;
7) When the cross section will produce a regular tetrahedron.
Accordingly, here the hyperplane intersects the tesseract along a plane on which, due to the limitations of the variables, a triangular region is allocated (an analogy - the plane intersected the cube along a straight line, on which, due to the constraints of the variables, a segment was allocated). In case 5) the hyperplane intersects exactly four three-dimensional faces of the tesseract, that is, four triangles are obtained that have pairwise common sides, in other words, forming a tetrahedron (how this can be calculated is correct). In case 6), the hyperplane intersects exactly eight three-dimensional faces of the tesseract, that is, eight triangles are obtained that have sequentially common sides, in other words, forming an octahedron. Case 7) is completely similar to case 5).
Let us illustrate this with a specific example. Namely, we study the section of a four-dimensional cube by a hyperplaneDue to variable restrictions, this hyperplane intersects the following three-dimensional faces: Edge intersects along a planeDue to the limitations of the variables, we have:We get a triangular area with verticesFurther,we get a triangleWhen a hyperplane intersects a facewe get a triangleWhen a hyperplane intersects a facewe get a triangleThus, the vertices of the tetrahedron have the following coordinates. As is easy to calculate, this tetrahedron is indeed regular.
conclusions
So, in the process of this research, the basic facts of multidimensional analytical geometry were studied, the features of constructing cubes of dimensions from 0 to 3 were studied, the structure of a four-dimensional cube was studied, a four-dimensional cube was analytically and geometrically described, models of developments and central projections of three-dimensional and four-dimensional cubes were made, three-dimensional cubes were analytically described objects resulting from the intersection of a four-dimensional cube with hyperplanes parallel to one of its three-dimensional faces, or with hyperplanes perpendicular to its main diagonal.
The conducted research made it possible to identify deep analogies in the structure and properties of cubes of different dimensions. The analogy technique used can be applied in research, for example,dimensional sphere ordimensional simplex. Namely,a dimensional sphere can be defined as a set of pointsdimensional space equidistant from a given point, which is called the center of the sphere. Further,a dimensional simplex can be defined as a partdimensional space limited by the minimum numberdimensional hyperplanes. For example, a one-dimensional simplex is a segment (a part of one-dimensional space, limited by two points), a two-dimensional simplex is a triangle (a part of two-dimensional space, limited by three lines), a three-dimensional simplex is a tetrahedron (a part of three-dimensional space, limited by four planes). Finally,we define the dimensional simplex as the partdimensional space, limitedhyperplane of dimension.
Note that, despite the numerous applications of the tesseract in some areas of science, this research is still largely a mathematical study.
Bibliography
1) Bugrov Ya.S., Nikolsky S.M.Higher mathematics, vol. 1 – M.: Bustard, 2005 – 284 p.
2) Quantum. Four-dimensional cube / Duzhin S., Rubtsov V., No. 6, 1986.
3) Quantum. How to draw dimensional cube / Demidovich N.B., No. 8, 1974.
In geometry hypercube- This n-dimensional analogy of a square ( n= 2) and cube ( n= 3). It is a closed convex figure consisting of groups of parallel lines located on opposite edges of the figure, and connected to each other at right angles.
This figure is also known as tesseract(tesseract). The tesseract is to the cube as the cube is to the square. More formally, a tesseract can be described as a regular convex four-dimensional polytope (polyhedron) whose boundary consists of eight cubic cells.
According to the Oxford English Dictionary, the word "tesseract" was coined in 1888 by Charles Howard Hinton and used in his book "A New Era of Thought." The word was derived from the Greek "τεσσερες ακτινες" ("four rays"), in the form of four coordinate axes. In addition, in some sources, the same figure was called tetracube(tetracube).
n-dimensional hypercube is also called n-cube.
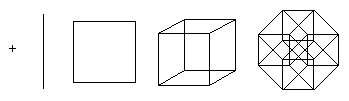
A point is a hypercube of dimension 0. If you shift the point by a unit of length, you get a segment of unit length - a hypercube of dimension 1. Further, if you shift the segment by a unit of length in a direction perpendicular to the direction of the segment, you get a cube - a hypercube of dimension 2. Shifting the square by a unit of length in the direction perpendicular to the plane of the square, a cube is obtained - a hypercube of dimension 3. This process can be generalized to any number of dimensions. For example, if you move a cube by one unit of length in the fourth dimension, you get a tesseract.
The hypercube family is one of the few regular polyhedra that can be represented in any dimension.
Elements of a hypercube
Dimension hypercube n has 2 n"sides" (a one-dimensional line has 2 points; a two-dimensional square - 4 sides; a three-dimensional cube - 6 faces; a four-dimensional tesseract - 8 cells). The number of vertices (points) of a hypercube is 2 n(for example, for a cube - 2 3 vertices).
Quantity m-dimensional hypercubes on the boundary n-cube equals
For example, on the boundary of a hypercube there are 8 cubes, 24 squares, 32 edges and 16 vertices.
| n-cube | Name | Vertex (0-face) |
Edge (1-face) |
Edge (2-face) |
Cell (3-face) |
(4-face) | (5-face) | (6-sided) | (7-face) | (8-face) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-cube | Dot | 1 | ||||||||
| 1-cube | Line segment | 2 | 1 | |||||||
| 2-cube | Square | 4 | 4 | 1 | ||||||
| 3-cube | Cube | 8 | 12 | 6 | 1 | |||||
| 4-cube | Tesseract | 16 | 32 | 24 | 8 | 1 | ||||
| 5-cube | Penteract | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6-cube | Hexeract | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7-cube | Hepteract | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8-cube | Octeract | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-cube | Eneneract | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Projection onto a plane
The formation of a hypercube can be represented in the following way:
- Two points A and B can be connected to form a line segment AB.
- Two parallel segments AB and CD can be connected to form a square ABCD.
- Two parallel squares ABCD and EFGH can be connected to form a cube ABCDEFGH.
- Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to form the hypercube ABCDEFGHIJKLMNOP.
The latter structure is not easy to visualize, but it is possible to depict its projection into two-dimensional or three-dimensional space. Moreover, projections onto a two-dimensional plane can be more useful by allowing the positions of the projected vertices to be rearranged. In this case, it is possible to obtain images that no longer reflect the spatial relationships of the elements within the tesseract, but illustrate the structure of the vertex connections, as in the examples below.

The first illustration shows how, in principle, a tesseract is formed by joining two cubes. This scheme is similar to the scheme for creating a cube from two squares. The second diagram shows that all the edges of the tesseract are the same length. This scheme also forces you to look for cubes connected to each other. In the third diagram, the vertices of the tesseract are located in accordance with the distances along the faces relative to the bottom point. This scheme is interesting because it is used as a basic scheme for the network topology of connecting processors when organizing parallel computing: the distance between any two nodes does not exceed 4 edge lengths, and there are many different paths for balancing the load.
Hypercube in art
The hypercube has appeared in science fiction literature since 1940, when Robert Heinlein, in the story “And He Built a Crooked House,” described a house built in the shape of a tesseract scan. In the story, this Next, this house collapses, turning into a four-dimensional tesseract. After this, the hypercube appears in many books and short stories.
The movie Cube 2: Hypercube is about eight people trapped in a network of hypercubes.
Salvador Dali's painting "Crucifixion (Corpus Hypercubus)", 1954, depicts Jesus crucified on a tesseract scan. This painting can be seen in the Metropolitan Museum of Art in New York.
Conclusion
A hypercube is one of the simplest four-dimensional objects, from which one can see the complexity and unusualness of the fourth dimension. And what looks impossible in three dimensions is possible in four, for example, impossible figures. So, for example, the bars of an impossible triangle in four dimensions will be connected at right angles. And this figure will look like this from all viewing points, and will not be distorted, unlike the implementations of an impossible triangle in three-dimensional space (see.
Back when I was a first-year student, I had a heated argument with one of my classmates. He said that a four-dimensional cube cannot be represented in any form, but I assured that it can be represented quite clearly. Then I even made a projection of a hypercube onto our three-dimensional space from paper clips... But let's talk about everything in order.
What is a hypercube and four-dimensional space
Our usual space has three dimensions. From a geometric point of view, this means that three mutually perpendicular lines can be indicated in it. That is, for any line you can find a second line perpendicular to the first, and for a pair you can find a third line perpendicular to the first two. It will no longer be possible to find a fourth line perpendicular to the existing three.
Four-dimensional space differs from ours only in that it has one more additional direction. If you already have three mutually perpendicular lines, then you can find a fourth one, such that it will be perpendicular to all three.
Hypercube it's just a cube in four-dimensional space.
Is it possible to imagine four-dimensional space and a hypercube?
This question is akin to the question: “is it possible to imagine the Last Supper by looking at the painting of the same name (1495-1498) by Leonardo da Vinci (1452-1519)?”
On the one hand, you, of course, will not imagine what Jesus saw (he is sitting facing the viewer), especially since you will not smell the garden outside the window and taste the food on the table, you will not hear the birds singing... You will not get a complete picture of what happened at that time evening, but it cannot be said that you will not learn anything new and that the picture is of no interest.
The situation is similar with the question of the hypercube. It is impossible to fully imagine it, but you can get closer to understanding what it is like.
Construction of a hypercube
0-dimensional cube
Let's start from the beginning - with a 0-dimensional cube. This cube contains 0 mutually perpendicular faces, that is, it is just a point.
1-dimensional cube
In one-dimensional space, we only have one direction. We move the point in this direction and get a segment.
This is a one-dimensional cube.
2 dimensional cube
We have a second dimension, we shift our one-dimensional cube (segment) in the direction of the second dimension and we get a square.
It is a cube in two-dimensional space.
3 dimensional cube
With the advent of the third dimension, we do the same: we move the square and get a regular three-dimensional cube.

4-dimensional cube (hypercube)
Now we have a fourth dimension. That is, we have at our disposal a direction perpendicular to all three previous ones. Let's use it exactly the same way. A four-dimensional cube will look like this.

Naturally, three-dimensional and four-dimensional cubes cannot be depicted on a two-dimensional screen plane. What I drew are projections. We'll talk about projections a little later, but for now a few bare facts and figures.
Number of vertices, edges, faces
Please note that the face of a hypercube is our ordinary three-dimensional cube. If you look closely at the drawing of a hypercube, you can actually find eight cubes.
Projections and vision of an inhabitant of four-dimensional space
A few words about vision
We live in a three-dimensional world, but we see it as two-dimensional. This is due to the fact that the retina of our eyes is located in a plane that has only two dimensions. This is why we are able to perceive two-dimensional pictures and find them similar to reality.
(Of course, thanks to accommodation, the eye can estimate the distance to an object, but this is a side effect associated with the optics built into our eyes.)
The eyes of an inhabitant of four-dimensional space must have a three-dimensional retina. Such a creature can immediately see the entire three-dimensional figure: all its faces and interiors. (In the same way, we can see a two-dimensional figure, all its faces and interiors.)
Thus, with the help of our organs of vision, we are not able to perceive a four-dimensional cube the way a resident of a four-dimensional space would perceive it. Alas. All that remains is to rely on your mind's eye and imagination, which, fortunately, have no physical limitations.
However, when depicting a hypercube on a plane, I am simply forced to make its projection onto two-dimensional space. Take this fact into account when studying the drawings.
Edge intersections
Naturally, the edges of the hypercube do not intersect. Intersections appear only in drawings. However, this should not come as a surprise, because the edges of a regular cube in the pictures also intersect.
Ribs lengths
It is worth noting that all faces and edges of a four-dimensional cube are equal. In the figure they are not equal only because they are located at different angles to the direction of view. However, it is possible to rotate a hypercube so that all projections have the same length.
By the way, in this figure eight cubes, which are the faces of a hypercube, are clearly visible.
The hypercube is empty inside
It’s hard to believe, but between the cubes that bound the hypercube, there is some space (a fragment of four-dimensional space).
To understand this better, let's look at a two-dimensional projection of an ordinary three-dimensional cube (I deliberately made it somewhat schematic).

Can you guess from it that there is some space inside the cube? Yes, but only by using your imagination. The eye does not see this space.
This happens because the edges located in the third dimension (which cannot be depicted in a flat drawing) have now turned into segments lying in the plane of the drawing. They no longer provide volume.
The squares enclosing the space of the cube overlapped each other. But one can imagine that in the original figure (a three-dimensional cube) these squares were located in different planes, and not one on top of the other in the same plane, as happened in the figure.
The situation is exactly the same with a hypercube. The cubes-faces of a hypercube do not actually overlap, as it seems to us on the projection, but are located in four-dimensional space.
Sweeps
So, a resident of four-dimensional space can see a three-dimensional object from all sides simultaneously. Can we see a three-dimensional cube from all sides at the same time? With the eye - no. But people have come up with a way to depict all the faces of a three-dimensional cube at the same time on a flat drawing. Such an image is called a scan.
Development of a three-dimensional cube
Everyone probably knows how the development of a three-dimensional cube is formed. This process is shown in the animation.

For clarity, the edges of the cube faces are made translucent.
It should be noted that we are able to perceive this two-dimensional picture only thanks to our imagination. If we consider the unfolding phases from a purely two-dimensional point of view, the process will seem strange and not at all clear.

It looks like the gradual appearance of first the outlines of distorted squares, and then their creeping into place while simultaneously taking on the required shape.
If you look at the unfolding cube in the direction of one of its faces (from this point of view the cube looks like a square), then the process of formation of the unfold is even less clear. Everything looks like squares creeping out from the initial square (not the unfolded cube).
But not visual scan only for eye.
How to understand 4-dimensional space?
It is thanks to your imagination that you can glean a lot of information from it.
Development of a four-dimensional cube
It is simply impossible to make the animated process of unfolding a hypercube at least somewhat visual. But this process can be imagined. (To do this, you need to look at it through the eyes of a four-dimensional being.)
The scan looks like this.

All eight cubes bounding the hypercube are visible here.
The edges that should align when folded are painted with the same colors. Faces for which pairs are not visible are left gray. After convolution, the topmost face of the top cube should align with the bottom edge of the bottom cube. (The unfolding of a three-dimensional cube is collapsed in a similar way.)
Please note that after convolution, all the faces of the eight cubes will come into contact, closing the hypercube. And finally, when imagining the process of folding, do not forget that when folding, it is not the overlapping of cubes that occurs, but the wrapping of them around a certain (hypercubic) four-dimensional area.
Salvador Dali (1904-1989) depicted the crucifixion many times, and crosses appear in many of his paintings. The painting “The Crucifixion” (1954) uses a hypercube scan.
Space-time and Euclidean four-dimensional space
I hope you were able to imagine the hypercube. But have you managed to come closer to understanding how the four-dimensional space-time in which we live works? Alas, not quite.
Here we talked about Euclidean four-dimensional space, but space-time has completely different properties. In particular, during any rotations, the segments always remain inclined to the time axis, either at an angle less than 45 degrees, or at an angle greater than 45 degrees.
I devoted a series of notes to the properties of space-time.
Three-dimensionality of the image
The world is three-dimensional. Its image is two-dimensional. An important task of painting and, now, photography is to convey the three-dimensionality of space. Some techniques were already mastered by the Romans, then they were forgotten and began to return to classical painting with the Renaissance.
 The main technique for creating three-dimensional space in painting is perspective. The railway rails, moving away from the viewer, visually narrow. In painting, the rails can be physically narrowed. In photography, perspective occurs automatically: the camera will photograph the rails as narrowed as the eye sees them. However, do not allow it to almost close: it will no longer look like a perspective, but a strange figure; There must be a noticeable gap between the rails, the sides of the street, and the banks of the river.
The main technique for creating three-dimensional space in painting is perspective. The railway rails, moving away from the viewer, visually narrow. In painting, the rails can be physically narrowed. In photography, perspective occurs automatically: the camera will photograph the rails as narrowed as the eye sees them. However, do not allow it to almost close: it will no longer look like a perspective, but a strange figure; There must be a noticeable gap between the rails, the sides of the street, and the banks of the river.
It is important to understand that linear perspective is the most primitive, realistic way of conveying the world.
Post navigation
It is no coincidence that its appearance is associated with theatrical scenery (Florensky, “Reverse Perspective”). The conventionality and simplicity of conveying a theatrical scene of small depth is very suitable for photography, which lacks the variety of techniques available in painting.
There are perspectives that are much more interesting than the linear one. In the works of Chinese masters there is a floating perspective, when objects are depicted simultaneously from below, above and in front. It was not a technical mistake by incompetent artists: the legendary author of this technique, Guo Xi, wrote that such a display allows one to realize the world in its totality. The technique of Russian icon painting is similar, in which the viewer can see the character’s face and back at the same time. An interesting technique of icon painting, also found among Western European artists, was reverse perspective, in which distant objects, on the contrary, are larger than close ones, emphasizing importance. Only in our days has it been established that such a perspective is correct: unlike distant objects, the close-up is actually perceived in reverse perspective (Rauschenbach). Using Photoshop, you can achieve reverse perspective by enlarging background objects. For a viewer accustomed to the laws of photography, such an image will look strange.
Introducing the corner of a building into the frame, from which the walls diverge in both directions, creates a semblance of an isometric perspective. The brain understands that the walls are at right angles and arranges the rest of the image accordingly. This perspective is more dynamic than the frontal one and more natural for the close-up. Simply introduce the end angles of objects and nearby buildings into the frame.
Due to the expansion, the isometric perspective is major, which is rarely suitable for a classical portrait. Linear perspective, due to narrowing, better conveys minor emotions.
At the shooting stage, the photographer has a number of tools available to him to emphasize perspective. Objects of equal width extending into the distance (tracks, streets, columns, furrows) by their narrowing and even simply moving away indicate to the viewer the three-dimensionality of space. The effect is stronger if you shoot from a low angle to increase perspective distortion. This is enough for landscape photography, but with a shallow image depth for interior photography, the effect is hardly noticeable. It can be enhanced a little in post-processing by narrowing the top of the image (Transform Perspective). However, in a landscape, an exaggerated perspective can look interesting.
Depth can be obvious in the meaning of the image: buildings are separated by a street or river. The diagonal emphasizes three-dimensionality; for example, a bridge over a river.
Objects of a size known to the viewer in the background set the scale and, accordingly, form the perspective. In landscape photography, this object could be a car, but in portrait photography, try bending your leg (away from the camera) under the chair so that it appears smaller while remaining visible. You can even make this leg a little smaller in post-processing.
The ornament conveys perspective by visually reducing the elements. An example would be large tiles on the floor, marking lines on the road.
There is a technique called hypertrophied foreground. Disproportionally large, it creates depth in the image. By comparing the scale of the foreground and the model, the eye comes to the conclusion that the model is much further away than it seems. The exaggeration should remain subtle so that the image is not perceived as an error. This technique works not only for post-processing, but also for shooting: distort the proportions by shooting with a 35 or 50mm lens. Shooting with a wide-angle lens stretches the space, enhancing its three-dimensionality by breaking the proportions. The effect is stronger if you shoot the model at close range, but beware of grotesque proportions: only the authors of religious images can depict a person larger than a building.
The intersection works great. If the apple partially covers the pear, then the brain will not be mistaken: the apple is in front of the pear. The model partially covers the furniture, thereby creating depth in the interior.
The alternation of light and dark spots also gives depth to the image. The brain knows from experience that nearby objects are lit approximately equally, so it interprets differently lit objects as being located at different distances. For this effect, the spots alternate in the direction of the perspective axis - deep into the image, and not across it. For example, when shooting a model lying away from the camera in a dark frame, place highlights near the buttocks and near the legs. You can lighten/darken areas in post-processing.
The sequence of increasingly dark objects is perceived to decrease. By gradually shading objects along the active line, you can get a subtle sense of perspective. Likewise, depth is conveyed by weakening the light: cast a strip of light across the furniture or on the floor.
A three-dimensional image can be obtained due to not only light, but also color contrast. This technique was known to Flemish painters, who placed bright colored spots on their still lifes. A red pomegranate and a yellow lemon next to each other will look three-dimensional even in flat frontal lighting. They will stand out especially well against the background of purple grapes: a warm color against a cold background. Bright colored surfaces emerge well from the darkness even with weak light, typical of still life. Color contrast works better with primary colors: red, yellow, blue, rather than shades.
On a black background, yellow comes forward, blue hides back. On a white background it’s the other way around. Color saturation enhances this effect. Why is this happening? The color yellow is never dark, so the brain refuses to believe that a yellow object can be immersed in a dark background, not illuminated. Blue, on the contrary, is dark.
Enhancing perspective in post-processing comes down to simulating atmospheric perception: distant objects appear lighter, blurrier, with reduced contrast in brightness, saturation and tone.
Besides long distances, atmospheric effects look natural in morning haze, fog, or a smoky bar. Consider the weather: on a cloudy day or at dusk, there may not be a significant difference between the foreground and background.
The strongest factor is brightness contrast. In the settings this is the usual contrast. Reduce the contrast of distant objects, raise the contrast of the foreground - and the image will become convex. We are not talking about the contrast between the foreground and background, but about the contrast of the background, which should be lower than the contrast of the foreground. This method is suitable not only for landscapes and genre photography, but also for studio portraits: raise the contrast of the front of the face, reduce the contrast on the hair, cheekbones, and clothes. Portrait filters do something similar, blurring the model's skin and leaving the eyes and lips harsh.
Contrast adjustment is the easiest way to do 3D image post-processing. Unlike other processes, the viewer will hardly notice any changes, which will allow maintaining maximum naturalness.
Blurring is similar to contrast reduction, but they are different processes. The image can be low contrast while remaining sharp. Due to limited depth of field, blurring distant objects remains the most popular way to convey three-dimensionality in photography, and can easily be enhanced by blurring distant subjects in post-production. Therefore, fewer details should be placed in the background - the brain does not expect distinguishable objects in the distance. Meanwhile, reducing the contrast better corresponds to natural perception: distant mountains are visible in low contrast, and not blurred, because when scanning the landscape, the eye is constantly refocused, and the problem of depth of field is alien to it. By blurring the background, you can at the same time sharpen the foreground. Additionally, in the foreground you can enhance the image lines (High Pass Filter or Clarity). It is the high sharpness of the foreground that explains the characteristic bump in the image of high-quality lenses. Beware: for the sake of a slight increase in three-dimensionality, you may make the image too rigid.
Lighter objects appear further away. This is due to the fact that in nature we see distant objects through the thickness of light-scattering air; distant mountains appear light. In landscape photography, therefore, you should be careful about the placement of light objects in the foreground.
Brighten distant objects. The further away they are, the more they blend in with the brightness and tone of the sky. Please note that horizontal objects (ground, sea) are better illuminated than vertical ones (walls, trees), so do not overdo it with lightening the latter. In any case, objects should remain noticeably lighter than the sky.
 Well, if you notice that dodging is another way to reduce the contrast in the brightness of the background. Darken the foreground slightly to enhance the bump effect.
Well, if you notice that dodging is another way to reduce the contrast in the brightness of the background. Darken the foreground slightly to enhance the bump effect.
It would seem that in the interior everything is the other way around. If on the street the eye is accustomed to the fact that the distance is bright, then in the room the light is often concentrated on the person, and the interior is immersed in darkness; the brain is accustomed to foreground lighting, not background lighting.
In interior images with shallow scene depth, unlike landscape images, the illuminated model protrudes from a dark background. But there is also an opposite factor: for 99% of his evolution, man observed the perspective in open areas, and with the advent of rooms, the brain had not yet had time to restructure. Vermeer preferred a light background for his portraits, and his portraits are really prominent. Lighting a vertical background, recommended in photography, not only separates the model from it, but also, by lightening the background, gives the image a slight three-dimensionality. Here we are faced with the fact that the brain analyzes the location of objects according to several factors, and they can be conflicting.
Studio lighting looks interesting, in which light spots lie on areas of the model remote from the camera. For example, the breast that is farthest from the camera is highlighted.
Reduce color saturation on distant objects: due to the thickness of the air separating us, distant mountains are desaturated almost to the level of monochrome and covered with a blue haze. The foreground saturation can be increased.
Since yellow is light, and blue and red are dark, the color contrast is also a contrast in brightness.
When desaturating the distant background, do not let it disappear from view. Often, on the contrary, you need to increase the saturation of the background in order to reveal it. This is more important than three-dimensionality.
A lot of 3D photography advice focuses on temperature contrast. In fact, this effect is very weak and is easily interrupted by brightness contrast. In addition, the temperature contrast is annoying and noticeable.
Very distant objects appear cooler in color because the air absorbs warm orange light. When photographing a model on the beach with ships on the horizon in the background, lower the color temperature of the distant sea and ships in post-processing. A model in a red swimsuit emerges from the blue sea, and a model in the yellow light of a street lamp emerges from the bluish twilight.
This is the essence of separate toning: we make the model warmer, the background cooler. The brain understands that there are no different color temperatures in the same plane, and perceives such a three-dimensional image, in which the model protrudes from the background. Split toning adds depth to landscapes: make the foreground warmer, the background cooler.
An important exception to separate toning: at sunrise and sunset, the distant background is not cold at all, but warm, with yellow and red-orange tones. The obvious solution - using a white model in a purple swimsuit - doesn't work because the sunset light casts a warm tint on the model's body as well.
Let's summarize: to give a photo three-dimensionality based on atmospheric effects, it is necessary to contrast the foreground and background. The main contrast is based on the usual contrast: the foreground is high-contrast, the background is low-contrast. The second contrast is in terms of sharpness: the foreground is sharp, the background is blurry. The third contrast is in terms of lightness: the foreground is dark, the background is light. The fourth contrast is in terms of saturation: the foreground colors are saturated, the background colors are desaturated. The fifth contrast is in temperature: the foreground is warm, the background is cold.
The listed factors are often multidirectional. Yellow is brighter than blue, and light objects appear further away from dark ones. It would be natural to expect that yellow would recede and blue would approach the viewer. In fact, it's the other way around: a warm color emerges from a cold background. That is, color turns out to be a stronger factor than brightness. Which, on reflection, is not surprising: yellow and red are clearly distinguishable only up close, and the viewer does not expect to see them at a great distance.
Bottom line: keep the background low contrast, washed out, light, desaturated, bluish. And be prepared for the fact that the viewer, accustomed to the hypertrophied 3D of films, will find the three-dimensionality you created to be barely noticeable or absent.
In portrait photography, it is better to rely on the proven chiaroscuro effect - the play of light and shadow on the model's face, which will make the image quite prominent. In genre photography, perspective gives the most noticeable three-dimensional effect. In a still life, the main factor will be the intersection (overlapping) of objects.
Don't get carried away with the prospect; it is just a background for the frontal plane on which your image flutters. In modern painting, which is far from realism, perspective is not held in high esteem.
Download the entire book: pdfepubazw3mobifb2litContents
Points (±1, ±1, ±1, ±1). In other words, it can be represented as the following set:
The tesseract is limited by eight hyperplanes, the intersection of which with the tesseract itself defines its three-dimensional faces (which are ordinary cubes). Each pair of non-parallel 3D faces intersect to form 2D faces (squares), and so on. Finally, the tesseract has 8 3D faces, 24 2D faces, 32 edges and 16 vertices.
Popular description
Let's try to imagine what a hypercube will look like without leaving three-dimensional space.
In a one-dimensional “space” - on a line - we select a segment AB of length L. On a two-dimensional plane at a distance L from AB, we draw a segment DC parallel to it and connect their ends. The result is a square CDBA. Repeating this operation with the plane, we obtain a three-dimensional cube CDBAGHFE. And by shifting the cube in the fourth dimension (perpendicular to the first three) by a distance L, we get the hypercube CDBAGHFEKLJIOPNM.
Construction of a tesseract on a plane
The one-dimensional segment AB serves as the side of the two-dimensional square CDBA, the square - as the side of the cube CDBAGHFE, which, in turn, will be the side of the four-dimensional hypercube. A straight line segment has two boundary points, a square has four vertices, a cube has eight. In a four-dimensional hypercube, there will thus be 16 vertices: 8 vertices of the original cube and 8 of the one shifted in the fourth dimension. It has 32 edges - 12 each give the initial and final positions of the original cube, and another 8 edges “draw” its eight vertices, which have moved to the fourth dimension. The same reasoning can be done for the faces of a hypercube. In two-dimensional space there is only one (the square itself), a cube has 6 of them (two faces from the moved square and four more that describe its sides). A four-dimensional hypercube has 24 square faces - 12 squares of the original cube in two positions and 12 squares from its twelve edges.
Just as the sides of a square are 4 one-dimensional segments, and the sides (faces) of a cube are 6 two-dimensional squares, so for a “four-dimensional cube” (tesseract) the sides are 8 three-dimensional cubes. The spaces of opposite pairs of tesseract cubes (that is, the three-dimensional spaces to which these cubes belong) are parallel. In the figure these are the cubes: CDBAGHFE and KLJIOPNM, CDBAKLJI and GHFEOPNM, EFBAMNJI and GHDCOPLK, CKIAGOME and DLJBHPNF.
In a similar way, we can continue our reasoning for hypercubes of a larger number of dimensions, but it is much more interesting to see how a four-dimensional hypercube will look for us, residents of three-dimensional space. For this we will use the already familiar method of analogies.
Let's take the wire cube ABCDHEFG and look at it with one eye from the side of the edge. We will see and can draw two squares on the plane (its near and far edges), connected by four lines - side edges. Similarly, a four-dimensional hypercube in three-dimensional space will look like two cubic “boxes” inserted into each other and connected by eight edges. In this case, the “boxes” themselves - three-dimensional faces - will be projected onto “our” space, and the lines connecting them will stretch in the direction of the fourth axis. You can also try to imagine the cube not in projection, but in a spatial image.
Just as a three-dimensional cube is formed by a square shifted by the length of its face, a cube shifted into the fourth dimension will form a hypercube. It is limited by eight cubes, which in perspective will look like some rather complex figure. The four-dimensional hypercube itself consists of an infinite number of cubes, just as a three-dimensional cube can be “cut” into an infinite number of flat squares.
By cutting the six faces of a three-dimensional cube, you can decompose it into a flat figure - a development. It will have a square on each side of the original face plus one more - the face opposite to it. And the three-dimensional development of a four-dimensional hypercube will consist of the original cube, six cubes “growing” from it, plus one more - the final “hyperface”.
The properties of a tesseract represent a continuation of the properties of geometric figures of lower dimension into four-dimensional space.
Projections
To two-dimensional space
This structure is difficult to imagine, but it is possible to project a tesseract into two-dimensional or three-dimensional spaces. In addition, projecting onto a plane makes it easy to understand the location of the vertices of the hypercube. In this way, it is possible to obtain images that no longer reflect the spatial relationships within the tesseract, but which illustrate the vertex connection structure, as in the following examples:

The third picture shows the tesseract in isometry, relative to the construction point. This representation is of interest when using a tesseract as the basis for a topological network to link multiple processors in parallel computing.
To three-dimensional space
One of the projections of a tesseract onto three-dimensional space represents two nested three-dimensional cubes, the corresponding vertices of which are connected by segments. The inner and outer cubes have different sizes in three-dimensional space, but in four-dimensional space they are equal cubes. To understand the equality of all tesseract cubes, a rotating tesseract model was created.
|
|
- The six truncated pyramids along the edges of the tesseract are images of equal six cubes. However, these cubes are to a tesseract as squares (faces) are to a cube. But in fact, the tesseract can be divided into an infinite number of cubes, just as a cube can be divided into an infinite number of squares, or a square into an infinite number of segments.
Another interesting projection of the tesseract onto three-dimensional space is a rhombic dodecahedron with its four diagonals connecting pairs of opposite vertices at large angles of the rhombuses. In this case, 14 of the 16 vertices of the tesseract are projected into 14 vertices of the rhombic dodecahedron, and the projections of the remaining 2 coincide in its center. In such a projection onto three-dimensional space, the equality and parallelism of all one-dimensional, two-dimensional and three-dimensional sides are preserved.
Stereo pair
A stereo pair of a tesseract is depicted as two projections onto three-dimensional space. This image of the tesseract was designed to represent depth as a fourth dimension. The stereo pair is viewed so that each eye sees only one of these images, a stereoscopic picture appears that reproduces the depth of the tesseract.
Tesseract unwrapping
The surface of a tesseract can be unfolded into eight cubes (similar to how the surface of a cube can be unfolded into six squares). There are 261 different tesseract designs. The unfolding of a tesseract can be calculated by plotting the connected angles on a graph.
Tesseract in art
- In Edwina A.'s "New Abbott Plain", the hypercube acts as a narrator.
- In one episode of The Adventures of Jimmy Neutron, the "boy genius" Jimmy invents a four-dimensional hypercube identical to the foldbox from the novel Glory Road (1963) by Robert Heinlein.
- Robert E. Heinlein has mentioned hypercubes in at least three science fiction stories. In "The House of Four Dimensions" ("The House That Teal Built"), he described a house built as an unwrapped tesseract, and then, due to an earthquake, "folded" in the fourth dimension and became a "real" tesseract.
- Heinlein's novel Glory Road describes a hyper-sized box that was larger on the inside than on the outside.
- Henry Kuttner's story "All Tenali Borogov" describes an educational toy for children from the distant future, similar in structure to a tesseract.
- In the novel by Alex Garland (), the term "tesseract" is used for the three-dimensional unfolding of a four-dimensional hypercube, rather than the hypercube itself. This is a metaphor designed to show that the cognitive system must be broader than the knowable.
- The plot of Cube 2: Hypercube centers on eight strangers trapped in a "hypercube", or network of connected cubes.
- The television series Andromeda uses tesseract generators as a plot device. They are primarily designed to manipulate space and time.
- Painting “The Crucifixion” (Corpus Hypercubus) by Salvador Dali ().
- The Nextwave comic book depicts a vehicle that includes 5 tesseract zones.
- In the album Voivod Nothingface one of the compositions is called “In my hypercube”.
- In Anthony Pearce's novel Route Cube, one of the International Development Association's orbiting moons is called a tesseract that has been compressed into 3 dimensions.
- In the series “Black Hole School” in the third season there is an episode “Tesseract”. Lucas presses a secret button and the school begins to “take shape like a mathematical tesseract.”
- The term “tesseract” and its derivative “tesseract” are found in Madeleine L’Engle’s story “A Wrinkle in Time.”
- TesseracT is the name of a British djent band.
- In the Marvel Cinematic Universe film series, the Tesseract is a key plot element, a cosmic artifact in the shape of a hypercube.
- In Robert Sheckley’s story “Miss Mouse and the Fourth Dimension,” an esoteric writer, an acquaintance of the author, tries to see the tesseract by staring for hours at the device he designed: a ball on a leg with rods stuck into it, on which cubes are mounted, pasted over with all sorts of esoteric symbols. The story mentions Hinton's work.
- In the films The First Avenger, The Avengers. Tesseract - the energy of the entire universe
Other names
- Hexadecachoron Hexadecachoron)
- Octochoron (English) Octachoron)
- Tetracube
- 4-Cube
- Hypercube (if the number of dimensions is not specified)
Notes
Literature
- Charles H. Hinton. Fourth Dimension, 1904. ISBN 0-405-07953-2
- Martin Gardner, Mathmatical Carnival, 1977. ISBN 0-394-72349-X
- Ian Stewart, Concepts of Modern Mathematics, 1995. ISBN 0-486-28424-7
Links
In Russian- Transformator4D program. Formation of models of three-dimensional projections of four-dimensional objects (including the Hypercube).
- A program that implements the construction of a tesseract and all its affine transformations, with source code in C++.
In English
- Mushware Limited - tesseract output program ( Tesseract Trainer, license compatible with GPLv2) and a first-person shooter in four-dimensional space ( Adanaxis; graphics are mainly three-dimensional; There is a GPL version in the OS repositories).
| Polyhedra | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Correct (Platonic solids) |
|||||||||
| Stellated dodecahedron Stellated icosidodecahedron Stellated icosahedron Stellated polyhedron Stellated octahedron | |||||||||
| Convex |
|
||||||||
| Formulas, theorems, theories |
|||||||||
| Other | |||||||||
Wikimedia Foundation.









