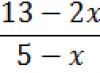Instructions

To make both methods more understandable, we can give a couple of examples.

Example 1: length midline trapezoid 10 cm, its area is 100 cm². To find the height of this trapezoid, you need to do:

h = 100/10 = 10 cm

Answer: the height of this trapezoid is 10 cm

Example 2: the area of ​​the trapezoid is 100 cm², the lengths of the bases are 8 cm and 12 cm. To find the height of this trapezoid, you need to perform the following action:

h = (2*100)/(8+12) = 200/20 = 10 cm

Answer: the height of this trapezoid is 20 cm

Please note

There are several types of trapezoids:
An isosceles trapezoid is a trapezoid in which sides are equal to each other.
A rectangular trapezoid is a trapezoid in which one of the internal corners equal to 90 degrees.
It is worth noting that in rectangular trapezoid height coincides with side length at right angle.
You can describe a circle around a trapezoid, or fit it inside a given figure. You can inscribe a circle only if the sum of its bases is equal to the sum of its opposite sides. A circle can only be described around isosceles trapezoid.

Useful advice

A parallelogram is a special case of a trapezoid, because the definition of a trapezoid does not in any way contradict the definition of a parallelogram. A parallelogram is a quadrilateral opposite sides which are parallel to each other. For a trapezoid, the definition refers only to a pair of its sides. Therefore, any parallelogram is also a trapezoid. The reverse statement is not true.

Sources:

• how to find the area of ​​a trapezoid formula

Tip 2: How to find the height of a trapezoid if the area is known

A trapezoid is a quadrilateral in which two of its four sides are parallel to each other. The parallel sides are the bases of the given one, the other two are the lateral sides of the given one. trapezoids. Find height trapezoids, if known square, it will be very easy.

Instructions

You need to figure out how to calculate square original trapezoids. There are several formulas for this, depending on the initial data: S = ((a+b)*h)/2, where a and b are bases trapezoids, and h is its height (Height trapezoids- perpendicular, lowered from one base trapezoids to another);
S = m*h, where m is line trapezoids(The middle line is a segment with bases trapezoids and connecting the midpoints of its sides).

To make it clearer, similar problems can be considered: Example 1: Given a trapezoid with square 68 cm², the middle line of which is 8 cm, you need to find height given trapezoids. In order to solve this problem, you need to use the previously derived formula:
h = 68/8 = 8.5 cm Answer: height of this trapezoids is 8.5 cmExample 2: Let y trapezoids square equals 120 cm², the length of the bases of this trapezoids 8 cm and 12 cm respectively, you need to find height this trapezoids. To do this, you need to apply one of the derived formulas:
h = (2*120)/(8+12) = 240/20 = 12 cmAnswer: given height trapezoids equal to 12 cm

Video on the topic

Please note

Any trapezoid has a number of properties:

The midline of a trapezoid is equal to half the sum of its bases;

A segment that connects the diagonals of a trapezoid equal to half differences in its bases;

If a straight line is drawn through the midpoints of the bases, then it will intersect the point of intersection of the diagonals of the trapezoid;

A circle can be inscribed in a trapezoid if the sum of the bases of the trapezoid is equal to the sum of its sides.

Use these properties when solving problems.

Tip 3: How to find the area of ​​a trapezoid if the bases are known

By geometric definition A trapezoid is a quadrilateral with only one pair of sides parallel. These sides are hers reasons. Distance between reasons called height trapezoids. Find square trapezoids possible using geometric formulas.

Instructions

Measure the bases and trapezoids ABCD. Usually they are given in tasks. Let in in this example tasks foundation AD (a) trapezoids will be equal to 10 cm, base BC (b) - 6 cm, height trapezoids BK (h) - 8 cm. Use geometric to find area trapezoids, if the lengths of its bases and heights are known - S= 1/2 (a+b)*h, where: - a - the size of the base AD trapezoids ABCD, - b - the value of the base BC, - h - the value of the height BK.

In order to feel confident and successfully solve problems in geometry lessons, it is not enough to learn the formulas. They need to be understood first. To be afraid, and even more so to hate formulas, is unproductive. In this article accessible language Various methods for finding the area of ​​a trapezoid will be analyzed. To better understand the corresponding rules and theorems, we will pay some attention to its properties. This will help you understand how the rules work and in what cases certain formulas should be applied.

Defining a trapezoid

What kind of figure is this overall? A trapezoid is a polygon with four corners and two parallel sides. The other two sides of the trapezoid can be inclined at different angles. Her parallel sides are called bases, and for non-parallel sides the name “sides” or “hips” is used. Such figures are quite common in everyday life. The contours of the trapezoid can be seen in the silhouettes of clothing, interior items, furniture, dishes and many others. Trapeze happens different types: scalene, equilateral and rectangular. We will examine their types and properties in more detail later in the article.

Properties of a trapezoid

Let us dwell briefly on the properties of this figure. The sum of the angles adjacent to any side is always 180°. It should be noted that all angles of a trapezoid add up to 360°. The trapezoid has the concept of a midline. If you connect the midpoints of the sides with a segment, this will be the middle line. It is designated m. The middle line has important properties: it is always parallel to the bases (we remember that the bases are also parallel to each other) and equal to their half-sum:

This definition must be learned and understood, because it is the key to solving many problems!

With a trapezoid, you can always lower the height to the base. An altitude is a perpendicular, often denoted by the symbol h, that is drawn from any point of one base to another base or its extension. The midline and height will help you find the area of ​​the trapezoid. Similar tasks are the most common in school course geometry and regularly appear among test and examination papers.

The simplest formulas for the area of ​​a trapezoid

Let's look at the two most popular and simple formulas used to find the area of ​​a trapezoid. It is enough to multiply the height by half the sum of the bases to easily find what you are looking for:

S = h*(a + b)/2.

In this formula, a, b denote the bases of the trapezoid, h - the height. For ease of perception, in this article, multiplication signs are marked with a symbol (*) in formulas, although in official reference books the multiplication sign is usually omitted.

Let's look at an example.

Given: a trapezoid with two bases equal to 10 and 14 cm, the height is 7 cm. What is the area of ​​the trapezoid?

Let's look at the solution to this problem. Using this formula, you first need to find the half-sum of the bases: (10+14)/2 = 12. So, the half-sum is equal to 12 cm. Now we multiply the half-sum by the height: 12*7 = 84. What we are looking for is found. Answer: The area of ​​the trapezoid is 84 square meters. cm.

Second famous formula states: the area of ​​a trapezoid is equal to the product of the midline and the height of the trapezoid. That is, it actually follows from the previous concept of the middle line: S=m*h.

Using diagonals for calculations

Another way to find the area of ​​a trapezoid is actually not that complicated. It is connected to its diagonals. Using this formula, to find the area, you need to multiply the half-product of its diagonals (d 1 d 2) by the sine of the angle between them:

S = ½ d 1 d 2 sin a.

Let's consider a problem that shows the application of this method. Given: a trapezoid with the length of the diagonals equal to 8 and 13 cm, respectively. The angle a between the diagonals is 30°. Find the area of ​​the trapezoid.

Solution. Using the above formula, it is easy to calculate what is required. As you know, sin 30° is 0.5. Therefore, S = 8*13*0.5=52. Answer: the area is 52 square meters. cm.

Finding the area of ​​an isosceles trapezoid

A trapezoid can be isosceles (isosceles). Its sides are the same and the angles at the bases are equal, which is well illustrated by the figure. An isosceles trapezoid has the same properties as a regular one, plus a number of special ones. A circle can be circumscribed around an isosceles trapezoid, and a circle can be inscribed within it.

What methods are there for calculating the area of ​​such a figure? The method below will require a lot of calculations. To use it, you need to know the values ​​of the sine (sin) and cosine (cos) of the angle at the base of the trapezoid. Their calculations require either Bradis tables or engineering calculator. Here is the formula:

S= c*sin a*(a - c*cos a),

Where With- lateral thigh, a- angle at the lower base.

An equilateral trapezoid has diagonals of equal length. The converse is also true: if a trapezoid has equal diagonals, then it is isosceles. From here following formula, which helps to find the area of ​​a trapezoid - the half product of the square of the diagonals and the sine of the angle between them: S = ½ d 2 sin a.

Finding the area of ​​a rectangular trapezoid

Known special case rectangular trapezoid. This is a trapezoid, in which one side (its thigh) adjoins the bases at a right angle. It has the properties of a regular trapezoid. In addition, she has very interesting feature. The difference in the squares of the diagonals of such a trapezoid is equal to the difference in the squares of its bases. All previously described methods for calculating area are used for it.

We use ingenuity

There is one trick that can help if you forget specific formulas. Let's take a closer look at what a trapezoid is. If we mentally divide it into parts, we will get familiar and understandable geometric shapes: a square or rectangle and a triangle (one or two). If the height and sides of the trapezoid are known, you can use the formulas for the area of ​​a triangle and a rectangle, and then add up all the resulting values.

Let's illustrate this following example. Given a rectangular trapezoid. Angle C = 45°, angles A, D are 90°. The upper base of the trapezoid is 20 cm, the height is 16 cm. You need to calculate the area of ​​the figure.

This figure obviously consists of a rectangle (if two angles are equal to 90°) and a triangle. Since the trapezoid is rectangular, therefore, its height is equal to its side, that is, 16 cm. We have a rectangle with sides of 20 and 16 cm, respectively. Now consider a triangle whose angle is 45°. We know that one side of it is 16 cm. Since this side is also the height of the trapezoid (and we know that the height descends to the base at a right angle), therefore, the second angle of the triangle is 90°. Hence the remaining angle of the triangle is 45°. As a consequence of this we get a rectangular isosceles triangle, whose two sides are the same. This means that the other side of the triangle is equal to the height, that is, 16 cm. All that remains is to calculate the area of ​​the triangle and the rectangle and add the resulting values.

The area of ​​a right triangle is equal to half the product of its legs: S = (16*16)/2 = 128. The area of ​​a rectangle is equal to the product of its width and length: S = 20*16 = 320. We found the required: area of ​​the trapezoid S = 128 + 320 = 448 sq. see. You can easily double-check yourself using the above formulas, the answer will be identical.

We use the Pick formula

S = M/2 + N - 1,

in this formula M is the number of nodes, i.e. intersections of the lines of the figure with the lines of the cell at the boundaries of the trapezoid (orange dots in the figure), N is the number of nodes inside the figure (blue dots). It is most convenient to use it when finding the area irregular polygon. However, the larger the arsenal of techniques used, the fewer errors and better the results.

Of course, the information provided does not exhaust the types and properties of a trapezoid, as well as methods for finding its area. This article provides an overview of its most important characteristics. In the decision geometric problems It is important to act gradually, start with easy formulas and problems, consistently consolidate understanding, and move to another level of complexity.

Collected together the most common formulas will help students navigate the various ways to calculate the area of ​​a trapezoid and better prepare for tests and tests on this topic.

AND . Now we can begin to consider the question of how to find the area of ​​a trapezoid. This task arises very rarely in everyday life, but sometimes it turns out to be necessary, for example, to find the area of ​​a room in the shape of a trapezoid, which is increasingly used in the construction of modern apartments, or in design renovation projects.

Trapezoid is geometric figure, formed by four intersecting segments, two of which are parallel to each other and are called the bases of a trapezoid. The other two segments are called the sides of the trapezoid. In addition, we will need another definition later. This is the middle line of the trapezoid, which is a segment connecting the midpoints of the sides and the height of the trapezoid, which is equal to the distance between the bases.
Like triangles, trapezoids have special types in the form of an isosceles (equal-sided) trapezoid, in which the lengths of the sides are the same, and a rectangular trapezoid, in which one of the sides forms a right angle with the bases.

Trapezes have some interesting properties:

1. The midline of the trapezoid is equal to half the sum of the bases and is parallel to them.
   
2. Isosceles trapezoids have equal sides and the angles they form with the bases.
   
3. The midpoints of the diagonals of a trapezoid and the point of intersection of its diagonals are on the same straight line.
   
4. If the sum of the sides of a trapezoid is equal to the sum of the bases, then a circle can be inscribed in it
   
5. If the sum of the angles formed by the sides of a trapezoid at any of its bases is 90, then the length of the segment connecting the midpoints of the bases is equal to their half-difference.
   
6. An isosceles trapezoid can be described by a circle. And vice versa. If a trapezoid fits into a circle, then it is isosceles.
   
7. The segment passing through the midpoints of the bases of an isosceles trapezoid will be perpendicular to its bases and represents the axis of symmetry.
   

How to find the area of ​​a trapezoid.

The area of ​​the trapezoid will be equal to half the sum of its bases multiplied by its height. In formula form, this is written as an expression:

where S is the area of ​​the trapezoid, a, b is the length of each of the bases of the trapezoid, h is the height of the trapezoid.

You can also expand any trapezoid into more simple figures: a rectangle and one or two triangles, and if it’s easier for you, then find the area of ​​the trapezoid as the sum of the areas of its constituent figures.

There's another one simple formula to calculate its area. According to it, the area of ​​a trapezoid is equal to the product of its midline by the height of the trapezoid and is written in the form: S = m*h, where S is the area, m is the length of the midline, h is the height of the trapezoid. This formula is more suitable for mathematics problems than for everyday problems, since in real conditions you won't know the length of the centerline without some preliminary calculations. And you will only know the lengths of the bases and sides.

In this case, the area of ​​the trapezoid can be found using the formula:

S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2

where S is the area, a,b are the bases, c,d-sides trapezoids.

There are several other ways to find the area of ​​a trapezoid. But, they are about as inconvenient as the last formula, which means there is no point in dwelling on them. Therefore, we recommend that you use the first formula from the article and wish you to always get accurate results.

Trapeze is called a quadrilateral whose only two the sides are parallel to each other.

They are called the bases of the figure, the remaining ones are called the sides. Parallelograms are considered special cases of the figure. There is also a curved trapezoid, which includes the graph of a function. Formulas for the area of ​​a trapezoid include almost all of its elements, and best solution is selected depending on the specified values.
The main roles in the trapezoid are assigned to the height and midline. Middle line- This is a line connecting the midpoints of the sides. Height trapezoid is held at right angles from top corner to the base.
The area of ​​a trapezoid through its height is equal to the product of half the sum of the lengths of the bases multiplied by the height:

If the average line is known according to the conditions, then this formula is significantly simplified, since it is equal to half the sum of the lengths of the bases:

If, according to the conditions, the lengths of all sides are given, then we can consider an example of calculating the area of ​​a trapezoid using these data:

Suppose we are given a trapezoid with bases a = 3 cm, b = 7 cm and sides c = 5 cm, d = 4 cm. let's find the area figures:

Area of ​​an isosceles trapezoid

An isosceles trapezoid, or, as it is also called, an isosceles trapezoid, is considered a separate case.
A special case is finding the area of ​​an isosceles (equilateral) trapezoid. The formula is derived in various ways– through diagonals, through angles adjacent to the base and the radius of the inscribed circle.
If the length of the diagonals is specified according to the conditions and the angle between them is known, you can use the following formula:

Remember that the diagonals of an isosceles trapezoid are equal to each other!

That is, knowing one of their bases, side and angle, you can easily calculate the area.

Area of ​​a curved trapezoid

A special case is curved trapezoid. It is located on the coordinate axis and is limited by the graph of a continuous positive function.

Its base is located on the X axis and is limited to two points:
Integrals help calculate area curved trapezoid.
The formula is written like this:

Let's consider an example of calculating the area of ​​a curved trapezoid. The formula requires some knowledge to work with certain integrals. First, let's look at the value of the definite integral:

Here F(a) is the value antiderivative function f(x) at point a, F(b) is the value of the same function f(x) at point b.

Now let's solve the problem. The figure shows a curved trapezoid, limited by function. Function
We need to find the area of ​​the selected figure, which is a curvilinear trapezoid bounded from above by the graph, on the right by the straight line x =(-8), on the left by the straight line x =(-10) and the OX axis below.
We will calculate the area of ​​this figure using the formula:

The conditions of the problem give us a function. Using it we will find the values ​​of the antiderivative at each of our points:


Now
Answer: The area of ​​a given curved trapezoid is 4.

There is nothing complicated in calculating this value. The only thing that is important is extreme care in calculations.

Area of ​​a trapezoid. Greetings! In this publication we will look at this formula. Why is she exactly like this and how to understand her. If there is understanding, then you don’t need to teach it. If you just want to look at this formula and urgently, then you can immediately scroll down the page))

Now in detail and in order.

A trapezoid is a quadrilateral, two sides of this quadrilateral are parallel, the other two are not. Those that are not parallel are the bases of the trapezoid. The other two are called sides.

If the sides are equal, then the trapezoid is called isosceles. If one of the sides is perpendicular to the bases, then such a trapezoid is called rectangular.

In its classic form, a trapezoid is depicted as follows - larger base is at the bottom, respectively, the smaller one is at the top. But no one forbids depicting her and vice versa. Here are the sketches:

Next important concept.

The midline of a trapezoid is a segment that connects the midpoints of the sides. The middle line is parallel to the bases of the trapezoid and equal to their half-sum.

Now let's delve deeper. Why is this so?

Consider a trapezoid with bases a and b and with the middle line l, and let's do some additional constructions: draw straight lines through the bases, and perpendiculars through the ends of the midline until they intersect with the bases:

*Letter designations for vertices and other points are not included intentionally to avoid unnecessary designations.

Look, triangles 1 and 2 are equal according to the second sign of equality of triangles, triangles 3 and 4 are the same. From the equality of triangles follows the equality of the elements, namely the legs (they are indicated in blue and red, respectively).

Now attention! If we mentally “cut off” the blue and red segments from the lower base, then we will be left with a segment (this is the side of the rectangle) equal to the middle line. Next, if we “glue” the cut blue and red segments to the upper base of the trapezoid, then we will also get a segment (this is also the side of the rectangle) equal to the midline of the trapezoid.

Got it? It turns out that the sum of the bases will be equal to the two middle lines of the trapezoid:

View another explanation

Let's do the following - construct a straight line passing through the lower base of the trapezoid and a straight line that will pass through points A and B:

We get triangles 1 and 2, they are equal along the side and adjacent angles (the second sign of equality of triangles). This means that the resulting segment (in the sketch it is indicated in blue) is equal to the upper base of the trapezoid.

Now consider the triangle:

*The midline of this trapezoid and the midline of the triangle coincide.

It is known that a triangle is equal to half of the base parallel to it, that is:

Okay, we figured it out. Now about the area of ​​the trapezoid.

Trapezoid area formula:

They say: the area of ​​a trapezoid is equal to the product of half the sum of its bases and height.

That is, it turns out that it is equal to the product of the center line and the height:

You've probably already noticed that this is obvious. Geometrically, this can be expressed this way: if we mentally cut off triangles 2 and 4 from the trapezoid and place them on triangles 1 and 3, respectively:

Then we get a rectangle in area equal to area our trapezoid. The area of ​​this rectangle will be equal to the product of the center line and the height, that is, we can write:

But the point here is not in writing, of course, but in understanding.

Download (view) article material in *pdf format

That's all. Good luck to you!

Best regards, Alexander.