The material presented in this topic is based on the information presented in the topic "Rational fractions. Decomposition of rational fractions into elementary (simple) fractions". I highly recommend that you at least skim through this topic before moving on to reading this material. In addition, we will need a table of indefinite integrals.
Let me remind you of a couple of terms. They were discussed in the corresponding topic, so here I will limit myself to a brief formulation.
The ratio of two polynomials $\frac(P_n(x))(Q_m(x))$ is called a rational function or rational fraction. The rational fraction is called correct, if $n< m$, т.е. если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе. В противном случае (если $n ≥ m$) дробь называется wrong.
Elementary (simplest) rational fractions are rational fractions four types:
- $\frac(A)(x-a)$;
- $\frac(A)((x-a)^n)$ ($n=2,3,4, \ldots$);
- $\frac(Mx+N)(x^2+px+q)$ ($p^2-4q< 0$);
- $\frac(Mx+N)((x^2+px+q)^n)$ ($p^2-4q< 0$; $n=2,3,4,\ldots$).
Note (desirable for a more complete understanding of the text): show\hide
Why is the condition $p^2-4q needed?< 0$ в дробях третьего и четвертого типов? Рассмотрим quadratic equation$x^2+px+q=0$. The discriminant of this equation is $D=p^2-4q$. Essentially, the condition $p^2-4q< 0$ означает, что $D < 0$. Если $D < 0$, то уравнение $x^2+px+q=0$ не имеет действительных корней. Т.е. выражение $x^2+px+q$ неразложимо на множители. Именно эта неразложимость нас и интересует.
For example, for the expression $x^2+5x+10$ we get: $p^2-4q=5^2-4\cdot 10=-15$. Since $p^2-4q=-15< 0$, то выражение $x^2+5x+10$ нельзя разложить на множители.
By the way, for this check it is not at all necessary that the coefficient of $x^2$ be equal to 1. For example, for $5x^2+7x-3=0$ we get: $D=7^2-4\cdot 5 \cdot (-3)=$109. Since $D > 0$, the expression $5x^2+7x-3$ is factorizable.
Examples of rational fractions (proper and improper), as well as examples of decomposition of a rational fraction into elementary ones can be found. Here we will be interested only in questions of their integration. Let's start with integrating elementary fractions. So, each of the four types of elementary fractions above is easy to integrate using the formulas below. Let me remind you that when integrating fractions of types (2) and (4), $n=2,3,4,\ldots$ are assumed. Formulas (3) and (4) require the fulfillment of the condition $p^2-4q< 0$.
\begin(equation) \int \frac(A)(x-a) dx=A\cdot \ln |x-a|+C \end(equation) \begin(equation) \int\frac(A)((x-a)^n )dx=-\frac(A)((n-1)(x-a)^(n-1))+C \end(equation) \begin(equation) \int \frac(Mx+N)(x^2 +px+q) dx= \frac(M)(2)\cdot \ln (x^2+px+q)+\frac(2N-Mp)(\sqrt(4q-p^2))\arctg\ frac(2x+p)(\sqrt(4q-p^2))+C \end(equation)
For $\int\frac(Mx+N)((x^2+px+q)^n)dx$ the substitution $t=x+\frac(p)(2)$ is made, after which the resulting interval is divided into two. The first will be calculated by entering under the differential sign, and the second will have the form $I_n=\int\frac(dt)((t^2+a^2)^n)$. This integral is taken using the recurrence relation
\begin(equation) I_(n+1)=\frac(1)(2na^2)\frac(t)((t^2+a^2)^n)+\frac(2n-1)(2na ^2)I_n,\; n\in N\end(equation)
The calculation of such an integral is discussed in example No. 7 (see the third part).
Scheme for calculating integrals of rational functions (rational fractions):
- If the integrand is elementary, then apply formulas (1)-(4).
- If the integrand is not elementary, then represent it as a sum of elementary fractions, and then integrate using formulas (1)-(4).
The above algorithm for integrating rational fractions has an undeniable advantage - it is universal. Those. using this algorithm you can integrate any rational fraction. That is why almost all changes of variables in the indefinite integral (Euler, Chebyshev substitutions, universal trigonometric substitution) are made in such a way that after this replacement we obtain a rational fraction under the interval. And then apply the algorithm to it. We will analyze the direct application of this algorithm using examples, after making a small note.
$$ \int\frac(7dx)(x+9)=7\ln|x+9|+C. $$
In principle, this integral is easy to obtain without mechanical application of the formula. If we take the constant $7$ out of the integral sign and take into account that $dx=d(x+9)$, we get:
$$ \int\frac(7dx)(x+9)=7\cdot \int\frac(dx)(x+9)=7\cdot \int\frac(d(x+9))(x+9 )=|u=x+9|=7\cdot\int\frac(du)(u)=7\ln|u|+C=7\ln|x+9|+C. $$
For detailed information, I recommend looking at the topic. It explains in detail how such integrals are solved. By the way, the formula is proved by the same transformations that were applied in this paragraph when solving it “manually”.
2) Again, there are two ways: use the ready-made formula or do without it. If you apply the formula, you should take into account that the coefficient in front of $x$ (number 4) will have to be removed. To do this, let’s simply take this four out of brackets:
$$ \int\frac(11dx)((4x+19)^8)=\int\frac(11dx)(\left(4\left(x+\frac(19)(4)\right)\right)^ 8)= \int\frac(11dx)(4^8\left(x+\frac(19)(4)\right)^8)=\int\frac(\frac(11)(4^8)dx) (\left(x+\frac(19)(4)\right)^8). $$
Now it’s time to apply the formula:
$$ \int\frac(\frac(11)(4^8)dx)(\left(x+\frac(19)(4)\right)^8)=-\frac(\frac(11)(4 ^8))((8-1)\left(x+\frac(19)(4) \right)^(8-1))+C= -\frac(\frac(11)(4^8)) (7\left(x+\frac(19)(4) \right)^7)+C=-\frac(11)(7\cdot 4^8 \left(x+\frac(19)(4) \right )^7)+C. $$
You can do without using the formula. And even without taking the constant $4$ out of brackets. If we take into account that $dx=\frac(1)(4)d(4x+19)$, we get:
$$ \int\frac(11dx)((4x+19)^8)=11\int\frac(dx)((4x+19)^8)=\frac(11)(4)\int\frac( d(4x+19))((4x+19)^8)=|u=4x+19|=\\ =\frac(11)(4)\int\frac(du)(u^8)=\ frac(11)(4)\int u^(-8)\;du=\frac(11)(4)\cdot\frac(u^(-8+1))(-8+1)+C= \\ =\frac(11)(4)\cdot\frac(u^(-7))(-7)+C=-\frac(11)(28)\cdot\frac(1)(u^7 )+C=-\frac(11)(28(4x+19)^7)+C. $$
Detailed explanations for finding such integrals are given in the topic “Integration by substitution (substitution under the differential sign)”.
3) We need to integrate the fraction $\frac(4x+7)(x^2+10x+34)$. This fraction has the structure $\frac(Mx+N)(x^2+px+q)$, where $M=4$, $N=7$, $p=10$, $q=34$. However, to make sure that this is really an elementary fraction of the third type, you need to check that the condition $p^2-4q is met< 0$. Так как $p^2-4q=10^2-4\cdot 34=-16 < 0$, то мы действительно имеем дело с интегрированием элементарной дроби третьего типа. Как и в предыдущих пунктах есть два пути для нахождения $\int\frac{4x+7}{x^2+10x+34}dx$. Первый путь - банально использовать формулу . Подставив в неё $M=4$, $N=7$, $p=10$, $q=34$ получим:
$$ \int\frac(4x+7)(x^2+10x+34)dx = \frac(4)(2)\cdot \ln (x^2+10x+34)+\frac(2\cdot 7-4\cdot 10)(\sqrt(4\cdot 34-10^2)) \arctg\frac(2x+10)(\sqrt(4\cdot 34-10^2))+C=\\ = 2\cdot \ln (x^2+10x+34)+\frac(-26)(\sqrt(36)) \arctg\frac(2x+10)(\sqrt(36))+C =2\cdot \ln (x^2+10x+34)+\frac(-26)(6) \arctg\frac(2x+10)(6)+C=\\ =2\cdot \ln (x^2+10x +34)-\frac(13)(3) \arctg\frac(x+5)(3)+C. $$
Let's solve the same example, but without using a ready-made formula. Let's try to isolate the derivative of the denominator in the numerator. What does this mean? We know that $(x^2+10x+34)"=2x+10$. It is the expression $2x+10$ that we have to isolate in the numerator. So far the numerator contains only $4x+7$, but this will not last long. Let's apply the following transformation to the numerator:
$$ 4x+7=2\cdot 2x+7=2\cdot (2x+10-10)+7=2\cdot(2x+10)-2\cdot 10+7=2\cdot(2x+10) -13. $$
Now the required expression $2x+10$ appears in the numerator. And our integral can be rewritten as follows:
$$ \int\frac(4x+7)(x^2+10x+34) dx= \int\frac(2\cdot(2x+10)-13)(x^2+10x+34)dx. $$
Let's split the integrand into two. Well, and, accordingly, the integral itself is also “bifurcated”:
$$ \int\frac(2\cdot(2x+10)-13)(x^2+10x+34)dx=\int \left(\frac(2\cdot(2x+10))(x^2 +10x+34)-\frac(13)(x^2+10x+34) \right)\; dx=\\ =\int \frac(2\cdot(2x+10))(x^2+10x+34)dx-\int\frac(13dx)(x^2+10x+34)=2\cdot \int \frac((2x+10)dx)(x^2+10x+34)-13\cdot\int\frac(dx)(x^2+10x+34). $$
Let's first talk about the first integral, i.e. about $\int \frac((2x+10)dx)(x^2+10x+34)$. Since $d(x^2+10x+34)=(x^2+10x+34)"dx=(2x+10)dx$, then the numerator of the integrand contains the differential of the denominator. In short, instead of the expression $( 2x+10)dx$ we write $d(x^2+10x+34)$.
Now let's say a few words about the second integral. Let's select a complete square in the denominator: $x^2+10x+34=(x+5)^2+9$. In addition, we take into account $dx=d(x+5)$. Now the sum of integrals we obtained earlier can be rewritten in a slightly different form:
$$ 2\cdot\int \frac((2x+10)dx)(x^2+10x+34)-13\cdot\int\frac(dx)(x^2+10x+34) =2\cdot \int \frac(d(x^2+10x+34))(x^2+10x+34)-13\cdot\int\frac(d(x+5))((x+5)^2+ 9). $$
If we make the substitution $u=x^2+10x+34$ in the first integral, then it will take the form $\int\frac(du)(u)$ and take easy to use second formula from . As for the second integral, the change $u=x+5$ is feasible for it, after which it will take the form $\int\frac(du)(u^2+9)$. This pure water eleventh formula from the table of indefinite integrals. So, returning to the sum of integrals, we have:
$$ 2\cdot\int \frac(d(x^2+10x+34))(x^2+10x+34)-13\cdot\int\frac(d(x+5))((x+ 5)^2+9) =2\cdot\ln(x^2+10x+34)-\frac(13)(3)\arctg\frac(x+5)(3)+C. $$
We received the same answer as when applying the formula, which, strictly speaking, is not surprising. In general, the formula is proved by the same methods that we used to find this integral. I believe that the attentive reader may have one question here, so I will formulate it:
Question No. 1
If we apply the second formula from the table of indefinite integrals to the integral $\int \frac(d(x^2+10x+34))(x^2+10x+34)$, then we get the following:
$$ \int \frac(d(x^2+10x+34))(x^2+10x+34)=|u=x^2+10x+34|=\int\frac(du)(u) =\ln|u|+C=\ln|x^2+10x+34|+C. $$
Why was there no module in the solution?
Answer to question #1
The question is completely natural. The module was missing only because the expression $x^2+10x+34$ for any $x\in R$ greater than zero. This is quite easy to show in several ways. For example, since $x^2+10x+34=(x+5)^2+9$ and $(x+5)^2 ≥ 0$, then $(x+5)^2+9 > 0$ . You can think differently, without using emphasis full square. Since $10^2-4\cdot 34=-16< 0$, то $x^2+10x+34 >0$ for any $x\in R$ (if this logical chain is surprising, I advise you to look graphic method solutions quadratic inequalities). In any case, since $x^2+10x+34 > 0$, then $|x^2+10x+34|=x^2+10x+34$, i.e. Instead of a module, you can use regular parentheses.
All points of example No. 1 have been solved, all that remains is to write down the answer.
Answer:
- $\int\frac(7dx)(x+9)=7\ln|x+9|+C$;
- $\int\frac(11dx)((4x+19)^8)=-\frac(11)(28(4x+19)^7)+C$;
- $\int\frac(4x+7)(x^2+10x+34)dx=2\cdot\ln(x^2+10x+34)-\frac(13)(3)\arctg\frac(x +5)(3)+C$.
Example No. 2
Find the integral $\int\frac(7x+12)(3x^2-5x-2)dx$.
At first glance, the integrand fraction $\frac(7x+12)(3x^2-5x-2)$ is very similar to an elementary fraction of the third type, i.e. by $\frac(Mx+N)(x^2+px+q)$. It seems that the only difference is the coefficient of $3$ in front of $x^2$, but it doesn’t take long to remove the coefficient (put it out of brackets). However, this similarity is apparent. For the fraction $\frac(Mx+N)(x^2+px+q)$ the condition $p^2-4q is mandatory< 0$, которое гарантирует, что знаменатель $x^2+px+q$ нельзя разложить на множители. Проверим, как обстоит дело с разложением на множители у знаменателя нашей дроби, т.е. у многочлена $3x^2-5x-2$.
Our coefficient before $x^2$ is not equal to one, therefore check the condition $p^2-4q< 0$ напрямую мы не можем. Однако тут нужно вспомнить, откуда взялось выражение $p^2-4q$. Это всего лишь дискриминант квадратного уравнения $x^2+px+q=0$. Если дискриминант less than zero, then the expression $x^2+px+q$ cannot be factorized. Let's calculate the discriminant of the polynomial $3x^2-5x-2$ located in the denominator of our fraction: $D=(-5)^2-4\cdot 3\cdot(-2)=49$. So, $D > 0$, therefore the expression $3x^2-5x-2$ can be factorized. This means that the fraction $\frac(7x+12)(3x^2-5x-2)$ is not an elemental fraction of the third type, and apply $\int\frac(7x+12)(3x^2-) to the integral 5x-2)dx$ formula is not possible.
Well, if the given rational fraction is not an elementary fraction, then it needs to be represented as a sum of elementary fractions and then integrated. In short, take advantage of the trail. How to decompose a rational fraction into elementary ones is written in detail. Let's start by factoring the denominator:
$$ 3x^2-5x-2=0;\\ \begin(aligned) & D=(-5)^2-4\cdot 3\cdot(-2)=49;\\ & x_1=\frac( -(-5)-\sqrt(49))(2\cdot 3)=\frac(5-7)(6)=\frac(-2)(6)=-\frac(1)(3); \\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot 3)=\frac(5+7)(6)=\frac(12)(6)=2.\ \\end(aligned)\\ 3x^2-5x-2=3\cdot\left(x-\left(-\frac(1)(3)\right)\right)\cdot (x-2)= 3\cdot\left(x+\frac(1)(3)\right)(x-2). $$
We present the subintercal fraction in this form:
$$ \frac(7x+12)(3x^2-5x-2)=\frac(7x+12)(3\cdot\left(x+\frac(1)(3)\right)(x-2) )=\frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2)). $$
Now let’s decompose the fraction $\frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))$ into elementary ones:
$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2)) =\frac(A)(x+\frac( 1)(3))+\frac(B)(x-2)=\frac(A(x-2)+B\left(x+\frac(1)(3)\right))(\left(x+ \frac(1)(3)\right)(x-2));\\ \frac(7)(3)x+4=A(x-2)+B\left(x+\frac(1)( 3)\right). $$
To find the coefficients $A$ and $B$ there are two standard ways: the method of undetermined coefficients and the method of substitution of partial values. Let's apply the partial value substitution method, substituting $x=2$ and then $x=-\frac(1)(3)$:
$$ \frac(7)(3)x+4=A(x-2)+B\left(x+\frac(1)(3)\right).\\ x=2;\; \frac(7)(3)\cdot 2+4=A(2-2)+B\left(2+\frac(1)(3)\right); \; \frac(26)(3)=\frac(7)(3)B;\; B=\frac(26)(7).\\ x=-\frac(1)(3);\; \frac(7)(3)\cdot \left(-\frac(1)(3) \right)+4=A\left(-\frac(1)(3)-2\right)+B\left (-\frac(1)(3)+\frac(1)(3)\right); \; \frac(29)(9)=-\frac(7)(3)A;\; A=-\frac(29\cdot 3)(9\cdot 7)=-\frac(29)(21).\\ $$
Since the coefficients have been found, all that remains is to write down the finished expansion:
$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))=\frac(-\frac(29)( 21))(x+\frac(1)(3))+\frac(\frac(26)(7))(x-2). $$
In principle, you can leave this entry, but I like a more accurate option:
$$ \frac(\frac(7)(3)x+4)(\left(x+\frac(1)(3)\right)(x-2))=-\frac(29)(21)\ cdot\frac(1)(x+\frac(1)(3))+\frac(26)(7)\cdot\frac(1)(x-2). $$
Returning to the original integral, we substitute the resulting expansion into it. Then we divide the integral into two, and apply the formula to each. I prefer to immediately place the constants outside the integral sign:
$$ \int\frac(7x+12)(3x^2-5x-2)dx =\int\left(-\frac(29)(21)\cdot\frac(1)(x+\frac(1) (3))+\frac(26)(7)\cdot\frac(1)(x-2)\right)dx=\\ =\int\left(-\frac(29)(21)\cdot\ frac(1)(x+\frac(1)(3))\right)dx+\int\left(\frac(26)(7)\cdot\frac(1)(x-2)\right)dx =- \frac(29)(21)\cdot\int\frac(dx)(x+\frac(1)(3))+\frac(26)(7)\cdot\int\frac(dx)(x-2 )dx=\\ =-\frac(29)(21)\cdot\ln\left|x+\frac(1)(3)\right|+\frac(26)(7)\cdot\ln|x- 2|+C. $$
Answer: $\int\frac(7x+12)(3x^2-5x-2)dx=-\frac(29)(21)\cdot\ln\left|x+\frac(1)(3)\right| +\frac(26)(7)\cdot\ln|x-2|+C$.
Example No. 3
Find the integral $\int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx$.
We need to integrate the fraction $\frac(x^2-38x+157)((x-1)(x+4)(x-9))$. The numerator contains a polynomial of the second degree, and the denominator contains a polynomial of the third degree. Since the degree of the polynomial in the numerator is less than the degree of the polynomial in the denominator, i.e. $2< 3$, то подынтегральная дробь является правильной. Разложение этой дроби на элементарные (простейшие) было получено в примере №3 на странице, посвящённой разложению рациональных дробей на элементарные. Полученное разложение таково:
$$ \frac(x^2-38x+157)((x-1)(x+4)(x-9))=-\frac(3)(x-1)+\frac(5)(x +4)-\frac(1)(x-9). $$
All we have to do is split the given integral into three and apply the formula to each. I prefer to immediately place the constants outside the integral sign:
$$ \int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx=\int\left(-\frac(3)(x-1) +\frac(5)(x+4)-\frac(1)(x-9) \right)dx=\\=-3\cdot\int\frac(dx)(x-1)+ 5\cdot \int\frac(dx)(x+4)-\int\frac(dx)(x-9)=-3\ln|x-1|+5\ln|x+4|-\ln|x- 9|+C. $$
Answer: $\int\frac(x^2-38x+157)((x-1)(x+4)(x-9))dx=-3\ln|x-1|+5\ln|x+ 4|-\ln|x-9|+C$.
Continuation of the analysis of examples of this topic is located in the second part.
A test on the integration of functions, including rational fractions, is given to 1st and 2nd year students. Examples of integrals will mainly be of interest to mathematicians, economists, and statisticians. These examples were asked on test work at LNU named after. I. Frank. The conditions of the following examples are “Find the integral” or “Calculate the integral”, so to save space and your time they were not written out.
Example 15. We came to the integration of fractional-rational functions. They occupy special place among integrals, because they require a lot of time to calculate and help teachers test your knowledge not only of integration. To simplify the function under the integral, we add and subtract an expression in the numerator that will allow us to split the function under the integral into two simple ones
As a result, we find one integral quite quickly, in the second we need to expand the fraction into a sum of elementary fractions 
When reduced to a common denominator, we obtain the following numerals
Next, open the brackets and group
We equate the value at equal degrees"X" on the right and left. As a result, we arrive at a system of three linear equations(SLAU) with three unknowns. 
How to solve systems of equations is described in other articles on the site. In the end you will receive next solution SLAU
A=4; B=-9/2; C=-7/2.
We substitute constants into the expansion of fractions into the simplest ones and perform integration
This concludes the example.
Example 16. Again we need to find the integral of a fractional rational function. To begin with cubic equation, which is contained in the denominator of the fraction, we will decompose it into simple factors 
Next, we decompose the fraction into its simplest forms 
Let's bring it together right side to the common denominator and open the brackets in the numerator. 
We equate the coefficients for the same degrees of the variable. Let's come to the SLAE again with three unknowns 
Let's substitute values A, B, C into the expansion and calculate the integral 
The first two terms give the logarithm, the last one is also easy to find.
Example 17. In the denominator of the fractional rational function we have the difference of cubes. Using the abbreviated multiplication formulas, we decompose it into two prime factors
Further received fractional function write down the amount simple fractions and bring them together to a common denominator 
In the numerator we get the following expression.
From it we form a system of linear equations to calculate 3 unknowns 
A=1/3; B=-1/3; C=1/3.
We substitute A, B, C into the formula and perform integration. As a result, we arrive at the following answer: 
Here the numerator of the second integral was converted into a logarithm, and the remainder under the integral gives the arctangent.
Similar examples There is a lot on the Internet about integrating rational fractions. You can find similar examples from the materials below.
A rational function is a fraction of the form , the numerator and denominator of which are polynomials or products of polynomials.
Example 1. Step 2.
.
We multiply the undetermined coefficients by polynomials that are not in this individual fraction, but which are in other resulting fractions:
Open the parentheses and equate the numerator of the original integrand to the resulting expression:
In both sides of the equality, we look for terms with the same powers of x and compose a system of equations from them:
.
We cancel all the X's and get equivalent system equations:
.
Thus, the final expansion of the integrand into a sum of simple fractions is:
.
Example 2. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
Now we begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:
Now you need to create and solve a system of equations. To do this, we equate the coefficients of the variable to the corresponding degree in the numerator of the original expression of the function and similar coefficients in the expression obtained at the previous step:
We solve the resulting system:
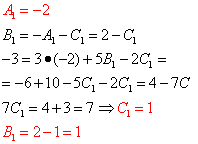
So, from here
.
Example 3. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
We begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:
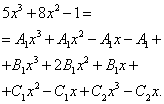
As in previous examples, we compose a system of equations:
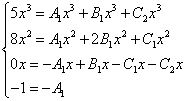
We reduce the x's and get an equivalent system of equations:
Solving the system, we get following values uncertain coefficients:
We obtain the final decomposition of the integrand into the sum of simple fractions:
.
Example 4. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
We already know from previous examples how to equate the numerator of the original fraction to the expression in the numerator obtained after decomposing the fraction into the sum of simple fractions and bringing this sum to a common denominator. Therefore, just for control purposes, we present the resulting system of equations:
Solving the system, we obtain the following values of the uncertain coefficients:
We obtain the final decomposition of the integrand into the sum of simple fractions:
Example 5. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
We independently reduce this sum to a common denominator, equating the numerator of this expression to the numerator of the original fraction. The result should be next system equations:
Solving the system, we obtain the following values of the uncertain coefficients:
.
We obtain the final decomposition of the integrand into the sum of simple fractions:
.
Example 6. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
We perform the same actions with this amount as in the previous examples. The result should be the following system of equations:
Solving the system, we obtain the following values of the uncertain coefficients:
.
We obtain the final decomposition of the integrand into the sum of simple fractions:
.
Example 7. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
After certain actions with the resulting amount, the following system of equations should be obtained:
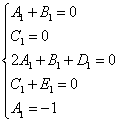
Solving the system, we obtain the following values of the uncertain coefficients:
We obtain the final decomposition of the integrand into the sum of simple fractions:
.
Example 8. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:
.
Let's make some changes to the actions that have already been brought to automaticity to obtain a system of equations. There is an artificial technique that in some cases helps to avoid unnecessary calculations. Bringing the sum of fractions to a common denominator, we obtain and equating the numerator of this expression to the numerator of the original fraction, we obtain.
Integration of rational functions Fractional - rational function The simplest rational fractions Decomposition of a rational fraction into simple fractions Integration of simple fractions General rule integration of rational fractions
polynomial of degree n. Fractional-rational function A fractional-rational function is a function equal to the ratio two polynomials: A rational fraction is called proper if the degree of the numerator is less than the degree of the denominator, that is, m< n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:)()()(x. Q x. P xf n m)()()(x. Q x. R x. L x. Q x. P
Fractional – rational function Reduce improper fraction To the right kind: 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 93 x 3 63 x 15 2 95 4 x xx 342 23 xxx 2 15 x
Simplest rational fractions Proper rational fractions of the form: They are called simplest rational fractions of types. ax A); 2(Nkk ax A k)04(2 2 qp qpxx NMx); 2; 04(2 2 Nkkqp qpxx NMx k V V,
Decomposition of a rational fraction into simple fractions Theorem: Any proper rational fraction, the denominator of which is factorized: can be represented, moreover, in a unique way in the form of a sum of simple fractions: s k qxpxxxxxx. Q)()()(22 2 11 2 21)()(x. Q x. P 1 xx A k k xx B)()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11)(qxpx Nx. M s ss qxpx Nx)
Decomposition of a rational fraction into simple fractions Let us explain the formulation of the theorem in following examples: To find the uncertain coefficients A, B, C, D..., two methods are used: the coefficient comparison method and the method of partial variable values. Let's look at the first method using an example. 3 2)3)(2(4 xx x 2 x A 3 3 2 21)3()3(3 x B x B 1 2 x DCx 22 22 2 11)1(1 xx Nx. M)1(3 22 3 xx x 2 21 x A 22 2)1)(4(987 xxx xx 4 x
Decomposition of a rational fraction into simple fractions Present the fraction as a sum of simple fractions: Let's bring the simplest fractions to a common denominator Equate the numerators of the resulting and original fractions Equate the coefficients at the same powers x)52)(1(332 2 2 xxx xx 1 x A 52 2 xx CBx )52)(1()1)(()52(2 2 xxx x. CBxxx. A 33252 222 xx. CBx. Cx. Bx. AAx. Ax 35 32 2 0 1 2 CAx BAx 2 3 1 C B A 52 23 1 1 2 xx x x
Integration of the simplest fractions Let's find the integrals of the simplest rational fractions: Let's look at the integration of type 3 fractions using an example. dx ax A k dx qpxx NMx 2 ax axd A)(Cax. Aln)(axdax. A k C k ax. A k
Integration of simple fractionsdx xx x 102 13 2 dx xx x 9)12(13 2 dx x x 9)1(13 2 dtdx tx tx 1 1 dt t t 9 1)1(3 2 dt t t 9 23 2 9 322 t dtt 9 9 2 3 2 2 t td 33 2 t arctg. C t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln
Integration of simple fractions Integral of this type using substitution: reduced to the sum of two integrals: The first integral is calculated by introducing t under the differential sign. The second integral is calculated using the recurrence formula: dx qpxx NMx k 2 V t p x 2 kk at dt N at dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt
Integration of simple fractions a = 1; k = 3 323)1(t dt tarctg t dt 1 21)1)(12(2222 322 1 21222 t t t dt)1(22 1 2 t t tarctg 2223)1)(13(2232 332 t t C t t tarctg 222)1 (4)1(
General rule for integrating rational fractions If the fraction is improper, then represent it as the sum of a polynomial and proper fraction. Having factorized the denominator of a proper rational fraction, represent it as a sum of simple fractions with undetermined coefficients Find uncertain odds the method of comparing coefficients or the method of partial values of a variable. Integrate the polynomial and the resulting sum of simple fractions.
Example Let's put the fraction in the correct form. dx xxx 23 35 2 442 35 xxxxxx 23 2 2 x 345 2 xxx 442 34 xxx x 2 234 242 xxx 4425 23 xxx xxx 23 35 2 442 xxx xx xx 23 2 2 2 48 52 5 xxx 5105 23 48 2 x x
Example Let's factorize the denominator of a proper fraction Let's represent the fraction as a sum of simple fractions Let's find the undetermined coefficients using the method of partial values of the variable xxx xx 23 2 2 48 2 2)1(48 xx xx 2)1(1 x C x B x A 2 2)1 ()1(xx Cxx. Bxx. A 48)1()1(22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2)1(3 1 124 xxx
Example dx xx 2 2)1(3 1 124 52 2 2)1(3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln
Here we present detailed solutions three examples of integrating the following rational fractions:
,
,
.
Example 1
Calculate the integral:
.
Solution
Here, under the integral sign there is a rational function, since integrand is a fraction of polynomials. Denominator polynomial degree ( 3 ) is less than the degree of the numerator polynomial ( 4 ). Therefore, first you need to select the whole part of the fraction.
1.
Let's select the whole part of the fraction. Divide x 4
by x 3 - 6 x 2 + 11 x - 6:
From here
.
2.
Let's factorize the denominator of the fraction. To do this, you need to solve the cubic equation:
.
6
1, 2, 3, 6, -1, -2, -3, -6
.
Let's substitute x = 1
:
.
1
. Divide by x - 1
:
From here
.
Solving a quadratic equation.
.
The roots of the equation are: , .
Then
.
3.
Let's break down the fraction into its simplest form.
.
So we found:
.
Let's integrate.
Answer
Example 2
Calculate the integral:
.
Solution
Here the numerator of the fraction is a polynomial of degree zero ( 1 = x 0). The denominator is a polynomial of the third degree. Since 0 < 3 , then the fraction is correct. Let's break it down into simple fractions.
1.
Let's factorize the denominator of the fraction. To do this, you need to solve the third degree equation:
.
Let's assume that it has at least one whole root. Then it is a divisor of the number 3
(member without x). That is, the whole root can be one of the numbers:
1, 3, -1, -3
.
Let's substitute x = 1
:
.
So, we have found one root x = 1
. Divide x 3 + 2 x - 3 on x - 1
:
So,
.
Solving the quadratic equation:
x 2 + x + 3 = 0.
Find the discriminant: D = 1 2 - 4 3 = -11. Since D< 0
, then the equation has no real roots. Thus, we obtained the factorization of the denominator:
.
2.
.
(x - 1)(x 2 + x + 3):
(2.1)
.
Let's substitute x = 1
. Then x - 1 = 0
,
.
Let's substitute in (2.1)
x = 0
:
1 = 3 A - C;
.
Let's equate to (2.1)
coefficients for x 2
:
;
0 = A + B;
.
.
3.
Let's integrate.
(2.2)
.
To calculate the second integral, we select the derivative of the denominator in the numerator and reduce the denominator to the sum of squares.
;
;
.
Calculate I 2
.
.
Since the equation x 2 + x + 3 = 0 has no real roots, then x 2 + x + 3 > 0. Therefore, the modulus sign can be omitted.
We deliver to (2.2)
:
.
Answer
Example 3
Calculate the integral:
.
Solution
Here under the integral sign there is a fraction of polynomials. Therefore, the integrand is a rational function. The degree of the polynomial in the numerator is equal to 3 . The degree of the polynomial of the denominator of the fraction is equal to 4 . Since 3 < 4 , then the fraction is correct. Therefore, it can be decomposed into simple fractions. But to do this you need to factorize the denominator.
1.
Let's factorize the denominator of the fraction. To do this, you need to solve the fourth degree equation:
.
Let's assume that it has at least one whole root. Then it is a divisor of the number 2
(member without x). That is, the whole root can be one of the numbers:
1, 2, -1, -2
.
Let's substitute x = -1
:
.
So, we have found one root x = -1
. Divide by x - (-1) = x + 1:
So,
.
Now we need to solve the third degree equation:
.
If we assume that this equation has an integer root, then it is a divisor of the number 2
(member without x). That is, the whole root can be one of the numbers:
1, 2, -1, -2
.
Let's substitute x = -1
:
.
So, we found another root x = -1
. It would be possible, as in the previous case, to divide the polynomial by , but we will group the terms:
.
Since the equation x 2 + 2 = 0
has no real roots, then we get the factorization of the denominator:
.
2.
Let's break down the fraction into its simplest form. We are looking for an expansion in the form:
.
We get rid of the denominator of the fraction, multiply by (x + 1) 2 (x 2 + 2):
(3.1)
.
Let's substitute x = -1
. Then x + 1 = 0
,
.
Let's differentiate (3.1)
:
;
.
Let's substitute x = -1
and take into account that x + 1 = 0
:
;
;
.
Let's substitute in (3.1)
x = 0
:
0 = 2 A + 2 B + D;
.
Let's equate to (3.1)
coefficients for x 3
:
;
1 = B + C;
.
So, we have found the decomposition into simple fractions:
.
3.
Let's integrate.
.
