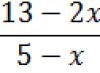I hope that after studying this article you will learn how to find the roots of a complete quadratic equation.
Using the discriminant, only complete quadratic equations are solved; to solve incomplete quadratic equations, other methods are used, which you will find in the article “Solving incomplete quadratic equations.”
What quadratic equations are called complete? This equations of the form ax 2 + b x + c = 0, where coefficients a, b and c are not equal to zero. So, to solve a complete quadratic equation, we need to calculate the discriminant D.
D = b 2 – 4ac.
Depending on the value of the discriminant, we will write down the answer.
If the discriminant is a negative number (D< 0),то корней нет.
If the discriminant is zero, then x = (-b)/2a. When the discriminant positive number(D > 0),
then x 1 = (-b - √D)/2a, and x 2 = (-b + √D)/2a.
For example. Solve the equation x 2– 4x + 4= 0.
D = 4 2 – 4 4 = 0
x = (- (-4))/2 = 2
Answer: 2.
Solve Equation 2 x 2 + x + 3 = 0.
D = 1 2 – 4 2 3 = – 23
Answer: no roots.
Solve Equation 2 x 2 + 5x – 7 = 0.
D = 5 2 – 4 2 (–7) = 81
x 1 = (-5 - √81)/(2 2)= (-5 - 9)/4= – 3.5
x 2 = (-5 + √81)/(2 2) = (-5 + 9)/4=1
Answer: – 3.5; 1.
So let’s imagine the solution of complete quadratic equations using the diagram in Figure 1.
Using these formulas you can solve any complete quadratic equation. You just need to be careful to the equation was written as a polynomial of the standard form
A x 2 + bx + c, otherwise you may make a mistake. For example, in writing the equation x + 3 + 2x 2 = 0, you can mistakenly decide that
a = 1, b = 3 and c = 2. Then
D = 3 2 – 4 1 2 = 1 and then the equation has two roots. And this is not true. (See solution to example 2 above).
Therefore, if the equation is not written as a polynomial of the standard form, first the complete quadratic equation must be written as a polynomial of the standard form (the monomial with the highest indicator degrees, that is A x 2 , then with less – bx and then a free member With.
When solving the reduced quadratic equation and a quadratic equation with an even coefficient in the second term, you can use other formulas. Let's get acquainted with these formulas. If in a complete quadratic equation the second term has an even coefficient (b = 2k), then you can solve the equation using the formulas shown in the diagram in Figure 2.
A complete quadratic equation is called reduced if the coefficient at x 2 equal to one and the equation will take the form x 2 + px + q = 0. Such an equation can be given for solution, or it can be obtained by dividing all coefficients of the equation by the coefficient A, standing at x 2 .
Figure 3 shows a diagram for solving the reduced square  equations. Let's look at an example of the application of the formulas discussed in this article.
equations. Let's look at an example of the application of the formulas discussed in this article.
Example. Solve the equation
3x 2 + 6x – 6 = 0.
Let's solve this equation using the formulas shown in the diagram in Figure 1.
D = 6 2 – 4 3 (– 6) = 36 + 72 = 108
√D = √108 = √(36 3) = 6√3
x 1 = (-6 - 6√3)/(2 3) = (6 (-1- √(3)))/6 = –1 – √3
x 2 = (-6 + 6√3)/(2 3) = (6 (-1+ √(3)))/6 = –1 + √3
Answer: –1 – √3; –1 + √3
You can notice that the coefficient of x in this equation even number, that is, b = 6 or b = 2k, whence k = 3. Then let’s try to solve the equation using the formulas given in the diagram of the figure D 1 = 3 2 – 3 (– 6) = 9 + 18 = 27
√(D 1) = √27 = √(9 3) = 3√3
x 1 = (-3 - 3√3)/3 = (3 (-1 - √(3)))/3 = – 1 – √3
x 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Answer: –1 – √3; –1 + √3. Noticing that all the coefficients in this quadratic equation are divisible by 3 and performing the division, we get the reduced quadratic equation x 2 + 2x – 2 = 0 Solve this equation using the formulas for the reduced quadratic  equations figure 3.
equations figure 3.
D 2 = 2 2 – 4 (– 2) = 4 + 8 = 12
√(D 2) = √12 = √(4 3) = 2√3
x 1 = (-2 - 2√3)/2 = (2 (-1 - √(3)))/2 = – 1 – √3
x 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Answer: –1 – √3; –1 + √3.
As we see, when solving this equation by various formulas we received the same answer. Therefore, having thoroughly mastered the formulas shown in the diagram in Figure 1, you will always be able to solve any complete quadratic equation.
website, when copying material in full or in part, a link to the source is required.
Bibliographic description: Gasanov A. R., Kuramshin A. A., Elkov A. A., Shilnenkov N. V., Ulanov D. D., Shmeleva O. V. Methods for solving quadratic equations // Young scientist. 2016. No. 6.1. P. 17-20..02.2019).
Our project is about ways to solve quadratic equations. Goal of the project: learn to solve quadratic equations in ways not included in the school curriculum. Task: find everything possible ways solving quadratic equations and learning how to use them yourself and introducing these methods to your classmates.
What are “quadratic equations”?
Quadratic equation - equation of the form ax2 + bx + c = 0, Where a, b, c- some numbers ( a ≠ 0), x- unknown.
The numbers a, b, c are called the coefficients of the quadratic equation.
- a is called the first coefficient;
- b is called the second coefficient;
- c - free member.
Who was the first to “invent” quadratic equations?
Some algebraic techniques for solving linear and quadratic equations were known 4000 years ago in Ancient Babylon. Ancient Babylonian found clay tablets, dated somewhere between 1800 and 1600 BC, are the earliest evidence of the study of quadratic equations. The same tablets outline methods for solving certain types of quadratic equations.
The need to solve equations not only of the first, but also of the second degree in ancient times was caused by the need to solve problems related to finding areas land plots and with earthworks of a military nature, as well as with the development of astronomy and mathematics itself.
The rule for solving these equations, set out in the Babylonian texts, essentially coincides with the modern one, but it is not known how the Babylonians arrived at this rule. Almost all cuneiform texts found so far provide only problems with solutions laid out in the form of recipes, with no indication as to how they were found. Despite high level development of algebra in Babylon, the cuneiform texts lack the concept of a negative number and general methods solving quadratic equations.
Babylonian mathematicians from about the 4th century BC. used the square complement method to solve equations with positive roots. Around 300 BC Euclid came up with a more general geometric method solutions. The first mathematician who found solutions to equations with negative roots in the form algebraic formula, was an Indian scientist Brahmagupta(India, 7th century AD).
Brahmagupta laid down a general rule for solving quadratic equations reduced to a unified canonical form:
ax2 + bx = c, a>0
The coefficients in this equation can also be negative. Brahmagupta's rule is essentially the same as ours.
Public competitions in solving problems were common in India. difficult tasks. One of the old Indian books says the following about such competitions: “As the sun eclipses the stars with its brilliance, so learned man will eclipse his glory in public assemblies by proposing and solving algebraic problems.” Problems were often presented in poetic form.
In an algebraic treatise Al-Khwarizmi a classification of linear and quadratic equations is given. The author counts 6 types of equations, expressing them as follows:
1) “Squares are equal to roots,” i.e. ax2 = bx.
2) “Squares are equal to numbers,” i.e. ax2 = c.
3) “The roots are equal to the number,” i.e. ax2 = c.
4) “Squares and numbers are equal to roots,” i.e. ax2 + c = bx.
5) “Squares and roots are equal to the number,” i.e. ax2 + bx = c.
6) “Roots and numbers are equal to squares,” i.e. bx + c == ax2.
For Al-Khwarizmi, who avoided the use of negative numbers, the terms of each of these equations are addends and not subtractables. In this case, equations that do not have positive solutions are obviously not taken into account. The author sets out methods for solving these equations using the techniques of al-jabr and al-mukabal. His decision, of course, does not completely coincide with ours. Not to mention that it is purely rhetorical, it should be noted, for example, that when solving an incomplete quadratic equation of the first type, Al-Khorezmi, like all mathematicians until the 17th century, does not take into account the zero solution, probably because in specific practical problems it doesn't matter. When solving complete quadratic equations of Al-Khwarizmi on partial numerical examples lays out the solution rules and then their geometric proofs.
Forms for solving quadratic equations following the model of Al-Khwarizmi in Europe were first set forth in the “Book of the Abacus,” written in 1202. Italian mathematician Leonard Fibonacci. The author independently developed some new algebraic examples solving problems and was the first in Europe to introduce negative numbers.
This book contributed to the spread of algebraic knowledge not only in Italy, but also in Germany, France and other European countries. Many problems from this book were used in almost all European textbooks of the 14th-17th centuries. General rule solving quadratic equations reduced to a unified canonical form x2 + bх = с for all possible combinations of signs and coefficients b, c, was formulated in Europe in 1544. M. Stiefel.
The derivation of the formula for solving a quadratic equation in general form is available from Vieta, but Vieta only recognized positive roots. Italian mathematicians Tartaglia, Cardano, Bombelli among the first in the 16th century. take into account, in addition to the positive, and negative roots. Only in the 17th century. thanks to the efforts Girard, Descartes, Newton and other scientists, the method of solving quadratic equations takes a modern form.
Let's look at several ways to solve quadratic equations.
Standard methods for solving quadratic equations from school curriculum:
- Factoring the left side of the equation.
- Method for selecting a complete square.
- Solving quadratic equations using the formula.
- Graphic solution quadratic equation.
- Solving equations using Vieta's theorem.
Let us dwell in more detail on the solution of reduced and unreduced quadratic equations using Vieta’s theorem.
Recall that to solve the above quadratic equations it is enough to find two numbers whose product is equal to free member, and the sum - to the second coefficient c opposite sign.
Example.x 2 -5x+6=0
You need to find numbers whose product is 6 and whose sum is 5. These numbers will be 3 and 2.
Answer: x 1 =2, x 2 =3.
But you can use this method for equations with the first coefficient not equal to one.
Example.3x 2 +2x-5=0
Take the first coefficient and multiply it by the free term: x 2 +2x-15=0
The roots of this equation will be numbers whose product is - 15 and whose sum is - 2. These numbers are 5 and 3. To find the roots original equation, divide the resulting roots by the first coefficient.
Answer: x 1 =-5/3, x 2 =1
6. Solving equations using the "throw" method.
Consider the quadratic equation ax 2 + bx + c = 0, where a≠0.
Multiplying both sides by a, we obtain the equation a 2 x 2 + abx + ac = 0.
Let ax = y, whence x = y/a; then we arrive at the equation y 2 + by + ac = 0, equivalent to the given one. We find its roots for 1 and 2 using Vieta’s theorem.
We finally get x 1 = y 1 /a and x 2 = y 2 /a.
With this method, the coefficient a is multiplied by the free term, as if “thrown” to it, which is why it is called the “throw” method. This method is used when you can easily find the roots of the equation using Vieta's theorem and, most importantly, when the discriminant is an exact square.
Example.2x 2 - 11x + 15 = 0.
Let’s “throw” the coefficient 2 to the free term and make a substitution and get the equation y 2 - 11y + 30 = 0.
According to converse of the theorem Vieta
y 1 = 5, x 1 = 5/2, x 1 = 2.5; y 2 = 6, x 2 = 6/2, x 2 = 3.
Answer: x 1 =2.5; X 2 = 3.
7. Properties of coefficients of a quadratic equation.
Let the quadratic equation ax 2 + bx + c = 0, a ≠ 0 be given.
1. If a+ b + c = 0 (i.e. the sum of the coefficients of the equation is zero), then x 1 = 1.
2. If a - b + c = 0, or b = a + c, then x 1 = - 1.
Example.345x 2 - 137x - 208 = 0.
Since a + b + c = 0 (345 - 137 - 208 = 0), then x 1 = 1, x 2 = -208/345.
Answer: x 1 =1; X 2 = -208/345 .
Example.132x 2 + 247x + 115 = 0
Because a-b+c = 0 (132 - 247 +115=0), then x 1 = - 1, x 2 = - 115/132
Answer: x 1 = - 1; X 2 =- 115/132
There are other properties of the coefficients of a quadratic equation. but their use is more complex.
8. Solving quadratic equations using a nomogram.
Fig 1. Nomogram
This is an old and currently forgotten method of solving quadratic equations, placed on p. 83 of the collection: Bradis V.M. Four-digit math tables. - M., Education, 1990.
Table XXII. Nomogram for solving the equation z 2 + pz + q = 0. This nomogram allows, without solving a quadratic equation, to determine the roots of the equation from its coefficients.
The curvilinear scale of the nomogram is built according to the formulas (Fig. 1):
Believing OS = p, ED = q, OE = a(all in cm), from Fig. 1 similarities of triangles SAN And CDF we get the proportion
which, after substitutions and simplifications, yields the equation z 2 + pz + q = 0, and the letter z means the mark of any point on a curved scale.

Rice. 2 Solving quadratic equations using a nomogram
Examples.
1) For the equation z 2 - 9z + 8 = 0 the nomogram gives the roots z 1 = 8.0 and z 2 = 1.0
Answer:8.0; 1.0.
2) Using a nomogram, we solve the equation
2z 2 - 9z + 2 = 0.
Divide the coefficients of this equation by 2, we get the equation z 2 - 4.5z + 1 = 0.
The nomogram gives roots z 1 = 4 and z 2 = 0.5.
Answer: 4; 0.5.
9. Geometric method solving quadratic equations.
Example.X 2 + 10x = 39.
In the original, this problem is formulated as follows: “The square and ten roots are equal to 39.”
Consider a square with side x, rectangles are constructed on its sides so that the other side of each of them is 2.5, therefore the area of each is 2.5x. The resulting figure is then completed to a new square ABCD, adding four squares in the corners. equal square, the side of each of them is 2.5, and the area is 6.25

Rice. 3 Graphic method solutions to the equation x 2 + 10x = 39
The area S of square ABCD can be represented as the sum of the areas of: the original square x 2, four rectangles (4∙2.5x = 10x) and four additional squares (6.25∙4 = 25), i.e. S = x 2 + 10x = 25. Replacing x 2 + 10x with the number 39, we get that S = 39 + 25 = 64, which means that the side of the square is ABCD, i.e. segment AB = 8. For the required side x of the original square we obtain
10. Solving equations using Bezout's theorem.
Bezout's theorem. The remainder of dividing the polynomial P(x) by the binomial x - α is equal to P(α) (that is, the value of P(x) at x = α).
If the number α is the root of the polynomial P(x), then this polynomial is divisible by x -α without a remainder.
Example.x²-4x+3=0
Р(x)= x²-4x+3, α: ±1,±3, α =1, 1-4+3=0. Divide P(x) by (x-1): (x²-4x+3)/(x-1)=x-3
x²-4x+3=(x-1)(x-3), (x-1)(x-3)=0
x-1=0; x=1, or x-3=0, x=3; Answer: x1 =2, x2 =3.
Conclusion: The ability to quickly and rationally solve quadratic equations is simply necessary to solve more complex equations, For example, fractional rational equations, equations higher degrees, biquadratic equations, and in high school trigonometric, exponential and logarithmic equations. Having studied all the found ways to solve quadratic equations, we can advise our classmates, except standard methods, solution by transfer method (6) and solution of equations using the properties of coefficients (7), since they are more accessible to understanding.
Literature:
- Bradis V.M. Four-digit math tables. - M., Education, 1990.
- Algebra 8th grade: textbook for 8th grade. general education institutions Makarychev Yu. N., Mindyuk N. G., Neshkov K. I., Suvorova S. B. ed. S. A. Telyakovsky 15th ed., revised. - M.: Education, 2015
- https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE%D0 %B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
- Glazer G.I. History of mathematics at school. Manual for teachers. / Ed. V.N. Younger. - M.: Education, 1964.
Goals:
- Introduce the concept of a reduced quadratic equation;
- “discover” the relationship between the roots and coefficients of the given quadratic equation;
- develop an interest in mathematics, showing through the example of Viet’s life that mathematics can be a hobby.
1. Checking homework
No. 309(g) x 1 =7, x 2 =
No. 311(g) x 1 =2, x 2 =-1
No. 312 (d) no roots
2. Repetition of learned material
Everyone has a table on their table. Find the correspondence between the left and right columns of the table.
| Verbal formulation | Literal expression |
| 1. Square trinomial | A. ah 2 =0 |
| 2. Discriminant | B. ax 2 +c=0, s< 0 |
| 3. Incomplete quadratic equation having one root equal to 0. | IN. D > 0 |
| 4. An incomplete quadratic equation, one root of which is 0 and the other is not equal to 0. | G. D< 0 |
| 5. Not a complete quadratic equation, the roots of which are equal in magnitude but opposite in sign. | D. akh 2 +in+c=0 |
| 6. Not a complete quadratic equation that has no real roots. | E. D=v 2 +4ac |
| 7. General view quadratic equation. | AND. x 2 +px+q=0 |
| 8. Condition under which a quadratic equation has two roots | Z. ah 2 +in+s |
| 9. Condition under which a quadratic equation has no roots | AND. ax 2 +c=0, c > 0 |
| 10. The condition under which a quadratic equation has two equal roots | TO. akh 2 +in=0 |
| 11. Reduced quadratic equation. | L. D = 0 |
Enter the correct answers in the table.
1-Z; 2-E; 3-A; 4-K; 5-B; 6-I; 7-D; 8-B; 9-G; 10-L; 11-F.
3. Consolidation of the studied material
Solve the equations:
a) -5x 2 + 8x -3=0;
Solution:
D=64 – 4(-5)(-3) = 4,
x 1 = x 2 = = a + b + c = -5+8-3=0
b) 2 x 2 +6x – 8 = 0;
Solution:
D=36 – 4 2 (-8)= 100,
x 1 = = x 2 = a + b + c = 2+6-8=0
c) 2009 x 2 +x – 2010 =0
Solution:
a + b + c = 2009+1 + (-2010) =0, then x 1 =1 x 2 =
4. Expansion of the school course
ax 2 +in+c=0, if a+b+c=0, then x 1 =1 x 2 =Let's consider solving the equations
a) 2x 2 + 5x +3 = 0
Solution:
D = 25 -24 = 1 x 1 = x 2 = a – b + c = 2-5 + 3 = 0
b) -4x 2 -5x -1 =0
Solution:
D = 25 – 16 = 9 x 1 = – 1 x 2 = a – b + c = -4-(-5) – 1 = 0
c)1150x 2 +1135x -15 = 0
Solution:
a – b+c = 1150-1135 +(-15) = 0 x 1 = – 1 x 2 =
ax 2 +in+c=0, if a-b+c=0, then x 1 = – 1 x 2 =
5. New theme
Let's check your completion of the first task. What new concepts did you encounter? 11 – f, i.e.
The given quadratic equation is x 2 + px + q = 0.
The topic of our lesson.
Let's fill out the following table.
The left column is in the notebooks and one student is at the blackboard.
Solving the equation akh 2 +in+c=0
Right column, more prepared student at the blackboard
Solving the equation x 2 + px + q = 0, with a = 1, b = p, c = q
The teacher (if necessary) helps, the rest are in notebooks.
6. Practical part
X 2 – 6 X + 8 = 0,
D = 9 – 8 = 1,
x 1 = 3 – 1 = 2
x 2 = 3 + 1 = 4
X 2 + 6 X + 8 = 0,
D = 9 – 8 = 0,
x 1 = -3 – 1 = -4
x 2 = -3 + 1 = -2
X 2 + 20 X + 51 = 0,
D = 100 – 51 = 49
x 1 = 10 – 7 = 3
x 2 = 10 + 7 = 17
X 2 – 20 X – 69 = 0,
D = 100 – 69 = 31
Based on the results of our calculations, we will fill out the table.
Equation no. r x 1+ x 2 q x 1 x 2 1 -6 6 8 8
Let's compare the results obtained with the coefficients of quadratic equations.
What conclusion can be drawn?
7. Historical background
For the first time, the relationship between the roots and coefficients of a quadratic equation was established by the famous French scientist Francois Viète (1540–1603).
François Viète was a lawyer by profession and worked for many years as an adviser to the king. And although mathematics was his hobby, or as they say, a hobby, thanks to hard work he achieved great results in it. Viet in 1591 introduced letter notation for unknowns and coefficients of equations. This made it possible to write roots and other properties of the equation using general formulas.
The disadvantage of Vieta's algebra was that it only recognized positive numbers. To avoid negative decisions, he replaced equations or looked for artificial solutions, which took a lot of time, complicated the solution and often led to errors.
Viète made many different discoveries, but he himself most valued the establishment of the relationship between the roots and coefficients of a quadratic equation, that is, the relationship called “Viète’s theorem.”
We will consider this theorem in the next lesson.
8. Generalization of knowledge
Questions:
- Which equation is called a reduced quadratic equation?
- What formula can be used to find the roots of the given quadratic equation?
- What determines the number of roots of the given quadratic equation?
- What is the discriminant of a reduced quadratic equation?
- How are the roots of the above quadratic equation and its coefficients related?
- Who made this connection?
9. Homework
clause 4.5, No. 321(b,f) No.322(a,d,g,h)
Fill out the table.
Equation Roots Sum of roots Product of roots X 2 – 8x + 7 = 0 1 and 7 8 7
Literature
CM. Nikolsky and others, “Algebra 8” textbook of the “MSU-School” series - M.: Prosveshchenie, 2007.
We continue to study the topic " solving equations" We have already become acquainted with linear equations and are moving on to getting acquainted with quadratic equations.
First we will look at what a quadratic equation is, how it is written in general form, and give related definitions. After this, we will use examples to examine in detail how incomplete quadratic equations are solved. Next, let's move on to solving complete equations, get the root formula, get acquainted with the discriminant of a quadratic equation and consider solutions typical examples. Finally, let's trace the connections between the roots and coefficients.
Page navigation.
What is a quadratic equation? Their types
First you need to clearly understand what a quadratic equation is. Therefore, it is logical to start a conversation about quadratic equations with the definition of a quadratic equation, as well as related definitions. After this, you can consider the main types of quadratic equations: reduced and unreduced, as well as complete and incomplete equations.
Definition and examples of quadratic equations
Definition.
Quadratic equation is an equation of the form a x 2 +b x+c=0, where x is a variable, a, b and c are some numbers, and a is non-zero.
Let's say right away that quadratic equations are often called equations of the second degree. This is due to the fact that the quadratic equation is algebraic equation second degree.
The stated definition allows us to give examples of quadratic equations. So 2 x 2 +6 x+1=0, 0.2 x 2 +2.5 x+0.03=0, etc. These are quadratic equations.
Definition.
Numbers a, b and c are called coefficients of the quadratic equation a·x 2 +b·x+c=0, and coefficient a is called the first, or the highest, or the coefficient of x 2, b is the second coefficient, or the coefficient of x, and c is the free term.
For example, let's take a quadratic equation of the form 5 x 2 −2 x −3=0, here the leading coefficient is 5, the second coefficient is equal to −2, and the free term is equal to −3. Note that when the coefficients b and/or c are negative, as in the example just given, then short form writing a quadratic equation of the form 5 x 2 −2 x−3=0, and not 5 x 2 +(−2) x+(−3)=0.
It is worth noting that when the coefficients a and/or b are equal to 1 or −1, they are usually not explicitly present in the quadratic equation, which is due to the peculiarities of writing such . For example, in the quadratic equation y 2 −y+3=0 the leading coefficient is one, and the coefficient of y is equal to −1.
Reduced and unreduced quadratic equations
Depending on the value of the leading coefficient, reduced and unreduced quadratic equations are distinguished. Let us give the corresponding definitions.
Definition.
A quadratic equation in which the leading coefficient is 1 is called given quadratic equation. Otherwise the quadratic equation is untouched.
According to this definition, quadratic equations x 2 −3·x+1=0, x 2 −x−2/3=0, etc. – given, in each of them the first coefficient is equal to one. A 5 x 2 −x−1=0, etc. - unreduced quadratic equations, their leading coefficients are different from 1.
From any unreduced quadratic equation, by dividing both sides by the leading coefficient, you can go to the reduced one. This action is an equivalent transformation, that is, the reduced quadratic equation obtained in this way has the same roots as the original unreduced quadratic equation, or, like it, has no roots.
Let us look at an example of how the transition from an unreduced quadratic equation to a reduced one is performed.
Example.
From the equation 3 x 2 +12 x−7=0, go to the corresponding reduced quadratic equation.
Solution.
We just need to divide both sides of the original equation by the leading coefficient 3, it is non-zero, so we can perform this action. We have (3 x 2 +12 x−7):3=0:3, which is the same, (3 x 2):3+(12 x):3−7:3=0, and then (3:3) x 2 +(12:3) x−7:3=0, from where . This is how we obtained the reduced quadratic equation, which is equivalent to the original one.
Answer:
Complete and incomplete quadratic equations
The definition of a quadratic equation contains the condition a≠0. This condition is necessary so that the equation a x 2 + b x + c = 0 is quadratic, since when a = 0 it actually becomes a linear equation of the form b x + c = 0.
As for the coefficients b and c, they can be equal to zero, both individually and together. In these cases, the quadratic equation is called incomplete.
Definition.
The quadratic equation a x 2 +b x+c=0 is called incomplete, if at least one of the coefficients b, c is equal to zero.
In turn
Definition.
Complete quadratic equation is an equation in which all coefficients are different from zero.
Such names were not given by chance. From the following reasoning it will become clear.
If the coefficient b is zero, then the quadratic equation takes the form a·x 2 +0·x+c=0, and it is equivalent to the equation a·x 2 +c=0. If c=0, that is, the quadratic equation has the form a·x 2 +b·x+0=0, then it can be rewritten as a·x 2 +b·x=0. And with b=0 and c=0 we get the quadratic equation a·x 2 =0. The resulting equations differ from the complete quadratic equation in that their left-hand sides do not contain either a term with the variable x, or a free term, or both. Hence their name - incomplete quadratic equations.
So the equations x 2 +x+1=0 and −2 x 2 −5 x+0.2=0 are examples of complete quadratic equations, and x 2 =0, −2 x 2 =0, 5 x 2 +3=0 , −x 2 −5 x=0 are incomplete quadratic equations.
Solving incomplete quadratic equations
From the information in the previous paragraph it follows that there is three types of incomplete quadratic equations:
- a·x 2 =0, the coefficients b=0 and c=0 correspond to it;
- a x 2 +c=0 when b=0 ;
- and a·x 2 +b·x=0 when c=0.
Let us examine in order how incomplete quadratic equations of each of these types are solved.
a x 2 =0
Let's start with solving incomplete quadratic equations in which the coefficients b and c are equal to zero, that is, with equations of the form a x 2 =0. The equation a·x 2 =0 is equivalent to the equation x 2 =0, which is obtained from the original by dividing both parts by a non-zero number a. Obviously, the root of the equation x 2 =0 is zero, since 0 2 =0. This equation has no other roots, which is explained by the fact that for any non-zero number p the inequality p 2 >0 holds, which means that for p≠0 the equality p 2 =0 is never achieved.
So, the incomplete quadratic equation a·x 2 =0 has a single root x=0.
As an example, we give the solution to the incomplete quadratic equation −4 x 2 =0. It is equivalent to the equation x 2 =0, its only root is x=0, therefore, the original equation has a single root zero.
A short solution in this case can be written as follows:
−4 x 2 =0 ,
x 2 =0,
x=0 .
a x 2 +c=0
Now let's look at how incomplete quadratic equations are solved in which the coefficient b is zero and c≠0, that is, equations of the form a x 2 +c=0. We know that moving a term from one side of the equation to the other with the opposite sign, as well as dividing both sides of the equation by a non-zero number, gives an equivalent equation. Therefore, we can carry out the following equivalent transformations incomplete quadratic equation a x 2 +c=0 :
- move from to right side, which gives the equation a x 2 =−c,
- and divide both sides by a, we get .
The resulting equation allows us to draw conclusions about its roots. Depending on the values of a and c, the value of the expression can be negative (for example, if a=1 and c=2, then ) or positive (for example, if a=−2 and c=6, then ), it is not zero , since by condition c≠0. Let's look at the cases separately.
If , then the equation has no roots. This statement follows from the fact that the square of any number is a non-negative number. It follows from this that when , then for any number p the equality cannot be true.
If , then the situation with the roots of the equation is different. In this case, if we remember about , then the root of the equation immediately becomes obvious; it is the number, since . It’s easy to guess that the number is also the root of the equation, indeed, . This equation has no other roots, which can be shown, for example, by contradiction. Let's do this.
Let us denote the roots of the equation just announced as x 1 and −x 1 . Suppose that the equation has one more root x 2, different from the indicated roots x 1 and −x 1. It is known that substituting its roots into an equation instead of x turns the equation into a correct numerical equality. For x 1 and −x 1 we have , and for x 2 we have . The properties of numerical equalities allow us to perform term-by-term subtraction of correct numerical equalities, so subtracting the corresponding parts of the equalities gives x 1 2 −x 2 2 =0. The properties of operations with numbers allow us to rewrite the resulting equality as (x 1 −x 2)·(x 1 +x 2)=0. We know that the product of two numbers is equal to zero if and only if at least one of them is equal to zero. Therefore, from the resulting equality it follows that x 1 −x 2 =0 and/or x 1 +x 2 =0, which is the same, x 2 =x 1 and/or x 2 =−x 1. So we came to a contradiction, since at the beginning we said that the root of the equation x 2 is different from x 1 and −x 1. This proves that the equation has no roots other than and .
Let us summarize the information in this paragraph. The incomplete quadratic equation a x 2 +c=0 is equivalent to the equation that
- has no roots if ,
- has two roots and , if .
Let's consider examples of solving incomplete quadratic equations of the form a·x 2 +c=0.
Let's start with the quadratic equation 9 x 2 +7=0. After moving the free term to the right side of the equation, it will take the form 9 x 2 =−7. Dividing both sides of the resulting equation by 9, we arrive at . Since the right side has a negative number, this equation has no roots, therefore, the original incomplete quadratic equation 9 x 2 +7 = 0 has no roots.
Let's solve another incomplete quadratic equation −x 2 +9=0. We move the nine to the right side: −x 2 =−9. Now we divide both sides by −1, we get x 2 =9. On the right side there is a positive number, from which we conclude that or . Then we write down the final answer: the incomplete quadratic equation −x 2 +9=0 has two roots x=3 or x=−3.
a x 2 +b x=0
It remains to deal with the solution of the last type of incomplete quadratic equations for c=0. Incomplete quadratic equations of the form a x 2 + b x = 0 allows you to solve factorization method. Obviously, we can, located on the left side of the equation, for which it is enough to take it out of brackets common multiplier x. This allows us to move from the original incomplete quadratic equation to an equivalent equation of the form x·(a·x+b)=0. And this equation is equivalent to a set of two equations x=0 and a·x+b=0, the latter of which is linear and has a root x=−b/a.
So, the incomplete quadratic equation a·x 2 +b·x=0 has two roots x=0 and x=−b/a.
To consolidate the material, we will analyze the solution to a specific example.
Example.
Solve the equation.
Solution.
Taking x out of brackets gives the equation . It is equivalent to two equations x=0 and . We solve the resulting linear equation: , and perform the division mixed number on common fraction, we find . Therefore, the roots of the original equation are x=0 and .
After gaining the necessary practice, solutions to such equations can be written briefly:
Answer:
x=0 , .
Discriminant, formula for the roots of a quadratic equation
To solve quadratic equations, there is a root formula. Let's write it down formula for the roots of a quadratic equation: , Where D=b 2 −4 a c- so-called discriminant of a quadratic equation. The entry essentially means that .
It is useful to know how the root formula was derived and how it is used in finding the roots of quadratic equations. Let's figure this out.
Derivation of the formula for the roots of a quadratic equation
Let us need to solve the quadratic equation a·x 2 +b·x+c=0. Let's perform some equivalent transformations:
- We can divide both sides of this equation by a non-zero number a, resulting in the following quadratic equation.
- Now let's highlight perfect square on its left side: . After this, the equation will take the form .
- At this stage, it is possible to transfer the last two terms to the right side with the opposite sign, we have .
- And let’s also transform the expression on the right side: .
As a result, we arrive at an equation that is equivalent to the original quadratic equation a·x 2 +b·x+c=0.
We have already solved equations similar in form in the previous paragraphs, when we examined. This allows you to do the following conclusions concerning the roots of the equation:
- if , then the equation does not have valid solutions;
- if , then the equation has the form , therefore, , from which its only root is visible;
- if , then or , which is the same as or , that is, the equation has two roots.
Thus, the presence or absence of roots of the equation, and therefore the original quadratic equation, depends on the sign of the expression on the right side. In turn, the sign of this expression is determined by the sign of the numerator, since the denominator 4·a 2 is always positive, that is, by the sign of the expression b 2 −4·a·c. This expression b 2 −4 a c was called discriminant of a quadratic equation and designated by the letter D. From here the essence of the discriminant is clear - based on its value and sign, they conclude whether the quadratic equation has real roots, and if so, what is their number - one or two.
Let's return to the equation and rewrite it using the discriminant notation: . And we draw conclusions:
- if D<0 , то это уравнение не имеет действительных корней;
- if D=0, then this equation has a single root;
- finally, if D>0, then the equation has two roots or, which can be rewritten in the form or, and after expanding and bringing the fractions to a common denominator we obtain.
So we derived the formulas for the roots of the quadratic equation, they have the form , where the discriminant D is calculated by the formula D=b 2 −4·a·c.
With their help, with a positive discriminant, you can calculate both real roots of a quadratic equation. When the discriminant is equal to zero, both formulas give the same value of the root, corresponding to the only solution quadratic equation. And when negative discriminant When we try to use the formula for the roots of a quadratic equation, we are faced with extracting the square root of a negative number, which takes us beyond the scope of the school curriculum. With a negative discriminant, the quadratic equation has no real roots, but has a pair complex conjugate roots, which can be found using the same root formulas we obtained.
Algorithm for solving quadratic equations using root formulas
In practice, when solving quadratic equations, you can immediately use the root formula to calculate their values. But this is more related to finding complex roots.
However, in school course algebra usually we're talking about not about complex, but about real roots of a quadratic equation. In this case, it is advisable, before using the formulas for the roots of a quadratic equation, to first find the discriminant, make sure that it is non-negative (otherwise, we can conclude that the equation does not have real roots), and only then calculate the values of the roots.
The above reasoning allows us to write algorithm for solving a quadratic equation. To solve the quadratic equation a x 2 +b x+c=0, you need to:
- using the discriminant formula D=b 2 −4·a·c, calculate its value;
- conclude that a quadratic equation has no real roots if the discriminant is negative;
- calculate the only root of the equation using the formula if D=0;
- find two real roots of a quadratic equation using the root formula if the discriminant is positive.
Here we just note that if the discriminant is equal to zero, you can also use the formula; it will give the same value as .
You can move on to examples of using the algorithm for solving quadratic equations.
Examples of solving quadratic equations
Let's consider solutions to three quadratic equations with positive, negative and equal to zero discriminant. Having dealt with their solution, by analogy it will be possible to solve any other quadratic equation. Let's begin.
Example.
Find the roots of the equation x 2 +2·x−6=0.
Solution.
In this case, we have the following coefficients of the quadratic equation: a=1, b=2 and c=−6. According to the algorithm, you first need to calculate the discriminant; to do this, we substitute the indicated a, b and c into the discriminant formula, we have D=b 2 −4·a·c=2 2 −4·1·(−6)=4+24=28. Since 28>0, that is, the discriminant greater than zero, then the quadratic equation has two real roots. Let's find them using the root formula, we get , here you can simplify the resulting expressions by doing moving the multiplier beyond the root sign followed by reduction of the fraction:
Answer:
Let's move on to the next typical example.
Example.
Solve the quadratic equation −4 x 2 +28 x−49=0 .
Solution.
We start by finding the discriminant: D=28 2 −4·(−4)·(−49)=784−784=0. Therefore, this quadratic equation has a single root, which we find as , that is,
Answer:
x=3.5.
It remains to consider solving quadratic equations with a negative discriminant.
Example.
Solve the equation 5·y 2 +6·y+2=0.
Solution.
Here are the coefficients of the quadratic equation: a=5, b=6 and c=2. We substitute these values into the discriminant formula, we have D=b 2 −4·a·c=6 2 −4·5·2=36−40=−4. The discriminant is negative, therefore, this quadratic equation has no real roots.
If you need to indicate complex roots, then we apply well-known formula roots of a quadratic equation, and perform actions with complex numbers
:
Answer:
there are no real roots, complex roots are: .
Let us note once again that if the discriminant of a quadratic equation is negative, then in school they usually immediately write down an answer in which they indicate that there are no real roots, and complex roots are not found.
Root formula for even second coefficients
The formula for the roots of a quadratic equation, where D=b 2 −4·a·c allows you to obtain a formula of a more compact form, allowing you to solve quadratic equations with an even coefficient for x (or simply with a coefficient of the form 2·n, for example, or 14· ln5=2·7·ln5 ). Let's get her out.
Let's say we need to solve a quadratic equation of the form a x 2 +2 n x+c=0. Let's find its roots using the formula we know. To do this, we calculate the discriminant D=(2 n) 2 −4 a c=4 n 2 −4 a c=4 (n 2 −a c), and then we use the root formula:
Let us denote the expression n 2 −a c as D 1 (sometimes it is denoted D "). Then the formula for the roots of the quadratic equation under consideration with the second coefficient 2 n will take the form  , where D 1 =n 2 −a·c.
, where D 1 =n 2 −a·c.
It is easy to see that D=4·D 1, or D 1 =D/4. In other words, D 1 is the fourth part of the discriminant. It is clear that the sign of D 1 is the same as the sign of D . That is, the sign D 1 is also an indicator of the presence or absence of roots of a quadratic equation.
So, to solve a quadratic equation with a second coefficient 2·n, you need
- Calculate D 1 =n 2 −a·c ;
- If D 1<0 , то сделать вывод, что действительных корней нет;
- If D 1 =0, then calculate the only root of the equation using the formula;
- If D 1 >0, then find two real roots using the formula.
Let's consider solving the example using the root formula obtained in this paragraph.
Example.
Solve the quadratic equation 5 x 2 −6 x −32=0 .
Solution.
The second coefficient of this equation can be represented as 2·(−3) . That is, you can rewrite the original quadratic equation in the form 5 x 2 +2 (−3) x−32=0, here a=5, n=−3 and c=−32, and calculate the fourth part of the discriminant: D 1 =n 2 −a·c=(−3) 2 −5·(−32)=9+160=169. Since its value is positive, the equation has two real roots. Let's find them using corresponding formula roots:
Note that it was possible to use the usual formula for the roots of a quadratic equation, but in this case more computational work would have to be performed.
Answer:
Simplifying the form of quadratic equations
Sometimes, before starting to calculate the roots of a quadratic equation using formulas, it doesn’t hurt to ask the question: “Is it possible to simplify the form of this equation?” Agree that in terms of calculations it will be easier to solve the quadratic equation 11 x 2 −4 x−6=0 than 1100 x 2 −400 x−600=0.
Typically, simplifying the form of a quadratic equation is achieved by multiplying or dividing both sides by a certain number. For example, in the previous paragraph it was possible to simplify the equation 1100 x 2 −400 x −600=0 by dividing both sides by 100.
A similar transformation is carried out with quadratic equations, the coefficients of which are not . In this case, we usually divide both sides of the equation by absolute values its coefficients. For example, let's take the quadratic equation 12 x 2 −42 x+48=0. absolute values of its coefficients: GCD(12, 42, 48)= GCD(GCD(12, 42), 48)= GCD(6, 48)=6. Dividing both sides of the original quadratic equation by 6, we arrive at the equivalent quadratic equation 2 x 2 −7 x+8=0.
And multiplying both sides of a quadratic equation is usually done to get rid of fractional odds. In this case, multiplication is carried out by the denominators of its coefficients. For example, if both sides of the quadratic equation are multiplied by LCM(6, 3, 1)=6, then it will take the simpler form x 2 +4·x−18=0.
In conclusion of this point, we note that they almost always get rid of the minus at the highest coefficient of a quadratic equation by changing the signs of all terms, which corresponds to multiplying (or dividing) both sides by −1. For example, usually we move from the quadratic equation −2 x 2 −3 x + 7 = 0 to the solution 2 x 2 + 3 x − 7 = 0 .
Relationship between roots and coefficients of a quadratic equation
The formula for the roots of a quadratic equation expresses the roots of the equation through its coefficients. Based on the root formula, you can obtain other relationships between roots and coefficients.
The most well-known and applicable formulas from Vieta’s theorem are of the form and . In particular, for the given quadratic equation, the sum of the roots is equal to the second coefficient with the opposite sign, and the product of the roots is equal to the free term. For example, by looking at the form of the quadratic equation 3 x 2 −7 x + 22 = 0, we can immediately say that the sum of its roots is equal to 7/3, and the product of the roots is equal to 22/3.
Using the already written formulas, you can obtain a number of other connections between the roots and coefficients of the quadratic equation. For example, you can express the sum of the squares of the roots of a quadratic equation through its coefficients: .
References.
- Algebra: textbook for 8th grade. general education institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edited by S. A. Telyakovsky. - 16th ed. - M.: Education, 2008. - 271 p. : ill. - ISBN 978-5-09-019243-9.
- Mordkovich A. G. Algebra. 8th grade. At 2 p.m. Part 1. Textbook for students educational institutions/ A. G. Mordkovich. - 11th ed., erased. - M.: Mnemosyne, 2009. - 215 p.: ill. ISBN 978-5-346-01155-2.
This topic may seem difficult at first due to many not so simple formulas. Not only do the quadratic equations themselves have long notations, but the roots are also found through the discriminant. In total, three new formulas are obtained. Not very easy to remember. This only works after common solution such equations. Then all the formulas will be remembered by themselves.
General view of a quadratic equation
Here we propose their explicit recording, when the most high degree written first, and then in descending order. There are often situations when the terms are inconsistent. Then it is better to rewrite the equation in descending order of the degree of the variable.
Let us introduce some notation. They are presented in the table below.
If we accept these notations, all quadratic equations are reduced to the following notation.

Moreover, the coefficient a ≠ 0. Let this formula be designated number one.
When an equation is given, it is not clear how many roots there will be in the answer. Because one of three options is always possible:
- the solution will have two roots;
- the answer will be one number;
- the equation will have no roots at all.
And until the decision is finalized, it is difficult to understand which option will appear in a particular case.
Types of recordings of quadratic equations
There may be different entries in tasks. They won't always look like general formula quadratic equation. Sometimes it will be missing some terms. What was written above is complete equation. If you remove the second or third term in it, you get something else. These records are also called quadratic equations, only incomplete.
Moreover, only terms with coefficients “b” and “c” can disappear. The number "a" cannot be equal to zero under any circumstances. Because in this case the formula turns into a linear equation. The formulas for the incomplete form of equations will be as follows:
So, there are only two types; in addition to complete ones, there are also incomplete quadratic equations. Let the first formula be number two, and the second - three.
Discriminant and dependence of the number of roots on its value
You need to know this number in order to calculate the roots of the equation. It can always be calculated, no matter what the formula of the quadratic equation is. In order to calculate the discriminant, you need to use the equality written below, which will have number four.
After substituting the coefficient values into this formula, you can get numbers with different signs. If the answer is yes, then the answer to the equation will be two different roots. If the number is negative, there will be no roots of the quadratic equation. If it is equal to zero, there will be only one answer.
How to solve a complete quadratic equation?
In fact, consideration of this issue has already begun. Because first you need to find a discriminant. After it is determined that there are roots of the quadratic equation, and their number is known, you need to use formulas for the variables. If there are two roots, then you need to apply the following formula.

Since it contains a “±” sign, there will be two values. The expression under the square root sign is the discriminant. Therefore, the formula can be rewritten differently.
Formula number five. From the same record it is clear that if the discriminant is equal to zero, then both roots will take the same values.
If solving quadratic equations has not yet been worked out, then it is better to write down the values of all coefficients before applying the discriminant and variable formulas. Later this moment will not cause difficulties. But at the very beginning there is confusion.

How to solve an incomplete quadratic equation?
Everything is much simpler here. There is no need for additional formulas. And those that have already been written down for the discriminant and the unknown will not be needed.
Let's first consider incomplete equation at number two. In this equality, it is necessary to take the unknown quantity out of brackets and solve the linear equation, which will remain in brackets. The answer will have two roots. The first one is necessarily equal to zero, because there is a multiplier consisting of the variable itself. The second one will be obtained by solving a linear equation.
The incomplete equation number three is solved by moving the number from the left side of the equality to the right. Then you need to divide by the coefficient facing the unknown. All that remains is to extract the square root and remember to write it down twice with opposite signs.

Below are some steps that will help you learn how to solve all kinds of equalities that turn into quadratic equations. They will help the student to avoid mistakes due to inattention. These shortcomings are the reason bad grades while studying the extensive topic “Quadratic equations (8th grade)”. Subsequently, these actions will not need to be performed constantly. Because a stable skill will appear.
- First you need to write the equation in standard form. That is, first the term with the most to a large extent variable, and then - without a degree and lastly - just a number.
- If a minus appears before the coefficient “a”, it can complicate the work for a beginner studying quadratic equations. It's better to get rid of it. For this purpose, the entire equality must be multiplied by “-1”. This means that all terms will change sign to the opposite.
- It is recommended to get rid of fractions in the same way. Simply multiply the equation by the appropriate factor so that the denominators cancel out.

Examples
It is required to solve the following quadratic equations:
x 2 − 7x = 0;
15 − 2x − x 2 = 0;
x 2 + 8 + 3x = 0;
12x + x 2 + 36 = 0;
(x+1) 2 + x + 1 = (x+1)(x+2).
The first equation: x 2 − 7x = 0. It is incomplete, so it is solved as described for formula number two.
After taking it out of brackets, it turns out: x (x - 7) = 0.
The first root takes the value: x 1 = 0. The second will be found from linear equation: x - 7 = 0. It is easy to see that x 2 = 7.
Second equation: 5x 2 + 30 = 0. Again incomplete. Only it is solved as described for the third formula.
After moving 30 to the right side of the equation: 5x 2 = 30. Now you need to divide by 5. It turns out: x 2 = 6. The answers will be the numbers: x 1 = √6, x 2 = - √6.
The third equation: 15 − 2х − x 2 = 0. Here and further, solving quadratic equations will begin with their rewriting in standard view: − x 2 − 2x + 15 = 0. Now it’s time to use the second useful advice and multiply everything by minus one. It turns out x 2 + 2x - 15 = 0. Using the fourth formula, you need to calculate the discriminant: D = 2 2 - 4 * (- 15) = 4 + 60 = 64. It is a positive number. From what is said above, it turns out that the equation has two roots. They need to be calculated using the fifth formula. It turns out that x = (-2 ± √64) / 2 = (-2 ± 8) / 2. Then x 1 = 3, x 2 = - 5.
The fourth equation x 2 + 8 + 3x = 0 is transformed into this: x 2 + 3x + 8 = 0. Its discriminant is equal to this value: -23. Since this number is negative, the answer to this task will be the following entry: “There are no roots.”
The fifth equation 12x + x 2 + 36 = 0 should be rewritten as follows: x 2 + 12x + 36 = 0. After applying the formula for the discriminant, the number zero is obtained. This means that it will have one root, namely: x = -12/ (2 * 1) = -6.
The sixth equation (x+1) 2 + x + 1 = (x+1)(x+2) requires transformations, which consist in bringing similar terms, before opening the brackets. In place of the first there will be the following expression: x 2 + 2x + 1. After the equality, this entry will appear: x 2 + 3x + 2. After similar terms are counted, the equation will take the form: x 2 - x = 0. It has become incomplete . Something similar to this has already been discussed a little higher. The roots of this will be the numbers 0 and 1.