Complex integrals
This article concludes the topic of indefinite integrals, and includes integrals that I find quite complex. The lesson was created at the repeated requests of visitors who expressed their wish that more difficult examples be analyzed on the site.
It is assumed that the reader of this text is well prepared and knows how to apply basic integration techniques. Dummies and people who are not very confident in integrals should refer to the very first lesson - Indefinite integral. Examples of solutions, where you can master the topic almost from scratch. More experienced students can become familiar with techniques and methods of integration that have not yet been encountered in my articles.
What integrals will be considered?
First we will consider integrals with roots, for the solution of which we successively use variable replacement And integration by parts. That is, in one example two techniques are combined at once. And even more.
Then we will get acquainted with interesting and original method of reducing the integral to itself. Quite a few integrals are solved this way.
The third issue of the program will be integrals from complex fractions, which flew past the cash desk in previous articles.
Fourthly, additional integrals from trigonometric functions will be analyzed. In particular, there are methods that avoid time-consuming universal trigonometric substitution.
(2) In the integrand function, we divide the numerator by the denominator term by term.
(3) We use the linearity property of the indefinite integral. In the last integral immediately put the function under the differential sign.
(4) We take the remaining integrals. Note that in a logarithm you can use parentheses rather than a modulus, since .
(5) We carry out a reverse replacement, expressing “te” from the direct replacement:
Masochistic students can differentiate the answer and get the original integrand, as I just did. No, no, I did the check in the right sense =)
As you can see, during the solution we had to use even more than two solution methods, so to deal with such integrals you need confident integration skills and quite a bit of experience.
In practice, of course, the square root is more common; here are three examples for solving it yourself:
Example 2
Find the indefinite integral
Example 3
Find the indefinite integral
Example 4
Find the indefinite integral
These examples are of the same type, so the complete solution at the end of the article will only be for Example 2; Examples 3-4 have the same answers. Which replacement to use at the beginning of decisions, I think, is obvious. Why did I choose examples of the same type? Often found in their role. More often, perhaps, just something like ![]() .
.
But not always, when under the arctangent, sine, cosine, exponential and other functions there is a root of a linear function, you have to use several methods at once. In a number of cases, it is possible to “get off easy,” that is, immediately after the replacement, a simple integral is obtained, which can be easily taken. The easiest of the tasks proposed above is Example 4, in which, after replacement, a relatively simple integral is obtained.
By reducing the integral to itself
A witty and beautiful method. Let's take a look at the classics of the genre:
Example 5
Find the indefinite integral
Under the root is a quadratic binomial, and trying to integrate this example can give the teapot a headache for hours. Such an integral is taken in parts and reduced to itself. In principle, it’s not difficult. If you know how.
Let us denote the integral under consideration by a Latin letter and begin the solution: ![]()
Let's integrate by parts: 

(1) Prepare the integrand function for term-by-term division.
(2) We divide the integrand function term by term. It may not be clear to everyone, but I’ll describe it in more detail:
(3) We use the linearity property of the indefinite integral.
(4) Take the last integral (“long” logarithm).
Now let's look at the very beginning of the solution: 
And to the end: 
What happened? As a result of our manipulations, the integral was reduced to itself!
Let's equate the beginning and the end: ![]()
Move to the left side with a change of sign: ![]()
And we move the two to the right side. As a result: ![]()
The constant, strictly speaking, should have been added earlier, but I added it at the end. I strongly recommend reading what the rigor is here:
Note:
More strictly, the final stage of the solution looks like this:
Thus:
The constant can be redesignated by . Why can it be redesignated? Because he still accepts it any values, and in this sense there is no difference between constants and.
As a result:
A similar trick with constant renotation is widely used in differential equations. And there I will be strict. And here I allow such freedom only in order not to confuse you with unnecessary things and to focus attention precisely on the integration method itself.
Example 6
Find the indefinite integral
Another typical integral for independent solution. Full solution and answer at the end of the lesson. There will be a difference with the answer in the previous example!
If under the square root there is a square trinomial, then the solution in any case comes down to two analyzed examples.
For example, consider the integral ![]() . All you need to do is first select a complete square:
. All you need to do is first select a complete square:
.
Next, a linear replacement is carried out, which does “without any consequences”:
, resulting in the integral . Something familiar, right?
Or this example, with a quadratic binomial:
Select a complete square:
And, after linear replacement, we obtain the integral, which is also solved using the algorithm already discussed.
Let's look at two more typical examples of how to reduce an integral to itself:
– integral of the exponential multiplied by sine;
– integral of the exponential multiplied by the cosine.
In the listed integrals by parts you will have to integrate twice:
Example 7
Find the indefinite integral
The integrand is the exponential multiplied by the sine.
We integrate by parts twice and reduce the integral to itself: ![]()



As a result of double integration by parts, the integral was reduced to itself. We equate the beginning and end of the solution:
We move it to the left side with a change of sign and express our integral: 
Ready. At the same time, it is advisable to comb the right side, i.e. take the exponent out of brackets, and place the sine and cosine in brackets in a “beautiful” order.
Now let's go back to the beginning of the example, or more precisely, to integration by parts:
We designated the exponent as. The question arises: is it the exponent that should always be denoted by ? Not necessary. In fact, in the considered integral fundamentally doesn't matter, what do we mean by , we could have gone the other way: 
Why is this possible? Because the exponential turns into itself (both during differentiation and integration), sine and cosine mutually turn into each other (again, both during differentiation and integration).
That is, we can also denote a trigonometric function. But, in the example considered, this is less rational, since fractions will appear. If you wish, you can try to solve this example using the second method; the answers must match.
Example 8
Find the indefinite integral
This is an example for you to solve on your own. Before you decide, think about what is more advantageous in this case to designate as , an exponential or a trigonometric function? Full solution and answer at the end of the lesson.
And, of course, do not forget that most of the answers in this lesson are quite easy to check by differentiation!
The examples considered were not the most complex. In practice, integrals are more common where the constant is both in the exponent and in the argument of the trigonometric function, for example: . Many people will get confused in such an integral, and I often get confused myself. The fact is that there is a high probability of fractions appearing in the solution, and it is very easy to lose something through carelessness. In addition, there is a high probability of an error in the signs; note that the exponent has a minus sign, and this introduces additional difficulty.
At the final stage, the result is often something like this:
Even at the end of the solution, you should be extremely careful and correctly understand the fractions: 
Integrating Complex Fractions
We are slowly approaching the equator of the lesson and begin to consider integrals of fractions. Again, not all of them are super complex, it’s just that for one reason or another the examples were a little “off topic” in other articles.
Continuing the theme of roots
Example 9
Find the indefinite integral
In the denominator under the root there is a quadratic trinomial plus an “appendage” in the form of an “X” outside the root. An integral of this type can be solved using a standard substitution.
We decide: ![]()
The replacement here is simple: ![]()
Let's look at life after replacement: 
(1) After substitution, we reduce the terms under the root to a common denominator.
(2) We take it out from under the root.
(3) The numerator and denominator are reduced by . At the same time, under the root, I rearranged the terms in a convenient order. With some experience, steps (1), (2) can be skipped by performing the commented actions orally.
(4) The resulting integral, as you remember from the lesson Integrating Some Fractions, is being decided complete square extraction method. Select a complete square.
(5) By integration we obtain an ordinary “long” logarithm.
(6) We carry out the reverse replacement. If initially , then back: .
(7) The final action is aimed at straightening the result: under the root we again bring the terms to a common denominator and take them out from under the root.
Example 10
Find the indefinite integral ![]()
This is an example for you to solve on your own. Here a constant is added to the lone “X”, and the replacement is almost the same: ![]()
The only thing you need to do additionally is to express the “x” from the replacement being carried out: ![]()
Full solution and answer at the end of the lesson.
Sometimes in such an integral there may be a quadratic binomial under the root, this does not change the method of solution, it will be even simpler. Feel the difference:
Example 11
Find the indefinite integral
Example 12
Find the indefinite integral
Brief solutions and answers at the end of the lesson. It should be noted that Example 11 is exactly binomial integral, the solution method of which was discussed in class Integrals of irrational functions.
Integral of an indecomposable polynomial of the 2nd degree to the power
(polynomial in denominator)
A more rare type of integral, but nevertheless encountered in practical examples.
Example 13
Find the indefinite integral
But let’s return to the example with lucky number 13 (honestly, I didn’t guess correctly). This integral is also one of those that can be quite frustrating if you don’t know how to solve.
The solution starts with an artificial transformation: 
I think everyone already understands how to divide the numerator by the denominator term by term.
The resulting integral is taken in parts: 

For an integral of the form ( – natural number) we derive recurrent reduction formula:
, Where ![]() – integral of a degree lower.
– integral of a degree lower.
Let us verify the validity of this formula for the solved integral.
In this case: , , we use the formula: 
As you can see, the answers are the same.
Example 14
Find the indefinite integral
This is an example for you to solve on your own. The sample solution uses the above formula twice in succession.
If under the degree is indivisible square trinomial, then the solution is reduced to a binomial by isolating the perfect square, for example:
What if there is an additional polynomial in the numerator? In this case, the method of indefinite coefficients is used, and the integrand function is expanded into a sum of fractions. But in my practice there is such an example never met, so I missed this case in the article Integrals of fractional-rational functions, I'll skip it now. If you still encounter such an integral, look at the textbook - everything is simple there. I don’t think it’s advisable to include material (even simple ones), the probability of encountering which tends to zero.
Integrating complex trigonometric functions
The adjective “complex” for most examples is again largely conditional. Let's start with tangents and cotangents in high powers. From the point of view of the solving methods used, tangent and cotangent are almost the same thing, so I will talk more about tangent, implying that the demonstrated method for solving the integral is valid for cotangent too.
In the above lesson we looked at universal trigonometric substitution for solving a certain type of integrals of trigonometric functions. The disadvantage of universal trigonometric substitution is that its use often results in cumbersome integrals with difficult calculations. And in some cases, universal trigonometric substitution can be avoided!
Let's consider another canonical example, the integral of one divided by sine:
Example 17
Find the indefinite integral
Here you can use universal trigonometric substitution and get the answer, but there is a more rational way. I will provide the complete solution with comments for each step:

(1) We use the trigonometric formula for the sine of a double angle.
(2) We carry out an artificial transformation: Divide in the denominator and multiply by .
(3) Using the well-known formula in the denominator, we transform the fraction into a tangent.
(4) We bring the function under the differential sign.
(5) Take the integral.
A couple of simple examples for you to solve on your own:
Example 18
Find the indefinite integral
Note: The very first step should be to use the reduction formula ![]() and carefully carry out actions similar to the previous example.
and carefully carry out actions similar to the previous example.
Example 19
Find the indefinite integral
Well, this is a very simple example.
Complete solutions and answers at the end of the lesson.
I think now no one will have problems with integrals: ![]() and so on.
and so on.
What is the idea of the method? The idea is to use transformations and trigonometric formulas to organize only tangents and the tangent derivative into the integrand. That is, we are talking about replacing: ![]() . In Examples 17-19 we actually used this replacement, but the integrals were so simple that we got by with an equivalent action - subsuming the function under the differential sign.
. In Examples 17-19 we actually used this replacement, but the integrals were so simple that we got by with an equivalent action - subsuming the function under the differential sign.
Similar reasoning, as I already mentioned, can be carried out for the cotangent.
There is also a formal prerequisite for applying the above replacement:
The sum of the powers of cosine and sine is a negative integer EVEN number, For example:
for the integral – a negative integer EVEN number.
! Note : if the integrand contains ONLY a sine or ONLY a cosine, then the integral is also taken for a negative odd degree (the simplest cases are in Examples No. 17, 18).
Let's look at a couple of more meaningful tasks based on this rule:
Example 20
Find the indefinite integral
The sum of the powers of sine and cosine: 2 – 6 = –4 is a negative integer EVEN number, which means that the integral can be reduced to tangents and its derivative: 
(1) Let's transform the denominator.
(2) Using the well-known formula, we obtain .
(3) Let's transform the denominator.
(4) We use the formula ![]() .
.
(5) We bring the function under the differential sign.
(6) We carry out replacement. More experienced students may not carry out the replacement, but it is still better to replace the tangent with one letter - there is less risk of getting confused.
Example 21
Find the indefinite integral
This is an example for you to solve on your own.
Hang in there, the championship rounds are about to begin =)
Often the integrand contains a “hodgepodge”:
Example 22
Find the indefinite integral ![]()
This integral initially contains a tangent, which immediately leads to an already familiar thought:

I will leave the artificial transformation at the very beginning and the remaining steps without comment, since everything has already been discussed above.
A couple of creative examples for your own solution:
Example 23
Find the indefinite integral ![]()
Example 24
Find the indefinite integral ![]()
Yes, in them, of course, you can lower the powers of sine and cosine, and use a universal trigonometric substitution, but the solution will be much more efficient and shorter if it is carried out through tangents. Full solution and answers at the end of the lesson
Solving integrals is an easy task, but only for a select few. This article is for those who want to learn to understand integrals, but know nothing or almost nothing about them. Integral... Why is it needed? How to calculate it? What are definite and indefinite integrals? If the only use you know of for an integral is to use a crochet hook shaped like an integral icon to get something useful out of hard-to-reach places, then welcome! Find out how to solve integrals and why you can't do without it.
We study the concept of "integral"
Integration was known back in Ancient Egypt. Of course, not in its modern form, but still. Since then, mathematicians have written many books on this topic. Especially distinguished themselves Newton And Leibniz , but the essence of things has not changed. How to understand integrals from scratch? No way! To understand this topic, you will still need a basic knowledge of the basics of mathematical analysis. We already have information about , necessary for understanding integrals, on our blog.
Indefinite integral
Let us have some function f(x) .
Indefinite integral function f(x) this function is called F(x) , whose derivative is equal to the function f(x) .
In other words, an integral is a derivative in reverse or an antiderivative. By the way, read about how in our article.

An antiderivative exists for all continuous functions. Also, a constant sign is often added to the antiderivative, since the derivatives of functions that differ by a constant coincide. The process of finding the integral is called integration.
Simple example:

In order not to constantly calculate antiderivatives of elementary functions, it is convenient to put them in a table and use ready-made values:

Definite integral
When dealing with the concept of an integral, we are dealing with infinitesimal quantities. The integral will help to calculate the area of a figure, the mass of a non-uniform body, the distance traveled during uneven movement, and much more. It should be remembered that an integral is the sum of an infinitely large number of infinitesimal terms.
As an example, imagine a graph of some function. How to find the area of a figure bounded by the graph of a function?

Using an integral! Let us divide the curvilinear trapezoid, limited by the coordinate axes and the graph of the function, into infinitesimal segments. This way the figure will be divided into thin columns. The sum of the areas of the columns will be the area of the trapezoid. But remember that such a calculation will give an approximate result. However, the smaller and narrower the segments, the more accurate the calculation will be. If we reduce them to such an extent that the length tends to zero, then the sum of the areas of the segments will tend to the area of the figure. This is a definite integral, which is written like this:

Points a and b are called limits of integration.
 Bari Alibasov and the group "Integral"
Bari Alibasov and the group "Integral" By the way! For our readers there is now a 10% discount on
Rules for calculating integrals for dummies
Properties of the indefinite integral
How to solve an indefinite integral? Here we will look at the properties of the indefinite integral, which will be useful when solving examples.
- The derivative of the integral is equal to the integrand:

- The constant can be taken out from under the integral sign:

- The integral of the sum is equal to the sum of the integrals. This is also true for the difference:
Properties of a definite integral
- Linearity:

- The sign of the integral changes if the limits of integration are swapped:

- At any points a, b And With:

We have already found out that a definite integral is the limit of a sum. But how to get a specific value when solving an example? For this there is the Newton-Leibniz formula:

Examples of solving integrals
Below we will consider several examples of finding indefinite integrals. We suggest you figure out the intricacies of the solution yourself, and if something is unclear, ask questions in the comments.

To reinforce the material, watch a video about how integrals are solved in practice. Don't despair if the integral is not given right away. Contact a professional service for students, and any triple or curved integral over a closed surface will be within your power.
The following formula is called integration by parts formula in the indefinite integral:
To apply the integration by parts formula, the integrand must be divided into two factors. One of them is denoted by u, and the rest refers to the second factor and is denoted by dv. Then by differentiation we find du and integration - function v. At the same time, for u dv- such a part of the integrand that can be easily integrated.
When is it beneficial to use the method of integration by parts? Then when the integrand contains :
1) - logarithmic functions, as well as inverse trigonometric functions (with the prefix "arc"), then, based on long-term experience of integration by parts, these functions are denoted by u;
2) , , - sine, cosine and exponent multiplied by P(x) is an arbitrary polynomial in x, then these functions are denoted by dv, and the polynomial is through u;
3) , , , , in this case integration by parts is applied twice.
Let us explain the value of the method of integration by parts using the example of the first case. Let the expression under the integral sign contain a logarithmic function (this will be example 1). By using integration by parts, such an integral is reduced to calculating the integral of only algebraic functions (most often a polynomial), that is, not containing a logarithmic or inverse trigonometric function. Using the integration by parts formula given at the very beginning of the lesson
we obtain in the first term (without an integral) a logarithmic function, and in the second term (under the integral sign) a function that does not contain a logarithm. The integral of an algebraic function is much simpler than the integral under the sign of which a logarithmic or inverse trigonometric function is found separately or together with an algebraic factor.
Thus, using integration by parts formulas integration is not performed immediately: finding a given integral is reduced to finding another. The meaning of the integration by parts formula is that as a result of its application, the new integral turns out to be tabular or at least becomes simpler than the original one.
The method of integration by parts is based on the use of the formula for differentiating the product of two functions:
then it can be written in the form
which was given at the very beginning of the lesson.
When finding by integrating the function v for it an infinite set of antiderivative functions is obtained. To apply the integration by parts formula, you can take any of them, and therefore the one that corresponds to an arbitrary constant WITH, equal to zero. Therefore, when finding the function v arbitrary constant WITH should not be entered.
The method of integration by parts has a very special application: it can be used to derive recurrent formulas for finding antiderivative functions when it is necessary to reduce the degree of functions under the integral sign. Reducing the degree is necessary when there are no tabular integrals for, for example, functions such as sines and cosines to powers greater than the second and their products. A recurrent formula is a formula for finding the next member of a sequence through the previous member. For the indicated cases, the goal is achieved by successively lowering the degree. So, if the integrand is a sine to the fourth power of x, then by integrating by parts you can find a formula for the integral of sine to the third power, and so on. The last paragraph of this lesson is devoted to the described task.
Applying integration by parts together
Example 1. Find the indefinite integral using the method of integration by parts:
Solution. In the integrand expression - the logarithm, which, as we already know, can be reasonably denoted by u. We believe that , .
We find (as already mentioned in the explanation for the theoretical reference, we immediately obtain a logarithmic function in the first term (without an integral), and a function that does not contain a logarithm in the second term (under the integral sign):

And again the logarithm...
Example 2. Find the indefinite integral:
Solution. Let , .
The logarithm is present in the square. This means that it needs to be differentiated as a complex function. We find
,
.
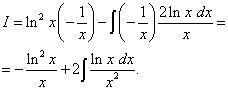
We again find the second integral by parts and obtain the already mentioned advantage (in the first term (without the integral) there is a logarithmic function, and in the second term (under the integral sign) there is a function that does not contain a logarithm).
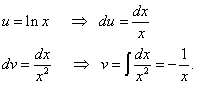

We find the original integral:

Example 3.
Solution. The arctangent, like the logarithm, is better denoted by u. So let , .
Then ,
.
Applying the integration by parts formula, we obtain:
![]()
We find the second integral by changing a variable.

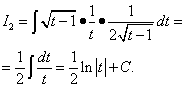
Returning to the variable x, we get
![]() .
.
We find the original integral:
![]() .
.
Example 4. Find the indefinite integral using the method of integration by parts:
Solution. It is better to denote the exhibitor by dv. We split the integrand into two factors. Believing that
Example 5. Find the indefinite integral using the method of integration by parts:
![]() .
.
Solution. Let , . Then , .
Using the integration by parts formula (1), we find:

Example 6. Find the indefinite integral by integration by parts:
Solution. The sine, like the exponential, can be conveniently denoted by dv. Let , .
Using the integration by parts formula, we find:
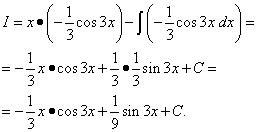
We apply integration by parts together again
Example 10. Find the indefinite integral by integration by parts:
![]() .
.
Solution. As in all similar cases, it is convenient to denote the cosine by dv. We denote , .
Then ![]() ,
.
,
.
Using the integration by parts formula, we obtain:
We also apply integration by parts to the second term. We denote , .
Using these notations, we integrate the mentioned term:

Now we find the required integral:

Among the integrals that can be solved by the method of integration by parts, there are also those that are not included in any of the three groups mentioned in the theoretical part, for which it is known from practice that it is better to denote by u, and what through dv. Therefore, in these cases, you need to use the consideration of convenience, also given in the paragraph “The essence of the method of integration by parts”: for u one should take a part of the integrand that does not become much more complicated during differentiation, but dv- such a part of the integrand that can be easily integrated. The last example of this lesson is the solution of just such an integral.
The integration by parts formula looks like:
.
The method of integration by parts consists of applying this formula. In practical application, it is worth noting that u and v are functions of the integration variable. Let the integration variable be designated as x (the symbol after the differential sign d at the end of the integral notation). Then u and v are functions of x: u(x) and v(x) .
Then
, .
And the formula for integration by parts takes the form:
.
That is, the integrand function must consist of the product of two functions:
,
one of which we denote as u: g(x) = u, and for the other the integral must be calculated (more precisely, the antiderivative must be found):
, then dv = f(x) dx .
In some cases f(x) = 1
.
,
That is, in the integral
we can put g(x) = u, x = v .
Summary
;
.
So, in this method, the integration by parts formula should be remembered and applied in two forms:
Integrals calculated by integration by parts
Integrals containing logarithms and inverse trigonometric (hyperbolic) functions
Integrals containing logarithms and inverse trigonometric or hyperbolic functions are often integrated by parts. In this case, the part that contains the logarithm or inverse trigonometric (hyperbolic) functions is denoted by u, the remaining part by dv.
, , , , , , .
Here are examples of such integrals, which are calculated by the method of integration by parts:
Integrals containing the product of a polynomial and sin x, cos x or e x
, , ,
where P(x) is a polynomial in x. When integrating, the polynomial P(x) is denoted by u, and e ax dx, cos ax dx or sin ax dx
- via dv.
, , .
Here are examples of such integrals:
Examples of calculating integrals using the method of integration by parts
Examples of integrals containing logarithms and inverse trigonometric functions
Example
Calculate the integral:
Detailed solution
Here the integrand contains a logarithm. Making substitutions u =,
ln x dv = x.
Then
,
.
2 dx
.
Then
.
We calculate the remaining integral:
At the end of the calculations, it is necessary to add the constant C, since the indefinite integral is the set of all antiderivatives. It could also be added in intermediate calculations, but this would only clutter up the calculations.
Shorter solution
.You can present the solution in a shorter version. To do this, you do not need to make substitutions with u and v, but you can group the factors and apply the integration by parts formula in the second form.
Answer
Examples of integrals containing logarithms and inverse trigonometric functions
Example
.
Examples of integrals containing the product of a polynomial and sin x, cos x or ex
Solution
Let us introduce the exponent under the differential sign:.
e - x dx = - e - x d(-x) = - d(e - x)
.
Let's integrate by parts.
.
.
.
We also use the method of integration by parts.
Finally we have. Integration by parts
- a method used to solve definite and indefinite integrals, when one of the integrands is easily integrable and the other is differentiable. A fairly common method for finding integrals, both indefinite and definite. The main sign when you need to use it is a certain function consisting of the product of two functions that cannot be integrated point-blank.
Formula
In order to successfully use this method, you need to understand and learn the formulas.
Formula for integration by parts in the indefinite integral:
$$ \int udv = uv - \int vdu $$
Formula for integration by parts in a definite integral:
$$ \int \limits_(a)^(b) udv = uv \bigg |_(a)^(b) - \int \limits_(a)^(b) vdu $$
Examples of solutions
| Let us consider in practice examples of solutions to integration by parts, which are often proposed by teachers during tests. Please note that under the integral symbol there is a product of two functions. This is a sign that this method is suitable for the solution. |
| Example 1 |
| Find the integral $ \int xe^xdx $ |
|
We see that the integrand consists of two functions, one of which, upon differentiation, instantly turns into unity, and the other is easily integrated. To solve the integral, we use the method of integration by parts. Let's assume $ u = x \rightarrow du=dx $ and $ dv = e^x dx \rightarrow v=e^x $ We substitute the found values into the first integration formula and get: $$ \int xe^x dx = xe^x - \int e^x dx = xe^x - e^x + C $$ If you cannot solve your problem, then send it to us. We will provide detailed solution. You will be able to view the progress of the calculation and gain information. This will help you get your grade from your teacher in a timely manner! |
| Answer |
|
$$ \int xe^x dx = xe^x - e^x + C $$ |
| Example 4 |
| Calculate the integral $ \int \limits_0 ^1 (x+5) 3^x dx $ |
| Find the integral $ \int xe^xdx $ |
|
By analogy with the previous solved examples, we will figure out which function to integrate without problems, which to differentiate. Please note that if we differentiate $ (x+5) $, then this expression will be automatically converted to unity, which will be to our advantage. So we do this: $$ u=x+5 \rightarrow du=dx, dv=3^x dx \rightarrow v=\frac(3^x)(ln3) $$ Now all unknown functions have been found and can be put into the second formula for integration by parts for a definite integral. $$ \int \limits_0 ^1 (x+5) 3^x dx = (x+5) \frac(3^x)(\ln 3) \bigg |_0 ^1 - \int \limits_0 ^1 \frac (3^x dx)(\ln 3) = $$ $$ = \frac(18)(\ln 3) - \frac(5)(\ln 3) - \frac(3^x)(\ln^2 3)\bigg| _0 ^1 = \frac(13)(\ln 3) - \frac(3)(\ln^2 3)+\frac(1)(\ln^2 3) = \frac(13)(\ln 3 )-\frac(4)(\ln^2 3) $$ |
| Answer |
| $$ \int\limits_0 ^1 (x+5)3^x dx = \frac(13)(\ln 3)-\frac(4)(\ln^2 3) $$ |








