Instructions
According to the property of an isosceles trapezoid, the segment n is equal to half the difference between the bases x and y. Therefore, the smaller base of the trapezoid y can be represented as the difference between the larger base and the segment n multiplied by two: y = x - 2*n.
Find the unknown smaller segment n. To do this, calculate one of the sides of the resulting right triangle. A triangle is formed by a height - h (leg), a side - a (hypotenuse) and a segment - n (leg). According to the Pythagorean theorem, the unknown leg n² = a² - h². Substitute numeric values and calculate the square of leg n. Take the square root of the resulting value - this will be the length of the segment n.
Substitute this value into the first equation to calculate y. The area of the trapezoid is calculated using the formula S = ((x + y)*h)/2. Express the unknown variable: y = 2*S/h – x.
Sources:
- height of an isosceles trapezoid
To define a quadrilateral such as a trapezoid, at least three of its sides must be defined. Therefore, for example, we can consider a problem in which the lengths of the diagonals are given trapezoids, as well as one of the side vectors.

Instructions
The figure from the problem conditions is presented in 1.B in this case it should be assumed that the one under consideration is ABCD, in which the lengths of the diagonals AC and BD are given, as well as side AB, represented by the vector a(ax,ay). The accepted initial data allows us to find both grounds trapezoids(both top and bottom). IN specific example the lower base AD will be found first.
Consider triangle ABD. The length of its side AB is equal to the absolute value of the vector a. Let |a|=sqrt((ax)^2+(ay)^2)=a, then cosф =ax/sqrt(((ax)^2+(ay)^2), as the direction cosine of a. Let the given diagonal BD has length p, and the desired AD length X. Then, according to the cosine theorem, P^2=a^2+ x^2-2axcosф. Or x^2-2axcosф+(a^2-p^2)=0.
To find the top grounds BC (its length is also denoted by x when searching), the module |a|=a is used, as well as the second diagonal BD=q and the cosine of the angle ABC, which is obviously equal to (n-ph).
Next we consider triangle ABC, to which, as before, the cosine theorem, and the following arises. Considering that cos(п-ф)=-cosф, based on the solution for AD, we can use the following formula, replacing p with q:ВС=- a*ax|sqrt(((ax)^2+(ay)^2) +sqrt((((a)^2)(ax^2))/(ax^2+ay^2))-a^2+q^2).
This is a square and, accordingly, has two roots. Thus, in this case it remains to choose only those roots that have positive value, since the length cannot be negative.
Example Let in trapezoids ABCD side side AB is specified by the vector a(1, sqrt3), p=4, q=6. Find grounds trapezoids.Solution. Using the algorithms obtained above, we can write: |a|=a=2, cosф=1/2. AD=1/2+sqrt(4/4 -4+16)=1/2 +sqrt(13)=(sqrt(13)+1)/2.BC=-1/2+sqrt(-3+36 )=(sqrt(33)-1)/2.
Video on the topic
A trapezoid is a quadrilateral in which two sides are parallel and the other two are not. The height of a trapezoid is a segment drawn perpendicularly between two parallel lines. Depending on the source data, it can be calculated in different ways.

You will need
- Knowledge of the sides, grounds, midline trapezoid, as well as, optionally, its area and/or perimeter.
Instructions
Let's say there is a trapezoid with the same data as in Figure 1. Let's draw 2 heights, we get , which has 2 smaller sides by the legs of right-angled triangles. Let us denote the smaller roll as x. It is located by dividing the difference in length between the larger and smaller bases. Then, by the Pythagorean theorem, the square of the height equal to the sum squares of the hypotenuse d and leg x. We extract from this sum and get the height h. (Fig. 2)

Video on the topic
Sources:
- how to calculate the height of a trapezoid
Mathematical figure with four corners is called a trapezoid if a pair of its opposite sides are parallel and the other pair is not. Parallel sides are called reasons trapezoids, the other two are lateral. In a rectangular trapezoids one of the angles at the side is straight.

Instructions
Task 1. Find the bases BC and AD trapezoids, if the length AC = f is known; side length CD = c and angle ADC = α. Solution: Consider a rectangular CED. The hypotenuse c and the angle between the hypotenuse and the leg EDC are known. Find the lengths CE and ED: using the angle formula CE = CD*sin(ADC); ED = CD*cos(ADC). So: CE = c*sinα; ED=c*cosα.
Consider the right triangle ACE. You know the hypotenuse AC and CE, find side AE using the rule: the sum of the squares of the legs is equal to the square of the hypotenuse. So: AE(2) = AC(2) - CE(2) = f(2) - c*sinα. Calculate square root from the right side of the equality. You found the top rectangular trapezoids.
The length of the base AD is the sum of the lengths of two segments AE and ED. AE = square root(f(2) - c*sinα); ED = c*cosα).So: AD = square root(f(2) - c*sinα) + c*cosα.You have found the lower base of the rectangular trapezoids.
Task 2. Find the bases BC and AD of the rectangular trapezoids, if the length of the diagonal is known BD = f; side length CD = c and angle ADC = α. Solution: Consider the right triangle CED. Find the lengths of the sides CE and ED: CE = CD*sin(ADC) = c*sinα; ED = CD*cos(ADC) = c*cosα.
Consider rectangle ABCE. By the property AB = CE = c*sinα. Consider the right triangle ABD. According to the property of a right triangle, the square of the hypotenuse is the sum of the squares of the legs. Therefore AD(2) = BD(2) - AB(2) = f(2) - c*sinα. You have found the lower base of the rectangular trapezoids AD = square root(f(2) - c*sinα).
According to the rectangle rule, BC = AE = AD - ED = square root(f(2) - c*sinα) - c*cosα.You have found the upper base of the rectangular trapezoids.
The smaller base of a trapezoid is one of its parallel sides, which has a minimum length. This value can be calculated in several ways using certain data.

You will need
- - calculator.
Instructions
If two lengths are known - the base and the midline - use the trapezoid property to calculate the smallest base. According to it, the midline of a trapezoid is identical to half the sum of the bases. In this case, the smallest base will be equal to the difference between twice the length of the middle line and the length of the large base of this figure.
If such parameters of the trapezoid as , height, length of the large base are known, then calculate the smallest base of this base based on the trapezoid. In this case end result obtained by subtracting from the difference between the quotient of twice the area and the height a parameter such as the length of the large base of the trapezoid.
Calculate the length of the side side on the other
In the materials of various tests and exams, they are very often found trapezoid problems, the solution of which requires knowledge of its properties.
Let's find out what interesting and useful properties a trapezoid has for solving problems.
After studying the properties of the midline of a trapezoid, one can formulate and prove property of a segment connecting the midpoints of the diagonals of a trapezoid. The segment connecting the midpoints of the diagonals of a trapezoid is equal to half the difference of the bases.
MO – middle line triangle ABC and equal to 1/2ВС (Fig. 1).
MQ is the middle line of triangle ABD and is equal to 1/2AD.
Then OQ = MQ – MO, therefore OQ = 1/2AD – 1/2BC = 1/2(AD – BC).
When solving many problems on a trapezoid, one of the main techniques is to draw two heights in it.
Consider the following task.
Let BT be the height of an isosceles trapezoid ABCD with bases BC and AD, with BC = a, AD = b. Find the lengths of the segments AT and TD.
Solution.
Solving the problem is not difficult (Fig. 2), but it allows you to get property of the height of an isosceles trapezoid drawn from the vertex obtuse angle : the height of an isosceles trapezoid drawn from the vertex of an obtuse angle divides larger base into two segments, the smaller of which is equal to half the difference of the bases, and the larger one is equal to half the sum of the bases.
When studying the properties of a trapezoid, you need to pay attention to such a property as similarity. So, for example, the diagonals of a trapezoid divide it into four triangles, and the triangles adjacent to the bases are similar, and the triangles adjacent to the sides are equal in size. This statement can be called property of triangles into which a trapezoid is divided by its diagonals. Moreover, the first part of the statement can be proven very easily through the sign of similarity of triangles at two angles. Let's prove second part of the statement.
Triangles BOC and COD have a common height (Fig. 3), if we take the segments BO and OD as their bases. Then S BOC /S COD = BO/OD = k. Therefore, S COD = 1/k · S BOC .
Similarly, triangles BOC and AOB have a common height if we take the segments CO and OA as their bases. Then S BOC /S AOB = CO/OA = k and S A O B = 1/k · S BOC .
From these two sentences it follows that S COD = S A O B.
Let's not dwell on the formulated statement, but find the relationship between the areas of the triangles into which the trapezoid is divided by its diagonals. To do this, let's solve the following problem.
Let point O be the intersection point of the diagonals of the trapezoid ABCD with the bases BC and AD. It is known that the areas of triangles BOC and AOD are equal to S 1 and S 2, respectively. Find the area of the trapezoid.
Since S COD = S A O B, then S ABC D = S 1 + S 2 + 2S COD.
From the similarity of triangles BOC and AOD it follows that BO/OD = √(S₁/S 2).
Therefore, S₁/S COD = BO/OD = √(S₁/S 2), which means S COD = √(S 1 · S 2).
Then S ABC D = S 1 + S 2 + 2√(S 1 · S 2) = (√S 1 + √S 2) 2.
Using similarity it is proved that property of a segment passing through the point of intersection of the diagonals of a trapezoid parallel to the bases.
Let's consider task:
Let point O be the intersection point of the diagonals of the trapezoid ABCD with the bases BC and AD. BC = a, AD = b. Find the length of the segment PK passing through the point of intersection of the diagonals of the trapezoid parallel to the bases. What segments is PK divided by point O (Fig. 4)?

From the similarity of triangles AOD and BOC it follows that AO/OC = AD/BC = b/a.
From the similarity of triangles AOP and ACB it follows that AO/AC = PO/BC = b/(a + b).
Hence PO = BC b / (a + b) = ab/(a + b).
Similarly, from the similarity of triangles DOK and DBC, it follows that OK = ab/(a + b).
Hence PO = OK and PK = 2ab/(a + b).
So, the proven property can be formulated as follows: the segment, parallel to the bases a trapezoid passing through the point of intersection of the diagonals and connecting two points on the sides is bisected by the point of intersection of the diagonals. Its length is the harmonic mean of the bases of the trapezoid.
Following four point property: in a trapezoid, the point of intersection of the diagonals, the point of intersection of the continuation of the sides, the midpoints of the bases of the trapezoid lie on the same line.
Triangles BSC and ASD are similar (Fig. 5) and in each of them the medians ST and SG divide the vertex angle S into equal parts. Therefore, points S, T and G lie on the same line.
In the same way, points T, O and G are located on the same line. This follows from the similarity of triangles BOC and AOD.
This means that all four points S, T, O and G lie on the same line.
You can also find the length of the segment dividing the trapezoid into two similar ones.
If trapezoids ALFD and LBCF are similar (Fig. 6), then a/LF = LF/b.
Hence LF = √(ab).
Thus, a segment dividing a trapezoid into two similar trapezoids has a length equal to the geometric mean of the lengths of the bases. 
Let's prove property of a segment dividing a trapezoid into two equal areas.
Let the area of the trapezoid be S (Fig. 7). h 1 and h 2 are parts of the height, and x is the length of the desired segment.
Then S/2 = h 1 (a + x)/2 = h 2 (b + x)/2 and
S = (h 1 + h 2) · (a + b)/2.
Let's create a system
(h 1 (a + x) = h 2 (b + x)
(h 1 · (a + x) = (h 1 + h 2) · (a + b)/2.
Deciding this system, we get x = √(1/2(a 2 + b 2)).
Thus, the length of the segment dividing the trapezoid into two equal ones is equal to √((a 2 + b 2)/2)(mean square of base lengths).
So, for the trapezoid ABCD with bases AD and BC (BC = a, AD = b) we proved that the segment:
1) MN, connecting the midpoints of the lateral sides of the trapezoid, is parallel to the bases and equal to their half-sum (average arithmetic numbers a and b);
2) PK passing through the point of intersection of the diagonals of the trapezoid parallel to the bases is equal to
2ab/(a + b) (harmonic mean of numbers a and b);
3) LF, which splits a trapezoid into two similar trapezoids, has a length equal to the average geometric numbers a and b, √(ab);
4) EH, dividing a trapezoid into two equal ones, has length √((a 2 + b 2)/2) (the root mean square of the numbers a and b).
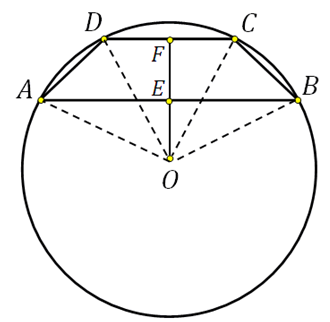
Sign and property of an inscribed and circumscribed trapezoid.
Property of an inscribed trapezoid: a trapezoid can be inscribed in a circle if and only if it is isosceles.
Properties of the described trapezoid. A trapezoid can be described around a circle if and only if the sum of the lengths of the bases is equal to the sum of the lengths of the sides.
Useful consequences of the fact that a circle is inscribed in a trapezoid:
1. The height of the circumscribed trapezoid is equal to two radii of the inscribed circle.
2. The side of the described trapezoid is visible from the center of the inscribed circle at a right angle.
The first is obvious. To prove the second corollary, it is necessary to establish that the angle COD is right, which is also not difficult. But knowing this corollary allows you to use a right triangle when solving problems.
Let's specify corollaries for an isosceles circumscribed trapezoid:
The height of an isosceles circumscribed trapezoid is the average geometric bases trapezoids
h = 2r = √(ab).
The considered properties will allow you to understand the trapezoid more deeply and ensure success in solving problems using its properties.
Still have questions? Don't know how to solve trapezoid problems?
To get help from a tutor -.
The first lesson is free!
blog.site, when copying material in full or in part, a link to the original source is required.
Circumscribed circle and trapezoid. Hello! There is one more publication for you, in which we will look at problems with trapezoids. The tasks are part of the mathematics exam. Here they are combined into a group; not just one trapezoid is given, but a combination of bodies - a trapezoid and a circle. Most of these problems are solved orally. But there are also some that need to be addressed. special attention, for example, task 27926.
What theory do you need to remember? This:
Problems with trapezoids that are available on the blog can be viewed Here.
27924. A circle is described around a trapezoid. The perimeter of the trapezoid is 22, the midline is 5. Find the side of the trapezoid.

Note that a circle can only be described around an isosceles trapezoid. We are given the middle line, which means we can determine the sum of the bases, that is:
This means the sum of the sides will be equal to 22–10=12 (perimeter minus the base). Since the sides of an isosceles trapezoid are equal, one side will be equal to six.
27925. The lateral side of an isosceles trapezoid is equal to its smaller base, the angle at the base is 60 0, the larger base is 12. Find the radius of the circumscribed circle of this trapezoid.

If you solved problems with a circle and a hexagon inscribed in it, then you will immediately voice the answer - the radius is 6. Why?
Look: an isosceles trapezoid with a base angle equal to 60 0 and equal sides AD, DC and CB, represents half of a regular hexagon:

In such a hexagon, the segment connecting opposite vertices passes through the center of the circle. *The center of the hexagon and the center of the circle coincide, more details
That is, the larger base of this trapezoid coincides with the diameter of the circumscribed circle. So the radius is six.
*Of course, we can consider the equality of triangles ADO, DOC and OCB. Prove that they are equilateral. Next, conclude that angle AOB is equal to 180 0 and point O is equidistant from vertices A, D, C and B, and therefore AO=OB=12/2=6.
27926. The bases of an isosceles trapezoid are 8 and 6. The radius of the circumscribed circle is 5. Find the height of the trapezoid.

Note that the center of the circumscribed circle lies on the axis of symmetry, and if we construct the height of the trapezoid passing through this center, then when it intersects with the bases it will divide them in half. Let's show this in the sketch and also connect the center to the vertices:

The segment EF is the height of the trapezoid, we need to find it.
In right triangle OFC we know the hypotenuse (this is the radius of the circle), FC=3 (since DF=FC). Using the Pythagorean theorem we can calculate OF:

In the right triangle OEB, we know the hypotenuse (this is the radius of the circle), EB=4 (since AE=EB). Using the Pythagorean theorem we can calculate OE:

Thus EF=FO+OE=4+3=7.
Now an important nuance!
In this problem, the figure clearly shows that the bases lie along different sides from the center of the circle, so the problem is solved this way.
What if the conditions did not include a sketch?
Then the problem would have two answers. Why? Look carefully - two trapezoids with given bases can be inscribed in any circle:
*That is, given the bases of the trapezoid and the radius of the circle, there are two trapezoids.
And the solution to the “second option” will be as follows.
Using the Pythagorean theorem we calculate OF:
Let's also calculate OE:

Thus EF=FO–OE=4–3=1.
Of course, in a problem with a short answer on the Unified State Examination there cannot be two answers, and a similar problem will not be given without a sketch. Therefore, pay special attention to the sketch! Namely: how the bases of the trapezoid are located. But in tasks with a detailed answer, this was present in past years (with a slightly more complicated condition). Those who considered only one option for the location of the trapezoid lost a point on this task.
27937. A trapezoid is circumscribed around a circle, the perimeter of which is 40. Find its midline.

Here we should immediately recall the property of a quadrilateral circumscribed about a circle:
Amounts opposite sides any quadrilateral circumscribed about a circle are equal.
In order to feel confident and successfully solve problems in geometry lessons, it is not enough to learn the formulas. They need to be understood first. To be afraid, and even more so to hate formulas, is unproductive. In this article accessible language will be analyzed various ways Finding the area of a trapezoid. To better understand the corresponding rules and theorems, we will pay some attention to its properties. This will help you understand how the rules work and in what cases certain formulas should be applied.
Defining a trapezoid
What kind of figure is this overall? A trapezoid is a polygon with four corners and two parallel sides. The other two sides of the trapezoid can be inclined at different angles. Her parallel sides are called bases, and for non-parallel sides the name “sides” or “hips” is used. Such figures are quite common in everyday life. The contours of the trapezoid can be seen in the silhouettes of clothing, interior items, furniture, dishes and many others. Trapeze happens different types: scalene, equilateral and rectangular. We will examine their types and properties in more detail later in the article.
Properties of a trapezoid

Let us dwell briefly on the properties of this figure. The sum of the angles adjacent to any side is always 180°. It should be noted that all angles of a trapezoid add up to 360°. The trapezoid has the concept of a midline. If you connect the midpoints of the sides with a segment, this will be the middle line. It is designated m. The middle line has important properties: it is always parallel to the bases (we remember that the bases are also parallel to each other) and equal to their half-sum:
This definition must be learned and understood, because it is the key to solving many problems!
With a trapezoid, you can always lower the height to the base. An altitude is a perpendicular, often denoted by the symbol h, that is drawn from any point of one base to another base or its extension. The midline and height will help you find the area of the trapezoid. Similar tasks are the most common in school course geometry and regularly appear among test and examination papers.
The simplest formulas for the area of a trapezoid

Let's look at the two most popular and simple formulas, with the help of which the area of a trapezoid is found. It is enough to multiply the height by half the sum of the bases to easily find what you are looking for:
S = h*(a + b)/2.
In this formula, a, b denote the bases of the trapezoid, h - the height. For ease of perception, in this article, multiplication signs are marked with a symbol (*) in formulas, although in official reference books the multiplication sign is usually omitted.
Let's look at an example.
Given: a trapezoid with two bases equal to 10 and 14 cm, the height is 7 cm. What is the area of the trapezoid?
Let's look at the solution to this problem. Using this formula, you first need to find the half-sum of the bases: (10+14)/2 = 12. So, the half-sum is equal to 12 cm. Now we multiply the half-sum by the height: 12*7 = 84. What we are looking for is found. Answer: The area of the trapezoid is 84 square meters. cm.
Second famous formula states: the area of a trapezoid is equal to the product of the midline and the height of the trapezoid. That is, it actually follows from the previous concept of the middle line: S=m*h.

Using diagonals for calculations
Another way to find the area of a trapezoid is actually not that complicated. It is connected to its diagonals. Using this formula, to find the area, you need to multiply the half-product of its diagonals (d 1 d 2) by the sine of the angle between them:
S = ½ d 1 d 2 sin a.
Let's consider a problem that shows the application of this method. Given: a trapezoid with the length of the diagonals equal to 8 and 13 cm, respectively. The angle a between the diagonals is 30°. Find the area of the trapezoid.
Solution. Using the above formula, it is easy to calculate what is required. As you know, sin 30° is 0.5. Therefore, S = 8*13*0.5=52. Answer: the area is 52 square meters. cm.
Finding the area of an isosceles trapezoid
A trapezoid can be isosceles. Its sides are the same and the angles at the bases are equal, which is well illustrated by the figure. Isosceles trapezoid has the same properties as the regular one, plus a number of special ones. A circle can be circumscribed around an isosceles trapezoid, and a circle can be inscribed within it.

What methods are there for calculating the area of such a figure? The method below will require a lot of calculations. To use it, you need to know the values of the sine (sin) and cosine (cos) of the angle at the base of the trapezoid. Their calculations require either Bradis tables or engineering calculator. Here is the formula:
S= c*sin a*(a - c*cos a),
Where With- lateral thigh, a- angle at the lower base.
An equilateral trapezoid has diagonals of equal length. The converse is also true: if a trapezoid has equal diagonals, then it is isosceles. From here following formula, which helps to find the area of a trapezoid - the half product of the square of the diagonals and the sine of the angle between them: S = ½ d 2 sin a.
Finding the area of a rectangular trapezoid

Known special case rectangular trapezoid. This is a trapezoid, in which one side (its thigh) adjoins the bases at a right angle. It has the properties of a regular trapezoid. In addition, she has very interesting feature. The difference in the squares of the diagonals of such a trapezoid is equal to the difference in the squares of its bases. All previously described methods for calculating area are used for it.
We use ingenuity
There is one trick that can help if you forget specific formulas. Let's take a closer look at what a trapezoid is. If we mentally divide it into parts, we will get familiar and understandable geometric shapes: a square or rectangle and a triangle (one or two). If the height and sides of the trapezoid are known, you can use the formulas for the area of a triangle and a rectangle, and then add up all the resulting values.
Let's illustrate this following example. Dana rectangular trapezoid. Angle C = 45°, angles A, D are 90°. The upper base of the trapezoid is 20 cm, the height is 16 cm. You need to calculate the area of the figure.
This figure obviously consists of a rectangle (if two angles are equal to 90°) and a triangle. Since the trapezoid is rectangular, therefore, its height is equal to its side, that is, 16 cm. We have a rectangle with sides of 20 and 16 cm, respectively. Now consider a triangle whose angle is 45°. We know that one side of it is 16 cm. Since this side is also the height of the trapezoid (and we know that the height descends to the base at a right angle), therefore, the second angle of the triangle is 90°. Hence the remaining angle of the triangle is 45°. As a consequence of this we get a rectangular isosceles triangle, whose two sides are the same. This means that the other side of the triangle is equal to the height, that is, 16 cm. It remains to calculate the area of the triangle and the rectangle and add the resulting values.
The area of a right triangle is equal to half the product of its legs: S = (16*16)/2 = 128. The area of a rectangle is equal to the product of its width and length: S = 20*16 = 320. We found the required: area of the trapezoid S = 128 + 320 = 448 sq. see. You can easily double-check yourself using the above formulas, the answer will be identical.
We use the Pick formula

Finally, we present another original formula that helps to find the area of a trapezoid. It is called the Pick formula. It is convenient to use when the trapezoid is drawn on checkered paper. Similar problems are often found in GIA materials. It looks like this:
S = M/2 + N - 1,
in this formula M is the number of nodes, i.e. intersections of the lines of the figure with the lines of the cell at the boundaries of the trapezoid (orange dots in the figure), N is the number of nodes inside the figure (blue dots). It is most convenient to use it when finding the area irregular polygon. However, the larger the arsenal of techniques used, the fewer errors and better the results.
Of course, the information provided does not exhaust the types and properties of a trapezoid, as well as methods for finding its area. This article provides an overview of its most important characteristics. When solving geometric problems, it is important to act gradually, start with easy formulas and problems, consistently consolidate your understanding, and move to another level of complexity.
Collected together the most common formulas will help students navigate the various ways to calculate the area of a trapezoid and better prepare for tests and tests on this topic.










