Let some continuous function f be given on a certain segment of the Ox axis. Let us assume that this function does not change its sign throughout the entire segment.
If f is a continuous and non-negative function on a certain segment, and F is its antiderivative on this segment, then the area of the curvilinear trapezoid S is equal to the increment of the antiderivative on this segment.
This theorem can be written as follows:
S = F(b) - F(a)
The integral of the function f(x) from a to b will be equal to S. Here and further, to denote the definite integral of some function f(x), with the limits of integration from a to b, we will use the following notation (a;b)∫f( x). Below is an example of how it will look.
Newton-Leibniz formula
This means that we can equate these two results. We obtain: (a;b)∫f(x)dx = F(b) - F(a), provided that F is an antiderivative for the function f on . This formula is called Newton - Leibniz formulas. It will be true for any continuous function f on an interval.
The Newton-Leibniz formula is used to calculate integrals. Let's look at a few examples:
Example 1: calculate the integral. Find the antiderivative for the integrand function x 2 . One of the antiderivatives will be the function (x 3)/3.
Now we use the Newton-Leibniz formula:
(-1;2)∫x 2 dx = (2 3)/3 - ((-1) 3)/3 = 3
Answer: (-1;2)∫x 2 dx = 3.
Example 2: calculate the integral (0;pi)∫sin(x)dx.
Find the antiderivative for the integrand function sin(x). One of the antiderivatives will be the -cos(x) function. Let's use the Newton-Leibniz formula:
(0;pi)∫cos(x)dx = -cos(pi) + cos(0) = 2.
Answer: (0;pi)∫sin(x)dx=2
Sometimes, for simplicity and convenience of recording, the increment of the function F on the segment (F(b)-F(a)) is written as follows:
![]()
Using this notation for the increment, the Newton-Leibniz formula can be rewritten as follows:
![]()
As noted above, this is just an abbreviation for ease of recording; this recording does not affect anything else. This notation and the formula (a;b)∫f(x)dx = F(b) - F(a) will be equivalent.
By a definite integral from a continuous function f(x) on the final segment [ a, b] (where ) is the increment of some of its antiderivatives on this segment. (In general, understanding will be noticeably easier if you repeat the topic of the indefinite integral) In this case, the notation is used
As can be seen in the graphs below (the increment of the antiderivative function is indicated by ), a definite integral can be either a positive or a negative number(It is calculated as the difference between the value of the antiderivative in the upper limit and its value in the lower limit, i.e. as F(b) - F(a)).

Numbers a And b are called the lower and upper limits of integration, respectively, and the segment [ a, b] – segment of integration.
Thus, if F(x) – some antiderivative function for f(x), then, according to the definition,
![]() (38)
(38)
Equality (38) is called Newton-Leibniz formula . Difference F(b) – F(a) is briefly written as follows:
Therefore, we will write the Newton-Leibniz formula like this:
![]() (39)
(39)
Let us prove that the definite integral does not depend on which antiderivative of the integrand is taken when calculating it. Let F(x) and F( X) are arbitrary antiderivatives of the integrand. Since these are antiderivatives of the same function, they differ by a constant term: Ф( X) = F(x) + C. That's why

This establishes that on the segment [ a, b] increments of all antiderivatives of the function f(x) match up.
Thus, to calculate a definite integral, it is necessary to find any antiderivative of the integrand, i.e. First you need to find the indefinite integral. Constant WITH excluded from subsequent calculations. Then the Newton-Leibniz formula is applied: the value of the upper limit is substituted into the antiderivative function b , further - the value of the lower limit a and the difference is calculated F(b) - F(a) . The resulting number will be a definite integral..
At a = b by definition accepted
Example 1.
Solution. First, let's find the indefinite integral:
Applying the Newton-Leibniz formula to the antiderivative
(at WITH= 0), we get
![]()
However, when calculating a definite integral, it is better not to find the antiderivative separately, but to immediately write the integral in the form (39).
Example 2. Calculate definite integral
Solution. Using formula
![]()
![]()
Properties of the definite integral
Theorem 2.The value of the definite integral does not depend on the designation of the integration variable, i.e.
![]() (40)
(40)
Let F(x) – antiderivative for f(x). For f(t) the antiderivative is the same function F(t), in which the independent variable is only designated differently. Hence,
![]()
Based on formula (39), the last equality means the equality of the integrals
Theorem 3.The constant factor can be taken out of the sign of the definite integral, i.e.
![]() (41)
(41)
Theorem 4.The definite integral of an algebraic sum of a finite number of functions is equal to the algebraic sum of definite integrals of these functions, i.e.
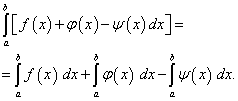 (42)
(42)
Theorem 5.If a segment of integration is divided into parts, then the definite integral over the entire segment is equal to the sum of definite integrals over its parts, i.e. If
![]() (43)
(43)
Theorem 6.When rearranging the limits of integration, the absolute value of the definite integral does not change, but only its sign changes, i.e.
![]() (44)
(44)
Theorem 7(mean value theorem). A definite integral is equal to the product of the length of the integration segment and the value of the integrand at some point inside it, i.e.
![]() (45)
(45)
Theorem 8.If the upper limit of integration is greater than the lower one and the integrand is non-negative (positive), then the definite integral is also non-negative (positive), i.e. If

Theorem 9.If the upper limit of integration is greater than the lower one and the functions and are continuous, then the inequality
can be integrated term by term, i.e.
![]() (46)
(46)
The properties of the definite integral make it possible to simplify the direct calculation of integrals.
Example 5. Calculate definite integral
![]()
Using Theorems 4 and 3, and when finding antiderivatives - table integrals (7) and (6), we obtain

Definite integral with variable upper limit
Let f(x) – continuous on the segment [ a, b] function, and F(x) is its antiderivative. Consider the definite integral
![]() (47)
(47)
and through t the integration variable is designated so as not to confuse it with the upper bound. When it changes X the definite integral (47) also changes, i.e. it is a function of the upper limit of integration X, which we denote by F(X), i.e.
![]() (48)
(48)
Let us prove that the function F(X) is an antiderivative for f(x) = f(t). Indeed, differentiating F(X), we get

because F(x) – antiderivative for f(x), A F(a) is a constant value.
Function F(X) – one of the infinite number of antiderivatives for f(x), namely the one that x = a goes to zero. This statement is obtained if in equality (48) we put x = a and use Theorem 1 of the previous paragraph.
Calculation of definite integrals by the method of integration by parts and the method of change of variable
![]()
where, by definition, F(x) – antiderivative for f(x). If we change the variable in the integrand
then, in accordance with formula (16), we can write
In this expression
antiderivative function for
In fact, its derivative, according to rule of differentiation of complex functions, is equal

Let α and β be the values of the variable t, for which the function
takes values accordingly a And b, i.e.

But, according to the Newton-Leibniz formula, the difference F(b) – F(a) There is
Newton - Leibniz formula
Main theorem of analysis or Newton - Leibniz formula gives a relationship between two operations: taking a definite integral and calculating the antiderivative
Formulation
Consider the integral of the function y = f(x) within a constant number a up to the number x, which we will consider variable. Let's write the integral in the following form:
This type of integral is called an integral with a variable upper limit. Using the mean value theorem in a definite integral, it is easy to show that this function is continuous and differentiable. And also the derivative of a given function at point x is equal to the integrable function itself. From this it follows that any continuous function has an antiderivative in the form of a quadrature: . And since the class of antiderivative functions of the function f differs by a constant, it is easy to show that: the definite integral of the function f is equal to the difference in the values of the antiderivatives at points b and a
Wikimedia Foundation.
- 2010.
- Total Probability Formula
Rayleigh-Jeans formula
See what the “Newton-Leibniz formula” is in other dictionaries: Newton-Leibniz formula
- The main theorem of analysis or Newton’s Leibniz formula gives the relationship between two operations: taking a definite integral and calculating the antiderivative Formulation Let’s consider the integral of the function y = f(x) in the range from a constant number a to... ... Wikipedia Finite Increment Formula
- This term has other meanings, see Lagrange’s Theorem. The finite increment formula or Lagrange's mean value theorem states that if a function is continuous on an interval and... Wikipedia Stokes formula
- Stokes' theorem is one of the main theorems of differential geometry and mathematical analysis on the integration of differential forms, which generalizes several theorems of analysis. Named after J. G. Stokes. Contents 1 General formulation 2… … Wikipedia NEWTON - LEIBNITZ FORMULA - a formula expressing the value of a definite integral of a given function f over a segment in the form of the difference between the values at the ends of the segment of any antiderivative F of this function. Named after I. Newton and G. Leibniz, because the rule … …
Mathematical Encyclopedia NEWTON-LEIBNITZ FORMULA - the basic formula of integral calculus. Expresses the connection between a definite integral of a function f(x) and any of its antiderivatives F(x) ...
Big Encyclopedic Dictionary- This term has other meanings, see List of objects named after Leibniz. This term has other meanings, see Leibniz Formula (meanings). The Leibniz formula in integral calculus is the rule... ... Wikipedia
Newton-Leibniz formula- Newton Leibniz formula, the basic formula of integral calculus. Expresses the connection between the definite integral of the function f(x) and any of its antiderivatives F(x). . * * * NEWTON LEIBNITZ FORMULA NEWTON LEIBNITZ FORMULA, basic formula... ... encyclopedic Dictionary
Rectangle formula
Trapezoid formula- Definite integral as the area of a figure Numerical integration (historical name: quadrature) calculation of the value of a definite integral (usually approximate), based on the fact that the value of the integral is numerically equal to the area... ... Wikipedia
Newton's theorem- Newton's Leibniz formula or the fundamental theorem of analysis gives the relationship between two operations: taking a definite integral and calculating the antiderivative. If it is continuous on a segment and any antiderivative of it on this segment has ... Wikipedia
Problem 1(about calculating the area of a curved trapezoid).
In the Cartesian rectangular coordinate system xOy, a figure is given (see figure) bounded by the x axis, straight lines x = a, x = b (a by a curvilinear trapezoid. It is required to calculate the area of a curvilinear trapezoid.
Solution. Geometry gives us recipes for calculating the areas of polygons and some parts of a circle (sector, segment). Using geometric considerations, we can only find an approximate value of the required area, reasoning as follows.
Let's split the segment [a; b] (base of a curved trapezoid) into n equal parts; this partition is carried out using points x 1, x 2, ... x k, ... x n-1. Let us draw straight lines through these points parallel to the y-axis. Then the given curvilinear trapezoid will be divided into n parts, into n narrow columns. The area of the entire trapezoid is equal to the sum of the areas of the columns.
Let us consider the k-th column separately, i.e. a curved trapezoid whose base is a segment. Let's replace it with a rectangle with the same base and height equal to f(x k) (see figure). The area of the rectangle is equal to \(f(x_k) \cdot \Delta x_k \), where \(\Delta x_k \) is the length of the segment; It is natural to consider the resulting product as an approximate value of the area of the kth column. 
If we now do the same with all the other columns, we will come to the following result: the area S of a given curvilinear trapezoid is approximately equal to the area S n of a stepped figure made up of n rectangles (see figure):
\(S_n = f(x_0)\Delta x_0 + \dots + f(x_k)\Delta x_k + \dots + f(x_(n-1))\Delta x_(n-1) \)
Here, for the sake of uniformity of notation, we assume that a = x 0, b = x n; \(\Delta x_0 \) - length of the segment, \(\Delta x_1 \) - length of the segment, etc.; in this case, as we agreed above, \(\Delta x_0 = \dots = \Delta x_(n-1) \)
So, \(S \approx S_n \), and this approximate equality is more accurate, the larger n.
By definition, it is believed that the required area of a curvilinear trapezoid is equal to the limit of the sequence (S n):
$$ S = \lim_(n \to \infty) S_n $$
Problem 2(about moving a point)
A material point moves in a straight line. The dependence of speed on time is expressed by the formula v = v(t). Find the movement of a point over a period of time [a; b].
Solution. If the movement were uniform, then the problem would be solved very simply: s = vt, i.e. s = v(b-a). For uneven movement, you have to use the same ideas on which the solution to the previous problem was based.
1) Divide the time interval [a; b] into n equal parts.
2) Consider a period of time and assume that during this period of time the speed was constant, the same as at time t k. So we assume that v = v(t k).
3) Let’s find the approximate value of the point’s movement over a period of time; we’ll denote this approximate value as s k
\(s_k = v(t_k) \Delta t_k \)
4) Find the approximate value of displacement s:
\(s \approx S_n \) where
\(S_n = s_0 + \dots + s_(n-1) = v(t_0)\Delta t_0 + \dots + v(t_(n-1)) \Delta t_(n-1) \)
5) The required displacement is equal to the limit of the sequence (S n):
$$ s = \lim_(n \to \infty) S_n $$
Let's summarize. Solutions to various problems were reduced to the same mathematical model. Many problems from various fields of science and technology lead to the same model in the process of solution. This means that this mathematical model must be specially studied.
The concept of a definite integral
Let us give a mathematical description of the model that was built in the three considered problems for the function y = f(x), continuous (but not necessarily non-negative, as was assumed in the considered problems) on the interval [a; b]:
1) split the segment [a; b] into n equal parts;
2) make up the sum $$ S_n = f(x_0)\Delta x_0 + f(x_1)\Delta x_1 + \dots + f(x_(n-1))\Delta x_(n-1) $$
3) calculate $$ \lim_(n \to \infty) S_n $$
In the course of mathematical analysis it was proven that this limit exists in the case of a continuous (or piecewise continuous) function. He is called a certain integral of the function y = f(x) over the segment [a; b] and denoted as follows:
\(\int\limits_a^b f(x) dx \)
The numbers a and b are called the limits of integration (lower and upper, respectively).
Let's return to the tasks discussed above. The definition of area given in Problem 1 can now be rewritten as follows:
\(S = \int\limits_a^b f(x) dx \)
here S is the area of the curved trapezoid shown in the figure above. This is geometric meaning of a definite integral.
The definition of the displacement s of a point moving in a straight line with a speed v = v(t) over the period of time from t = a to t = b, given in Problem 2, can be rewritten as follows:
Newton - Leibniz formula
First, let's answer the question: what is the connection between the definite integral and the antiderivative?
The answer can be found in Problem 2. On the one hand, the displacement s of a point moving in a straight line with a speed v = v(t) over the period of time from t = a to t = b is calculated by the formula
\(S = \int\limits_a^b v(t) dt \)
On the other hand, the coordinate of a moving point is an antiderivative for speed - let's denote it s(t); this means that the displacement s is expressed by the formula s = s(b) - s(a). As a result we get:
\(S = \int\limits_a^b v(t) dt = s(b)-s(a) \)
where s(t) is the antiderivative of v(t).
The following theorem was proven in the course of mathematical analysis.
Theorem. If the function y = f(x) is continuous on the interval [a; b], then the formula is valid
\(S = \int\limits_a^b f(x) dx = F(b)-F(a) \)
where F(x) is the antiderivative of f(x).
The given formula is usually called Newton-Leibniz formula in honor of the English physicist Isaac Newton (1643-1727) and the German philosopher Gottfried Leibniz (1646-1716), who received it independently of each other and almost simultaneously.
In practice, instead of writing F(b) - F(a), they use the notation \(\left. F(x)\right|_a^b \) (it is sometimes called double substitution) and, accordingly, rewrite the Newton-Leibniz formula in this form:
\(S = \int\limits_a^b f(x) dx = \left. F(x)\right|_a^b \)
When calculating a definite integral, first find the antiderivative, and then carry out a double substitution.
Based on the Newton-Leibniz formula, we can obtain two properties of the definite integral.
Property 1. The integral of the sum of functions is equal to the sum of the integrals:
\(\int\limits_a^b (f(x) + g(x))dx = \int\limits_a^b f(x)dx + \int\limits_a^b g(x)dx \)
Property 2. The constant factor can be taken out of the integral sign:
\(\int\limits_a^b kf(x)dx = k \int\limits_a^b f(x)dx \)
Calculating the areas of plane figures using a definite integral

Using the integral, you can calculate the areas not only of curved trapezoids, but also of plane figures of a more complex type, for example, the one shown in the figure. The figure P is limited by straight lines x = a, x = b and graphs of continuous functions y = f(x), y = g(x), and on the segment [a; b] the inequality \(g(x) \leq f(x) \) holds. To calculate the area S of such a figure, we will proceed as follows:
\(S = S_(ABCD) = S_(aDCb) - S_(aABb) = \int\limits_a^b f(x) dx - \int\limits_a^b g(x) dx = \)
\(= \int\limits_a^b (f(x)-g(x))dx \)
So, the area S of a figure bounded by straight lines x = a, x = b and graphs of functions y = f(x), y = g(x), continuous on the segment and such that for any x from the segment [a; b] the inequality \(g(x) \leq f(x) \) is satisfied, calculated by the formula
\(S = \int\limits_a^b (f(x)-g(x))dx \)
Table of indefinite integrals (antiderivatives) of some functions
$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch ) x +C $$Preview:
To use presentation previews, create a Google account and log in to it: https://accounts.google.com
Slide captions:
Integral. Newton–Leibniz formula. Compiled by: Mathematics teacher of State Educational Institution of Educational Institution PU No. 27 Shchelyayur Semyashkina Irina Vasilievna
Objective of the lesson: Introduce the concept of an integral and its calculation using the Newton-Leibniz formula, using knowledge about the antiderivative and the rules for its calculation; Illustrate the practical application of the integral using examples of finding the area of a curved trapezoid; Reinforce what you have learned during the exercises.
Definition: Let a positive function f(x) be given, defined on a finite segment [ a;b ] . The integral of a function f(x) on [ a;b ] is the area of its curvilinear trapezoid. y=f(x) b a 0 x y
Designation: “integral from a to b eff from x de x”
Historical information: Leibniz derived the notation for the integral from the first letter of the word “Summa”. Newton did not propose an alternative symbolism for the integral in his works, although he tried various options. The term integral itself was coined by Jacob Bernoulli. S umma Isaac Newton Gottfried Wilhelm von Leibniz Jacob Bernoulli
Euler introduced the notation for the indefinite integral. Jean Baptiste Joseph Fourier Leonard Euler The design of the definite integral in the form we are familiar with was invented by Fourier.
Newton - Leibniz formula
Example 1. Calculate the definite integral: = Solution:
Example 2. Calculate definite integrals: 5 9 1
Example 3. S y x Calculate the area of the figure bounded by the lines and the x-axis. First, let's find the intersection points of the x-axis with the graph of the function. To do this, let's solve the equation. = Solution: S =
y x S A B D C Example 4. Calculate the area of the figure bounded by the lines and Find the intersection points (abscissa) of these lines by solving the equation S=S BADC - S BAC S BADC = = S BAC = S = 9 – 4.5 = 4.5 see example 1 Solution:
SINCWAIN RULES 1 line - the theme of the syncwine 1 word 2 line - 2 adjectives describing the signs and properties of the topic 3 line - 3 verbs describing the nature of the action 4 line - a short sentence of 4 words showing your personal attitude to the topic 5 line - 1 word, synonym or your association theme of the subject .
Integral 2. Definite, positive Count, add, multiply 4. Calculate using the Newton-Leibniz formula 5. Area
List of used literature: textbook by A.N. Kolmagorov. and others. Algebra and beginnings of analysis 10 - 11 grades.
Thank you for your attention! “TALENT is 99% of labor and 1% of ability” folk wisdom
Example 1. Calculate the definite integral: = Solution: example 4
Preview:
Subject: mathematics (algebra and beginnings of analysis), grade: 11th grade.
Lesson topic: "Integral. Newton-Leibniz formula."
Lesson type: Learning new material.
Lesson duration: 45 minutes.
Lesson objectives: introduce the concept of an integral and its calculation using the Newton-Leibniz formula, using knowledge about the antiderivative and the rules for its calculation; illustrate the practical application of the integral using examples of finding the area of a curved trapezoid; consolidate what you have learned during the exercises.
Lesson objectives:
Educational:
- form the concept of integral;
- developing skills in calculating a definite integral;
- developing skills in the practical application of the integral to find the area of a curvilinear trapezoid.
Educational:
- developing students’ cognitive interest, developing mathematical speech, the ability to observe, compare, and draw conclusions;
- develop interest in the subject using ICT.
Educational:
- to intensify interest in acquiring new knowledge, developing accuracy and accuracy when calculating the integral and making drawings.
Equipment: PC, Microsoft Windows 2000/XP operating system, MS Office 2007 program: Power Point, Microsoft Word; multimedia projector, screen.
Literature: textbook by Kolmagorov A.N. and others. Algebra and beginnings of analysis 10-11 grades.
Technologies: ICT, individual training.
DURING THE CLASSES
Lesson stage | Teacher activities | Student activities | Time |
|
Introductory part | ||||
Organizing time | Greets, checks students' readiness for the lesson, organizes attention. Distributes supporting notes. | Listen, write down the date. | 3 min |
|
Communicating the topic and objectives of the lesson | Updating basic knowledge and subjective experience with access to the goals of the lesson. | Listen and write down the topic of the lesson in your notebook.Actively involved in mental activity. Analyze, compare, draw conclusions to reach the goals of the lesson. | Presentation ICT 3 min |
|
Main part of the lesson Presentation of new material with an accompanying test of knowledge of past topics. | ||||
Definition of the integral (slide 3) | Gives a definition. ICT What is a curved trapezoid? | A figure bounded by the graph of a function, a segment and straight lines x=a and x=b. | 10 min |
|
Integral notation (slide 4) | Introduces the notation for the integral and how it is read. | Listen, write down. | ||
History of the integral (slides 5 and 6) | Tells the history of the term "integral". | Listen and write down briefly. | ||
Newton–Leibniz formula (slide 7) | Gives the Newton–Leibniz formula. What does F stand for in the formula? | Listen, take notes, answer the teacher’s questions. Antiderivative. | ||
The final part of the lesson. | ||||
Fixing the material. Solving examples using the material studied | ||||
Example 1 (slide 8) | Analyzes the solution to the example, asking questions about finding antiderivatives for the integrands. | Listen, write down, show knowledge of the table of antiderivatives. | 20 minutes |
|
Example 2 (slide 9). Examples for students to solve independently. | Supervises the solution of examples. | Complete the task one by one, commenting (individual learning technology), listen to each other, write down, show knowledge of past topics. | ||
Example 3 (slide 10) | Analyzes the solution to the example. How to find the intersection points of the x-axis with the graph of a function? | They listen, answer questions, show knowledge of past topics, and write down. Equate the integrand to 0 and solve the equation. | ||
Example 4 (slide 11) | Analyzes the solution to the example. How to find the intersection points (abscissas) of function graphs? Determine the type of triangle ABC. How to find the area of a right triangle? | They listen and answer questions. Equate the functions to each other and solve the resulting equation. Rectangular. where a and b are the legs of a right triangle. | ||
Summing up the lesson (slides 12 and 13) | Organizes work on compiling syncwine. | Participate in the preparation of syncwine. Analyze, compare, draw conclusions on the topic. | 5 minutes. |
|
Homework assignment according to difficulty level. | Gives homework and explains. | Listen, write down. | 1 min. |
|
Assessing students' work in class. | Evaluates the work of students in the lesson and analyzes it. | They are listening. | 1 min |
Preview:
Basic summary on the topic “Integral. Newton-Leibniz formula."
Definition: Let a positive function be given f(x) , defined on a finite segment.Integral of the function f(x) onis called the area of its curvilinear trapezoid. | ||
Designation: Reads: “integral from a to b ef from x de x” | ||
Newton - Leibniz formula | ||
Example 1. Calculate the definite integral: Solution: | ||
Example 3. and x-axis. Solution: | ||
Example 3. Calculate the area of a figure bounded by lines And . |








