Ball (sphere)
Spherical surface. Ball (sphere). Ball sections: circles.
Archimedes' theorem. Parts of the ball: spherical segment,
spherical layer, spherical belt, spherical sector.
Spherical surface - This locus of points(those. manynumber of all points)in space, equidistant from one point O , which is called the center of the spherical surface (Fig.90). Radius AOi diameter AB are defined in the same way as in a circle.
Ball (sphere) - This a body bounded by a spherical surface. Can get the ball by rotating the semicircle ( or circle ) around the diameter. All plane sections of the ball are circles ( Fig.90 ). The largest circle lies in a section passing through the center of the ball and is called big circle. Its radius is equal to the radius of the ball. Any two large circles intersect along the diameter of the ball ( AB, fig.91 ).This diameter is also the diameter of intersecting great circles. Through two points of a spherical surface located at the ends of the same diameter(A and B, Fig.91 ), you can draw countless large circles. For example, an infinite number of meridians can be drawn through the Earth's poles.
The volume of the sphere is one and a half times less than the volume of the cylinder circumscribed around it. (Fig.92 ), A the surface of the ball is one and a half times less than the total surface of the same cylinder ( Archimedes' theorem):
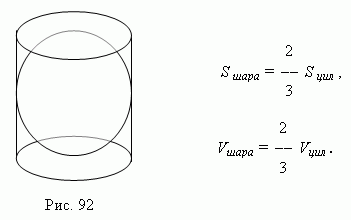
Here S ball And V ball - the surface and volume of the ball, respectively;
S cyl And V cyl - the total surface and volume of the circumscribed cylinder.
Parts of the ball. Part of a ball (sphere) ), cut off from it by some plane ( ABC, Fig.93), called ball(spherical ) segment. Circle ABC called basis ball segment. Line segment MN perpendicular drawn from the center N circle ABC until it intersects with a spherical surface, is called height ball segment. Dot M called top ball segment.
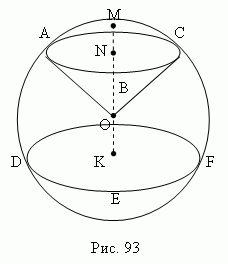
Part of a sphere enclosed between two parallel planes ABC and DEF intersecting a spherical surface (Fig. 93), called spherical layer; the curved surface of a spherical layer is called ball belt(zone). Circles ABC and DEF – grounds ball belt. Distance N.K. between the bases of the spherical belt - its height. The part of the ball bounded by the curved surface of a spherical segment ( AMCB, Fig.93) and conical surface OABC , the base of which is the base of the segment ( ABC ), and the vertex is the center of the ball O , called spherical sector.
A ball and a sphere are, first of all, geometric figures, and if a ball is a geometric body, then a sphere is the surface of a ball. These figures were of interest many thousands of years ago BC.
Subsequently, when it was discovered that the Earth is a ball and the sky is a celestial sphere, a new fascinating direction in geometry was developed - geometry on a sphere or spherical geometry. In order to talk about the size and volume of a ball, you must first define it.
Ball
A ball of radius R with a center at point O in geometry is a body that is created by all points in space that have a common property. These points are located at a distance not exceeding the radius of the ball, that is, they fill the entire space less than the radius of the ball in all directions from its center. If we consider only those points that are equidistant from the center of the ball, we will consider its surface or the shell of the ball.
How can I get the ball? We can cut a circle out of paper and start rotating it around its own diameter. That is, the diameter of the circle will be the axis of rotation. The formed figure will be a ball. Therefore, the ball is also called a body of revolution. Because it can be formed by rotating a flat figure - a circle.
Let's take some plane and cut our ball with it. Just like we cut an orange with a knife. The piece that we cut off from the ball is called a spherical segment.
In Ancient Greece, they knew how to not only work with a ball and sphere as geometric figures, for example, use them in construction, but also knew how to calculate the surface area of a ball and the volume of a ball.
A sphere is another name for the surface of a ball. A sphere is not a body - it is the surface of a body of revolution. However, since both the Earth and many bodies have a spherical shape, for example a drop of water, the study of geometric relationships inside the sphere has become widespread.
For example, if we connect two points of a sphere with each other by a straight line, then this straight line is called a chord, and if this chord passes through the center of the sphere, which coincides with the center of the ball, then the chord is called the diameter of the sphere.
If we draw a straight line that touches the sphere at just one point, then this line will be called a tangent. In addition, this tangent to the sphere at this point will be perpendicular to the radius of the sphere drawn to the point of contact.
If we extend the chord to a straight line in one direction or the other from the sphere, then this chord will be called a secant. Or we can say it differently - the secant to the sphere contains its chord.
Ball volume
The formula for calculating the volume of a ball is:
where R is the radius of the ball.
If you need to find the volume of a spherical segment, use the formula:
V seg =πh 2 (R-h/3), h is the height of the spherical segment.
Surface area of a ball or sphere
To calculate the area of a sphere or the surface area of a ball (they're the same thing):
where R is the radius of the sphere.
Archimedes was very fond of the ball and sphere, he even asked to leave a drawing on his tomb in which a ball was inscribed in a cylinder. Archimedes believed that the volume of a ball and its surface are equal to two-thirds of the volume and surface of the cylinder in which the ball is inscribed.”
In Chapter 2 we will continue “structural geometry” and talk about the structure and properties of the most important spatial figures - ball and sphere, cylinders and cones, prisms and pyramids. Most objects created by human hands - buildings, cars, furniture, dishes, etc. ., etc., consists of parts shaped like these figures.
§ 4. SPHERE AND BALL
After straight lines and planes, the sphere and ball are the simplest, but very important spatial figures rich in various properties. Whole books have been written about the geometric properties of a ball and its surface - a sphere. Some of these properties were known to ancient Greek geometers, and some were discovered more recently, in recent years. These properties (together with the laws of natural science) explain why, for example, celestial bodies and fish eggs are spherical in shape, why bathyscaphes and soccer balls are made in the shape of a ball, why ball bearings are so common in technology, etc. We can prove only the simplest properties of the ball. Proofs of other, albeit very important properties, often require the use of completely non-elementary methods, although the formulation of such properties can be very simple: for example, among all bodies having a given surface area, the ball has the largest volume.
4.1. Definitions of sphere and ball.
A sphere and a ball are defined in space in exactly the same way as a circle and a circle on a plane. A sphere is a figure consisting of all points in space remote from a given one.
different points to the same (positive) distance.
This point is called the center of the sphere, and the distance is its radius (Fig. 4.1).
So, a sphere with center O and radius R is a figure formed by all points X of space for which
A ball is a figure formed by all points in space located at a distance no greater than a given (positive) distance from a given point. This point is called the center of the ball, and this distance is its radius.
So, a ball with center O and radius R is a figure formed by all points X of space for which
Those points X of a ball with center O and radius R for which they form a sphere. They say that this sphere encloses a given ball or that it is its surface.
About the same points X of the ball for which they say that they lie inside the ball.
The radius of a sphere (and ball) is called not only the distance, but also any segment connecting the center with a point on the sphere.
GEOMETRY
Section II. STEREOMETRY
§22. BALL. SPHERE.
1. Definition of ball and sphere. Elements of ball and sphere.
A bullet is a geometric body formed by the rotation of a circle around an axis containing its diameter (Fig. 500).
The center of the circle that rotates is called the center of the ball, the radius of the circle is the radius of the ball, and the diameter of the circle is the diameter of the ball. In Figure 500, point O is the center of the ball, OA and OB are the radii of the ball, and AB is the diameter of the ball.
The surface of a ball is called a sphere.
The center, radius and diameter of a sphere are also the center, radius and diameter of a sphere.
All points on the sphere are at the same distance, equal to the radius, from the center of the sphere. Other points of the ball that do not belong to the sphere are called internal points; such points are said to lie inside the sphere. The internal points of the ball are located from the center of the ball at a distance that is less than the radius.
Thus we come to another definition of sphere and ball.
A sphere is a surface that consists of all points in space equidistant from the same point. This point is called the center of the sphere, and the distance from the center of the sphere to any of its points is the radius of the sphere.
A bullet is a geometric body that consists of all points in space located at a distance not greater than a given point from a given point. This point is called the center of the ball, and this distance is called the radius of the ball.
Example. The radius of the sphere is 3.5 cm. Point A is located inside or outside the sphere if it is distant from the center of the sphere: 1) cm, 2) cm.
A ball is a body consisting of all points in space that are located at a distance not greater than a given one from a given point. This point is called the center of the ball, and this distance is called the radius of the ball. The boundary of a ball is called a spherical surface or sphere. The points of the sphere are all points of the ball that are removed from the center at a distance equal to the radius. Any segment that connects the center of a ball to a point on the spherical surface is also called a radius. The segment passing through the center of the ball and connecting two points on the spherical surface is called the diameter. The ends of any diameter are called diametrically opposed points of the ball.
A ball is a body of revolution, just like a cone and a cylinder. A ball is obtained by rotating a semicircle around its diameter as an axis.
The surface area of the ball can be found using the formulas:
where r is the radius of the ball, d is the diameter of the ball.
The volume of the ball is found by the formula:
V = 4 / 3 πr 3,
where r is the radius of the ball.
Theorem. Every section of a ball by a plane is a circle. The center of this circle is the base of the perpendicular drawn from the center of the ball onto the cutting plane.
Based on this theorem, if a ball with center O and radius R is intersected by the plane α, then the cross-section results in a circle of radius r with center K. The radius of the section of the ball by the plane can be found by the formula
From the formula it is clear that planes equidistant from the center intersect the ball in equal circles. The radius of the section is greater, the closer the cutting plane is to the center of the ball, that is, the smaller the distance OK. The greatest radius has a section by a plane passing through the center of the ball. The radius of this circle is equal to the radius of the ball.
The plane passing through the center of the ball is called the center plane. The section of a ball by the diametrical plane is called a great circle, and the section of a sphere is called a great circle, and the section of a sphere is called a great circle.
Theorem. Any diametrical plane of a ball is its plane of symmetry. The center of the ball is its center of symmetry.
The plane that passes through point A of the spherical surface and is perpendicular to the radius drawn to point A is called the tangent plane. Point A is called the tangent point.
Theorem. The tangent plane has only one common point with the ball - the point of contact.
A straight line that passes through point A of a spherical surface perpendicular to the radius drawn to this point is called a tangent.
Theorem. An infinite number of tangents pass through any point on the spherical surface, and all of them lie in the tangent plane of the ball.
A spherical segment is the part of a ball cut off from it by a plane. Circle ABC is the base of the spherical segment. The perpendicular segment MN drawn from the center N of circle ABC to the intersection with the spherical surface is the height of the spherical segment. Point M is the vertex of the spherical segment.
The surface area of a spherical segment can be calculated using the formula:
The volume of a spherical segment can be found using the formula:
V = πh 2 (R – 1/3h),
where R is the radius of the great circle, h is the height of the spherical segment.
A spherical sector is obtained from a spherical segment and a cone as follows. If a spherical segment is smaller than a hemisphere, then the spherical segment is complemented by a cone, the vertex of which is in the center of the ball, and the base is the base of the segment. If the segment is larger than a hemisphere, then the specified cone is removed from it.
A spherical sector is a part of a ball bounded by a curved surface of a spherical segment (in our figure, this is AMCB) and a conical surface (in our figure, this is OABC), the base of which is the base of the segment (ABC), and the vertex is the center of the ball O.
The volume of the spherical sector is found by the formula:
V = 2/3 πR 2 H.
A spherical layer is a part of a ball enclosed between two parallel planes (planes ABC and DEF in the figure) intersecting the spherical surface. The curved surface of the spherical layer is called a spherical belt (zone). Circles ABC and DEF are the bases of the spherical belt. The distance NK between the bases of the spherical belt is its height.
website, when copying material in full or in part, a link to the original source is required.
