પરિપત્ર સમીકરણ અને તેની એપ્લિકેશન દ્વારા ડેલૌનેય સ્થિતિને તપાસવા માટે અલ્ગોરિધમનું ઑપ્ટિમાઇઝેશન

હું તમને બે ત્રિકોણ માટે Delaunay સ્થિતિને ઝડપથી કેવી રીતે તપાસવી તે વિશે એક રહસ્ય કહીશ.
વાસ્તવમાં, ઑપ્ટિમાઇઝેશનનું વર્ણન થોડું ઓછું કરવામાં આવ્યું છે (જુઓ "સર્કલ સમીકરણ દ્વારા ડેલૌનેય સ્થિતિને તપાસવા માટે અલ્ગોરિધમનું ઑપ્ટિમાઇઝેશન"), પરંતુ હું તમને બધું જ ક્રમમાં જણાવીશ.

મારા કિસ્સામાં, પ્લેનને આદિમ ક્ષેત્રો (ત્રિકોણ) માં વિભાજીત કરવા માટે ઇમેજ ટ્રેસિંગમાં ત્રિકોણનો ઉપયોગ થાય છે. જેમ તમે જાણો છો, તે ઘણા તબક્કામાં પણ વહેંચાયેલું છે: ગોઠવણ, સીમાઓ ઓળખવી, સીમાઓની આસપાસ ચાલવું, રૂપરેખા સાફ કરવી. આ સૌથી સામાન્ય શબ્દોમાં છે. મને લાગે છે કે, હું સૌથી મુશ્કેલ તબક્કે રોકવા માંગુ છું: વિમાનને સાફ કરવું.

પ્રવેશદ્વાર પર

આકૃતિ 1

શું કરવું

શોધો

અલ્ગોરિધમ

આકૃતિ 2

આકૃતિ 3

આકૃતિ 4

બીજી એક વાત: આગલા ત્રિકોણને સાચવતી વખતે, શિરોબિંદુઓને ઘડિયાળની દિશામાં ટ્રાવર્સલમાં (જમણી સંકલન પ્રણાલીમાં) રેકોર્ડ કરવું જરૂરી છે. આ ભવિષ્યમાં કમ્પ્યુટિંગ સંસાધનોને ઘટાડવા માટે ઉપયોગી થશે.

2) જ્યાં સુધી આપણે સમગ્ર પ્લેનને સ્વિપ ન કરીએ ત્યાં સુધી પગલું 1 નું પુનરાવર્તન કરો.

3) જો ત્યાં અનેક સિક્વન્સ હોય, એટલે કે. એક, અને તેની અંદર એક અથવા વધુ આંતરિક રૂપરેખા છે (આકૃતિ 1). અહીં દરેક ક્રમને અલગથી ધ્યાનમાં લેવો જરૂરી છે. ચાલો બીજો આંતરિક સમોચ્ચ લઈએ. એક બાહ્ય અને એક આંતરિકમાંથી આપણે બે સિંગલ સર્કિટ બનાવીશું. આ કરવા માટે, તમારે એક સર્કિટથી બીજા સર્કિટમાં બે "બંદરો" શોધવાની જરૂર છે. "બંદરો" માટેની સ્થિતિ: તેઓ એકબીજા સાથે છેદે ન હોવા જોઈએ (તેમના છેડાને પણ સ્પર્શ ન કરવો જોઈએ), અને તેઓ સમોચ્ચ રેખાઓ સાથે છેદે ન જોઈએ (આકૃતિ 5).

આકૃતિ 5

આકૃતિ 6
4) આગળ, તમારે એક પછી એક તમામ આંતરિક સિક્વન્સ પહેલેથી જ રચાયેલી સિક્વન્સમાં દાખલ કરવી જોઈએ, એકબીજાથી અલગ (બિંદુ 3). તમારે તેને નવા સમાવિષ્ટ સાથે મર્જ કરવાની જરૂર છે. વ્યાખ્યા પ્રમાણે, કોઈપણ આંતરિક ક્રમ અન્ય લોકો સાથે સ્પર્શતો નથી અથવા છેદતો નથી (બંને એક બાહ્ય અને તમામ સંભવિત આંતરિક), તેથી બધું સરળતાથી ચાલશે.
બંદરો (આકૃતિ 6) મળ્યા પછી, વર્તમાન અલ્ગોરિધમના પોઈન્ટ 1 અને 2 (આકૃતિ 7) નો ઉપયોગ કરીને નવા સિક્વન્સનું નિર્માણ કરવું અને તેમને બાયપાસ કરવું સરળ છે.

આકૃતિ 7

5) 4થા તબક્કા પછી આપણી પાસે ત્રિકોણની યાદી છે (આકૃતિ 8). એવું લાગે છે કે કાર્ય પહેલેથી જ પૂર્ણ થઈ ગયું છે, પરંતુ જે બાકી છે તે ચિત્રને સુંદર બનાવવાનું છે: તપાસો કે ડેલૌનેય શરત પૂર્ણ થઈ છે (આકૃતિ 9).

આકૃતિ 8

આકૃતિ 9

6) આગળ જોઈને, હું તમને છઠ્ઠા મુદ્દા વિશે જણાવીશ. તેમાં સ્ટેપ નંબર 5 નો ઉપયોગ કરીને મેળવેલ ત્રિકોણની યાદીમાંથી ક્રમિક રીતે દોડવાનો સમાવેશ થાય છે. પ્રથમ, આપણે બધા ત્રિકોણને "ગંદા" તરીકે ચિહ્નિત કરીએ છીએ. દરેક ચક્રમાં આપણે દરેક ત્રિકોણ માટે Delaunay સ્થિતિ તપાસીએ છીએ. જો શરત પૂરી ન થાય, તો અમે ફરીથી બનાવીએ છીએ અને પડોશીઓ અને વર્તમાન ત્રિકોણને "ગંદા" તરીકે ચિહ્નિત કરીએ છીએ. જો શરત પૂરી થાય છે, તો અમે તેને સ્વચ્છ ચિહ્નિત કરીએ છીએ. મારા અલ્ગોરિધમના અમલીકરણમાં, દરેક ત્રિકોણમાં તેના પડોશીઓ સાથે એક લિંક છે. આ કિસ્સામાં, બિંદુ 6 સૌથી ઝડપી કાર્ય કરે છે.

પાંચમા તબક્કા વિશે વધુ

કમ્પ્યુટિંગ પાવર #1: 10 ગુણાકાર/ભાગાકાર અને 13 ઉમેરો/બાદબાકી.
કમ્પ્યુટિંગ પાવર #2: 29 ગુણાકાર/ભાગાકાર કામગીરી અને 24 સરવાળો/બાદબાકી કામગીરી.

કોમ્પ્યુટીંગ પાવરના દૃષ્ટિકોણથી, જે પુસ્તકમાં ઉદાહરણ તરીકે ગણવામાં આવે છે, વિકલ્પ નંબર 1 વધુ નફાકારક છે. મેં તેનો અમલ કર્યો હોત, જો નહીં... (આકૃતિ 10). જેમ જેમ તે બહાર આવ્યું છે, આ પદ્ધતિને "કન્વેયર" પર મૂક્યા પછી, અનિશ્ચિતતા પરિણમી. આ એક વિકલ્પ છે જ્યારે કોણ A પોતે 180 ડિગ્રી કરતા વધારે હોય. તે પુસ્તકમાં વ્યક્તિગત ખાનગી પદ્ધતિઓમાંની એક તરીકે ગણવામાં આવે છે. અને આ સાથે, તેની બધી લાવણ્ય, પારદર્શિતા અને પ્રદર્શન અદૃશ્ય થઈ જાય છે. અને તે પણ પાછળથી બહાર આવ્યું કે પદ્ધતિ નંબર 2 ખૂબ જ નોંધપાત્ર રીતે ઑપ્ટિમાઇઝ કરી શકાય છે.

આકૃતિ 10

પરિપત્ર સમીકરણ દ્વારા ડેલૉનાય સ્થિતિને તપાસવા માટે અલ્ગોરિધમનું ઑપ્ટિમાઇઝેશન

તેથી અમારી પાસે છે:
A(x1, y1), B(x2, y2), C(x3, y3) બિંદુઓમાંથી પસાર થતા વર્તુળના સમીકરણ દ્વારા બિંદુ M(X, Y) બિંદુ માટેની સ્થિતિને આ રીતે લખી શકાય છે:

(a ⋅ (X^2 + Y^ 2) − b ⋅ X + c ⋅ Y − d) ⋅ ચિહ્ન a ≥ 0

વિગતો ઉત્તમ પુસ્તકમાં મળી શકે છે. (ના, હું લેખક નથી)
તેથી, સાઇન a એ ટ્રાવર્સલ દિશાનું ચિહ્ન છે, શરૂઆતથી જ મેં ત્રિકોણ ઘડિયાળની દિશામાં બનાવ્યા છે, તેથી તેને અવગણી શકાય છે (તે એકની બરાબર છે).

A(x1 - X, y1 - Y), B(x2 - X, y2 - Y), B(x3 - X, y3 - Y);

D>=0

આકૃતિ 11

સરળ છે ને?

પુસ્તક મુજબ, ફરીથી,

(x1^2 + y1^2)*(y2*x3 - x2*y3) + (x2^2 + y2^2)*(x1*y3 - y1*x3) + (x3^2 + y3^2)* (y1*x2 - x1*y2)<= 0

અમારી પાસે છે: 15 ગુણાકાર/ભાગાકાર ક્રિયાઓ અને 14 સરવાળો/બાદબાકીની ક્રિયાઓ.

તમારા ધ્યાન બદલ આભાર. હું ટીકાની રાહ જોઈ રહ્યો છું.

વપરાયેલ સાહિત્યની સૂચિ

ટેપ્લોવ એ.એ., સ્નાતક, MSTU નામ આપવામાં આવ્યું N.E. બૌમન, ડિપાર્ટમેન્ટ ઓફ કોમ્પ્યુટર સોફ્ટવેર એન્ડ ઇન્ફોર્મેશન ટેક્નોલોજીસ, મોસ્કો, [ઇમેઇલ સુરક્ષિત]

માયકોવ કે.એ., ડોકટર ઓફ ટેકનિકલ સાયન્સ, પ્રોફેસર, મોસ્કો સ્ટેટ ટેકનિકલ યુનિવર્સિટીનું નામ N.E. બૌમન, ડિપાર્ટમેન્ટ ઓફ કોમ્પ્યુટર સોફ્ટવેર એન્ડ ઇન્ફોર્મેશન ટેક્નોલોજીસ, મોસ્કો, [ઇમેઇલ સુરક્ષિત]

સંશોધિત અલ્ગોરિધમનો
Delaunay ત્રિકોણ

ઉચ્ચ પ્રદર્શન અને ઓછા સંસાધન વપરાશ સાથે Delaunay ત્રિકોણ પદ્ધતિઓના તુલનાત્મક વિશ્લેષણના પરિણામો રજૂ કરવામાં આવ્યા છે. અનુગામી આધુનિકીકરણ માટે પ્રોટોટાઇપની પસંદગી વાસ્તવિક સમયમાં ગતિશીલ ત્રિ-પરિમાણીય વસ્તુઓના નિર્માણના સંબંધમાં વ્યવહારિક રીતે જરૂરી વિગતો સાથે પ્રમાણિત છે. વિતરણ ઘનતા અનુસાર ત્રિકોણ બિંદુઓની શ્રેણીના અંતરાલ પાર્ટીશન માટે એક અલ્ગોરિધમ પ્રસ્તાવિત છે, જે હાર્ડવેર અમલીકરણમાં ભૂલોને ટાળવા માટે પરવાનગી આપે છે. સૂચિત સંશોધિત Delaunay ત્રિકોણ અલ્ગોરિધમનું વિશ્લેષણ હાથ ધરવામાં આવે છે

પરિચય

આપેલ સ્તરની વિગત સાથે ડાયનેમિક 3D ઑબ્જેક્ટ બનાવવાના સંસાધનની તીવ્રતા નક્કી કરતા તબક્કાઓમાંથી એક ત્રિકોણ છે. વ્યવહારમાં, ત્રિકોણ પદ્ધતિનો પ્રોટોટાઇપ નક્કી કરવાની જરૂર છે જે ઉચ્ચ પ્રદર્શન અને ઓછી સંસાધન તીવ્રતાની જરૂરિયાતને સંતોષે છે, ચોક્કસ વર્ગની સમસ્યાઓ માટે અનુગામી ફેરફાર સાથે.

હલ કરવાના કાર્યોને સેટ કરી રહ્યા છીએ

અજ્ઞાત વિતરણ કાયદા સાથે પોઈન્ટના અનુરૂપ સમૂહ દ્વારા વર્ણવેલ 3D ઑબ્જેક્ટ્સને મોડેલ કરવાની જરૂરિયાત દ્વારા સંખ્યાબંધ વ્યવહારિક સમસ્યાઓ દર્શાવવામાં આવે છે. આવી સમસ્યાઓનું ઉદાહરણ પર્વતમાળા અથવા જટિલ અને અનિયમિત સપાટીની રચનાઓનું મોડેલિંગ છે, જેની ઊંચાઈઓ અગાઉ રિમોટ સેન્સિંગ દ્વારા મેળવવામાં આવે છે. આ કિસ્સામાં, ત્રિકોણની ઉચ્ચતમ "ચોક્કસતાની ડિગ્રી" સુનિશ્ચિત કરીને, બિંદુઓના મૂળ સમૂહ પર ત્રિકોણ કરવું જરૂરી છે, જે સરવાળાના લઘુત્તમ મૂલ્ય સાથે "પાતળા" ત્રિકોણના નિર્માણને બાકાત દ્વારા વર્ગીકૃત થયેલ છે. ઘેરાયેલા વર્તુળોની ત્રિજ્યાની.

ત્રિકોણની "નિયમિતતાની ડિગ્રી" ની સમસ્યા ત્રિકોણ દ્વારા ઉકેલવામાં આવે છે જે ડેલૌનેય સ્થિતિને સંતોષે છે.

જાણીતા ડેલૌનેય ત્રિકોણ અલ્ગોરિધમ્સને નીચેની ચાર શ્રેણીઓમાં વિભાજિત કરી શકાય છે: પુનરાવર્તિત અલ્ગોરિધમ્સ, મર્જિંગ અલ્ગોરિધમ્સ, ટુ-પાસ અલ્ગોરિધમ્સ અને સ્ટેપવાઇઝ; આ અલ્ગોરિધમ્સની મુખ્ય લાક્ષણિકતાઓ નીચે ચર્ચા કરવામાં આવી છે.

Delaunay ત્રિકોણ બનાવવા માટે પુનરાવર્તિત અલ્ગોરિધમ્સ

પુનરાવર્તિત અલ્ગોરિધમ્સ આંશિક રીતે બાંધવામાં આવેલા ડેલૌનેય ત્રિકોણમાં પોઈન્ટનો ક્રમિક ઉમેરણ અમલમાં મૂકે છે. પુનરાવર્તિત Delaunay અલ્ગોરિધમ્સની જટિલતાને O(N2) તરીકે વ્યાખ્યાયિત કરવામાં આવે છે, અને બિંદુઓના સમાન વિતરણના કિસ્સામાં - O(N). પુનરાવર્તિત Delaunay અલ્ગોરિધમ્સના ગેરફાયદામાં પુનરાવર્તિત લૂપ્સની મોટી સંખ્યા, સ્રોત ડેટાની રચના પર સૉર્ટિંગ અલ્ગોરિધમની અવલંબન, અને દરેક લૂપમાં Delaunay સ્થિતિ તપાસવાની જરૂરિયાત છે. પુનરાવર્તિત Delaunay અલ્ગોરિધમ્સના ફાયદા અમલીકરણની સરળતા અને ઇનપુટ ડેટાના ચોક્કસ સેટ પર આધારિત અસરકારક સોર્ટિંગ અલ્ગોરિધમ પસંદ કરવાની ઉચ્ચ ઝડપ છે.

મર્જ કરીને Delaunay ત્રિકોણ બનાવવા માટેના અલ્ગોરિધમ્સ

મર્જ અલ્ગોરિધમ્સ પોઈન્ટના મૂળ સમૂહના વિભાજનને સંખ્યાબંધ સબસેટમાં અમલમાં મૂકે છે, જેમાં સંખ્યાબંધ ઉકેલોના અનુગામી મર્જ સાથે ત્રિકોણ બનાવવામાં આવે છે. મર્જિંગ એલ્ગોરિધમ્સની સરેરાશ જટિલતા O(N) છે. મર્જિંગ એલ્ગોરિધમ્સ નિરર્થકતા દ્વારા વર્ગીકૃત કરવામાં આવે છે, જે "સાંકડી" પટ્ટાઓ માટે બહિર્મુખ વિસ્તારો બનાવવાની જરૂરિયાત દ્વારા નિર્ધારિત કરવામાં આવે છે, અને પરિણામે, લાંબા, "સાંકડા" ત્રિકોણની રચના, મર્જ કરતી વખતે ફરીથી બનાવવામાં આવે છે. મર્જર એલ્ગોરિધમ્સ ઉચ્ચ પ્રદર્શન ધરાવે છે, જે તેમના વ્યવહારુ લાભને નિર્ધારિત કરે છે.

Delaunay ત્રિકોણ બનાવવા માટે બે-પાસ અલ્ગોરિધમ્સ

ટુ-પાસ એલ્ગોરિધમ્સની ફાયદાકારક વિશેષતા એ છે કે પ્રથમ ચક્રમાં ડેલૌનાય સ્થિતિને ધ્યાનમાં લીધા વિના ચોક્કસ ત્રિકોણ બનાવવામાં આવે છે, જે ડેલૌનાય સ્થિતિ અનુસાર બીજા તબક્કામાં સંશોધિત થાય છે. બે-પાસ અલ્ગોરિધમ્સની જટિલતા સરેરાશ O(N) છે, અને ઓછામાં ઓછા અનુકૂળ કિસ્સામાં - O(N 2) . ટુ-પાસ ડેલૌનેય અલ્ગોરિધમ્સનો ગેરલાભ એ દરેક પટ્ટા માટે મોટી સંખ્યામાં પ્રકારની જરૂરિયાત છે. તે જ સમયે, આ અલ્ગોરિધમ ઉચ્ચ પ્રદર્શન દ્વારા વર્ગીકૃત થયેલ છે, કારણ કે આગળનો ત્રિકોણ જે ત્રિકોણમાં આવે છે તે ડેલૌનાય સ્થિતિના સંતોષ માટે તપાસવામાં આવતો નથી, જેને નોંધપાત્ર હાર્ડવેર સંસાધનોની જરૂર છે.

Delaunay ત્રિકોણ બનાવવા માટે સ્ટેપ-બાય-સ્ટેપ અલ્ગોરિધમ્સ

સ્ટેપ-બાય-સ્ટેપ કન્સ્ટ્રક્શન એલ્ગોરિધમ્સ માત્ર ત્રિકોણ અમલમાં મૂકે છે જે અંતિમ ત્રિકોણમાં ડેલૌનેય સ્થિતિને સંતોષે છે અને તેથી પુનઃનિર્માણની જરૂર નથી. પોઈન્ટની મોટી સાંદ્રતા સાથે, સ્ટેપ-બાય-સ્ટેપ સેલ્યુલર અલ્ગોરિધમનો ઉપયોગ અવ્યવહારુ છે. આ અલ્ગોરિધમની જટિલતા સરેરાશ O(N) છે, અને સૌથી ખરાબ કિસ્સામાં - O(N 2).

Delaunay ત્રિકોણમાં ફેરફાર કરવા માટે પ્રોટોટાઇપ પસંદ કરી રહ્યા છીએ

વાસ્તવિક સમયમાં ડાયનેમિક 3D ઑબ્જેક્ટ્સ બનાવવાની સમસ્યાના વ્યવહારુ લક્ષણો, ઉચ્ચ પ્રદર્શન અને ઓછી સંસાધન તીવ્રતા તરીકે ડેલૌનેય ત્રિકોણ અલ્ગોરિધમ્સ માટેની આવી આવશ્યકતાઓને નિર્ધારિત કરે છે. ઉપરોક્ત પૃથ્થકરણ પરિણામો પરથી નીચે મુજબ, ગણવામાં આવેલ અલ્ગોરિધમ્સ આ જરૂરિયાતોને પૂર્ણપણે સંતોષતા નથી. તેથી, એક અલ્ગોરિધમ બનાવવાની જરૂર છે કે જે ત્રિકોણ વિસ્તારના વિભાજન પર નિર્ભર ન હોય કે જે ત્રિકોણના જ બિંદુઓ ધરાવે છે, અને વર્તમાન ત્રિકોણને મૂળ ત્રિકોણમાં ઉમેરવાની દરેક પુનરાવૃત્તિ પર ડેલૌનેય સ્થિતિ તપાસવાની જરૂર નથી. .

તુલનાત્મક વિશ્લેષણના ઉપરોક્ત પરિણામો પરથી તે અનુસરે છે કે બે-પાસ ડેલૌનેય ત્રિકોણ ગાણિતીક નિયમો, ખાસ કરીને ટુ-પાસ ચાહક અલ્ગોરિધમ, માત્ર ઉચ્ચ પ્રદર્શન અને ઓછી સંસાધન તીવ્રતાના માપદંડને આંશિક રીતે સંતોષે છે.

જો કે, આ પ્રકારના અલ્ગોરિધમ્સને રીઅલ-ટાઇમ સમસ્યાઓ પર લાગુ પડતી વખતે કામગીરી વધારવા માટે ફેરફારની જરૂર છે. બે-પાસ ચાહક અલ્ગોરિધમ પોઈન્ટના સમૂહનું કેન્દ્ર નક્કી કરવા માટે નિરર્થક છે. OX અથવા OY નો ઉપયોગ કરીને સમૂહના બિંદુ કેન્દ્રનું સંકલન નક્કી કરતી વખતે, મોટી સંખ્યામાં બિંદુઓ સાથે અંકગણિત સરેરાશના મૂલ્યની ગણતરી કરવી અયોગ્ય છે, અને બિંદુ કોઓર્ડિનેટ્સના મોટા મૂલ્યો સાથે, ડેટા ઓવરફ્લો થઈ શકે છે, જે પ્રોગ્રામની ભૂલ અથવા નિષ્ફળતા તરફ દોરી જશે. તેથી, ત્રિકોણ બિંદુઓના તમામ મૂલ્યોને X અક્ષ સાથે અંતરાલોમાં Δx 1, Δx 2, Δx 3 ... Δx n અને Y અક્ષ સાથે Δy 1, Δy 2, Δy 3 માં વિભાજીત કરવાની સલાહ આપવામાં આવે છે. ... Δy n. X અને Y અક્ષો સાથે સંબંધિત અંતરાલો સાથે જોડાયેલા બિંદુઓની સંખ્યા નક્કી કરવી પણ જરૂરી છે.

• x c - સમૂહ બિંદુના કેન્દ્રનું x-સંકલન;
• X અક્ષ પર Δх i – i-th અંતરાલ;
• X મહત્તમ - બધા ત્રિકોણ બિંદુઓ વચ્ચે X અક્ષ સાથે મહત્તમ મૂલ્ય;
• X મિનિટ - બધા ત્રિકોણ બિંદુઓ વચ્ચે X અક્ષ સાથે લઘુત્તમ મૂલ્ય;

• y c - સમૂહ બિંદુના કેન્દ્રનું y-સંકલન;
• n i – i-th અંતરાલ પર પોઈન્ટની સંખ્યા;
• Y અક્ષ પર Δy i – i-th અંતરાલ;
• Y મહત્તમ - બધા ત્રિકોણ બિંદુઓ વચ્ચે Y અક્ષ સાથે મહત્તમ મૂલ્ય;
• Y મિનિટ - બધા ત્રિકોણ બિંદુઓ વચ્ચે Y અક્ષ સાથેનું લઘુત્તમ મૂલ્ય.

ત્રિકોણના અનુગામી તબક્કા ક્લાસિક ચાહક અલ્ગોરિધમનો અનુસાર અમલમાં મૂકવામાં આવે છે. વિકસિત સંશોધિત ચાહક આકારના ડેલૌનેય ત્રિકોણ અલ્ગોરિધમનો આકૃતિ ફિગમાં બતાવવામાં આવ્યો છે. 1.

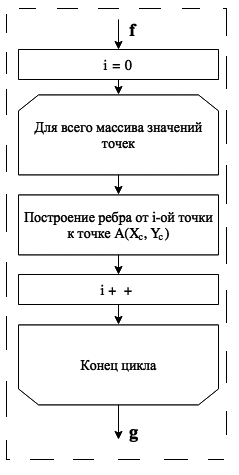પ્રસ્તુત યોજનામાં સૌથી વધુ શ્રમ-સઘન તબક્કાઓ બહિર્મુખમાં ત્રિકોણને વર્ગીકૃત કરવા અને બાંધવાના તબક્કા છે. મર્જિંગ અલ્ગોરિધમને સોર્ટિંગ અલ્ગોરિધમ તરીકે પસંદ કરવામાં આવ્યું હતું, અને ગ્રેહામ અલ્ગોરિધમને બહિર્મુખ ત્રિકોણ બનાવવા માટે અલ્ગોરિધમ તરીકે પસંદ કરવામાં આવ્યું હતું. બંને અલ્ગોરિધમ્સ સ્વીકાર્ય સમયે કાર્ય કરે છે અને તેમના પ્રતિનિધિઓમાં વ્યવહારિક દ્રષ્ટિએ સૌથી વધુ પસંદ કરવામાં આવે છે.

સંશોધિત ચાહક આકારના ડેલૌનેય ત્રિકોણ અલ્ગોરિધમનું વિશ્લેષણ

ફિગમાં બતાવેલ એકમાંથી. આકૃતિનો 1 બતાવે છે કે સંશોધિત ચાહક અલ્ગોરિધમનો ઉપયોગ કરીને ત્રિકોણ બનાવવા માટેનું સમય મૂલ્ય અભિવ્યક્તિ દ્વારા નક્કી કરવામાં આવે છે:

• T 1 , T 2 - અનુક્રમે X અને Y અક્ષો સાથે અંતરાલોની શ્રેષ્ઠ સંખ્યાની ગણતરી માટે સમય મૂલ્યો;
• T 3 , T 4 - ગણતરી સમયના મૂલ્યો X મિનિટ અને X મહત્તમ, અનુક્રમે;
• T 5 , T 6 – ગણતરીના સમયના મૂલ્યો અનુક્રમે Y મિનિટ અને Y મહત્તમ;
• T 7 , T 8 - અનુક્રમે X અને Y અક્ષો સાથે અંતરાલ મૂલ્યોની ગણતરી માટે સમય મૂલ્યો;
• T 9 - બિંદુ A(X c ,Y c) ને સંબંધિત એરેના દરેક બિંદુના ધ્રુવીય ખૂણાની ગણતરી માટે સમય મૂલ્ય;
• T 10 - બિંદુ A(X c ,Y c) ના સાપેક્ષ ધ્રુવીય કોણ દ્વારા તમામ બિંદુઓને મર્જ કરીને વર્ગીકરણ સમયનું મૂલ્ય;
• T 11 – એરેના દરેક બિંદુથી બિંદુ A(X c ,Y c) સુધીની ધાર બાંધવા માટેનું સમય મૂલ્ય;
• T 12 – બહિર્મુખ ત્રિકોણ પૂર્ણ કરવા માટે સમય મૂલ્ય;
• T 13 – ત્રિકોણ પુનઃનિર્માણ સમયનું મૂલ્ય જે ડેલૌનેય સ્થિતિને સંતોષે છે;
• n – બિંદુ સંકલન મૂલ્યોની શ્રેણી.

ચાલો દરેક સમયની અવલંબનને અલગથી ધ્યાનમાં લઈએ.

X અને Y અક્ષ સાથે અંતરાલોની શ્રેષ્ઠ સંખ્યા નક્કી કરતી વખતે, અમે સ્ટર્જના નિયમનો ઉપયોગ કરીએ છીએ, જે મુજબ અંતરાલો n ની સંખ્યા આ રીતે નક્કી કરવામાં આવે છે:

• N એ જથ્થાના અવલોકનોની કુલ સંખ્યા છે;
• [x] - સંખ્યા x નો પૂર્ણાંક ભાગ.

તે સ્પષ્ટ છે કે સમય નિર્ભરતા T 1 અને T 2 ની સતત રજૂઆત c 1 અને c 2 છે.

X min , X max , Y min , Y max મૂલ્યો નક્કી કરવાના તબક્કે સ્યુડોકોડ આના જેવો દેખાશે:

Xmin ← એમ

i માટે ← 1 થી લંબાઈ(M) – 1

જો Xmin › M[i]

Xmin ← M[i]

Xmax ← એમ

i માટે ← 1 થી લંબાઈ(M) – 1

જો Xmax< M[i]

Xmax ← M[i]

યમીન ← એમ

i માટે ← 1 થી લંબાઈ(M) – 1

જો Ymin › M[i]

Ymin ← M[i]

Ymax ← એમ

i માટે ← 1 થી લંબાઈ(M) – 1

જો Ymax< M[i]

Ymax ← M[i]

ઉપરોક્ત સ્યુડોકોડ પરથી સ્પષ્ટપણે જોઈ શકાય છે કે x અથવા y ની મહત્તમ અથવા લઘુત્તમ કિંમત શોધવાનો સમય એક રેખીય અવલંબન O(N) ધરાવે છે, તેથી, T 3 (n), T 4 (n), T 5 (n) , T 6 (n) , અનુક્રમે સમય લાક્ષણિકતા O(N) ધરાવે છે.

X અક્ષ સાથે અંતરાલોના મૂલ્યો નક્કી કરવા માટેની રેખાકૃતિ ફિગમાં બતાવવામાં આવી છે. 2.

ઉપર પ્રસ્તુત રેખાકૃતિમાંથી, O(N) ની રેખીય સમય અવલંબન પણ દૃશ્યમાન છે, કારણ કે બિંદુ એરેના મૂલ્યોના કોઓર્ડિનેટ્સનો સંપૂર્ણ સમૂહ મૂલ્યો નક્કી કરવામાં સામેલ છે. Y અક્ષ સાથે અંતરાલોના મૂલ્યો નક્કી કરવા માટેની યોજનામાં સમાન માળખું અને સમય લાક્ષણિકતાઓ છે, તેથી, T 7 (n) અને T 8 (n) માટે સમય અવલંબન ફોર્મ O(N) ધરાવે છે.

પોઈન્ટના મૂળ એરે માટે ધ્રુવીય ખૂણાના મૂલ્યો નક્કી કરવા માટેની યોજના ફિગમાં બતાવવામાં આવી છે. 3.

સ્યુડોકોડ સ્વરૂપમાં, આ રેખાકૃતિ આના જેવો દેખાશે:

પોઈન્ટ થી પોઈન્ટ માટે

# જો બિંદુ 1 લી અને 4 થી ક્વાર્ટર વચ્ચે સંકલન અક્ષ પર આવેલું છે

જો point.x ≥ Xc અને point.y = Yc

બિંદુ.કોણ ← 0

# જો બિંદુ પ્રથમ ક્વાર્ટરમાં સખત રીતે આવેલું હોય

અન્યથા જો point.x > Xc અને point.y > Yc

ફાઉન્ડેશન ← |point.x – Xc|

Point.angle ← arctg(લંબ/પાયો)

# જો બિંદુ 1 લી અને 2 જી ક્વાર્ટર વચ્ચે સંકલન અક્ષ પર આવેલું છે

બાકી જો point.x = Xc અને point.y > Yc

બિંદુ.કોણ ← p/2

# જો બિંદુ બીજા ક્વાર્ટરમાં સખત રીતે આવેલું હોય

અન્યથા જો point.x< Xc and point.y >Yc

ફાઉન્ડેશન ← |point.y – Yc|

Point.angle ← p/2 + arctg(લંબ/પાયો)

# જો બિંદુ II અને III ક્વાર્ટર વચ્ચે સંકલન અક્ષ પર આવેલું છે

જો બિંદુ.x< Xc and point.y = Yc

બિંદુ.કોણ ← પૃષ્ઠ

# જો બિંદુ ત્રીજા ક્વાર્ટરમાં સખત રીતે આવેલું હોય

જો બિંદુ.x< Xc and point.y >Yc

ફાઉન્ડેશન ← |point.x – Xc|

લંબ ← |point.y – Yc|

બિંદુ.કોણ ← p + આર્ક્ટન(લંબ/પાયો)

# જો બિંદુ III અને IV ક્વાર્ટર વચ્ચે સંકલન અક્ષ પર આવેલું છે

જો point.x = Xc અને point.y< Yc

બિંદુ.કોણ ← 3p/2

# જો બિંદુ IV ક્વાર્ટરમાં સખત રીતે આવેલું હોય

જો point.x > Xc અને point.y< Yc

ફાઉન્ડેશન ← |point.y – Yc|

લંબ ← |point.x – Xc|

Point.angle ← 3p/2 + arctg(લંબ/પાયો)

દેખીતી રીતે, બિંદુ કોઓર્ડિનેટ્સના મૂળ એરે માટે ધ્રુવીય ખૂણાના મૂલ્યો નક્કી કરવા માટે સમયની લાક્ષણિકતા O(N) સ્વરૂપ ધરાવે છે, તેથી, T 9 (n) = O(N).

માં બતાવ્યા પ્રમાણે, મર્જ સૉર્ટ O(N) ની સમય અવલંબન ધરાવે છે, તેથી T 10 (n) = O(NlnN).

મૂળ એરેના બિંદુઓને જોડતી ધાર બાંધવા માટેની રેખાકૃતિ ફિગમાં બતાવવામાં આવી છે. 4.

ઉપરોક્ત સર્કિટનો સ્યુડોકોડ આના જેવો દેખાશે:

i માટે ← 0 થી લંબાઈ (પોઇન્ટ્સ) – 1

દોરો(Xc,Yc,Points[i].x, Points[i].y)

સમયનો પ્રતિભાવ પણ રેખીય છે, તેથી T 11 (n) = O(N).

બહિર્મુખમાં પરિણામી ત્રિકોણની પૂર્ણતા ગ્રેહામના અલ્ગોરિધમ અનુસાર હાથ ધરવામાં આવે છે. પ્રક્રિયાનો ઇનપુટ ડેટા એ પોઈન્ટ Q નો સમૂહ છે, જ્યાં |Q|≥3. તે ફંક્શનને Top(S) કહે છે, જે તેના સમાવિષ્ટોને બદલ્યા વિના સ્ટેક Sની ટોચ પરના બિંદુને પરત કરે છે. વધુમાં, ફંક્શન NextToTop(S) નો પણ ઉપયોગ થાય છે, જે સ્ટેક S માં સ્થિત એક બિંદુ આપે છે, જે ટોચના બિંદુની નીચે એક સ્થાન આપે છે; સ્ટેક S યથાવત છે.

ગ્રેહામ(Q)

ચાલો p 0 એ ન્યૂનતમ સંકલન સાથે Q સમૂહમાંથી એક બિંદુ છે.

ચાલો ‹p 1 , p 2 ,...,p N › – સમૂહ Q ના બિંદુઓ, સૉર્ટ કરેલ

ધ્રુવીય કોણ વધારવાના ક્રમમાં.

દબાણ(p 0 ,S)

દબાણ(p 1 ,S)

i=2 થી N do માટે

જ્યારે બિન્દુ NextToTop(S), Top(S) અને pi દ્વારા રચાયેલ કોણ,

બિન-ડાબે વળાંક બનાવો

# જ્યારે આ દ્વારા રચાયેલી તૂટેલી રેખા સાથે આગળ વધવું

# બિંદુઓ, ચળવળ સીધી અથવા જમણી તરફ કરવામાં આવે છે

ડૂ પૉપ(એસ)

દબાણ(pi,S)

પરત એસ

ગ્રેહામ પ્રક્રિયાનો ચાલવાનો સમય O(NlnN) છે, જ્યાં N=લંબાઈ(Q). તે બતાવવાનું સરળ છે કે જ્યારે લૂપમાં O(N) સમય લાગશે, અને ધ્રુવીય ખૂણાને સૉર્ટ કરવામાં O(NlnN) સમય લાગશે, જે ગ્રેહામ પ્રક્રિયાના સામાન્ય એસિમ્પ્ટોટિક વર્તનને સૂચિત કરે છે, તેથી, T 12 (n) = O (NlnN).

ત્રિકોણના પુનઃનિર્માણની સમયની લાક્ષણિકતા જે ડેલૌનેય સ્થિતિને સંતોષે છે, જેમ કે માં બતાવ્યા પ્રમાણે, એક રેખીય અવલંબન O(N) ધરાવે છે, આમ T 13 (n) = O(N).

જો આપણે તમામ જોવા મળેલી સમય લાક્ષણિકતાઓને અભિવ્યક્તિ (3) માં બદલીએ, તો પરિણામી સમય અવલંબન આના જેવું દેખાશે:

T(n) = c 1 +c 2 +O(N)+O(N)+O(N)+O(N)+O(N)+O(N)+O(N)+ +O(NlnN) )+O(N)+O(NlnN)+O(N)

T(n) = O(NlnN)

સંશોધિત ડેલૌનેય ત્રિકોણ અલ્ગોરિધમના સમયની લાક્ષણિકતાઓનું સૈદ્ધાંતિક વિશ્લેષણ સૂચિત અલ્ગોરિધમની કાર્યક્ષમતા અને ઉચ્ચ પ્રદર્શનની પુષ્ટિ કરે છે.

તારણો

વ્યવહારિક રીતે લોકપ્રિય ડેલૌનેય ત્રિકોણ ગાણિતીક નિયમોના તુલનાત્મક વિશ્લેષણના પરિણામે, તે દર્શાવવામાં આવ્યું છે કે ધ્યાનમાં લેવામાં આવેલી પદ્ધતિઓ વાસ્તવિક સમયમાં ગતિશીલ ત્રિ-પરિમાણીય વસ્તુઓના નિર્માણ માટેની જરૂરિયાતોને પૂર્વનિર્ધારિત વિગતો સાથે સંતોષતી નથી, અને તેથી, ત્યાં એક વ્યવહારુ છે. તેમના સુધારાની જરૂર છે. પંખા-આકારના બે-પાસ ડેલૌનેય ત્રિકોણ અલ્ગોરિધમનો ફેરફાર પ્રસ્તાવિત છે, જેનું કાર્યાત્મક લક્ષણ ત્રિકોણ બિંદુઓના કોઓર્ડિનેટ એરેના સમૂહના કેન્દ્રના મૂલ્યોની ગણતરી કરવા માટે છે. X અને Y અક્ષો સંશોધિત ડેલૌનેય ત્રિકોણ અલ્ગોરિધમના સમયની લાક્ષણિકતાઓનું વિશ્લેષણ કરવામાં આવે છે. આ ગણતરીઓ સામૂહિક બિંદુના કેન્દ્રના કોઓર્ડિનેટ્સ નક્કી કરતી વખતે પોઈન્ટ્સની વિશાળ શ્રેણી પર પ્રભાવને નોંધપાત્ર રીતે સુધારવાનું શક્ય બનાવે છે અને ડેટા ઓવરફ્લો ટાળે છે, અને તેથી સોફ્ટવેર અમલીકરણમાં ભૂલો.

1. નુટ ડી.ઇ. પ્રોગ્રામિંગની કળા. વોલ્યુમ 1. મૂળભૂત ગાણિતીક નિયમો. – એમ.: વિલિયમ્સ, 2008. – 680 પૃષ્ઠ.
2. નુટ ડી.ઇ. પ્રોગ્રામિંગની કળા. વોલ્યુમ 3. સૉર્ટિંગ અને સર્ચિંગ. – એમ.: વિલિયમ્સ, 2008. – 800 પૃષ્ઠ.
3. મેન્ડેલબ્રોટ B. પ્રકૃતિની ખંડિત ભૂમિતિ. – એમ.: કોમ્પ્યુટર સંશોધન સંસ્થા, 2002. – 656 પૃષ્ઠ.
4. Skvortsov A.V. Delaunay ત્રિકોણ અને તેની અરજી. – ટોમ્સ્ક: ટોમ્સ્ક યુનિવર્સિટી પબ્લિશિંગ હાઉસ, 2002. – 128 પૃષ્ઠ.
5. સ્કવોર્ટ્સોવ એ.વી. રેખીય સમયમાં ડેલૌનાય ત્રિકોણનું નિર્માણ. – ટોમ્સ્ક: ટોમ્સ્ક યુનિવર્સિટી પબ્લિશિંગ હાઉસ, 1999. – P.120-126.
6. સ્કવોર્ટ્સોવ એ.વી., મિર્ઝા એન.એસ. ત્રિકોણ બનાવવા અને વિશ્લેષણ કરવા માટેના અલ્ગોરિધમ્સ. – ટોમ્સ્ક: ટોમ્સ્ક યુનિવર્સિટી પબ્લિશિંગ હાઉસ, 2006. – 168 પૃષ્ઠ.
7. થોમસ એચ. કોર્મન, ચાર્લ્સ આઈ. લીસેરોન, રોનાલ્ડ એલ. રિવેસ્ટ, ક્લિફોર્ડ સ્ટેઈન. અલ્ગોરિધમ્સ: બાંધકામ અને વિશ્લેષણ, 3જી આવૃત્તિ.: અનુવાદ. અંગ્રેજીમાંથી – એમ.: વિલિયમ્સ, 2013. – 1328 પૃષ્ઠ.
8. શૈદુરોવ વી.વી. મલ્ટિગ્રીડ મર્યાદિત તત્વ પદ્ધતિઓ. – એમ.: નૌકા, 1989. – 288 પૃષ્ઠ.
9. સ્ટર્જ એચ. (1926). વર્ગ-અંતરાલની પસંદગી. જે. આમેર. આંકડાશાસ્ત્રી. એસો., 21, 65-66.

મુખ્ય શબ્દો:વર્ચ્યુઅલ રિયાલિટી, આપેલ બિંદુઓની શ્રેણી પર ત્રિકોણ, ડેલૌનેય ત્રિકોણ, ગતિશીલ ત્રિ-પરિમાણીય વસ્તુઓનું નિર્માણ.

સંશોધિત ડેલૌનાયનું ત્રિકોણ અલ્ગોરિધમ

ટેપ્લોવ એ.એ., સ્નાતક, MSTU બૌમન, "સોફ્ટવેર અને માહિતી તકનીકી વિભાગ", મોસ્કો, [ઇમેઇલ સુરક્ષિત]

માઇકોવ કે.એ., ડોકટર ઓફ ટેકનિકલ સાયન્સ, પ્રોફેસર, MSTU બૌમન, "સોફ્ટવેર એન્ડ ઇન્ફોર્મેશન ટેક્નોલોજીસ" વિભાગ, મોસ્કો, [ઇમેઇલ સુરક્ષિત]

અમૂર્ત:ઉચ્ચ પ્રદર્શન અને ઓછા સંસાધન વપરાશ સાથે ડેલૌનાયના ત્રિકોણની વર્ચ્યુઅલ રીતે લોકપ્રિય પદ્ધતિઓના તુલનાત્મક વિશ્લેષણના પરિણામો આ લેખમાં વર્ણવવામાં આવ્યા છે. ચોક્કસ ડિગ્રી સાથે વાસ્તવિક સમયમાં ગતિશીલ 3-D ઑબ્જેક્ટ્સ બનાવવાના ઉદ્દેશ્ય સાથે વધુ આધુનિકીકરણ માટેની પદ્ધતિની પસંદગી વાજબી છે. ડેલૌનાયના ત્રિકોણના ફાઇબરવાળા બે-પાસ અલ્ગોરિધમના મુખ્ય તબક્કાઓમાંના એકમાં ફેરફાર કરવામાં આવ્યો છે. વિતરણની ઘનતા અનુસાર ત્રિકોણના સેલ એરેના અંતરાલ પાર્ટીશન માટે અલ્ગોરિધમનો પ્રસ્તાવ છે, જે હાર્ડવેર અમલીકરણમાં ભૂલોને ટાળવા માટે પરવાનગી આપે છે.

કીવર્ડ્સ:વર્ચ્યુઅલ રિયાલિટી, આપેલ સેલ એરે પર ત્રિકોણ, ડેલૌનેયનું ત્રિકોણ, ગતિશીલ 3-ડી ઑબ્જેક્ટનું નિર્માણ.

VKontakte

પોઈન્ટ S ના મર્યાદિત સમૂહ માટે ત્રિકોણ એ સમૂહ S ના તમામ બિંદુઓને બંધ કરીને બહિર્મુખ હલ CH(S) ને ત્રિકોણ કરવાની સમસ્યા છે. ત્રિકોણમાં સીધા રેખાના ભાગો એકબીજાને છેદતા નથી - તેઓ ફક્ત S સમૂહ સાથે જોડાયેલા સામાન્ય બિંદુઓ પર જ મળી શકે છે. સીધી રેખાના ભાગો ત્રિકોણને બંધ કરે છે, અમે તેમને પાંસળી ગણીશું. ફિગ માં. આકૃતિ 1 બિંદુઓના સમાન સમૂહ માટે ત્રિકોણના બે અલગ-અલગ સંસ્કરણો બતાવે છે (આપણે આ આંકડાઓમાં દોરેલા વર્તુળોને અસ્થાયી રૂપે અવગણીશું).

ચોખા. 1

આપેલ બિંદુ S ના સમૂહ માટે, આપણે જોઈ શકીએ છીએ કે સમૂહ S ના તમામ બિંદુઓને સીમા બિંદુઓમાં વિભાજિત કરી શકાય છે - તે બિંદુઓ જે બહિર્મુખ હલ CH(S) ની સીમા પર આવેલા છે અને આંતરિક બિંદુઓ - જે બહિર્મુખની અંદર આવેલા છે. હલ CH(S). તમે ત્રિકોણ S ના પરિણામે મેળવેલી ધારને પણ વર્ગીકૃત કરી શકો છો શેલ પાંસળીઅને આંતરિક પાંસળી. હલની કિનારીઓ બહિર્મુખ હલ CH(S) ની સીમા સાથે સ્થિત કિનારીઓનો સમાવેશ કરે છે, અને આંતરિક કિનારીઓ અન્ય તમામ કિનારીઓનો સમાવેશ કરે છે જે બહિર્મુખ હલની અંદર ત્રિકોણનું નેટવર્ક બનાવે છે. નોંધ કરો કે દરેક શેલ ધાર બે અડીને આવેલા સીમા બિંદુઓને જોડે છે, જ્યારે આંતરિક કિનારીઓ કોઈપણ પ્રકારના બે બિંદુઓને જોડી શકે છે. ખાસ કરીને, જો આંતરિક ધાર બે સીમા બિંદુઓને જોડે છે, તો તે બહિર્મુખ હલ CH(S) નો તાર છે. એ પણ નોંધો કે ત્રિકોણની દરેક ધાર એ બે ક્ષેત્રોની સીમા છે: દરેક આંતરિક ધાર બે ત્રિકોણ વચ્ચે છે, અને શેલની દરેક ધાર ત્રિકોણ અને અનંત સમતલ વચ્ચે છે.

બિંદુઓનો કોઈપણ સમૂહ, કેટલાક તુચ્છ કિસ્સાઓ સિવાય, ત્રિકોણની એક કરતાં વધુ પદ્ધતિને મંજૂરી આપે છે. પરંતુ ત્યાં એક નોંધપાત્ર મિલકત છે: આપેલ સમૂહ માટે ત્રિકોણની કોઈપણ પદ્ધતિ ત્રિકોણની સમાન સંખ્યા નક્કી કરે છે, જે પ્રમેયમાંથી અનુસરે છે:

બિંદુઓના સમૂહના ત્રિકોણ પરનું પ્રમેય.ધારો કે પોઈન્ટ S ના સમૂહમાં n>3 પોઈન્ટ છે અને તે બધા સમરેખા નથી. વધુમાં, તેમાંથી i બિંદુઓ આંતરિક છે (એટલે ​​​​કે, બહિર્મુખ હલ CH(S) ની અંદર આવેલા છે. પછી, સમૂહ S ના ત્રિકોણની કોઈપણ પદ્ધતિ બરાબર n + i - 2 ત્રિકોણમાં પરિણમશે.

પ્રમેયને સાબિત કરવા માટે, આપણે સૌ પ્રથમ n-i સીમા બિંદુઓના ત્રિકોણને ધ્યાનમાં લઈએ છીએ. બહિર્મુખ બહુકોણના બધા શિરોબિંદુઓ હોવાથી, આવા ત્રિકોણ (n - i) - 2 ત્રિકોણમાં પરિણમશે. (આ ચકાસવું મુશ્કેલ નથી અને વધુમાં, તે બતાવી શકાય છે કે કોઈપણ ત્રિકોણ મનસ્વી m-બાજુવાળા બહુકોણ - બહિર્મુખ અથવા બિન-બહિર્મુખ - m - 2 ત્રિકોણ ધરાવે છે). હવે ચાલો તપાસીએ કે જ્યારે બાકીના i આંતરિક બિંદુઓ ઉમેરવામાં આવે ત્યારે ત્રિકોણનું શું થશે, દરેક વખતે એક. અમે દાવો કરીએ છીએ કે આવા દરેક બિંદુને ઉમેરવાથી ત્રિકોણની સંખ્યામાં બે વધારો થાય છે. આંતરિક બિંદુ ઉમેરતી વખતે, બે પરિસ્થિતિઓ ઊભી થઈ શકે છે, જે ફિગમાં બતાવેલ છે. 2. પ્રથમ, બિંદુ કેટલાક ત્રિકોણની અંદર હોઈ શકે છે અને પછી આવા ત્રિકોણને ત્રણ નવા ત્રિકોણ દ્વારા બદલવામાં આવે છે. બીજું, જો કોઈ બિંદુ ત્રિકોણ ધારમાંથી એક સાથે એકરુપ હોય, તો આ ધારને અડીને આવેલા બે ત્રિકોણમાંથી પ્રત્યેકને બે નવા ત્રિકોણથી બદલવામાં આવે છે. તે અનુસરે છે કે બધા i બિંદુઓ ઉમેર્યા પછી, ત્રિકોણની કુલ સંખ્યા (n - i - 2) + (2i), અથવા ફક્ત n + i - 2 થશે.

ચોખા. 2

આ વિભાગમાં, અમે Delaunay triangulation તરીકે ઓળખાતા વિશિષ્ટ પ્રકારના ત્રિકોણ બનાવવા માટે એક અલ્ગોરિધમ રજૂ કરીશું. આ ત્રિકોણ એ અર્થમાં સારી રીતે સંતુલિત છે કે જે ત્રિકોણ રચાય છે તે સમકોણાકાર હોય છે. ઉદાહરણ તરીકે, ફિગમાં બતાવેલ ત્રિકોણ. 1a ડેલૌનાય ત્રિકોણ પ્રકારને આભારી હોઈ શકે છે, અને ફિગમાં. 1b ત્રિકોણમાં ઘણા બધા વિસ્તરેલ ત્રિકોણ હોય છે અને તે ડેલૌનાય પ્રકારને આભારી નથી. ફિગ માં. આકૃતિ 3 મોટી સંખ્યામાં બિંદુઓના સમૂહ માટે ડેલૌનાય ત્રિકોણનું ઉદાહરણ બતાવે છે.

ચોખા. 3

Delaunay ત્રિકોણ રચવા માટે, અમને ઘણી નવી વ્યાખ્યાઓની જરૂર છે. પોઈન્ટનો સમૂહ ગોળાકાર ગણવામાં આવે છે જો ત્યાં એક વર્તુળ હોય કે જેના પર સમૂહના તમામ બિંદુઓ આવેલા હોય. આવા વર્તુળને આપેલ બિંદુઓના સમૂહ માટે પરિક્રમા કરવામાં આવશે. ત્રિકોણનું ઘેરાયેલું વર્તુળ તેના ત્રણેય (બિન-કોલિનિયર) શિરોબિંદુઓમાંથી પસાર થાય છે. એવું કહેવાય છે કે જો વર્તુળની અંદર સમૂહ Sમાંથી કોઈ બિંદુઓ ન હોય તો આપેલ બિંદુઓના સમૂહના સંદર્ભમાં વર્તુળ બિંદુ-મુક્ત હશે પરંતુ, જો કે, સમૂહ Sમાંથી બિંદુઓ વર્તુળ પર સ્થિત હોઈ શકે છે સૌથી વધુ બિંદુ મુક્ત.

જો દરેક ત્રિકોણ માટેનું પરિઘ બિંદુઓથી મુક્ત હોય તો S બિંદુઓના સમૂહનું ત્રિકોણ એક Delaunay ત્રિકોણ હશે. ત્રિકોણ રેખાકૃતિ ફિગમાં. આકૃતિ 1a બે વર્તુળો બતાવે છે જેમાં સ્પષ્ટપણે તેમની અંદર અન્ય બિંદુઓ શામેલ નથી (તમે અન્ય ત્રિકોણ માટે વર્તુળો દોરી શકો છો તેની ખાતરી કરવા માટે કે તેઓ સમૂહના બિંદુઓથી પણ મુક્ત છે). આ નિયમ ફિગમાં આકૃતિમાં જોવા મળતો નથી. 16 - બીજા ત્રિકોણનો એક બિંદુ દોરેલા વર્તુળની અંદર આવે છે, તેથી, આ ગ્રિન્ગ્યુલેશન ડેલૌનાય પ્રકારનું નથી.

ત્રિકોણ અલ્ગોરિધમને સરળ બનાવવા માટે સેટ S માંના બિંદુઓ વિશે બે ધારણાઓ કરી શકાય છે. પ્રથમ, ત્રિકોણ બિલકુલ અસ્તિત્વમાં રહે તે માટે, આપણે ધારવું જોઈએ કે સમૂહ Sમાં ઓછામાં ઓછા ત્રણ બિંદુઓ છે અને તે સમરેખા નથી. બીજું, ડેલૌનેય ત્રિકોણ અદ્વિતીય હોવા માટે, તે જરૂરી છે કે સમૂહ Sમાંથી કોઈ ચાર બિંદુઓ સમાન પરિઘ પર ન હોય. તે જોવાનું સરળ છે કે આવી ધારણા વિના ડેલૌનાય ત્રિકોણ અનન્ય નહીં હોય, કારણ કે એક પરિક્રમાવાળા વર્તુળ પરના 4 બિંદુઓ આપણને બે અલગ-અલગ ડેલૌનાય ત્રિકોણને સમજવાની મંજૂરી આપે છે.

અમારું અલ્ગોરિધમ વર્તમાન ત્રિકોણ એક સમયે એક ત્રિકોણને સતત વધારીને કાર્ય કરે છે. શરૂઆતમાં, વર્તમાન ત્રિકોણમાં શેલની એક ધાર હોય છે; દરેક પુનરાવૃત્તિ પર, અલ્ગોરિધમ એક નવો ત્રિકોણ શોધે છે જે જોડે છે સરહદવર્તમાન ત્રિકોણ.

સીમાની વ્યાખ્યા વર્તમાન ત્રિકોણની તુલનામાં ડેલૌનાય ત્રિકોણની ધાર માટે નીચેની વર્ગીકરણ યોજના પર આધારિત છે. દરેક ધાર હોઈ શકે છે સૂવું, જીવંતઅથવા મૃત:

• ઊંઘની પાંસળી: ડેલૌનાય ત્રિકોણની ધાર નિષ્ક્રિય હોય છે જો તે હજી સુધી અલ્ગોરિધમ દ્વારા શોધાયેલ ન હોય;
• જીવંત પાંસળી: જો તે મળી આવે તો પાંસળી જીવંત છે, પરંતુ માત્ર એક નજીકનો વિસ્તાર જાણીતો છે;
• મૃત પાંસળી: એક ધાર મૃત માનવામાં આવે છે જો તે મળી આવે અને બંને બાજુના વિસ્તારો જાણીતા હોય.

શરૂઆતમાં, બહિર્મુખ i લોબની એકમાત્ર ધાર જીવંત છે - એક અનબાઉન્ડ પ્લેન તેની બાજુમાં છે, અને અન્ય તમામ કિનારીઓ નિષ્ક્રિય છે. જેમ જેમ અલ્ગોરિધમ કામ કરે છે તેમ, કિનારીઓ ઊંઘમાંથી જીવતા મૃત તરફ જાય છે. દરેક તબક્કે સીમા જીવંત કિનારીઓનો સમૂહ ધરાવે છે.

દરેક પુનરાવૃત્તિ પર, સીમાની ધારોમાંથી કોઈપણ એક પસંદ કરવામાં આવે છે અને તે પ્રક્રિયાને આધિન છે, જેમાં એક અજ્ઞાત પ્રદેશની શોધનો સમાવેશ થાય છે કે જેની ધાર e છે, જો આ પ્રદેશ ત્રિકોણ f છે, જે દ્વારા વ્યાખ્યાયિત કરવામાં આવે છે ધાર e ના અંતિમ બિંદુઓ અને કેટલાક ત્રીજા શિરોબિંદુ v, પછી ધાર e મૃત બની જાય છે, કારણ કે તેની બાજુના બંને વિસ્તારો હવે જાણીતા છે. ત્રિકોણ t ની અન્ય બે ધારોમાંથી દરેક નીચેની સ્થિતિમાં સ્થાનાંતરિત થાય છે: ઊંઘમાંથી જીવંત અથવા જીવંતમાંથી મૃત સુધી. અહીં શિરોબિંદુ v કહેવામાં આવશે જોડાણધાર e સાથે નહિંતર, જો અજ્ઞાત પ્રદેશ અનંત સમતલ હોય, તો ધાર e મૃત્યુ પામે છે. આ કિસ્સામાં, ધાર e પાસે સંયોજક શિરોબિંદુ નથી.

ફિગ માં. આકૃતિ 4 અલ્ગોરિધમનું સંચાલન બતાવે છે, જ્યાં ક્રિયા ઉપરથી નીચે સુધી થાય છે અને જમણી તરફ મહિમા થાય છે. દરેક તબક્કે સરહદ જાડા રેખા સાથે પ્રકાશિત થાય છે.

અલ્ગોરિધમનો અમલ delaunayTriangulate પ્રોગ્રામમાં થાય છે. પ્રોગ્રામને n પોઈન્ટની એરે આપવામાં આવે છે અને ડેલૌનેય ત્રિકોણનું પ્રતિનિધિત્વ કરતા ત્રિકોણની સૂચિ આપે છે. અમલીકરણ ભૌમિતિક ડેટા સ્ટ્રક્ચર વિભાગમાંથી પરિપત્ર સૂચિ વર્ગ અને વર્ગોનો ઉપયોગ કરે છે. ડિક્શનરી ક્લાસ એ કોઈપણ ડિક્શનરી હોઈ શકે છે જે જરૂરી ઑપરેશનને સપોર્ટ કરે છે. ઉદાહરણ તરીકે, તમે #define Dictionary RandomizedSearchTree ને ઓવરરાઇડ કરી શકો છો.

યાદી * (બિંદુ s, int n) ( બિંદુ p; યાદી *ત્રિકોણ = નવી યાદી ; શબ્દકોશ

સરહદ (એજસીએમપી);

એજ *e = hullEdge(s, n);

Int edgeCmp (Edge *a, Edge *b) ( જો (a->org< b->org) વળતર 1;< b->જો (a->org > b->org) 1 પરત કરે છે;

જો (a->ડેસ્ટ

ડેસ્ટ) રીટર્ન -1;

જો (a->dest > b->dest) પરત 1;

પરત 0; ) સરહદ એક પગલાથી બીજા પગલામાં કેવી રીતે બદલાય છે, અને આ ફેરફારોને પ્રતિબિંબિત કરવા માટે અપડેટફ્રન્ટિયર ફંક્શન બોર્ડરના કિનારી શબ્દકોશને કેવી રીતે સંશોધિત કરે છે? જ્યારે નવો ત્રિકોણ t સીમા સાથે જોડાયેલ હોય છે, ત્યારે ત્રિકોણની ત્રણ ધારની સ્થિતિ બદલાય છે. સીમાને અડીને આવેલ ત્રિકોણની ધાર જીવંતમાંથી મૃતમાં બદલાય છે. UpdateFrontier ફંક્શન આ ધારને અવગણી શકે છે કારણ કે જ્યારે removeMin ફંક્શનને કૉલ કરવામાં આવે ત્યારે તેને ડિક્શનરીમાંથી પહેલેથી જ કાઢી નાખવું જોઈએ. ત્રિકોણ ટીની બાકીની બે કિનારીઓમાંથી દરેક તેની સ્થિતિને ઊંઘમાંથી જીવંતમાં બદલી નાખે છે, જો તે અગાઉ શબ્દકોશમાં નોંધાયેલ ન હોય અથવા જીવંતમાંથી મૃત સુધી, જો ધાર પહેલેથી જ શબ્દકોશમાં હોય. ફિગ માં. 5 બંને કેસ બતાવે છે. આકૃતિ મુજબ, અમે જીવંત ધાર af ને પ્રક્રિયા કરીએ છીએ અને, તે બિંદુ b એ તેનો સંયોજક છે તે શોધ્યા પછી, આપણે વર્તમાન ત્રિકોણમાં ત્રિકોણ afb ઉમેરીએ છીએ. પછી આપણે શબ્દકોશમાં એજ fb શોધીએ છીએ અને, કારણ કે તે હજી ત્યાં નથી અને તે પ્રથમ વખત શોધાયું છે, તેની સ્થિતિ ઊંઘમાંથી જીવંત સુધી બદલાય છે. શબ્દકોશને સંપાદિત કરવા માટે, અમે કિનારી fb ને ફેરવીશું જેથી તેની બાજુમાં આવેલ અજાણ્યો પ્રદેશ તેની જમણી બાજુ આવે અને આ ધારને શબ્દકોશમાં લખી શકાય. પછી આપણે શબ્દકોશમાં એજ ba શોધીશું - કારણ કે તે તેમાં છે, તે પહેલેથી જ જીવંત છે (તેની બાજુમાં આવેલો જાણીતો વિસ્તાર ત્રિકોણ abc છે). તેના માટે અજ્ઞાત પ્રદેશ, ત્રિકોણ afb, હમણાં જ શોધાયેલ હોવાથી, આ ધાર શબ્દકોશમાંથી દૂર કરવામાં આવી છે.

અપડેટફ્રન્ટિયર ફંક્શન ફ્રન્ટિયર ડિક્શનરીને સંપાદિત કરે છે, જેમાં બિંદુ a થી બિંદુ b સુધીની ધારની સ્થિતિ બદલાય છે:

ચોખા. 5< n; i++) if (s[i] < s[m]) m = i; swap(s, s[m]); for (m = 1, i = 2; i < n; i++) { int с = s[i].classify (s, s[m]); if ((c == LEFT) || (C == BETWEEN)) m = i; } return new Edge(s, s[m]); }

રદબાતલ અપડેટફ્રન્ટિયર (શબ્દકોષ

&ફ્રન્ટીયર, પોઈન્ટ &a, પોઈન્ટ &b) ( Edge *e = new Edge (a, b); if (frontier.find (e)) frontier.remove(e); else ( e->flip(); frontier.insert( e);

ત્રિકોણ ફંક્શન પેરામીટર તરીકે તેને પસાર કરેલા ત્રણ બિંદુઓ માટે બહુકોણ બનાવે છે અને પરત કરે છે:

બિન-ઓવરલેપિંગ ત્રિકોણનું નેટવર્ક બનાવવાની સમસ્યા એ કોમ્પ્યુટેશનલ ભૂમિતિમાં મૂળભૂત મુદ્દાઓમાંની એક છે અને સપાટીના મોડેલિંગ અને અવકાશી સમસ્યાઓ ઉકેલવા માટે કોમ્પ્યુટર ગ્રાફિક્સ અને ભૌગોલિક માહિતી પ્રણાલીઓમાં વ્યાપકપણે ઉપયોગમાં લેવાય છે.

બિન-ઓવરલેપિંગ ત્રિકોણનું નેટવર્ક બનાવવાની સમસ્યા સૌપ્રથમ 1934 માં સોવિયેત ગણિતશાસ્ત્રી બી.એન. ડેલોનના કાર્યમાં ઉભી થઈ હતી, જેમણે અનુરૂપ પરિસ્થિતિઓની રચના કરી હતી.

ગણિતમાં, આપેલ બિંદુઓમાંથી ત્રિકોણ બાંધવાનું કાર્ય એ છે કે તેઓને એકબીજા સાથે જોડાયેલા ન હોય તેવા ભાગો દ્વારા જોડીમાં જોડવાનું કાર્ય છે જેથી ત્રિકોણનું નેટવર્ક રચાય. તેના મુખ્ય ઘટકો છે (ફિગ. 5.3): ગાંઠો (ત્રિકોણના શિરોબિંદુઓ), કિનારીઓ (બાજુઓ) અને ચહેરાઓ (ત્રિકોણ પોતે). બાંધવામાં આવેલ ત્રિકોણ બહિર્મુખ (જો તે મોડેલિંગ વિસ્તારને આવરી લેતો લઘુત્તમ બહુકોણ હોય), બિન-બહિર્મુખ (જો ત્રિકોણ બહિર્મુખ ન હોય તો) અને શ્રેષ્ઠ (જો બધી ધારની લંબાઈનો સરવાળો ન્યૂનતમ હોય તો) હોઈ શકે છે.

આવા ત્રિકોણના નેટવર્કને ડેલૌનેય ત્રિકોણ કહેવામાં આવે છે જો તે અમુક શરતોને સંતોષે છે:

મૂળ બિંદુઓમાંથી કોઈ પણ ત્રિકોણ (ફિગ. 5.3);

ત્રિકોણ બહિર્મુખ છે અને ઉપર ઘડવામાં આવેલી ડેલૌનેય સ્થિતિને સંતોષે છે;

તમામ ત્રિકોણના લઘુત્તમ ખૂણાઓનો સરવાળો એ તમામ શક્ય ત્રિકોણમાંથી મહત્તમ છે;

ત્રિકોણની આસપાસ વર્ણવેલ વર્તુળોની ત્રિજ્યાનો સરવાળો તમામ સંભવિત ત્રિકોણમાં ન્યૂનતમ છે.

ડેલૌનાય ત્રિકોણ બનાવવા માટે ઉપરોક્ત માપદંડોમાંથી પ્રથમ, જેને પરિપત્ર કહેવાય છે, તે મુખ્ય પૈકી એક છે અને સામાન્ય ચહેરાવાળા ત્રિકોણની કોઈપણ જોડી માટે તપાસવામાં આવે છે. માપદંડનું ગાણિતિક અર્થઘટન ફિગમાંથી અનુસરે છે. 5.3:

(5.2)

ડેલૌનેય ત્રિકોણ બાંધવાની ઘણી રીતો છે, જે તાજેતરમાં ત્રિકોણ જાળી બાંધવાની સૌથી લોકપ્રિય પદ્ધતિઓમાંની એક છે. રાહત મોડલ બનાવવા માટે ઘણી GIS સિસ્ટમોમાં તેનો ઉપયોગ થાય છે.

જ્યારે દ્વિ-પરિમાણીય અવકાશ પર લાગુ કરવામાં આવે છે, ત્યારે તે નીચે પ્રમાણે ઘડવામાં આવે છે: એકબીજા સાથે જોડાયેલા બિન-ઓવરલેપિંગ ત્રિકોણની સિસ્ટમ સૌથી નાની પરિમિતિ ધરાવે છે જો રચના ત્રિકોણ (ફિગ. 5.4) ની આસપાસ વર્ણવેલ કોઈપણ વર્તુળોની અંદર કોઈ પણ શિરોબિંદુ ન આવે.

ચોખા. 5.4. Delaunay ત્રિકોણ

આનો અર્થ એ છે કે આવા ત્રિકોણ સાથેના પરિણામી ત્રિકોણ સમભુજની શક્ય તેટલી નજીક છે, અને વિપરીત શિરોબિંદુમાંથી પરિણામી ત્રિકોણની દરેક બાજુ અનુરૂપ અર્ધ-વિમાનના તમામ સંભવિત બિંદુઓથી મહત્તમ કોણ પર દૃશ્યમાન છે. આ બરાબર શ્રેષ્ઠ ત્રિકોણ છે જેની કિનારીઓ સાથે રેખીય પ્રક્ષેપ સામાન્ય રીતે આઇસોલિન બનાવવા માટે કરવામાં આવે છે.

Delaunay ત્રિકોણ બનાવવા માટે ઘણા અલ્ગોરિધમ નીચેના પ્રમેયનો ઉપયોગ કરે છે.

પ્રમેય 1. ડેલૌનાય ત્રિકોણ એબીડી અને એસીડી (ફિગ. 5.5) ત્રિકોણની જોડીમાં ડેલૌનેય સ્થિતિને સંતોષતા ન હોય તેવા સંલગ્ન ત્રિકોણ ABC અને BCDની જોડીને અનુક્રમે ગોઠવીને બિંદુઓની સમાન સિસ્ટમનો ઉપયોગ કરીને અન્ય કોઈપણ ત્રિકોણમાંથી મેળવી શકાય છે.

ચોખા. 5.5.. ત્રિકોણનું પુનઃનિર્માણ જે ડેલૌનેય સ્થિતિને સંતોષતા નથી

આ પુનઃનિર્માણ કામગીરીને ઘણીવાર ફ્લિપ કહેવામાં આવે છે. આ પ્રમેય વ્યક્તિને ક્રમિક રીતે ડેલૌનેય ત્રિકોણ બનાવવાની મંજૂરી આપે છે, પ્રથમ કેટલાક ત્રિકોણનું નિર્માણ કરે છે, અને પછી ક્રમિક રીતે તેને ડેલૌનાય સ્થિતિના અર્થમાં સુધારે છે. અડીને આવેલા ત્રિકોણની જોડી માટે ડેલૉનાય સ્થિતિ તપાસતી વખતે, તમે વ્યાખ્યાનો સીધો ઉપયોગ કરી શકો છો, પરંતુ કેટલીકવાર ઉપર સૂચિબદ્ધ શરતોના આધારે અન્ય પદ્ધતિઓનો ઉપયોગ કરવામાં આવે છે.

આ પરિસ્થિતિઓમાં, સમગ્ર ત્રિકોણની કુલ લાક્ષણિકતા દેખાય છે (ન્યૂનતમ ખૂણાઓનો સરવાળો અથવા ત્રિજ્યાનો સરવાળો), જેને ઑપ્ટિમાઇઝ કરીને કોઈ ડેલૌનેય ત્રિકોણ મેળવી શકે છે.

ઉપર સૂચવ્યા મુજબ, ત્રિકોણ બાંધતી વખતે કરવામાં આવતી સૌથી મહત્વપૂર્ણ ક્રિયાઓમાંની એક ત્રિકોણની આપેલ જોડી માટે ડેલૌનેય સ્થિતિ તપાસી રહી છે. Delaunay triangulation ની વ્યાખ્યા અને અનુરૂપ શરતોના આધારે, સામાન્ય રીતે વ્યવહારમાં ઘણી ચકાસણી પદ્ધતિઓનો ઉપયોગ કરવામાં આવે છે:

- પરિપત્ર સમીકરણ દ્વારા તપાસવું;

- પૂર્વ-ગણતરીવાળા વર્તુળ સાથે તપાસો;

- વિરોધી ખૂણાઓનો સરવાળો તપાસો;

- વિરોધી ખૂણાઓના સરવાળાની સંશોધિત તપાસ.

ઘણી પ્રણાલીઓ પ્રી-કમ્પ્યુટેડ સર્કલ સાથે ટેસ્ટ કરે છે. પૂર્વ-ગણતરી કરેલ વર્તુળો દ્વારા ચકાસણી અલ્ગોરિધમનો મુખ્ય વિચાર દરેક બાંધેલા ત્રિકોણ માટે કેન્દ્ર અને તેની આસપાસ વર્ણવેલ વર્તુળના ત્રિજ્યાની પૂર્વ-ગણતરી કરવાનો છે, ત્યારબાદ ડેલૌનેય સ્થિતિ તપાસવાથી કેન્દ્ર સુધીના અંતરની ગણતરી કરવામાં ઘટાડો થશે. આ વર્તુળની અને ત્રિજ્યા સાથે પરિણામની તુલના. આસપાસ વર્ણવેલ વર્તુળનું કેન્દ્ર અને ત્રિજ્યા r , , , r 2 = (b 2 + c 2 - 4аd)/4а 2 તરીકે શોધી શકાય છે, જ્યાં મૂલ્યો a, b, c, dસૂત્રો દ્વારા નિર્ધારિત (5.3)

(5.3)

આ વર્તુળના સમીકરણ માટે બીજી એન્ટ્રી છે:

(5.5.)

(5.6)

પછી માટે Delaunay શરત ત્યારે જ સંતુષ્ટ થશે જ્યારે અન્ય કોઈપણ ત્રિકોણ બિંદુ માટે તે હશે:

(x 0 – x C) 2 + (y 0 – y C) 2 ≥ r 2 . (5.7)

હાલમાં, Delaunay ત્રિકોણ બનાવવા માટે ઘણા અલ્ગોરિધમ્સ છે. ઘણા જાણીતા અલ્ગોરિધમ્સ ડેલૌનાય ત્રિકોણ વ્યાખ્યાનો ગૌણ ત્રિકોણ લક્ષણ તરીકે ઉપયોગ કરે છે. તેથી, આવા અલ્ગોરિધમ્સમાં નીચેની નબળાઈઓ નોંધવામાં આવે છે:

- એલ્ગોરિધમ્સ સતત ગણતરી કરેલ ત્રિકોણમિતિ કાર્યોનો ઉપયોગ કરે છે, જે પ્રક્રિયાને નાટકીય રીતે ધીમું કરે છે;

- પોઈન્ટ અને બેઝ સેગમેન્ટ વચ્ચેના સંબંધનો અભ્યાસ કરતી વખતે, ખૂબ જ નાના ખૂણો ઉદ્ભવે છે, અને જ્યારે ત્રિકોણમિતિ ફંક્શનનો ઉપયોગ થાય છે, ત્યારે કમ્પ્યુટરમાં ડેટા રજૂઆતોની મર્યાદિત ચોકસાઈને કારણે ક્રમ અદૃશ્ય થઈ જવાનો અને 0 દ્વારા વિભાજીત થવાનો ભય હંમેશા રહે છે; સતત વધારાની પ્રક્રિયા.

સૌથી વધુ જાણીતા સોફ્ટવેર ઉત્પાદનો ત્રિકોણ બનાવવા માટે મુખ્ય, પ્રાથમિક સિદ્ધાંત તરીકે ખાલી બોલ પ્રમેયનો ઉપયોગ કરીને ડેલૌનેય ત્રિકોણ બનાવે છે. અલ્ગોરિધમ આના જેવો દેખાય છે:

- બિંદુઓનો સંપૂર્ણ સમૂહ ત્રિકોણમાં વહેંચાયેલો છે, એટલે કે. ત્રણ બિંદુઓના સંયોજનો બનાવવામાં આવે છે;

- દરેક સંયોજન માટે, પરિમાણિત વર્તુળ અને તેના કેન્દ્રના કોઓર્ડિનેટ્સ જોવા મળે છે;

- જો વર્તમાન સંયોજનના વર્તુળની અંદર એક પણ બિંદુ બાકી ન હોય, તો પછી આ સંયોજન ત્રિકોણ છે - ડેલૌનાય ત્રિકોણનો ભાગ.

આ અલ્ગોરિધમના ફાયદાઓમાં શામેલ છે:

- ત્રિકોણમિતિ કાર્યોના ઉપયોગનો અભાવ, જે બાંધકામ પ્રક્રિયાને ધીમું કરતું નથી;

- ડેલૌનાય ત્રિકોણનું સીધું બાંધકામ, કોઈપણ પ્રારંભિક બાંધકામો વિના;

- તમામ ગણતરીઓ અને પરિવર્તનની સરળતા;

– પરિણામે, ત્રિકોણ ગ્રીડ વ્યક્તિગત રેખાઓને બદલે ઘણા ત્રિકોણ દ્વારા દર્શાવવામાં આવે છે.

આ રીતે બાંધવામાં આવેલ ત્રિકોણ એ આઇસોલાઇન્સ બનાવવા માટે ભૌમિતિક આધાર છે.

Delaunay ત્રિકોણ બનાવવા માટેના અલ્ગોરિધમ્સને સંખ્યાબંધ જૂથોમાં વિભાજિત કરી શકાય છે, જે ઉપયોગમાં લેવાતા ઇનપુટ ડેટાના બંધારણમાં, કોમ્પ્યુટેશનલ કામગીરીનું પ્રમાણ, પ્રારંભિક જગ્યા વગેરેમાં ભિન્ન છે. ચાલો તેમાંથી કેટલાકને ધ્યાનમાં લઈએ.

મર્જિંગ એલ્ગોરિધમ્સમાં સ્ત્રોત બિંદુઓના સમૂહને સબસેટમાં વિભાજીત કરવા, તેમાંથી દરેક પર ત્રિકોણ બાંધવા અને પછી તેમને એક નેટવર્કમાં જોડવાનો સમાવેશ થાય છે. આમાંના એક અલ્ગોરિધમનો સાર નીચે મુજબ આવે છે.

પ્રારંભિક બિંદુઓના સમૂહને ઊભી રેખાઓ દ્વારા બે અથવા વધુ ભાગોમાં વિભાજિત કરવામાં આવે છે, ત્યારબાદ તેમાંથી દરેકને આડી અને ઊભી રેખાઓ દ્વારા લગભગ સમાન ભાગોમાં વિભાજિત કરવામાં આવે છે. પરિણામે, પ્રારંભિક બિંદુઓનો સમગ્ર વિસ્તાર ત્રણ અથવા ચાર બિંદુઓ (ફિગ. 2.4) ના આદિકાળમાં વિભાજિત થાય છે, જેની સાથે એક અથવા બે ત્રિકોણ બાંધવામાં આવે છે.

આ ત્રિકોણને એક નેટવર્કમાં ભેળવીને બે બેઝલાઈન બનાવીને કરવામાં આવે છે (P 0 P 1 અને P 2 P 3, ચોખા. 5.7.a), બેઝ લાઇન (ફિગ. 5.7, b) પર લંબરૂપ દ્વિભાજક પર કેન્દ્રિત ચલ ત્રિજ્યાના વર્તુળો દોરવા, વર્તુળ (બિંદુ) પર પડતા નોડની શોધ એ, ચોખા. 5.7. c) અને નવા ત્રિકોણનું નિર્માણ (P 0 P 1 A).આ કિસ્સામાં, હાલના ત્રિકોણને કાઢી નાખવાની જરૂર પડી શકે છે (ઉદાહરણ તરીકે, P 0 AB).

પુનરાવર્તિત અલ્ગોરિધમ્સ ડેલૌનેય માપદંડ અનુસાર તેના એક સાથે સુધારણા અને પુનઃનિર્માણ સાથે આંશિક રીતે બાંધવામાં આવેલા ત્રિકોણમાં ક્રમિક રીતે પોઈન્ટ ઉમેરવાના વિચાર પર આધારિત છે. સામાન્ય રીતે, તેમાં ઘણા પગલાંઓ શામેલ છે અને પ્રથમ ત્રણ પ્રારંભિક બિંદુઓ પર ત્રિકોણ બાંધવા અને આગલા બિંદુને મૂકવા માટે ઘણા વિકલ્પોની શોધખોળ કરવા માટે નીચે ઉકાળવામાં આવે છે. ખાસ કરીને, મોડેલિંગ વિસ્તારની સીમાની બહાર, હાલના નોડ અથવા ધાર પર, બાંધેલા ત્રિકોણની અંદર, વગેરે માટે વિકલ્પો ધ્યાનમાં લેવામાં આવે છે. આમાંના દરેક વિકલ્પોમાં ચોક્કસ કામગીરી કરવાનો સમાવેશ થાય છે: ધારને બે ભાગમાં વિભાજીત કરવી, ચહેરા પર ત્રણ, વગેરે; જે પછી પરિણામી ત્રિકોણને ડેલૌનેય સ્થિતિ અને જરૂરી પુનઃનિર્માણ માટે ચકાસવામાં આવે છે.

ટુ-પાસ અલ્ગોરિધમ્સમાં પ્રથમ કેટલાક ત્રિકોણનું નિર્માણ, ડેલૌનેય શરતોને અવગણીને અને પછી આ શરતો અનુસાર તેનું પુનઃનિર્માણ સામેલ છે. અલ્ગોરિધમનો ઉપયોગ કરવાનું ઉદાહરણ ફિગમાં બતાવવામાં આવ્યું છે. 5.8.

બનાવેલ રાહત મોડેલને વાસ્તવિકની નજીક લાવવા માટે, તેના રેખીય અને ક્ષેત્રીય માળખાકીય તત્વોને ધ્યાનમાં લેવામાં આવે છે અને પ્રદર્શિત થાય છે તેની ખાતરી કરવા માટે તેમાં વધારાના ઘટકો દાખલ કરવામાં આવે છે. આવા વધારાના તત્વો એ માળખાકીય રેખાઓ છે જેનો વ્યાપકપણે ટોપોગ્રાફીમાં ઉપયોગ થાય છે જે "રાહત હાડપિંજર" ને વ્યાખ્યાયિત કરે છે: વોટરશેડ, થલવેગ્સ, પટ્ટાઓ, ખડકો, તરંગો, તળાવો, કોતરો, દરિયાકિનારા, કૃત્રિમ માળખાઓની સીમાઓ વગેરે, જેની સંપૂર્ણતા એક પ્રકારનું સર્જન કરે છે. Delaunay ત્રિકોણ માટે ફ્રેમ. આ માળખાકીય રેખાઓ ત્રિકોણમાં ત્રિકોણની કિનારીઓ તરીકે રજૂ કરવામાં આવે છે, જે પૃથ્વીની સપાટીની સામાન્ય અસમાનતાની પૃષ્ઠભૂમિ સામે વાસ્તવિક રાહત તત્વોનું મોડેલિંગ પ્રાપ્ત કરે છે. આવી કિનારીઓને સ્ટ્રક્ચરલ (નિશ્ચિત, નૉન-કોન્ફિગરેબલ) કહેવામાં આવે છે, અન્ય ત્રિકોણની ધારને છેદતી નથી અને પછીથી બદલાતી નથી.

બ્રેકલાઈનને ધ્યાનમાં લઈને સપાટીના મોડેલના નિર્માણની સમસ્યાને અવરોધિત ડેલૌનાય ત્રિકોણ કહેવામાં આવે છે જો ડેલૌનાય સ્થિતિઓ અડીને આવેલા ત્રિકોણની કોઈપણ જોડી માટે સંતુષ્ટ હોય કે જે બ્રેકલાઈન દ્વારા અલગ ન હોય. સંશોધકો માને છે કે સૌથી વધુ અસરકારક રીત પુનરાવર્તિત અલ્ગોરિધમનો ઉપયોગ કરીને આવા ત્રિકોણ બનાવવાનો છે.

Delaunay ત્રિકોણ બનાવવા માટેના અલ્ગોરિધમ્સ નોડ્સના કોઓર્ડિનેટ્સની વાસ્તવિક અથવા પૂર્ણાંક રજૂઆત સાથે અમલમાં મૂકવામાં આવે છે, જે પ્રક્રિયાની ઝડપ અને ચોકસાઈને નોંધપાત્ર રીતે વધારી શકે છે, પરંતુ મેચિંગ નોડ્સને શોધવા અને બાકાત રાખવાની સમસ્યાઓને જન્મ આપે છે.

ટીઆઈએન મોડેલ સરળતાથી ગાંઠો ખસેડીને, નવા દાખલ કરીને, વર્તમાનને કાઢીને, એક અથવા અનેક ધારની સ્થિતિ બદલીને, નવી માળખાકીય રેખાઓ રજૂ કરીને, વગેરે દ્વારા સરળતાથી સંપાદિત થાય છે. આવા ફેરફારો હંમેશા અડીને આવેલા ત્રિકોણના નાના જૂથને અસર કરે છે, તેને ફરીથી બનાવવાની જરૂર નથી. સમગ્ર નેટવર્ક અને કર્સરને અનુરૂપ તત્વ પર નિર્દેશ કરીને ઓન લાઇન હાથ ધરવામાં આવે છે.

ચોકસાઈ વિશે:

લાક્ષણિક રાહત તત્વો (ઉદાહરણ તરીકે, વોટરશેડ અને થલવેગ્સ) પર પિકેટ્સ મૂકીને, અમે ગાબડાંમાં નાના તત્વોને અવગણીએ છીએ. ત્રિકોણની આવી કિનારીઓ સાથે સમોચ્ચ રેખાઓ1 બનાવતી વખતે, એક ભૂલ થાય છે, જે ભૂપ્રદેશની અસમાનતા અને ભૂપ્રદેશના ઝોકના કોણ પર આધાર રાખે છે. ઉદાહરણ તરીકે, રાહતના સર્વેક્ષણમાં સરેરાશ ભૂલ 2 થી 10 ડિગ્રી સુધી સપાટીના ઝોકના ખૂણા પર રાહત ક્રોસ-સેક્શનના 1/3 કરતા વધુ ન હોવી જોઈએ. તે ગણતરી કરી શકાય છે કે 0.5 મીટરના રાહત વિભાગ સાથે, ચૂકી ગયેલ અસમાનતાનું મહત્તમ મૂલ્ય (એટલે ​​​​કે, અડીને આવેલા પિકેટ્સમાંથી પસાર થતી સીધી રેખામાંથી જમીનની સપાટીનું વિચલન) (0.5/3) * cos10° થી વધુ ન હોવું જોઈએ. = 0.16 મી.

પરિવહન કરાયેલ માટીના જથ્થાને નિર્ધારિત કરવાની ચોકસાઈ માટે, બિનહિસાબી રાહત વિગત દ્વારા કબજે કરાયેલ વિસ્તાર પણ મહત્વપૂર્ણ છે. ચાલો કહીએ કે પિકેટની બે જોડી વચ્ચે 20x20 મીટરના ચોરસમાં મહત્તમ 0.15 મીટરની ઊંચાઈ સાથે નળાકાર બહિર્મુખતા છે તે ગણતરી કરવી સરળ છે કે જ્યારે આ સપાટીને માત્ર બે ત્રિકોણ સાથે રજૂ કરવામાં આવે ત્યારે તેને ધ્યાનમાં ન લેવાથી લગભગ 40 m3 ની ભૂલ. એટલું નહીં, પરંતુ 1 હેક્ટરના પ્લોટ માટે, જે ટેકરી અથવા ઢોળાવના ઉપરના (સામાન્ય રીતે બહિર્મુખ) ભાગ પર સ્થિત છે, તમને 40 * 25 = 1000 m3 વધારાની માટી મળે છે. જો તમે પિકેટ્સ બમણી વાર લો (એટલે ​​કે દર 10 મીટર), તો ભૂલ ચાર ગણી ઘટશે અને હેક્ટર દીઠ 250 m3 જેટલી થશે. આ પરિબળને અગાઉથી ધ્યાનમાં લઈ શકાય છે, કારણ કે સપાટ રાહતના હકારાત્મક સ્વરૂપો સામાન્ય રીતે બહિર્મુખ આકાર ધરાવે છે, જ્યારે નકારાત્મક સ્વરૂપો અંતર્મુખ આકાર ધરાવે છે. જો સર્વે કરવા માટેના વિસ્તારમાં રાહત અંગેનો અંદાજિત ડેટા હોય, તો સપાટીની વક્રતાની ત્રિજ્યા અને પિકેટની આવશ્યક ઘનતા સમોચ્ચ રેખાઓ અથવા વ્યક્તિગત ઊંચાઈના મૂલ્યો પરથી સરળતાથી ગણતરી કરી શકાય છે.

વ્યાખ્યાન માળખું વ્યાખ્યાઓ એપ્લિકેશનના ક્ષેત્રો એપ્લિકેશનના ક્ષેત્રો ડેલૌનાય ત્રિકોણના ગુણધર્મો ડેલૌનાય ત્રિકોણના ગુણધર્મો ડેલૌનાય ત્રિકોણ બાંધવા માટેની પદ્ધતિઓ ડેલૌનાય ત્રિકોણ બાંધવા માટેની પદ્ધતિઓ પગલું-દર-પગલાં ઇનપુટ પદ્ધતિઓ પગલું-દર-પગલા ઇનપુટ પદ્ધતિઓ પગલું-દર-પગલાં ઇનપુટ પદ્ધતિઓ સ્ટેપ-બાય-સ્ટેપ પદ્ધતિ -બાય-સ્ટેપ સેમ્પલિંગ પદ્ધતિઓ વિઘટન પદ્ધતિઓ વિઘટન પદ્ધતિઓ સ્કેનિંગ પદ્ધતિઓ સ્કેનિંગ પદ્ધતિઓ બે-પાસ પદ્ધતિઓ બે-પાસ પદ્ધતિઓ

ત્રિકોણ ત્રિકોણ એ એક પ્લેનર ગ્રાફ છે જેના આંતરિક પ્રદેશો બધા ત્રિકોણ છે. ત્રિકોણ એ એક પ્લેનર ગ્રાફ છે જેના આંતરિક પ્રદેશો બધા ત્રિકોણ છે. શબ્દ "ત્રિકોણ" શબ્દ છે "ત્રિકોણ" એ આલેખ છે; આલેખ ગ્રાફ બાંધકામ પ્રક્રિયા. ગ્રાફ બાંધકામ પ્રક્રિયા. બિંદુ S ના સમૂહ માટે ત્રિકોણ સમસ્યા એ ત્રિકોણ ગ્રાફ મેળવવા માટે સમૂહ S ના તમામ બિંદુઓને અસંબંધિત ભાગો સાથે જોડવાની સમસ્યા છે. બિંદુ S ના સમૂહ માટે ત્રિકોણ સમસ્યા એ ત્રિકોણ ગ્રાફ મેળવવા માટે સમૂહ S ના તમામ બિંદુઓને અસંબંધિત ભાગો સાથે જોડવાની સમસ્યા છે. ત્રિકોણની વ્યાખ્યા પોઈન્ટનો સમૂહ S

શ્રેષ્ઠ ત્રિકોણ એ ગ્રાફની તમામ કિનારીઓની લંબાઈના લઘુત્તમ સરવાળા સાથેનું ત્રિકોણ છે. શ્રેષ્ઠ ત્રિકોણ એ ગ્રાફની તમામ કિનારીઓની લંબાઈના લઘુત્તમ સરવાળા સાથેનું ત્રિકોણ છે. ! એક લોકપ્રિય, પરંતુ ખૂબ જ સમય માંગી લેતી સમસ્યા O(2 n)! વ્યવહારમાં, શ્રેષ્ઠ ત્રિકોણનો ઉપયોગ થાય છે: "લોભી" ત્રિકોણ O(N 2 *logN) "લોભી" ત્રિકોણ O(N 2 *logN) Delaunay triangulation O(N*logN) Delaunay triangulation O(N*logN) ) વ્યાખ્યા શ્રેષ્ઠ ત્રિકોણ

Delaunay triangulation (DT(S)) એક બહિર્મુખ ત્રિકોણ છે જે Delaunay સ્થિતિને સંતોષે છે: Delaunay triangulation (DT(S)) એક બહિર્મુખ ત્રિકોણ છે જે Delaunay સ્થિતિને સંતોષે છે: આલેખના કોઈપણ શિરોબિંદુઓ આસપાસના પરિઘની અંદર ન આવવા જોઈએ. તેના કોઈપણ ત્રિકોણ. ગ્રાફના કોઈપણ શિરોબિંદુઓ તેના કોઈપણ ત્રિકોણની આસપાસના વર્તુળની અંદર ન આવવા જોઈએ. ડેલૌનાય ત્રિકોણની વ્યાખ્યા ડેલૌનાય સ્થિતિ સંતુષ્ટ છે ડેલૌનાય સ્થિતિ સંતુષ્ટ નથી B.N. Delaunay()

અન્ય વીજી સમસ્યાઓમાં ડેલૌનેય ત્રિકોણનો ઉપયોગ અન્ય વીજી સમસ્યાઓમાં પોઈન્ટ્સના સમૂહનો ન્યૂનતમ વ્યાપ પોઈન્ટના સમૂહનો ન્યૂનતમ વ્યાપ ઝોન) મહત્તમ ખાલી વર્તુળ શોધવું મહત્તમ ખાલી વર્તુળ શોધવું, વગેરે , ઔદ્યોગિક મોડેલો, રમતોમાં મોડેલો, GIS માં રાહતો, શિલ્પો, ઔદ્યોગિક .મોડેલ, રમતોમાં મોડેલો, મોડેલોનું સંખ્યાત્મક વિશ્લેષણ Isolines, Isoclines, FEM મોડેલોનું સંખ્યાત્મક વિશ્લેષણ. Isolines, Isoclins, FEM.

કોઈપણ બહિર્મુખ ત્રિકોણના ગુણધર્મો 1. n બિંદુઓના સમૂહ માટે જેમાંથી m આંતરિક ત્રિકોણ ત્રિકોણની સંખ્યા = n + m – 2 ત્રિકોણ ત્રિકોણની સંખ્યા = n + m – 2 ત્રિકોણ ધારની સંખ્યા 3n – 6 ત્રિકોણ ધારની સંખ્યા 3n – 6 ઉદાહરણ: પોઈન્ટ (n) – 13 પોઈન્ટ્સ (n) – 13 આંતરિક (m) – 4 આંતરિક (m) – 4 ત્રિકોણ – 15 = ત્રિકોણ – 15 = ધાર – 26 3*13-6 = 33 ધાર – 26 3 *13-6 = 33

ડેલૌનાય ત્રિકોણના ગુણધર્મો 2. ડેલૌનાય ત્રિકોણમાં તમામ સંભવિત ત્રિકોણ વચ્ચેના તમામ ત્રિકોણના લઘુત્તમ ખૂણાઓનો મહત્તમ સરવાળો હોય છે. 3. ડેલૌનાય ત્રિકોણમાં તમામ સંભવિત ત્રિકોણમાં ત્રિકોણની આસપાસ વર્ણવેલ વર્તુળોની ત્રિજ્યાનો લઘુત્તમ સરવાળો છે. Delaunay triangulation NOT Delaunay triangulation

Delaunay ત્રિકોણ બનાવવા માટેની પદ્ધતિઓ સ્ટેપ-બાય-સ્ટેપ ઇનપુટ પદ્ધતિઓ સ્ટેપ-બાય-સ્ટેપ ઇનપુટ પદ્ધતિઓ પુનરાવર્તિત અલ્ગોરિધમ્સ () પુનરાવર્તિત અલ્ગોરિધમ્સ () સ્ટેપ-બાય-સ્ટેપ સેમ્પલિંગ પદ્ધતિઓ સ્ટેપ-બાય-સ્ટેપ સેમ્પલિંગ પદ્ધતિઓ ડાયરેક્ટ (સ્ટેપ-બાય-સ્ટેપ) બાંધકામ અલ્ગોરિધમ્સ (3) ડાયરેક્ટ (સ્ટેપ-બાય-સ્ટેપ) કન્સ્ટ્રક્શન એલ્ગોરિધમ્સ (3) વિઘટન પદ્ધતિઓ વિઘટન પદ્ધતિઓ અલ્ગોરિધમ્સને મર્જ કરો (2 ) અલ્ગોરિધમ્સ મર્જ કરો (2) સ્કેનિંગ પદ્ધતિઓ સ્કેનિંગ પદ્ધતિઓ પોઈન્ટ ઉમેરવાના બદલાયેલા ક્રમ સાથે પુનરાવર્તિત અલ્ગોરિધમ્સ (1.4) સાથે પુનરાવર્તિત અલ્ગોરિધમ્સ પોઈન્ટ ઉમેરવાનો બદલાયેલો ક્રમ (1.4) ટુ-પાસ એલ્ગોરિધમ્સ (4) ટુ-પાસ એલ્ગોરિધમ્સ (4)

સ્ટેપ-બાય-સ્ટેપ ઇનપુટ પદ્ધતિઓ પુનરાવર્તિત અલ્ગોરિધમ્સ () ડેલૌનેય ત્રિકોણ બનાવવા માટે પુનરાવર્તિત અલ્ગોરિધમ્સની સામાન્ય યોજના 1. પ્રથમ ત્રણ બિંદુઓ પર એક ત્રિકોણ બનાવો 2. સેટ S 3 ના બાકીના તમામ બિંદુઓ p i દ્વારા લૂપ કરો. બિંદુની સૌથી નજીક ત્રિકોણ t j શોધો વર્તમાન ત્રિકોણનો p i 4. જો બિંદુ p i ત્રિકોણ t j ની બહાર હોય, તો નજીકની ધાર પર ત્રિકોણ બનાવો. 5. જો બિંદુ p i ત્રિકોણ t j ની અંદર હોય, તો ત્રિકોણને ત્રણ ભાગમાં વહેંચો. 6. જો બિંદુ p i એક ધાર પર હોય, તો બાજુના ત્રિકોણને જોડીમાં વિભાજીત કરો. 7. જો પડોશીઓ માટે Delaunay સ્થિતિનું ઉલ્લંઘન થાય છે, તો પછી પડોશી ત્રિકોણ ફરીથી બનાવો. ત્રિકોણ શોધને ઝડપી બનાવવા માટેના વિકલ્પો: ત્રિકોણ અનુક્રમણિકા (વૃક્ષો) – O(લોગ n) ત્રિકોણ અનુક્રમણિકા (વૃક્ષો) – O(લોગ એન) ત્રિકોણ કેશીંગ (મેશ) – O(ઓ) ત્રિકોણ કેશીંગ (મેશ) – O(ઓ)

સ્ટેપ-બાય-સ્ટેપ સેમ્પલિંગની પદ્ધતિઓ ડાયરેક્ટ (સ્ટેપ-બાય-સ્ટેપ) કન્સ્ટ્રક્શન માટે અલ્ગોરિધમ્સ (3) જે પહેલાથી જ બાંધવામાં આવ્યું છે તેને રિબિલ્ડ કર્યા વિના તરત જ જરૂરી ત્રિકોણ બનાવો. ડેલૌનાય ત્રિકોણના સીધા બાંધકામ માટે એલ્ગોરિધમ્સની સામાન્ય યોજના બિનપ્રોસેસ કરેલ ધારના સ્ટેકનો ઉપયોગ કરવો અનુકૂળ છે. 1. બિંદુઓના સમૂહના બહિર્મુખ હલની કોઈપણ ધાર q શોધો. 2. ધાર q ને કાચી ધારના સ્ટેકમાં દબાણ કરો. 3. કાચા કિનારીઓનો સ્ટેક ખાલી ન થાય ત્યાં સુધી લૂપ કરો. 4. સ્ટેકમાંથી પોપ એજ v. 5. કિનારી v માટે, એક બિંદુ p શોધો જે Delaunay સ્થિતિ (Delaunay પાડોશી) ને સંતોષે છે 6. જો Delaunay પાડોશી p મળે, તો 7. કિનારી v થી બિંદુ p સુધીનો ત્રિકોણ બનાવો. 8. નવા ત્રિકોણની નવી કિનારીઓને કાચી ધારના સ્ટેક પર દબાણ કરો. Delaunay પડોશી શોધને વેગ આપવા માટેના વિકલ્પો: k-D-ટ્રી સાથે પોઈન્ટ ઈન્ડેક્સીંગ - O(log n) ઈન્ડેક્સીંગ પોઈન્ટ with a k-D-ટ્રી - O(log n) પોઈન્ટનું સેલ્યુલર ઈન્ડેક્સીંગ - O(c) પોઈન્ટનું સેલ્યુલર ઈન્ડેક્સીંગ - O(c) )

લોભી Delaunay ત્રિકોણ અલ્ગોરિધમની પ્રક્રિયા

વિઘટન પદ્ધતિઓ અલ્ગોરિધમ્સને મર્જ કરો (2) સબસેટમાં પાર્ટીશન, સ્વતંત્ર પ્રક્રિયા, પરિણામો મર્જ કરો. મર્જિંગ એલ્ગોરિધમ્સની સામાન્ય યોજના 0. જો સેટ S માં 3 થી વધુ પોઈન્ટ ન હોય, તો સીધું જ બાંધો અન્યથા 1. પોઈન્ટ S ના સમૂહને લગભગ સમાન સબસેટમાં વિભાજીત કરો. 1. પોઈન્ટ S ના સમૂહને લગભગ સમાન સબસેટમાં વિભાજીત કરો. 2. સબસેટ્સ માટે ત્રિકોણનું બાંધકામ. 2. સબસેટ્સ માટે ત્રિકોણનું બાંધકામ. 3. પરિણામી ત્રિકોણને એકમાં મર્જ કરો. 3. પરિણામી ત્રિકોણને એકમાં મર્જ કરો. ઉપગણોમાં વિભાજનની પદ્ધતિઓ ઓર્થોગોનલ સીધી રેખાઓ ઓર્થોગોનલ સીધી રેખાઓ બહિર્મુખ હલના વ્યાસ દ્વારા બહિર્મુખ હલના વ્યાસ દ્વારા પટ્ટાઓ પટ્ટાઓ

મર્જિંગ એલ્ગોરિધમ્સ (2) ત્રિકોણને મર્જ કરવા માટેની પદ્ધતિઓ “કાઢી નાખો અને બનાવો” (બાંધકામ પહેલાં તપાસો) “કાઢી નાખો અને બનાવો” (બાંધકામ પહેલાં તપાસો) “બિલ્ડ અને ફરીથી બનાવો” (બાંધકામ પછી તપાસો) “બિલ્ડ અને ફરીથી બનાવો” (બાંધકામ પછી તપાસો) “ બિલ્ડ, રિબિલ્ડિંગ" (બાંધકામ દરમિયાન તપાસો) "બિલ્ડ, રિબિલ્ડિંગ" (બાંધકામ દરમિયાન તપાસો)

પોઈન્ટ ઉમેરવાના સંશોધિત ક્રમ સાથે પુનરાવર્તિત પદ્ધતિઓની સામાન્ય યોજના 1. પોઈન્ટ ગોઠવો (ઈવેન્ટ પોઈન્ટ્સની સૂચિ બનાવો) 2. તમામ ઘટના બિંદુઓ દ્વારા ચક્ર સ્કેન કરો 3. દરેક બિંદુ p i માટે, પહેલાના ત્રિકોણ પર ત્રિકોણ બનાવો. 4. જો પડોશીઓ માટે Delaunay સ્થિતિનું ઉલ્લંઘન થાય છે, તો પછી પડોશી ત્રિકોણ ફરીથી બનાવો. સ્કેનિંગ પદ્ધતિઓ પોઈન્ટ ઉમેરવાના સંશોધિત ક્રમ સાથે પુનરાવર્તિત અલ્ગોરિધમ્સ (1.4)

સ્કેનિંગ પદ્ધતિઓ ઇવેન્ટ પોઈન્ટ ઓર્ડર કરવા માટેની પદ્ધતિઓ રેક્ટીલીનિયર રેક્ટીલીનિયર ધ્રુવીય (ગોળાકાર, પંખા આકારની) ધ્રુવીય (ગોળાકાર, પંખાના આકારની) સ્ટ્રાઈપ સ્ક્વેર સ્ક્વેર હિલ્બર્ટ વક્ર દ્વારા હિલ્બર્ટ વળાંક દ્વારા ઝેડ-કોડ દ્વારા ઝેડ-કોડ લક્ષ્યો: તરત જ મહત્તમ બનાવો સારા ત્રિકોણ તરત જ મહત્તમ સારા ત્રિકોણ બનાવો લેન ફેરફારોની સંખ્યા ઓછી કરો લેન ફેરફારોની સંખ્યા ઓછી કરો

ડેલૌનાય ત્રિકોણ પદ્ધતિની સારાંશ લાક્ષણિકતાઓ ત્રિકોણ પદ્ધતિ સરેરાશ સમય સૌથી ખરાબ સમયે સેકન્ડ/ટી અમલીકરણની સરળતા. સ્ટેપ-બાય-સ્ટેપ ઇનપુટ મેથડ્સ સ્ટેપ-બાય-સ્ટેપ ઇનપુટ મેથડ ઇટરેટિવ એલ્ગોરિધમ્સ () ઇટરરેટિવ એલ્ગોરિધમ્સ ()O(n)- O(n 3/2) O(n 2) 1.5-9.2 2-5 સ્ટેપ-બાય સ્ટેપ સેમ્પલિંગ પદ્ધતિઓ સ્ટેપ-બાય-સ્ટેપ સેમ્પલિંગ પદ્ધતિઓ સીધી બાંધકામ પદ્ધતિ (3) સીધી બાંધકામ પદ્ધતિ (3) O(n)- O(n 2) O(n 2) -2 વિઘટન પદ્ધતિઓ વિઘટન પદ્ધતિઓ વિઘટન પદ્ધતિઓ (2) મર્જ પદ્ધતિઓ (2) 2) O(n)- O(nlogn) O (nlogn)- O(n 2) 2.5-4.52-3 સ્કેનિંગ પદ્ધતિઓ સ્કેનિંગ પદ્ધતિઓ પોઈન્ટ ઉમેરવાના બદલાયેલા ક્રમ સાથે પુનરાવર્તિત (1.4) પોઈન્ટ ઉમેરવાના બદલાયેલા ક્રમ સાથે પુનરાવર્તિત ( 1.4)O(n) O(n 2) 1 ,9-5,34-5 ટુ-પાસ પદ્ધતિઓ (4) ટુ-પાસ પદ્ધતિઓ (4) O(n) - O(n 2) O(nlogn)- O (n 2) 2.2-15.41-5 Skvortsov ભલામણ કરે છે: ગતિશીલ કેશીંગ સાથે પુનરાવર્તિત અલ્ગોરિધમ

આજે તે શું છે? Delaunay ત્રિકોણ વિશે! વ્યાખ્યા વ્યાખ્યા એપ્લિકેશનના ક્ષેત્રો એપ્લિકેશનના ક્ષેત્રો ડેલૌનાય ત્રિકોણના ગુણધર્મો ડેલૌનાય ત્રિકોણના ગુણધર્મો ડેલૌનાય ત્રિકોણ બનાવવા માટેની પદ્ધતિઓ ડેલૌનેય ત્રિકોણ બનાવવા માટેની પદ્ધતિઓ પગલું-દર-પગલાં ઇનપુટ પદ્ધતિઓ પગલું-દર-પગલું ઇનપુટ પદ્ધતિઓ પગલું-દર-પગલું ઇનપુટ પદ્ધતિઓ પગલું-દર-પગલાં-નમૂના લેવાની પદ્ધતિ -સ્ટેપ સેમ્પલિંગ પદ્ધતિઓ વિઘટન પદ્ધતિઓ વિઘટન પદ્ધતિઓ સ્કેનિંગ પદ્ધતિઓ સ્કેનિંગ પદ્ધતિઓ બે-પાસ પદ્ધતિઓ બે-પાસ પદ્ધતિઓ