સૂચનાઓ. ઓનલાઈન ઉકેલવા માટે, તમારે સમીકરણનો પ્રકાર પસંદ કરવો પડશે અને અનુરૂપ મેટ્રિસિસનું પરિમાણ સેટ કરવું પડશે.
જ્યાં A, B, C એ ઉલ્લેખિત મેટ્રિક્સ છે, X એ ઇચ્છિત મેટ્રિક્સ છે. ફોર્મ (1), (2) અને (3) ના મેટ્રિક્સ સમીકરણો વ્યસ્ત મેટ્રિક્સ A -1 દ્વારા ઉકેલવામાં આવે છે. જો અભિવ્યક્તિ A·X - B = C આપવામાં આવે છે, તો તમારે પહેલા મેટ્રિસિસ C + B ઉમેરવાની જરૂર છે અને A·X = D, જ્યાં D = C + B (). જો અભિવ્યક્તિ A*X = B 2 આપવામાં આવે છે, તો મેટ્રિક્સ B નો પ્રથમ વર્ગ હોવો જોઈએ. મેટ્રિસિસ પરની મૂળભૂત કામગીરીઓથી પોતાને પરિચિત કરવાની પણ ભલામણ કરવામાં આવે છે.ઉદાહરણ નંબર 1. વ્યાયામ. મેટ્રિક્સ સમીકરણનો ઉકેલ શોધો
ઉકેલ. ચાલો સૂચિત કરીએ:
પછી મેટ્રિક્સ સમીકરણ ફોર્મમાં લખવામાં આવશે: A·X·B = C.
મેટ્રિક્સ A નો નિર્ણાયક detA=-1 બરાબર છે
A એ બિન-એકવચન મેટ્રિક્સ હોવાથી, ત્યાં એક વ્યસ્ત મેટ્રિક્સ A -1 છે. ડાબી બાજુના સમીકરણની બંને બાજુઓને A -1 વડે ગુણાકાર કરો: આ સમીકરણની ડાબી બાજુએ A -1 વડે અને જમણી બાજુએ B -1 વડે ગુણાકાર કરો: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . ત્યારથી A A -1 = B B -1 = E અને E X = X E = X, પછી X = A -1 C B -1
વ્યસ્ત મેટ્રિક્સ A -1: ![]()
ચાલો વ્યસ્ત મેટ્રિક્સ B -1 શોધીએ.
ટ્રાન્સપોઝ્ડ મેટ્રિક્સ B T:
વ્યસ્ત મેટ્રિક્સ B -1: ![]()
અમે સૂત્રનો ઉપયોગ કરીને મેટ્રિક્સ X શોધીએ છીએ: X = A -1 ·C·B -1 ![]()
જવાબ:
ઉદાહરણ નંબર 2. વ્યાયામ.મેટ્રિક્સ સમીકરણ ઉકેલો ![]()
ઉકેલ. ચાલો સૂચિત કરીએ:
પછી મેટ્રિક્સ સમીકરણ ફોર્મમાં લખવામાં આવશે: A·X = B.
મેટ્રિક્સ A નો નિર્ધારક detA=0 છે
A એ એકવચન મેટ્રિક્સ હોવાથી (નિર્ધારક 0 છે), તેથી સમીકરણનો કોઈ ઉકેલ નથી.
ઉદાહરણ નંબર 3. વ્યાયામ. મેટ્રિક્સ સમીકરણનો ઉકેલ શોધો
ઉકેલ. ચાલો સૂચિત કરીએ:
પછી મેટ્રિક્સ સમીકરણ ફોર્મમાં લખવામાં આવશે: X A = B.
મેટ્રિક્સ A નો નિર્ણાયક detA=-60 છે
A એ બિન-એકવચન મેટ્રિક્સ હોવાથી, ત્યાં એક વ્યસ્ત મેટ્રિક્સ A -1 છે. ચાલો જમણી બાજુના સમીકરણની બંને બાજુઓને A -1 વડે ગુણાકાર કરીએ: X A A -1 = B A -1, જ્યાંથી આપણે શોધીએ છીએ કે X = B A -1
ચાલો વ્યસ્ત મેટ્રિક્સ A -1 શોધીએ.
ટ્રાન્સપોઝ્ડ મેટ્રિક્સ A T: 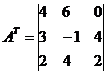
વ્યસ્ત મેટ્રિક્સ A -1: 
અમે સૂત્રનો ઉપયોગ કરીને મેટ્રિક્સ X શોધીએ છીએ: X = B A -1 
જવાબ: > 
ચાલો આપણે સમીકરણોની સિસ્ટમોના બે પ્રકારના ઉકેલોનું વિશ્લેષણ કરીએ:
1. અવેજી પદ્ધતિનો ઉપયોગ કરીને સિસ્ટમને હલ કરવી.
2. સિસ્ટમ સમીકરણોના ટર્મ-બાય-ટર્મ સરવાળા (બાદબાકી) દ્વારા સિસ્ટમને હલ કરવી.
સમીકરણોની સિસ્ટમ ઉકેલવા માટે અવેજી પદ્ધતિ દ્વારાતમારે એક સરળ અલ્ગોરિધમનું પાલન કરવાની જરૂર છે:
1. એક્સપ્રેસ. કોઈપણ સમીકરણમાંથી આપણે એક ચલ વ્યક્ત કરીએ છીએ.
2. અવેજી. અમે પરિણામી મૂલ્યને વ્યક્ત કરેલ ચલને બદલે બીજા સમીકરણમાં બદલીએ છીએ.
3. પરિણામી સમીકરણને એક ચલ વડે ઉકેલો. અમે સિસ્ટમનો ઉકેલ શોધી કાઢીએ છીએ.
નક્કી કરવા માટે ટર્મ-બાય-ટર્મ એડિશન (બાદબાકી) પદ્ધતિ દ્વારા સિસ્ટમજરૂર છે:
1. એક ચલ પસંદ કરો જેના માટે આપણે સમાન ગુણાંક બનાવીશું.
2. અમે સમીકરણો ઉમેરી અથવા બાદ કરીએ છીએ, પરિણામે એક ચલ સાથે સમીકરણ થાય છે.
3. પરિણામી રેખીય સમીકરણ ઉકેલો. અમે સિસ્ટમનો ઉકેલ શોધી કાઢીએ છીએ.
સિસ્ટમનો ઉકેલ એ ફંક્શન ગ્રાફના આંતરછેદ બિંદુઓ છે.
ચાલો ઉદાહરણોનો ઉપયોગ કરીને સિસ્ટમોના ઉકેલને વિગતવાર ધ્યાનમાં લઈએ.
ઉદાહરણ #1:
ચાલો અવેજી પદ્ધતિ દ્વારા હલ કરીએ
અવેજી પદ્ધતિનો ઉપયોગ કરીને સમીકરણોની સિસ્ટમ ઉકેલવી2x+5y=1 (1 સમીકરણ)
x-10y=3 (બીજું સમીકરણ)
1. એક્સપ્રેસ
તે જોઈ શકાય છે કે બીજા સમીકરણમાં 1 ના ગુણાંક સાથે ચલ x છે, જેનો અર્થ છે કે બીજા સમીકરણમાંથી ચલ x વ્યક્ત કરવાનું સૌથી સરળ છે.
x=3+10y
2.આપણે તેને વ્યક્ત કર્યા પછી, અમે ચલ x ને બદલે પ્રથમ સમીકરણમાં 3+10y ને બદલીએ છીએ.
2(3+10y)+5y=1
3. પરિણામી સમીકરણને એક ચલ વડે ઉકેલો.
2(3+10y)+5y=1 (કૌંસ ખોલો)
6+20y+5y=1
25વર્ષ=1-6
25y=-5 |: (25)
y=-5:25
y=-0.2
સમીકરણ પદ્ધતિનો ઉકેલ એ ગ્રાફના આંતરછેદ બિંદુઓ છે, તેથી આપણે x અને y શોધવાની જરૂર છે, કારણ કે આંતરછેદ બિંદુ x અને y ધરાવે છે, ચાલો x શોધીએ, જ્યાં આપણે તેને વ્યક્ત કરીએ છીએ, ત્યાં આપણે y ને બદલીએ છીએ .
x=3+10y
x=3+10*(-0.2)=1
પોઈન્ટ લખવાનો રિવાજ છે પ્રથમ સ્થાને આપણે ચલ x લખીએ છીએ, અને બીજા સ્થાને ચલ y.
જવાબ: (1; -0.2)
ઉદાહરણ #2:
ચાલો ટર્મ-બાય-ટર્મ એડિશન (બાદબાકી) પદ્ધતિનો ઉપયોગ કરીને હલ કરીએ.
ઉમેરણ પદ્ધતિનો ઉપયોગ કરીને સમીકરણોની સિસ્ટમ ઉકેલવી3x-2y=1 (1 સમીકરણ)
2x-3y=-10 (બીજું સમીકરણ)
1. આપણે ચલ પસંદ કરીએ છીએ, ચાલો કહીએ કે આપણે x પસંદ કરીએ છીએ. પ્રથમ સમીકરણમાં, ચલ x નો ગુણાંક 3 છે, બીજામાં - 2. આપણે ગુણાંક સમાન બનાવવાની જરૂર છે, આ માટે આપણને સમીકરણોનો ગુણાકાર કરવાનો અથવા કોઈપણ સંખ્યા દ્વારા ભાગાકાર કરવાનો અધિકાર છે. આપણે પ્રથમ સમીકરણને 2 વડે અને બીજાને 3 વડે ગુણાકાર કરીએ છીએ અને કુલ ગુણાંક 6 મેળવીએ છીએ.
3x-2y=1 |*2
6x-4y=2
2x-3y=-10 |*3
6x-9y=-30
2. રેખીય સમીકરણને ઉકેલવા માટે પ્રથમ સમીકરણમાંથી બીજાને બાદ કરો.
__6x-4y=2
5y=32 | :5
y=6.4
3. એક્સ શોધો. આપણે કોઈપણ સમીકરણોમાં મળેલા y ને બદલીએ છીએ, ચાલો પ્રથમ સમીકરણમાં કહીએ.
3x-2y=1
3x-2*6.4=1
3x-12.8=1
3x=1+12.8
3x=13.8 |:3
x=4.6
આંતરછેદ બિંદુ x=4.6 હશે; y=6.4
જવાબ: (4.6; 6.4)
શું તમે મફતમાં પરીક્ષાની તૈયારી કરવા માંગો છો? શિક્ષક ઓનલાઇન મફતમાં. મજાક નથી.
ગણિત ઉકેલવા માટે. ઝડપથી શોધો ગાણિતિક સમીકરણ ઉકેલવુંમોડમાં ઓનલાઇન. વેબસાઇટ www.site પરવાનગી આપે છે સમીકરણ ઉકેલોલગભગ કોઈપણ આપેલ બીજગણિત, ત્રિકોણમિતિઅથવા અતીન્દ્રિય સમીકરણ ઓનલાઇન. ગણિતની લગભગ કોઈ પણ શાખાનો અભ્યાસ વિવિધ તબક્કામાં કરતી વખતે તમારે નક્કી કરવાનું હોય છે સમીકરણો ઓનલાઇન. તરત જ જવાબ મેળવવા માટે, અને સૌથી અગત્યનું સચોટ જવાબ મેળવવા માટે, તમારે એક સંસાધનની જરૂર છે જે તમને આ કરવાની મંજૂરી આપે. સાઇટ www.site માટે આભાર સમીકરણો ઓનલાઇન ઉકેલોથોડી મિનિટો લાગશે. ગણિત ઉકેલતી વખતે www.site નો મુખ્ય ફાયદો સમીકરણો ઓનલાઇન- આ આપેલા પ્રતિભાવની ઝડપ અને ચોકસાઈ છે. સાઇટ કોઈપણ ઉકેલવા માટે સક્ષમ છે બીજગણિત સમીકરણો ઓનલાઇન, ત્રિકોણમિતિ સમીકરણો ઓનલાઇન, અતીન્દ્રિય સમીકરણો ઓનલાઇન, અને પણ સમીકરણોમોડમાં અજાણ્યા પરિમાણો સાથે ઓનલાઇન. સમીકરણોશક્તિશાળી ગાણિતિક ઉપકરણ તરીકે સેવા આપે છે ઉકેલોવ્યવહારુ સમસ્યાઓ. મદદ સાથે ગાણિતિક સમીકરણોહકીકતો અને સંબંધોને વ્યક્ત કરવું શક્ય છે જે પ્રથમ નજરમાં મૂંઝવણભર્યા અને જટિલ લાગે છે. અજ્ઞાત માત્રા સમીકરણોમાં સમસ્યાની રચના કરીને શોધી શકાય છે ગાણિતિકસ્વરૂપમાં ભાષા સમીકરણોઅને નક્કી કરોમોડમાં કાર્ય પ્રાપ્ત કર્યું ઓનલાઇનવેબસાઇટ www.site પર. કોઈપણ બીજગણિતીય સમીકરણ, ત્રિકોણમિતિ સમીકરણઅથવા સમીકરણોસમાવતી ગુણાતીતસુવિધાઓ તમે સરળતાથી કરી શકો છો નક્કી કરોઑનલાઇન અને ચોક્કસ જવાબ મેળવો. કુદરતી વિજ્ઞાનનો અભ્યાસ કરતી વખતે, તમારે અનિવાર્યપણે જરૂરિયાતનો સામનો કરવો પડે છે સમીકરણો ઉકેલવા. આ કિસ્સામાં, જવાબ ચોક્કસ હોવો જોઈએ અને મોડમાં તરત જ મેળવવો આવશ્યક છે ઓનલાઇન. તેથી માટે ગાણિતિક સમીકરણો ઓનલાઇન ઉકેલવાઅમે www.site સાઇટની ભલામણ કરીએ છીએ, જે તમારા માટે અનિવાર્ય કેલ્ક્યુલેટર બનશે બીજગણિત સમીકરણો ઓનલાઈન ઉકેલો, ત્રિકોણમિતિ સમીકરણો ઓનલાઇન, અને પણ અતીન્દ્રિય સમીકરણો ઓનલાઇનઅથવા સમીકરણોઅજાણ્યા પરિમાણો સાથે. વિવિધના મૂળ શોધવાની વ્યવહારિક સમસ્યાઓ માટે ગાણિતિક સમીકરણોસ્ત્રોત www.. ઉકેલવું સમીકરણો ઓનલાઇનતમારી જાતને, તેનો ઉપયોગ કરીને પ્રાપ્ત જવાબ તપાસવા માટે ઉપયોગી છે ઓનલાઇન સમીકરણ ઉકેલવેબસાઇટ www.site પર. તમારે સમીકરણ યોગ્ય રીતે લખવાની જરૂર છે અને તરત જ મેળવો ઓનલાઈન સોલ્યુશન, જે પછી જે બાકી રહે છે તે સમીકરણના તમારા ઉકેલ સાથે જવાબની તુલના કરવાનું છે. જવાબ તપાસવામાં એક મિનિટથી વધુ સમય લાગશે નહીં, તે પૂરતું છે સમીકરણ ઓનલાઇન ઉકેલોઅને જવાબોની સરખામણી કરો. આ તમને ભૂલો ટાળવામાં મદદ કરશે નિર્ણયઅને સમયસર જવાબ સુધારો જ્યારે ઓનલાઇન સમીકરણો ઉકેલવાતે બનો બીજગણિત, ત્રિકોણમિતિ, ગુણાતીતઅથવા સમીકરણઅજાણ્યા પરિમાણો સાથે.
અમે તમારા ધ્યાન પર લાવીએ છીએ તે મફત કેલ્ક્યુલેટરમાં ગાણિતિક ગણતરીઓ માટેની શક્યતાઓનું સમૃદ્ધ શસ્ત્રાગાર છે. તે તમને પ્રવૃત્તિના વિવિધ ક્ષેત્રોમાં ઑનલાઇન કેલ્ક્યુલેટરનો ઉપયોગ કરવાની મંજૂરી આપે છે: શૈક્ષણિક, વ્યાવસાયિકઅને વ્યાપારી. અલબત્ત, ઑનલાઇન કેલ્ક્યુલેટરનો ઉપયોગ ખાસ કરીને લોકપ્રિય છે વિદ્યાર્થીઓઅને શાળાના બાળકો, તે તેમના માટે વિવિધ ગણતરીઓ કરવાનું ખૂબ સરળ બનાવે છે.
તે જ સમયે, કેલ્ક્યુલેટર વ્યવસાયના કેટલાક ક્ષેત્રોમાં અને વિવિધ વ્યવસાયોના લોકો માટે ઉપયોગી સાધન બની શકે છે. અલબત્ત, વ્યવસાય અથવા કાર્યમાં કેલ્ક્યુલેટરનો ઉપયોગ કરવાની જરૂરિયાત મુખ્યત્વે પ્રવૃત્તિના પ્રકાર દ્વારા નક્કી કરવામાં આવે છે. જો તમારો વ્યવસાય અને વ્યવસાય સતત ગણતરીઓ અને ગણતરીઓ સાથે સંકળાયેલા છે, તો તે ઇલેક્ટ્રોનિક કેલ્ક્યુલેટરને અજમાવવા અને ચોક્કસ કાર્ય માટે તેની ઉપયોગિતાની ડિગ્રીનું મૂલ્યાંકન કરવા યોગ્ય છે.
આ ઓનલાઈન કેલ્ક્યુલેટર કરી શકે છે
- એક લીટીમાં લખેલા પ્રમાણભૂત ગાણિતિક કાર્યોને યોગ્ય રીતે કરો જેમ કે - 12*3-(7/2) અને આપણે ઓનલાઈન કેલ્ક્યુલેટરમાં મોટી સંખ્યાઓ ગણી શકીએ તેના કરતા મોટી સંખ્યાઓ પર પ્રક્રિયા કરી શકીએ છીએ. ત્યાં 34 અક્ષરો છે અને આ મર્યાદા બિલકુલ નથી).
- સિવાય સ્પર્શક, કોસાઇન, સાઈનઅને અન્ય પ્રમાણભૂત કાર્યો - કેલ્ક્યુલેટર ગણતરી કામગીરીને સમર્થન આપે છે આર્કટેન્જેન્ટ, આર્કોટેન્જેન્ટઅને અન્ય.
- આર્સેનલમાં ઉપલબ્ધ છે લઘુગણક, ફેક્ટોરિયલઅને અન્ય રસપ્રદ સુવિધાઓ
- આ ઓનલાઈન કેલ્ક્યુલેટર ગ્રાફ કેવી રીતે બનાવવો તે જાણે છે!!!
આલેખને પ્લોટ કરવા માટે, સેવા એક વિશિષ્ટ બટનનો ઉપયોગ કરે છે (ગ્રાફ ગ્રે રંગમાં દોરવામાં આવે છે) અથવા આ કાર્ય (પ્લોટ) નું અક્ષર પ્રતિનિધિત્વ કરે છે. ઑનલાઇન કેલ્ક્યુલેટરમાં ગ્રાફ બનાવવા માટે, ફંક્શન લખો: પ્લોટ(ટેન(x)),x=-360..360.
અમે સ્પર્શક માટે સૌથી સરળ આલેખ લીધો, અને દશાંશ બિંદુ પછી અમે X ચલની શ્રેણી -360 થી 360 સુધી દર્શાવી.
તમે કોઈપણ ચલોની સંખ્યા સાથે એકદમ કોઈપણ કાર્ય બનાવી શકો છો, ઉદાહરણ તરીકે આ: પ્લોટ(cos(x)/3z, x=-180..360,z=4)અથવા વધુ જટિલ કે જેની સાથે તમે આવી શકો છો. ચલ X ની વર્તણૂક પર ધ્યાન આપો - થી અને થી અંતરાલ બે બિંદુઓનો ઉપયોગ કરીને સૂચવવામાં આવે છે.
આ ઑનલાઇન કેલ્ક્યુલેટરની એકમાત્ર નકારાત્મક (જોકે તેને ગેરલાભ કહેવું મુશ્કેલ છે) એ છે કે તે ગોળા અને અન્ય ત્રિ-પરિમાણીય આકૃતિઓ બનાવી શકતું નથી - માત્ર એક વિમાન.
ગણિત કેલ્ક્યુલેટરનો ઉપયોગ કેવી રીતે કરવો
1. ડિસ્પ્લે (કેલ્ક્યુલેટર સ્ક્રીન) દાખલ કરેલ અભિવ્યક્તિ અને સામાન્ય પ્રતીકોમાં તેની ગણતરીનું પરિણામ દર્શાવે છે, જેમ આપણે કાગળ પર લખીએ છીએ. આ ક્ષેત્ર ફક્ત વર્તમાન વ્યવહાર જોવા માટે છે. જ્યારે તમે ઇનપુટ લાઇનમાં ગાણિતિક અભિવ્યક્તિ ટાઇપ કરો છો ત્યારે એન્ટ્રી ડિસ્પ્લે પર દેખાય છે.
2. અભિવ્યક્તિ ઇનપુટ ફીલ્ડ અભિવ્યક્તિને રેકોર્ડ કરવા માટે બનાવાયેલ છે જેની ગણતરી કરવાની જરૂર છે. અહીં એ નોંધવું જોઈએ કે કોમ્પ્યુટર પ્રોગ્રામમાં વપરાતા ગાણિતિક ચિહ્નો આપણે સામાન્ય રીતે કાગળ પર વાપરીએ છીએ તેટલા જ હોતા નથી. દરેક કેલ્ક્યુલેટર કાર્યની ઝાંખીમાં, તમને ચોક્કસ કામગીરી માટે યોગ્ય હોદ્દો અને કેલ્ક્યુલેટરમાં ગણતરીઓના ઉદાહરણો મળશે. નીચે આ પૃષ્ઠ પર કેલ્ક્યુલેટરમાં તમામ સંભવિત કામગીરીની સૂચિ છે, જે તેમની સાચી જોડણી પણ સૂચવે છે.
3. ટૂલબાર - આ કેલ્ક્યુલેટર બટનો છે જે અનુરૂપ કામગીરી દર્શાવતા ગાણિતિક પ્રતીકોના મેન્યુઅલ ઇનપુટને બદલે છે. કેટલાક કેલ્ક્યુલેટર બટનો (વધારાના કાર્યો, યુનિટ કન્વર્ટર, મેટ્રિસિસ અને સમીકરણો, આલેખ ઉકેલવા) ટાસ્કબારને નવા ક્ષેત્રો સાથે પૂરક બનાવે છે જ્યાં ચોક્કસ ગણતરી માટેનો ડેટા દાખલ કરવામાં આવે છે. "ઇતિહાસ" ફીલ્ડમાં ગાણિતિક અભિવ્યક્તિઓ લખવાના ઉદાહરણો તેમજ તમારી છ સૌથી તાજેતરની એન્ટ્રીઓ શામેલ છે.
મહેરબાની કરીને નોંધ કરો કે જ્યારે તમે વધારાના ફંક્શન્સ, યુનિટ કન્વર્ટર, મેટ્રિસિસ અને સમીકરણો ઉકેલવા અને ગ્રાફ બનાવવા માટે બટનો દબાવો છો, ત્યારે સમગ્ર કેલ્ક્યુલેટર પેનલ ડિસ્પ્લેના ભાગને આવરી લેતા ઉપર જાય છે. જરૂરી ફીલ્ડ્સ ભરો અને પૂર્ણ-કદનું પ્રદર્શન જોવા માટે "I" કી (ચિત્રમાં લાલ રંગમાં પ્રકાશિત) દબાવો.
4. આંકડાકીય કીપેડમાં સંખ્યાઓ અને અંકગણિત ચિહ્નો હોય છે. "C" બટન અભિવ્યક્તિ એન્ટ્રી ફીલ્ડમાંની સંપૂર્ણ એન્ટ્રી કાઢી નાખે છે. એક પછી એક અક્ષરો કાઢી નાખવા માટે, તમારે ઇનપુટ લાઇનની જમણી બાજુના તીરનો ઉપયોગ કરવાની જરૂર છે.
અભિવ્યક્તિના અંતે હંમેશા કૌંસ બંધ કરવાનો પ્રયાસ કરો. મોટાભાગના ઓપરેશન્સ માટે આ મહત્વપૂર્ણ નથી; ઓનલાઈન કેલ્ક્યુલેટર દરેક વસ્તુની યોગ્ય ગણતરી કરશે. જો કે, કેટલાક કિસ્સાઓમાં ભૂલો થઈ શકે છે. ઉદાહરણ તરીકે, જ્યારે અપૂર્ણાંક શક્તિમાં વધારો કરવામાં આવે છે, ત્યારે બંધ કૌંસ ઘાતાંકમાંના અપૂર્ણાંકના છેદને આધારના છેદમાં જવા માટેનું કારણ બનશે. બંધ કૌંસ ડિસ્પ્લે પર આછા રાખોડી રંગમાં બતાવવામાં આવે છે અને જ્યારે રેકોર્ડિંગ પૂર્ણ થાય ત્યારે બંધ કરવું જોઈએ.
| કી | પ્રતીક | ઓપરેશન |
|---|---|---|
| pi | pi | સતત પી |
| ઇ | ઇ | યુલર નંબર |
| % | % | ટકા |
| () | () | કૌંસ ખોલો/બંધ કરો |
| , | , | અલ્પવિરામ |
| પાપ | પાપ(?) | કોણની સાઈન |
| cos | cos(?) | કોસાઇન |
| રાતા | ટેન(વાય) | સ્પર્શક |
| સિંહ | સિંહ() | હાયપરબોલિક સાઈન |
| કોશ | cosh() | હાઇપરબોલિક કોસાઇન |
| તન્હ | તનહ() | હાયપરબોલિક સ્પર્શક |
| પાપ -1 | અસિન() | રિવર્સ સાઈન |
| cos -1 | acos() | વ્યસ્ત કોસાઇન |
| ટેન -1 | atan() | વિપરીત સ્પર્શક |
| સિંહ -1 | asinh() | વ્યસ્ત હાયપરબોલિક સાઈન |
| cosh -1 | acosh() | વ્યસ્ત હાઇપરબોલિક કોસાઇન |
| tanh -1 | atanh() | વ્યસ્ત અતિપરવલય સ્પર્શક |
| x 2 | ^2 | સ્ક્વેરિંગ |
| x 3 | ^3 | ક્યુબ |
| x y | ^ | ઘાત |
| 10 x | 10^() | આધાર 10 માટે ઘાત |
| e x | EXP() | યુલરની સંખ્યાનું ઘાતીકરણ |
| vx | sqrt(x) | ચોરસ મૂળ |
| 3 વીએક્સ | sqrt3(x) | 3જી મૂળ |
| yvx | sqrt(x,y) | રુટ નિષ્કર્ષણ |
| લોગ 2 x | log2(x) | દ્વિસંગી લઘુગણક |
| લોગ | લોગ(x) | દશાંશ લઘુગણક |
| ln | ln(x) | કુદરતી લઘુગણક |
| લોગ y x | લોગ(x,y) | લઘુગણક |
| I/II | અતિરિક્ત કાર્યોને નાનું કરો/કોલ કરો | |
| એકમ | યુનિટ કન્વર્ટર | |
| મેટ્રિક્સ | મેટ્રિસિસ | |
| ઉકેલો | સમીકરણો અને સમીકરણોની સિસ્ટમો | |
| આલેખન | ||
| વધારાના કાર્યો (કી II સાથે કૉલ કરો) | ||
| મોડ | મોડ | શેષ સાથે વિભાજન |
| ! | ! | ફેક્ટોરિયલ |
| i/j | i/j | કાલ્પનિક એકમ |
| રી | ફરી() | સમગ્ર વાસ્તવિક ભાગને અલગ પાડવો |
| ઇમ | હું() | વાસ્તવિક ભાગને બાદ કરતાં |
| |x| | abs() | નંબર મોડ્યુલસ |
| અર્ગ | arg() | કાર્ય દલીલ |
| nCr | ncr() | બાયનોમિનલ ગુણાંક |
| જીસીડી | gcd() | જીસીડી |
| એલસીએમ | lcm() | એનઓસી |
| સરવાળો | રકમ() | તમામ ઉકેલોનું કુલ મૂલ્ય |
| fac | ફેક્ટરાઇઝ () | પ્રાઇમ ફેક્ટરાઇઝેશન |
| તફાવત | તફાવત() | ભિન્નતા |
| ડિગ્રી | ડિગ્રીઓ | |
| રેડ | રેડિયન | |
આ વિડિયોમાં આપણે રેખીય સમીકરણોના સંપૂર્ણ સેટનું વિશ્લેષણ કરીશું જે સમાન અલ્ગોરિધમનો ઉપયોગ કરીને ઉકેલવામાં આવે છે - તેથી જ તેને સૌથી સરળ કહેવામાં આવે છે.
પ્રથમ, ચાલો વ્યાખ્યાયિત કરીએ: રેખીય સમીકરણ શું છે અને કયું સૌથી સરળ કહેવાય છે?
રેખીય સમીકરણ એ એક છે જેમાં માત્ર એક જ ચલ હોય છે, અને માત્ર પ્રથમ ડિગ્રી સુધી.
સૌથી સરળ સમીકરણનો અર્થ છે બાંધકામ:
અન્ય તમામ રેખીય સમીકરણો અલ્ગોરિધમનો ઉપયોગ કરીને સરળમાં ઘટાડવામાં આવે છે:
- કૌંસ વિસ્તૃત કરો, જો કોઈ હોય તો;
- સમાન ચિન્હની એક બાજુએ ચલ ધરાવતાં શબ્દો અને ચલ વગરના શબ્દોને બીજી તરફ ખસેડો;
- સમાન ચિહ્નની ડાબી અને જમણી બાજુએ સમાન શરતો આપો;
- પરિણામી સમીકરણને $x$ ચલના ગુણાંક દ્વારા વિભાજીત કરો.
અલબત્ત, આ અલ્ગોરિધમ હંમેશા મદદ કરતું નથી. હકીકત એ છે કે કેટલીકવાર આ બધી યુક્તિઓ પછી ચલનો ગુણાંક $x$ શૂન્યની બરાબર થાય છે. આ કિસ્સામાં, બે વિકલ્પો શક્ય છે:
- સમીકરણનો કોઈ ઉકેલ નથી. ઉદાહરણ તરીકે, જ્યારે $0\cdot x=8$ જેવું કંઈક બહાર આવે છે, એટલે કે. ડાબી બાજુ શૂન્ય છે, અને જમણી બાજુ શૂન્ય સિવાયની સંખ્યા છે. નીચેની વિડિઓમાં આપણે આ પરિસ્થિતિ શા માટે શક્ય છે તેના ઘણા કારણો જોઈશું.
- ઉકેલ એ બધી સંખ્યાઓ છે. એકમાત્ર કેસ જ્યારે આ શક્ય હોય ત્યારે સમીકરણ $0\cdot x=0$ સુધી ઘટાડી દેવામાં આવ્યું હોય. તે તદ્દન તાર્કિક છે કે અમે ગમે તે $x$ અવેજી કરીએ, તે હજુ પણ "શૂન્ય એ શૂન્ય સમાન છે", એટલે કે. સાચી સંખ્યાત્મક સમાનતા.
હવે ચાલો જોઈએ કે આ બધું વાસ્તવિક જીવનના ઉદાહરણોનો ઉપયોગ કરીને કેવી રીતે કાર્ય કરે છે.
સમીકરણો ઉકેલવાના ઉદાહરણો
આજે આપણે રેખીય સમીકરણો સાથે કામ કરી રહ્યા છીએ, અને માત્ર સૌથી સરળ. સામાન્ય રીતે, એક રેખીય સમીકરણનો અર્થ થાય છે કોઈપણ સમાનતા જેમાં બરાબર એક ચલ હોય છે, અને તે માત્ર પ્રથમ ડિગ્રી સુધી જાય છે.
આવા બાંધકામો લગભગ સમાન રીતે હલ કરવામાં આવે છે:
- સૌ પ્રથમ, તમારે કૌંસને વિસ્તૃત કરવાની જરૂર છે, જો ત્યાં કોઈ હોય (આપણા છેલ્લા ઉદાહરણની જેમ);
- પછી સમાન ભેગું કરો
- છેલ્લે, ચલને અલગ કરો, એટલે કે. ચલ સાથે જોડાયેલી દરેક વસ્તુને ખસેડો - જે શરતોમાં તે સમાયેલ છે - એક બાજુએ, અને તેના વિના બાકી રહેલ દરેક વસ્તુને બીજી બાજુ ખસેડો.
પછી, એક નિયમ તરીકે, તમારે પરિણામી સમાનતાની દરેક બાજુએ સમાન લાવવાની જરૂર છે, અને તે પછી જે બાકી રહે છે તે "x" ના ગુણાંક દ્વારા વિભાજીત કરવાનું છે, અને અમને અંતિમ જવાબ મળશે.
સિદ્ધાંતમાં, આ સરસ અને સરળ લાગે છે, પરંતુ વ્યવહારમાં, ઉચ્ચ શાળાના અનુભવી વિદ્યાર્થીઓ પણ એકદમ સરળ રેખીય સમીકરણોમાં અપમાનજનક ભૂલો કરી શકે છે. સામાન્ય રીતે, કૌંસ ખોલતી વખતે અથવા "પ્લસ" અને "માઈનસ" ની ગણતરી કરતી વખતે ભૂલો કરવામાં આવે છે.
વધુમાં, એવું બને છે કે રેખીય સમીકરણમાં કોઈ ઉકેલો નથી, અથવા તે ઉકેલ એ સમગ્ર સંખ્યા રેખા છે, એટલે કે. કોઈપણ સંખ્યા. આપણે આજના પાઠમાં આ સૂક્ષ્મતા જોઈશું. પરંતુ અમે શરૂઆત કરીશું, જેમ તમે પહેલાથી જ સમજી ગયા છો, સરળ કાર્યો સાથે.
સરળ રેખીય સમીકરણો ઉકેલવા માટેની યોજના
પ્રથમ, ચાલો હું ફરી એકવાર સરળ રેખીય સમીકરણો ઉકેલવા માટેની આખી યોજના લખું:
- જો કોઈ હોય તો કૌંસને વિસ્તૃત કરો.
- અમે ચલોને અલગ પાડીએ છીએ, એટલે કે. અમે "X's" ધરાવતી દરેક વસ્તુને એક બાજુએ અને "X's" વગરની દરેક વસ્તુને બીજી તરફ ખસેડીએ છીએ.
- અમે સમાન શરતો રજૂ કરીએ છીએ.
- આપણે દરેક વસ્તુને "x" ના ગુણાંક દ્વારા વિભાજીત કરીએ છીએ.
અલબત્ત, આ યોજના હંમેશા કામ કરતી નથી; તેમાં કેટલીક સૂક્ષ્મતા અને યુક્તિઓ છે, અને હવે આપણે તેમને જાણીશું.
સરળ રેખીય સમીકરણોના વાસ્તવિક ઉદાહરણો ઉકેલવા
કાર્ય નંબર 1
પ્રથમ પગલા માટે આપણે કૌંસ ખોલવાની જરૂર છે. પરંતુ તેઓ આ ઉદાહરણમાં નથી, તેથી અમે આ પગલું છોડી દઈએ છીએ. બીજા પગલામાં આપણે ચલોને અલગ કરવાની જરૂર છે. મહેરબાની કરીને નોંધ કરો: અમે ફક્ત વ્યક્તિગત શરતો વિશે વાત કરી રહ્યા છીએ. ચાલો તેને લખીએ:
અમે ડાબી અને જમણી બાજુએ સમાન શરતો રજૂ કરીએ છીએ, પરંતુ આ અહીં પહેલાથી જ કરવામાં આવ્યું છે. તેથી, અમે ચોથા પગલા પર આગળ વધીએ છીએ: ગુણાંક દ્વારા વિભાજીત કરો:
\[\frac(6x)(6)=-\frac(72)(6)\]
તો અમને જવાબ મળ્યો.
કાર્ય નંબર 2
આપણે આ સમસ્યામાં કૌંસ જોઈ શકીએ છીએ, તેથી ચાલો તેને વિસ્તૃત કરીએ:
ડાબી અને જમણી બંને બાજુએ આપણે લગભગ સમાન ડિઝાઇન જોઈએ છીએ, પરંતુ ચાલો એલ્ગોરિધમ અનુસાર કાર્ય કરીએ, એટલે કે. ચલોને અલગ કરી રહ્યા છીએ:
અહીં કેટલાક સમાન છે:
આ કયા મૂળમાં કામ કરે છે? જવાબ: કોઈપણ માટે. તેથી, આપણે લખી શકીએ કે $x$ કોઈપણ સંખ્યા છે.
કાર્ય નંબર 3
ત્રીજું રેખીય સમીકરણ વધુ રસપ્રદ છે:
\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]
અહીં ઘણા કૌંસ છે, પરંતુ તેઓ કોઈ પણ વસ્તુ દ્વારા ગુણાકાર કરતા નથી, તેઓ ફક્ત વિવિધ ચિહ્નો દ્વારા આગળ આવે છે. ચાલો તેમને તોડીએ:
અમે બીજું પગલું કરીએ છીએ જે અમને પહેલાથી જ જાણીતું છે:
\[-x+x+2x=15-6-12+3\]
ચાલો ગણિત કરીએ:
અમે છેલ્લું પગલું હાથ ધરીએ છીએ - દરેક વસ્તુને "x" ના ગુણાંક દ્વારા વિભાજીત કરો:
\[\frac(2x)(x)=\frac(0)(2)\]
રેખીય સમીકરણો ઉકેલતી વખતે યાદ રાખવા જેવી બાબતો
જો આપણે ખૂબ સરળ કાર્યોને અવગણીએ, તો હું નીચે મુજબ કહેવા માંગુ છું:
- મેં ઉપર કહ્યું તેમ, દરેક રેખીય સમીકરણનો ઉકેલ હોતો નથી - કેટલીકવાર ફક્ત કોઈ મૂળ હોતા નથી;
- જો ત્યાં મૂળ હોય તો પણ, તેમાં શૂન્ય હોઈ શકે છે - તેમાં કંઈ ખોટું નથી.
શૂન્ય એ અન્યની સમાન સંખ્યા છે; તમારે તેની સાથે કોઈપણ રીતે ભેદભાવ કરવો જોઈએ નહીં અથવા જો તમે શૂન્ય મેળવો છો, તો તમે કંઈક ખોટું કર્યું છે.
અન્ય લક્ષણ કૌંસના ઉદઘાટન સાથે સંબંધિત છે. મહેરબાની કરીને નોંધ કરો: જ્યારે તેમની સામે "માઈનસ" હોય, ત્યારે અમે તેને દૂર કરીએ છીએ, પરંતુ કૌંસમાં અમે ચિહ્નોને વિરુદ્ધ. અને પછી આપણે તેને પ્રમાણભૂત અલ્ગોરિધમ્સનો ઉપયોગ કરીને ખોલી શકીએ છીએ: આપણે ઉપરની ગણતરીમાં જે જોયું છે તે મેળવીશું.
આ સરળ હકીકતને સમજવાથી તમને હાઈસ્કૂલમાં મૂર્ખ અને નુકસાનકારક ભૂલો કરવાનું ટાળવામાં મદદ મળશે, જ્યારે આવી વસ્તુઓ કરવાનું સ્વીકાર્ય માનવામાં આવે છે.
જટિલ રેખીય સમીકરણો ઉકેલવા
ચાલો વધુ જટિલ સમીકરણો તરફ આગળ વધીએ. હવે બાંધકામો વધુ જટિલ બનશે અને વિવિધ પરિવર્તનો કરતી વખતે એક ચતુર્ભુજ કાર્ય દેખાશે. જો કે, આપણે આનાથી ડરવું જોઈએ નહીં, કારણ કે જો, લેખકની યોજના અનુસાર, આપણે એક રેખીય સમીકરણ હલ કરી રહ્યા છીએ, તો પછી પરિવર્તન પ્રક્રિયા દરમિયાન ચતુર્ભુજ કાર્ય ધરાવતા તમામ મોનોમિઅલ્સ આવશ્યકપણે રદ થશે.
ઉદાહરણ નંબર 1
દેખીતી રીતે, પ્રથમ પગલું કૌંસ ખોલવાનું છે. ચાલો આ ખૂબ જ કાળજીપૂર્વક કરીએ:
હવે ચાલો ગોપનીયતા પર એક નજર કરીએ:
\[-x+6((x)^(2))-6((x)^(2))+x=-12\]
અહીં કેટલાક સમાન છે:
દેખીતી રીતે, આ સમીકરણનો કોઈ ઉકેલ નથી, તેથી અમે જવાબમાં આ લખીશું:
\[\varnothing\]
અથવા ત્યાં કોઈ મૂળ નથી.
ઉદાહરણ નંબર 2
અમે સમાન ક્રિયાઓ કરીએ છીએ. પ્રથમ પગલું:
ચાલો દરેક વસ્તુને ચલ સાથે ડાબી તરફ ખસેડીએ, અને તેના વિના - જમણી તરફ:
અહીં કેટલાક સમાન છે:
દેખીતી રીતે, આ રેખીય સમીકરણનો કોઈ ઉકેલ નથી, તેથી અમે તેને આ રીતે લખીશું:
\[\varnothing\],
અથવા ત્યાં કોઈ મૂળ નથી.
ઉકેલની ઘોંઘાટ
બંને સમીકરણો સંપૂર્ણપણે હલ થઈ ગયા છે. ઉદાહરણ તરીકે આ બે અભિવ્યક્તિઓનો ઉપયોગ કરીને, અમને ફરી એકવાર ખાતરી થઈ કે સરળ રેખીય સમીકરણોમાં પણ, બધું એટલું સરળ ન હોઈ શકે: ત્યાં કાં તો એક, અથવા કોઈ પણ, અથવા અનંત ઘણા મૂળ હોઈ શકે છે. અમારા કિસ્સામાં, અમે બે સમીકરણો ધ્યાનમાં લીધા છે, બંનેનું કોઈ મૂળ નથી.
પરંતુ હું તમારું ધ્યાન બીજી હકીકત તરફ દોરવા માંગુ છું: કૌંસ સાથે કેવી રીતે કામ કરવું અને જો તેમની સામે માઇનસ ચિહ્ન હોય તો તેને કેવી રીતે ખોલવું. આ અભિવ્યક્તિને ધ્યાનમાં લો:
ખોલતા પહેલા, તમારે દરેક વસ્તુને "X" વડે ગુણાકાર કરવાની જરૂર છે. મહેરબાની કરીને નોંધ કરો: ગુણાકાર દરેક વ્યક્તિગત શબ્દ. અંદર બે પદ છે - અનુક્રમે, બે પદ અને ગુણાકાર.
અને આ મોટે ભાગે પ્રાથમિક, પરંતુ ખૂબ જ મહત્વપૂર્ણ અને ખતરનાક પરિવર્તનો પૂર્ણ થયા પછી જ, તમે કૌંસને એ હકીકતના દૃષ્ટિકોણથી ખોલી શકો છો કે તેના પછી માઇનસ ચિહ્ન છે. હા, હા: ફક્ત હવે, જ્યારે પરિવર્તન પૂર્ણ થાય છે, ત્યારે આપણે યાદ રાખીએ છીએ કે કૌંસની સામે માઈનસ ચિહ્ન છે, જેનો અર્થ છે કે નીચેની દરેક વસ્તુ ફક્ત ચિહ્નોને બદલે છે. તે જ સમયે, કૌંસ પોતે અદૃશ્ય થઈ જાય છે અને, સૌથી અગત્યનું, આગળનો "માઈનસ" પણ અદૃશ્ય થઈ જાય છે.
અમે બીજા સમીકરણ સાથે તે જ કરીએ છીએ:
તે આકસ્મિક નથી કે હું આ નાની, મોટે ભાગે નજીવી હકીકતો પર ધ્યાન આપું છું. કારણ કે સમીકરણો ઉકેલવા એ હંમેશા પ્રાથમિક પરિવર્તનનો ક્રમ હોય છે, જ્યાં સ્પષ્ટ અને સક્ષમ રીતે સરળ ક્રિયાઓ કરવામાં અસમર્થતા એ હકીકત તરફ દોરી જાય છે કે ઉચ્ચ શાળાના વિદ્યાર્થીઓ મારી પાસે આવે છે અને ફરીથી આવા સરળ સમીકરણોને હલ કરવાનું શીખે છે.
અલબત્ત, એવો દિવસ આવશે જ્યારે તમે આ કૌશલ્યોને સ્વચાલિતતાના મુદ્દા પર હાંસલ કરશો. તમારે દરેક વખતે આટલા બધા રૂપાંતરણો કરવા પડશે નહીં; તમે બધું એક લીટી પર લખશો. પરંતુ જ્યારે તમે માત્ર શીખતા હોવ, ત્યારે તમારે દરેક ક્રિયાને અલગથી લખવાની જરૂર છે.
વધુ જટિલ રેખીય સમીકરણો ઉકેલવા
હવે આપણે જે ઉકેલવા જઈ રહ્યા છીએ તે ભાગ્યે જ સરળ કાર્ય કહી શકાય, પરંતુ અર્થ એ જ રહે છે.
કાર્ય નંબર 1
\[\left(7x+1 \જમણે)\left(3x-1 \right)-21((x)^(2))=3\]
ચાલો પહેલા ભાગમાં તમામ ઘટકોનો ગુણાકાર કરીએ:
ચાલો થોડી ગોપનીયતા કરીએ:
અહીં કેટલાક સમાન છે:
ચાલો છેલ્લું પગલું પૂર્ણ કરીએ:
\[\frac(-4x)(4)=\frac(4)(-4)\]
અહીં અમારો અંતિમ જવાબ છે. અને, એ હકીકત હોવા છતાં કે હલ કરવાની પ્રક્રિયામાં અમારી પાસે ચતુર્ભુજ કાર્ય સાથે ગુણાંક હતા, તેઓએ એકબીજાને રદ કર્યા, જે સમીકરણને રેખીય બનાવે છે અને ચતુર્ભુજ નથી.
કાર્ય નંબર 2
\[\left(1-4x \જમણે)\left(1-3x \right)=6x\left(2x-1 \જમણે)\]
ચાલો પ્રથમ પગલું કાળજીપૂર્વક કરીએ: પ્રથમ કૌંસમાંથી દરેક ઘટકને બીજામાંથી દરેક ઘટક દ્વારા ગુણાકાર કરો. રૂપાંતરણ પછી કુલ ચાર નવા પદો હોવા જોઈએ:
હવે ચાલો દરેક ટર્મમાં ગુણાકાર કાળજીપૂર્વક કરીએ:
ચાલો “X” સાથેના શબ્દોને ડાબી બાજુએ અને તે વગરના શબ્દોને જમણી બાજુએ ખસેડીએ:
\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]
અહીં સમાન શરતો છે:
ફરી એકવાર અમને અંતિમ જવાબ મળ્યો છે.
ઉકેલની ઘોંઘાટ
આ બે સમીકરણો વિશેની સૌથી મહત્વની નોંધ નીચે મુજબ છે: જલદી આપણે એક કરતાં વધુ પદ ધરાવતા કૌંસનો ગુણાકાર કરવાનું શરૂ કરીએ છીએ, આ નીચેના નિયમ અનુસાર કરવામાં આવે છે: આપણે પ્રથમમાંથી પ્રથમ પદ લઈએ છીએ અને દરેક તત્વ સાથે ગુણાકાર કરીએ છીએ. બીજું; પછી આપણે પ્રથમમાંથી બીજું તત્વ લઈએ છીએ અને તે જ રીતે બીજામાંથી દરેક તત્વ સાથે ગુણાકાર કરીએ છીએ. પરિણામે, અમારી પાસે ચાર પદ હશે.
બીજગણિત રકમ વિશે
આ છેલ્લા ઉદાહરણ સાથે, હું વિદ્યાર્થીઓને યાદ અપાવવા માંગુ છું કે બીજગણિત રકમ શું છે. શાસ્ત્રીય ગણિતમાં, $1-7$ દ્વારા અમારો અર્થ એક સરળ બાંધકામ છે: એકમાંથી સાત બાદ કરો. બીજગણિતમાં, અમારો આનો અર્થ નીચે મુજબ છે: “એક” નંબરમાં આપણે બીજી સંખ્યા ઉમેરીએ છીએ, એટલે કે “માઈનસ સાત”. આ રીતે બીજગણિતનો સરવાળો સામાન્ય અંકગણિતના સરવાળાથી અલગ પડે છે.
જલદી, તમામ રૂપાંતરણો, દરેક ઉમેરણો અને ગુણાકાર કરતી વખતે, તમે ઉપર વર્ણવેલ સમાન બાંધકામો જોવાનું શરૂ કરો છો, બહુપદી અને સમીકરણો સાથે કામ કરતી વખતે તમને બીજગણિતમાં કોઈ સમસ્યા નહીં હોય.
છેલ્લે, ચાલો આપણે થોડા વધુ ઉદાહરણો જોઈએ જે આપણે હમણાં જ જોયા છે તેના કરતાં પણ વધુ જટિલ હશે, અને તેને ઉકેલવા માટે આપણે આપણા પ્રમાણભૂત અલ્ગોરિધમને સહેજ વિસ્તૃત કરવું પડશે.
અપૂર્ણાંક સાથે સમીકરણો ઉકેલવા
આવા કાર્યોને ઉકેલવા માટે, અમારે અમારા અલ્ગોરિધમમાં વધુ એક પગલું ઉમેરવું પડશે. પરંતુ પ્રથમ, ચાલો હું તમને અમારા અલ્ગોરિધમનો યાદ અપાવી દઉં:
- કૌંસ ખોલો.
- અલગ ચલો.
- સમાન લાવો.
- ગુણોત્તર દ્વારા ભાગાકાર કરો.
અરે, આ અદ્ભુત અલ્ગોરિધમ, તેની તમામ અસરકારકતા માટે, જ્યારે આપણી સામે અપૂર્ણાંક હોય ત્યારે તે સંપૂર્ણપણે યોગ્ય નથી. અને આપણે નીચે જે જોઈશું તેમાં, આપણી પાસે બંને સમીકરણોમાં ડાબી અને જમણી બાજુએ અપૂર્ણાંક છે.
આ કિસ્સામાં કેવી રીતે કામ કરવું? હા, તે ખૂબ જ સરળ છે! આ કરવા માટે, તમારે અલ્ગોરિધમમાં એક વધુ પગલું ઉમેરવાની જરૂર છે, જે પ્રથમ ક્રિયા પહેલાં અને પછી બંને કરી શકાય છે, એટલે કે, અપૂર્ણાંકોથી છુટકારો મેળવવો. તેથી અલ્ગોરિધમ નીચે મુજબ હશે:
- અપૂર્ણાંકોથી છુટકારો મેળવો.
- કૌંસ ખોલો.
- અલગ ચલો.
- સમાન લાવો.
- ગુણોત્તર દ્વારા ભાગાકાર કરો.
"અપૂર્ણાંકોથી છૂટકારો મેળવવા" નો અર્થ શું છે? અને આ પ્રથમ ધોરણના પગલા પછી અને પહેલા બંને શા માટે કરી શકાય? હકીકતમાં, અમારા કિસ્સામાં, તમામ અપૂર્ણાંક તેમના છેદમાં સંખ્યાત્મક છે, એટલે કે. દરેક જગ્યાએ છેદ માત્ર એક સંખ્યા છે. તેથી, જો આપણે સમીકરણની બંને બાજુઓને આ સંખ્યા વડે ગુણાકાર કરીએ, તો આપણે અપૂર્ણાંકોથી છૂટકારો મેળવીશું.
ઉદાહરણ નંબર 1
\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=(x)^(2))-1\]
ચાલો આ સમીકરણમાંના અપૂર્ણાંકોથી છુટકારો મેળવીએ:
\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left((x)^(2))-1 \right)\cdot 4\]
મહેરબાની કરીને નોંધ કરો: દરેક વસ્તુને એકવાર "ચાર" વડે ગુણાકાર કરવામાં આવે છે, એટલે કે. ફક્ત તમારી પાસે બે કૌંસ હોવાનો અર્થ એ નથી કે તમારે દરેકને "ચાર" વડે ગુણાકાર કરવો પડશે. ચાલો નીચે લખીએ:
\[\left(2x+1 \right)\left(2x-3 \right)=\left((x)^(2))-1 \right)\cdot 4\]
ચાલો હવે વિસ્તૃત કરીએ:
અમે ચલને અલગ કરીએ છીએ:
અમે સમાન શરતોનો ઘટાડો કરીએ છીએ:
\[-4x=-1\left| :\left(-4 \જમણે) \જમણે.\]
\[\frac(-4x)(-4)=\frac(-1)(-4)\]
અમને અંતિમ ઉકેલ મળ્યો છે, ચાલો બીજા સમીકરણ તરફ આગળ વધીએ.
ઉદાહરણ નંબર 2
\[\frac(\left(1-x \right)\left(1+5x \right))(5)+(x)^(2)=1\]
અહીં આપણે બધી સમાન ક્રિયાઓ કરીએ છીએ:
\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]
\[\frac(4x)(4)=\frac(4)(4)\]
સમસ્યા હલ થાય છે.
તે, હકીકતમાં, હું તમને આજે કહેવા માંગતો હતો.
કી પોઈન્ટ્સ
મુખ્ય તારણો છે:
- રેખીય સમીકરણો ઉકેલવા માટેનું અલ્ગોરિધમ જાણો.
- કૌંસ ખોલવાની ક્ષમતા.
- ચિંતા કરશો નહીં જો તમારી પાસે ક્યાંક ચતુર્ભુજ કાર્યો છે, મોટે ભાગે, તેઓ વધુ પરિવર્તનની પ્રક્રિયામાં ઘટાડવામાં આવશે.
- રેખીય સમીકરણોમાં ત્રણ પ્રકારના મૂળ હોય છે, સૌથી સરળ પણ: એક જ મૂળ, આખી સંખ્યા રેખા એક મૂળ હોય છે, અને કોઈ મૂળ નથી.
હું આશા રાખું છું કે આ પાઠ તમને બધા ગણિતની વધુ સમજણ માટે એક સરળ, પરંતુ ખૂબ જ મહત્વપૂર્ણ વિષયમાં માસ્ટર કરવામાં મદદ કરશે. જો કંઈક સ્પષ્ટ ન હોય, તો સાઇટ પર જાઓ અને ત્યાં પ્રસ્તુત ઉદાહરણો ઉકેલો. ટ્યુન રહો, ઘણી વધુ રસપ્રદ વસ્તુઓ તમારી રાહ જોઈ રહી છે!








