મેટ્રિક્સના વ્યસ્ત શોધવાનું એક જટિલ ઉદાહરણ. વ્યસ્ત મેટ્રિક્સ શોધવા માટેની પદ્ધતિઓ

આપેલ મેટ્રિક્સ માટેનું વ્યસ્ત મેટ્રિક્સ એવું મેટ્રિક્સ છે, જે મૂળ મેટ્રિક્સનો ગુણાકાર કરે છે જેના દ્વારા ઓળખ મેટ્રિક્સ મળે છે: વ્યસ્ત મેટ્રિક્સની હાજરી માટે ફરજિયાત અને પર્યાપ્ત શરત એ છે કે મૂળ મેટ્રિક્સનો નિર્ધારક શૂન્યની બરાબર નથી (જે બદલામાં સૂચવે છે કે મેટ્રિક્સ ચોરસ હોવો જોઈએ). જો મેટ્રિક્સનો નિર્ણાયક શૂન્ય સમાન હોય, તો તેને એકવચન કહેવામાં આવે છે અને આવા મેટ્રિક્સમાં વ્યસ્ત નથી. ઉચ્ચ ગણિતમાં, વ્યસ્ત મેટ્રિસિસ મહત્વપૂર્ણ છે અને તેનો ઉપયોગ સંખ્યાબંધ સમસ્યાઓ ઉકેલવા માટે થાય છે. ઉદાહરણ તરીકે, ચાલુ વ્યસ્ત મેટ્રિક્સ શોધવીસમીકરણોની સિસ્ટમો ઉકેલવા માટે મેટ્રિક્સ પદ્ધતિ બનાવવામાં આવી હતી. અમારી સેવા સાઇટ પરવાનગી આપે છે વ્યસ્ત મેટ્રિક્સની ઓનલાઇન ગણતરી કરોબે પદ્ધતિઓ: ગૌસ-જોર્ડન પદ્ધતિ અને બીજગણિત ઉમેરણોના મેટ્રિક્સનો ઉપયોગ કરીને. પ્રથમમાં મેટ્રિક્સની અંદર મોટી સંખ્યામાં પ્રાથમિક રૂપાંતરણોનો સમાવેશ થાય છે, બીજામાં તમામ ઘટકોમાં નિર્ણાયક અને બીજગણિતીય ઉમેરણોની ગણતરીનો સમાવેશ થાય છે. મેટ્રિક્સના નિર્ણાયકની ઓનલાઇન ગણતરી કરવા માટે, તમે અમારી અન્ય સેવાનો ઉપયોગ કરી શકો છો - મેટ્રિક્સના નિર્ણાયકની ઓનલાઇન ગણતરી

સાઇટ માટે વ્યસ્ત મેટ્રિક્સ શોધો

વેબસાઇટતમને શોધવા માટે પરવાનગી આપે છે વ્યસ્ત મેટ્રિક્સ ઓનલાઇનઝડપી અને મફત. સાઇટ પર, અમારી સેવાનો ઉપયોગ કરીને ગણતરીઓ કરવામાં આવે છે અને પરિણામ શોધવા માટે વિગતવાર ઉકેલ સાથે આપવામાં આવે છે વ્યસ્ત મેટ્રિક્સ. સર્વર હંમેશા માત્ર સચોટ અને સાચો જવાબ આપે છે. વ્યાખ્યા દ્વારા કાર્યોમાં વ્યસ્ત મેટ્રિક્સ ઓનલાઇન, તે જરૂરી છે કે નિર્ણાયક મેટ્રિસિસશૂન્ય હતું, અન્યથા વેબસાઇટઅસલ મેટ્રિક્સનો નિર્ણાયક શૂન્ય સમાન છે તે હકીકતને કારણે વ્યસ્ત મેટ્રિક્સ શોધવાની અશક્યતાની જાણ કરશે. શોધવાનું કાર્ય વ્યસ્ત મેટ્રિક્સગણિતની ઘણી શાખાઓમાં જોવા મળે છે, જે બીજગણિતની સૌથી મૂળભૂત વિભાવનાઓમાંની એક છે અને લાગુ સમસ્યાઓમાં ગાણિતિક સાધન છે. સ્વતંત્ર વ્યસ્ત મેટ્રિક્સની વ્યાખ્યાગણતરીમાં ટાઈપો અથવા નાની ભૂલો ટાળવા માટે નોંધપાત્ર પ્રયત્નો, ઘણો સમય, ગણતરીઓ અને મહાન કાળજીની જરૂર છે. તેથી અમારી સેવા વ્યસ્ત મેટ્રિક્સ ઓનલાઈન શોધવુંતમારા કાર્યને વધુ સરળ બનાવશે અને ગાણિતિક સમસ્યાઓ ઉકેલવા માટે એક અનિવાર્ય સાધન બની જશે. ભલે તમે વ્યસ્ત મેટ્રિક્સ શોધોજાતે, અમે અમારા સર્વર પર તમારું સોલ્યુશન તપાસવાની ભલામણ કરીએ છીએ. અમારી વેબસાઈટ પર તમારું મૂળ મેટ્રિક્સ દાખલ કરો ઈન્વર્સ મેટ્રિક્સની ઓનલાઈન ગણતરી કરો અને તમારો જવાબ તપાસો. અમારી સિસ્ટમ ક્યારેય ભૂલો કરતી નથી અને શોધતી નથી વ્યસ્ત મેટ્રિક્સમોડમાં આપેલ પરિમાણ ઓનલાઇનતરત! વેબસાઇટ પર વેબસાઇટતત્વોમાં અક્ષર પ્રવેશો માન્ય છે મેટ્રિક્સ, આ કિસ્સામાં વ્યસ્ત મેટ્રિક્સ ઓનલાઇનસામાન્ય પ્રતીકાત્મક સ્વરૂપમાં રજૂ કરવામાં આવશે.

એક ચોરસ મેટ્રિક્સ આપવા દો. તમારે વ્યસ્ત મેટ્રિક્સ શોધવાની જરૂર છે.

પ્રથમ માર્ગ. વ્યસ્ત મેટ્રિક્સના અસ્તિત્વ અને વિશિષ્ટતાનો પ્રમેય 4.1 તેને શોધવા માટેની એક રીત સૂચવે છે.

1. આ મેટ્રિક્સના નિર્ણાયકની ગણતરી કરો. જો, તો વ્યસ્ત મેટ્રિક્સ અસ્તિત્વમાં નથી (મેટ્રિક્સ એકવચન છે).

2. મેટ્રિક્સ તત્વોના બીજગણિતીય પૂરકમાંથી મેટ્રિક્સ બનાવો.

3. સંલગ્ન મેટ્રિક્સ મેળવવા માટે મેટ્રિક્સને સ્થાનાંતરિત કરો .

4. સંલગ્ન મેટ્રિક્સના તમામ ઘટકોને નિર્ણાયક દ્વારા વિભાજીત કરીને વ્યસ્ત મેટ્રિક્સ (4.1) શોધો

બીજી રીત. વ્યસ્ત મેટ્રિક્સ શોધવા માટે, તમે પ્રાથમિક પરિવર્તનનો ઉપયોગ કરી શકો છો.

1. આપેલ મેટ્રિક્સને સમાન ક્રમનું ઓળખ મેટ્રિક્સ સોંપીને બ્લોક મેટ્રિક્સ બનાવો.

2. મેટ્રિક્સની પંક્તિઓ પર કરવામાં આવેલ પ્રાથમિક પરિવર્તનનો ઉપયોગ કરીને, તેના ડાબા બ્લોકને તેના સરળ સ્વરૂપમાં લાવો. આ કિસ્સામાં, બ્લોક મેટ્રિક્સને તે સ્વરૂપમાં ઘટાડવામાં આવે છે જ્યાં ઓળખ મેટ્રિક્સમાંથી પરિવર્તનના પરિણામે મેળવેલ ચોરસ મેટ્રિક્સ છે.

3. જો , તો બ્લોક મેટ્રિક્સના વ્યસ્ત સમાન છે, એટલે કે જો, તો મેટ્રિક્સમાં વ્યસ્ત નથી.

હકીકતમાં, મેટ્રિક્સની પંક્તિઓના પ્રાથમિક પરિવર્તનની મદદથી, તેના ડાબા બ્લોકને સરળ સ્વરૂપમાં ઘટાડી શકાય છે (જુઓ. ફિગ. 1.5). આ કિસ્સામાં, બ્લોક મેટ્રિક્સ ફોર્મમાં રૂપાંતરિત થાય છે જ્યાં સમાનતાને સંતોષતું પ્રાથમિક મેટ્રિક્સ છે. જો મેટ્રિક્સ બિન-ડિજનરેટ છે, તો પછી રિમાર્કસ 3.3 ના ફકરા 2 અનુસાર તેનું સરળ સ્વરૂપ ઓળખ મેટ્રિક્સ સાથે એકરુપ છે. પછી સમાનતામાંથી તે અનુસરે છે. જો મેટ્રિક્સ એકવચન છે, તો તેનું સરળ સ્વરૂપ ઓળખ મેટ્રિક્સથી અલગ છે, અને મેટ્રિક્સમાં વ્યસ્ત નથી.

11. મેટ્રિક્સ સમીકરણો અને તેમના ઉકેલ. SLAE રેકોર્ડિંગનું મેટ્રિક્સ સ્વરૂપ. SLAE ને ઉકેલવા માટે મેટ્રિક્સ પદ્ધતિ (વિપરીત મેટ્રિક્સ પદ્ધતિ) અને તેની લાગુ પડતી શરતો.

મેટ્રિક્સ સમીકરણો ફોર્મના સમીકરણો છે: A*X=C; X*A=C;દરેક SLAE સાથે અનેક મેટ્રિસિસ સાંકળવામાં આવી શકે છે; વધુમાં, SLAE પોતે મેટ્રિક્સ સમીકરણના રૂપમાં લખી શકાય છે. SLAE (1) માટે, નીચેના મેટ્રિક્સને ધ્યાનમાં લો:

મેટ્રિક્સ A કહેવાય છે સિસ્ટમનું મેટ્રિક્સ. આ મેટ્રિક્સના તત્વો આપેલ SLAE ના ગુણાંકનું પ્રતિનિધિત્વ કરે છે.

મેટ્રિક્સ A˜ કહેવાય છે વિસ્તૃત મેટ્રિક્સ સિસ્ટમ. તે સિસ્ટમ મેટ્રિક્સમાં મફત શબ્દો b1,b2,...,bm ધરાવતી કૉલમ ઉમેરીને મેળવવામાં આવે છે. સામાન્ય રીતે આ કૉલમ સ્પષ્ટતા માટે ઊભી રેખા દ્વારા અલગ કરવામાં આવે છે.

કૉલમ મેટ્રિક્સ B કહેવાય છે મફત સભ્યોનું મેટ્રિક્સ, અને કૉલમ મેટ્રિક્સ X છે અજાણ્યાઓનું મેટ્રિક્સ.

ઉપર રજૂ કરાયેલ સંકેતનો ઉપયોગ કરીને, SLAE (1) ને મેટ્રિક્સ સમીકરણના સ્વરૂપમાં લખી શકાય છે: A⋅X=B.

નોંધ

સિસ્ટમ સાથે સંકળાયેલ મેટ્રિસિસ વિવિધ રીતે લખી શકાય છે: બધું વિચારણા હેઠળના SLAE ના ચલ અને સમીકરણોના ક્રમ પર આધારિત છે. પરંતુ કોઈ પણ સંજોગોમાં, આપેલ SLAE ના દરેક સમીકરણમાં અજાણ્યાઓનો ક્રમ સમાન હોવો જોઈએ.

મેટ્રિક્સ પદ્ધતિ SLAE ને ઉકેલવા માટે યોગ્ય છે જેમાં સમીકરણોની સંખ્યા અજાણ્યા ચલોની સંખ્યા સાથે મેળ ખાય છે અને સિસ્ટમના મુખ્ય મેટ્રિક્સનો નિર્ધારક શૂન્યથી અલગ છે. જો સિસ્ટમમાં ત્રણ કરતાં વધુ સમીકરણો હોય, તો વ્યસ્ત મેટ્રિક્સ શોધવા માટે નોંધપાત્ર કોમ્પ્યુટેશનલ પ્રયત્નોની જરૂર પડે છે, તેથી, આ કિસ્સામાં તેનો ઉપયોગ કરવાની સલાહ આપવામાં આવે છે. ગૌસીયન પદ્ધતિ.

12. સજાતીય SLAE, તેમના બિન-શૂન્ય ઉકેલોના અસ્તિત્વ માટેની શરતો. સજાતીય SLAE ના આંશિક ઉકેલોના ગુણધર્મો.

રેખીય સમીકરણને સજાતીય કહેવામાં આવે છે જો તેનો મુક્ત શબ્દ શૂન્ય સમાન હોય અને અન્યથા અસંગત હોય. સજાતીય સમીકરણો ધરાવતી સિસ્ટમને સજાતીય કહેવામાં આવે છે અને તેનું સામાન્ય સ્વરૂપ છે:

13 રેખીય સ્વતંત્રતાનો ખ્યાલ અને સજાતીય SLAE ના આંશિક ઉકેલોની અવલંબન. ફન્ડામેન્ટલ સિસ્ટમ ઑફ સોલ્યુશન્સ (FSD) અને તેનું નિર્ધારણ. એફએસઆર દ્વારા સજાતીય SLAE ના સામાન્ય ઉકેલનું પ્રતિનિધિત્વ.

કાર્ય સિસ્ટમ y 1 (x ), y 2 (x ), …, y n (x ) કહેવાય છે રેખીય રીતે નિર્ભરઅંતરાલ પર ( a , b ), જો ત્યાં એક જ સમયે શૂન્યની બરાબર ન હોય તેવા સ્થિર ગુણાંકનો સમૂહ હોય, જેમ કે આ કાર્યોનું રેખીય સંયોજન શૂન્ય પર સમાન હોય છે ( a , b માટે . જો સમાનતા ફક્ત માટે જ શક્ય છે, તો ફંક્શન સિસ્ટમ y 1 (x ), y 2 (x ), …, y n (x ) કહેવાય છે રેખીય રીતે સ્વતંત્રઅંતરાલ પર ( a , b ). બીજા શબ્દોમાં કહીએ તો, કાર્યો y 1 (x ), y 2 (x ), …, y n (x ) રેખીય રીતે નિર્ભરઅંતરાલ પર ( a , b જો ત્યાં શૂન્યની બરાબર હોય તો ( a , b ) તેમનું બિન-તુચ્છ રેખીય સંયોજન. કાર્યો y 1 (x ),y 2 (x ), …, y n (x ) રેખીય રીતે સ્વતંત્રઅંતરાલ પર ( a , b ), જો માત્ર તેમનું તુચ્છ રેખીય સંયોજન સમાન રીતે શૂન્ય પર ( a , b ).

મૂળભૂત નિર્ણય પ્રણાલી (FSR)એક સમાન SLAE કૉલમની આ સિસ્ટમનો આધાર છે.

એફએસઆરમાં તત્વોની સંખ્યા સિસ્ટમ મેટ્રિક્સના રેન્ક બાદ સિસ્ટમના અજાણ્યાઓની સંખ્યા જેટલી છે. મૂળ સિસ્ટમનો કોઈપણ ઉકેલ એ એફએસઆરના ઉકેલોનું રેખીય સંયોજન છે.

પ્રમેય

બિન-સજાતીય SLAE નો સામાન્ય ઉકેલ એ બિન-સમાન્ય SLAE ના ચોક્કસ દ્રાવણના સરવાળા અને અનુરૂપ સજાતીય SLAE ના સામાન્ય ઉકેલ જેટલો છે.

1 . જો સ્તંભો સમીકરણોની સજાતીય પ્રણાલીના ઉકેલો છે, તો તેમાંથી કોઈપણ રેખીય સંયોજન પણ સજાતીય પ્રણાલીનો ઉકેલ છે.

ખરેખર, સમાનતાઓમાંથી તે તેને અનુસરે છે

તે ઉકેલોનું રેખીય સંયોજન એ સજાતીય સિસ્ટમનો ઉકેલ છે.

2. જો સજાતીય પ્રણાલીના મેટ્રિક્સનો ક્રમ સમાન હોય, તો સિસ્ટમમાં રેખીય રીતે સ્વતંત્ર ઉકેલો હોય છે.

ખરેખર, એકસમાન પ્રણાલીના સામાન્ય ઉકેલ માટે સૂત્રો (5.13) નો ઉપયોગ કરીને, અમે વિશિષ્ટ ઉકેલો શોધીએ છીએ, જે નીચે આપેલા મુક્ત ચલો આપે છે. માનક મૂલ્ય સેટ (દરેક વખતે એમ માની લઈએ કે ફ્રી ચલોમાંનું એક એક બરાબર છે અને બાકીનું શૂન્ય બરાબર છે):

જે રેખીય રીતે સ્વતંત્ર છે. હકીકતમાં, જો તમે આ કૉલમ્સમાંથી મેટ્રિક્સ બનાવો છો, તો તેની છેલ્લી પંક્તિઓ ઓળખ મેટ્રિક્સ બનાવે છે. પરિણામે, છેલ્લી લીટીઓમાં સ્થિત ગૌણ શૂન્યની બરાબર નથી (તે એકની બરાબર છે), એટલે કે. મૂળભૂત છે. તેથી, મેટ્રિક્સનો ક્રમ સમાન હશે. આનો અર્થ એ છે કે આ મેટ્રિક્સના તમામ કૉલમ રેખીય રીતે સ્વતંત્ર છે (પ્રમેય 3.4 જુઓ).

સજાતીય સિસ્ટમના રેખીય સ્વતંત્ર ઉકેલોના કોઈપણ સંગ્રહને કહેવામાં આવે છે ઉકેલોની મૂળભૂત સિસ્ટમ (સેટ). .

14 માઇનોર ઓફ ધ ઓર્ડર, બેઝિક માઇનોર, મેટ્રિક્સનો રેન્ક. મેટ્રિક્સની રેન્કની ગણતરી.

મેટ્રિક્સ A નો ક્રમ k માઇનોર એ તેના કેટલાક ચોરસ સબમેટ્રિક્સ ક્રમ k નો નિર્ણાયક છે.

m x n પરિમાણના મેટ્રિક્સ Aમાં, ક્રમ r ના નાનાને મૂળભૂત કહેવામાં આવે છે જો તે શૂન્ય ન હોય, અને ઉચ્ચ ક્રમના તમામ સગીર, જો તેઓ અસ્તિત્વમાં હોય, તો શૂન્ય સમાન છે.

મેટ્રિક્સ A ના સ્તંભો અને પંક્તિઓ, જેના આંતરછેદ પર બેઝિસ માઇનોર છે, તેને A ની બેઝિક કૉલમ્સ અને પંક્તિઓ કહેવામાં આવે છે.

પ્રમેય 1. (મેટ્રિક્સના ક્રમ પર). કોઈપણ મેટ્રિક્સ માટે, ગૌણ ક્રમ એ પંક્તિ ક્રમની બરાબર અને કૉલમ ક્રમની બરાબર છે.

પ્રમેય 2. (નાના આધારે). દરેક મેટ્રિક્સ કૉલમ તેના આધાર કૉલમના રેખીય સંયોજનમાં વિઘટિત થાય છે.

મેટ્રિક્સનો ક્રમ (અથવા માઇનોર રેન્ક) એ બેઝિસ માઇનોરનો ક્રમ છે અથવા બીજા શબ્દોમાં કહીએ તો, સૌથી મોટો ક્રમ કે જેના માટે બિન-શૂન્ય સગીર અસ્તિત્વ ધરાવે છે. શૂન્ય મેટ્રિક્સની રેન્કને વ્યાખ્યા દ્વારા 0 ગણવામાં આવે છે.

ચાલો નાના ક્રમના બે સ્પષ્ટ ગુણધર્મોની નોંધ લઈએ.

1) ટ્રાન્સપોઝિશન દરમિયાન મેટ્રિક્સનો રેન્ક બદલાતો નથી, કારણ કે જ્યારે મેટ્રિક્સ ટ્રાન્સપોઝ થાય છે, ત્યારે તેના તમામ સબમેટ્રિક્સ ટ્રાન્સપોઝ થાય છે અને સગીર બદલાતા નથી.

2) જો A' એ મેટ્રિક્સ A નું સબમેટ્રિક્સ છે, તો A' ની રેન્ક A ના રેન્ક કરતાં વધી જતી નથી, કારણ કે A' માં શામેલ બિન-શૂન્ય સગીર પણ A માં શામેલ છે.

15. પરિમાણીય અંકગણિત વેક્ટરનો ખ્યાલ. વેક્ટરની સમાનતા. વેક્ટર્સ પરની ક્રિયાઓ (ઉમેરો, બાદબાકી, સંખ્યા દ્વારા ગુણાકાર, મેટ્રિક્સ દ્વારા ગુણાકાર). વેક્ટર્સનું રેખીય સંયોજન.

ઓર્ડર કરેલ સંગ્રહ nવાસ્તવિક અથવા જટિલ સંખ્યાઓ કહેવામાં આવે છે n-પરિમાણીય વેક્ટર. નંબરો કહેવામાં આવે છે વેક્ટર કોઓર્ડિનેટ્સ.

બે (શૂન્ય સિવાયના) વેક્ટર aઅને bસમાન હોય છે જો તેઓ સમાન રીતે નિર્દેશિત હોય અને સમાન મોડ્યુલ હોય. બધા શૂન્ય વેક્ટર સમાન ગણવામાં આવે છે. અન્ય તમામ કિસ્સાઓમાં, વેક્ટર સમાન નથી.

વેક્ટર ઉમેરણ. વેક્ટર ઉમેરવાની બે રીતો છે: 1. સમાંતરગ્રામ નિયમ. વેક્ટર ઉમેરવા માટે અને, અમે બંનેના મૂળ એક જ બિંદુ પર મૂકીએ છીએ. આપણે સમાંતરગ્રામ સુધી બનાવીએ છીએ અને તે જ બિંદુથી આપણે સમાંતરગ્રામનો કર્ણ દોરીએ છીએ. આ વેક્ટરનો સરવાળો હશે.

2. વેક્ટર ઉમેરવાની બીજી પદ્ધતિ ત્રિકોણ નિયમ છે. ચાલો એ જ વેક્ટર લઈએ અને . આપણે પ્રથમ વેક્ટરના અંતમાં બીજાની શરૂઆત ઉમેરીશું. હવે ચાલો પ્રથમની શરૂઆત અને બીજાના અંતને જોડીએ. આ વેક્ટરનો સરવાળો છે અને . સમાન નિયમનો ઉપયોગ કરીને, તમે ઘણા વેક્ટર ઉમેરી શકો છો. અમે તેમને એક પછી એક ગોઠવીએ છીએ, અને પછી પ્રથમની શરૂઆતને છેલ્લાના અંત સાથે જોડીએ છીએ.

વેક્ટરની બાદબાકી. વેક્ટરને વેક્ટરની વિરુદ્ધ દિશામાન કરવામાં આવે છે. વેક્ટરની લંબાઈ સમાન છે. હવે તે સ્પષ્ટ છે કે વેક્ટર બાદબાકી શું છે. વેક્ટર વચ્ચેનો તફાવત અને વેક્ટર અને વેક્ટરનો સરવાળો છે.

સંખ્યા વડે વેક્ટરનો ગુણાકાર

વેક્ટરને સંખ્યા k વડે ગુણાકાર કરવાથી એક વેક્ટર ઉત્પન્ન થાય છે જેની લંબાઈ k લંબાઇના ગણી હોય છે. જો k શૂન્ય કરતા વધારે હોય તો તે વેક્ટર સાથે સહદિશાત્મક હોય છે અને જો k શૂન્ય કરતા ઓછું હોય તો વિરુદ્ધ દિશા નિર્દેશિત હોય છે.

વેક્ટર્સનું સ્કેલર ઉત્પાદન એ વેક્ટરની લંબાઈ અને તેમની વચ્ચેના ખૂણાના કોસાઈનનું ઉત્પાદન છે.જો વેક્ટર કાટખૂણે હોય, તો તેમનું સ્કેલર ઉત્પાદન શૂન્ય છે. અને આ રીતે વેક્ટરના કોઓર્ડિનેટ્સ અને સ્કેલર ઉત્પાદનને વ્યક્ત કરવામાં આવે છે.

વેક્ટર્સનું રેખીય સંયોજન

વેક્ટર્સનું રેખીય સંયોજન વેક્ટર કહેવાય છે

જ્યાં - રેખીય સંયોજન ગુણાંક. જો જો તે બિન-તુચ્છ હોય તો સંયોજનને તુચ્છ કહેવામાં આવે છે.

16 અંકગણિત વેક્ટરનું સ્કેલર ઉત્પાદન. વેક્ટરની લંબાઈ અને વેક્ટર વચ્ચેનો કોણ. વેક્ટર ઓર્થોગોનાલિટીનો ખ્યાલ.

a અને b વેક્ટરનો સ્કેલર ગુણાંક એ સંખ્યા છે

સ્કેલર પ્રોડક્ટનો ઉપયોગ ગણતરી કરવા માટે થાય છે: 1) તેમની વચ્ચેનો કોણ શોધવો; 3) વેક્ટરની લંબાઈની ગણતરી કરવી;

સેગમેન્ટ AB ની લંબાઈને બિંદુ A અને B વચ્ચેનું અંતર કહેવામાં આવે છે. A અને B વેક્ટર વચ્ચેના ખૂણાને કોણ α = (a, b), 0≤ α ≤P કહેવામાં આવે છે. જેના દ્વારા તમારે 1 વેક્ટરને ફેરવવાની જરૂર છે જેથી તેની દિશા અન્ય વેક્ટર સાથે એકરુપ થાય. પૂરી પાડવામાં આવેલ છે કે તેમની ઉત્પત્તિ એકરુપ છે.

ઓર્ટોમ a એ વેક્ટર છે જેની લંબાઈ અને દિશા a છે.

17. વેક્ટરની સિસ્ટમ અને તેનું રેખીય સંયોજન. રેખીય અવલંબન અને વેક્ટર્સની સિસ્ટમની સ્વતંત્રતાનો ખ્યાલ. વેક્ટર્સની સિસ્ટમની રેખીય અવલંબન માટે જરૂરી અને પર્યાપ્ત પરિસ્થિતિઓ પર પ્રમેય.

વેક્ટર a1,a2,...,an ની સિસ્ટમને લીનિયરલી ડિપેન્ડન્ટ કહેવામાં આવે છે જો ત્યાં સંખ્યાઓ λ1,λ2,...,λn હોય કે તેમાંથી ઓછામાં ઓછી એક શૂન્ય હોય અને λ1a1+λ2a2+...λnan=0 . નહિંતર, સિસ્ટમને રેખીય રીતે સ્વતંત્ર કહેવામાં આવે છે.

બે વેક્ટર a1 અને a2 જો તેમની દિશાઓ એકસરખી અથવા વિરુદ્ધ હોય તો તેમને કોલિનિયર કહેવામાં આવે છે.

ત્રણ વેક્ટર a1, a2 અને a3ને કોપ્લાનર કહેવામાં આવે છે જો તેઓ અમુક સમતલની સમાંતર હોય.

રેખીય અવલંબન માટે ભૌમિતિક માપદંડ:

a) સિસ્ટમ (a1,a2) રેખીય રીતે નિર્ભર છે જો અને માત્ર જો વેક્ટર a1 અને a2 સમરેખા હોય.

b) સિસ્ટમ (a1,a2,a3) રેખીય રીતે નિર્ભર છે જો અને માત્ર જો વેક્ટર a1,a2 અને a3 કોપ્લાનર હોય.

પ્રમેય (રેખીય અવલંબન માટે જરૂરી અને પર્યાપ્ત સ્થિતિ સિસ્ટમોવેક્ટર.)

વેક્ટર સિસ્ટમ વેક્ટર જગ્યાછે રેખીયઆશ્રિત જો અને માત્ર જો સિસ્ટમના વેક્ટરમાંથી એક અન્યની દ્રષ્ટિએ રેખીય રીતે વ્યક્ત કરવામાં આવે વેક્ટરઆ સિસ્ટમ.

કોરોલરી 1. વેક્ટર સ્પેસમાં વેક્ટર્સની સિસ્ટમ રેખીય રીતે સ્વતંત્ર હોય છે જો અને માત્ર જો સિસ્ટમના કોઈપણ વેક્ટર આ સિસ્ટમના અન્ય વેક્ટર્સની દ્રષ્ટિએ રેખીય રીતે વ્યક્ત ન હોય.2. શૂન્ય વેક્ટર અથવા બે સમાન વેક્ટર ધરાવતી વેક્ટર્સની સિસ્ટમ રેખીય રીતે આધારિત છે.

વ્યસ્ત મેટ્રિક્સ શોધવી- એક સમસ્યા જે ઘણીવાર બે પદ્ધતિઓ દ્વારા હલ થાય છે:

• બીજગણિત ઉમેરણોની પદ્ધતિ, જેમાં નિર્ણાયકો શોધવા અને મેટ્રિસિસ ટ્રાન્સપોઝ કરવાની જરૂર છે;
• અજાણ્યાઓને દૂર કરવાની ગૌસીયન પદ્ધતિ, જેમાં મેટ્રિસીસના પ્રાથમિક રૂપાંતર કરવાની જરૂર છે (પંક્તિઓ ઉમેરો, સમાન સંખ્યા દ્વારા પંક્તિઓનો ગુણાકાર કરો, વગેરે).

જેઓ ખાસ કરીને વિચિત્ર છે, ત્યાં અન્ય પદ્ધતિઓ છે, ઉદાહરણ તરીકે, રેખીય પરિવર્તનની પદ્ધતિ. આ પાઠમાં આપણે આ પદ્ધતિઓનો ઉપયોગ કરીને વ્યસ્ત મેટ્રિક્સ શોધવા માટે ઉલ્લેખિત ત્રણ પદ્ધતિઓ અને અલ્ગોરિધમ્સનું વિશ્લેષણ કરીશું.

વ્યસ્ત મેટ્રિક્સ એ, આવા મેટ્રિક્સ કહેવામાં આવે છે

એ
. (1)

વ્યસ્ત મેટ્રિક્સ , જે આપેલ ચોરસ મેટ્રિક્સ માટે શોધવાની જરૂર છે એ, આવા મેટ્રિક્સ કહેવામાં આવે છે

જેનું ઉત્પાદન મેટ્રિસિસ એજમણી બાજુએ ઓળખ મેટ્રિક્સ છે, એટલે કે.
. (1)

ઓળખ મેટ્રિક્સ એ એક કર્ણ મેટ્રિક્સ છે જેમાં તમામ કર્ણ તત્વો એક સમાન હોય છે.

પ્રમેય.દરેક બિન-એકવચન (નૉન-ડિજનરેટ, બિન-એકવચન) ચોરસ મેટ્રિક્સ માટે, એક વ્યસ્ત મેટ્રિક્સ શોધી શકે છે, અને માત્ર એક. વિશિષ્ટ (ડિજનરેટ, એકવચન) ચોરસ મેટ્રિક્સ માટે, વ્યસ્ત મેટ્રિક્સ અસ્તિત્વમાં નથી.

ચોરસ મેટ્રિક્સ કહેવાય છે ખાસ નથી(અથવા બિન-અધોગતિ, બિન-એકવચન), જો તેનો નિર્ણાયક શૂન્ય નથી, અને ખાસ(અથવા અધોગતિ, એકવચન) જો તેનો નિર્ણાયક શૂન્ય છે.

મેટ્રિક્સનો વ્યસ્ત માત્ર ચોરસ મેટ્રિક્સ માટે જ શોધી શકાય છે. સ્વાભાવિક રીતે, વ્યસ્ત મેટ્રિક્સ પણ ચોરસ અને આપેલ મેટ્રિક્સ જેવા જ ક્રમમાં હશે. એક મેટ્રિક્સ કે જેના માટે વ્યસ્ત મેટ્રિક્સ શોધી શકાય છે તેને ઇન્વર્ટિબલ મેટ્રિક્સ કહેવામાં આવે છે.

માટે વ્યસ્ત મેટ્રિક્સ સંખ્યાના વ્યસ્ત સાથે સંબંધિત સામ્યતા છે. દરેક નંબર માટે a, શૂન્યની બરાબર નથી, આવી સંખ્યા છે bકે કામ aઅને bએક સમાન: ab= 1. નંબર bસંખ્યાનો વ્યસ્ત કહેવાય છે b. ઉદાહરણ તરીકે, નંબર 7 માટે પારસ્પરિક 1/7 છે, કારણ કે 7*1/7=1.

બીજગણિત ઉમેરણોની પદ્ધતિનો ઉપયોગ કરીને વ્યસ્ત મેટ્રિક્સ શોધવું (સંલગ્ન મેટ્રિક્સ)

બિન-એકવચન ચોરસ મેટ્રિક્સ માટે એવ્યસ્ત એ મેટ્રિક્સ છે

મેટ્રિક્સનો નિર્ણાયક ક્યાં છે એ, a એ મેટ્રિક્સ સાથે સંકળાયેલ મેટ્રિક્સ છે એ.

ચોરસ મેટ્રિક્સ સાથે જોડાણ એસમાન ક્રમનું મેટ્રિક્સ છે, જેનાં તત્વો મેટ્રિક્સ A ના સંદર્ભમાં સ્થાનાંતરિત મેટ્રિક્સના નિર્ણાયકના અનુરૂપ ઘટકોના બીજગણિતીય પૂરક છે. આમ, જો

તે

અને

બીજગણિત ઉમેરણોની પદ્ધતિનો ઉપયોગ કરીને વ્યસ્ત મેટ્રિક્સ શોધવા માટેનું અલ્ગોરિધમ

1. આ મેટ્રિક્સનો નિર્ણાયક શોધો એ. જો નિર્ણાયક શૂન્યની બરાબર હોય, તો વ્યસ્ત મેટ્રિક્સ શોધવાનું બંધ થઈ જાય છે, કારણ કે મેટ્રિક્સ એકવચન છે અને તેનો વ્યસ્ત અસ્તિત્વમાં નથી.

2. આદર સાથે ટ્રાન્સપોઝ કરેલ મેટ્રિક્સ શોધો એ.

3. સ્ટેપ 2 માં મળેલ મેરીટ્ઝના બીજગણિતીય પૂરક તરીકે યુનિયન મેટ્રિક્સના તત્વોની ગણતરી કરો.

4. સૂત્ર (2) લાગુ કરો: મેટ્રિક્સ નિર્ણાયકના વ્યસ્તનો ગુણાકાર કરો એ, પગલું 4 માં મળેલ યુનિયન મેટ્રિક્સ માટે.

5. આ મેટ્રિક્સનો ગુણાકાર કરીને સ્ટેપ 4 માં મેળવેલ પરિણામ તપાસો એવ્યસ્ત મેટ્રિક્સ સુધી. જો આ મેટ્રિક્સનું ઉત્પાદન ઓળખ મેટ્રિક્સ સમાન હોય, તો વ્યસ્ત મેટ્રિક્સ યોગ્ય રીતે મળી આવ્યું હતું. નહિંતર, ઉકેલ પ્રક્રિયા ફરીથી શરૂ કરો.

ઉદાહરણ 1.મેટ્રિક્સ માટે

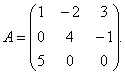
વ્યસ્ત મેટ્રિક્સ શોધો.

ઉકેલ. વ્યસ્ત મેટ્રિક્સ શોધવા માટે, તમારે મેટ્રિક્સનો નિર્ણાયક શોધવાની જરૂર છે એ. આપણે ત્રિકોણના નિયમ દ્વારા શોધીએ છીએ:

તેથી, મેટ્રિક્સ એ- બિન-એકવચન (બિન-અધોગતિ, બિન-એકવચન) અને તેના માટે એક વ્યસ્ત છે.

ચાલો આ મેટ્રિક્સ સાથે જોડાયેલ મેટ્રિક્સ શોધીએ એ.

ચાલો મેટ્રિક્સના સંદર્ભમાં સ્થાનાંતરિત મેટ્રિક્સ શોધીએ એ:

અમે મેટ્રિક્સના સંદર્ભમાં સ્થાનાંતરિત મેટ્રિક્સના બીજગણિતીય પૂરક તરીકે સંબંધિત મેટ્રિક્સના ઘટકોની ગણતરી કરીએ છીએ એ:

તેથી, મેટ્રિક્સ મેટ્રિક્સ સાથે જોડાયેલું છે એ, ફોર્મ ધરાવે છે

ટિપ્પણી.તત્વોની ગણતરી કરવાનો અને મેટ્રિક્સને સ્થાનાંતરિત કરવાનો ક્રમ અલગ હોઈ શકે છે. તમે પહેલા મેટ્રિક્સના બીજગણિતીય પૂરકની ગણતરી કરી શકો છો એ, અને પછી બીજગણિતીય પૂરક મેટ્રિક્સને સ્થાનાંતરિત કરો. પરિણામ યુનિયન મેટ્રિક્સના સમાન ઘટકો હોવા જોઈએ.

ફોર્મ્યુલા (2) ને લાગુ કરીને, આપણે મેટ્રિક્સને મેટ્રિક્સથી વિપરીત શોધીએ છીએ એ:

ગૌસીઅન અજાણી નાબૂદી પદ્ધતિનો ઉપયોગ કરીને વ્યસ્ત મેટ્રિક્સ શોધવું

ગૌસિયન એલિમિનેશન પદ્ધતિનો ઉપયોગ કરીને મેટ્રિક્સના વ્યસ્ત શોધવાનું પ્રથમ પગલું મેટ્રિક્સને સોંપવાનું છે એસમાન ક્રમનું ઓળખ મેટ્રિક્સ, તેમને ઊભી પટ્ટીથી અલગ કરે છે. અમને ડ્યુઅલ મેટ્રિક્સ મળશે. ચાલો આ મેટ્રિક્સની બંને બાજુઓને વડે ગુણાકાર કરીએ, પછી આપણને મળે છે

,

ગૌસીઅન અજાણી નાબૂદી પદ્ધતિનો ઉપયોગ કરીને વ્યસ્ત મેટ્રિક્સ શોધવા માટે અલ્ગોરિધમ

1. મેટ્રિક્સ માટે એસમાન ક્રમનું ઓળખ મેટ્રિક્સ સોંપો.

2. પરિણામી દ્વિ મેટ્રિક્સનું રૂપાંતર કરો જેથી તેની ડાબી બાજુએ તમને એકમ મેટ્રિક્સ મળે, પછી જમણી બાજુએ, ઓળખ મેટ્રિક્સની જગ્યાએ, તમને આપોઆપ એક વ્યસ્ત મેટ્રિક્સ મળે. મેટ્રિક્સ એડાબી બાજુ પ્રાથમિક મેટ્રિક્સ પરિવર્તન દ્વારા ઓળખ મેટ્રિક્સમાં રૂપાંતરિત થાય છે.

2. જો મેટ્રિક્સ ટ્રાન્સફોર્મેશનની પ્રક્રિયામાં હોય એઓળખ મેટ્રિક્સમાં કોઈપણ પંક્તિ અથવા કોઈપણ કૉલમમાં ફક્ત શૂન્ય હશે, પછી મેટ્રિક્સનો નિર્ધારક શૂન્ય સમાન છે, અને પરિણામે, મેટ્રિક્સ એએકવચન હશે, અને તેમાં વ્યસ્ત મેટ્રિક્સ નથી. આ કિસ્સામાં, વ્યસ્ત મેટ્રિક્સનું વધુ નિર્ધારણ અટકે છે.

ઉદાહરણ 2.મેટ્રિક્સ માટે

વ્યસ્ત મેટ્રિક્સ શોધો.

અને અમે તેને રૂપાંતરિત કરીશું જેથી ડાબી બાજુએ આપણને ઓળખ મેટ્રિક્સ મળે. અમે પરિવર્તન શરૂ કરીએ છીએ.

ડાબી અને જમણી મેટ્રિક્સની પ્રથમ પંક્તિને (-3) વડે ગુણાકાર કરો અને તેને બીજી પંક્તિમાં ઉમેરો, અને પછી પ્રથમ પંક્તિને (-4) વડે ગુણાકાર કરો અને તેને ત્રીજી પંક્તિમાં ઉમેરો, પછી આપણને મળશે

.

અનુગામી રૂપાંતરણોમાં કોઈ અપૂર્ણાંક સંખ્યાઓ નથી તેની ખાતરી કરવા માટે, ચાલો પહેલા દ્વિ મેટ્રિક્સની ડાબી બાજુએ બીજી હરોળમાં એક એકમ બનાવીએ. આ કરવા માટે, બીજી લીટીને 2 વડે ગુણાકાર કરો અને તેમાંથી ત્રીજી લીટી બાદ કરો, તો આપણને મળશે

.

ચાલો પ્રથમ લીટીને બીજી સાથે ઉમેરીએ અને પછી બીજી લીટીને (-9) વડે ગુણાકાર કરીએ અને તેને ત્રીજી લીટી સાથે ઉમેરીએ. પછી આપણને મળે છે

.

પછી ત્રીજી લાઇનને 8 વડે વિભાજીત કરો

.

ત્રીજી લીટીને 2 વડે ગુણાકાર કરો અને તેને બીજી લીટીમાં ઉમેરો. તે તારણ આપે છે:

.

ચાલો બીજી અને ત્રીજી લાઈનો અદલાબદલી કરીએ, પછી આપણને આખરે મળશે:

.

આપણે જોઈએ છીએ કે ડાબી બાજુ આપણી પાસે ઓળખ મેટ્રિક્સ છે, તેથી, જમણી બાજુ આપણી પાસે વ્યસ્ત મેટ્રિક્સ છે. આમ:

.

તમે મૂળ મેટ્રિક્સને મળેલા વ્યસ્ત મેટ્રિક્સ વડે ગુણાકાર કરીને ગણતરીઓની સાચીતા ચકાસી શકો છો:

પરિણામ એક વ્યસ્ત મેટ્રિક્સ હોવું જોઈએ.

ઉદાહરણ 3.મેટ્રિક્સ માટે

વ્યસ્ત મેટ્રિક્સ શોધો.

ઉકેલ. ડ્યુઅલ મેટ્રિક્સનું સંકલન

અને અમે તેને રૂપાંતરિત કરીશું.

આપણે પ્રથમ લીટીને 3 વડે અને બીજી 2 વડે ગુણાકાર કરીએ છીએ, અને બીજીમાંથી બાદ કરીએ છીએ, અને પછી આપણે પ્રથમ લીટીને 5 વડે અને ત્રીજી લીટીને 2 વડે ગુણાકાર કરીએ છીએ અને ત્રીજી લીટીમાંથી બાદ કરીએ છીએ, પછી આપણને મળે છે.

.

આપણે પ્રથમ લીટીને 2 વડે ગુણાકાર કરીએ છીએ અને તેને બીજીમાં ઉમેરીએ છીએ, અને પછી ત્રીજી લીટીમાંથી બીજી બાદ કરીએ છીએ, પછી આપણને મળે છે.

.

આપણે જોઈએ છીએ કે ડાબી બાજુની ત્રીજી લીટીમાં બધા તત્વો શૂન્ય સમાન છે. તેથી, મેટ્રિક્સ એકવચન છે અને તેમાં કોઈ વ્યસ્ત મેટ્રિક્સ નથી. અમે વ્યસ્ત મેરિટ્ઝ શોધવાનું બંધ કરીએ છીએ.

ઘણા ગુણધર્મમાં વ્યુત્ક્રમ સમાન.

જ્ઞાનકોશીય YouTube

1 / 5

✪ મેટ્રિક્સનું વ્યસ્ત કેવી રીતે શોધવું - bezbotvy

✪ વ્યસ્ત મેટ્રિક્સ (શોધવાની 2 રીતો)

✪ વ્યસ્ત મેટ્રિક્સ #1

✪ 2015-01-28. વ્યસ્ત 3x3 મેટ્રિક્સ

✪ 2015-01-27. વ્યસ્ત મેટ્રિક્સ 2x2

સબટાઈટલ

વ્યસ્ત મેટ્રિક્સના ગુણધર્મો

• det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), ક્યાં det (\displaystyle \\det )નિર્ણાયક સૂચવે છે.
• (A B) − 1 = B − 1 A − 1 (\Displaystyle \ (AB)^(-1)=B^(-1)A^(-1))બે ચોરસ ઇન્વર્ટિબલ મેટ્રિસિસ માટે A (\Displaystyle A)અને B (\Displaystyle B).
• (A T) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), ક્યાં (... .) T (\displaystyle (...)^(T))ટ્રાન્સપોઝ કરેલ મેટ્રિક્સ સૂચવે છે.
• (k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1))કોઈપણ ગુણાંક માટે k ≠ 0 (\ડિસ્પ્લેસ્ટાઈલ k\not =0).
• E − 1 = E (\Displaystyle \E^(-1)=E).
• જો રેખીય સમીકરણોની સિસ્ટમ હલ કરવી જરૂરી હોય, તો (b એ શૂન્ય ન હોય તેવા વેક્ટર છે) જ્યાં x (\displaystyle x)ઇચ્છિત વેક્ટર છે, અને જો A − 1 (\Displaystyle A^(-1))અસ્તિત્વમાં છે, તો પછી x = A − 1 b (\displaystyle x=A^(-1)b). નહિંતર, કાં તો સોલ્યુશન સ્પેસનું પરિમાણ શૂન્ય કરતા વધારે છે, અથવા ત્યાં કોઈ ઉકેલો નથી.

વ્યસ્ત મેટ્રિક્સ શોધવા માટેની પદ્ધતિઓ

જો મેટ્રિક્સ ઇન્વર્ટિબલ હોય, તો ઇન્વર્સ મેટ્રિક્સ શોધવા માટે તમે નીચેની પદ્ધતિઓમાંથી એકનો ઉપયોગ કરી શકો છો:

ચોક્કસ (સીધી) પદ્ધતિઓ

ગૌસ-જોર્ડન પદ્ધતિ

ચાલો બે મેટ્રિસિસ લઈએ: ધ એઅને સિંગલ ઇ. ચાલો મેટ્રિક્સ રજૂ કરીએ એગૉસ-જોર્ડન પદ્ધતિનો ઉપયોગ કરીને ઓળખ મેટ્રિક્સ પર, પંક્તિઓ સાથે પરિવર્તન લાગુ કરો (તમે કૉલમ સાથે પણ પરિવર્તનો લાગુ કરી શકો છો, પરંતુ એકબીજા સાથે નહીં). દરેક ઑપરેશનને પ્રથમ મેટ્રિક્સ પર લાગુ કર્યા પછી, તે જ ઑપરેશન બીજા પર લાગુ કરો. જ્યારે પ્રથમ મેટ્રિક્સથી એકમ સ્વરૂપમાં ઘટાડો પૂર્ણ થાય છે, ત્યારે બીજા મેટ્રિક્સ સમાન હશે A−1.

ગૌસીયન પદ્ધતિનો ઉપયોગ કરતી વખતે, પ્રથમ મેટ્રિક્સને ડાબી બાજુએ પ્રાથમિક મેટ્રિક્સમાંથી એક દ્વારા ગુણાકાર કરવામાં આવશે. Λ i (\Displaystyle \Lambda _(i))(મુખ્ય કર્ણ પરની સાથે ટ્રાન્સવેક્શન અથવા વિકર્ણ મેટ્રિક્સ, એક સ્થિતિ સિવાય):

તમામ કામગીરી લાગુ કર્યા પછીનો બીજો મેટ્રિક્સ સમાન હશે Λ (\Displaystyle \Lambda), એટલે કે, તે ઇચ્છિત હશે. અલ્ગોરિધમ જટિલતા - O (n 3) (\Displaystyle O(n^(3))).

બીજગણિત પૂરક મેટ્રિક્સનો ઉપયોગ કરીને

મેટ્રિક્સનો મેટ્રિક્સ વ્યસ્ત A (\Displaystyle A), ફોર્મમાં રજૂ કરી શકાય છે

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

જ્યાં adj (A) (\displaystyle (\mbox(adj))(A))- સંલગ્ન મેટ્રિક્સ;

અલ્ગોરિધમની જટિલતા નિર્ણાયક O det ની ગણતરી કરવા માટે અલ્ગોરિધમની જટિલતા પર આધાર રાખે છે અને O(n²)·O det ની બરાબર છે.

LU/LUP વિઘટનનો ઉપયોગ

મેટ્રિક્સ સમીકરણ A X = I n (\displaystyle AX=I_(n))વ્યસ્ત મેટ્રિક્સ માટે X (\Displaystyle X)સંગ્રહ તરીકે ગણી શકાય n (\Displaystyle n)ફોર્મની સિસ્ટમો A x = b (\displaystyle Ax=b). ચાલો સૂચિત કરીએ i (\ પ્રદર્શન શૈલી i)મેટ્રિક્સની મી કૉલમ X (\Displaystyle X)દ્વારા X i (\displaystyle X_(i)); પછી A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\displaystyle i=1,\ldots ,n), કારણ કે i (\ પ્રદર્શન શૈલી i)મેટ્રિક્સની મી કૉલમ I n (\ displaystyle I_(n))એકમ વેક્ટર છે e i (\ displaystyle e_(i)). બીજા શબ્દોમાં કહીએ તો, વ્યસ્ત મેટ્રિક્સ શોધવું એ સમાન મેટ્રિક્સ અને વિવિધ જમણી બાજુઓ સાથે n સમીકરણો ઉકેલવા માટે નીચે આવે છે. LUP વિઘટન (O(n³) સમય કર્યા પછી, દરેક n સમીકરણોને ઉકેલવામાં O(n²) સમય લાગે છે, તેથી કાર્યના આ ભાગમાં પણ O(n³) સમયની જરૂર પડે છે.

જો મેટ્રિક્સ A બિન-એકવચન છે, તો તેના માટે LUP વિઘટનની ગણતરી કરી શકાય છે P A = L U (\ displaystyle PA=LU). દો P A = B (\Displaystyle PA=B), B − 1 = D (\Displaystyle B^(-1)=D). પછી વ્યસ્ત મેટ્રિક્સના ગુણધર્મોમાંથી આપણે લખી શકીએ: D = U − 1 L − 1 (\displaystyle D=U^(-1)L^(-1)). જો તમે આ સમાનતાને U અને L વડે ગુણાકાર કરો છો, તો તમે ફોર્મની બે સમાનતા મેળવી શકો છો U D = L − 1 (\displaystyle UD=L^(-1))અને D L = U − 1 (\displaystyle DL=U^(-1)). આ સમાનતાઓમાંની પ્રથમ n² રેખીય સમીકરણોની સિસ્ટમ છે n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2)))જેમાંથી જમણી બાજુઓ ઓળખાય છે (ત્રિકોણાકાર મેટ્રિસિસના ગુણધર્મોમાંથી). બીજા માટે n² રેખીય સમીકરણોની સિસ્ટમ પણ રજૂ કરે છે n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2)))જેમાંથી જમણી બાજુઓ જાણીતી છે (ત્રિકોણાકાર મેટ્રિસિસના ગુણધર્મોમાંથી પણ). તેઓ એકસાથે n² સમાનતાઓની સિસ્ટમનું પ્રતિનિધિત્વ કરે છે. આ સમાનતાઓનો ઉપયોગ કરીને, અમે મેટ્રિક્સ D ના તમામ n² તત્વોને વારંવાર નિર્ધારિત કરી શકીએ છીએ. પછી સમાનતા (PA) −1 = A −1 P −1 = B −1 = D. આપણે સમાનતા મેળવીએ છીએ. A − 1 = D P (\displaystyle A^(-1)=DP).

LU વિઘટનનો ઉપયોગ કરવાના કિસ્સામાં, મેટ્રિક્સ Dના કૉલમના ક્રમચયની જરૂર નથી, પરંતુ જો મેટ્રિક્સ A બિન-એકવચન હોય તો પણ ઉકેલ અલગ પડી શકે છે.

અલ્ગોરિધમની જટિલતા O(n³) છે.

પુનરાવર્તિત પદ્ધતિઓ

શુલ્ટ્ઝ પદ્ધતિઓ

( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\ displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),\\U_( k+1)=U_(k)\સમ _(i=0)^(n)\Psi _(k)^(i)\અંત(કેસ)))

ભૂલ અંદાજ

પ્રારંભિક અંદાજ પસંદ કરી રહ્યા છીએ

અહીં ધ્યાનમાં લેવામાં આવતી પુનરાવર્તિત મેટ્રિક્સ વ્યુત્ક્રમ પ્રક્રિયાઓમાં પ્રારંભિક અંદાજ પસંદ કરવાની સમસ્યા અમને તેમને સ્વતંત્ર સાર્વત્રિક પદ્ધતિઓ તરીકે સમજવાની મંજૂરી આપતી નથી જે સીધી વ્યુત્ક્રમ પદ્ધતિઓ સાથે સ્પર્ધા કરે છે, ઉદાહરણ તરીકે, મેટ્રિસિસના LU વિઘટન પર. પસંદ કરવા માટે કેટલીક ભલામણો છે U 0 (\Displaystyle U_(0)), શરતની પરિપૂર્ણતાની ખાતરી કરવી ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (મેટ્રિક્સની સ્પેક્ટ્રલ ત્રિજ્યા એકતા કરતા ઓછી છે), જે પ્રક્રિયાના કન્વર્જન્સ માટે જરૂરી અને પર્યાપ્ત છે. જો કે, આ કિસ્સામાં, સૌપ્રથમ, ઇન્વર્ટિબલ મેટ્રિક્સ A અથવા મેટ્રિક્સના સ્પેક્ટ્રમ માટેના અંદાજ ઉપરથી જાણવાની જરૂર છે. A A T (\ ડિસ્પ્લેસ્ટાઇલ AA^(T))(એટલે ​​​​કે, જો A એ સપ્રમાણ હકારાત્મક ચોક્કસ મેટ્રિક્સ છે અને ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), પછી તમે લઈ શકો છો U 0 = α E (\Displaystyle U_(0)=(\alpha )E), ક્યાં ; જો A એ મનસ્વી બિન-એકવચન મેટ્રિક્સ છે અને ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), પછી તેઓ માને છે U 0 = α A T (\Displaystyle U_(0)=(\alpha )A^(T)), જ્યાં પણ α ∈ (0 , 2 β) (\displaystyle \alpha \in \left(0,(\frac (2)(\beta ))\right)); તમે, અલબત્ત, પરિસ્થિતિને સરળ બનાવી શકો છો અને તે હકીકતનો લાભ લઈ શકો છો ρ (A A T) ≤ k A A T k (\ displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), મૂકો U 0 = A T ‖ A A T ‖ (\Displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). બીજું, આ રીતે પ્રારંભિક મેટ્રિક્સનો ઉલ્લેખ કરતી વખતે, તેની કોઈ ગેરેંટી નથી ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|)નાનું હશે (કદાચ તે બહાર પણ આવશે ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), અને કન્વર્જન્સ દરનો ઉચ્ચ ક્રમ તરત જ જાહેર કરવામાં આવશે નહીં.

ઉદાહરણો

મેટ્રિક્સ 2x2

(\displaystyle \mathbf (A) ^(-1)=(\begin(bmatrix)a&b\\c&d\\\end(bmatrix))^(-1)=(\frac (1)(\det(\mathbf) (A))))(\begin(bmatrix)\,\,\,d&\!\!-b\\-c&\,a\\\end(bmatrix))=(\frac (1)(ad- bc))(\begin(bmatrix)\,\,\,d&\!\!-b\\-c&\,a\\\end(bmatrix)).) 2x2 મેટ્રિક્સનું વ્યુત્ક્રમ ફક્ત તે શરત હેઠળ જ શક્ય છે.

a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0)વ્યાખ્યા 1:

મેટ્રિક્સને એકવચન કહેવામાં આવે છે જો તેનો નિર્ણાયક શૂન્ય હોય.વ્યાખ્યા 2:

મેટ્રિક્સને બિન-એકવચન કહેવામાં આવે છે જો તેનો નિર્ણાયક શૂન્ય સમાન ન હોય. મેટ્રિક્સ "A" કહેવાય છેવ્યસ્ત મેટ્રિક્સ

, જો શરત A*A-1 = A-1 *A = E (એકમ મેટ્રિક્સ) સંતુષ્ટ છે.

ચોરસ મેટ્રિક્સ ફક્ત ત્યારે જ ઉલટાવી શકાય તેવું છે જો તે બિન-એકવચન હોય.

વ્યસ્ત મેટ્રિક્સની ગણતરી કરવાની યોજના: ∆ 1) જો મેટ્રિક્સ "A" ના નિર્ણાયકની ગણતરી કરો

A = 0, તો વ્યસ્ત મેટ્રિક્સ અસ્તિત્વમાં નથી.

2) મેટ્રિક્સ "A" ના તમામ બીજગણિત પૂરક શોધો.

3) બીજગણિત ઉમેરણોનું મેટ્રિક્સ બનાવો (Aij)

4) બીજગણિતીય પૂરક (Aij )T ના મેટ્રિક્સને સ્થાનાંતરિત કરો

5) ટ્રાન્સપોઝ કરેલ મેટ્રિક્સને આ મેટ્રિક્સના નિર્ધારકના વ્યસ્ત વડે ગુણાકાર કરો.

6) તપાસ કરો:

પ્રથમ નજરમાં તે જટિલ લાગે છે, પરંતુ હકીકતમાં બધું ખૂબ સરળ છે. બધા ઉકેલો સરળ અંકગણિત કામગીરી પર આધારિત છે, ઉકેલ કરતી વખતે મુખ્ય વસ્તુ એ છે કે "-" અને "+" ચિહ્નો સાથે મૂંઝવણમાં ન આવવું અને તેમને ગુમાવવું નહીં.

કાર્ય: નીચેના ચિત્રમાં બતાવેલ વ્યસ્ત મેટ્રિક્સ "A" શોધો:

1. પ્રથમ વસ્તુ મેટ્રિક્સ "A" ના નિર્ણાયકને શોધવાનું છે:

સમજૂતી:

અમે અમારા નિર્ણાયકને તેના મૂળભૂત કાર્યોનો ઉપયોગ કરીને સરળ બનાવ્યા છે. પ્રથમ, અમે 2જી અને 3જી લીટીઓમાં પ્રથમ લીટીના તત્વો ઉમેર્યા, એક સંખ્યા દ્વારા ગુણાકાર.

બીજું, અમે નિર્ણાયકની 2 જી અને 3 જી કૉલમ બદલી, અને તેના ગુણધર્મો અનુસાર, અમે તેની સામેનું ચિહ્ન બદલ્યું.

ત્રીજે સ્થાને, અમે બીજી લાઇનના સામાન્ય પરિબળ (-1)ને બહાર કાઢ્યા, ત્યાંથી ચિહ્ન ફરીથી બદલ્યું, અને તે હકારાત્મક બન્યું. અમે ઉદાહરણની શરૂઆતમાંની જેમ જ લાઇન 3 ને પણ સરળ બનાવીએ છીએ.

આપણી પાસે ત્રિકોણાકાર નિર્ણાયક છે જેના કર્ણની નીચેના તત્વો શૂન્યના બરાબર છે, અને ગુણધર્મ 7 દ્વારા તે કર્ણ તત્વોના ગુણાંક સમાન છે. અંતે અમને મળ્યું ∆ A = 26, તેથી વ્યસ્ત મેટ્રિક્સ અસ્તિત્વમાં છે.

A11 = 1*(3+1) = 4

A12 = -1*(9+2) = -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. આગળનું પગલું પરિણામી ઉમેરણોમાંથી મેટ્રિક્સનું સંકલન કરવાનું છે:

5. આ મેટ્રિક્સને નિર્ણાયકના વ્યસ્ત વડે ગુણાકાર કરો, એટલે કે 1/26 વડે:

6. હવે આપણે ફક્ત તપાસ કરવાની જરૂર છે:

પરીક્ષણ દરમિયાન, અમને એક ઓળખ મેટ્રિક્સ પ્રાપ્ત થયો, તેથી, ઉકેલ એકદમ યોગ્ય રીતે હાથ ધરવામાં આવ્યો હતો.

વ્યસ્ત મેટ્રિક્સની ગણતરી કરવાની 2 રીત.

1. પ્રાથમિક મેટ્રિક્સ ટ્રાન્સફોર્મેશન

2. પ્રાથમિક કન્વર્ટર દ્વારા વિપરિત મેટ્રિક્સ.

પ્રાથમિક મેટ્રિક્સ ટ્રાન્સફોર્મેશનમાં શામેલ છે:

1. શૂન્યની બરાબર ન હોય તેવી સંખ્યા વડે શબ્દમાળાનો ગુણાકાર કરવો.

2. કોઈપણ લીટીમાં બીજી લીટી ઉમેરીને સંખ્યા વડે ગુણાકાર થાય છે.

3. મેટ્રિક્સની પંક્તિઓ સ્વેપ કરો.

4. પ્રાથમિક પરિવર્તનની સાંકળ લાગુ કરીને, આપણે બીજું મેટ્રિક્સ મેળવીએ છીએ.

એ -1 = ?

1. (A|E) ~ (E|A -1 )

2.એ -1 * A = E

ચાલો વાસ્તવિક સંખ્યાઓ સાથેના વ્યવહારુ ઉદાહરણનો ઉપયોગ કરીને આને જોઈએ.

વ્યાયામ:વ્યસ્ત મેટ્રિક્સ શોધો.

ઉકેલ:

ચાલો તપાસીએ:

ઉકેલ પર થોડી સ્પષ્ટતા:

પ્રથમ, અમે મેટ્રિક્સની પંક્તિઓ 1 અને 2 ને ફરીથી ગોઠવી, પછી પ્રથમ પંક્તિનો (-1) દ્વારા ગુણાકાર કર્યો.

તે પછી, અમે પ્રથમ પંક્તિનો (-2) દ્વારા ગુણાકાર કર્યો અને તેને મેટ્રિક્સની બીજી પંક્તિ સાથે ઉમેરી. પછી આપણે લીટી 2 ને 1/4 વડે ગુણાકાર કરીએ છીએ.

રૂપાંતરણનો અંતિમ તબક્કો બીજી લાઇનને 2 વડે ગુણાકાર કરવો અને તેને પ્રથમ સાથે ઉમેરવાનો હતો. પરિણામે, આપણી પાસે ડાબી બાજુએ ઓળખ મેટ્રિક્સ છે, તેથી, વ્યસ્ત મેટ્રિક્સ એ જમણી બાજુનું મેટ્રિક્સ છે.

તપાસ કર્યા પછી, અમને ખાતરી થઈ કે નિર્ણય સાચો હતો.

જેમ તમે જોઈ શકો છો, વ્યસ્ત મેટ્રિક્સની ગણતરી કરવી ખૂબ જ સરળ છે.

આ વ્યાખ્યાનના અંતે, હું આવા મેટ્રિક્સના ગુણધર્મો પર થોડો સમય પસાર કરવા માંગુ છું.