સૈદ્ધાંતિક મિકેનિક્સ, સમૂહના કેન્દ્રની ગતિની ગતિશીલતા. સિસ્ટમ ડાયનેમિક્સના સામાન્ય પ્રમેય

વ્યાખ્યાન 3. ગતિશાસ્ત્રના સામાન્ય પ્રમેય

ભૌતિક બિંદુઓની સિસ્ટમની ગતિશીલતાસૈદ્ધાંતિક મિકેનિક્સની એક મહત્વપૂર્ણ શાખા છે. અહીં આપણે મુખ્યત્વે સ્વતંત્રતાના ડિગ્રીની મર્યાદિત સંખ્યા સાથે યાંત્રિક પ્રણાલીઓ (સામગ્રી બિંદુઓની સિસ્ટમો) ની ગતિ વિશેની સમસ્યાઓને ધ્યાનમાં લઈએ છીએ - સ્વતંત્ર પરિમાણોની મહત્તમ સંખ્યા જે સિસ્ટમની સ્થિતિ નક્કી કરે છે. સિસ્ટમની ગતિશીલતાનું મુખ્ય કાર્ય એ કઠોર શરીર અને યાંત્રિક પ્રણાલીઓના ગતિના નિયમોનો અભ્યાસ છે.

સિસ્ટમની ગતિનો અભ્યાસ કરવાનો સૌથી સરળ અભિગમ, જેમાં સમાવેશ થાય છે એનભૌતિક બિંદુઓ, સિસ્ટમના દરેક વ્યક્તિગત બિંદુની હિલચાલને ધ્યાનમાં લેતા નીચે આવે છે. આ કિસ્સામાં, સિસ્ટમના દરેક બિંદુ પર કાર્ય કરતી તમામ દળો, બિંદુઓ વચ્ચેની ક્રિયાપ્રતિક્રિયાના દળો સહિત, નિર્ધારિત કરવી આવશ્યક છે.

ન્યૂટનના બીજા નિયમ (1.2) અનુસાર દરેક બિંદુના પ્રવેગને નિર્ધારિત કરીને, અમે દરેક બિંદુ માટે બીજા ક્રમની ગતિના ત્રણ અકાશીય વિભેદક નિયમો મેળવીએ છીએ, એટલે કે. 3 એન સમગ્ર સિસ્ટમ માટે ગતિના વિભેદક નિયમો.

સિસ્ટમના દરેક બિંદુ માટે આપેલ દળો અને પ્રારંભિક પરિસ્થિતિઓના આધારે યાંત્રિક પ્રણાલીની ગતિના સમીકરણો શોધવા માટે, પરિણામી વિભેદક કાયદાઓ એકીકૃત હોવા જોઈએ. આ સમસ્યા બે ભૌતિક બિંદુઓના કિસ્સામાં પણ મુશ્કેલ છે જે ફક્ત સાર્વત્રિક આકર્ષણ (બે-શરીરની સમસ્યા) ના નિયમ અનુસાર ક્રિયાપ્રતિક્રિયા દળોના પ્રભાવ હેઠળ આગળ વધે છે, અને ત્રણ ક્રિયાપ્રતિક્રિયાના બિંદુઓ (ત્રણ-શરીરની સમસ્યા) ના કિસ્સામાં અત્યંત મુશ્કેલ છે. ).

તેથી, સમસ્યાઓ ઉકેલવા માટેની પદ્ધતિઓ શોધવી જરૂરી છે જે ઉકેલી શકાય તેવા સમીકરણો તરફ દોરી જાય અને યાંત્રિક પ્રણાલીની હિલચાલનો ખ્યાલ આપે. ગતિશીલતાના સામાન્ય પ્રમેય, ગતિના વિભેદક નિયમોનું પરિણામ હોવાથી, અમને સંકલન દરમિયાન ઊભી થતી જટિલતાને ટાળવા અને જરૂરી પરિણામો મેળવવાની મંજૂરી આપે છે.

3. 1. સામાન્ય નોંધો

અમે યાંત્રિક સિસ્ટમના બિંદુઓને સૂચકાંકો સાથે નંબર આપીશું i, j, kવગેરે, જે તમામ મૂલ્યો દ્વારા ચાલે છે 1, 2, 3… એન, ક્યાં એન - સિસ્ટમના બિંદુઓની સંખ્યા. સંબંધિત ભૌતિક જથ્થાઓ k th બિંદુ બિંદુ તરીકે સમાન અનુક્રમણિકા દ્વારા નિયુક્ત કરવામાં આવે છે. ઉદાહરણ તરીકે, અનુક્રમે ત્રિજ્યા વેક્ટર અને ઝડપ વ્યક્ત કરો kમી બિંદુ.

સિસ્ટમના દરેક બિંદુ પર બે મૂળના દળો દ્વારા કાર્ય કરવામાં આવે છે: પ્રથમ, એવા દળો કે જેના સ્ત્રોત સિસ્ટમની બહાર હોય છે, જેને કહેવામાં આવે છે. બાહ્યદળો અને નિયુક્ત; બીજું, આપેલ સિસ્ટમના અન્ય બિંદુઓમાંથી દળો, કહેવાય છે આંતરિકદળો અને નિયુક્ત. આંતરિક દળો ન્યૂટનના ત્રીજા નિયમને સંતોષે છે. ચાલો કોઈપણ રાજ્યમાં સમગ્ર યાંત્રિક પ્રણાલી પર કાર્ય કરતી આંતરિક દળોના સરળ ગુણધર્મોને ધ્યાનમાં લઈએ.

પ્રથમ મિલકત. સિસ્ટમના તમામ આંતરિક દળોનો ભૌમિતિક સરવાળો (આંતરિક દળોનો મુખ્ય વેક્ટર) શૂન્ય બરાબર છે.

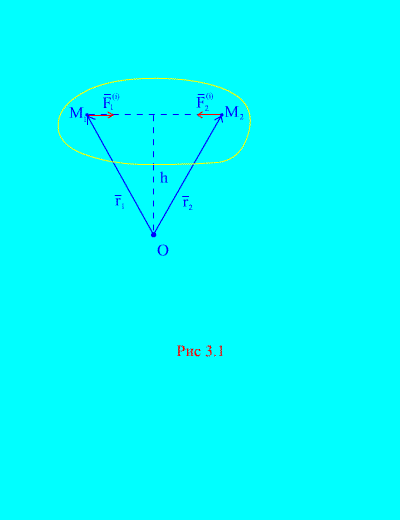
ખરેખર, જો આપણે સિસ્ટમના કોઈપણ બે મનસ્વી મુદ્દાઓને ધ્યાનમાં લઈએ, ઉદાહરણ તરીકે અને (ફિગ. 3.1), પછી તેમના માટે , કારણ કે ક્રિયા અને પ્રતિક્રિયા દળો હંમેશા તીવ્રતામાં સમાન હોય છે, ક્રિયાની એક રેખા સાથે વિરુદ્ધ દિશામાં કાર્ય કરે છે, જે ક્રિયાપ્રતિક્રિયાના બિંદુઓને જોડે છે. આંતરિક દળોના મુખ્ય વેક્ટરમાં ક્રિયાપ્રતિક્રિયા કરતી બિંદુઓના દળોની જોડી હોય છે, તેથી

(3.1)

બીજી મિલકત. અવકાશમાં મનસ્વી બિંદુને સંબંધિત તમામ આંતરિક દળોની ક્ષણોનો ભૌમિતિક સરવાળો શૂન્ય બરાબર છે.

ચાલો દળોની ક્ષણોની સિસ્ટમ અને બિંદુને સંબંધિત ધ્યાનમાં લઈએ વિશે(ફિગ. 3.1). થી (ફિગ. 3.1). તે સ્પષ્ટ છે

,

કારણ કે બંને દળો પાસે સમાન હાથ અને વેક્ટર ક્ષણોની વિરુદ્ધ દિશાઓ છે. બિંદુને સંબંધિત આંતરિક દળોની મુખ્ય ક્ષણ વિશેઆવા સમીકરણોના વેક્ટર સરવાળાનો સમાવેશ કરે છે અને તે શૂન્યની બરાબર છે. આથી,

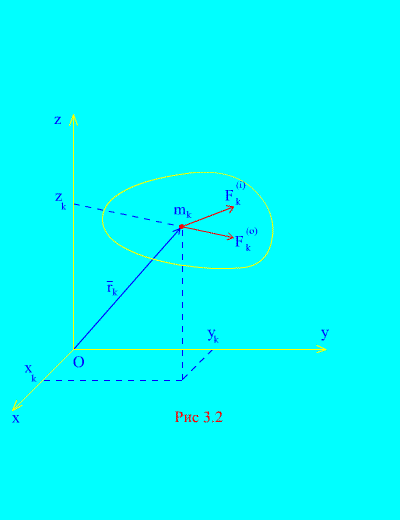
બાહ્ય અને આંતરિક દળોને યાંત્રિક સિસ્ટમ પર કાર્ય કરવા દો એનપોઈન્ટ (ફિગ. 3.2). જો બાહ્ય દળોના પરિણામ અને તમામ આંતરિક દળોના પરિણામને સિસ્ટમના દરેક બિંદુ પર લાગુ કરવામાં આવે, તો કોઈપણ માટે kસિસ્ટમના મી બિંદુએ, ગતિના વિભેદક સમીકરણો દોરી શકાય છે. આવા કુલ સમીકરણો હશે એન:

અને નિશ્ચિત સંકલન અક્ષો પર અંદાજોમાં 3 એન:

(3.4)

વેક્ટર સમીકરણો (3.3) અથવા સમકક્ષ સ્કેલર સમીકરણો (3.4) સમગ્ર સિસ્ટમના ભૌતિક બિંદુઓની ગતિના વિભેદક નિયમોનું પ્રતિનિધિત્વ કરે છે. જો બધા બિંદુઓ એક પ્લેન અથવા એક સીધી રેખાની સમાંતર આગળ વધે છે, તો પ્રથમ કિસ્સામાં સમીકરણોની સંખ્યા (3.4) હશે 2 એન, બીજામાં એન.

ઉદાહરણ 1.બ્લોક પર ફેંકવામાં આવેલા અક્ષમ્ય કેબલ દ્વારા બે સમૂહ એકબીજા સાથે જોડાયેલા છે (ફિગ. 3.3). ઘર્ષણ દળોની અવગણના, તેમજ બ્લોક અને કેબલના સમૂહ, લોડ અને કેબલ તણાવની હિલચાલનો કાયદો નક્કી કરે છે.

ઉકેલ. સિસ્ટમમાં બે મટીરીયલ બોડીનો સમાવેશ થાય છે (એક અક્ષમ કેબલ દ્વારા જોડાયેલ) એક જ ધરીની સમાંતર આગળ વધી રહી છે. એક્સ.ચાલો ધરી પરના અંદાજોમાં ગતિના વિભેદક નિયમો લખીએ એક્સદરેક શરીર માટે.

જમણા વજનને પ્રવેગ સાથે ઘટવા દો, પછી ડાબું વજન પ્રવેગ સાથે વધશે. અમે માનસિક રીતે પોતાને કનેક્શન (કેબલ) થી મુક્ત કરીએ છીએ અને તેને પ્રતિક્રિયાઓ સાથે બદલીએ છીએ અને (ફિગ. 3.3). શરીરને મુક્ત ગણીને, ચાલો ધરી પર પ્રક્ષેપણમાં ગતિના વિભેદક નિયમો દોરીએ. એક્સ(એટલે ​​કે થ્રેડ ટેન્શન આંતરિક દળો છે, અને ભારનું વજન બાહ્ય છે):

ત્યારથી અને (શરીરો એક અક્ષમ કેબલ દ્વારા જોડાયેલા છે), અમે મેળવીએ છીએ

પ્રવેગક અને કેબલ તણાવ માટે આ સમીકરણો ઉકેલવા ટી, અમને મળે છે

.

નોંધ કરો કે કેબલમાં તણાવ અનુરૂપ લોડના ગુરુત્વાકર્ષણ બળ જેટલું નથી.

3. 2. સમૂહના કેન્દ્રની ગતિ પર પ્રમેય

તે જાણીતું છે કે પ્લેનમાં સખત શરીર અને યાંત્રિક સિસ્ટમ ખૂબ જટિલ રીતે ખસેડી શકે છે. શરીર અને યાંત્રિક પ્રણાલીની ગતિ અંગેનું પ્રથમ પ્રમેય નીચે પ્રમાણે આવી શકે છે: k.-l ફેંકો. એક સાથે જોડાયેલ ઘણા નક્કર શરીરનો સમાવેશ થતો પદાર્થ. તે સ્પષ્ટ છે કે તે પેરાબોલામાં ઉડશે. બિંદુની હિલચાલનો અભ્યાસ કરતી વખતે આ બહાર આવ્યું હતું. જો કે, હવે પદાર્થ એક બિંદુ નથી. પેરાબોલામાં ફરતા કેટલાક અસરકારક કેન્દ્રની આસપાસ તેની ઉડાન દરમિયાન તે વળે છે અને લહેરાવે છે. જટિલ પદાર્થોની હિલચાલ વિશે પ્રથમ પ્રમેય કહે છે કે ચોક્કસ અસરકારક કેન્દ્ર એ ગતિશીલ પદાર્થના સમૂહનું કેન્દ્ર છે. સમૂહનું કેન્દ્ર શરીરમાં જ સ્થિત હોવું જરૂરી નથી; તે તેની બહાર ક્યાંક સૂઈ શકે છે.

પ્રમેય. યાંત્રિક પ્રણાલીના સમૂહનું કેન્દ્ર સમગ્ર સિસ્ટમના દળના સમાન સમૂહ સાથે ભૌતિક બિંદુ તરીકે ફરે છે, જેના પર સિસ્ટમ પર કાર્ય કરતી તમામ બાહ્ય શક્તિઓ લાગુ થાય છે.

પ્રમેયને સાબિત કરવા માટે, અમે ગતિના વિભેદક નિયમો (3.3) ને નીચેના સ્વરૂપમાં ફરીથી લખીએ છીએ:

(3.5)

જ્યાં એન - સિસ્ટમના બિંદુઓની સંખ્યા.

ચાલો એકસાથે સમીકરણો શબ્દ દ્વારા શબ્દ ઉમેરીએ:

(A)

પસંદ કરેલ સંકલન પ્રણાલીની તુલનામાં યાંત્રિક સિસ્ટમના સમૂહના કેન્દ્રની સ્થિતિ સૂત્ર (2.1) દ્વારા નક્કી કરવામાં આવે છે: જ્યાં એમ- સિસ્ટમનો સમૂહ. પછી સમાનતાની ડાબી બાજુ (a) લખવામાં આવશે

સમાનતાની જમણી બાજુનો પ્રથમ સરવાળો (a) બાહ્ય દળોના મુખ્ય વેક્ટર જેટલો છે, અને છેલ્લો, આંતરિક દળોના ગુણધર્મ દ્વારા, શૂન્ય જેટલો છે. પછી સમાનતા (a), ધ્યાનમાં રાખીને (b), ફરીથી લખવામાં આવશે

, (3.6)

તે સિસ્ટમના સમૂહનું ઉત્પાદન અને તેના સમૂહના કેન્દ્રનું પ્રવેગક સિસ્ટમ પર કાર્ય કરતી તમામ બાહ્ય શક્તિઓના ભૌમિતિક સરવાળો સમાન છે.

સમીકરણ (3.6) થી તે અનુસરે છે કે આંતરિક દળો સમૂહના કેન્દ્રની હિલચાલને સીધી અસર કરતા નથી. જો કે, કેટલાક કિસ્સાઓમાં તેઓ સિસ્ટમ પર લાગુ બાહ્ય દળોના દેખાવનું કારણ છે. આમ, કારના ડ્રાઇવિંગ વ્હીલ્સને પરિભ્રમણમાં ચલાવતા આંતરિક બળો તેના પર કાર્ય કરવા માટે વ્હીલ રિમ પર લાગુ બાહ્ય સંલગ્નતા બળનું કારણ બને છે.

ઉદાહરણ 2.મિકેનિઝમ, વર્ટિકલ પ્લેનમાં સ્થિત છે, તે આડા સરળ પ્લેન પર સ્થાપિત થયેલ છે અને તેની સાથે સપાટી પર સખત રીતે નિશ્ચિત બાર સાથે જોડાયેલ છે. પ્રતિઅને એલ (ફિગ. 3.4).

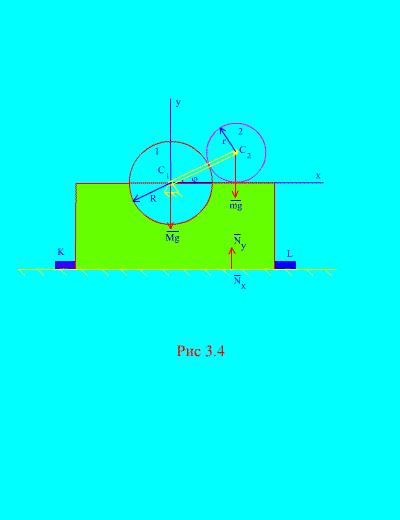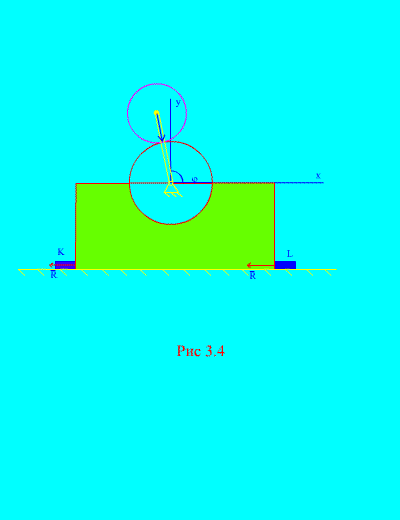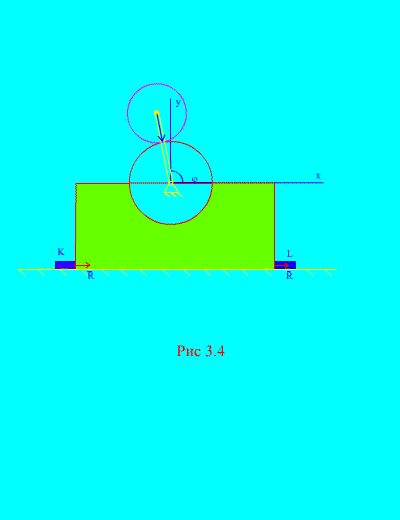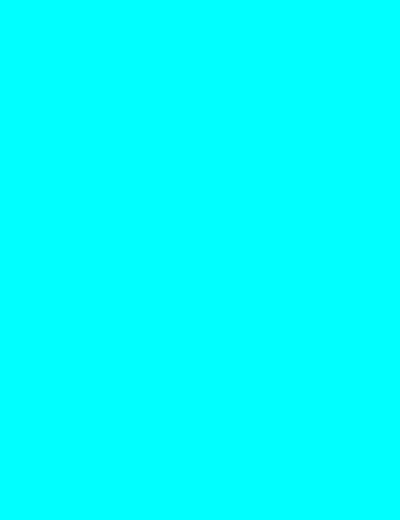
ડિસ્ક 1 ત્રિજ્યા આરગતિહીન ડિસ્ક 2 માસ mઅને ત્રિજ્યા આર ક્રેન્ક, લંબાઈ સાથે જોડાયેલ આર+ આરબિંદુ પર સી 2. ક્રેન્ક સતત ફરે છે

કોણીય ઝડપ. પ્રારંભિક ક્ષણે, ક્રેન્કે જમણી આડી સ્થિતિ પર કબજો કર્યો. ક્રેન્કના સમૂહની અવગણના કરીને, જો ફ્રેમ અને વ્હીલ 1 નો કુલ દળ સમાન હોય તો બાર પર કામ કરતા મહત્તમ આડી અને ઊભી દળો નક્કી કરો. એમ.બારની ગેરહાજરીમાં મિકેનિઝમના વર્તનને પણ ધ્યાનમાં લો.

ઉકેલ. સિસ્ટમમાં બે સમૂહનો સમાવેશ થાય છે ( એન=2 ): નિશ્ચિત ડિસ્ક 1 ફ્રેમ અને મૂવેબલ ડિસ્ક સાથે 2. અક્ષને દિશામાન કરો ખાતેસ્થિર ડિસ્કના ગુરુત્વાકર્ષણ કેન્દ્ર દ્વારા ઊભી રીતે ઉપર તરફ, અક્ષ એક્સ- આડી પ્લેન સાથે.

ચાલો સમૂહ (3.6) ના કેન્દ્રની ગતિ પર સંકલન સ્વરૂપમાં પ્રમેય લખીએ

આ સિસ્ટમના બાહ્ય દળો છે: ફ્રેમનું વજન અને નિશ્ચિત ડિસ્ક - એમજી, ખસેડતી ડિસ્ક વજન - મિલિગ્રામ, - બોલ્ટ્સની કુલ આડી પ્રતિક્રિયા, - પ્લેનની સામાન્ય કુલ પ્રતિક્રિયા. આથી,

પછી ગતિના નિયમો (b) ફરીથી લખવામાં આવશે

ચાલો યાંત્રિક પ્રણાલીના સમૂહના કેન્દ્રના કોઓર્ડિનેટ્સની ગણતરી કરીએ:

; (જી)

પરથી જોઈ શકાય છે (ફિગ. 3.4), , , (ક્રેન્ક એંગલ), . આ અભિવ્યક્તિઓને (d) માં બદલવી અને સમયના સંદર્ભમાં બીજા ડેરિવેટિવ્સની ગણતરી કરવી tથી , , અમને તે મળે છે

(d)

(c) અને (e) ને (b) માં બદલીને, આપણે શોધીએ છીએ

બાર પર કામ કરતું આડું દબાણ સૌથી વધુ અને ઓછામાં ઓછું હોય છે cos = 1 તદનુસાર, એટલે કે

જ્યારે હોરીઝોન્ટલ પ્લેન પર મિકેનિઝમનું દબાણ સૌથી વધુ અને સૌથી નીચું મૂલ્ય ધરાવે છે પાપ તદનુસાર, એટલે કે

હકીકતમાં, ગતિશીલતાની પ્રથમ સમસ્યા હલ કરવામાં આવી છે: સિસ્ટમ (ડી) ના સમૂહના કેન્દ્રની ગતિના જાણીતા સમીકરણો અનુસાર, ચળવળમાં સામેલ દળો પુનઃસ્થાપિત થાય છે.

બારની ગેરહાજરીમાં કેઅને એલ (ફિગ. 3.4), મિકેનિઝમ આડી પ્લેન ઉપર ઉછળવાનું શરૂ કરી શકે છે. આ ત્યારે થશે જ્યારે, એટલે કે. જ્યારે, તે અનુસરે છે કે ક્રેન્કના પરિભ્રમણનો કોણીય વેગ, જેના પર મિકેનિઝમ ઉછળે છે, તે સમાનતાને સંતોષે છે

.

3. 3. સમૂહના કેન્દ્રની ગતિના સંરક્ષણનો કાયદો

જો સિસ્ટમ પર કામ કરતા બાહ્ય દળોનું મુખ્ય વેક્ટર શૂન્ય બરાબર હોય, એટલે કે. , પછી થી(3.6)તે અનુસરે છે કે દળના કેન્દ્રની પ્રવેગકતા શૂન્ય છે, તેથી, દળના કેન્દ્રની ગતિ તીવ્રતા અને દિશામાં સ્થિર છે. જો, ખાસ કરીને, પ્રારંભિક ક્ષણે સમૂહનું કેન્દ્ર આરામ પર હોય, તો પછી તે સમગ્ર સમય માટે આરામ કરે છે જ્યારે બાહ્ય દળોનો મુખ્ય વેક્ટર શૂન્ય સમાન હોય છે.

આ પ્રમેયમાંથી કેટલાક કોરોલરીઓ અનુસરે છે.

· એકલા આંતરિક દળો સિસ્ટમના સમૂહના કેન્દ્રની હિલચાલની પ્રકૃતિને બદલી શકતા નથી.

· જો સિસ્ટમ પર કામ કરતા બાહ્ય દળોનો મુખ્ય વેક્ટર શૂન્ય હોય, તો સમૂહનું કેન્દ્ર આરામ પર હોય છે અથવા એકસરખી અને સરખી રીતે આગળ વધે છે.

· જો અમુક નિશ્ચિત અક્ષ પર સિસ્ટમના બાહ્ય દળોના મુખ્ય વેક્ટરનું પ્રક્ષેપણ શૂન્ય બરાબર હોય, તો આ અક્ષ પર સિસ્ટમના સમૂહના કેન્દ્રના વેગનું પ્રક્ષેપણ બદલાતું નથી.

· કઠોર શરીર પર લાગુ દળોની જોડી તેના સમૂહના કેન્દ્રની હિલચાલને બદલી શકતી નથી (તે શરીરને માત્ર સમૂહના કેન્દ્રની આસપાસ ફેરવવાનું કારણ બની શકે છે).

ચાલો સમૂહના કેન્દ્રની ગતિના સંરક્ષણના કાયદાને સમજાવતા ઉદાહરણને ધ્યાનમાં લઈએ.

ઉદાહરણ 3.બ્લોક દ્વારા ફેંકવામાં આવેલા અક્ષમ થ્રેડ દ્વારા બે સમૂહો જોડાયેલા છે (ફિગ. 3.5), એક સમૂહ સાથે ફાચર પર નિશ્ચિત એમ.ફાચર એક સરળ આડી પ્લેન પર રહે છે. પ્રાથમિક ક્ષણે તંત્ર આરામમાં હતું. પ્લેન સાથે ફાચરનું વિસ્થાપન શોધો જ્યારે પ્રથમ ભાર ઊંચાઈ સુધી ઘટે છે એન.બ્લોક અને થ્રેડના સમૂહને અવગણો.

ઉકેલ.ભાર સાથે ફાચર પર કામ કરતી બાહ્ય શક્તિઓ ગુરુત્વાકર્ષણ છે, અને એમજી, તેમજ સરળ આડી સપાટીની સામાન્ય પ્રતિક્રિયા N. પરિણામે,

પ્રારંભિક ક્ષણે સિસ્ટમ આરામ પર હોવાથી, અમારી પાસે છે.

ચાલો સિસ્ટમના દળના કેન્દ્રના કોઓર્ડિનેટ્સ અને તે સમયે ગણતરી કરીએ t 1 જ્યારે ભારનું વજન થાય છે gઊંચાઈ સુધી ઉતરશે એચ.

ક્ષણ માટે:

,

જ્યાં , , એક્સ- અનુક્રમે, g, g અને ફાચરના વજનવાળા ભારના સમૂહના કેન્દ્રના કોઓર્ડિનેટ્સ એમg.

ચાલો ધારીએ કે સમયની ક્ષણે ફાચર ધરીની સકારાત્મક દિશામાં આગળ વધે છે બળદરકમ દ્વારા એલ, જો ભારનું વજન ઉંચાઈ સુધી ઘટી જાય એન.પછી, ક્ષણ માટે

કારણ કે ફાચર સાથેના ભારો ત્યાં જશે એલજમણી તરફ, અને ભાર ફાચર સાથે ઉપર તરફ જશે. ત્યારથી, પછી ગણતરીઓ પછી આપણને મળે છે

.

3.4. સિસ્ટમ ચળવળ જથ્થો

3.4.1. સિસ્ટમ વેગની ગણતરી

સામગ્રી બિંદુનો વેગ એ બિંદુના સમૂહ અને તેના વેગ વેક્ટરના ગુણાંક સમાન વેક્ટર જથ્થો છે

વેગના માપનનું એકમ -

યાંત્રિક સિસ્ટમનો વેગ એ સિસ્ટમના વ્યક્તિગત બિંદુઓના વેગનો વેક્ટર સરવાળો છે, એટલે કે.

જ્યાં એન - સિસ્ટમના બિંદુઓની સંખ્યા.

યાંત્રિક પ્રણાલીની ગતિને સિસ્ટમના સમૂહના સંદર્ભમાં વ્યક્ત કરી શકાય છે એમઅને સમૂહના કેન્દ્રની ગતિ. ખરેખર,

તે સિસ્ટમનો વેગ સમગ્ર સિસ્ટમના સમૂહના ઉત્પાદન અને તેના સમૂહના કેન્દ્રની ગતિ સમાન છે.દિશા દિશા સમાન છે (ફિગ. 3.6)

લંબચોરસ અક્ષો પરના અંદાજોમાં આપણી પાસે છે

જ્યાં , , એ સિસ્ટમના સમૂહના કેન્દ્રના વેગના અંદાજો છે.

અહીં એમ- યાંત્રિક સિસ્ટમનો સમૂહ; જ્યારે સિસ્ટમ ફરે છે ત્યારે બદલાતું નથી.

સખત શરીરની ગતિના જથ્થાની ગણતરી કરતી વખતે આ પરિણામોનો ઉપયોગ કરવા માટે ખાસ કરીને અનુકૂળ છે.

સૂત્ર (3.7) પરથી તે સ્પષ્ટ છે કે જો કોઈ યાંત્રિક પ્રણાલી એવી રીતે આગળ વધે છે કે તેના સમૂહનું કેન્દ્ર સ્થિર રહે છે, તો સિસ્ટમની ગતિ શૂન્ય સમાન રહે છે.

3.4.2. પ્રાથમિક અને સંપૂર્ણ બળ આવેગ

સમય જતાં ભૌતિક બિંદુ પર બળની ક્રિયા તાપ્રાથમિક આવેગ દ્વારા વર્ગીકૃત કરી શકાય છે. સમય જતાં કુલ બળ આવેગ t, અથવા બળ આવેગ, સૂત્ર દ્વારા નિર્ધારિત

અથવા અક્ષ કોઓર્ડિનેટ્સ પરના અંદાજોમાં

(3.8a)

બળ આવેગનું એકમ છે.

3.4.3. સિસ્ટમના વેગમાં ફેરફાર પર પ્રમેય

બાહ્ય અને આંતરિક દળોને સિસ્ટમના બિંદુઓ પર લાગુ થવા દો. પછી સિસ્ટમના દરેક બિંદુ માટે આપણે ગતિના વિભેદક નિયમો લાગુ કરી શકીએ છીએ (3.3), તે ધ્યાનમાં રાખીને :

.

સિસ્ટમના તમામ મુદ્દાઓનો સારાંશ, અમે મેળવીએ છીએ

આંતરિક દળોની મિલકત દ્વારા અને વ્યાખ્યા દ્વારા અમારી પાસે

(3.9)

દ્વારા આ સમીકરણની બંને બાજુનો ગુણાકાર તા, અમે વિભેદક સ્વરૂપમાં વેગમાં ફેરફાર પર એક પ્રમેય મેળવીએ છીએ:

, (3.10)

તે યાંત્રિક પ્રણાલીનો વિભેદક વેગ યાંત્રિક પ્રણાલીના બિંદુઓ પર કાર્ય કરતી તમામ બાહ્ય દળોના પ્રાથમિક આવેગોના વેક્ટર સરવાળાની બરાબર છે.

0 થી સમયાંતરે બંને બાજુઓ (3.10) ના અવિભાજ્યની ગણતરી t, આપણે પ્રમેયને મર્યાદિત અથવા અભિન્ન સ્વરૂપમાં મેળવીએ છીએ

(3.11)

સંકલન અક્ષો પરના અંદાજોમાં આપણી પાસે હશે

સમય જતાં યાંત્રિક પ્રણાલીના વેગમાં ફેરફારt, તે જ સમય દરમિયાન યાંત્રિક પ્રણાલીના બિંદુઓ પર કાર્ય કરતા બાહ્ય દળોના તમામ આવેગના વેક્ટર સરવાળો સમાન છે.

ઉદાહરણ 4.લોડ વજન m બળના પ્રભાવ હેઠળ આરામથી વલણવાળા વિમાનથી નીચે ઉતરે છે એફ, સમયના પ્રમાણસર: , ક્યાં (ફિગ. 3.7). શરીર પછી શું ગતિ પ્રાપ્ત કરશે t ચળવળની શરૂઆત પછીની સેકંડ, જો વલણવાળા પ્લેન પરના ભારના સ્લાઇડિંગ ઘર્ષણનો ગુણાંક બરાબર હોય f.

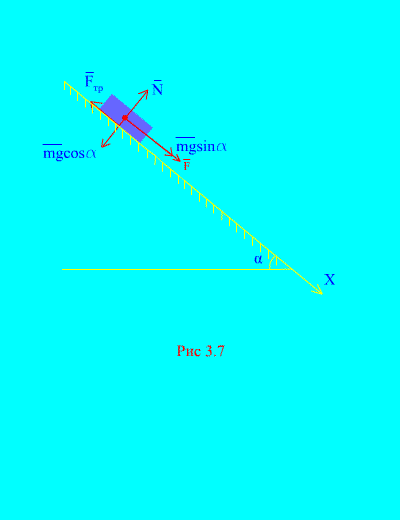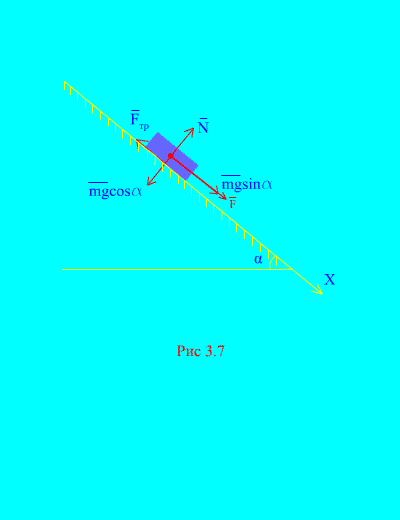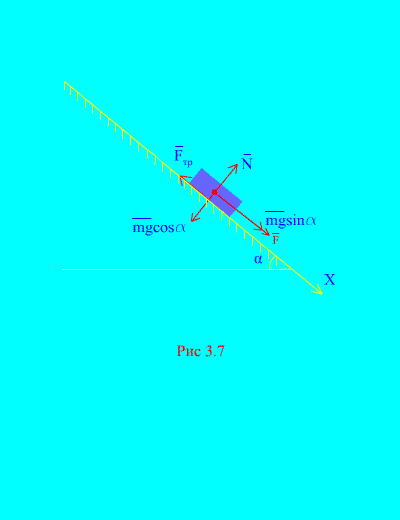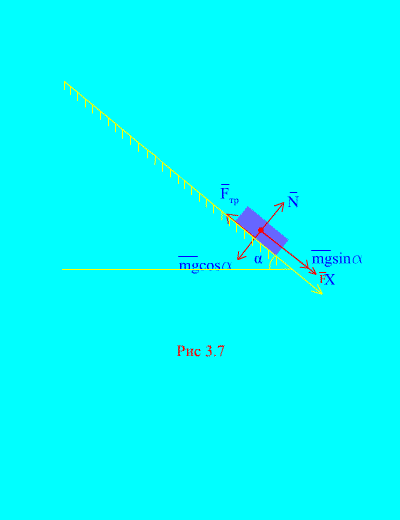
ઉકેલ.ચાલો ભાર પર લાગુ દળોનું નિરૂપણ કરીએ: મિલિગ્રામ - ભાર ગુરુત્વાકર્ષણ બળ, એનપ્લેનની સામાન્ય પ્રતિક્રિયા છે, પ્લેન પરના ભારનું સ્લાઇડિંગ ઘર્ષણ બળ છે, અને . માં તમામ દળોની દિશા બતાવવામાં આવી છે (ફિગ. 3.7).

ચાલો ધરીને દિશામાન કરીએ એક્સનીચે તરફ વળેલું પ્લેન સાથે. ચાલો ધરી પર પ્રક્ષેપણમાં વેગ (3.11) માં ફેરફાર વિશે પ્રમેય લખીએ. એક્સ:

(A)

શરત મુજબ, કારણ કે સમયની પ્રારંભિક ક્ષણે ભાર આરામ પર હતો. x અક્ષ પરના તમામ દળોના આવેગના અંદાજોનો સરવાળો બરાબર છે

આથી,

,

.

3.4.4. ગતિના સંરક્ષણના નિયમો

સંરક્ષણ કાયદાઓ વેગમાં ફેરફાર પર પ્રમેયના વિશેષ કેસ તરીકે મેળવવામાં આવે છે. બે વિશેષ કેસો શક્ય છે.

· જો સિસ્ટમ પર લાગુ તમામ બાહ્ય દળોનો વેક્ટર સરવાળો શૂન્ય સમાન હોય, એટલે કે. , પછી પ્રમેયમાંથી તે અનુસરે છે (3.9) , શું ,

તે જો સિસ્ટમના બાહ્ય દળોનો મુખ્ય વેક્ટર શૂન્ય હોય, તો સિસ્ટમની ગતિનું પ્રમાણ તીવ્રતા અને દિશામાં સ્થિર છે.

· જો કોઈપણ સંકલન ધરી પર બાહ્ય દળોના મુખ્ય વેક્ટરનું પ્રક્ષેપણ શૂન્ય બરાબર હોય, ઉદાહરણ તરીકે ઓક્સ, એટલે કે. , તો પછી આ અક્ષ પર વેગનું પ્રક્ષેપણ એક સ્થિર મૂલ્ય છે.

ચાલો વેગના સંરક્ષણના કાયદાને લાગુ કરવાના ઉદાહરણને ધ્યાનમાં લઈએ.

ઉદાહરણ 5.બેલિસ્ટિક લોલક એ લાંબા થ્રેડ પર સ્થગિત સમૂહ સાથેનું શરીર છે (ફિગ. 3.8).

સમૂહની બુલેટ, ઝડપ સાથે આગળ વધી રહી છે વીઅને સ્થિર શરીરને અથડાવીને, તેમાં અટવાઈ જાય છે, અને શરીર ભટકાઈ જાય છે. જો શરીર ઊંચાઈએ પહોંચ્યું તો બુલેટની ઝડપ કેટલી હતી h ?

ઉકેલ.અટકી ગયેલી બુલેટ સાથેના શરીરને ગતિ પ્રાપ્ત કરવા દો. પછી, બે સંસ્થાઓની ક્રિયાપ્રતિક્રિયા દરમિયાન વેગના સંરક્ષણના કાયદાનો ઉપયોગ કરીને, આપણે લખી શકીએ છીએ .

યાંત્રિક ઊર્જાના સંરક્ષણના કાયદાનો ઉપયોગ કરીને ઝડપની ગણતરી કરી શકાય છે . પછી . પરિણામે આપણે શોધીએ છીએ

.

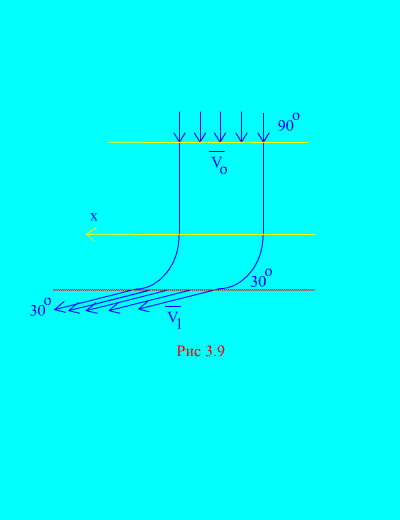
ઉદાહરણ 6. પાણી સ્થિર ચેનલમાં પ્રવેશ કરે છે (ફિગ. 3.9)વેરિયેબલ ક્રોસ-સેક્શન આડી તરફના ખૂણા પર ઝડપ સાથે; પ્રવેશદ્વાર પર ચેનલનો ક્રોસ-વિભાગીય વિસ્તાર; ચેનલમાંથી બહાર નીકળતી વખતે પાણીની ગતિ ક્ષિતિજ સાથે કોણ બનાવે છે.

ચેનલની દિવાલો પર પાણીની પ્રતિક્રિયાના આડા ઘટકને નિર્ધારિત કરો. પાણીની ઘનતા .

ઉકેલ.અમે પાણી પર ચેનલની દિવાલો દ્વારા કરવામાં આવતી પ્રતિક્રિયાના આડા ઘટકને નિર્ધારિત કરીશું. આ બળ તીવ્રતામાં સમાન છે અને ઇચ્છિત બળના ચિહ્નમાં વિરુદ્ધ છે. અમારી પાસે, (3.11a) અનુસાર,

. (A)

અમે સમય દરમિયાન ચેનલમાં પ્રવેશતા પ્રવાહીના જથ્થાના સમૂહની ગણતરી કરીએ છીએ:

મૂલ્ય આરએવી 0 કહેવાય છે બીજો સમૂહ - એકમ સમય દીઠ પાઇપના કોઈપણ વિભાગમાંથી વહેતા પ્રવાહીનો સમૂહ.

તે જ સમય દરમિયાન નહેરમાંથી સમાન પ્રમાણમાં પાણી છોડે છે. પ્રારંભિક અને અંતિમ ગતિ શરતમાં આપવામાં આવે છે.

ચાલો સમાનતા (a) ની જમણી બાજુની ગણતરી કરીએ, જે સિસ્ટમ (પાણી) પર લાગુ બાહ્ય દળોની આડી અક્ષ પર અંદાજોનો સરવાળો નક્કી કરે છે. એકમાત્ર આડી બળ એ પરિણામી દિવાલ પ્રતિક્રિયાનો આડી ઘટક છે આરએક્સ. પાણીની સ્થિર હિલચાલ દરમિયાન આ બળ સતત રહે છે. એ કારણે

. (વી)

(b) અને (c) ને (a) માં બદલીને, આપણને મળે છે

3.5. સિસ્ટમની ગતિશીલ ક્ષણ

3.5.1. સિસ્ટમના વેગનો મુખ્ય ક્ષણ

અમુક બિંદુ A, જેને કેન્દ્ર કહેવાય છે તેની સાપેક્ષ સિસ્ટમના દળ સાથે બિંદુનો ત્રિજ્યા વેક્ટર ગણો (ફિગ. 3.10).

એક બિંદુની ગતિની ગતિ (ગતિ ક્ષણ). કેન્દ્ર A થી સંબંધિતવેક્ટર કહેવાય છે , સૂત્ર દ્વારા નક્કી કરવામાં આવે છે

. (3.12)

આ કિસ્સામાં, વેક્ટર કેન્દ્રમાંથી પસાર થતા પ્લેન પર લંબ નિર્દેશિત એઅને વેક્ટર .

અક્ષની સાપેક્ષ બિંદુની ગતિ (ગતિ ક્ષણ).આ અક્ષ પર પસંદ કરેલ કોઈપણ કેન્દ્રને સંબંધિત બિંદુના વેગના ક્ષણના આ અક્ષ પર પ્રક્ષેપણ કહેવાય છે.

કેન્દ્ર A ની સાપેક્ષ સિસ્ટમની વેગની મુખ્ય ક્ષણ (ગતિ ક્ષણ).જથ્થો કહેવાય છે

(3.13)

અક્ષની તુલનામાં સિસ્ટમની વેગની મુખ્ય ક્ષણ (ગતિ ક્ષણ).સિસ્ટમના વેગના મુખ્ય ક્ષણના આ અક્ષ પરના પ્રક્ષેપણને આના પર પસંદ કરેલ કોઈપણની તુલનામાં કહેવામાં આવે છે. કેન્દ્ર અક્ષ.

3.5.2. પરિભ્રમણની ધરી વિશે ફરતા સખત શરીરની ગતિશીલ ક્ષણ

ચાલો નિશ્ચિત બિંદુને સંરેખિત કરીએ વિશેપરિભ્રમણની ધરી પર પડેલું શરીર વિશેz, કોઓર્ડિનેટ સિસ્ટમની ઉત્પત્તિ સાથે ઓહુz, જેની ધરીઓ શરીર સાથે ફરશે (ફિગ. 3.11). કોઓર્ડિનેટ્સની ઉત્પત્તિની તુલનામાં શરીરના બિંદુના ત્રિજ્યા વેક્ટર તરીકે અક્ષ પર તેનું પ્રક્ષેપણ , , દ્વારા સૂચવવામાં આવશે; અમે 0, 0, () જેવા સમાન અક્ષો પર શરીરના કોણીય વેગ વેક્ટરના અંદાજો દર્શાવીએ છીએ.

ચાલો નિશ્ચિત સંકલન પ્રણાલીની તુલનામાં ભૌતિક પદાર્થોની ચોક્કસ સિસ્ટમની હિલચાલને ધ્યાનમાં લઈએ, જ્યારે સિસ્ટમ મુક્ત ન હોય, તો જો આપણે સિસ્ટમ પર લાદવામાં આવેલા જોડાણોને છોડી દઈએ અને તેની ક્રિયાને અનુરૂપ પ્રતિક્રિયાઓ સાથે બદલીએ તો તે મુક્ત ગણી શકાય.

ચાલો સિસ્ટમ પર લાગુ તમામ દળોને બાહ્ય અને આંતરિકમાં વિભાજીત કરીએ; બંનેમાં કાઢી નાખવાની પ્રતિક્રિયાઓ શામેલ હોઈ શકે છે

જોડાણો ચાલો અને બિંદુ A ને સંબંધિત મુખ્ય વેક્ટર અને બાહ્ય દળોની મુખ્ય ક્ષણ સૂચવીએ.

1. વેગમાં ફેરફાર પર પ્રમેય.જો સિસ્ટમની ગતિનું પ્રમાણ છે, તો (જુઓ)

એટલે કે, પ્રમેય માન્ય છે: સિસ્ટમના વેગનો સમય વ્યુત્પન્ન તમામ બાહ્ય દળોના મુખ્ય વેક્ટર સમાન છે.

વેક્ટરને તેની અભિવ્યક્તિ દ્વારા બદલીને સિસ્ટમનું દળ ક્યાં છે, દળના કેન્દ્રનો વેગ છે, સમીકરણ (4.1) ને અલગ સ્વરૂપ આપી શકાય છે:

આ સમાનતાનો અર્થ એ છે કે સિસ્ટમના દળનું કેન્દ્ર ભૌતિક બિંદુની જેમ ફરે છે જેનું દળ સિસ્ટમના દળ જેટલું હોય છે અને જેના પર બળ લાગુ કરવામાં આવે છે જે સિસ્ટમના તમામ બાહ્ય દળોના મુખ્ય વેક્ટરની ભૌમિતિક રીતે સમાન હોય છે. છેલ્લું વિધાન સિસ્ટમના દળના કેન્દ્ર (જડતાનું કેન્દ્ર) ની ગતિ પર પ્રમેય કહેવાય છે.

જો પછી (4.1) થી તે અનુસરે છે કે વેક્ટર વેક્ટર તીવ્રતા અને દિશામાં સ્થિર છે. તેને કોઓર્ડિનેટ અક્ષ પર પ્રક્ષેપિત કરીને, અમે સિસ્ટમના ડબલ કેપના વિભેદક સમીકરણો, ત્રણ સ્કેલર ફર્સ્ટ ઇન્ટિગ્રલ મેળવીએ છીએ:

આ ઇન્ટિગ્રલ્સને મોમેન્ટમ ઇન્ટિગ્રલ્સ કહેવામાં આવે છે. જ્યારે દળના કેન્દ્રની ગતિ સ્થિર હોય છે, એટલે કે, તે એકસરખી અને સરખી રીતે આગળ વધે છે.

જો કોઈપણ એક ધરી પર બાહ્ય દળોના મુખ્ય વેક્ટરનું પ્રક્ષેપણ, ઉદાહરણ તરીકે, અક્ષ પર, શૂન્ય સમાન હોય, તો આપણી પાસે એક પ્રથમ અવિભાજ્ય છે, અથવા જો મુખ્ય વેક્ટરના બે અંદાજો શૂન્ય સમાન હોય, તો ત્યાં બે છે. ગતિના અભિન્ન અંગો.

2. કોણીય વેગમાં ફેરફાર પર પ્રમેય. A ને અવકાશમાં કેટલાક મનસ્વી બિંદુ (ખસેડવાની અથવા સ્થિર) રહેવા દો, જે સમગ્ર હિલચાલ દરમિયાન સિસ્ટમના કોઈપણ વિશિષ્ટ સામગ્રી બિંદુ સાથે સુસંગત હોય તે જરૂરી નથી. પોઈન્ટ A ની સાપેક્ષમાં ભૌતિક પ્રણાલીની ગતિશીલ ક્ષણમાં ફેરફાર પરના પ્રમેય દ્વારા અમે નિશ્ચિત સંકલન પ્રણાલીમાં તેની ઝડપને દર્શાવીએ છીએ

જો બિંદુ A નિશ્ચિત છે, તો સમાનતા (4.3) એક સરળ સ્વરૂપ લે છે:

આ સમાનતા એક નિશ્ચિત બિંદુને સંબંધિત સિસ્ટમના કોણીય વેગના તફાવત વિશે પ્રમેયને વ્યક્ત કરે છે: સિસ્ટમના કોણીય વેગનો સમય વ્યુત્પન્ન, અમુક નિશ્ચિત બિંદુની તુલનામાં ગણવામાં આવે છે, તે તમામ બાહ્ય દળોના સંબંધિત મુખ્ય ક્ષણની સમાન છે. આ બિંદુ સુધી.

જો પછી (4.4) મુજબ કોણીય મોમેન્ટમ વેક્ટર તીવ્રતા અને દિશામાં સ્થિર છે. તેને કોઓર્ડિનેટ અક્ષો પર પ્રક્ષેપિત કરીને, અમે ડબલ સિસ્ટમના વિભેદક સમીકરણોના સ્કેલર ફર્સ્ટ ઇન્ટિગ્રલ મેળવીએ છીએ:

આ ઇન્ટિગ્રલ્સને મોમેન્ટમ ઇન્ટિગ્રલ અથવા એરિયા ઇન્ટિગ્રલ કહેવામાં આવે છે.

જો બિંદુ A સિસ્ટમના સમૂહના કેન્દ્ર સાથે એકરુપ હોય, તો સમાનતા (4.3) ની જમણી બાજુનું પ્રથમ પદ અદૃશ્ય થઈ જાય છે અને કોણીય ગતિમાં ફેરફાર પર પ્રમેય લેખનનું સમાન સ્વરૂપ ધરાવે છે (4.4) ના કિસ્સામાં એક નિશ્ચિત બિંદુ A. નોંધ (જુઓ. p. 4 § 3), કે વિચારણા હેઠળના કિસ્સામાં, સમાનતા (4.4) ની ડાબી બાજુએ સિસ્ટમના સંપૂર્ણ કોણીય વેગને સિસ્ટમના સમાન કોણીય વેગ દ્વારા બદલી શકાય છે. દળના કેન્દ્રની તુલનામાં તેની ગતિમાં.

સિસ્ટમના દળના કેન્દ્રમાંથી પસાર થતી સતત દિશાની અમુક અક્ષો અથવા અક્ષ હોઈએ અને આ અક્ષની સાપેક્ષ સિસ્ટમની ગતિશીલ ક્ષણ હોઈએ. (4.4) થી તે અનુસરે છે

અક્ષની તુલનામાં બાહ્ય દળોની ક્ષણ ક્યાં છે. જો સમગ્ર ચળવળ દરમિયાન અમારી પાસે પ્રથમ અભિન્ન છે

S.A. ચૅપ્લિગિનના કાર્યોમાં, ગતિ ગતિમાં ફેરફાર અંગેના પ્રમેયના કેટલાક સામાન્યીકરણો પ્રાપ્ત થયા હતા, જે પછી રોલિંગ બોલ પરની સંખ્યાબંધ સમસ્યાઓના ઉકેલ માટે લાગુ કરવામાં આવ્યા હતા. યાંત્રિક ક્ષણમાં ફેરફાર પરના પ્રમેયના વધુ સામાન્યીકરણો અને સખત શારીરિક ગતિશીલતાની સમસ્યાઓમાં તેમના ઉપયોગો કાર્યોમાં સમાયેલ છે. આ કાર્યોના મુખ્ય પરિણામો ગતિશીલ ગતિમાં પરિવર્તનના પ્રમેય સાથે સંબંધિત છે, જે સતત અમુક ગતિશીલ બિંદુ Aમાંથી પસાર થાય છે. ચાલો આ અક્ષ સાથે નિર્દેશિત એકમ વેક્ટર બનીએ. સમાનતાની બંને બાજુઓ (4.3) દ્વારા સ્કેલર રીતે ગુણાકાર કરીને અને તેના બે ભાગોમાં શબ્દ ઉમેરવાથી આપણને મળે છે.

જ્યારે કાઇનેમેટિક સ્થિતિ પૂરી થાય છે

સમીકરણ (4.5) (4.7) થી અનુસરે છે. અને જો સમગ્ર ચળવળ દરમિયાન સ્થિતિ (4.8) સંતુષ્ટ હોય, તો પ્રથમ અભિન્ન (4.6) અસ્તિત્વમાં છે.

જો સિસ્ટમના કનેક્શન આદર્શ હોય અને વર્ચ્યુઅલ ડિસ્પ્લેસમેન્ટ્સ વચ્ચે, સિસ્ટમને અક્ષની ફરતે કઠોર શરીર તરીકે પરિભ્રમણ કરવાની મંજૂરી આપે છે અને, પછી અક્ષની તુલનામાં પ્રતિક્રિયાઓની મુખ્ય ક્ષણ અને શૂન્યની બરાબર છે, અને પછી મૂલ્ય સમીકરણની જમણી બાજુ (4.5) અક્ષ અને . આ ક્ષણની શૂન્યની સમાનતા અને સંબંધની માન્યતા (4.8) અવિભાજ્ય (4.6) ના અસ્તિત્વ માટે વિચારણા હેઠળના કિસ્સામાં હશે.

જો ધરીની દિશા અને સ્થિર હોય, તો શરત (4.8) ફોર્મમાં લખવામાં આવશે

આ સમાનતાનો અર્થ એ છે કે દળના કેન્દ્રના વેગના અંદાજો અને ધરી પર અને આના લંબરૂપ સમતલ પર બિંદુ A ના વેગના અનુમાન સમાંતર છે. S.A. Chaplygin ના કાર્યમાં, (4.9) ને બદલે, ઓછી સામાન્ય સ્થિતિની પરિપૂર્ણતા જરૂરી છે જ્યાં X એ મનસ્વી સ્થિર મૂલ્ય છે.

નોંધ કરો કે શરત (4.8) બિંદુની પસંદગી પર આધારિત નથી. ખરેખર, P ને ધરી પર મનસ્વી બિંદુ બનવા દો. પછી

અને તેથી

નિષ્કર્ષમાં, અમે રેઝાલના સમીકરણો (4.1) અને (4.4) ના ભૌમિતિક અર્થઘટનની નોંધ કરીએ છીએ: વેક્ટરના છેડાના સંપૂર્ણ વેગ વેક્ટર અને તે અનુક્રમે મુખ્ય વેક્ટર અને બિંદુ A ને સંબંધિત તમામ બાહ્ય દળોના મુખ્ય ક્ષણની સમાન હોય છે. .

સમસ્યાઓના નિરાકરણમાં સ્વાસ્થ્ય વીમાનો ઉપયોગ અમુક મુશ્કેલીઓ સાથે સંકળાયેલો છે. તેથી, વધારાના સંબંધો સામાન્ય રીતે ગતિ અને દળોની લાક્ષણિકતાઓ વચ્ચે સ્થાપિત થાય છે, જે વ્યવહારુ એપ્લિકેશન માટે વધુ અનુકૂળ છે. આવા સંબંધો છે ગતિશાસ્ત્રના સામાન્ય પ્રમેય.તેઓ, OMS ના પરિણામો હોવાને કારણે, ચળવળના કેટલાક વિશેષ રીતે રજૂ કરાયેલા પગલાં અને બાહ્ય દળોની લાક્ષણિકતાઓના પરિવર્તનની ગતિ વચ્ચે સંબંધ સ્થાપિત કરે છે.

વેગના પરિવર્તન પર પ્રમેય. ચાલો મટીરીયલ પોઈન્ટ (ફિગ. 3.4) ના વેક્ટર ઓફ વેક્ટર (આર. ડેસકાર્ટેસ) નો ખ્યાલ રજૂ કરીએ:

I i = t V જી (3.9)

ચોખા. 3.4.

સિસ્ટમ માટે અમે ખ્યાલ રજૂ કરીએ છીએ સિસ્ટમના વેગનું મુખ્ય વેક્ટરભૌમિતિક રકમ તરીકે:

Q = Y, m " V r

OZMS અનુસાર: Xu, -^=i) , અથવા X

આર (ઇ).

ધ્યાનમાં લેતા કે /w, = const આપણને મળે છે: -Ym,!" = R(E)

અથવા અંતિમ સ્વરૂપમાં

dO/di = A (E (3.11)

તે સિસ્ટમના વેગના મુખ્ય વેક્ટરના સમયના સંદર્ભમાં પ્રથમ વ્યુત્પન્ન બાહ્ય દળોના મુખ્ય વેક્ટર સમાન છે.

સમૂહના કેન્દ્રની ગતિ પર પ્રમેય. સિસ્ટમના સમૂહનું કેન્દ્રભૌમિતિક બિંદુ કહેવાય છે જેની સ્થિતિ પર આધાર રાખે છે ટી,વગેરે સમૂહ /g/ ના વિતરણમાંથી, સિસ્ટમમાં અને સમૂહના કેન્દ્રના ત્રિજ્યા વેક્ટર માટે અભિવ્યક્તિ દ્વારા નિર્ધારિત થાય છે (ફિગ. 3.5):

જ્યાં જી એસ -સમૂહના કેન્દ્રનો ત્રિજ્યા વેક્ટર.

ચોખા. 3.5.

ચાલો કૉલ કરીએ = સિસ્ટમના સમૂહ સાથે ટી.અભિવ્યક્તિનો ગુણાકાર કર્યા પછી

(3.12) છેદ પર લાગુ કરવું અને પરિણામની બંને બાજુઓને અલગ પાડવું

અમારી પાસે મૂલ્યવાન સમાનતા હશે: g s t s = ^t.U. = 0, અથવા 0 = t s U s.

આમ, સિસ્ટમનો મુખ્ય વેક્ટર વેક્ટર સિસ્ટમના સમૂહના ઉત્પાદન અને સમૂહના કેન્દ્રના વેગ જેટલો છે. વેગમાં ફેરફાર (3.11) પર પ્રમેયનો ઉપયોગ કરીને, અમે મેળવીએ છીએ:

t s dU s / dі = A (E) ,અથવા

ફોર્મ્યુલા (3.13) સમૂહના કેન્દ્રની હિલચાલ પર પ્રમેય વ્યક્ત કરે છે: સિસ્ટમના સમૂહનું કેન્દ્ર ભૌતિક બિંદુ તરીકે આગળ વધે છે જેમાં સિસ્ટમનો સમૂહ હોય છે, જેના પર બાહ્ય દળોના મુખ્ય વેક્ટર દ્વારા કાર્ય કરવામાં આવે છે.

કોણીય વેગમાં ફેરફાર પર પ્રમેય. ચાલો આપણે પદાર્થ બિંદુના કોણીય વેગના ખ્યાલને તેના ત્રિજ્યા વેક્ટર અને વેક્ટરના વેક્ટર ઉત્પાદન તરીકે રજૂ કરીએ:

ઓહ માટે = blએક્સ કે, (3.14)

જ્યાં OI થી -નિશ્ચિત બિંદુની તુલનામાં ભૌતિક બિંદુના વેગની ક્ષણ વિશે(ફિગ. 3.6).

હવે આપણે મિકેનિકલ સિસ્ટમના કોણીય વેગને ભૌમિતિક સરવાળો તરીકે વ્યાખ્યાયિત કરીએ છીએ:

К() = X કો, = ШУ, ? O-15>

ભિન્નતા (3.15), અમે મેળવીએ છીએ:

Ґ સેકન્ડ--- એક્સ t i U. + ગુએક્સ t i

તે ધ્યાનમાં લેતા = U G U iએક્સ t i u i= 0, અને સૂત્ર (3.2), અમે મેળવીએ છીએ:

сіК а /с1ї - ї 0 .

(3.6) માં બીજા અભિવ્યક્તિના આધારે, આપણી પાસે આખરે સિસ્ટમના કોણીય ગતિમાં ફેરફાર પર એક પ્રમેય હશે:

નિશ્ચિત કેન્દ્ર O ની સાપેક્ષ યાંત્રિક પ્રણાલીના વેગના ક્ષણનું પ્રથમ વખત વ્યુત્પન્ન એ સમાન કેન્દ્રની સાપેક્ષે આ સિસ્ટમ પર કાર્ય કરતી બાહ્ય દળોની મુખ્ય ક્ષણ સમાન છે.

સંબંધ (3.16) મેળવતી વખતે, એવું માનવામાં આવતું હતું વિશે- નિશ્ચિત બિંદુ. જો કે, તે બતાવી શકાય છે કે અન્ય સંખ્યાબંધ કેસોમાં સંબંધનું સ્વરૂપ (3.16) બદલાશે નહીં, ખાસ કરીને, જો સમતલ ગતિમાં ક્ષણ બિંદુ દળના કેન્દ્રમાં પસંદ કરવામાં આવે છે, વેગ અથવા પ્રવેગના તાત્કાલિક કેન્દ્ર. વધુમાં, જો બિંદુ વિશેમૂવિંગ મટીરીયલ પોઈન્ટ સાથે સુસંગત છે, આ બિંદુ માટે લખાયેલ સમાનતા (3.16) ઓળખ 0 = 0 માં ફેરવાશે.

ગતિ ઊર્જામાં ફેરફાર પર પ્રમેય. જ્યારે યાંત્રિક સિસ્ટમ ફરે છે, ત્યારે સિસ્ટમની "બાહ્ય" અને આંતરિક ઊર્જા બંને બદલાય છે. જો આંતરિક દળોની લાક્ષણિકતાઓ, મુખ્ય વેક્ટર અને મુખ્ય ક્ષણ, મુખ્ય વેક્ટરમાં ફેરફાર અને પ્રવેગની સંખ્યાના મુખ્ય ક્ષણને અસર કરતી નથી, તો પછી સિસ્ટમની ઊર્જા સ્થિતિની પ્રક્રિયાઓના મૂલ્યાંકનમાં આંતરિક દળોનો સમાવેશ કરી શકાય છે.તેથી, જ્યારે સિસ્ટમની ઊર્જામાં ફેરફારને ધ્યાનમાં લેતા, ત્યારે વ્યક્તિગત બિંદુઓની હિલચાલને ધ્યાનમાં લેવી જરૂરી છે, જેના પર આંતરિક દળો પણ લાગુ થાય છે.

સામગ્રી બિંદુની ગતિ ઊર્જાને જથ્થા તરીકે વ્યાખ્યાયિત કરવામાં આવે છે

T^tuTsg. (3.17)

યાંત્રિક સિસ્ટમની ગતિ ઊર્જા સિસ્ટમના ભૌતિક બિંદુઓની ગતિ ઊર્જાના સરવાળા જેટલી છે:

આ ધ્યાન માં રાખો ટી > 0.

ચાલો બળ વેક્ટર અને વેગ વેક્ટરના સ્કેલર ઉત્પાદન તરીકે બળ શક્તિને વ્યાખ્યાયિત કરીએ:

ઘણી વાર ગતિના વિભેદક સમીકરણોની સિસ્ટમને એકીકૃત કર્યા વિના યાંત્રિક પ્રણાલીની ગતિના મહત્વપૂર્ણ લક્ષણોને ઓળખવાનું શક્ય છે. ગતિશાસ્ત્રના સામાન્ય પ્રમેયને લાગુ કરીને આ પ્રાપ્ત થાય છે.

5.1. મૂળભૂત ખ્યાલો અને વ્યાખ્યાઓ

બાહ્ય અને આંતરિક દળો.યાંત્રિક પ્રણાલીમાં બિંદુ પર કાર્ય કરતું કોઈપણ બળ આવશ્યકપણે સક્રિય બળ અથવા જોડાણ પ્રતિક્રિયા છે. સિસ્ટમના બિંદુઓ પર કાર્ય કરતા દળોના સંપૂર્ણ સમૂહને બે વર્ગોમાં અલગ અલગ રીતે વિભાજિત કરી શકાય છે: બાહ્ય દળો અને આંતરિક દળો (સૂચકાંકો e અને i - લેટિન શબ્દો externus - external અને internus - આંતરિકમાંથી). બાહ્ય દળો તે છે જે સિસ્ટમના બિંદુઓ અને સંસ્થાઓના બિંદુઓ પર કાર્ય કરે છે જે વિચારણા હેઠળની સિસ્ટમનો ભાગ નથી. વિચારણા હેઠળના સિસ્ટમના બિંદુઓ અને સંસ્થાઓ વચ્ચેની ક્રિયાપ્રતિક્રિયાના દળોને આંતરિક કહેવામાં આવે છે.

આ વિભાજન વિચારણા હેઠળની યાંત્રિક પ્રણાલીમાં સંશોધક દ્વારા કયા ભૌતિક બિંદુઓ અને સંસ્થાઓનો સમાવેશ થાય છે તેના પર આધાર રાખે છે. જો આપણે વધારાના બિંદુઓ અને સંસ્થાઓનો સમાવેશ કરીને સિસ્ટમની રચનાને વિસ્તૃત કરીએ, તો કેટલાક બળો કે જે અગાઉની સિસ્ટમ માટે બાહ્ય હતા તે વિસ્તૃત સિસ્ટમ માટે આંતરિક બની શકે છે.

આંતરિક દળોના ગુણધર્મો.આ દળો સિસ્ટમના ભાગો વચ્ચેની ક્રિયાપ્રતિક્રિયાના દળો હોવાથી, તેઓ "બે" માં આંતરિક દળોની સંપૂર્ણ સિસ્ટમમાં પ્રવેશ કરે છે, જે ક્રિયા-પ્રતિક્રિયા સ્વયંસિદ્ધ અનુસાર ગોઠવાય છે. આવા દરેક "બે" માં શક્તિઓ હોય છે

મુખ્ય વેક્ટર અને મનસ્વી કેન્દ્ર વિશેની મુખ્ય ક્ષણ શૂન્યની બરાબર છે. આંતરિક દળોની સંપૂર્ણ પ્રણાલીમાં ફક્ત "બે" નો સમાવેશ થાય છે

1) આંતરિક દળોની સિસ્ટમનો મુખ્ય વેક્ટર શૂન્ય છે,

2) મનસ્વી બિંદુને સંબંધિત આંતરિક દળોની સિસ્ટમની મુખ્ય ક્ષણ શૂન્યની બરાબર છે.

સિસ્ટમનો સમૂહ એ સિસ્ટમની રચના કરતા તમામ બિંદુઓ અને સંસ્થાઓના માસ mk નો અંકગણિત સરવાળો છે:

સમૂહનું કેન્દ્રયાંત્રિક પ્રણાલીનું (જડતાનું કેન્દ્ર) એ ભૌમિતિક બિંદુ C છે, ત્રિજ્યા વેક્ટર અને કોઓર્ડિનેટ્સ જે સૂત્રો દ્વારા નક્કી કરવામાં આવે છે.

સિસ્ટમ બનાવતા બિંદુઓના ત્રિજ્યા વેક્ટર અને કોઓર્ડિનેટ્સ ક્યાં છે.

એક સમાન ગુરુત્વાકર્ષણ ક્ષેત્રમાં સ્થિત કઠોર શરીર માટે, સમૂહના કેન્દ્ર અને ગુરુત્વાકર્ષણના કેન્દ્રની સ્થિતિઓ એકરૂપ થાય છે, આ વિવિધ ભૌમિતિક બિંદુઓ છે.

જડતા સંદર્ભ પ્રણાલી સાથે, બિન-જડતી સંદર્ભ પ્રણાલી જે અનુવાદમાં આગળ વધે છે તેને ઘણીવાર એકસાથે ગણવામાં આવે છે. તેના સંકલન અક્ષો (કોનિગ અક્ષો) પસંદ કરવામાં આવે છે જેથી મૂળ C સતત યાંત્રિક પ્રણાલીના સમૂહના કેન્દ્ર સાથે સુસંગત રહે. વ્યાખ્યા અનુસાર, સમૂહનું કેન્દ્ર કોએનિગ અક્ષોમાં સ્થિર છે અને કોઓર્ડિનેટ્સના મૂળ પર સ્થિત છે.

સિસ્ટમની જડતાની ક્ષણઅક્ષની સાપેક્ષ એ અક્ષ સુધીના તેમના અંતરના વર્ગો દ્વારા સિસ્ટમના તમામ બિંદુઓના સમૂહ mk ના ઉત્પાદનના સરવાળા સમાન સ્કેલર જથ્થો છે:

જો યાંત્રિક સિસ્ટમ સખત શરીર છે, તો 12 શોધવા માટે તમે સૂત્રનો ઉપયોગ કરી શકો છો

ઘનતા ક્યાં છે, શરીર દ્વારા કબજે કરેલ વોલ્યુમ.

સમૂહના કેન્દ્રની ગતિ પર પ્રમેય.યાંત્રિક પ્રણાલીની ગતિના વિભેદક સમીકરણો. યાંત્રિક પ્રણાલીના સમૂહના કેન્દ્રની ગતિ પર પ્રમેય. સમૂહના કેન્દ્રની ગતિના સંરક્ષણનો કાયદો.

વેગના પરિવર્તન પર પ્રમેય.સામગ્રી બિંદુની ગતિનો જથ્થો. બળનો પ્રાથમિક આવેગ. સંકલન અક્ષો પર મર્યાદિત સમયગાળા માટે આવેગ અને તેના પ્રક્ષેપણ માટે દબાણ કરો. વિભેદક અને મર્યાદિત સ્વરૂપોમાં ભૌતિક બિંદુના વેગમાં ફેરફાર પર પ્રમેય.

યાંત્રિક પ્રણાલીની ગતિની માત્રા; સિસ્ટમના સમૂહ અને તેના સમૂહના કેન્દ્રની ગતિ દ્વારા તેની અભિવ્યક્તિ. વિભેદક અને મર્યાદિત સ્વરૂપોમાં યાંત્રિક સિસ્ટમના વેગમાં ફેરફાર પર પ્રમેય. યાંત્રિક ગતિના સંરક્ષણનો કાયદો

(શરીરનો ખ્યાલ અને ચલ સમૂહનો એક બિંદુ. મેશેરસ્કીનું સમીકરણ. ત્સિઓલકોવ્સ્કીનું સૂત્ર.)

કોણીય વેગમાં ફેરફાર પર પ્રમેય.કેન્દ્રની સાપેક્ષ અને અક્ષની સાપેક્ષમાં ભૌતિક બિંદુના વેગની ક્ષણ. ભૌતિક બિંદુના કોણીય વેગમાં ફેરફાર પર પ્રમેય. કેન્દ્રીય શક્તિ. કેન્દ્રીય બળના કિસ્સામાં સામગ્રી બિંદુના કોણીય ગતિનું સંરક્ષણ. (ક્ષેત્ર વેગનો ખ્યાલ. વિસ્તારોનો કાયદો.)

કેન્દ્રની સાપેક્ષ અને ધરીની સાપેક્ષમાં યાંત્રિક પ્રણાલીની વેગ અથવા ગતિની મુખ્ય ક્ષણ. પરિભ્રમણની ધરી વિશે ફરતા સખત શરીરની ગતિશીલ ક્ષણ. યાંત્રિક પ્રણાલીના ગતિશીલ ક્ષણમાં ફેરફાર પર પ્રમેય. મિકેનિકલ સિસ્ટમના કોણીય વેગના સંરક્ષણનો કાયદો. (દળના કેન્દ્રના સંદર્ભમાં સંબંધિત ગતિમાં યાંત્રિક પ્રણાલીના કોણીય વેગમાં ફેરફાર પર પ્રમેય.)

ગતિ ઊર્જામાં ફેરફાર પર પ્રમેય.ભૌતિક બિંદુની ગતિ ઊર્જા. બળનું પ્રાથમિક કાર્ય; પ્રારંભિક કાર્યની વિશ્લેષણાત્મક અભિવ્યક્તિ. તેની અરજીના બિંદુના અંતિમ વિસ્થાપન પર બળ દ્વારા કરવામાં આવેલ કાર્ય. ગુરુત્વાકર્ષણ, સ્થિતિસ્થાપક બળ અને ગુરુત્વાકર્ષણ બળનું કાર્ય. વિભેદક અને મર્યાદિત સ્વરૂપોમાં ભૌતિક બિંદુની ગતિ ઊર્જામાં ફેરફાર પર પ્રમેય.

યાંત્રિક પ્રણાલીની ગતિ ઊર્જા. અનુવાદની ગતિ દરમિયાન, નિશ્ચિત અક્ષની આસપાસ પરિભ્રમણ દરમિયાન અને ગતિના સામાન્ય કિસ્સામાં (ખાસ કરીને, પ્લેન-સમાંતર ગતિ દરમિયાન) કઠોર શરીરની ગતિ ઊર્જાની ગણતરી માટેના સૂત્રો. વિભેદક અને મર્યાદિત સ્વરૂપોમાં યાંત્રિક પ્રણાલીની ગતિ ઊર્જામાં ફેરફાર પર પ્રમેય. નક્કર શરીરમાં આંતરિક દળો દ્વારા કરવામાં આવતા કાર્યનો સરવાળો શૂન્ય બરાબર છે. નિશ્ચિત ધરીની આસપાસ ફરતા કઠોર શરીર પર લાગુ દળોનું કાર્ય અને શક્તિ.

બળ ક્ષેત્રનો ખ્યાલ. સંભવિત બળ ક્ષેત્ર અને બળ કાર્ય. બળ કાર્ય દ્વારા બળ અંદાજોની અભિવ્યક્તિ. સમાન સંભવિત સપાટીઓ. સંભવિત બળ ક્ષેત્રમાં બિંદુના અંતિમ વિસ્થાપન પર બળનું કાર્ય. સંભવિત ઊર્જા. સંભવિત બળ ક્ષેત્રોના ઉદાહરણો: સમાન ગુરુત્વાકર્ષણ ક્ષેત્ર અને ગુરુત્વાકર્ષણ ક્ષેત્ર. યાંત્રિક ઊર્જાના સંરક્ષણનો કાયદો.

સખત શરીરની ગતિશીલતા.કઠોર શરીરની અનુવાદાત્મક ગતિના વિભેદક સમીકરણો. નિશ્ચિત અક્ષની આસપાસ કઠોર શરીરના પરિભ્રમણ માટે વિભેદક સમીકરણ. ભૌતિક લોલક. કઠોર શરીરની સમતલ ગતિના વિભેદક સમીકરણો.

ડી'એલેમ્બર્ટનો સિદ્ધાંત.ભૌતિક બિંદુ માટે ડી'એલેમ્બર્ટનો સિદ્ધાંત; જડતા બળ. મિકેનિકલ સિસ્ટમ માટે ડી'એલેમ્બર્ટનો સિદ્ધાંત. કઠોર શરીરના બિંદુઓના જડતા દળોને કેન્દ્રમાં લાવવું; મુખ્ય વેક્ટર અને જડતા દળોની મુખ્ય ક્ષણ.

(નિશ્ચિત ધરીની આસપાસ કઠોર શરીરના પરિભ્રમણ દરમિયાન બેરિંગ્સની ગતિશીલ પ્રતિક્રિયાઓનું નિર્ધારણ. જ્યારે પરિભ્રમણની અક્ષ એ શરીરની જડતાની મુખ્ય કેન્દ્રિય ધરી હોય ત્યારે.)

શક્ય હલનચલનનો સિદ્ધાંત અને ગતિશીલતાના સામાન્ય સમીકરણ.યાંત્રિક સિસ્ટમ પર લાદવામાં આવેલા જોડાણો. ભૌતિક બિંદુ અને યાંત્રિક સિસ્ટમની સંભવિત (અથવા વર્ચ્યુઅલ) હિલચાલ. સિસ્ટમની સ્વતંત્રતાની ડિગ્રીની સંખ્યા. આદર્શ જોડાણો. શક્ય હલનચલનનો સિદ્ધાંત. ગતિશીલતાનું સામાન્ય સમીકરણ.

સામાન્યકૃત કોઓર્ડિનેટ્સ (લેગ્રેન્જ સમીકરણો) માં સિસ્ટમની ગતિના સમીકરણો.સિસ્ટમના સામાન્યકૃત કોઓર્ડિનેટ્સ; સામાન્ય ગતિ. સામાન્યકૃત કોઓર્ડિનેટ્સમાં પ્રાથમિક કાર્યની અભિવ્યક્તિ. સામાન્યીકૃત દળો અને તેમની ગણતરી; સંભવિત સાથેના દળોનો કેસ. સામાન્યકૃત કોઓર્ડિનેટ્સમાં સિસ્ટમના સંતુલન માટેની શરતો. સામાન્યકૃત કોઓર્ડિનેટ્સ અથવા બીજા પ્રકારના લેગ્રેન્જ સમીકરણોમાં સિસ્ટમની ગતિના વિભેદક સમીકરણો. સંભવિત દળોના કિસ્સામાં લેગ્રેન્જ સમીકરણો; લેગ્રેન્જ ફંક્શન (કાઇનેટિક સંભવિત).

સંતુલન સ્થિરતાનો ખ્યાલ. સિસ્ટમના સ્થિર સંતુલનની સ્થિતિ અને તેમના ગુણધર્મોની નજીક એક ડિગ્રી સ્વતંત્રતા સાથે યાંત્રિક સિસ્ટમના નાના મુક્ત કંપનો.

અસર સિદ્ધાંતના તત્વો.અસરની ઘટના. પ્રભાવ બળ અને અસર આવેગ. ભૌતિક બિંદુ પર અસર બળની ક્રિયા. અસર પર યાંત્રિક સિસ્ટમના વેગમાં ફેરફાર પર પ્રમેય. સ્થિર સપાટી પર શરીરની સીધી કેન્દ્રિય અસર; સ્થિતિસ્થાપક અને સ્થિતિસ્થાપક અસરો. અસર પુનઃપ્રાપ્તિ ગુણાંક અને તેના પ્રાયોગિક નિર્ધારણ. બે સંસ્થાઓની સીધી કેન્દ્રીય અસર. કાર્નોટનું પ્રમેય.

ગ્રંથસૂચિ

પાયાની

બ્યુટેનિન એન.વી., લન્ટ્સ યા-એલ., મર્કિન ડી.આર.સૈદ્ધાંતિક મિકેનિક્સનો કોર્સ. T. 1, 2. M., 1985 અને અગાઉની આવૃત્તિઓ.

ડોબ્રોનરોવોવ વી.વી., નિકિટિન એન.એન.સૈદ્ધાંતિક મિકેનિક્સનો કોર્સ. એમ., 1983.

સ્ટાર્ઝિન્સ્કી વી. એમ.સૈદ્ધાંતિક મિકેનિક્સ. એમ., 1980.

ટાર્ગ એસ. એમ.સૈદ્ધાંતિક મિકેનિક્સનો ટૂંકો અભ્યાસક્રમ. એમ., 1986 અને અગાઉની આવૃત્તિઓ.

યાબ્લોન્સ્કી એ.એ., નિકિફોરોવા વી. એમ.સૈદ્ધાંતિક મિકેનિક્સનો કોર્સ. ભાગ 1. એમ., 1984 અને અગાઉની આવૃત્તિઓ.

યબ્લોન્સ્કી એ. એ.સૈદ્ધાંતિક મિકેનિક્સનો કોર્સ. ભાગ 2. એમ., 1984 અને અગાઉની આવૃત્તિઓ.

મેશેરસ્કી આઇ. વી.સૈદ્ધાંતિક મિકેનિક્સ પર સમસ્યાઓનો સંગ્રહ. એમ., 1986 અને અગાઉની આવૃત્તિઓ.

સૈદ્ધાંતિક મિકેનિક્સ/Ed પર સમસ્યાઓનો સંગ્રહ. કે.એસ. કોલેસ્નિકોવા. એમ., 1983.

વધારાનુ

બેટ M. I., Dzhanelidze G. Yu., Kelzon A. S.ઉદાહરણો અને સમસ્યાઓમાં સૈદ્ધાંતિક મિકેનિક્સ. ભાગો 1, 2. M., 1984 અને અગાઉની આવૃત્તિઓ.

સૈદ્ધાંતિક મિકેનિક્સ/5razhnichen/so પર સમસ્યાઓનો સંગ્રહ N. A., કાન V. L., Mintzberg B. L.અને અન્ય., 1987.

નોવોઝિલોવ આઇ.વી., ઝત્સેપિન એમ. એફ.સૈદ્ધાંતિક મિકેનિક્સમાં સામાન્ય કમ્પ્યુટર-આધારિત ગણતરીઓ. એમ., 1986,

સૈદ્ધાંતિક મિકેનિક્સ / એડમાં અભ્યાસક્રમ માટે સોંપણીઓનો સંગ્રહ. એ. એ. યાબ્લોન્સ્કી. એમ., 1985 અને અગાઉની આવૃત્તિઓ (સમસ્યા ઉકેલવાના ઉદાહરણો સમાવે છે).