પંક્તિઓ (સ્તંભો). કેટલીક પંક્તિઓ (કૉલમ્સ)ને રેખીય રીતે સ્વતંત્ર કહેવામાં આવે છે જો તેમાંથી કોઈ પણ અન્યની દ્રષ્ટિએ રેખીય રીતે વ્યક્ત કરી શકાતી નથી. પંક્તિ સિસ્ટમનો ક્રમ હંમેશા કૉલમ સિસ્ટમના ક્રમ સમાન હોય છે, અને આ સંખ્યાને મેટ્રિક્સનો ક્રમ કહેવામાં આવે છે.
મેટ્રિક્સનો ક્રમ આ મેટ્રિક્સના તમામ સંભવિત બિન-શૂન્ય સગીરોના ઓર્ડરમાં સર્વોચ્ચ છે. કોઈપણ કદના શૂન્ય મેટ્રિક્સનો ક્રમ શૂન્ય છે. જો બીજા ક્રમના તમામ સગીર શૂન્ય છે, તો પછી રેન્ક એક છે, વગેરે.
મેટ્રિક્સ રેન્ક - છબીનું પરિમાણ મંદ (im (A)) (\displaystyle \dim(\operatorname (im) (A)))રેખીય ઓપરેટર કે જેને મેટ્રિક્સ અનુરૂપ છે.
સામાન્ય રીતે મેટ્રિક્સનો ક્રમ A (\Displaystyle A)દ્વારા સૂચિત રંગ A (\displaystyle \operatorname (rang) A), r A (\displaystyle \operatorname (r) A), rg A (\displaystyle \operatorname (rg) A)અથવા રેન્ક A (\Displaystyle \operatorname (rank) A). છેલ્લો વિકલ્પ અંગ્રેજી ભાષા માટે લાક્ષણિક છે, જ્યારે પ્રથમ બે જર્મન, ફ્રેન્ચ અને અન્ય ઘણી ભાષાઓ માટે છે.
જ્ઞાનકોશીય YouTube
-
1 / 5
ચાલો એક લંબચોરસ મેટ્રિક્સ હોઈએ.
પછી, વ્યાખ્યા દ્વારા, મેટ્રિક્સનો ક્રમ A (\Displaystyle A)છે:
પ્રમેય (રેન્ક નક્કી કરવાની શુદ્ધતા વિશે).મેટ્રિક્સના તમામ સગીરોને દો A m × n (\Displaystyle A_(m\times n))ઓર્ડર k (\ ડિસ્પ્લેસ્ટાઇલ k)શૂન્ય સમાન છે ( M k = 0 (\ displaystyle M_(k)=0)). પછી ∀ M k + 1 = 0 (\displaystyle \forall M_(k+1)=0), જો તેઓ અસ્તિત્વમાં છે.
સંબંધિત વ્યાખ્યાઓ
ગુણધર્મો
- પ્રમેય (આધારિત નાના વિશે):દો r = રંગ A , M r (\displaystyle r=\operatorname (rang) A,M_(r))- મેટ્રિક્સના બેઝિસ માઇનોર A (\Displaystyle A), પછી:
- પરિણામો:
- પ્રમેય (પ્રાથમિક રૂપાંતરણો હેઠળ ક્રમના વિચલન વિશે):ચાલો પ્રાથમિક રૂપાંતરણો દ્વારા એકબીજા પાસેથી મેળવેલા મેટ્રિસિસ માટે સંકેત રજૂ કરીએ. પછી નીચેનું વિધાન સાચું છે: જો A ∼ B (\Displaystyle A\sim B), તો તેમની રેન્ક સમાન છે.
- ક્રોનેકર-કેપેલી પ્રમેય:રેખીય બીજગણિત સમીકરણોની સિસ્ટમ સુસંગત છે જો અને માત્ર જો તેના મુખ્ય મેટ્રિક્સનો ક્રમ તેના વિસ્તૃત મેટ્રિક્સના ક્રમની સમાન હોય. વિશેષ રીતે:
- સિસ્ટમના મુખ્ય ચલોની સંખ્યા સિસ્ટમના રેન્ક જેટલી છે.
- એક સુસંગત સિસ્ટમ વ્યાખ્યાયિત કરવામાં આવશે (તેનું સોલ્યુશન અનન્ય છે) જો સિસ્ટમની રેન્ક તેના તમામ ચલોની સંખ્યા જેટલી હોય.
- સિલ્વેસ્ટરની અસમાનતા:જો એઅને બીમાપ મેટ્રિસિસ m x nઅને n x k, તે
આ નીચેની અસમાનતાનો ખાસ કિસ્સો છે.
- ફ્રોબેનિયસની અસમાનતા:જો AB, BC, ABC યોગ્ય રીતે વ્યાખ્યાયિત કરવામાં આવે તો
લીનિયર ટ્રાન્સફોર્મેશન અને મેટ્રિક્સ રેન્ક
દો A (\Displaystyle A)- માપ મેટ્રિક્સ m × n (\displaystyle m\times n)મેદાનની ઉપર C (\Displaystyle C)(અથવા R (\ ડિસ્પ્લેસ્ટાઇલ R)). દો T (\Displaystyle T)- અનુરૂપ રેખીય પરિવર્તન A (\Displaystyle A)પ્રમાણભૂત ધોરણે; તેનો અર્થ એ છે કે T (x) = A x (\displaystyle T(x)=Ax). મેટ્રિક્સ રેન્ક A (\Displaystyle A) પરિવર્તન શ્રેણીનું પરિમાણ છે T (\Displaystyle T).
પદ્ધતિઓ
મેટ્રિક્સનો ક્રમ શોધવા માટે ઘણી પદ્ધતિઓ છે:
- પ્રાથમિક પરિવર્તન પદ્ધતિ
- સગીરોની સરહદની પદ્ધતિ
અમે વિષયની એક મહત્વપૂર્ણ વ્યવહારિક એપ્લિકેશનને પણ ધ્યાનમાં લઈશું: સુસંગતતા માટે રેખીય સમીકરણોની સિસ્ટમનો અભ્યાસ.
મેટ્રિક્સનો ક્રમ શું છે?
લેખના રમૂજી એપિગ્રાફમાં સત્યનો મોટો જથ્થો છે. અમે સામાન્ય રીતે "રેન્ક" શબ્દને અમુક પ્રકારની વંશવેલો સાથે જોડીએ છીએ, મોટેભાગે કારકિર્દીની સીડી સાથે. વ્યક્તિ પાસે જેટલું વધુ જ્ઞાન, અનુભવ, ક્ષમતાઓ, જોડાણો વગેરે છે. - તેની સ્થિતિ અને તકોની શ્રેણી જેટલી ઊંચી છે. યુવાની દ્રષ્ટિએ, રેન્ક એ "ઊભાપણું" ની સામાન્ય ડિગ્રીનો સંદર્ભ આપે છે.
અને આપણા ગાણિતિક ભાઈઓ સમાન સિદ્ધાંતો પર જીવે છે. ચાલો થોડા રેન્ડમને વોક માટે લઈએ શૂન્ય મેટ્રિસિસ:
ચાલો તેના વિશે વિચારીએ, જો મેટ્રિક્સમાં બધા શૂન્ય, તો પછી આપણે કયા રેન્ક વિશે વાત કરી શકીએ? દરેક વ્યક્તિ "કુલ શૂન્ય" અનૌપચારિક અભિવ્યક્તિથી પરિચિત છે. મેટ્રિસિસના સમાજમાં બધું બરાબર સમાન છે:
શૂન્ય મેટ્રિક્સનો ક્રમકોઈપણ કદ શૂન્ય બરાબર છે.
નૉૅધ : શૂન્ય મેટ્રિક્સ ગ્રીક અક્ષર "થીટા" દ્વારા સૂચવવામાં આવે છે
મેટ્રિક્સના ક્રમને વધુ સારી રીતે સમજવા માટે, હવે પછી હું મદદ કરવા માટે સામગ્રીનો ઉપયોગ કરીશ વિશ્લેષણાત્મક ભૂમિતિ. શૂન્ય ધ્યાનમાં લો વેક્ટરઆપણી ત્રિ-પરિમાણીય જગ્યા, જે કોઈ ચોક્કસ દિશા નિર્ધારિત કરતી નથી અને નિર્માણ માટે નકામી છે affine આધાર. બીજગણિતીય દૃષ્ટિકોણથી, આ વેક્ટરના કોઓર્ડિનેટ્સ લખેલા છે મેટ્રિક્સ"એક બાય ત્રણ" અને તાર્કિક (સૂચિત ભૌમિતિક અર્થમાં)ધારો કે આ મેટ્રિક્સનો ક્રમ શૂન્ય છે.
હવે ચાલો થોડા જોઈએ બિન-શૂન્ય કૉલમ વેક્ટરઅને પંક્તિ વેક્ટર:
દરેક ઉદાહરણમાં ઓછામાં ઓછું એક બિન-શૂન્ય તત્વ હોય છે, અને તે કંઈક છે!કોઈપણ બિન-શૂન્ય પંક્તિ વેક્ટર (કૉલમ વેક્ટર) નો રેન્ક એક સમાન છે
અને સામાન્ય રીતે કહીએ તો - જો મેટ્રિક્સમાં હોય મનસ્વી કદત્યાં ઓછામાં ઓછું એક બિન-શૂન્ય તત્વ છે, પછી તેનો ક્રમ ઓછું નહીંએકમો.
બીજગણિત પંક્તિ વેક્ટર અને કૉલમ વેક્ટર અમુક હદ સુધી અમૂર્ત છે, તેથી ચાલો ફરીથી ભૌમિતિક જોડાણ તરફ વળીએ. બિન-શૂન્ય વેક્ટરઅવકાશમાં ખૂબ જ ચોક્કસ દિશા નિર્ધારિત કરે છે અને બાંધકામ માટે યોગ્ય છે આધાર, તેથી મેટ્રિક્સનો ક્રમ એક સમાન ગણવામાં આવશે.
સૈદ્ધાંતિક માહિતી : રેખીય બીજગણિતમાં, વેક્ટર એ વેક્ટર સ્પેસનું એક તત્વ છે (8 સ્વયંસિદ્ધ દ્વારા વ્યાખ્યાયિત), જે, ખાસ કરીને, વાસ્તવિક સંખ્યાઓની ક્રમાંકિત પંક્તિ (અથવા કૉલમ) રજૂ કરી શકે છે જેમાં વાસ્તવિક સંખ્યા દ્વારા સરવાળો અને ગુણાકારની ક્રિયાઓ કરવામાં આવે છે. તેમને માટે. વેક્ટર વિશે વધુ વિગતવાર માહિતી લેખમાં મળી શકે છે રેખીય પરિવર્તનો.
રેખીય રીતે નિર્ભર(એકબીજા દ્વારા વ્યક્ત). ભૌમિતિક દૃષ્ટિકોણથી, બીજી લાઇનમાં કોલિનિયર વેક્ટરના કોઓર્ડિનેટ્સ છે
, જે આ બાબતને બિલ્ડીંગમાં બિલકુલ આગળ વધારી ન હતી ત્રિ-પરિમાણીય આધાર, આ અર્થમાં અનાવશ્યક છે. આમ, આ મેટ્રિક્સનો ક્રમ પણ એક સમાન છે.ચાલો વેક્ટરના કોઓર્ડિનેટ્સને કૉલમમાં ફરીથી લખીએ ( મેટ્રિક્સ સ્થાનાંતરિત કરો):
ક્રમની દ્રષ્ટિએ શું બદલાયું છે? કંઈ નહીં. કૉલમ પ્રમાણસર છે, જેનો અર્થ છે કે ક્રમ એક સમાન છે. માર્ગ દ્વારા, નોંધ કરો કે ત્રણેય રેખાઓ પણ પ્રમાણસર છે. તેઓ કોઓર્ડિનેટ્સ દ્વારા ઓળખી શકાય છે ત્રણપ્લેનના સમરેખા વેક્ટર, જેમાંથી માત્ર એક"ફ્લેટ" આધાર બાંધવા માટે ઉપયોગી. અને આ અમારી ક્રમની ભૌમિતિક સમજ સાથે સંપૂર્ણપણે સુસંગત છે.
ઉપરના ઉદાહરણમાંથી એક મહત્વપૂર્ણ નિવેદન નીચે મુજબ છે:
પંક્તિઓમાં મેટ્રિક્સનો ક્રમ કૉલમમાંના મેટ્રિક્સના ક્રમ જેટલો છે. મેં પહેલેથી જ અસરકારક વિશેના પાઠમાં આનો થોડો ઉલ્લેખ કર્યો છે નિર્ણાયકની ગણતરી માટેની પદ્ધતિઓ.
નૉૅધ : પંક્તિઓની રેખીય અવલંબન એ સ્તંભોની રેખીય અવલંબન (અને ઊલટું) સૂચવે છે. પરંતુ સમય બચાવવા માટે, અને આદતની બહાર, હું લગભગ હંમેશા શબ્દમાળાઓની રેખીય અવલંબન વિશે વાત કરીશ.
ચાલો આપણા પ્રિય પાલતુને તાલીમ આપવાનું ચાલુ રાખીએ. ચાલો ત્રીજી પંક્તિના મેટ્રિક્સમાં બીજા કોલિનિયર વેક્ટરના કોઓર્ડિનેટ્સ ઉમેરીએ
:
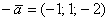શું તેમણે ત્રિ-પરિમાણીય આધાર બાંધવામાં અમને મદદ કરી? અલબત્ત નહીં. ત્રણેય વેક્ટર એક જ પાથ પર આગળ પાછળ ચાલે છે અને મેટ્રિક્સનો ક્રમ એક સમાન છે. તમે ગમે તેટલા કોલિનિયર વેક્ટર લઈ શકો છો, કહો, 100, તેમના કોઓર્ડિનેટ્સને “એકસો બાય ત્રણ” મેટ્રિક્સમાં મૂકો, અને આવા ગગનચુંબી ઈમારતનો ક્રમ હજુ પણ એક જ રહેશે.
ચાલો મેટ્રિક્સથી પરિચિત થઈએ, જેની પંક્તિઓ રેખીય રીતે સ્વતંત્ર. ત્રિ-પરિમાણીય આધાર બાંધવા માટે બિન-કોલિનિયર વેક્ટરની જોડી યોગ્ય છે. આ મેટ્રિક્સનો ક્રમ બે છે.
મેટ્રિક્સનો ક્રમ શું છે? રેખાઓ પ્રમાણસર નથી લાગતી... તેથી, સિદ્ધાંતમાં, તે ત્રણ છે. જો કે, આ મેટ્રિક્સનો રેન્ક પણ બે છે. મેં પ્રથમ બે લીટીઓ ઉમેરી અને પરિણામ તળિયે લખ્યું, એટલે કે. રેખીય રીતે વ્યક્તપ્રથમ બે મારફતે ત્રીજી લાઇન. ભૌમિતિક રીતે, મેટ્રિક્સની પંક્તિઓ ત્રણના કોઓર્ડિનેટ્સને અનુરૂપ છે કોપ્લાનર વેક્ટર, અને આ ત્રણ વચ્ચે નોન-કોલિનિયર સાથીઓની જોડી છે.
જેમ તમે જોઈ શકો છો, રેખીય અવલંબનમાનવામાં આવેલ મેટ્રિક્સમાં સ્પષ્ટ નથી, અને આજે આપણે તેને ખુલ્લામાં કેવી રીતે લાવવું તે શીખીશું.
મને લાગે છે કે ઘણા લોકો અનુમાન કરી શકે છે કે મેટ્રિક્સનો રેન્ક શું છે!
એક મેટ્રિક્સનો વિચાર કરો જેની પંક્તિઓ રેખીય રીતે સ્વતંત્ર. વેક્ટર રચે છે affine આધાર, અને આ મેટ્રિક્સનો ક્રમ ત્રણ છે.
જેમ તમે જાણો છો, ત્રિ-પરિમાણીય અવકાશનો કોઈપણ ચોથો, પાંચમો, દસમો વેક્ટર આધાર વેક્ટરની દ્રષ્ટિએ રેખીય રીતે વ્યક્ત કરવામાં આવશે. તેથી, જો તમે મેટ્રિક્સમાં કોઈપણ સંખ્યાની પંક્તિઓ ઉમેરો છો, તો તેનો ક્રમ હજુ ત્રણ બરાબર હશે.
સમાન તર્ક મોટા કદના મેટ્રિસિસ માટે હાથ ધરવામાં આવી શકે છે (અલબત્ત, કોઈપણ ભૌમિતિક અર્થ વિના).
વ્યાખ્યા : મેટ્રિક્સનો ક્રમ એ રેખીય રીતે સ્વતંત્ર પંક્તિઓની મહત્તમ સંખ્યા છે. અથવા: મેટ્રિક્સનો ક્રમ એ રેખીય રીતે સ્વતંત્ર કૉલમ્સની મહત્તમ સંખ્યા છે. હા, તેમની સંખ્યા હંમેશા સમાન હોય છે.
ઉપરોક્તમાંથી એક મહત્વપૂર્ણ વ્યવહારુ માર્ગદર્શિકા પણ અનુસરે છે: મેટ્રિક્સનો ક્રમ તેના ન્યૂનતમ પરિમાણ કરતાં વધી જતો નથી. ઉદાહરણ તરીકે, મેટ્રિક્સમાં
ચાર પંક્તિઓ અને પાંચ કૉલમ. ન્યૂનતમ પરિમાણ ચાર છે, તેથી, આ મેટ્રિક્સનો ક્રમ ચોક્કસપણે 4 કરતાં વધી જશે નહીં.હોદ્દો: વિશ્વ સિદ્ધાંત અને વ્યવહારમાં મેટ્રિક્સના રેન્કને નિયુક્ત કરવા માટે સામાન્ય રીતે સ્વીકૃત ધોરણો નથી: - જેમ તેઓ કહે છે, એક અંગ્રેજ એક વસ્તુ લખે છે, એક જર્મન બીજી. તેથી, અમેરિકન અને રશિયન નરક વિશેના પ્રખ્યાત મજાકના આધારે, ચાલો મૂળ શબ્દ સાથે મેટ્રિક્સનો ક્રમ સૂચવીએ. દાખ્લા તરીકે: . અને જો મેટ્રિક્સ "અનામી" છે, જેમાંથી ઘણા છે, તો તમે ખાલી લખી શકો છો.
સગીરોનો ઉપયોગ કરીને મેટ્રિક્સનો રેન્ક કેવી રીતે શોધવો?
જો મારી દાદી પાસે તેના મેટ્રિક્સમાં પાંચમી કૉલમ હોય, તો તેણે 4ઠ્ઠા ક્રમના બીજા નાનાની ગણતરી કરવી પડશે ("વાદળી", "રાસ્પબેરી" + 5મી કૉલમ).
નિષ્કર્ષ: બિન-શૂન્ય સગીરનો મહત્તમ ક્રમ ત્રણ છે, જેનો અર્થ થાય છે.
કદાચ દરેક વ્યક્તિએ આ વાક્યને સંપૂર્ણ રીતે સમજી શક્યું નથી: 4 થી ક્રમનો સગીર શૂન્ય સમાન છે, પરંતુ 3જા ક્રમના સગીરોમાં એક બિન-શૂન્ય હતો - તેથી મહત્તમ ક્રમ બિન-શૂન્યનાના અને ત્રણ બરાબર.
પ્રશ્ન એ ઊભો થાય છે કે શા માટે તરત જ નિર્ધારકની ગણતરી કરવામાં આવતી નથી? સારું, પ્રથમ, મોટાભાગના કાર્યોમાં મેટ્રિક્સ ચોરસ હોતું નથી, અને બીજું, જો તમને બિન-શૂન્ય મૂલ્ય મળે તો પણ, કાર્ય મોટે ભાગે નકારવામાં આવશે, કારણ કે તેમાં સામાન્ય રીતે પ્રમાણભૂત "બોટમ-અપ" સોલ્યુશન શામેલ હોય છે. અને ધ્યાનમાં લેવાયેલા ઉદાહરણમાં, 4 થી ક્રમનો શૂન્ય નિર્ણાયક અમને જણાવવા દે છે કે મેટ્રિક્સનો ક્રમ માત્ર ચાર કરતા ઓછો છે.
મારે કબૂલ કરવું જ પડશે, સગીરોની સરહદની પદ્ધતિને વધુ સારી રીતે સમજાવવા માટે મેં મારી જાતનું વિશ્લેષણ કર્યું તે સમસ્યા સાથે હું આવ્યો છું. વાસ્તવિક વ્યવહારમાં, બધું સરળ છે:
ઉદાહરણ 2
એજ માઇનર્સ પદ્ધતિનો ઉપયોગ કરીને મેટ્રિક્સનો ક્રમ શોધો
ઉકેલ અને જવાબ પાઠના અંતે છે.
અલ્ગોરિધમ ક્યારે સૌથી ઝડપી કામ કરે છે? ચાલો એ જ ચાર-બાય-ચાર મેટ્રિક્સ પર પાછા ફરીએ.
. દેખીતી રીતે, "સારા" ના કિસ્સામાં ઉકેલ સૌથી ટૂંકો હશે ખૂણે સગીરો: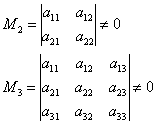
અને, જો, પછી, અન્યથા - .
વિચારસરણી બિલકુલ કાલ્પનિક નથી - એવા ઘણા ઉદાહરણો છે જ્યાં સમગ્ર બાબત માત્ર કોણીય સગીરો સુધી મર્યાદિત છે.
જો કે, કેટલાક કિસ્સાઓમાં બીજી પદ્ધતિ વધુ અસરકારક અને પ્રાધાન્યક્ષમ છે:
ગૌસીયન પદ્ધતિનો ઉપયોગ કરીને મેટ્રિક્સનો ક્રમ કેવી રીતે શોધવો?
ફકરો એવા વાચકો માટે બનાવાયેલ છે જેઓ પહેલેથી જ પરિચિત છે ગૌસીયન પદ્ધતિઅને વધુ કે ઓછા તેના પર હાથ મેળવ્યો.
તકનીકી દૃષ્ટિકોણથી, પદ્ધતિ નવલકથા નથી:
1) પ્રાથમિક રૂપાંતરણોનો ઉપયોગ કરીને, અમે મેટ્રિક્સને સ્ટેપવાઇઝ ફોર્મમાં ઘટાડીએ છીએ;
2) મેટ્રિક્સની રેન્ક પંક્તિઓની સંખ્યા જેટલી છે.
તે એકદમ સ્પષ્ટ છે કે ગૌસીયન પદ્ધતિનો ઉપયોગ કરવાથી મેટ્રિક્સનો ક્રમ બદલાતો નથી, અને અહીં સાર અત્યંત સરળ છે: અલ્ગોરિધમ મુજબ, પ્રાથમિક પરિવર્તન દરમિયાન, બધી બિનજરૂરી પ્રમાણસર (રેખીય રીતે આધારિત) પંક્તિઓ ઓળખવામાં આવે છે અને દૂર કરવામાં આવે છે, પરિણામે "શુષ્ક અવશેષ" - રેખીય સ્વતંત્ર પંક્તિઓની મહત્તમ સંખ્યા.
ચાલો જૂના પરિચિત મેટ્રિક્સને ત્રણ કોલિનિયર વેક્ટરના કોઓર્ડિનેટ્સ સાથે રૂપાંતરિત કરીએ:
(1) પ્રથમ લીટી બીજી લીટીમાં ઉમેરવામાં આવી હતી, તેને –2 વડે ગુણાકાર કરવામાં આવ્યો હતો. પ્રથમ લાઇન ત્રીજી લાઇનમાં ઉમેરવામાં આવી હતી.
(2) શૂન્ય રેખાઓ દૂર કરવામાં આવે છે.
આમ, એક લીટી બાકી છે, તેથી. કહેવાની જરૂર નથી, આ 2જી ક્રમના નવ શૂન્ય સગીરોની ગણતરી કરવા અને પછી જ નિષ્કર્ષ દોરવા કરતાં વધુ ઝડપી છે.
હું તમને તે પોતે જ યાદ કરાવું છું બીજગણિત મેટ્રિક્સકંઈપણ બદલી શકાતું નથી, અને પરિવર્તન ફક્ત રેન્ક નક્કી કરવાના હેતુ માટે કરવામાં આવે છે! માર્ગ દ્વારા, ચાલો ફરી એકવાર પ્રશ્ન પર ધ્યાન આપીએ, કેમ નહીં? સ્ત્રોત મેટ્રિક્સ
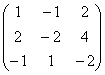મેટ્રિક્સ અને પંક્તિની માહિતીથી મૂળભૂત રીતે અલગ હોય તેવી માહિતી વહન કરે છે. કેટલાક ગાણિતિક મોડેલોમાં (કોઈ અતિશયોક્તિ નથી), એક નંબરમાં તફાવત જીવન અને મૃત્યુની બાબત હોઈ શકે છે. ...મને પ્રાથમિક અને માધ્યમિક શાળાના ગણિતના શિક્ષકો યાદ આવ્યા જેમણે અલ્ગોરિધમમાંથી સહેજ અચોક્કસતા અથવા વિચલન માટે નિર્દયતાથી ગ્રેડમાં 1-2 પોઇન્ટનો ઘટાડો કર્યો હતો. અને તે ખૂબ જ નિરાશાજનક હતું જ્યારે, દેખીતી રીતે બાંયધરીકૃત "A" ને બદલે, તે "સારું" અથવા તો ખરાબ બન્યું. સમજણ ઘણી પાછળથી આવી - આપણે ઉપગ્રહો, પરમાણુ શસ્ત્રો અને પાવર પ્લાન્ટ્સ મનુષ્યને કેવી રીતે સોંપી શકીએ? પરંતુ ચિંતા કરશો નહીં, હું આ વિસ્તારોમાં કામ કરતો નથી =)ચાલો વધુ અર્થપૂર્ણ કાર્યો તરફ આગળ વધીએ, જ્યાં, અન્ય વસ્તુઓની સાથે, આપણે મહત્વપૂર્ણ કોમ્પ્યુટેશનલ તકનીકોથી પરિચિત થઈશું. ગૌસ પદ્ધતિ:
ઉદાહરણ 3
પ્રાથમિક પરિવર્તનનો ઉપયોગ કરીને મેટ્રિક્સનો ક્રમ શોધો
ઉકેલ: એક "ચાર બાય પાંચ" મેટ્રિક્સ આપવામાં આવે છે, જેનો અર્થ છે કે તેની રેન્ક ચોક્કસપણે 4 કરતાં વધુ નથી.
પ્રથમ કૉલમમાં, ત્યાં કોઈ 1 અથવા -1 નથી, તેથી, ઓછામાં ઓછું એક એકમ મેળવવા માટે વધારાની ક્રિયાઓ જરૂરી છે. સાઇટના અસ્તિત્વ દરમિયાન, મને વારંવાર પ્રશ્ન પૂછવામાં આવ્યો છે: "શું પ્રાથમિક પરિવર્તન દરમિયાન કૉલમ ફરીથી ગોઠવવાનું શક્ય છે?" અહીં, અમે પ્રથમ અને બીજી કૉલમ ફરીથી ગોઠવી છે, અને બધું સારું છે! મોટા ભાગના કાર્યોમાં જ્યાં તેનો ઉપયોગ થાય છે ગૌસીયન પદ્ધતિ, કૉલમ ખરેખર ફરીથી ગોઠવી શકાય છે. પરંતુ જરૂર નથી. અને મુદ્દો ચલો સાથે સંભવિત મૂંઝવણમાં પણ નથી, મુદ્દો એ છે કે ઉચ્ચ ગણિતના શાસ્ત્રીય અભ્યાસક્રમમાં આ ક્રિયા પરંપરાગત રીતે ધ્યાનમાં લેવામાં આવતી નથી, તેથી આવી હકારને ખૂબ જ કુટિલ રીતે જોવામાં આવશે (અથવા બધું ફરીથી કરવાની ફરજ પાડવામાં આવશે).
બીજો મુદ્દો નંબરોથી સંબંધિત છે. જ્યારે તમે તમારો નિર્ણય લો છો, ત્યારે નીચેના અંગૂઠાના નિયમનો ઉપયોગ કરવો મદદરૂપ છે: પ્રાથમિક પરિવર્તન, જો શક્ય હોય તો, મેટ્રિક્સ નંબરો ઘટાડવો જોઈએ. છેવટે, એક, બે, ત્રણ કરતાં, ઉદાહરણ તરીકે, 23, 45 અને 97 સાથે કામ કરવું ખૂબ સરળ છે. અને પ્રથમ ક્રિયાનો હેતુ ફક્ત પ્રથમ કૉલમમાં એક મેળવવા માટે જ નહીં, પણ સંખ્યાઓને દૂર કરવાનો પણ છે. 7 અને 11.
પ્રથમ સંપૂર્ણ ઉકેલ, પછી ટિપ્પણીઓ:
(1) પ્રથમ લીટી બીજી લીટીમાં ઉમેરવામાં આવી હતી, તેને –2 વડે ગુણાકાર કરવામાં આવ્યો હતો. પ્રથમ લીટી ત્રીજી લીટીમાં ઉમેરવામાં આવી હતી, તેને –3 વડે ગુણાકાર કરવામાં આવ્યો હતો. અને ઢગલા પર: 1 લી લીટી 4 થી લીટીમાં ઉમેરવામાં આવી હતી, -1 દ્વારા ગુણાકાર કરવામાં આવ્યો હતો.
(2) છેલ્લી ત્રણ લીટીઓ પ્રમાણસર છે. 3 જી અને 4 થી લાઇન દૂર કરવામાં આવી હતી, બીજી લાઇન પ્રથમ સ્થાને ખસેડવામાં આવી હતી.
(3) પ્રથમ લીટી બીજી લીટીમાં ઉમેરવામાં આવી હતી, તેને –3 વડે ગુણાકાર કરવામાં આવ્યો હતો.
એચેલોન સ્વરૂપમાં ઘટાડાવામાં આવેલ મેટ્રિક્સમાં બે પંક્તિઓ છે.
જવાબ આપો:
હવે ચાર-બાય-ચાર મેટ્રિક્સને ત્રાસ આપવાનો તમારો વારો છે:
ઉદાહરણ 4
ગૌસીયન પદ્ધતિનો ઉપયોગ કરીને મેટ્રિક્સનો ક્રમ શોધો
હું તમને તે યાદ કરાવું છું ગૌસીયન પદ્ધતિઅસ્પષ્ટ કઠોરતા સૂચિત કરતું નથી, અને તમારો નિર્ણય મોટે ભાગે મારા નિર્ણયથી અલગ હશે. પાઠના અંતે કાર્યનું સંક્ષિપ્ત ઉદાહરણ.
મેટ્રિક્સનો રેન્ક શોધવા માટે મારે કઈ પદ્ધતિનો ઉપયોગ કરવો જોઈએ?
વ્યવહારમાં, તે ઘણીવાર જણાવવામાં આવતું નથી કે રેન્ક શોધવા માટે કઈ પદ્ધતિનો ઉપયોગ કરવો જોઈએ. આવી પરિસ્થિતિમાં, સ્થિતિનું વિશ્લેષણ કરવું જોઈએ - કેટલાક મેટ્રિસિસ માટે તે સગીરો દ્વારા ઉકેલવા માટે વધુ તર્કસંગત છે, જ્યારે અન્ય લોકો માટે તે પ્રાથમિક પરિવર્તન લાગુ કરવા માટે વધુ નફાકારક છે:
ઉદાહરણ 5
મેટ્રિક્સનો ક્રમ શોધો
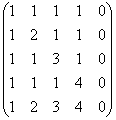
ઉકેલ: પ્રથમ પદ્ધતિ કોઈક રીતે તરત જ અદૃશ્ય થઈ જાય છે =)
થોડું ઊંચું, મેં મેટ્રિક્સના કૉલમ્સને સ્પર્શ ન કરવાની સલાહ આપી, પરંતુ જ્યારે શૂન્ય કૉલમ હોય, અથવા પ્રમાણસર/સંયોજક કૉલમ હોય, તો તે હજી પણ કાપવા યોગ્ય છે:
(1) પાંચમી કૉલમ શૂન્ય છે, તેને મેટ્રિક્સમાંથી દૂર કરો. આમ, મેટ્રિક્સનો ક્રમ ચાર કરતા વધુ નથી. પ્રથમ લીટીને –1 વડે ગુણાકાર કરવામાં આવ્યો હતો. ગૌસ પદ્ધતિની આ બીજી સહી વિશેષતા છે, જે નીચેની ક્રિયાને સુખદ ચાલમાં ફેરવે છે:
(2) બધી લીટીઓમાં, બીજીથી શરૂ કરીને, પ્રથમ લીટી ઉમેરવામાં આવી હતી.
(3) પ્રથમ લીટીને –1 વડે ગુણાકાર કરવામાં આવી હતી, ત્રીજી લીટીને 2 વડે ભાગવામાં આવી હતી, ચોથી લીટીને 3 વડે ભાગવામાં આવી હતી. બીજી લીટીને –1 વડે ગુણાકાર કરીને પાંચમી લીટીમાં ઉમેરવામાં આવી હતી.
(4) ત્રીજી લીટી પાંચમી લીટીમાં ઉમેરવામાં આવી હતી, તેને –2 વડે ગુણાકાર કરવામાં આવ્યો હતો.
(5) છેલ્લી બે લીટીઓ પ્રમાણસર છે, પાંચમી કાઢી નાખવામાં આવી છે.
પરિણામ 4 લીટીઓ છે.
જવાબ આપો:
સ્વતંત્ર સંશોધન માટે માનક પાંચ માળની ઇમારત:
ઉદાહરણ 6
મેટ્રિક્સનો ક્રમ શોધો
પાઠના અંતે ટૂંકો ઉકેલ અને જવાબ.
એ નોંધવું જોઇએ કે "મેટ્રિક્સ રેન્ક" વાક્ય વ્યવહારમાં વારંવાર આવતું નથી, અને મોટાભાગની સમસ્યાઓમાં તમે તેના વિના સંપૂર્ણપણે કરી શકો છો. પરંતુ એક કાર્ય છે જ્યાં પ્રશ્નમાંનો ખ્યાલ મુખ્ય પાત્ર છે, અને અમે આ પ્રાયોગિક એપ્લિકેશનને જોઈને લેખને સમાપ્ત કરીશું:
સુસંગતતા માટે રેખીય સમીકરણોની સિસ્ટમનો અભ્યાસ કેવી રીતે કરવો?
ઘણીવાર, ઉકેલ ઉપરાંત રેખીય સમીકરણોની સિસ્ટમોશરત અનુસાર, સૌ પ્રથમ તેને સુસંગતતા માટે તપાસવું જરૂરી છે, એટલે કે, કોઈપણ ઉકેલ અસ્તિત્વમાં છે તે સાબિત કરવા માટે. દ્વારા આવા ચકાસણીમાં મુખ્ય ભૂમિકા ભજવવામાં આવે છે ક્રોનેકર-કેપેલી પ્રમેય, જે હું જરૂરી સ્વરૂપમાં ઘડીશ:
જો રેન્ક સિસ્ટમ મેટ્રિસિસક્રમ સમાન વિસ્તૃત મેટ્રિક્સ સિસ્ટમ, પછી સિસ્ટમ સુસંગત છે, અને જો આ સંખ્યા અજાણ્યાઓની સંખ્યા સાથે એકરુપ હોય, તો ઉકેલ અનન્ય છે.
આમ, સુસંગતતા માટે સિસ્ટમનો અભ્યાસ કરવા માટે સમાનતા તપાસવી જરૂરી છે
, ક્યાં - સિસ્ટમ મેટ્રિક્સ(પાઠમાંથી પરિભાષા યાદ રાખો ગૌસ પદ્ધતિ), એ - વિસ્તૃત સિસ્ટમ મેટ્રિક્સ(એટલે કે ચલોના ગુણાંક સાથેનો મેટ્રિક્સ + મફત શરતોનો કૉલમ).દરેક મેટ્રિક્સમાં, બે રેન્ક સંકળાયેલા હોઈ શકે છે: એક પંક્તિ ક્રમ (પંક્તિ સિસ્ટમનો ક્રમ) અને કૉલમ ક્રમ (કૉલમ સિસ્ટમનો ક્રમ).
પ્રમેય
મેટ્રિક્સની પંક્તિ રેન્ક તેના કૉલમ રેન્કની બરાબર છે.
મેટ્રિક્સ રેન્ક
વ્યાખ્યા
મેટ્રિક્સ રેન્ક$A$ એ તેની પંક્તિઓ અથવા કૉલમ્સની સિસ્ટમનો ક્રમ છે.
$\operatorname(rang) A$ દ્વારા સૂચિત
વ્યવહારમાં, મેટ્રિક્સનો ક્રમ શોધવા માટે, નીચેના વિધાનનો ઉપયોગ કરવામાં આવે છે: મેટ્રિક્સનો ક્રમ એચેલોન સ્વરૂપમાં મેટ્રિક્સને ઘટાડ્યા પછી બિન-શૂન્ય પંક્તિઓની સંખ્યા જેટલો હોય છે.
મેટ્રિક્સની પંક્તિઓ (સ્તંભો) પર પ્રાથમિક રૂપાંતરણો તેના ક્રમમાં ફેરફાર કરતા નથી.
સ્ટેપ મેટ્રિક્સનો ક્રમ તેની બિન-શૂન્ય પંક્તિઓની સંખ્યા જેટલો છે.
ઉદાહરણ
કસરત.મેટ્રિક્સ $ A=\left(\begin(array)(cccc)(0) અને (4) અને (10) અને (1) \\ (4) અને (8) અને (18) અને ( 7) \ \ (10) અને (18) અને (40) અને (17) \\ (1) અને (7) અને (17) અને (3)\અંત(એરે)\જમણે) $
ઉકેલ.તેની પંક્તિઓ પર પ્રાથમિક રૂપાંતરણોનો ઉપયોગ કરીને, અમે મેટ્રિક્સ $A$ ને એકલન સ્વરૂપમાં ઘટાડીએ છીએ. આ કરવા માટે, પ્રથમ ત્રીજી લાઇનમાંથી બીજા બે બાદબાકી કરો:
$$ A \sim \left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & (7) \\ (2) અને (2) અને (4) અને (3) \\ (1) અને (7) અને (17) અને (3)\અંત(એરે)\જમણે) $$
બીજી લીટીમાંથી આપણે ચોથી લીટીને બાદ કરીએ છીએ, 4 વડે ગુણાકાર કરીએ છીએ; ત્રીજા - બે ચોથામાંથી:
$$ A \sim \left(\begin(array)(rrrr)(0) & (4) & (10) & (1) \\ (0) & (-20) & (-50) & (-5) ) \\ (0) અને (-12) અને (-30) અને (-3) \\ (1) અને (7) અને (17) અને (3)\અંત(એરે)\જમણે) $$
અમે પ્રથમ પાંચને બીજી લાઇનમાં અને ત્રીજી ત્રણને ત્રીજી લાઇનમાં ઉમેરીએ છીએ:
$$ A \sim \left(\begin(array)(cccc)(0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) અને (0) અને (0) અને (0) \\ (1) અને (7) અને (17) અને (3)\અંત(એરે)\જમણે) $$
પ્રથમ અને બીજી લીટીઓ સ્વેપ કરો:
$$ A \sim \left(\begin(array)(cccc)(0) & (0) & (0) & (0) \\ (0) & (4) & (10) & (1) \\ (0) અને (0) અને (0) અને (0) \\ (1) અને (7) અને (17) અને (3)\અંત(એરે)\જમણે) $$
$$ A \sim \left(\begin(array)(cccc)(1) & (7) & (17) & (3) \\ (0) & (4) & (10) & (1) \\ (0) અને (0) અને (0) અને (0) \\ (0) અને (0) અને (0) અને (0)\અંત(એરે)\જમણે) \Rightarrow \operatorname(rang) A=2 $$
જવાબ આપો.$ \operatorname(rang) A=2 $
સગીરોની સરહદની પદ્ધતિ
મેટ્રિક્સનો ક્રમ શોધવા માટેની બીજી પદ્ધતિ આ પ્રમેય પર આધારિત છે - નાની ધારની પદ્ધતિ. આ પદ્ધતિનો સાર એ સગીરોને શોધવાનો છે, નીચલા ઓર્ડરથી શરૂ કરીને અને ઉચ્ચ લોકો તરફ જવાનું. જો $n$th ક્રમની સગીર શૂન્યની બરાબર ન હોય, અને $n+1$th ક્રમની તમામ સગીર શૂન્યની બરાબર હોય, તો મેટ્રિક્સનો ક્રમ $n$ ની બરાબર હશે.
ઉદાહરણ
કસરત.મેટ્રિક્સ $ A=\left(\begin(array)(rrrr)(1) & (2) & (-1) & (-2) \\ (2) & (4) & (3) નો ક્રમ શોધો & (0 ) \\ (-1) & (-2) & (6) & (6)\end(એરે)\right) $ માઇનોર એજિંગ પદ્ધતિનો ઉપયોગ કરીને.
ઉકેલ.ન્યૂનતમ ક્રમના સગીર એ પ્રથમ ક્રમના સગીર છે, જે મેટ્રિક્સ $A$ ના ઘટકો સમાન છે. ઉદાહરણ તરીકે, નાના $ M_(1)=1 \neq 0 $ ને ધ્યાનમાં લો. પ્રથમ પંક્તિ અને પ્રથમ કૉલમમાં સ્થિત છે. અમે તેને બીજી હરોળ અને બીજા સ્તંભની મદદથી સરહદ કરીએ છીએ, અમને માઇનોર $ M_(2)^(1)=\left| \begin(એરે)(ll)(1) & (2) \\ (2) & (4)\end(એરે)\right|=0 $ ; ચાલો બીજા ક્રમના બીજા નાનાને ધ્યાનમાં લઈએ, આ માટે આપણે ગૌણ $M_1$ ને બીજી હરોળ અને ત્રીજા સ્તંભની મદદથી સરહદ કરીએ છીએ, પછી આપણી પાસે માઈનોર $ M_(2)^(2)=\left| \begin(array)(rr)(1) & (-1) \\ (2) & (3)\end(array)\right|=5 \neq 0 $, એટલે કે, મેટ્રિક્સનો ક્રમ છે બે કરતાં ઓછું નહીં. આગળ, અમે ત્રીજા ક્રમના સગીરોને ધ્યાનમાં લઈએ છીએ જે સગીર $ M_(2)^(2) $ ની સરહદ ધરાવે છે. આવા બે સગીર છે: બીજા કૉલમ સાથે અથવા ચોથા કૉલમ સાથે ત્રીજી પંક્તિનું સંયોજન. ચાલો આ સગીરોની ગણતરી કરીએ.
કેટલાક મેટ્રિક્સ આપવા દો:
.ચાલો આ મેટ્રિક્સમાં પસંદ કરીએ
મનસ્વી શબ્દમાળાઓ અને 
મનસ્વી કૉલમ 
. પછી નિર્ણાયક 
મી ક્રમ, મેટ્રિક્સ તત્વોથી બનેલો 
, પસંદ કરેલ પંક્તિઓ અને કૉલમ્સના આંતરછેદ પર સ્થિત છે, તેને માઇનોર કહેવામાં આવે છે 
મી ઓર્ડર મેટ્રિક્સ 
.વ્યાખ્યા 1.13.મેટ્રિક્સ રેન્ક
આ મેટ્રિક્સના બિન-શૂન્ય માઇનોરનો સૌથી મોટો ક્રમ છે.મેટ્રિક્સના ક્રમની ગણતરી કરવા માટે, વ્યક્તિએ તેના સૌથી નીચલા ક્રમના તમામ સગીરોને ધ્યાનમાં લેવું જોઈએ અને, જો તેમાંથી ઓછામાં ઓછું એક શૂન્યથી અલગ હોય, તો ઉચ્ચ ક્રમના સગીરોને ધ્યાનમાં લેવા આગળ વધો. મેટ્રિક્સની રેન્ક નક્કી કરવા માટેના આ અભિગમને બોર્ડરિંગ મેથડ (અથવા સગીરોને કિનારી કરવાની પદ્ધતિ) કહેવામાં આવે છે.
સમસ્યા 1.4.સગીરોની સરહદની પદ્ધતિનો ઉપયોગ કરીને, મેટ્રિક્સનો ક્રમ નક્કી કરો
.
.પ્રથમ ક્રમની ધારને ધ્યાનમાં લો, ઉદાહરણ તરીકે,
. પછી અમે કેટલાક સેકન્ડ-ઓર્ડર એજિંગને ધ્યાનમાં લેવા આગળ વધીએ છીએ.દાખ્લા તરીકે,
.છેલ્લે, ચાલો ત્રીજા-ક્રમની સરહદનું વિશ્લેષણ કરીએ.
.તેથી બિન-શૂન્ય સગીરનો સર્વોચ્ચ ક્રમ 2 છે, તેથી
.સમસ્યા 1.4 ઉકેલતી વખતે, તમે નોંધ કરી શકો છો કે સંખ્યાબંધ બીજા ક્રમની સરહદી સગીરો બિનશૂન્ય છે. આ સંદર્ભમાં, નીચેનો ખ્યાલ લાગુ પડે છે.
વ્યાખ્યા 1.14.મેટ્રિક્સનો બેઝિસ માઇનોર એ કોઈપણ બિન-શૂન્ય સગીર છે જેનો ક્રમ મેટ્રિક્સના ક્રમ સમાન છે.
પ્રમેય 1.2.(આધારિત ગૌણ પ્રમેય). આધાર પંક્તિઓ (આધારિત કૉલમ) રેખીય રીતે સ્વતંત્ર છે.
નોંધ કરો કે મેટ્રિક્સની પંક્તિઓ (સ્તંભો) રેખીય રીતે નિર્ભર હોય છે જો અને માત્ર જો તેમાંના ઓછામાં ઓછા એકને અન્યના રેખીય સંયોજન તરીકે રજૂ કરી શકાય.
પ્રમેય 1.3.રેખીય રીતે સ્વતંત્ર મેટ્રિક્સ પંક્તિઓની સંખ્યા રેખીય સ્વતંત્ર મેટ્રિક્સ કૉલમની સંખ્યા જેટલી છે અને તે મેટ્રિક્સની રેન્ક જેટલી છે.
પ્રમેય 1.4.(નિર્ધારક શૂન્યની બરાબર હોવા માટે જરૂરી અને પર્યાપ્ત શરત). નિર્ણાયક માટે ક્રમમાં
-મો ઓર્ડર 
શૂન્યની બરાબર હતી, તે જરૂરી અને પર્યાપ્ત છે કે તેની પંક્તિઓ (સ્તંભો) રેખીય રીતે આધારિત હોય.તેની વ્યાખ્યાના આધારે મેટ્રિક્સની રેન્કની ગણતરી કરવી ખૂબ જ બોજારૂપ છે. ઉચ્ચ ઓર્ડરના મેટ્રિસિસ માટે આ ખાસ કરીને મહત્વપૂર્ણ બની જાય છે. આ સંદર્ભમાં, વ્યવહારમાં, મેટ્રિક્સના ક્રમની ગણતરી પ્રમેય 10.2 - 10.4, તેમજ મેટ્રિક્સ સમાનતા અને પ્રાથમિક પરિવર્તનની વિભાવનાઓના ઉપયોગના આધારે કરવામાં આવે છે.
વ્યાખ્યા 1.15.બે મેટ્રિસિસ
અને 
સમકક્ષ કહેવાય છે જો તેમની રેન્ક સમાન હોય, એટલે કે. 
.જો મેટ્રિસિસ
અને 
સમકક્ષ છે, પછી નોંધ કરો 
.પ્રમેય 1.5.પ્રાથમિક પરિવર્તનને કારણે મેટ્રિક્સનો ક્રમ બદલાતો નથી.
અમે પ્રાથમિક મેટ્રિક્સ ટ્રાન્સફોર્મેશન કહીશું
મેટ્રિક્સ પર નીચેની કોઈપણ કામગીરી:અનુરૂપ પંક્તિઓ સાથે કૉલમ અને કૉલમ સાથે પંક્તિઓ બદલીને;
મેટ્રિક્સ પંક્તિઓ ફરીથી ગોઠવવી;
એક રેખાને પાર કરવી જેના તત્વો બધા શૂન્ય છે;
શૂન્ય સિવાયની સંખ્યા દ્વારા શબ્દમાળાનો ગુણાકાર;
એક લીટીના તત્વોમાં ઉમેરવાથી બીજી લીટીના અનુરૂપ તત્વોનો સમાન સંખ્યા વડે ગુણાકાર થાય છે
.પ્રમેયની કોરોલરી 1.5.જો મેટ્રિક્સ
મેટ્રિક્સમાંથી મેળવેલ 
પ્રાથમિક રૂપાંતરણોની મર્યાદિત સંખ્યાનો ઉપયોગ કરીને, પછી મેટ્રિક્સ 
અને 
સમકક્ષ છે.મેટ્રિક્સની રેન્કની ગણતરી કરતી વખતે, તેને મર્યાદિત સંખ્યામાં પ્રાથમિક પરિવર્તનનો ઉપયોગ કરીને ટ્રેપેઝોઇડલ સ્વરૂપમાં ઘટાડવું જોઈએ.
વ્યાખ્યા 1.16.જ્યારે, શૂન્ય સિવાયના સર્વોચ્ચ ક્રમના કિનારી નાનામાં, કર્ણની નીચેના બધા તત્વો અદૃશ્ય થઈ જાય ત્યારે અમે ટ્રેપેઝોઇડલને મેટ્રિક્સના પ્રતિનિધિત્વનું સ્વરૂપ કહીશું. દાખ્લા તરીકે:
.
અહીં
, મેટ્રિક્સ તત્વો 
શૂન્ય પર જાઓ. પછી આવા મેટ્રિક્સની રજૂઆતનું સ્વરૂપ ટ્રેપેઝોઇડલ હશે.નિયમ પ્રમાણે, ગૌસીયન અલ્ગોરિધમનો ઉપયોગ કરીને મેટ્રિસીસને ટ્રેપેઝોઇડલ આકારમાં ઘટાડવામાં આવે છે. ગૌસ અલ્ગોરિધમનો વિચાર એ છે કે, મેટ્રિક્સની પ્રથમ પંક્તિના ઘટકોને સંબંધિત પરિબળો દ્વારા ગુણાકાર કરીને, તે પ્રાપ્ત થાય છે કે તત્વની નીચે સ્થિત પ્રથમ સ્તંભના તમામ ઘટકો
, શૂન્ય તરફ વળશે. પછી, બીજા સ્તંભના ઘટકોને અનુરૂપ પરિબળો દ્વારા ગુણાકાર કરીને, અમે ખાતરી કરીએ છીએ કે બીજા કૉલમના તમામ ઘટકો તત્વની નીચે સ્થિત છે. 
, શૂન્ય તરફ વળશે. પછી એ જ રીતે આગળ વધો.સમસ્યા 1.5.મેટ્રિક્સને ટ્રેપેઝોઇડલ આકારમાં ઘટાડીને તેની રેન્ક નક્કી કરો.
.ગૌસીયન અલ્ગોરિધમનો ઉપયોગ કરવાનું સરળ બનાવવા માટે, તમે પ્રથમ અને ત્રીજી લાઇનને સ્વેપ કરી શકો છો.
.તે સ્પષ્ટ છે કે અહીં
. જો કે, પરિણામને વધુ ભવ્ય સ્વરૂપમાં લાવવા માટે, તમે આગળ કૉલમનું રૂપાંતર કરવાનું ચાલુ રાખી શકો છો.
.
