Какое еще название имеет прямоугольная система координат. Прямоугольная система координат

Для определения положения точки в пространстве мы будем использовать декартовы прямоугольные координаты (рис.2).

Декартова прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY, OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. Ось OX называется осью абсцисс (или просто абсциссой), ось OY - осью ординат (ординатой), ось OZ - осью аппликат (апп ликатой).

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки параллельно плоскостям YOZ, XOZ и XOY соответственно.

Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A.

Символически это записывают так:

или привязывают запись координат к конкретной точке с помощью индекса:

x A , y A , z A ,

Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче, приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка B лежала не как на рисунке — на луче OX, а на его продолжении в обратную сторону от точки O (на отрицательной части оси OX), то абсцисса x точки A была бы отрицательной (минус расстоянию OB). Аналогично и для двух других осей.

Координатные оси OX, OY, OZ, изображенные на рис. 2, образуют правую систему координат. Это означает, что если смотреть на плоскость YOZ вдоль положительного направления оси OX, то движение оси OY в сторону оси OZ будет проходить по часовой стрелке. Эту ситуацию можно описать при помощи правила буравчика : если буравчик (винт с правой резьбой) вращать по направлению от оси OY к оси OZ, то он будет двигаться вдоль положительного направления оси OX.

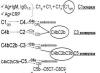
Векторы единичной длины, направленные вдоль координатных осей, называются координатными ортами. Их обозначают обычно как (рис. 3). Встречается так же обозначение Орты составляют базис координатной системы.

В случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

1. Прямоугольная система координат на плоскости

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X "X и Y "Y O , которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси Y "Y вверх, ось X "X смотрела направо.

Четыре угла (I, II, III, IV), образованные осями координат X "X и Y "Y , называются координатными углами или квадрантами (см. рис. 1).

Положение точки A на плоскости определяется двумя координатами x и y . Координата x равна длине отрезка OB , координата y - длине отрезка OC в выбранных единицах измерения . Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y "Y и X "X соответственно. Координата x называется абсциссой точки A , координата y - ординатой точки A . Записывают так: А (x , y )

Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату.

2. Полярные координаты.

Полярная сетка, на которой отложено несколько углов с пометками в градусах.

Полярная система координат - двумерная система координат, в которой каждая точка на плоскости определяется двумя числами - углом и расстоянием. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде расстояний и углов; в более распространенной, декартовой или прямоугольной системе координат, такие отношения можно установить только путем применения тригонометрических уравнений.

Полярная система координат задается лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается φ, равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

Определенная таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.

3. Деление отрезков в данном отношении.

Требуется разделить отрезок АВ, соединяющий точки A(x1;y1) и В(х2;y2) в заданном отношении λ > 0, т. е..jpg" align="left" width="84 height=84" height="84">

Решение : Введем в рассмотрение векторы https://pandia.ru/text/78/214/images/image006_41.gif" width="18" height="13 src=">..gif" width="79" height="15 src=">, т. е. и т. е..

Уравнение (9.1) принимает вид

Учитывая, что равные векторы имеют равные координаты, получаем:

https://pandia.ru/text/78/214/images/image014_27.gif" width="56 height=28" height="28"> (9.2) и

https://pandia.ru/text/78/214/images/image016_26.gif" width="60 height=29" height="29"> (9.3)

Формулы (9.2) и (9.3) называются формулами деления отрезка в данном отношении . В частности, при λ = 1, т. е..gif" width="54" height="29 src=">. В этом случае точка М(х;у) является серединой отрезка АВ.

Замечание:

Если λ = 0, то это означает, что точки A и Μ совпадают, если λ < 0, то точка Μ лежит вне отрезка АВ - говорят, что точка M делит отрезок АВ внешним образом , т. к. в противном случае , т. е. AM + MB = 0, т. е. АВ = 0).

4. Расстояние между точками.

Требуется найти расстояние d между точками A(x1;y1) и В(х2;y2) плоскости .

Решение : Искомое расстояние d равно длине вектора , т. е.

5. Уравнение прямой, проходящей через две точки.

Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) иM2(x2, y2, z2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:

.

Кроме того, для точки М1 можно записать:

.

Решая совместно эти уравнения, получим:

.

Это уравнение прямой, проходящей через две точки в пространстве.

6. Определители 2-го порядка.

Значение определителя 2-го порядка легко вычисляется по определению используя формулу.

7. Определители 3-го порядка.

https://pandia.ru/text/78/214/images/image030_15.gif" width="120" height="61 src="> схема вычисления определителя методом треугольника, т. о.:

https://pandia.ru/text/78/214/images/image034_15.gif" width="72" height="51 src=">DIV_ADBLOCK251">

9. Решение СЛУ методом Крамера.

Теорема Крамера: Система N уравнения с N неизвестными, Определитель которых отличен от нуля, всегда имеет решение, при том единственное. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы с заменой столбца коэффициентов при искомом неизвестных на столбец искомых членов.

Данная система уравнений будет иметь единственное решение только тогда, когда определитель составленный из коэффициентов при X1 - n не будет равен нулю. Обозначим этот определитель знаком - Δ. Если этот определитель не равен нулю, то решаем дальше. Тогда каждый Xi = Δi / Δ, где Δi - это определитель составленный из коэффициентов при X1 - n, только значения коэффициентов в i - ом стольбце заменены на значения за знаком равенства в сисетеме уравнений, а Δ - это главный определитель

Система N-го порядкаhttps://pandia.ru/text/78/214/images/image037_14.gif" width="112" height="46">.gif" width="79" height="46">.gif" width="264" height="48">.gif" width="120" height="29">DIV_ADBLOCK252">

10. Решение СЛУ матричным методом.

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

https://pandia.ru/text/78/214/images/image046_13.gif" width="75" height="41"> и матрицы столбцы неизвестных и свободных членов

Найдем произведение

https://pandia.ru/text/78/214/images/image049_13.gif" width="108" height="41"> или короче A ∙X=B .

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т. к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением .

Пусть определитель матрицы отличен от нуля |A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1 , обратную матрице A : https://pandia.ru/text/78/214/images/image051_13.gif" width="168" height="59">

Решить матричным способом следующую систему уравнений:

Внимание: Нули появляются, если нет одной переменной, т. е., например, если Х3 не дан в условии, то он автоматически равен нулю. Так же и с Х1 и Х2

https://pandia.ru/text/78/214/images/image057_9.gif" width="56 height=54" height="54">

https://pandia.ru/text/78/214/images/image065_8.gif" width="160 height=51" height="51">

Ответ:

# а) Дано:

https://pandia.ru/text/78/214/images/image074_5.gif" width="59 height=16" height="16"> Ответ:

https://pandia.ru/text/78/214/images/image081_5.gif" width="106" height="50 src=">

Найдем обратную матрицу.

Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.

https://pandia.ru/text/78/214/images/image083_4.gif" width="172" height="52 src=">

Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.

https://pandia.ru/text/78/214/images/image085_5.gif" width="187" height="53 src=">

Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1. Квадратная матрица, получившаяся правее единичной и есть обратная к главной.

https://pandia.ru/text/78/214/images/image087_4.gif" width="172" height="52 src=">

11. Векторы. Сложение векторов.

http://www. bigpi. *****/encicl/articles/15/1001553/1001553A. htm

Вектором называют величину, характеризуемую числовым значением, направлением в пространстве и складывающейся с другой, себе подобной величиной геометрически .

Графически векторы изображаются в виде направленных отрезков прямой определенной длины, как https://pandia.ru/text/78/214/images/image089_5.gif" width="17" height="17 src="> или DIV_ADBLOCK254">

Сложение векторов: Суммой векторов a(a1; a2) и b(b1; b2) называется вектор c(a1+b1; a2+b2). Для любых векторов a(a1; a2), b(b1; b2), c(с1; с2) справедливы равенства:

Теорема : Каковы бы ни были три точки A, B и C, имеет место векторное равенство https://pandia.ru/text/78/214/images/image094_4.gif" width="126" height="49">

При сложении двух векторов часто используют так называемое «правило параллелограмма ». При этом строят параллелограмм, используя слагаемые векторы в качестве его смежных сторон. Диагональ параллелограмма, проведённая из точки, где соединяются начала векторов, и является искомой суммой (рис. 4, слева).

Легко видеть (рис. 4, справа), что это правило приводит к тому же результату, что и указанный выше способ. При сложении более двух векторов «правило параллелограмма » практически не используется из-за громоздкости построений. Сложение векторов коммутативно, то есть,
а + b = b + а .

И еще, сумма определенного числа векторов не зависит от порядка, в котором они складываются, то есть, (а + b ) + d = a + (b + d ). В этом случае говорят, что сложение векторов ассоциативно, то есть для него выполняется сочетательный закон.

12. Скалярное произведение векторов.

http://www. dpva. info/Guide/GuideMathematics/linearAlgebra/ScalarVectorsMultiplication/

Скалярное произведение векторов - это операция над двумя векторами, результатом которой является число (не вектор).

https://pandia.ru/text/78/214/images/image097_5.gif" width="86" height="23">

Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Необходимо заметить, что угол между двумя векторами - это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать.

Непосредственно из определения следуют следующие простейшие свойства:

1. Скалярное произведение произвольного вектора а на себя же (скалярный квадрат вектора а) всегда неотрицательно, и равно квадрату длины этого вектора. Причем скалярный квадрат вектора равен нулю тогда и только тогда, когда данный вектор - нулевой.

2. Скалярное произведение любых перпендикулярных векторов a и b равно нулю.

3. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перепендикулярны или хотя бы один из них - нулевой.

4. Скалярное произведение двух векторов a и b положительно тогда и только тогда, когда между ними острый угол.

5. Скалярное произведение двух векторов a и b отрицательно тогда и только тогда, когда между ними тупой угол.

Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами.

(Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто :

Пусть есть вектор AB, А - начало вектора, В - конец, и координаты этих точек

А=(a1,a2,a3), В=(b1,b2,b3)

Тогда координаты вектора АВ:

АВ={b1-a1, b2-a2, b3-a3}.

Аналогично в двухмерном пространстве - просто отсутствуют третьи координаты)

Итак, пусть даны два вектора, заданные набором своих координат:

а) В двухмерном пространстве(на плоскости) ..gif" width="49" height="19 src=">

Тогда их скалярное произведение можно вычислить по формуле:

б) В трехмерном пространстве: ;

Аналогично двухмерному случаю, их скалярное произведение вычисляется по формуле:

DIV_ADBLOCK257">

Итак, пусть у нас есть два вектора: https://pandia.ru/text/78/214/images/image104_4.gif" width="73" height="23 src=">

И нам нужно найти угол между ними. С помощью их координат найдем их длины, а затем просто приравняем две формулы для скалярного произведения. Таким образом мы получим косинус искомого угла.

Длина вектора а вычисляется как корень из скалярного квадрата вектора а , который мы вычислим по формуле для скалярного произведения векторов, заданных координатами:

https://pandia.ru/text/78/214/images/image107_3.gif" width="365" height="23">

Значит, ,

Искомый угол найден.

13. Векторное произведение.

http://www. dpva. info/Guide/GuideMathematics/linearAlgebra/vectorVectorsMultiplication/

Векторное произведение двух векторов а и b - это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими свойствами:

https://pandia.ru/text/78/214/images/image111_3.gif" width="83" height="27">, где a и b .

3) Вектор направлен таким образом, что если привести вектора https://pandia.ru/text/78/214/images/image117_3.gif" width="13" height="24 src=">.gif" width="13" height="24"> до вектора будет ПРОТИВ часовой стрелки.

Для большей ясности приведем пример - на рисунке справа вектор - векторное произведение векторов а и b. Как сказано в определении, мы привели все три вектора к общему началу, и тогда, если смотреть на вектора a и b с конца вектора , кратчайший поворот от вектора а до вектора b будет против часовой стрелки.

https://pandia.ru/text/78/214/images/image119_3.gif" width="76" height="25">

Так же, непосредственно из определения следует, что для любого скалярного множителя k (числа) верно следующее:

det A https://pandia.ru/text/78/214/images/image182_2.gif" width="56 height=32" height="32">

7.2 Нахождение Определителя Матрицы 3-го порядка по правилу треугольника

DIV_ADBLOCK261">

Каждому элементу квадратной Матрицы (порядок которых больше, или равен трем), можно поставить в соответствие два числа, называемые МИНОРОМ или АЛГЕБРАИЧЕСКИМ ДОПОЛНЕНИЕМ. Минором элемента Aij квадратной Матрицы А (любого порядка) называется ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ, получаемый из Матрицы А методом вычеркивания строки и столбца, на пересечении которых стоит элемент Aij. Знак M - обозначение Минора.

https://pandia.ru/text/78/214/images/image034_15.gif" width="72" height="51 src=">.gif" width="35" height="19">

https://pandia.ru/text/78/214/images/image194_1.gif" width="96 height=82" height="82">

Пусть А = некоторая Матрица III-го порядка, тогда определитель матрицы А равен:

Замечание: Определитель можно вычислить по элементам любой строки или любого столбца данной Матрицы.

# Найти определитель Матрицы по элементам первой строки и первого столбца:

https://pandia.ru/text/78/214/images/image201_0.gif" width="58" height="56 src=">

https://pandia.ru/text/78/214/images/image203_0.gif" width="253" height="34 src=">

7.3 ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ n-го порядка

Пусть А - квадратная Матрица n-го порядка. Тогда, Определитель Матрицы n-го порядка будет выглядеть так:

Разложив по элементам 1 строки найти элементы Матрицы А

DIV_ADBLOCK262">

2) a12=0*(2*0*1+1*0*0+1*2*0)-0*(0*0*0+1*1*1+2*0*2)=0

3) a13=2*(2*2*1+1*1*0+0*0*2)-2*(0*2*0+1*0*1+2*2*1)=0

4) a14=-1*(2*2*0+1*1*1+0*0*0)-1*(1*2*0+1*0*0+2*1*0)=-1

6. ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛИТЕЛЯ

1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (транспонировать)

2. При перестановке двух строк или столбцов, Определение изменит свой знак на противоположный.

3. Общий множитель всех элементов строки (столбца) можно вынести за знак определителя

4. Определитель с двумя одинаковыми строками или столбцами всегда равен нулю.

5. Если элементы двух строк (столбцов) определителя пропорциональны то определитель равен нулю.

6. Если в какой-то строке или столбце определителя прибавить соответственно элементы другой строки или столбца, умноженные на одно и то же число, то определитель не изменит своей величины.

https://pandia.ru/text/78/214/images/image208_0.gif" width="48" height="12"> и т. д.

Треугольный определитель - это тот определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали - нули, равен произведению элементов главной диагонали.

https://pandia.ru/text/78/214/images/image210_0.gif" width="37" height="28 src=">DIV_ADBLOCK263">

Если обратная Матрица А существует, то Матрицу называют ОБРАТИМОЙ. Нахождение квадратной Матрицы имеет большое значение при решении системных линейных уравнений.

17. Обратная матрица.

http://www. mathelp. *****/book1/omatrix. htm

1. Найти Определитель Матирицы А

2. Найти алгибраическое дополнение всех элементов Матрицы А (Aij) и записать новую Матрицу

3. Транспонировать новую Матрицу

4. Умножить транспонированную Матрицу на число, обратное определителю. (Например: к числу 6 обратным определителем будет число )

Обозначим ∆ =det A. Для того, чтобы квадратная Матрица А имела обратную, необходимо и достаточно, чтобы Матрица была не вырожденной (отличной от нуля). Матрица, обратная матрице А, обозначается через А-1, так что В = А-1..gif" width="12" height="19 src=">.gif" width="82" height="34 src="> - нормирующий множитель плоскости, знак которого выбирается противоположным знаку D , если произвольно, если D = 0 .

21. Кривые 2-го (уравнение окружности).

Определение 11.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс , при пересечении образующих обеих полостей – гипербола , а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола .

Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных.

Классификация кривых второго порядка

Невырожденные кривые

невырожденной , если Могут возникать следующие варианты:

Невырожденная кривая второго порядка называется центральной, если

· эллипс - при условии D > 0 и ΔI < 0;

частный случай эллипса - окружность - при условии I 2 = 4D или a 11 = a 22,a 12 = 0;

мнимый эллипс (ни одной вещественной точки) - при условии ΔI > 0;

· гипербола - при условии D < 0;

Невырожденная кривая второго порядка называется нецентральной, если ΔI = 0

· парабола - при условии D = 0.

Вырожденные кривые: Кривая второго порядка называется вырожденной , если Δ = 0. Могут возникать следующие варианты:

· вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) - при условии D > 0;

· пара вещественных пересекающихся прямых (вырожденная гипербола) - при условии D < 0;

· вырожденная парабола - при условии D = 0:

· пара вещественных параллельных прямых - при условии B < 0;

· одна вещественная прямая (две слившиеся параллельные прямые) - при условии B = 0;

· пара мнимых параллельных прямых (ни одной вещественной точки) - при условии B > 0.

22. Эллипс и его уравнение.

Определение 11.2. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами , есть величина постоянная.

Замечание. При совпадении точек F 1 и F 2 эллипс превращается в окружность.

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.

Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a >2b ), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

Тогда https://pandia.ru/text/78/214/images/image264.gif" width="141" height="122 src=">

Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.

|r 1 - r 2 | = 2a , откуда. Если обозначить b ² = c ² - a ², отсюда можно получить https://pandia.ru/text/78/214/images/image267.gif" width="38" height="30 src=">.gif" width="87" height="44 src="> , (11.3`)

для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5) Отношение расстояния ri от точки гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Доказательство можно провести так же, как и для эллипса.

23. Парабола.

Определение 11.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой .

Для вывода уравнения параболы выберем декартову систему координат так, чтобы ее началом была середина перпендикуляра FD , опущенного из фокуса на директрису, а координатные оси располагались параллельно и перпендикулярно директрисе. Пусть длина отрезка FD

D O F x равна р . Тогда из равенства r = d следует, что https://pandia.ru/text/78/214/images/image271.gif" width="101 height=38" height="38">,

Алгебраическими преобразованиями это уравнение можно привести к виду:

y ² = 2px , (11.4) называемому каноническим уравнением параболы .

Величина р называется параметром параболы.

Свойства параболы :

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:

Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e <1), гиперболу (при e >1) или параболу (при е =1).

Приведение уравнения второго порядка к каноническому виду.

Определение 11.9. Линия, определяемая общим уравнением второго порядка

https://pandia.ru/text/78/214/images/image274.gif" width="103 height=19" height="19"> можно задать матрицу

https://pandia.ru/text/78/214/images/image276.gif" width="204" height="24 src="> (в предположении, что λ .

В случае, когда одно из собственных чисел матрицы А равно 0, уравнение (11.5) в результате двух преобразований координат можно привести к виду: , (11.8) являющимся каноническим уравнением параболы.

24. Прямоугольные координаты в пространстве.

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX , OY и OZ . Оси координат пересекаются в точке O , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX - ось абсцисс, OY - ось ординат, OZ - ось аппликат.

Если большой палец правой руки принять за направление X , указательный за направление Y , а средний за направление Z , то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY , если этот поворот наблюдать со стороны положительного направления оси OZ . Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. рис. 2).

Положение точки A в пространстве определяется тремя координатами x , y и z . Координата x равна длине отрезка OB , координата y - длине отрезка OC , координата z - длине отрезка OD в выбранных единицах измерения. Отрезки OB , OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ , XOZ и XOY соответственно. Координата x называется абсциссой точки A , координата y - ординатой точки A , координата z - аппликатой точки A . Записывают так: .

Дадим теперь понятие о методе координат на плоскости, т. е. укажем способ, позволяющий определять положение точек плоскости с помощью чисел.

Возьмем две взаимно перпендикулярные прямые и на каждой из них установим положительное направление. Эти прямые, относительно которых мы будем определять положение точек плоскости, называются осями координат. Оси координат обычно располагают так, как это указано на рис. 6: одну - горизонтально и положительное направление на ней выбирают слева направо, а другую - вертикально и положительное направление на ней - снизу вверх. Одна из осей (обычно горизонтальная) называется осью абсцисс (ось Ох), а другая -

осью ординат (ось Оу). Точка пересечения осей координат называется началом координат (на рис. 6 начало координат обозначено буквой О). Наконец, выберем единицу масштаба (мы всегда будем предполагать, что на обеих осях координат выбрана одна и та же единица масштаба).

Теперь положение любой точки плоскости можно будет определить числами - координатами этой точки. Действительно, всякой точке М плоскости соответствуют на осях координат две точки Р и Q, являющиеся ее проекциями на эти оси (рис. 6) и, обратно, зная точки на осях координат, можно построить единственную точку М на плоскости, для которой Р и Q являются проекциями на эти оси. Таким образом, определение положения точки М плоскости сводится к определению положений ее проекций Р и Q на координатные оси.

Но мы уже знаем, что положение точки на оси вполне определяется координатой. Пусть - координата точки Р на оси абсцисс и у - координата точки Q на оси ординат . Числа х и у вполне определяют положение точки М на плоскости и называются координатами точки; при этом называется абсциссой точки М, а у - ее ординатой.

Таким образом, абсциссой точки называется величина направленного отрезка оси Ох, началом которого является начало координат, а концом - проекция точки на эту ось; ординатой точки называется величина направленного отрезка оси Оу, началом которого является начало координат, а концом - проекция точки на ось ординат.

Итак, положение любой точки плоскости вполне определяется заданием пары чисел х и у, первое из которых является абсциссой точки, а второе - ее ординатой.

Координаты точки условимся писать в скобках, рядом с буквой, обозначающей эту точку, ставя на первом месте абсциссу, а на втором - ординату и разделяя их запятой: При указанном на рис. 6 расположении координатных осей для всех точек плоскости, лежащих вправо от оси Оу (оси ординат), абсцисса положительна, а для точек, лежащих влево от оси Оу, - отрицательна. Точки самой оси Оу имеют абсциссу, равную нулю. Совершенно так же точки плоскости, лежащие выше оси Ох (оси абсцисс), имеют положительную ординату у, а точки, лежащие ниже оси отрицательную. Точки самой оси Ох имеют ордииату, равную нулю. Начало координат имеет координаты (0, 0).

Оси координат делят плоскость на четыре части, называемые четвертями или квадрантами (иногда их также называют координатными

углами). Часть плоскости, заключенная между положительными полуосями Ох и Оу, называется первым квадрантом. Дальше нумерация квадрантов идет против часовой стрелки (рис. 7). Для всех точек 1 квадранта для точек II квадранта в III квадранте и в IV квадранте

Координаты, которые принимаются здесь для определения положения точки плоскости, называются прямоугольными координатами, так как точка М плоскости получается пересечением двух прямых РМ и QM (рис. 6), встречающихся под прямым углом, а также декартовыми по имени математика и философа Декарта, который в 1637 году опубликовал первый труд по аналитической геометрии.

Декартова прямоугольная система координат не является единственной координатной системой, позволяющей определять положения точек плоскости (см. § 11 этой главы), но она является наиболее простой и мы в дальнейшем будем пользоваться преимущественно ею. Из описанного метода координат вытекает решение двух основных задач.

Задача I. По данной точке М найти ее координаты.

Из данной точки М опускаем перпендикуляры на оси Основания этих перпендикуляров - точки Р и Q - определят обе искомые координаты. Первая координата точки М, ее абсцисса, равна величине направленного отрезка ОР оси Вторая же координата точки ее ордината, равна величине направленного отрезка OQ оси

Задача И. Зная координаты точки М, построить эту точку.

Отложим по оси Ох от точки О отрезок длиною единиц вправо, если и влево, если Конец этого отрезка - точка Р - будет проекцией искомой точки М на ось Ох, откладывая по оси Оу от точки О отрезок длиною единиц вверх, если и вниз, если получим точку Q - проекцию искомой точки на ось Оу. Зная же Р и Q, легко по этим точкам, как проекциям, построить искомую точку М. Для этого нужно провести через Р и Q прямые, параллельные осям координат; в пересечении этих прямых получится искомая точка

Замечание. Если мы условимся рассматривать направленные отрезки РМ и QM (рис. 6) как отрезки осей, направления которых совпадают с направлениями параллельных им координатных осей, то абсцисса точки М будет выражаться не только величиной отрезка ОР,

но и равной ей величиной отрезка QM. Ордината той же точки будет одинаково выражаться как величиной отрезка OQ, так и равной ей величиной отрезка РМ. Направленные отрезки OP, QM, OQ и РМ будем называть координатными отрезками точки М. Тогда при решении рассмотренных двух основных задач нет необходимости определять обе проекции точки М, достаточно определить только одну, например проекцию на ось абсцисс. Так, в задаче 1 опускаем из данной точки М перпендикуляр на ось абсцисс. Его основание Р определяет проекцию точки М на эту ось. Величина направленного отрезка ОР даст абсциссу данной точки, а величина отрезка РМ - ординату у.

Пример. Построить точку по координатам Откладываем вправо от О по оси абсцисс отрезок длиною в 2 единицы; через конец Р этого отрезка проводим прямую, параллельную оси ординат, и на ней откладываем вниз от Р отрезок длиною в 3 единицы; конец этого отрезка и есть искомая точка М.

Таким образом, в выбранной системе координат каждой точке плоскости соответствует вполне определенная пара координат х и у и, обратно, всякая пара действительных чисел х, у определяет на плоскости единственную точку, абсцисса которой равна х, а ордината у. Поэтому задать точку, это значит задать ее координаты; найти точку, значит найти ее координаты.

Если на плоскости или в трехмерном пространстве ввести систему координат, то мы получим возможность описывать геометрические фигуры и их свойства с помощью уравнений и неравенств, то есть, мы сможем использовать методы алгебры. Поэтому понятие системы координат очень важно.

В этой статье мы покажем как задается прямоугольная декартова система координат на плоскости и в трехмерном пространстве и выясним как определяются координаты точек. Для наглядности приведем графические иллюстрации.

Навигация по странице.

Прямоугольная декартова система координат на плоскости.

Введем прямоугольную систему координат на плоскости.

Для этого проведем на плоскости две взаимно перпендикулярные прямые, выберем на каждой из них положительное направление , указав его стрелочкой, и выберем на каждой из них масштаб (единицу измерения длины). Обозначим точку пересечения этих прямых буквой О и будем считать ее началом отсчета . Так мы получили прямоугольную систему координат на плоскости.

Каждую из прямых с выбранным началом отсчета О , направлением и масштабом называют координатной прямой или координатной осью .

Прямоугольную систему координат на плоскости обычно обозначают Oxy , где Ox и Oy – ее координатные оси. Ось Ox называют осью абсцисс , а ось Oy – осью ординат .

Сейчас условимся с изображением прямоугольной системы координат на плоскости.

Обычно единица измерения длины на осях Ox и Oy выбирается одинаковая и откладывается от начала координат на каждой координатной оси в положительном направлении (отмечается штришком на координатных осях и рядом записывается единица), ось абсцисс направляется вправо, а ось ординат – вверх. Все остальные варианты направления координатных осей сводятся к озвученному (ось Ox - вправо, ось Oy - вверх) при помощи поворота системы координат на некоторый угол относительно начала координат и взгляда на нее с другой стороны плоскости (при необходимости).

Прямоугольную систему координат часто называют декартовой, так как ее на плоскости впервые ввел Рене Декарт. Еще чаще прямоугольную систему координат называют прямоугольной декартовой системой координат, собирая все воедино.

Прямоугольная система координат в трехмерном пространстве.

Аналогично задается прямоугольная система координат Oxyz в трехмерном евклидовом пространстве, только берется не две, а три взаимно перпендикулярных прямых. Другими словами, к координатным осям Оx и Oy добавляется координатная ось Oz , которую называют осью аппликат .

В зависимости от направления координатных осей различают правую и левую прямоугольные системы координат в трехмерном пространстве.

Если смотреть с положительного направления оси Oz и кратчайший поворот от положительного направления оси Ox к положительному направлению оси Oy происходит против хода часовой стрелки, то система координат называется правой .

Если смотреть с положительного направления оси Oz и кратчайший поворот от положительного направления оси Ox к положительному направлению оси Oy происходит по ходу часовой стрелки, то система координат называется левой .

Координаты точки в декартовой системе координат на плоскости.

Сначала рассмотрим координатную прямую Ox и возьмем некоторую точку M на ней.

Каждому действительному числу соответствует единственная точка M на этой координатной прямой. К примеру, точке, расположенной на координатной прямой на расстоянии от начала отсчета в положительном направлении, соответствует число , а числу -3 соответствует точка, расположенная на расстоянии 3 от начала отсчета в отрицательном направлении. Числу 0 соответствует начало отсчета.

С другой стороны, каждой точке M на координатной прямой Ox соответствует действительное число . Это действительное число есть ноль, если точка M совпадает с началом отсчета (с точкой O ). Это действительное число положительно и равно длине отрезка OM в данном масштабе, если точка M удалена от начала отсчета в положительном направлении. Это действительное число отрицательно и равно длине отрезка OM со знаком минус, если точка M удалена от начала отсчета в отрицательном направлении.

Число называется координатой точки M на координатной прямой.

Теперь рассмотрим плоскость с введенной прямоугольной декартовой системой координат. Отметим на этой плоскости произвольную точку М .

Пусть - проекция точки M на прямую Ox , а - проекции точки M на координатную прямую Oy (при необходимости смотрите статью ). То есть, если через точку M провести прямые, перпендикулярные координатным осям Ox и Oy , то точками пересечения этих прямых с прямыми Ox и Oy являются соответственно точки и .

Пусть точке на координатной оси Ox соответствует число , а точке на оси Oy - число .

Каждой точке М плоскости в заданной прямоугольной декартовой системе координат соответствует единственная упорядоченная пара действительных чисел , называемых координатами точки M на плоскости. Координату называют абсциссой точки М , а - ординатой точки М .

Верно и обратное утверждение: каждой упорядоченной паре действительных чисел соответствует точка М плоскости в заданной системе координат.

Координаты точки в прямоугольной системе координат в трехмерном пространстве.

Покажем как определяются координаты точки М в прямоугольной системе координат, заданной в трехмерном пространстве.

Пусть и - проекции точки M на координатные оси Ox , Oy и Oz соответственно. Пусть этим точкам на координатных осях Ox , Oy и Oz соответствуют действительные числа и .