Sudėtingi integralai
Šis straipsnis užbaigia neapibrėžtų integralų temą ir apima integralus, kurie, mano nuomone, yra gana sudėtingi. Pamoka buvo sukurta ne kartą paprašius lankytojų, kurie išreiškė pageidavimą, kad svetainėje būtų analizuojami sunkesni pavyzdžiai.
Daroma prielaida, kad šio teksto skaitytojas yra gerai pasiruošęs ir žino, kaip taikyti pagrindinius integravimo būdus. Manekenai ir žmonės, kurie nelabai pasitiki integralais, turėtų kreiptis į pačią pirmąją pamoką - Neapibrėžtas integralas. Sprendimų pavyzdžiai, kur galite įvaldyti temą beveik nuo nulio. Labiau patyrę studentai gali susipažinti su integravimo technikomis ir metodais, su kuriais dar nebuvo susidurta mano straipsniuose.
Kokie integralai bus svarstomi?
Pirmiausia apsvarstysime integralus su šaknimis, kurių sprendimui nuosekliai naudojame kintamasis pakeitimas Ir integravimas dalimis. Tai yra, viename pavyzdyje iš karto derinami du būdai. Ir dar daugiau.
Tada susipažinsime su įdomiais ir originaliais integralo redukavimo į save metodą. Taip išspręsta nemažai integralų.
Trečiasis programos numeris bus integralai iš sudėtingų trupmenų, kurie ankstesniuose straipsniuose praskriejo pro kasą.
Ketvirta, bus analizuojami papildomi integralai iš trigonometrinių funkcijų. Visų pirma, yra metodų, kuriais išvengiama daug laiko reikalaujančio universalaus trigonometrinio pakeitimo.
(2) Integrando funkcijoje skaitiklį padalijame iš vardiklio termino.
(3) Mes naudojame neapibrėžto integralo tiesiškumo savybę. Paskutiniame integralu iš karto funkciją padėkite po diferencialo ženklu.
(4) Imame likusius integralus. Atminkite, kad logaritme galite naudoti skliaustus, o ne modulį, nes .
(5) Atliekame atvirkštinį pakeitimą, išreikšdami „te“ iš tiesioginio pakeitimo:
Mazochistiniai studentai gali atskirti atsakymą ir gauti pradinį integrandą, kaip aš ką tik padariau. Ne, ne, patikrinau teisinga prasme =)
Kaip matote, sprendimo metu teko naudoti net daugiau nei du sprendimo būdus, todėl norint susidoroti su tokiais integralais reikia patikimų integravimo įgūdžių ir nemažos patirties.
Praktiškai, žinoma, kvadratinė šaknis yra labiau paplitusi, čia yra trys pavyzdžiai, kaip ją išspręsti patys:
2 pavyzdys
Raskite neapibrėžtą integralą
3 pavyzdys
Raskite neapibrėžtą integralą
4 pavyzdys
Raskite neapibrėžtą integralą
Šie pavyzdžiai yra to paties tipo, todėl išsamus sprendimas straipsnio pabaigoje bus skirtas tik 2 pavyzdžiams. Kurį pakaitalą naudoti sprendimų pradžioje, manau, akivaizdu. Kodėl pasirinkau to paties tipo pavyzdžius? Dažnai sutinkami jų vaidmenyje. Dažniau galbūt tiesiog kažkas panašaus ![]() .
.
Bet ne visada, kai pagal arctangento, sinuso, kosinuso, eksponentinės ir kitas funkcijas yra tiesinės funkcijos šaknis, reikia vienu metu naudoti kelis metodus. Daugeliu atvejų galima „išlipti lengvai“, tai yra, iškart po pakeitimo gaunamas paprastas integralas, kurį galima lengvai paimti. Lengviausia iš aukščiau pasiūlytų užduočių yra 4 pavyzdys, kuriame pakeitus gaunamas gana paprastas integralas.
Sumažinant integralą į save
Šmaikštus ir gražus metodas. Pažvelkime į šio žanro klasiką:
5 pavyzdys
Raskite neapibrėžtą integralą
Po šaknimi yra kvadratinis dvinaris, o bandant integruoti šį pavyzdį arbatinukui gali skaudėti galvą kelias valandas. Toks integralas paimamas dalimis ir redukuojamas į save. Iš principo tai nėra sunku. Jei žinai kaip.
Pažymėkime nagrinėjamą integralą lotyniška raide ir pradėkime sprendimą: ![]()
Integruokime dalimis: 

(1) Paruoškite integrando funkciją dalijimui po terminus.
(2) Integrando funkcijos terminą padalijame iš termino. Gal ne visiems aišku, bet aprašysiu plačiau:
(3) Mes naudojame neapibrėžto integralo tiesiškumo savybę.
(4) Paimkite paskutinį integralą („ilgasis“ logaritmas).
Dabar pažvelkime į pačią sprendimo pradžią: 
Ir iki galo: 
Kas atsitiko? Dėl mūsų manipuliacijų integralas buvo sumažintas iki savęs!
Sulyginkime pradžią ir pabaigą: ![]()
Pereikite į kairę pusę pakeisdami ženklą: ![]()
Ir mes perkeliame abu į dešinę pusę. Kaip rezultatas: ![]()
Konstanta, griežtai tariant, turėjo būti pridėta anksčiau, bet aš ją pridėjau pabaigoje. Labai rekomenduoju perskaityti, koks griežtumas čia:
Pastaba:
Tiksliau, galutinis sprendimo etapas atrodo taip:
Taigi:
Konstantą gali pakeisti . Kodėl jis gali būti pakeistas? Nes jis vis tiek tai priima bet koks reikšmės, ir šia prasme nėra skirtumo tarp konstantų ir.
Kaip rezultatas:
Panaši gudrybė su nuolatine renotacija yra plačiai naudojama diferencialines lygtis. O ten aš būsiu griežtas. O štai tokią laisvę leidžiu tik tam, kad nesupainiočiau jūsų su nereikalingais dalykais ir sutelkčiau dėmesį būtent į patį integravimo būdą.
6 pavyzdys
Raskite neapibrėžtą integralą
Kitas tipiškas nepriklausomo sprendimo integralas. Visas sprendimas ir atsakymas pamokos pabaigoje. Bus skirtumas nuo atsakymo ankstesniame pavyzdyje!
Jei po kvadratine šaknimi yra kvadratinis trinaris, tada sprendimas bet kuriuo atveju yra du analizuoti pavyzdžiai.
Pavyzdžiui, apsvarstykite integralą ![]() . Viskas, ką jums reikia padaryti, tai pirma pasirinkite visą kvadratą:
. Viskas, ką jums reikia padaryti, tai pirma pasirinkite visą kvadratą:
.
Toliau atliekamas linijinis pakeitimas, kuris tai daroma „be jokių pasekmių“:
, todėl gaunamas integralas . Kažkas pažįstamo, tiesa?
Arba šis pavyzdys su kvadratiniu dvinariu:
Pasirinkite visą kvadratą:
Ir po tiesinio pakeitimo gauname integralą, kuris taip pat išsprendžiamas naudojant jau aptartą algoritmą.
Pažvelkime į dar du tipinius pavyzdžius, kaip sumažinti integralą į save:
– eksponentinės integralas, padaugintas iš sinuso;
– eksponento integralas, padaugintas iš kosinuso.
Išvardytuose integraluose pagal dalis turėsite integruoti du kartus:
7 pavyzdys
Raskite neapibrėžtą integralą
Integrandas yra eksponentas, padaugintas iš sinuso.
Integruojame dalimis du kartus ir integralą sumažiname į save: ![]()



Dėl dvigubo integravimo dalimis integralas buvo sumažintas iki savęs. Sulyginame sprendimo pradžią ir pabaigą:
Pakeisdami ženklą perkeliame jį į kairę pusę ir išreiškiame integralą: 
Paruošta. Tuo pačiu patartina šukuoti dešinįjį šoną, t.y. išimkite eksponentą iš skliaustų, o skliausteliuose sudėkite sinusą ir kosinusą „gražia“ tvarka.
Dabar grįžkime į pavyzdžio pradžią, tiksliau, prie integravimo dalimis:
Rodiklį pažymėjome kaip. Kyla klausimas: ar laipsnis visada turi būti žymimas ? Nebūtinai. Tiesą sakant, laikomame integralu iš esmės nesvarbu, ką turime omenyje sakydami , galėjome eiti kitu keliu: 
Kodėl tai įmanoma? Kadangi eksponentas virsta savimi (tiek diferencijuojant, tiek integruojant), sinusas ir kosinusas abipusiai virsta vienas kitu (vėlgi – tiek diferencijuojant, tiek integruojant).
Tai yra, mes taip pat galime žymėti trigonometrinę funkciją. Tačiau nagrinėjamame pavyzdyje tai mažiau racionalu, nes atsiras trupmenos. Jei norite, galite pabandyti išspręsti šį pavyzdį naudodami antrąjį metodą, atsakymai turi sutapti.
8 pavyzdys
Raskite neapibrėžtą integralą
Tai pavyzdys, kurį galite išspręsti patys. Prieš nuspręsdami pagalvokite, ką šiuo atveju naudingiau žymėti , eksponentinę ar trigonometrinę funkciją? Visas sprendimas ir atsakymas pamokos pabaigoje.
Ir, žinoma, nepamirškite, kad daugumą šios pamokos atsakymų gana lengva patikrinti diferencijuojant!
Nagrinėjami pavyzdžiai nebuvo patys sudėtingiausi. Praktikoje integralai yra labiau paplitę, kai konstanta yra ir laipsnyje, ir trigonometrinės funkcijos argumente, pavyzdžiui: . Daugelis žmonių susipainios dėl tokio integralo, o aš dažnai susipainioju. Faktas yra tai, kad yra didelė tikimybė, kad tirpale atsiras trupmenos, ir labai lengva ką nors prarasti dėl neatsargumo. Be to, yra didelė ženklų klaidos tikimybė, atkreipkite dėmesį, kad eksponentas turi minuso ženklą, ir tai sukelia papildomų sunkumų.
Paskutiniame etape rezultatas dažnai būna maždaug toks:
Net sprendimo pabaigoje turėtumėte būti ypač atsargūs ir teisingai suprasti trupmenas: 
Sudėtingų trupmenų integravimas
Pamažu artėjame prie pamokos pusiaujo ir pradedame svarstyti trupmenų integralus. Vėlgi, ne visi jie yra labai sudėtingi, tiesiog dėl vienokių ar kitokių priežasčių pavyzdžiai buvo šiek tiek „ne į temą“ kituose straipsniuose.
Tęsiant šaknų temą
9 pavyzdys
Raskite neapibrėžtą integralą
Vardiklyje po šaknimi yra kvadratinis trinaris ir „X“ formos „priedas“, esantis už šaknies ribų. Šio tipo integralas gali būti išspręstas naudojant standartinį pakaitalą.
Mes nusprendžiame: ![]()
Pakeitimas čia yra paprastas: ![]()
Pažvelkime į gyvenimą po pakeitimo: 
(1) Pakeitę šaknies terminus sumažiname iki bendro vardiklio.
(2) Išimame iš po šaknies.
(3) Skaitiklis ir vardiklis sumažinami . Tuo pačiu metu pagal šaknį pertvarkiau sąlygas patogia tvarka. Turint tam tikrą patirtį, žingsnius (1), (2) galima praleisti, komentuojamus veiksmus atliekant žodžiu.
(4) Gautas integralas, kaip prisimenate iš pamokos Kai kurių trupmenų integravimas, sprendžiama pilnas kvadrato ištraukimo metodas. Pasirinkite visą kvadratą.
(5) Integruodami gauname įprastą „ilgąjį“ logaritmą.
(6) Atliekame atvirkštinį pakeitimą. Jei iš pradžių , tada atgal: .
(7) Paskutiniu veiksmu siekiama ištiesinti rezultatą: po šaknimi vėl sujungiame terminus į bendrą vardiklį ir išimame juos iš po šaknies.
10 pavyzdys
Raskite neapibrėžtą integralą ![]()
Tai pavyzdys, kurį galite išspręsti patys. Čia prie vienetinio „X“ pridedama konstanta, o pakeitimas yra beveik toks pat: ![]()
Vienintelis dalykas, kurį jums reikia padaryti, yra išreikšti „x“ iš atliekamo pakeitimo: ![]()
Visas sprendimas ir atsakymas pamokos pabaigoje.
Kartais tokiame integrale po šaknimi gali būti kvadratinis dvinaris, tai sprendimo būdo nekeičia, bus dar paprasčiau. Pajuskite skirtumą:
11 pavyzdys
Raskite neapibrėžtą integralą
12 pavyzdys
Raskite neapibrėžtą integralą
Trumpi sprendimai ir atsakymai pamokos pabaigoje. Reikėtų pažymėti, kad 11 pavyzdys yra būtent toks binominis integralas, kurio sprendimo būdas buvo aptartas klasėje Iracionaliųjų funkcijų integralai.
Neskaidomo 2-ojo laipsnio daugianario integralas į laipsnį
(polinomas vardiklyje)
Retesnis integralo tipas, tačiau vis dėlto sutinkamas praktiniuose pavyzdžiuose.
13 pavyzdys
Raskite neapibrėžtą integralą
Bet grįžkime prie pavyzdžio su laimingu skaičiumi 13 (tiesą sakant, aš neatspėjau teisingai). Šis integralas taip pat yra vienas iš tų, kurie gali būti gana varginantys, jei nežinote, kaip išspręsti.
Sprendimas prasideda dirbtine transformacija: 
Manau, visi jau supranta, kaip dalyti skaitiklį iš vardiklio termino iš termino.
Gautas integralas paimamas dalimis: 

Formos ( – natūralusis skaičius) integralą išvedame pasikartojantis sumažinimo formulė:
, Kur ![]() – laipsniu žemesnis integralas.
– laipsniu žemesnis integralas.
Patikrinkime šios formulės pagrįstumą išspręstam integralui.
Šiuo atveju: , , naudojame formulę: 
Kaip matote, atsakymai yra tie patys.
14 pavyzdys
Raskite neapibrėžtą integralą
Tai pavyzdys, kurį galite išspręsti patys. Mėginio tirpalui naudojama aukščiau pateikta formulė du kartus iš eilės.
Jei pagal laipsnį yra nedalomas kvadratinis trinaris, tada sprendimas sumažinamas iki dvejetainio, išskiriant tobulą kvadratą, pavyzdžiui:
Ką daryti, jei skaitiklyje yra papildomas daugianomas? Šiuo atveju naudojamas neapibrėžtųjų koeficientų metodas, o integrandas išplečiamas į trupmenų sumą. Bet mano praktikoje yra toks pavyzdys niekada nesusitiko, todėl šiame straipsnyje praleidau šį atvejį Trupmeninių-racionalių funkcijų integralai, dabar praleisiu. Jei vis tiek susiduriate su tokiu integralu, pažiūrėkite į vadovėlį – ten viskas paprasta. Manau, kad nepatartina įtraukti medžiagos (net ir paprastos), kurios tikimybė susidurti yra lygi nuliui.
Sudėtingų trigonometrinių funkcijų integravimas
Daugumos pavyzdžių būdvardis „sudėtingas“ vėlgi yra sąlyginis. Pradėkime nuo liestinių ir kotangentų didelėmis galiomis. Naudojamų sprendimo būdų požiūriu tangentas ir kotangentas yra beveik tas pats dalykas, todėl kalbėsiu plačiau apie liestinę, o tai reiškia, kad parodytas integralo sprendimo metodas galioja ir kotangentui.
Aukščiau pateiktoje pamokoje mes apžvelgėme universalus trigonometrinis pakeitimas tam tikro tipo trigonometrinių funkcijų integralams išspręsti. Universalaus trigonometrinio pakeitimo trūkumas yra tas, kad jį naudojant dažnai susidaro sudėtingi integralai ir sudėtingi skaičiavimai. Ir kai kuriais atvejais galima išvengti universalaus trigonometrinio pakeitimo!
Panagrinėkime kitą kanoninį pavyzdį, vieno, padalyto iš sinuso, integralą:
17 pavyzdys
Raskite neapibrėžtą integralą
Čia galite naudoti universalų trigonometrinį pakeitimą ir gauti atsakymą, tačiau yra racionalesnis būdas. Pateiksiu visą sprendimą su komentarais kiekvienam žingsniui:

(1) Mes naudojame trigonometrinę dvigubo kampo sinuso formulę.
(2) Atliekame dirbtinę transformaciją: padalykite į vardiklį ir padauginkite iš .
(3) Vardiklyje naudodami gerai žinomą formulę, trupmeną paverčiame liestine.
(4) Funkciją pateikiame po diferencialiniu ženklu.
(5) Paimkite integralą.
Keletas paprastų pavyzdžių, kuriuos galite išspręsti patys:
18 pavyzdys
Raskite neapibrėžtą integralą
Pastaba: pats pirmasis žingsnis turėtų būti sumažinimo formulės naudojimas ![]() ir atidžiai atlikite veiksmus, panašius į ankstesnį pavyzdį.
ir atidžiai atlikite veiksmus, panašius į ankstesnį pavyzdį.
19 pavyzdys
Raskite neapibrėžtą integralą
Na, tai labai paprastas pavyzdys.
Užbaigti sprendimai ir atsakymai pamokos pabaigoje.
Manau, kad dabar niekas neturės problemų su integralais: ![]() ir tt
ir tt
Kokia metodo idėja? Idėja yra naudoti transformacijas ir trigonometrines formules, kad būtų galima organizuoti tik liestinės ir liestinės išvestinę į integrandą. Tai yra, mes kalbame apie pakeitimą: ![]() . 17–19 pavyzdžiuose iš tikrųjų naudojome šį pakeitimą, tačiau integralai buvo tokie paprasti, kad mums pavyko atlikti lygiavertį veiksmą – funkciją įtraukus į diferencialo ženklą.
. 17–19 pavyzdžiuose iš tikrųjų naudojome šį pakeitimą, tačiau integralai buvo tokie paprasti, kad mums pavyko atlikti lygiavertį veiksmą – funkciją įtraukus į diferencialo ženklą.
Panašus samprotavimas, kaip jau minėjau, gali būti atliktas ir kotangentui.
Taip pat yra formali išankstinė sąlyga, norint taikyti pirmiau nurodytą pakeitimą:
Kosinuso ir sinuso laipsnių suma yra neigiamas sveikasis skaičius LYGINIS skaičius, Pavyzdžiui:
integralui – neigiamas sveikasis LYGINIS skaičius.
! Pastaba : jei integralas turi TIK sinusą arba TIK kosinusą, tai integralas taip pat imamas neigiamam nelyginiam laipsniui (paprasčiausi atvejai yra pavyzdžiuose Nr. 17, 18).
Pažvelkime į keletą prasmingesnių užduočių, pagrįstų šia taisykle:
20 pavyzdys
Raskite neapibrėžtą integralą
Sinuso ir kosinuso laipsnių suma: 2 – 6 = –4 yra neigiamas sveikasis skaičius LYGINIS skaičius, o tai reiškia, kad integralas gali būti sumažintas iki liestinių ir jo išvestinės: 
(1) Transformuokime vardiklį.
(2) Naudodami gerai žinomą formulę gauname .
(3) Transformuokime vardiklį.
(4) Mes naudojame formulę ![]() .
.
(5) Funkciją pateikiame po diferencialiniu ženklu.
(6) Mes atliekame pakeitimą. Labiau patyrę studentai gali neatlikti keitimo, tačiau liestinę vis tiek geriau pakeisti viena raide – mažesnė rizika susipainioti.
21 pavyzdys
Raskite neapibrėžtą integralą
Tai pavyzdys, kurį galite išspręsti patys.
Laikykitės, čempionato etapai tuoj prasidės =)
Dažnai integrandas turi „maišytą“:
22 pavyzdys
Raskite neapibrėžtą integralą ![]()
Šis integralas iš pradžių turi liestinę, kuri iškart veda į jau pažįstamą mintį:

Dirbtinę transformaciją paliksiu pačioje pradžioje ir likusius žingsnius be komentarų, nes viskas jau buvo aptarta aukščiau.
Keletas kūrybingų pavyzdžių jūsų sprendimui:
23 pavyzdys
Raskite neapibrėžtą integralą ![]()
24 pavyzdys
Raskite neapibrėžtą integralą ![]()
Taip, juose, žinoma, galite sumažinti sinuso ir kosinuso laipsnius ir naudoti universalųjį trigonometrinį pakaitalą, tačiau sprendimas bus daug efektyvesnis ir trumpesnis, jei jis bus atliktas per tangentus. Visas sprendimas ir atsakymai pamokos pabaigoje
Integralų sprendimas yra lengvas uždavinys, tačiau tik kai kuriems iš jų. Šis straipsnis skirtas tiems, kurie nori išmokti suprasti integralus, bet nieko arba beveik nieko apie juos nežino. Integral... Kam to reikia? Kaip jį apskaičiuoti? Kas yra apibrėžtieji ir neapibrėžtieji integralai? Jei vienintelis integralas, kurį žinote, yra naudoti nėrimo kabliuką, panašų į integralo piktogramą, kad gautumėte ką nors naudingo iš sunkiai pasiekiamų vietų, sveiki atvykę! Sužinokite, kaip išspręsti integralus ir kodėl be jo neapsieisite.
Mes tiriame „integralo“ sąvoką
Integracija buvo žinoma dar Senovės Egipte. Žinoma, ne savo modernia forma, bet vis tiek. Nuo tada matematikai parašė daug knygų šia tema. Ypač pasižymėjo Niutonas Ir Leibnicas , bet dalykų esmė nepasikeitė. Kaip suprasti integralus nuo nulio? Jokiu būdu! Norėdami suprasti šią temą, jums vis tiek reikės pagrindinių matematinės analizės pagrindų žinių. Informacijos apie , būtinos integralams suprasti, jau turime savo tinklaraštyje.
Neapibrėžtas integralas
Leiskite mums atlikti tam tikrą funkciją f(x) .
Neapibrėžta integralinė funkcija f(x) ši funkcija vadinama F(x) , kurios išvestinė lygi funkcijai f(x) .
Kitaip tariant, integralas yra atvirkštinė arba antiderivatinė išvestinė. Beje, apie tai skaitykite mūsų straipsnyje.

Visoms nuolatinėms funkcijoms egzistuoja antidarinys. Taip pat prie antidarinio dažnai pridedamas pastovus ženklas, nes konstanta besiskiriančių funkcijų išvestiniai sutampa. Integralo radimo procesas vadinamas integracija.
Paprastas pavyzdys:

Kad nebūtų nuolat skaičiuojami elementariųjų funkcijų antidariniai, patogu juos sudėti į lentelę ir naudoti paruoštas reikšmes:

Apibrėžtasis integralas
Nagrinėdami integralo sąvoką, turime reikalą su be galo mažais dydžiais. Integralas padės apskaičiuoti figūros plotą, nevienodo kūno masę, nuvažiuotą atstumą netolygaus judėjimo metu ir dar daugiau. Reikia atsiminti, kad integralas yra be galo daug be galo mažų narių suma.
Kaip pavyzdį įsivaizduokite kokios nors funkcijos grafiką. Kaip rasti figūros plotą, kurį riboja funkcijos grafikas?

Naudojant integralą! Kreivinę trapeciją, apribotą koordinačių ašimis ir funkcijos grafiku, padalinkime į be galo mažus segmentus. Tokiu būdu figūra bus padalinta į plonus stulpelius. Stulpelių plotų suma bus trapecijos plotas. Tačiau atminkite, kad toks skaičiavimas duos apytikslį rezultatą. Tačiau kuo mažesni ir siauresni segmentai, tuo tikslesnis bus skaičiavimas. Jei sumažinsime juos tiek, kad ilgis būtų linkęs į nulį, tada segmentų plotų suma bus linkusi į figūros plotą. Tai yra apibrėžtas integralas, parašytas taip:

Taškai a ir b vadinami integracijos ribomis.
 Baris Alibasovas ir grupė „Integral“
Baris Alibasovas ir grupė „Integral“ Beje! Mūsų skaitytojams dabar taikoma 10% nuolaida
Manekenų integralų skaičiavimo taisyklės
Neapibrėžtinio integralo savybės
Kaip išspręsti neapibrėžtą integralą? Čia pažvelgsime į neapibrėžtinio integralo savybes, kurios pravers sprendžiant pavyzdžius.
- Integralo išvestinė lygi integrandui:

- Konstantą galima išimti iš po integralo ženklo:

- Sumos integralas lygus integralų sumai. Tai pasakytina ir apie skirtumą:
Apibrėžtinio integralo savybės
- Tiesiškumas:

- Integralo ženklas pasikeičia, jei integravimo ribos keičiamos:

- At bet koks taškų a, b Ir Su:

Jau išsiaiškinome, kad apibrėžtasis integralas yra sumos riba. Bet kaip gauti konkrečią vertę sprendžiant pavyzdį? Tam yra Niutono-Leibnizo formulė:

Integralų sprendimo pavyzdžiai
Toliau apžvelgsime keletą neapibrėžtų integralų radimo pavyzdžių. Siūlome patiems išsiaiškinti sprendimo subtilybes, o jei kas neaišku, užduoti klausimus komentaruose.

Norėdami sustiprinti medžiagą, žiūrėkite vaizdo įrašą apie tai, kaip integralai sprendžiami praktiškai. Nenusiminkite, jei integralas pateikiamas ne iš karto. Susisiekite su profesionalia studentų aptarnavimo tarnyba ir bet koks trigubas arba išlenktas integralas ant uždaro paviršiaus bus jūsų galioje.
Ši formulė vadinama integravimas pagal dalių formulę neapibrėžtame integralu:
Norint taikyti integravimo dalimis formulę, integrandą reikia padalyti į du veiksnius. Vienas iš jų žymimas u, o likusi dalis nurodo antrąjį veiksnį ir žymima dv. Tada diferencijuodami randame du o integracija – funkcija v. Tuo pačiu metu, už u dv- tokia integrando dalis, kurią galima lengvai integruoti.
Kada naudinga naudoti integravimo dalimis metodą? Tada kada integrandas yra :
1) - logaritminės funkcijos, taip pat atvirkštinės trigonometrinės funkcijos (su priešdėliu "lankas"), tada, remiantis ilgalaike integravimo dalimis patirtimi, šios funkcijos žymimos u;
2) , , - sinusas, kosinusas ir eksponentas, padaugintas iš P(x) yra savavališkas x daugianomas, tada šios funkcijos žymimos dv, o daugianomas yra per u;
3) , , , , šiuo atveju integravimas dalimis taikomas du kartus.
Paaiškinkime integravimo dalimis metodo reikšmę pirmojo atvejo pavyzdžiu. Tegul išraiškoje po integralo ženklu yra logaritminė funkcija (tai bus 1 pavyzdys). Naudojant integravimą dalimis, toks integralas sumažinamas iki tik algebrinių funkcijų (dažniausiai daugianario) integralo, ty neturinčio logaritminės ar atvirkštinės trigonometrinės funkcijos. Integravimo dalimis formulės naudojimas, pateikta pačioje pamokos pradžioje
pirmuoju nariu (be integralo) gauname logaritminę funkciją, o antruoju nariu (po integralo ženklu) funkciją, kurioje nėra logaritmo. Algebrinės funkcijos integralas yra daug paprastesnis nei integralas, po kurio ženklu logaritminė arba atvirkštinė trigonometrinė funkcija randama atskirai arba kartu su algebriniu koeficientu.
Taigi, naudojant integravimas dalių formulėmis integracija atliekama ne iš karto: duoto integralo radimas sumažinamas iki kito. Integravimo dalimis formulės prasmė ta, kad ją pritaikius naujas integralas tampa lentelės pavidalu arba bent jau tampa paprastesnis už pradinį.
Integravimo pagal dalis metodas pagrįstas formulės, skirtos atskirti dviejų funkcijų sandaugą, naudojimu:
tada jis gali būti parašytas formoje
kuri buvo duota pačioje pamokos pradžioje.
Kai randama integruojant funkciją v jam gaunamas begalinis antidarinių funkcijų rinkinys. Norėdami taikyti integravimo pagal dalis formulę, galite paimti bet kurią iš jų, taigi ir tą, kuri atitinka savavališką konstantą SU, lygus nuliui. Todėl ieškant funkciją v savavališka konstanta SU neturėtų būti įvestas.
Integravimo dalimis metodas turi labai ypatingą pritaikymą: juo galima išvesti pasikartojančias formules antiderivatinėms funkcijoms rasti, kai reikia sumažinti funkcijų laipsnį po integralo ženklu. Sumažinti laipsnį būtina, kai nėra lentelių integralų, skirtų, pavyzdžiui, funkcijoms, tokioms kaip sinusai ir kosinusai į laipsnius, didesnius už antrąjį ir jų sandaugoms. Pasikartojanti formulė yra formulė, skirta rasti kitą sekos narį per ankstesnį narį. Nurodytais atvejais tikslas pasiekiamas nuosekliai mažinant laipsnį. Taigi, jei integrandas yra sinusas iki ketvirtosios laipsnio x, tai naudojant integravimo dalimis metodą galima rasti sinuso integralo į trečiąjį laipsnį formulę ir pan. Paskutinė šios pamokos pastraipa skirta aprašytai užduočiai.
Integracijos taikymas dalimis kartu
1 pavyzdys. Raskite neapibrėžtą integralą integravimo dalimis metodu:
Sprendimas. Integrando išraiškoje - logaritmas, kuris, kaip jau žinome, gali būti pagrįstai žymimas u. Mes tikime, kad,.
Randame (kaip jau buvo minėta teorinės nuorodos paaiškinime, pirmajame naryje iškart gauname logaritminę funkciją (be integralo), o antrajame (po integralo ženklu) – funkciją be logaritmo:

Ir vėl logaritmas...
2 pavyzdys. Raskite neapibrėžtą integralą:
Sprendimas. Tegul,.
Logaritmas yra kvadrate. Tai reiškia, kad ją reikia diferencijuoti kaip sudėtingą funkciją. Mes randame
,
.
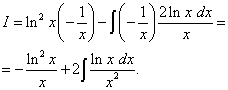
Antrąjį integralą vėlgi randame dalimis ir gauname jau minėtą pranašumą (pirmajame naryje (be integralo) yra logaritminė funkcija, o antrajame (po integralo ženklu) funkcija, kurioje nėra logaritmas).
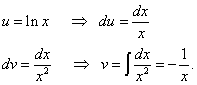

Mes randame originalų integralą:

3 pavyzdys.
Sprendimas. Arktangentas, kaip ir logaritmas, geriau žymimas u. Taigi tegul,.
Tada,
.
Taikydami integravimo dalimis formulę, gauname:
![]()
Antrąjį integralą randame pakeitę kintamąjį.

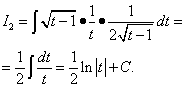
Grįžtant prie kintamojo x, gauname
![]() .
.
Mes randame originalų integralą:
![]() .
.
4 pavyzdys. Raskite neapibrėžtąjį integralą integruodami dalimis:
Sprendimas. Geriau rodiklį žymėti dv. Integrandą padalijome į du veiksnius. Tikėdamas tuo
5 pavyzdys. Raskite neapibrėžtąjį integralą integravimo dalimis metodu:
![]() .
.
Sprendimas. Tegul,. Tada,.
Naudodami integravimo pagal dalis formulę (1), randame:
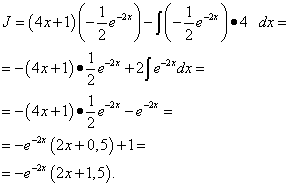
6 pavyzdys. Raskite neapibrėžtą integralą integruodami dalimis:
Sprendimas. Sinusą, kaip ir eksponentinį, galima patogiai žymėti dv. Tegul,.
Naudodami integravimo pagal dalis formulę randame:
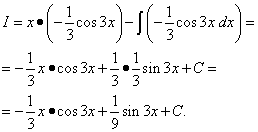
Integraciją dalimis vėl taikome kartu
10 pavyzdys. Raskite neapibrėžtą integralą integruodami dalimis:
![]() .
.
Sprendimas. Kaip ir visais panašiais atvejais, patogu kosinusą žymėti dv. Mes žymime ,.
Tada ![]() ,
.
,
.
Naudodami integravimo dalimis formulę, gauname:
Integraciją dalimis taikome ir antrajam terminui. Mes žymime ,.
Naudodami šiuos užrašus integruojame minėtą terminą:

Dabar randame reikiamą integralą:

Tarp integralų, kuriuos galima išspręsti integravimo dalimis metodu, yra ir tokių, kurie nepatenka į nė vieną iš trijų teorinėje dalyje paminėtų grupių, kuriems iš praktikos žinoma, kad geriau žymėti u, o per ką dv. Todėl tokiais atvejais reikia atsižvelgti į patogumą, taip pat pateiktą pastraipoje „Integravimo dalimis metodo esmė“: u reikėtų paimti integrando dalį, kuri diferencijuojant netaps daug sudėtingesnė, bet dv- tokia integrando dalis, kurią galima lengvai integruoti. Paskutinis šios pamokos pavyzdys yra būtent tokio integralo sprendimas.
Integravimo pagal dalis formulė atrodo taip:
.
Integravimo dalimis metodas susideda iš šios formulės taikymo. Praktikoje verta paminėti, kad u ir v yra integravimo kintamojo funkcijos. Tegul integravimo kintamasis žymimas kaip x (simbolis po diferencialinio ženklo d integralo žymėjimo pabaigoje). Tada u ir v yra x funkcijos: u(x) ir v(x) .
Tada
, .
Ir integravimo pagal dalis formulė yra tokia:
.
Tai reiškia, kad integrando funkcija turi būti sudaryta iš dviejų funkcijų sandaugos:
,
iš kurių vieną žymime u: g(x) = u, o kitam reikia apskaičiuoti integralą (tiksliau, reikia rasti antidarinį):
, tada dv = f(x) dx .
Kai kuriais atvejais f(x) = 1
.
,
Tai yra, integralu
galime dėti g(x) = u, x = v .
Tęsti
;
.
Taigi, taikant šį metodą, integravimo pagal dalis formulę reikia atsiminti ir taikyti dviem formomis:
Integralai, apskaičiuoti integruojant dalimis
Integralai, kuriuose yra logaritmų ir atvirkštinių trigonometrinių (hiperbolinių) funkcijų
Integralai, kuriuose yra logaritmų ir atvirkštinių trigonometrinių ar hiperbolinių funkcijų, dažnai integruojami dalimis. Šiuo atveju dalis, kurioje yra logaritmas arba atvirkštinės trigonometrinės (hiperbolinės) funkcijos, žymima u, likusi dalis – dv.
, , , , , , .
Štai tokių integralų, kurie apskaičiuojami integravimo dalimis metodu, pavyzdžiai:
Integralai, kuriuose yra daugianario sandauga ir sin x, cos x arba e x
, , ,
čia P(x) yra x daugianomas. Integruojant daugianomas P(x) žymimas u, o e ax dx, cos ax dx arba nuodėmės kirvis dx
- per dv.
, , .
Štai tokių integralų pavyzdžiai:
Integralų skaičiavimo taikant integravimo dalimis metodą pavyzdžiai
Integralų, kuriuose yra logaritmų ir atvirkštinių trigonometrinių funkcijų, pavyzdžiai
Pavyzdys
Apskaičiuokite integralą:
Detalus sprendimas
Čia integrandas turi logaritmą. Pakeitimų darymas u =,
ln x dv = x.
Tada
,
.
2 dx
.
Tada
.
Apskaičiuojame likusį integralą:
Skaičiavimų pabaigoje būtina pridėti konstantą C, nes neapibrėžtasis integralas yra visų antidarinių aibė. Jis taip pat gali būti įtrauktas į tarpinius skaičiavimus, tačiau tai tik sujauktų skaičiavimus.
Trumpesnis sprendimas
.Galite pateikti sprendimą trumpesniu variantu. Norėdami tai padaryti, jums nereikia keisti u ir v, tačiau galite sugrupuoti veiksnius ir pritaikyti integravimo pagal dalis formulę antroje formoje.
Atsakymas
Integralų, kuriuose yra logaritmų ir atvirkštinių trigonometrinių funkcijų, pavyzdžiai
Pavyzdys
.
Integralų, kuriuose yra daugianario ir sin x, cos x arba ex sandauga, pavyzdžiai
Sprendimas
Įveskime eksponentą po diferencialo ženklu:.
e - x dx = - e - x d(-x) = - d(e - x)
.
Integruokime dalimis.
.
.
.
Taip pat naudojame integravimo dalimis metodą.
Pagaliau turime. Integravimas dalimis
– metodas, naudojamas apibrėžtiesiems ir neapibrėžtiesiems integralams spręsti, kai vienas iš integrandų yra lengvai integruojamas, o kitas – diferencijuotas. Gana paplitęs metodas ieškant integralų, tiek neapibrėžtų, tiek apibrėžtų. Pagrindinis ženklas, kai reikia jį naudoti, yra tam tikra funkcija, susidedanti iš dviejų funkcijų sandaugos, kurių negalima integruoti taške.
Formulė
Norint sėkmingai naudoti šį metodą, reikia suprasti ir išmokti formules.
Neapibrėžtinio integralo integravimo dalimis formulė:
$$ \int udv = uv - \int vdu $$
Integravimo dalimis į apibrėžtąjį integralą formulė:
$$ \int \limits_(a)^(b) udv = uv \bigg |_(a)^(b) - \int \limits_(a)^(b) vdu $$
Sprendimų pavyzdžiai
| Praktiškai panagrinėkime integravimo dalimis sprendimų, kuriuos dažnai siūlo mokytojai testų metu, pavyzdžius. Atkreipkite dėmesį, kad po integralo simboliu yra dviejų funkcijų sandauga. Tai ženklas, kad šis metodas tinka sprendimui. |
| 1 pavyzdys |
| Raskite integralą $ \int xe^xdx $ |
|
Matome, kad integrandas susideda iš dviejų funkcijų, iš kurių viena, diferencijavus, akimirksniu virsta vienybe, o kita lengvai integruojama. Integralui išspręsti naudojame integravimo dalimis metodą. Tarkime, kad $ u = x \rightarrow du=dx $ ir $ dv = e^x dx \rightarrow v=e^x $ Rastas reikšmes pakeičiame į pirmąją integravimo formulę ir gauname: $$ \int xe^x dx = xe^x - \int e^x dx = xe^x - e^x + C $$ Jei negalite išspręsti savo problemos, atsiųskite ją mums. Pateiksime išsamų sprendimą. Galėsite stebėti skaičiavimo eigą ir gauti informacijos. Tai padės jums laiku gauti pažymį iš savo mokytojo! |
| Atsakymas |
|
$$ \int xe^x dx = xe^x - e^x + C $$ |
| 4 pavyzdys |
| Apskaičiuokite integralą $ \int \limits_0 ^1 (x+5) 3^x dx $ |
| Raskite integralą $ \int xe^xdx $ |
|
Analogiškai su ankstesniais išspręstais pavyzdžiais išsiaiškinsime, kurią funkciją be problemų integruoti, kurią atskirti. Atkreipkite dėmesį, kad jei atskirsime $ (x+5) $, tada ši išraiška bus automatiškai konvertuojama į vienybę, o tai mums bus naudinga. Taigi mes darome taip: $$ u=x+5 \rightarrow du=dx, dv=3^x dx \rightarrow v=\frac(3^x)(ln3) $$ Dabar visos nežinomos funkcijos buvo rastos ir gali būti įtrauktos į antrąją formulę integravimui dalimis apibrėžtam integralui. $$ \int \limits_0 ^1 (x+5) 3^x dx = (x+5) \frac(3^x)(\ln 3) \bigg |_0 ^1 - \int \limits_0 ^1 \frac (3^x dx)(\ln 3) = $$ $$ = \frac(18)(\ln 3) - \frac(5)(\ln 3) - \frac(3^x)(\ln^2 3)\bigg| _0 ^1 = \frac(13)(\ln 3) - \frac(3)(\ln^2 3)+\frac(1)(\ln^2 3) = \frac(13)(\ln 3) )-\frac(4)(\ln^2 3) $$ |
| Atsakymas |
| $$ \int\limits_0 ^1 (x+5)3^x dx = \frac(13)(\ln 3)-\frac(4)(\ln^2 3) $$ |








