Pristatymas pamokai „Trikampių panašumo praktiniai pritaikymai“. Trikampio panašumo praktiniai pritaikymai

2.

Vidutinės tiesės teorema.

Tėčio veltiniai batai ir tavo;….

(tęsti).

Gyvenime kalbame apie panašius objektus, o geometrijoje – apie panašius objektus. Tai reiškia, kad mūsų teoriją galima pritaikyti šiems dalykams. Pažvelkime į mus supančio pasaulio trikampių panašumo teoriją.

Suformuluokime pamokos temą.

Darbas poromis:

KAM

A Ar tiesa, kad: ?ABC ∞ ?A1B1C1, jei ∠A = 46° ∠B = 64° ∠A1 = 46° ∠C1 = 70°

L Ar tiesa, kad: ?ABC ∞ ?A1B1C1, jei AB=13m A1B1=58m P?ABC =25m, tai P?A1B1C1 =100m

b Ar tiesa, kad: ?ABC ∞ ?A1B1C1, jei AB=15m A1B1=45m S?A1B1C1 =27 m2, tai S?ABC =100m2

KAM

L

F

A Ar tiesa, kad jei, tada

Patikrinkite: kokį žodį gavai? - "Alfa".

* Šiek tiek informacijos:

• Mūsų saulės sistemoje 1 žvaigždė yra saulė.
• Žvaigždės – žvaigždyne ryškiausia žvaigždyno žvaigždė vadinama „Alfa“.
• Žvaigždės yra mūsų nepasiekiami objektai, tačiau jie yra tiriami ir atstumas iki jų randamas.

Kaip tai padaryti?

Atstumo iki neprieinamo taško nustatymas. Tarkime, kad reikia rasti atstumą nuo taško A iki nepasiekiamo taško B. Norėdami tai padaryti, pasirinkite tašką C žemėje, nubrėžkite atkarpą AC ir išmatuokite ją. Tada, naudodami astrolabiją, išmatuojame kampus ∠A ir ∠C. Ant popieriaus lapo pastatome kokį nors trikampį?A1B1C1, kuriame ∠A1=∠A, ∠C1=∠C, ir išmatuojame šio trikampio kraštinių A1B1 ir A1C1 ilgius.

Kadangi?ABC ∞ ?A1B1C1, tada =, iš kur. Naudodami žinomus atstumus AC, A1C1 ir A1B1 randame atstumą AB.

Skaičiavimams supaprastinti patogu sukonstruoti trikampį?A1B1C1, kad A1C1: AC = 1:1000. Pavyzdžiui, jei AC = 130 m, atstumas A1C1 lygus 130 mm. Šiuo atveju = 1000, todėl išmatuodami atstumą A1B1 milimetrais iš karto gauname atstumą AB metrais.

Pavyzdys. Tegul AC = 130 m, ∠A = 73° ir ∠C = 58°. Ant popieriaus sukonstruojame trikampį?A1B1C1, kad ∠A1 = 73° ir ∠С1 = 58°, A1C1 = 130mm, ir išmatuokite atkarpą A1B1. Jis lygus 153 mm, taigi reikiamas atstumas yra 153 m.

4.

Kunigas arogantiškai tęsė:

CAB ∞ ?BDE (2 kampais)

• C = ∠B (pagal sąlygą)
• B = ∠E = 90°

Atsakymas: 146 m.

AB=2,1 m AE=6,3 m CB=1,7 m

1. Trikampiai yra panašūs 2 kampais.

ABC ∞ ?AED (2 kampais)

• A – bendras
• B = ∠E = 90°

Atsakymas: 5,1 m.

Pavyzdys:

O! Pavargęs

Vos neatsilieka nuo mokytojo

Peržiūrėkite dokumento turinį
„Geometrijos pamokos tema „Trikampių panašumo praktiniai pritaikymai“ santrauka. »

Savivaldybės švietimo įstaiga

„Pavadinta jūrų kariūnų mokykla. Admirolas P. G. Kotovas“.

Geometrijos pamoka (8 klasė)

Tema: „Praktinis trikampio panašumo pritaikymas“.

Skirmantas Natalija Rudolfovna

aukštosios matematikos mokytojas

Darbo adresas:

164520, Archangelsko sritis,

Severodvinskas, Šv. Komsomolskaya, 7,

darbo telefonas 55-20-86

Severodvinskas

Pamokos tikslai ir uždaviniai:

parodyti trikampių panašumo panaudojimą atliekant matavimo darbus ant žemės;

parodyti teorijos ir praktikos ryšį;

supažindinti mokinius su įvairiais objekto aukščio ir atstumo iki neprieinamo objekto nustatymo būdais;

ugdyti gebėjimą pritaikyti įgytas žinias sprendžiant įvairias tokio pobūdžio problemas.

Vystantis

didinti studentų susidomėjimą geometrijos studijomis;

intensyvinti mokinių pažintinę veiklą;

formuoti matematinei veiklai būdingas ir produktyviam visuomenės gyvenimui reikalingas mąstymo savybes.

Švietimo

motyvuoti mokinių domėjimąsi dalyku, įtraukiant juos į praktinių problemų sprendimą.

Pamokos eiga:

1.Namų darbų tikrinimas.

2. Testas „Ar tai tiesa...“ (darbas poromis) – teorijos kartojimas.

3. Užduotis Nr. 1. Atstumo iki neprieinamo taško nustatymas (sąsiuvinių pildymas su mokytoju).

4. Užduotis Nr. 2. Objekto aukščio nustatymas:

A). per visą jo šešėlio ilgį (pažiūrėkite į paruoštą sprendimą vadovėlyje, patys nubraižykite 1 variantą savo sąsiuviniuose).

b). ant stulpo (išardykite pagal paruoštą sprendimą vadovėlyje, patys savo sąsiuviniuose nubraižykite 2 variantą).

V). naudojant veidrodį (pasiūlyti analizuoti problemą Nr. 581).

5. Pamokos rezultatai, namų darbai Nr.581,583.

1. Namų darbų tikrinimas. 550(1) paruošto sprendimo paaiškinimas.

Duota: piešimas.

Trikampiai yra panašūs 2 kampais.

∆BAD ∞ ∆KCB (2 kampais)

∠B = ∠K (pagal sąlygą)

∠A = ∠C = 90°

2. Mokytojas: „Vaikinai, mes išstudijavome visą trikampių panašumo teoriją“.

Mes svarstėme panašumo panaudojimą įrodinėdami teoremas.

Kokias teoremas mes įrodėme?

Vidutinės tiesės teorema.

Trikampio medianų savybė.

Kasdieniame gyvenime esame apsupti tos pačios formos daiktų.

Pavyzdys: - teniso ir futbolo kamuolys;

Tėčio veltiniai batai ir tavo;….

(tęsti).

Gyvenime kalbame apie panašius objektus, o geometrijoje – apie panašius objektus. Tai reiškia, kad mūsų teoriją galima pritaikyti šiems dalykams. Pažvelkime į mus supančio pasaulio trikampių panašumo teoriją.

Suformuluokime pamokos temą.

Studentai: „Praktinis trikampių panašumo pritaikymas“.

Mokytojas: „Kad galėtume pritaikyti teoriją, turime ją gerai žinoti. Pakartokime:

Darbas poromis:

Ar šis teiginys teisingas? Jei tiesa, palikite raidę prieš teiginį, kitu atveju perbraukite.

Testas „Ar tai tiesa...“ (darbas poromis) – teorijos kartojimas.

KAM Ar tiesa, kad: panašiuose trikampiuose panašios kraštinės yra lygios.

A Ar tiesa, kad: ∆ABC ∞ ∆A 1 B 1 C 1, jei ∠A = 46° ∠B = 64° ∠A1 = 46° ∠C1 = 70°

L Ar tiesa, kad: ∆ABC ∞ ∆A 1 B 1 C 1, jei AB=13m A1B1=58m P ∆ ABC =25m, tai P ∆ A 1 B 1 C 1 =100m

b Ar tiesa, kad: ∆ABC ∞ ∆A1B1C1, jei AB=15m A1B1=45m S ∆ A 1 B 1 C 1 =27 m 2, tai S ∆ ABC =100m 2

KAM Ar tiesa, kad: panašiuose trikampiuose atitinkami kampai yra proporcingi

L Ar tiesa (trumpas trikampių panašumo kriterijaus teiginys) "Trikampiai yra panašūs trimis kampais"

F Ar tiesa (trumpas trikampių panašumo kriterijaus teiginys) „Trikampiai yra panašūs dviem proporcingomis kraštinėmis ir kampu tarp jų?

A Ar tiesa, kad jei, tada

Patikrinkite: kokį žodį gavai? - "Alfa".

* Šiek tiek informacijos:

• Mūsų saulės sistemoje 1 žvaigždė yra saulė.

  Visos kitos žvaigždės yra už mūsų saulės sistemos ribų.

  Žvaigždės yra žvaigždyne, o ryškiausia žvaigždyno žvaigždė vadinama „Alfa“.

  Žvaigždės yra mūsų nepasiekiami objektai, tačiau jie yra tiriami ir atstumas iki jų randamas.

Kaip tai padaryti?

3. Užduotis Nr. 1. Atstumo iki nepasiekiamo taško nustatymas (su mokytoju pildyti užrašus sąsiuviniuose).

Atstumo iki neprieinamo taško nustatymas. Tarkime, kad reikia rasti atstumą nuo taško A iki nepasiekiamo taško B. Norėdami tai padaryti, pasirinkite tašką C žemėje, nubrėžkite atkarpą AC ir išmatuokite ją. Tada, naudodami astrolabiją, išmatuojame kampus ∠A ir ∠C. Ant popieriaus lapo pastatome kokį nors trikampį ∆A 1 B 1 C 1, kuriame ∠A 1 =∠A, ∠C 1 =∠C, ir išmatuojame kraštinių A 1 B 1 ir A 1 C 1 ilgius. šis trikampis.

Kadangi ∆ABC ∞ ∆A 1 B 1 C 1 , tai = , iš kur. Naudodami žinomus atstumus AC, A 1 C 1 ir A 1 B 1 randame atstumą AB.

Skaičiavimams supaprastinti patogu sukonstruoti trikampį ∆A 1 B 1 C 1 taip, kad A 1 C 1: AC = 1:1000. Pavyzdžiui, jei AC = 130 m, tada atstumas A 1 C 1 lygus 130 mm. Šiuo atveju = 1000, todėl išmatavę atstumą A 1 B 1 milimetrais, iš karto gauname atstumą AB metrais.

Pavyzdys. Tegul AC = 130 m, ∠A = 73° ir ∠C = 58°. Ant popieriaus sukonstruojame trikampį ∆A 1 B 1 C 1 taip, kad ∠A 1 = 73° ir ∠C 1 = 58°, A 1 C 1 = 130 mm, ir išmatuokite atkarpą A 1 B 1. Jis lygus 153 mm, taigi reikiamas atstumas yra 153 m.

4. Mokytojas: Grįžkime prie žemiškų reikalų. Graikijos mokslininkai išsprendė daug praktinių problemų, kurių anksčiau jiems nepavyko išspręsti. Pavyzdžiui, šešis šimtmečius prieš Kristų graikų išminčius Talis iš Mileto mokė egiptiečius nustatyti piramidės aukštį pagal jos šešėlio ilgį.

Kaip tai atsitiko, aprašyta Ya.I. Perelman "Pramoginė geometrija". Talis, pasak legendos, pasirinko dieną ir valandą, kai jo paties šešėlio ilgis buvo lygus jo ūgiui; šiuo momentu piramidės aukštis taip pat turi būti lygus jos metamo šešėlio ilgiui. Tai, ko gero, vienintelis atvejis, kai žmogus pasinaudojo savo šešėliu. Paklausykime palyginimo. (sako vienas iš mokinių).

„Pavargęs šiaurinis nepažįstamasis atvyko į Didžiosios Hapio šalį. Saulė jau leidosi, kai jis priėjo prie nuostabių faraono rūmų ir kažką pasakė tarnams. Jie akimirksniu atidarė jam duris ir įvedė į priėmimo salę. Ir štai jis stovi dulkėtu lauko apsiaustu, o priešais jį paauksuotame soste sėdi įžūlūs kunigai, amžinųjų gamtos paslapčių sergėtojai.

kas tu toks? – paklausė vyriausiasis kunigas.

Mano vardas Talis. Aš esu kilęs iš Mileto.

Kunigas arogantiškai tęsė:

Vadinasi, tu gyrėsi, kad gali išmatuoti piramidės aukštį į ją neįkopdamas? - juokdamiesi pasilenkė kunigai.

Bus gerai, – pašaipiai tęsė kunigas, – jei suklysite ne daugiau kaip šimtu uolekčių.

Galiu išmatuoti piramidės aukštį ir nutolti ne daugiau kaip puse uolekties. Aš tai padarysiu rytoj.

Kunigų veidai aptemo. Koks įžūlumas! Šis nepažįstamasis tvirtina, kad gali suprasti, ko jie, Didžiojo Egipto kunigai, negali.

Gerai, pasakė faraonas. – Prie rūmų yra piramidė, žinome jos aukštį. Rytoj mes patikrinsime jūsų meną“.

Kitą dieną Talis rado ilgą lazdą ir įsmeigė ją į žemę kiek toliau nuo piramidės. Laukiau tam tikro momento. Jis išmatavo lazdos šešėlį ir piramidės šešėlį. Palyginęs realių objektų aukščių santykius su jų šešėlių ilgiais, Talis nustatė piramidės aukštį.

Užduotis Nr. 2. Objekto aukščio nustatymas:

A). per visą jo šešėlio ilgį (pažiūrėkite į paruoštą sprendimą vadovėlyje, patys nubraižykite 1 variantą savo sąsiuviniuose).

CB = 8,4 m BE = 1022 m AB = 1,2 m ∠C = ∠B

Trikampiai yra panašūs 2 kampais.

∆CAB ∞ ∆BDE (2 kampais)

∠C = ∠B (pagal sąlygą)

∠B = ∠E = 90°

Atsakymas: 146 m.

b). ant stulpo (išardykite pagal paruoštą sprendimą vadovėlyje, patys savo sąsiuviniuose nubraižykite 2 variantą).

AB=2,1 m AE=6,3 m CB=1,7 m

Trikampiai yra panašūs 2 kampais.

∆ABC ∞ ∆AED (2 kampais)

∠A – bendras

∠B = ∠E = 90°

Atsakymas: 5,1 m.

V). naudojant veidrodį (pasiūlyti analizuoti problemą Nr. 581 (D/z)).

Norėdami nustatyti medžio aukštį, galite naudoti veidrodį, kaip parodyta paveikslėlyje. Šviesos spindulys FD, atsispindėjęs nuo veidrodžio taške D, patenka į žmogaus akį (taškas B). Nustatykite medžio aukštį, jei AC=165 cm, BC=12 cm, AD=120 cm, DE=4,8 m, ∠1 = ∠2.

5. Mokytojas: Apibendrinkime pamoką:

Šiandien klasėje sužinojome apie įvairius objekto aukščio matavimo būdus; atstumas iki neprieinamo taško; pritaikė panašumo teoriją.

Suformuluokite savo požiūrį į pamoką sakiniu ar fraze, pradėdami ją raide, įtraukta į žodį „panašumas“

Pavyzdys:

O! Pavargęs

Vos neatsilieka nuo mokytojo

Pristatymas „Praktiniai trikampio panašumo pritaikymai“ padės mokytojams aiškiau ir suprantamiau paaiškinti vieną iš svarbių geometrijos kurso pamokų aštuntokams. Medžiaga nėra tokia paprasta, kaip gali pasirodyti iš pirmo žvilgsnio. Tam reikia skirti pakankamai dėmesio, kad moksleiviai gerai suprastų šią temą. Ateityje trigonometriniai uždaviniai atsiras praktikoje atliekant namų darbus ir testus. Kad aštuntos klasės mokiniai pasirodytų aukštu lygiu, būtina, kad jie nepraleistų nei vienos pamokos, nes tiek geometrijos, tiek algebros temos yra tarpusavyje susijusios.

Pristatymas turi aiškią struktūrą. Skaidrėse elementai rodomi nuosekliai. Tekstas nesudėtingas ir parašytas taip, kad mokiniai jį suprastų kuo geriau. Nėra atitraukiančių ryškių spalvų, fono raštų ir pan.

1-2 skaidrės (Pristatymo tema „Trikampio panašumo praktiniai pritaikymai“, pavyzdys)

Pirmoje daugialypės terpės failo skaidrėje prašoma atlikti konstravimo užduotį. Reikia gauti trikampį, turintį du žinomus kampus ir trečiojo kampo viršūnėje pusiausvyrą. Kaip tai turėtų būti įgyvendinta?

Žemiau paryškinti trys elementai. Pirmasis elementas yra atkarpa, kuri dėl to bus gauto trikampio pusiausvyra. Kiti du elementai yra nurodyti kampai. Matome, kad jų priemonės skiriasi. Tai reiškia, kad gauname lygiašonį trikampį. Belieka sukonstruoti reikiamą figūrą.

Dėl konstrukcijos mes gavome trikampį, kurio pagrinde yra du iš anksto nustatyti kampai. Tačiau nubrėžę atkarpą, lygiagrečią pagrindui, einančią per apatinę pusiausvyros viršūnę, gausime norimą figūrą. Be to, matote, kad pirmojo ir antrojo trikampių pagrindų kampai yra lygūs, o jų viršūnė yra ta pati. Tai byloja apie jų lygybę.

3–4 skaidrės (pavyzdžiai)

Kitoje skaidrėje turime du panašius trikampius. Be to, atidžiai išnagrinėję juos, galite sužinoti, kad jie yra stačiakampiai. Šioje skaidrėje bus kalbama apie aukščio nustatymą. Kadangi trikampiai yra panašūs pagal pirmąjį ženklą, jų aukščių santykis bus lygus jų kojų, į kurias aukščiai praleisti, santykiui. Iš proporcijos galite išreikšti norimą aukštį.

Kad būtų aiškiau, toliau pateikiamas pavyzdys su skaitinėmis reikšmėmis. Jei aštuntokai negali jų išspręsti patys, tuomet galite parodyti jiems sprendimą iš tos pačios skaidrės. Panašiai galite rasti kitas puses, naudodamiesi žiniomis apie panašius trikampius.

5 skaidrė (pavyzdys)

Pirmiausia turite išnagrinėti figūras. Kaip matote, jie yra panašūs. Juk jie turi du vienodus kampus, o tai rodo, kad pirmasis trikampių panašumo ženklas yra patenkintas.
Remdamiesi trikampių panašumu, galime užrašyti atitinkamų kraštinių proporcingą santykį. Iš gautos lygybės galime išreikšti reikiamą pusę. Norint geriau suprasti, pateikiamas pavyzdys su skaitinėmis reikšmėmis. Mažo trikampio pagrindas yra tūkstantį kartų mažesnis už didelio trikampio pagrindą. Taip pat žinomi šių pagrindų ilgiai.

Skaitinis sprendimas pateikiamas kitoje skaidrėje. Čia taip pat pateikiami kampų matai. Išreikškime reikiamą pusę iš lygybės, kurią gavome paskutinėje skaidrėje. Tada pakeiskime turimus duomenis. Taigi gauname norimos pusės ilgį. Kitaip tariant, mes gavome atstumą iki netinkamo taško.

Taigi šio daugialypės terpės failo dėka moksleiviai susipažins su panašių trikampių konstravimu, taip pat išmoks rasti tam tikro trikampio aukštį, žinodami informaciją apie panašaus trikampio kraštines. Labai svarbu, kad aštuntos klasės mokiniai išmoktų sudaryti proporcijas ir su jomis dirbti, tai yra išreikšti kai kuriuos lygybės elementus.

Geometrijos pamoka 8 klasėje tema "Trikampių panašumo praktinis pritaikymas" 2016-2017 mokslo metams.

"" Geometrija yra galingiausia
priemonė paaštrinti mūsų protą
gebėjimus ir suteikia galimybę teisingai
galvok ir mąstyk“.
G. Galilėjus

Pamokos tikslas: mokyti taikyti teorines žinias sprendžiant praktinio turinio problemas.

Užduotys:

Švietimas:

apibendrinti ir sisteminti žinias tema: „Trikampių panašumo ženklai“;

ugdyti gebėjimus apibendrinti, abstrahuoti ir konkretizuoti tiriamų objektų ir santykių savybes bei pritaikyti jas sprendžiant praktines problemas;

toliau ugdyti mokinių įgūdžius naudojant trikampių panašumo ženklus sprendžiant uždavinius.

Švietimas:

ugdyti loginį mąstymą, gebėjimą lyginti, apibendrinti, daryti išvadas;

ugdyti mokinių susidomėjimą studijuojamu dalyku;

mokinių kūrybinių gebėjimų ugdymas

ugdyti gebėjimus apibendrinti, abstrahuoti ir konkretizuoti tiriamų objektų ir santykių savybes bei pritaikyti jas sprendžiant praktines problemas.

Švietimas:

formuoti pažintinės veiklos motyvus,

estetinis mokinių ugdymas.

ugdyti gebėjimą įvertinti savo žinių apie temą lygį;

žodinės kalbos kultūros ugdymas, pažintinis susidomėjimas;

Įranga :

• multimedijos projektorius, ekranas;

  pristatymas kartu su pamoka ;

  dalomoji medžiaga.

Pamokos tipas: praktinis seminaras apie problemų sprendimą

Pamokos struktūra:

Organizacinis momentas.

Pagrindinių žinių atnaujinimas:
A) mokinių mokymosi žinių tikrinimas;
b) teorinės medžiagos kartojimas;
V) žodinis problemų sprendimas.

Psichologinis palengvėjimas

Problemų sprendimo seminaras: smagių problemų sprendimas.

Minutė mankštos (akims, pečių juostos įtampai sumažinti)

Papildoma medžiaga

Namų darbai.

Grupinis darbas

Pamokos santrauka. Atspindys. Savigarba

Naudota literatūra:

Geometrija, 7-9: vadovėlis. bendrajam lavinimui institucijos/ [L.S. Atanasjanas, V.F. Butuzovas, S.B. Kadomtsev ir kt.] – 16 leid. – M.: Švietimas; UAB "Maskva" vadovėlis“, 2006 m

Geometrijos mokymasis 7-9 klasėse: Metodas. rekomendacijos studijoms: Knyga. mokytojui/ L.S. Atanasjanas, V.F. Butuzovas, Yu.A. Glazkovas ir kiti - M.: Išsilavinimas, 1997 m.

IR AŠ. Depmanas skaičių pasaulis. Pasakojimai apie matematiką – L.: Vaikų literatūra, 1975 m.

Pamokos eiga

I. Organizacinis momentas.

II. Mokytojo žodis apie šios pamokos tikslą.

Trikampis yra paprasčiausia geometrinė figūra, pažįstama nuo vaikystės. Geometrijos pamokose dažniausiai kreipiamės į trikampį. Ši figūra kupina daug įdomių ir paslaptingų dalykų, tokių kaip Bermudų trikampis, kuriame laivai ir lėktuvai dingsta be pėdsakų.Vienas išminčius pasakė: „Aukščiausias dvasios pasireiškimas yra protas. Aukščiausia proto apraiška yra geometrija. Geometrijos langelis yra trikampis. Jis yra neišsemiamas kaip Visata. Tai viena pagrindinių mokyklinio planimetrijos kurso temų. Geometrijoje, fizikoje ir astronomijoje plačiai naudojamas gebėjimas spręsti problemas naudojant panašumo ypatybes.

Šiandienos pamoką skirsime problemų sprendimui šia tema: “Praktinis trikampio panašumo taikymas “ Tai seminaro pamoka, kurioje apžvelgsime panašumo bruožų panaudojimą sprendžiant linksmas problemas.

Užsirašykite pamokos datą, klasės darbą ir temą.

III. Pagrindinių žinių atnaujinimas.

Kad pamoka būtų sėkminga, reikia pakartoti teorinę medžiagą. Tačiau pirmiausia patikrinkime, kaip įvaldėte namų darbų medžiagą.

Taigi, aš siūlau jums nedidelį 3-5 minučių testą.

a) Testavimas tema „Trikampių panašumo ženklai“

b) Teorinės medžiagos kartojimas:

Dabar prašau atsakyti į mano klausimus:

Kokie trikampiai vadinami panašiais?

Kurios trikampio kraštinės vadinamos panašiomis?

Kas yra panašumo koeficientas? (skaičius k lygus panašių pusių santykiui)

Kokie yra trikampių panašumo požymiai?

Koks yra dviejų panašių trikampių plotų santykis?

c) Žodinis problemų sprendimas:

- Pavadinkite panašius trikampius. Kuo jie panašūs?

-Įvardykite panašių trikampių savybes

IV. Psichologinis palengvėjimas

V. Pramoginių problemų sprendimas.

Geometrija yra ne tik trikampių, lygiagretainių ir apskritimų savybių mokslas. Geometrija yra visas pasaulis, supantis mus nuo gimimo. Juk viskas, ką matome aplinkui, vienaip ar kitaip susiję su geometrija, niekas neaplenkia jos dėmesingo žvilgsnio. Geometrija padeda žmogui vaikščioti po pasaulį plačiai atmerktomis akimis, moko atidžiai apsidairyti ir įžvelgti įprastų dalykų grožį, žiūrėti ir mąstyti, mąstyti ir daryti išvadas.

Geometrija yra vienas seniausių mokslų. Ji atsirado praktinės žmonių veiklos pagrindu ir kūrimosi pradžioje daugiausia tarnavo praktiniams tikslams. Vėliau geometrija susiformavo kaip savarankiškas mokslas, nagrinėjantis geometrines figūras.

Studijuodamas geometriją susipažinote su panašiomis figūromis. Šiandien aptarsime, kaip tokių trikampių savybes galima panaudoti atliekant įvairius lauko matavimus. Apsvarstykime užduotis:

objekto aukščio nustatymas; nustatant atstumą iki neprieinamo objekto

O dabar noriu jums pasiūlyti seną problemą.

1 problema . Graikų išminčius Talis nustatė piramidės aukštį Egipte šešis šimtmečius prieš Kristų. Jis pasinaudojo jos šešėliu. Aukščiausios piramidės papėdėje susirinkę kunigai ir faraonas suglumę žiūrėjo į šiaurinį atvykėlį, spėliojusį didžiulės konstrukcijos aukštį.
Talis, pasak legendos, pasirinko dieną ir valandą, kai jo paties šešėlio ilgis buvo lygus jo ūgiui; šiuo momentu piramidės aukštis taip pat turėtų būti lygus jos metamo šešėlio ilgiui. Žinoma, šešėlio ilgis turėjo būti
skaičiuoti nuo piramidės kvadratinio pagrindo vidurio; Thalesas galėjo tiesiogiai išmatuoti šio pagrindo plotį.

Taigi, Talis išmokė egiptiečius nustatyti piramidės aukštį pagal jos šešėlio ilgį:

Kaip tai buvo padaryta, aišku iš nuotraukos.

Jis išmatavo lazdos šešėlį ir piramidės šešėlį. Palyginęs realių objektų aukščių ir jų šešėlių ilgių santykį, Talis nustatė piramidės aukštį.

Pakeiskime šį metodą taip, kad saulėtą dieną galėtumėte naudoti bet kokį šešėlį, nesvarbu, kokio ilgio jis bebūtų. Tegul stulpas yra 1 m ilgio, o jo šešėlis 1,2 m. Raskite medžio aukštį, jeijo šešėlis yra 6 m.

AB yra lazdos ilgis,DE– piramidės aukštis.

 ABC yra panašus INDE(dviejuose kampuose):

 SVA= INED=90°;

 DIA = DBE, nes atitinka AS||DB ir sekantas NE (saulės spinduliai krinta lygiagrečiai)

;
.

Taigi Talis rado piramidės aukštį.

Tačiau Thales pasiūlytas metodas ne visada taikomas. Kodėl?

Objekto aukščio nustatymas.

Yra keletas paprastų būdų, kaip nustatyti objektų aukštį. Pavyzdžiui, tokie metodai pateikti medžiotojo-sportininko žinyne.

6 skaidrė

Prie šešėlio . Saulėtą dieną nesunku pagal šešėlį išmatuoti objekto, tarkime, medžio aukštį. Tiesiog reikia vadovautis tokia taisykle: matuojamo medžio aukštis yra tiek kartų didesnis už jums žinomo objekto (pavyzdžiui, lazdos ar ginklo) aukštį, kiek kartų medžio šešėlis yra didesnis už lazdos šešėlį. Jei pagal mūsų matavimus ginklo ar lazdos šešėlis yra du kartus didesnis už pistoleto ar lazdos ilgį, tada medžio aukštis bus pusė jo šešėlio ilgio. Tuo pačiu atveju, kai ginklo ar lazdos šešėlis lygus jo ilgiui, medžio aukštis taip pat lygus jo šešėliui.

2 uždavinys. Šerlokas Holmsas

Išilgai stulpo . Šis metodas gali būti naudojamas, kai nėra saulės ir nematyti šešėlių nuo objektų. Norėdami išmatuoti, turite paimti stulpą, kurio ilgis lygus jūsų ūgiui. Šis stulpas turi būti įrengtas tokiu atstumu nuo medžio, kad gulint būtų galima matyti medžio viršūnę tiesia linija su stulpo viršūnės tašku. Tada medžio aukštis bus lygus linijai, nubrėžtai nuo galvos iki medžio pagrindo.

3 užduotis. Kitas, taip pat labai paprastas aukštų objektų matavimo būdas, vaizdingai aprašytas Žiulio Verno savo garsiajame romane.„Paslaptingoji sala“ . Ar kas nors skaitė šį romaną?

…Paėmęs tiesų, 12 pėdų ilgio stulpą, inžinierius jį išmatavo kuo tiksliau, palygindamas su savo ūgiu, kuris jam buvo gerai žinomas. Nepasiekęs 500 pėdų nuo granitinės sienos, kuri iškilo vertikaliai, inžinierius įsmeigė maždaug dviejų pėdų stulpą į smėlį ir, tvirtai jį sutvirtinęs, svambalo pagalba pastatė vertikaliai.
Tada jis pasitraukė nuo stulpo į tokį atstumą, kad, gulėdamas ant smėlio, toje pačioje tiesėje matytų ir stulpo galą, ir keteros kraštą. Šį tašką jis atsargiai pažymėjo kaiščiu

– Ar esate susipažinę su geometrijos pradmenimis? – paklausė jis Herberto, pakildamas nuo žemės.
-Taip
– Ar prisimenate panašių trikampių savybes?
– Jų panašios pusės yra proporcingos.
- Teisingai. Taigi: dabar pastatysiu du panašius stačiuosius trikampius. Mažesniame ant vienos kojos bus vertikalus stulpas, o kitoje – atstumas nuo kaiščio iki stulpo pagrindo; Hipotenuzė yra mano regėjimo linija. Kito trikampio kojelės bus: vertikali siena, kurios aukštį norime nustatyti ir atstumą nuo kaiščio iki šios sienos pagrindo; hipotenuzė yra mano žvilgsnio linija, sutampanti su pirmojo trikampio hipotenuzos kryptimi...

Taigi stulpo ilgis yra 10 pėdų (ft = 30 cm). Atstumas nuo kaiščio iki stulpo yra 15 pėdų, nuo sienos iki stulpo 500 pėdų. Raskite uolos aukštį

Įdomios užduotys? Yra daug tokių gražių problemų, kurias galima išspręsti naudojant panašumo ypatybes.

Problemos Nr. 579 sprendimas,

Objekto aukščio nustatymas per balą . Šį būdą galima sėkmingai naudoti po lietaus, kai ant žemės atsiranda daug balų. Matavimas atliekamas taip: netoli matuojamo objekto raskite balą ir atsistokite šalia jos, kad ji tilptų tarp jūsų ir objekto. Po to randamas taškas, iš kurio matosi vandenyje atsispindinčio objekto viršus. Matuojamas objektas, pavyzdžiui, medis, bus tiek kartų aukštesnis už jus, kiek atstumas nuo jo iki balos yra didesnis nei atstumas nuo balos iki jūsų.

Vietoj balos galite naudoti veidrodį, padėtą ​​horizontaliai valgau. Padėtas veidrodishorizontaliai ir grįžkite iš jo į tašką, kuriame stovėdamas stebėtojas veidrodyje mato medžio viršūnę. Šviesos spindulysFD, atsispindi nuo veidrodžio taškeD, patenka į žmogaus akis.

 ABDpanašus EFD(dviejuose kampuose):

 VAD=  FED=90°;

 ADB = EDF, nes Kritimo kampas lygus atspindžio kampui.

Panašiuose trikampiuose panašios kraštinės yra proporcingos:

;
.

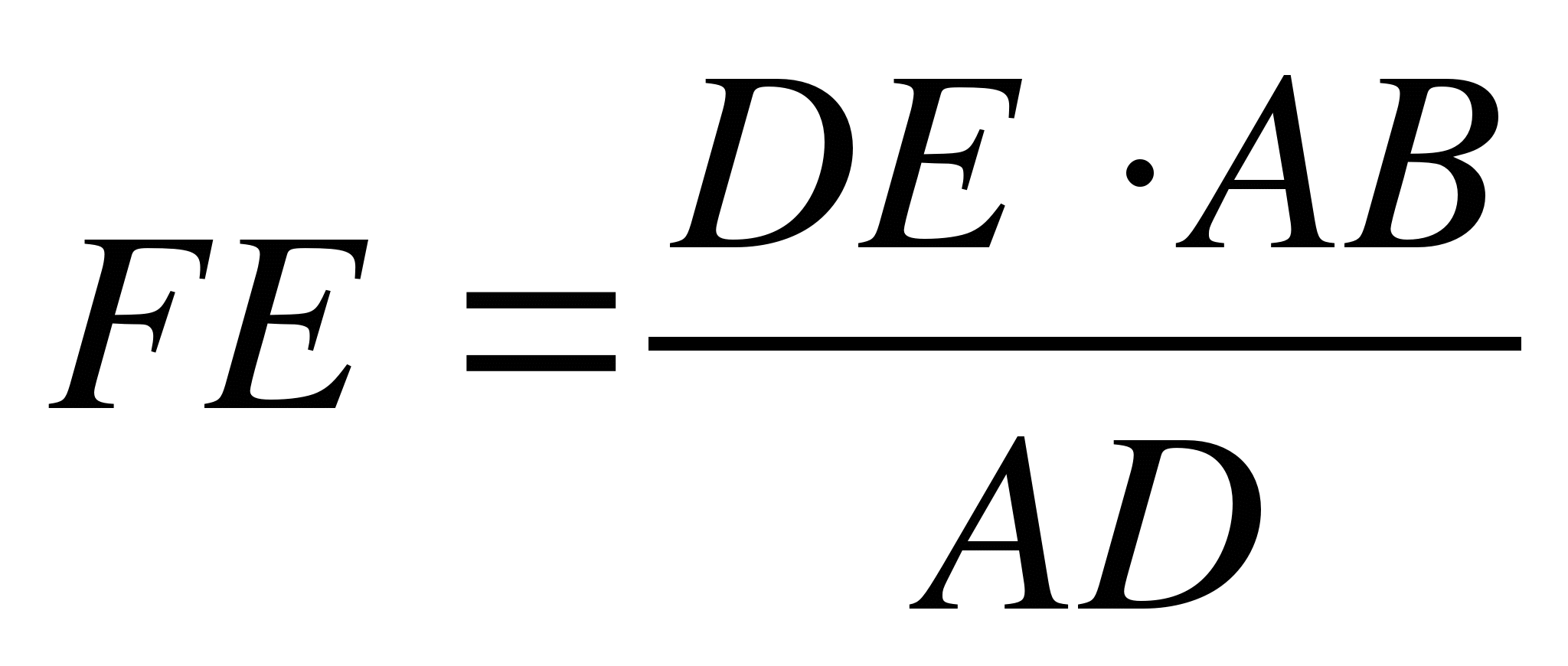Taigi randamas objekto aukštis.

Objekto aukščio nustatymas naudojant veidrodį . №581

Darbas ant žemės

Papildoma medžiaga. 7.1. Norint „atlikti“ ilgas atkarpas ant žemės, tokia technika vadinamakabo tiesiai. Ši technika yra tokia:

Pirmiausia pažymėti kai kurie taškai A ir B Tam naudojami du etapai – maždaug 2 m ilgio stulpai, nusmailinti viename gale, kad būtų galima įsmeigti į žemę. Trečiasis etapas (taškas C) dedamas taip, kad taškuose A ir B esantys etapai jį uždengtų nuo stebėtojo, esančio taške A. Kitas etapas dedamas taip, kad jį uždengtų taškuose B ir C esantys etapai ir kt. .

7.2. Kampai ant žemės matuojami naudojant specialius prietaisus. Paprasčiausias iš jų yraastrolabija. Astrolabija susideda iš dviejų dalių: disko, padalinto į laipsnius, ir liniuotės (alidados), besisukančios aplink disko centrą. Alidados galuose yra du siauri langai, kuriais galima nustatyti tam tikra kryptimi.

Norint išmatuoti AOB ant žemės statomas trikojis su astrolabe taip, kad svambalas, pakabintas nuo disko centro, būtų tiksliai virš taško O. Tada išilgai vienos iš kraštų OA arba OB įrengiama alidada, o priešais esanti pertvara pažymėtas alidade indikatorius. Tada pasukite alidadą, nukreipdami jį į kitą matuojamo kampo pusę, ir pažymėkite padalą, prieš kurią bus alidadės rodyklė. Skaitymo skirtumas suteikia laipsnio matą AOB.

Kampai ant žemės matuojami naudojant specialius prietaisus.

Medkirčio taisyklė

Atstumo iki neprieinamo taško nustatymas

Pirmiausia reikia atsiminti, kiek ilgio tiesios linijos nubrėžiamos ant žemės ir matuojami kampai.

kabo tiesiai .

astrolabija .

11 skaidrė

 A ir C. Jie statomi ant popieriaus lapo A 1 IN 1 SU 1 , kas turi A= A 1 Ir C= SU 1 1 IN 1 ir A 1 SU 1 .

Pagal statybas ABC yra panašus A 1 IN 1 SU 1 (dviejuose kampuose).

1) Norėdami „atlikti“ ilgas atkarpas ant žemės, naudokite techniką, vadinamąkabo tiesiai .

Kampus ant žemės galima matuoti naudojant specialų prietaisą -astrolabija .

11 skaidrė

Tarkime, kad reikia rasti atstumą nuo taško A iki nepasiekiamo objekto B. Norėdami tai padaryti, pasirinkite tašką C žemėje, nubrėžkite atkarpą AC ir išmatuokite ją. Tada, naudodami astrolabiją, išmatuokite A ir C. Jie statomi ant popieriaus lapo A 1 IN 1 SU 1 , kas turi A= A 1 Ir C= SU 1 . Tada išmatuokite kraštinių A ilgį 1 ;
.

Taigi buvo rastas atstumas iki nepasiekiamo taško

582 uždavinių sprendimas,

№583 . Praktinė užduotis.

Siūloma, dirbant poromis, išspręsti uždavinį Nr.583.

Jame siūloma išmatuoti upės plotį, naudojant trikampių panašumą.

Problemos brėžinys yra vadovėlyje. Turite paaiškinti, kaip buvo gautas toks brėžinys, įrodyti trikampių panašumą ir atlikti skaičiavimus.

12 skaidrė

V. Savarankiškas darbas grupėse

Užduotys 1,2,3,4 skaidrė (33-36)

VI. Namų darbai:

P.64, Nr.580 582

VI. Pamokos santrauka. Įvertinimai.

– Ką naujo sužinojai šiandien?

Šiandien pamokoje dirbote su paprasčiausia geometrine figūra, vadinama „geometrijos ląstele“, naudodamiesi trikampių panašumo ženklais, išmokote teisingai mąstyti, lyginti, apibendrinti, daryti išvadas, taip lavindami savo protinius sugebėjimus.

Pamokos santrauka

Pamokos tema: „Praktiniai trikampio panašumo pritaikymai“

Mokytojas: Kiseleva N.E.

MBOU "Nikolskaya vidurinė mokykla Nr. 9"

tema: geometrija

klasė: 8

Pamokos tikslai ir uždaviniai:

Švietimo

Vystantis

• formuoti matematinei veiklai būdingas mąstymo savybes, būtinas produktyviam visuomenės gyvenimui.

Švietimo

Įranga:

• interaktyvus kompleksas;
• lentelę, skirtą pamokai lydėti;
• didaktinė medžiaga problemų sprendimui;
• praktinio darbo aprašymas;
• planšetė, skirta užfiksuoti gautus matavimus;
• mikro skaičiuotuvas;
• ruletė;
• veidrodis;

Pamokos tipas:

Pamokos struktūra:

1. Organizacinis momentas
2. Pamokos tikslų išdėstymas
3. Žinių atnaujinimas
4. Dirba praktinius darbus
5. Praktinio darbo rezultatų įvertinimas
6. Atmintinės kūrimas
7. Problemų sprendimas
8. Namų darbai.
9. Atspindys

Pamokos eiga

1. Organizacinis punktas:

Mokinių sveikinimas, dėmesio sutelkimas.

2 skaidrė.

Mūsų pamokos epigrafas bus garsaus Rusijos laivų statytojo Aleksejaus Nikolajevičiaus Krylovo žodžiai „Teorija be praktikos yra mirusi arba bevaisė, praktika be teorijos neįmanoma arba pražūtinga. Teorija reikalauja žinių, o praktika – įgūdžių“.

2. Problemos išdėstymas ir pamokos tikslas:

Mokytojas: Vaikinai, kokią temą studijavote paskutinėse geometrijos pamokose?

Mokiniai: panašūs trikampiai

Panašių trikampių ženklai

Mokytojas: Šiandien pamokoje spręsdami uždavinius taikysime panašių trikampių savybes. Prisiminkime aptrauktą medžiagą.

3. Bazinių žinių atnaujinimas.

Užduočių sprendimas naudojant paruoštus brėžinius naudojant interaktyvią lentą.

Klausimai studentams.

1. Kokius trikampius matote piešiniuose?
2. Kokie jie kampai?
3. Kuo šie trikampiai panašūs?
4. Kas yra panašumo koeficientas?
5. Koks yra šių problemų panašumo koeficientas?
6. Ką rodo panašumo koeficientas?
7. Raskite, koks yra atkarpos AB ilgis?

Studentai daryti išvadą: atkarpos AB ilgis yra k kartų didesnis už kito trikampio panašios kraštinės ilgį

Mokytojas: Dabar pereikime prie problemų sprendimo realiame gyvenime.

Kaip sužinoti nepasiekiamo objekto aukštį? medis, stulpas, pastatas, uola... naudojant panašių trikampių savybes.

Paklausykite palyginimo apie tai, kaip Talis nustatė piramidės aukštį ir nurodykite, kaip jis tai padarė?

„Šiaurinis nepažįstamasis atvyko pavargęs į Didžiosios Hapio žemę. Saulė jau leidosi, kai jis priėjo prie nuostabių faraono rūmų ir kažką pasakė tarnams. Jie akimirksniu atidarė jam duris ir nuvedė į priėmimo salę. Ir štai jis stovi dulkėtu kelioniniu apsiaustu, o priešais jį paauksuotame soste sėdi faraonas. Šalia stovi įžūlūs kunigai, amžinųjų gamtos paslapčių sergėtojai.

kas tu toks? – paklausė vyriausiasis kunigas.

Mano vardas Talis. Aš esu kilęs iš Mileto.

Kunigas arogantiškai tęsė:

Vadinasi, tu gyrėsi, kad gali išmatuoti piramidės aukštį į ją neįkopdamas? - juokdamiesi pasilenkė kunigai. — Bus gerai, — pašaipiai tęsė kunigas, — jei suklysi ne daugiau kaip šimtu uolekčių.

Galiu išmatuoti piramidės aukštį ir nutolti ne daugiau kaip puse uolekties. Aš tai padarysiu rytoj. - atsakė Talis.

Kunigų veidai aptemo. Koks įžūlumas! Šis nepažįstamasis tvirtina, kad gali suprasti, ko jie, Didžiojo Egipto kunigai, negali.

Gerai, pasakė faraonas. – Prie rūmų yra piramidė, žinome jos aukštį. Rytoj mes patikrinsime jūsų meną.

Kitą dieną Talis nustatė piramidės aukštį.

Mokiniai pateikia paaiškinimus.

Mokytojas: Geometrija visada išspręsdavo gyvenimo jai iškilusias problemas. Graikų mokslininkai išsprendė daug praktinių problemų, kurių žmonės iki tol negalėjo išspręsti.

Tai tiesa, Thales išmokė egiptiečius nustatyti piramidės aukštį pagal jos šešėlio ilgį:

Kaip tai buvo padaryta, aišku iš atvirkštinės lentelės skaidrės.

Mokytojas: Praktiškai nepasiekiamo objekto aukštį galime išmatuoti naudodami stulpą. Šis metodas gali būti naudojamas, kai nėra saulės ir nematyti šešėlių nuo objektų. Paaiškinkite naudodami panašių trikampių savybes.

Mokiniai pateikia paaiškinimus.

Mokytojas : Dabar nepasiekiamo objekto aukščiui nustatyti naudosime kitą būdą ir mums padės daiktas – veidrodis. Atlikime praktinius darbus.

Veidrodis pastatomas horizontaliai ir perkeliamas iš jo atgal į tašką, kuriame stovėdamas stebėtojas mato objekto viršų veidrodyje. Šviesos spindulys, atsispindėjęs nuo veidrodžio tam tikrame taške, patenka į žmogaus akį. Atsiminkite: kritimo kampas lygus atspindžio kampui (atspindėjimo dėsnis).

Kokius segmentus reikia išmatuoti norint nustatyti spintelės aukštį?

4. Praktinis darbas „Daikto aukščio matavimas“

Darbo tikslas:

Raskite mokyklos biuro aukštį.

Įrankiai: veidrodis, matavimo juosta, mikro skaičiuotuvas, užrašų popierius.

Darbo aprašymas:

Darbą atliksite kaip grupė.

Paskirstykite pareigas!

Pasirinkite stebėtoją, techniką, inžinierių, skaičiavimo specialistą.

1. Padėkite veidrodį ant horizontalaus, lygaus paviršiaus toliau nuo stebimo taško.
2. Stebėtojas tolsta nuo veidrodžio, kol pamato stebimą tašką veidrodžio centre.
3. Inžinierius kruopščiai nupiešia piešinį ant popieriaus ir paaiškina technika kokius matavimus atlikti.Dirbdami su matavimo juostomis ir veidrodžiais laikykitės saugos taisyklių.Gauti duomenys pažymimi brėžinyje.
4. Grupė išsprendžia problemą ir Skaičiuoklė atlieka skaičiavimus mikroskaičiuotuvu.
5. Įveskite duomenis į lentelę interaktyvioje lentoje.
6. Įvertinkite rezultatą ir padarykite išvadą.

Gauti rezultatai įrašomi į lentelę

1. Praktinio darbo rezultatų gavimas ir įvertinimas

Mes kalbame apie klaidą. Norint gauti tikslesnį rezultatą, eksperimentą reikia pakartoti keletą kartų ir rasti vidutinę reikšmę.

Taigi, vaikinai, vasarą eksperimentą galite pakartoti neturėdami po ranka matavimo juostos ir veidrodžio. Pagalvokite, kas gali pakeisti matavimo juostą, o kokį veidrodį?

Mokiniai: Matavimo juostą pakeis žmogaus žingsnis (65-75 cm), o veidrodį – bala.

Kur galime pritaikyti įgytas žinias ir įgūdžius?

1. Atmintinė

Pamokos pabaigoje mokytojas išdalina mokiniams priminimus.

7. Problemų sprendimas

Iš modulio „Reali matematika“ matematikos atvirojo GIA uždavinių banko siūloma poromis išspręsti tris uždavinius.

Užduotis Nr.1

2 užduotis

Nustatykite medžio aukštį naudodami veidrodį, jei žmogus yra 153 cm ūgio. Atstumas nuo veidrodžio centro iki žmogaus yra 1,2 m, o nuo veidrodžio centro iki medžio yra 4,8 m.

Užduotis Nr.3

1,6 m ūgio vyras stovi 10 žingsnių nuo stulpo, ant kurio kabo žibintas. Žmogaus šešėlis yra 5 žingsniai. Kokiame aukštyje yra žibintas?

Atsakymai į lentelę įrašomi naudojant interaktyvią lentą

8. Namų darbai: Nr.579, Nr.583

9. Atspindys "Piramidė"

Ką kultūroje simbolizuoja geometrinis kūnas

bet koks verslas, kuriame aiškiai matomi visi augimo ir užbaigimo etapai.

Mokiniai ant piramidės priklijuoja atitinkamos spalvos kraštą.

1. Išvada

Geometrija – mokslas, turintis visas krištolo stiklo savybes, vienodai skaidrus samprotavimuose, nepriekaištingas įrodymais, aiškūs atsakymai, harmoningai derinantis minties skaidrumą ir žmogaus proto grožį. Geometrija nėra visiškai suprantamas mokslas, ir galbūt jūsų laukia daug atradimų. Linkiu sėkmės toliau studijuojant mokslą.

Ačiū už pamoką.

Peržiūra:

Geometrijos pamokos savianalizė

„Praktiniai trikampio panašumo pritaikymai“

klasė: 8

Ši pamoka paremta skyriumi „Panašūs trikampiai“, pirmąja pamoka bloke „Panašumo taikymas“. Toliau pateikiamas bloko tęsinys, kuriame aptariami kiti praktiniai panašumo panaudojimo būdai.

Pamokos tipas: kompleksinio žinių taikymo pamoka

Planuodamas pamoką išsikeliu sau šiuos tikslus ir uždavinius:

Švietimo

• parodyti trikampių panašumo panaudojimą atliekant matavimo darbus ant žemės;
• parodyti teorijos ir praktikos ryšį;
• ugdyti mokinių gebėjimus panaudoti panašių trikampių teoriją sprendžiant įvairias problemas.

Vystantis

• didinti mokinių susidomėjimą geometrija;
• intensyvinti mokinių pažintinę veiklą;
• formuoti matematinei veiklai būdingas ir produktyviam visuomenės gyvenimui reikalingas mąstymo savybes.

Švietimo

• ugdyti gebėjimą dirbti komandoje;
• ugdyti pasitikėjimą bendravimu.

Manau, kad kurdamas pamokos planą stengiausi šiuos tikslus derinti ir padaryti visapusiškus. Tačiau mano prioritetinės užduotys liko siekti, kad mokiniai suprastų praktinę įgytų žinių reikšmę.

Pamokos struktūra buvo sukurta aiškiai pagal tokio tipo pamokas. Algoritmo buvo laikomasi. Tai reiškia, kad visi etapai buvo baigti:

• žinių, reikalingų jų kūrybiškam žinių pritaikymui, atnaujinimas;
• žinių ir veiklos metodų apibendrinimas ir sisteminimas;
• visuotinių auklėjamųjų veiksmų formavimas;
• visuotinės švietėjiškos veiklos kontrolė.

Stengiausi pateikti logišką ryšį tarp atskirų etapų, kiekvieno etapo pabaigoje užduodamas klausimas yra kito etapo užduotis.

Pagrindinis dėmesys skiriamas tam, kad studentas gebėtų sukurti matematinį realios situacijos modelį ir, panaudodamas anksčiau įgytas žinias, gebėtų išspręsti problemą.

Pamokos pradžioje naudojau frontalinį darbą, kuris leido atnaujinti mokinių žinias. Tada buvo iškelta problema, kuri leido motyvuoti studentus tolesniam darbui. Susidarė reali situacija, kurią mokiniai sprendė grupėje, atlikdami praktinius darbus. Žinių kontrolės etape mokiniai sprendė praktinio turinio matematikos uždavinius, su kuriais susiduriama valstybinėje baigiamojoje atestacijoje, dirbdami poromis.

Šios pamokos klasė tapo platforma praktinei užduočiai atlikti. Pamokoje buvo naudojamas interaktyvus kompleksas, kuris leido padidinti pamokos tankumą ir suteikti aiškumo.

Atlikdamas praktinį darbą taikiau sisteminės veiklos metodą. Keičiant veiklos rūšis buvo galima išvengti mokinių perkrovos.

Mokinių susidomėjimą palaikė praktinė užduočių orientacija ir nestandartinis matavimų atlikimo būdas. Taip pat įdomių istorinių faktų.

Stengiausi užkariauti vaikus, sukurti patogias sąlygas, pasitelkdama intonaciją, malonų požiūrį, šypseną. Kritinėje situacijoje nusprendžiau išlaikyti ramybę. Būkite pasirengę bet kokiam įvykių posūkiui.

Pamokos pradžioje paminėtos Egipto piramidės ir piramidė, kuri leido apmąstyti žinias, buvo savotiškas atskaitos signalas. Tikiuosi, kad tai leido vaikams prisiminti praktinius būdus, kaip išmatuoti nepasiekiamo objekto aukštį ir prireikus juos pritaikyti.

Tikiu, kad užsibrėžti tikslai buvo pasiekti.

UŽTIKRINU. Mokyklos direktorius E. N. Polikarpova

Peržiūra:

Užduotis Nr.1

1 m aukščio medis yra 8 žingsniai nuo šviestuvo stulpo ir meta 4 žingsnių ilgio šešėlį. Nustatykite žibinto stulpo aukštį.

2 užduotis