3 paskaita. Bendrosios dinamikos teoremos
Materialių taškų sistemos dinamika yra svarbi teorinės mechanikos šaka. Čia daugiausia nagrinėjamos mechaninių sistemų (medžiagų taškų sistemų) judėjimo problemos, turinčios baigtinį laisvės laipsnių skaičių – maksimalų nepriklausomų parametrų, lemiančių sistemos padėtį, skaičių. Pagrindinis sistemos dinamikos uždavinys – standaus kūno ir mechaninių sistemų judėjimo dėsnių tyrimas.
Paprasčiausias būdas tirti sistemos judėjimą, susidedantis iš N materialių taškų, reikia atsižvelgti į kiekvieno atskiro sistemos taško judesius. Šiuo atveju turi būti nustatytos visos jėgos, veikiančios kiekvieną sistemos tašką, įskaitant sąveikos tarp taškų jėgas.
Nustatę kiekvieno taško pagreitį pagal antrąjį Niutono dėsnį (1.2), kiekvienam taškui gauname po tris antros eilės skaliarinius diferencialinius judėjimo dėsnius, t.y. 3 N visos sistemos diferencialiniai judėjimo dėsniai.
Norint rasti mechaninės sistemos judėjimo lygtis pagal duotąsias jėgas ir kiekvieno sistemos taško pradines sąlygas, reikia integruoti gautus diferencinius dėsnius. Ši problema sudėtinga net dviejų materialių taškų, kurie juda tik veikiami sąveikos jėgų pagal visuotinės traukos dėsnį (dviejų kūnų problema), o trijų sąveikaujančių taškų atveju – itin sudėtinga (trijų kūnų problema). ).
Todėl būtina rasti problemų sprendimo metodus, kurie leistų susidaryti išsprendžiamas lygtis ir susidarytų supratimą apie mechaninės sistemos judėjimą. Bendrosios dinamikos teoremos, būdamos diferencinių judėjimo dėsnių pasekmė, leidžia išvengti sudėtingumo, atsirandančio integruojant, ir gauti reikiamus rezultatus.
3. 1. Bendrosios pastabos
Mechaninės sistemos taškus sunumeruosime indeksais i, j, k ir tt, kurie eina per visas vertybes 1, 2, 3… N, Kur N – sistemos taškų skaičius. Fiziniai kiekiai, susiję su k taškas žymimas tuo pačiu indeksu kaip ir taškas. Pavyzdžiui, atitinkamai išreikškite spindulio vektorių ir greitį k taškas.
Kiekvieną sistemos tašką veikia dviejų šaltinių jėgos: pirma, jėgos, kurių šaltiniai yra už sistemos ribų, vadinamos išorės pajėgos ir paskirtos ; antra, jėgos iš kitų tam tikros sistemos taškų, vadinamos vidinis pajėgos ir paskirtos . Vidinės jėgos tenkina trečiąjį Niutono dėsnį. Panagrinėkime paprasčiausias vidinių jėgų, veikiančių visą mechaninę sistemą bet kurioje būsenoje, savybes.
Pirmas turtas. Visų sistemos vidinių jėgų geometrinė suma (pagrindinis vidinių jėgų vektorius) yra lygi nuliui.
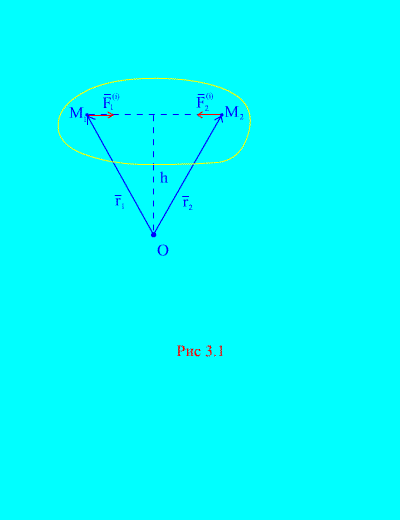
Iš tiesų, jei atsižvelgsime į bet kuriuos du savavališkus sistemos taškus, pavyzdžiui, ir (3.1 pav.), tada jiems ![]() , nes veikimo ir reakcijos jėgos visada yra vienodo dydžio, veikiančios pagal vieną veikimo liniją priešinga kryptimi, kuri jungia sąveikaujančius taškus. Pagrindinis vidinių jėgų vektorius susideda iš sąveikaujančių taškų jėgų porų, todėl
, nes veikimo ir reakcijos jėgos visada yra vienodo dydžio, veikiančios pagal vieną veikimo liniją priešinga kryptimi, kuri jungia sąveikaujančius taškus. Pagrindinis vidinių jėgų vektorius susideda iš sąveikaujančių taškų jėgų porų, todėl
![]() (3.1)
(3.1)
Antrasis turtas. Visų vidinių jėgų momentų geometrinė suma, palyginti su savavališku erdvės tašku, yra lygi nuliui.
Panagrinėkime jėgų momentų ir santykinio su tašku sistemą APIE(3.1 pav.). Iš (3.1 pav.). tai aišku
![]() ,
,
nes abi jėgos turi tas pačias kryptis ir priešingas vektorinių momentų kryptis. Pagrindinis vidinių jėgų momentas taško atžvilgiu APIE susideda iš tokių išraiškų vektorinės sumos ir yra lygi nuliui. Vadinasi,
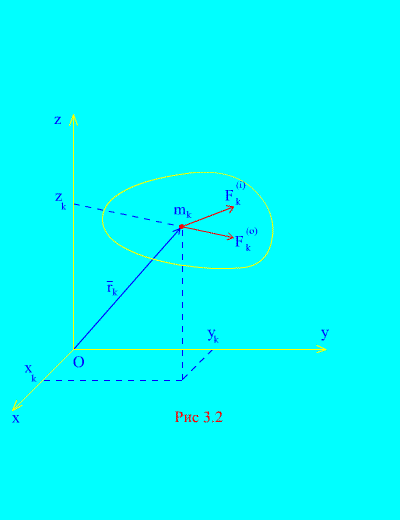
Tegul išorinės ir vidinės jėgos veikia mechaninę sistemą, susidedančią iš N taškų (3.2 pav.). Jei išorinių jėgų ir visų vidinių jėgų atstumas taikomi kiekvienam sistemos taškui, tai bet kuriam k sistemos taške, galima sudaryti diferencialines judėjimo lygtis. Tokių lygčių bus iš viso N:
ir projekcijose į fiksuotas koordinačių ašis 3 N:
![]() (3.4)
(3.4)
Vektorinės lygtys (3.3) arba lygiavertės skaliarinės lygtys (3.4) vaizduoja visos sistemos materialių taškų judėjimo diferencialinius dėsnius. Jei visi taškai juda lygiagrečiai vienai plokštumai arba vienai tiesei, tada lygčių (3.4) skaičius pirmuoju atveju bus 2 N, antrajame N.

1 pavyzdys. Dvi masės yra sujungtos viena su kita per bloką permestu netiesiamu kabeliu (3.3 pav.). Nepaisydami trinties jėgų, taip pat į bloko ir troso masę, nustatomas apkrovų judėjimo ir troso įtempimo dėsnis.
Sprendimas. Sistema susideda iš dviejų medžiaginių kūnų (sujungtų nepratęsiu kabeliu), judančių lygiagrečiai tai pačiai ašiai X. Užrašykime diferencialinius judėjimo dėsnius projekcijose į ašį X kiekvienam kūnui.
Leiskite dešiniajam svoriui kristi su pagreičiu, tada kairysis svoris pakils pagreičiu. Psichiškai išsivaduojame iš ryšio (kabelio) ir pakeičiame jį reakcijomis ir (3.3 pav.). Laikydami kūnus laisvus, sudarykime diferencinius judėjimo dėsnius projekcijoje į ašį X(tai reiškia, kad sriegio įtempimai yra vidinės jėgos, o apkrovų svoris yra išorinis):
Kadangi ir (kūnai sujungti netiesiamu kabeliu), gauname
Šių pagreičio ir kabelio įtempimo lygčių sprendimas T, gauname
 .
.
Atkreipkite dėmesį, kad troso įtempimas nėra lygus atitinkamos apkrovos gravitacijos jėgai.
3. 2. Masės centro judėjimo teorema
Yra žinoma, kad standus kūnas ir mechaninė sistema plokštumoje gali judėti gana sudėtingai. Pirmąją kūno ir mechaninės sistemos judėjimo teoremą galima pasiekti taip: mesti k.-l. objektas, susidedantis iš daugybės tarpusavyje sujungtų kietų kūnų. Aišku, kad jis skris parabole. Tai paaiškėjo tiriant taško judėjimą. Tačiau dabar objektas nėra taškas. Skrydžio metu jis sukasi ir siūbuoja aplink kokį nors veiksmingą centrą, kuris juda parabole. Pirmoji teorema apie sudėtingų objektų judėjimą sako, kad tam tikras efektyvusis centras yra judančio objekto masės centras. Masės centras nebūtinai yra pačiame kūne, jis gali būti kur nors už jo ribų.
Teorema. Mechaninės sistemos masės centras juda kaip materialus taškas, kurio masė lygi visos sistemos masei, kuriam taikomos visos sistemą veikiančios išorinės jėgos.
Norėdami įrodyti teoremą, perrašome diferencialinius judėjimo dėsnius (3.3) tokia forma:
![]() (3.5)
(3.5)
Kur N – sistemos taškų skaičius.
Sudėkime lygtis po terminą:
 (A)
(A)
Mechaninės sistemos masės centro padėtis pasirinktos koordinačių sistemos atžvilgiu nustatoma pagal (2.1) formulę:  Kur M– sistemos masė. Tada bus parašyta kairioji lygybės (a) pusė
Kur M– sistemos masė. Tada bus parašyta kairioji lygybės (a) pusė
Pirmoji suma dešinėje lygybės (a) pusėje yra lygi pagrindiniam išorinių jėgų vektoriui, o paskutinė, pagal vidinių jėgų savybę, yra lygi nuliui. Tada lygybė (a), atsižvelgiant į (b), bus perrašyta
![]() , (3.6)
, (3.6)
tie. sistemos masės ir jos masės centro pagreičio sandauga lygi visų sistemą veikiančių išorinių jėgų geometrinei sumai.
Iš (3.6) lygties išplaukia, kad vidinės jėgos neturi tiesioginės įtakos masės centro judėjimui. Tačiau kai kuriais atvejais jie yra išorinių jėgų, veikiančių sistemą, atsiradimo priežastis. Taigi vidinės jėgos, varančios automobilio varomuosius ratus, sukelia išorinę sukibimo jėgą, veikiančią rato ratlankį.
2 pavyzdys. Mechanizmas, esantis vertikalioje plokštumoje, sumontuotas horizontalioje lygioje plokštumoje ir pritvirtintas prie jo standžiai pritvirtintais strypais prie paviršiaus KAM Ir L (3.4 pav.).
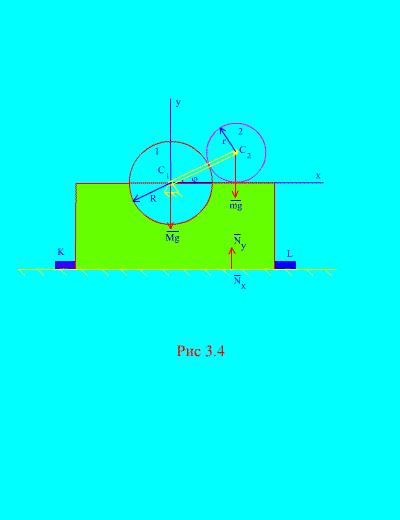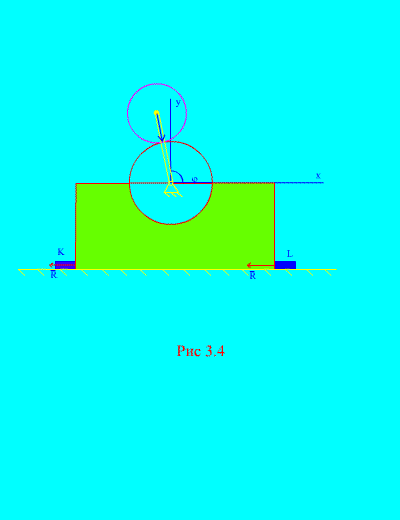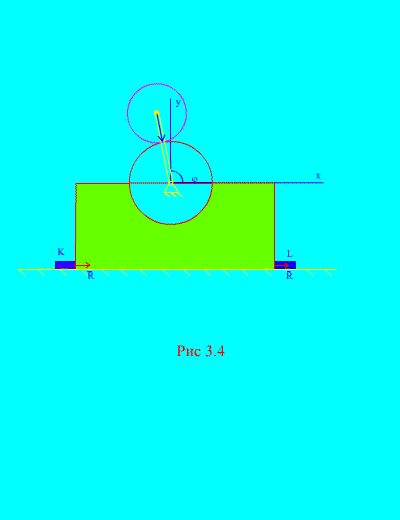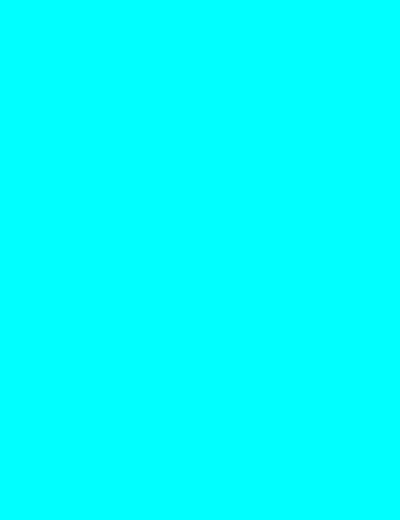
1 disko spindulys R nejudėdamas. 2 disko masė m ir spindulys r pritvirtintas prie švaistiklio, ilgis R+ r taške C 2. Švaistiklis sukasi pastoviai
kampinis greitis. Iš pradžių švaistiklis užėmė tinkamą horizontalią padėtį. Nepaisydami švaistiklio masės, nustatykite didžiausias horizontalias ir vertikalias jėgas, veikiančias strypus, jei bendra rėmo ir rato 1 masė yra lygi M. Taip pat apsvarstykite mechanizmo elgesį, kai nėra strypų.
Sprendimas. Sistema susideda iš dviejų masių ( N=2 ): fiksuotas diskas 1 su rėmeliu ir kilnojamasis diskas 2. Nukreipkite ašį adresu per nejudančio disko svorio centrą vertikaliai aukštyn, ašis X– išilgai horizontalios plokštumos.
Masės centro judėjimo teoremą (3.6) parašykime koordinačių forma
Šios sistemos išorinės jėgos yra: rėmo ir fiksuoto disko svoris - Mg, judančio disko svoris - mg, - visa horizontali varžtų reakcija, - normali bendra plokštumos reakcija. Vadinasi,
Tada judėjimo dėsniai (b) bus perrašyti
Apskaičiuokime mechaninės sistemos masės centro koordinates:
 ; (G)
; (G)
kaip matyti iš (3.4 pav.), , , ![]() (suktuvo kampas),
(suktuvo kampas), ![]() . Šių išraiškų pakeitimas į (d) ir antrųjų išvestinių apskaičiavimas laiko atžvilgiu t iš , mes tai gauname
. Šių išraiškų pakeitimas į (d) ir antrųjų išvestinių apskaičiavimas laiko atžvilgiu t iš , mes tai gauname
 (e)
(e)
Pakeitę (c) ir (e) į (b), randame

Horizontalus slėgis, veikiantis strypus, yra didžiausias ir mažiausias, kai cos = 1 atitinkamai, t.y.
![]()
![]()
Mechanizmo slėgis horizontalioje plokštumoje turi didžiausias ir mažiausias vertes, kai nuodėmė atitinkamai, t.y.
![]()
![]()
Tiesą sakant, pirmoji dinamikos problema buvo išspręsta: pagal žinomas sistemos masės centro judėjimo lygtis (d) atkuriamos judėjime dalyvaujančios jėgos.
Nesant barų K Ir L (3.4 pav.), mechanizmas gali pradėti šokinėti virš horizontalios plokštumos. Tai įvyks, kai, t.y. kai , tai reiškia, kad švaistiklio sukimosi kampinis greitis, kuriuo mechanizmas atsimuša, turi tenkinti lygybę
 .
.
3. 3. Masės centro judėjimo likimo dėsnis
Jei pagrindinis sistemą veikiančių išorinių jėgų vektorius lygus nuliui, t.y. , tada nuo(3.6)Iš to išplaukia, kad masės centro pagreitis lygus nuliui, todėl masės centro greitis yra pastovus pagal dydį ir kryptį. Jei pradiniu momentu masės centras yra ramybės būsenoje, tada jis yra ramybės būsenoje visą laiką, o pagrindinis išorinių jėgų vektorius yra lygus nuliui.
Iš šios teoremos išplaukia keletas išvadų.
· Vien vidinės jėgos negali pakeisti sistemos masės centro judėjimo pobūdžio.
· Jei pagrindinis išorinių jėgų, veikiančių sistemą, vektorius yra lygus nuliui, tai masės centras yra ramybės būsenoje arba juda tolygiai ir tiesia linija.
· Jei pagrindinio sistemos išorinių jėgų vektoriaus projekcija į kokią nors fiksuotą ašį lygi nuliui, tai sistemos masės centro greičio projekcija į šią ašį nekinta.
· Jėgų pora, veikiančia standųjį kūną, negali pakeisti jo masės centro judėjimo (dėl to kūnas gali suktis tik apie masės centrą).
Panagrinėkime pavyzdį, iliustruojantį masės centro judėjimo išsaugojimo dėsnį.

3 pavyzdys. Dvi masės sujungiamos per bloką išmestu netiesiu siūlu (3.5 pav.), pritvirtintas ant pleišto su mase M. Pleištas remiasi į lygią horizontalią plokštumą. Iš pradžių sistema buvo ramybės būsenoje. Raskite pleišto poslinkį išilgai plokštumos, kai pirmoji apkrova nuleidžiama į aukštį N. Nepaisykite bloko ir sriegio masės.
Sprendimas. Išorinės jėgos, veikiančios pleištą kartu su apkrovomis, yra gravitacija, ir Mg, taip pat normali lygaus horizontalaus paviršiaus reakcija N. Vadinasi,
Kadangi iš pradžių sistema buvo ramybės būsenoje, mes turime .
Apskaičiuokime sistemos masės centro koordinates šiuo momentu t 1 kai krovinys sveria g nusileis į aukštį H.
Šiuo metu:
 ,
,
Kur , , X– atitinkamai g, g sveriančių krovinių ir pleišto masės centro koordinates Mg.
Tarkime, kad pleištas laiko momentu juda teigiama ašies kryptimi Jautis pagal sumą L, jei krovinio svoris nukrenta iki aukščio N. Tada kol kas
nes kroviniai kartu su pleištu pajudės į Lį dešinę, o krovinys judės aukštyn išilgai pleišto. Nuo tada po skaičiavimų gauname
 .
.
3.4. Sistemos judėjimo kiekis
3.4.1. Sistemos impulso apskaičiavimas
Materialaus taško impulsas yra vektorinis dydis, lygus taško masės ir jo greičio vektoriaus sandaugai
Impulso matavimo vienetas -
Mechaninės sistemos impulsas – tai atskirų sistemos taškų impulsų vektorinė suma, t.y.
Kur N – sistemos taškų skaičius.
Mechaninės sistemos impulsą galima išreikšti sistemos mase M ir masės centro greitį. tikrai,
tie. Sistemos impulsas lygus visos sistemos masės ir jos masės centro greičio sandaugai. Kryptis yra tokia pati kaip kryptis (3.6 pav.)

Projekcijose į stačiakampes ašis turime
kur , , yra sistemos masės centro greičio projekcijos.
Čia M– mechaninės sistemos masė; nesikeičia, kai sistema juda.
Šiuos rezultatus ypač patogu naudoti skaičiuojant standžių kūnų judėjimo dydžius.
Iš (3.7) formulės aišku, kad jeigu mechaninė sistema juda taip, kad jos masės centras lieka nejudantis, tai sistemos impulsas lieka lygus nuliui.
3.4.2. Elementarus ir visos jėgos impulsas
Jėgos veikimas materialiame taške laikui bėgant dt galima apibūdinti elementariu impulsu. Bendras jėgos impulsas laikui bėgant t, arba jėgos impulsas, nustatomas pagal formulę
arba projekcijose į ašies koordinates
 (3.8a)
(3.8a)
Jėgos impulso vienetas yra.
3.4.3. Sistemos impulso kitimo teorema
Tegul sistemos taškams taikomos išorinės ir vidinės jėgos. Tada kiekvienam sistemos taškui galime taikyti diferencinius judėjimo dėsnius (3.3), turėdami omenyje, kad ![]() :
:
 .
.
Susumavus visus sistemos taškus, gauname
Pagal vidinių jėgų savybę ir pagal apibrėžimą ![]() mes turime
mes turime
 (3.9)
(3.9)
Abi šios lygties puses padauginus iš dt, gauname teoremą apie impulso pokytį diferencine forma:
![]() , (3.10)
, (3.10)
tie. mechaninės sistemos diferencinis impulsas lygus visų išorinių jėgų, veikiančių mechaninės sistemos taškus, elementariųjų impulsų vektorinei sumai.
Apskaičiuojant abiejų pusių integralą (3.10) laikui bėgant nuo 0 iki t, teoremą gauname baigtinės arba integralinės formos
 (3.11)
(3.11)
Projekcijose į koordinačių ašis turėsime
Mechaninės sistemos impulso pokytis laikui bėgantt, yra lygi visų išorinių jėgų impulsų, veikiančių mechaninės sistemos taškus per tą patį laiką, vektorinei sumai.
4 pavyzdys. Krovinio svoris m veikiamas jėgos nusileidžia pasvirusia plokštuma iš ramybės F, proporcingas laikui: , kur (3.7 pav.). Kokį greitį įgaus kūnas t sekundės po judėjimo pradžios, jei apkrovos slydimo trinties koeficientas pasvirusioje plokštumoje yra lygus f.
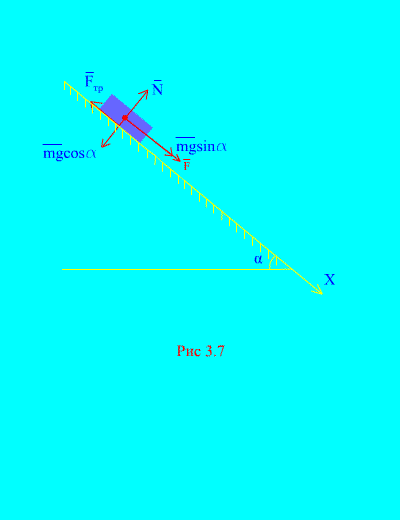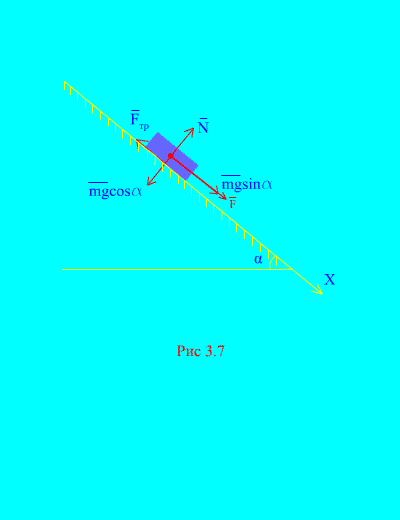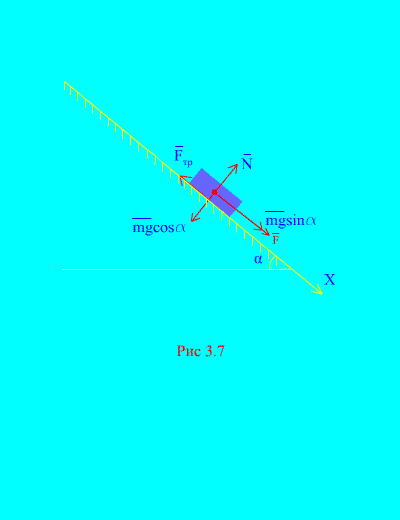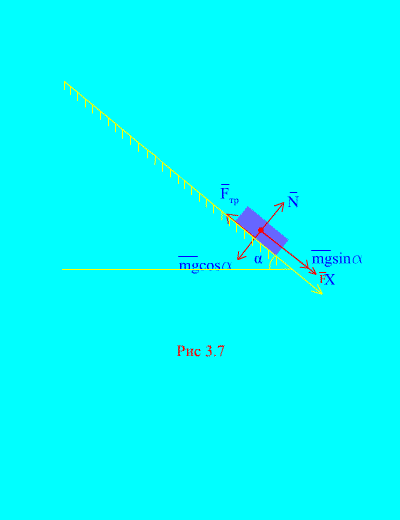
Sprendimas. Pavaizduokime jėgas, veikiančias apkrovą: mg - apkrovos gravitacijos jėga, N yra normali plokštumos reakcija, yra plokštumos apkrovos slydimo trinties jėga ir . Visų jėgų kryptis parodyta (3.7 pav.).
Nukreipkime ašį X išilgai pasvirusios plokštumos žemyn. Parašykime teoremą apie impulso pokytį (3.11) projekcijoje į ašį X:
 (A)
(A)
Pagal sąlygą, nes pradiniu laiko momentu krovinys buvo ramybės būsenoje. Visų jėgų impulsų projekcijų į x ašį suma lygi

Vadinasi,
 ,
,
 .
.
3.4.4. Impulso išsaugojimo dėsniai
Konservavimo dėsniai gaunami kaip specialieji impulso kitimo teoremos atvejai. Galimi du ypatingi atvejai.
· Jeigu visų sistemą veikiančių išorinių jėgų vektorinė suma lygi nuliui, t.y. , tada iš teoremos išplaukia (3.9) , Ką ,
tie. jei pagrindinis sistemos išorinių jėgų vektorius lygus nuliui, tai sistemos judėjimo dydis yra pastovus pagal dydį ir kryptį.
· Jei pagrindinio išorinių jėgų vektoriaus projekcija į bet kurią koordinačių ašį lygi nuliui, pavyzdžiui, Ox, t.y. , tada impulso projekcija į šią ašį yra pastovi vertė.
Panagrinėkime impulso tvermės dėsnio taikymo pavyzdį.

5 pavyzdys. Balistinė švytuoklė yra masės kūnas, pakabintas ant ilgo sriegio (3.8 pav.).
Masės kulka, judanti greičiu V ir atsitrenkęs į nejudantį kūną, jame įstringa ir kūnas nukrypsta. Koks buvo kulkos greitis, jei kūnas pakilo į aukštį h ?
Sprendimas. Tegul kūnas su įstrigusia kulka įgauna greitį. Tada, naudodamiesi judesio tvermės dėsniu dviejų kūnų sąveikos metu, galime rašyti ![]() .
.
Greitis gali būti apskaičiuojamas naudojant mechaninės energijos tvermės dėsnį  . Tada . Dėl to randame
. Tada . Dėl to randame
 .
.
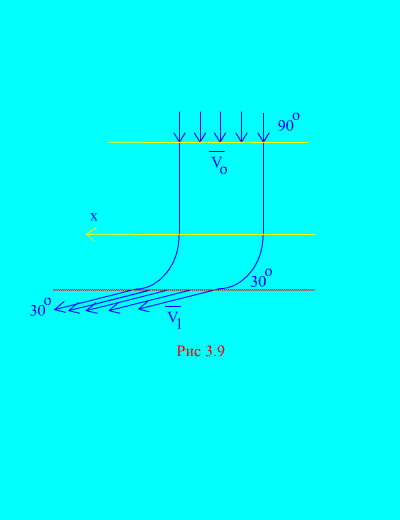
6 pavyzdys. Vanduo patenka į stacionarų kanalą (3.9 pav.) kintamas skerspjūvis su greičiu kampu į horizontalę; kanalo skerspjūvio plotas prie įėjimo; vandens greitis prie išėjimo iš kanalo sudaro kampą su horizontu.
Nustatykite horizontalųjį reakcijos komponentą, kurį vanduo turi ant kanalo sienelių. Vandens tankis  .
.
Sprendimas. Nustatysime kanalo sienelių sukeltos reakcijos ant vandens horizontalųjį komponentą. Ši jėga yra lygi norimai jėgai ir yra priešinga ženklu. Pagal (3.11a)
 . (A)
. (A)
Apskaičiuojame skysčio, patenkančio į kanalą per laiką t, tūrio masę:
Reikšmė rAV 0 vadinama antroji masė – skysčio masė, tekanti per bet kurią vamzdžio dalį per laiko vienetą.
Per tą patį laiką iš kanalo išeina toks pat vandens kiekis. Pradinis ir galutinis greičiai nurodyti sąlygoje.
Apskaičiuokime dešinę lygybės (a) pusę, kuri apibrėžia sistemą (vandenį) veikiančių išorinių jėgų projekcijų į horizontaliąją ašį sumą. Vienintelė horizontali jėga yra gautos sienos reakcijos horizontalioji dalis Rx. Ši jėga yra pastovi esant pastoviam vandens judėjimui. Štai kodėl
 . (V)
. (V)
Pakeitę (b) ir (c) į (a), gauname
3.5. Kinetinis sistemos momentas
3.5.1. Pagrindinis sistemos impulso momentas

Leisti būti spindulio vektorius taško, kurio masė sistemos, palyginti su tam tikru tašku A, vadinamas centru (3.10 pav.).
Taško judesio momentas (kinetinis momentas). palyginti su centru A vadinamas vektoriumi , nustatoma pagal formulę
![]() . (3.12)
. (3.12)
Šiuo atveju vektorius nukreiptas statmenai plokštumai, einančiai per centrą A ir vektorius .
Taško judesio momentas (kinetinis momentas) ašies atžvilgiu vadinama taško momento momento projekcija į šią ašį bet kurio šioje ašyje pasirinkto centro atžvilgiu.
Pagrindinis sistemos impulso momentas (kinetinis momentas) centro A atžvilgiu vadinamas kiekiu
 (3.13)
(3.13)
Pagrindinis sistemos impulso momentas (kinetinis momentas) ašies atžvilgiu vadinama pagrindinio sistemos impulso momento projekcija į šią ašį, palyginti su bet kuriuo pasirinktu centrinė ašis.
3.5.2. Besisukančio standaus kūno kinetinis momentas apie sukimosi ašį
Sulygiuokime fiksuotą tašką APIE kūnas guli ant sukimosi ašies APIEz, su koordinačių sistemos pradžia Ohoz, kurių ašys suksis kartu su kūnu (3.11 pav.). Leisti būti spindulio vektorius kūno taško atžvilgiu koordinačių pradžios jo projekcija ašyje bus pažymėta , , . Kūno kampinio greičio vektoriaus projekcijas žymime tose pačiose ašyse kaip 0, 0, ().
Panagrinėkime tam tikros materialių objektų sistemos judėjimą fiksuotos koordinačių sistemos atžvilgiu.
Visas sistemai taikomas jėgas padalinkime į išorines ir vidines; abu gali apimti reakcijas į išmestą
jungtys. Pažymime pagrindinį vektorių ir pagrindinį išorinių jėgų momentą taško A atžvilgiu.
1. Impulso kitimo teorema. Jei yra sistemos judesio kiekis, tada (žr.
tai galioja teorema: sistemos impulso laiko išvestinė lygi pagrindiniam visų išorinių jėgų vektoriui.
Pakeitus vektorių jo išraiška, kur yra sistemos masė, yra masės centro greitis, (4.1) lygtis gali būti suteikta kitokia forma:
Ši lygybė reiškia, kad sistemos masės centras juda kaip materialus taškas, kurio masė lygi sistemos masei ir kuriam taikoma jėga, geometriškai lygi pagrindiniam visų išorinių sistemos jėgų vektoriui. Paskutinis teiginys vadinamas sistemos masės centro (inercijos centro) judėjimo teorema.
Jei tada iš (4.1) seka, kad impulso vektorius yra pastovus pagal dydį ir kryptį. Projektuodami jį į koordinačių ašį, gauname tris pirmuosius skaliarinius integralus, sistemos dvigubos dangtelio diferencialines lygtis:
Šie integralai vadinami impulso integralais. Kai masės centro greitis yra pastovus, tai yra, jis juda tolygiai ir tiesiai.
Jei pagrindinio išorinių jėgų vektoriaus projekcija bet kurioje ašyje, pavyzdžiui, ašyje, yra lygi nuliui, tada turime vieną pirmąjį integralą arba jei dvi pagrindinio vektoriaus projekcijos yra lygios nuliui, tada yra dvi impulso integralai.
2. Kinetinio impulso kitimo teorema. Tegu A yra koks nors savavališkas erdvės taškas (judantis arba nejudantis), kuris nebūtinai sutampa su kokiu nors konkrečiu materialiu sistemos tašku per visą judėjimo laiką. Jo greitį fiksuotoje koordinačių sistemoje žymime Teorema apie medžiagos sistemos kinetinio momento pokytį taško A atžvilgiu turi tokią formą
![]()
Jei taškas A yra fiksuotas, tada lygybė (4.3) įgauna paprastesnę formą:
Ši lygybė išreiškia teoremą apie sistemos kampinio momento kitimą fiksuoto taško atžvilgiu: sistemos kampinio momento laiko išvestinė, apskaičiuota tam tikro fiksuoto taško atžvilgiu, yra lygi visų išorinių jėgų pagrindiniam momentui, susijusiam su fiksuotu tašku. iki šio taško.
Jei tada pagal (4.4) kampinio momento vektorius yra pastovus pagal dydį ir kryptį. Projektuodami jį į koordinačių ašis, gauname dvigubos sistemos diferencialinių lygčių pirmuosius skaliarinius integralus:
Šie integralai vadinami momento integralais arba ploto integralais.
Jei taškas A sutampa su sistemos masės centru, tada pirmasis narys dešinėje lygybės (4.3) pusėje išnyksta ir teorema apie kampinio momento pokytį turi tokią pat rašymo formą (4.4) kaip ir fiksuotas taškas A. Atkreipkite dėmesį (žr. p. 4 § 3), kad nagrinėjamu atveju sistemos absoliutus kampinis impulsas kairėje lygybės pusėje (4.4) gali būti pakeistas lygiu sistemos kampiniu momentu. jo judėjime masės centro atžvilgiu.
Leisti yra tam tikra pastovi ašis arba pastovios krypties ašis, einanti per sistemos masės centrą, ir tegul yra sistemos kinetinis momentas šios ašies atžvilgiu. Iš (4.4) išplaukia, kad
kur yra išorinių jėgų momentas ašies atžvilgiu. Jei viso judesio metu turime pirmąjį integralą
S. A. Chaplygino darbuose buvo gauti keli teoremos apibendrinimai apie kinetinį impulsą, kurie vėliau buvo pritaikyti sprendžiant daugybę riedančių rutuliukų problemų. Darbuose pateikiami tolesni teoremos apibendrinimai dėl mechaninio momento kitimo ir jų pritaikymo standžiosios kūno dinamikos problemose. Pagrindiniai šių darbų rezultatai yra susiję su teorema apie kinetinio impulso kitimą judančiojo, nuolat einančio per kurį nors judantį tašką A, pokytį. Tebūnie vienetinis vektorius, nukreiptas išilgai šios ašies. Skaliariškai padauginę iš abiejų lygybės pusių (4.3) ir pridėję terminą prie dviejų jo dalių, gauname
Kai įvykdoma kinematinė sąlyga
(4.5) lygtis išplaukia iš (4.7). Ir jei sąlyga (4.8) tenkinama viso judėjimo metu, tai egzistuoja pirmasis integralas (4.6).
Jei sistemos jungtys yra idealios ir leidžia tarp virtualių poslinkių sistemą, kaip standųjį kūną, suktis apie ašį ir tada pagrindinis reakcijų momentas ašies atžvilgiu ir yra lygus nuliui, o tada reikšmė dešinioji lygties pusė (4.5) reiškia pagrindinį visų išorinių aktyviųjų jėgų momentą ašies ir atžvilgiu. Šio momento lygybė nuliui ir ryšio (4.8) galiojimas nagrinėjamu atveju bus pakankamos sąlygos integralui (4.6) egzistuoti.
Jei ir ašies kryptis yra pastovi, tada sąlyga (4.8) bus įrašyta formoje
![]()
Ši lygybė reiškia, kad masės centro greičio ir taško A greičio projekcijos ašyje ir jai statmenoje plokštumoje yra lygiagrečios. S.A. Chaplygino darbe vietoj (4.9) reikia įvykdyti ne tokią bendrą sąlygą, kur X yra savavališka pastovi reikšmė.
Atkreipkite dėmesį, kad sąlyga (4.8) nepriklauso nuo taško pasirinkimo . Iš tiesų, tegul P yra savavališkas ašies taškas. Tada
ir todėl
Apibendrinant, atkreipiame dėmesį į Rézal geometrinį (4.1) ir (4.4) lygčių aiškinimą: vektorių galų absoliutūs greičio vektoriai ir yra atitinkamai lygūs pagrindiniam vektoriui ir visų išorinių jėgų pagrindiniam momentui taško A atžvilgiu. .
Sveikatos draudimo naudojimas sprendžiant problemas yra susijęs su tam tikrais sunkumais. Todėl tarp judėjimo charakteristikų ir jėgų dažniausiai nustatomi papildomi ryšiai, kurie yra patogesni praktiniam pritaikymui. Tokie santykiai yra bendrosios dinamikos teoremos. Jie, būdami OMS pasekmės, nustato ryšį tarp kai kurių specialiai įvestų judėjimo priemonių kitimo greičio ir išorinių jėgų savybių.
Impulso kitimo teorema. Įveskime materialaus taško impulso vektoriaus (R. Dekarto) sampratą (3.4 pav.):
I i = t V G (3.9)
Ryžiai. 3.4.
Sistemai pristatome koncepciją pagrindinis sistemos impulso vektorius kaip geometrinė suma:
Q = Y, m " V r
Pagal OZMS: Xu, -^=i) arba X
R (E) .
Atsižvelgdami į tai, kad /w, = const gauname: -Ym,!" = R(E)
arba galutine forma
dO/di = A (E (3.11)
tie. pirmoji pagrindinio sistemos impulso vektoriaus išvestinė laiko atžvilgiu yra lygi pagrindiniam išorinių jėgų vektoriui.
Masės centro judėjimo teorema. Sistemos masės centras vadinamas geometriniu tašku, kurio padėtis priklauso nuo T, ir tt iš masės pasiskirstymo /g/, sistemoje ir nustatomas masės centro spindulio vektoriaus išraiška (3.5 pav.):

Kur g s - masės centro spindulio vektorius.

Ryžiai. 3.5.
Skambinam = t su sistemos mase. Padauginus išraišką
taikant (3.12) vardikliui ir diferencijuojant abi rezultato puses
turėsime vertingą lygybę: g s t s = ^t.U. = 0 arba 0 = t s U s.
Taigi pagrindinis sistemos impulso vektorius yra lygus sistemos masės ir masės centro greičio sandaugai. Naudodami impulso kitimo teoremą (3.11), gauname:
t s dU s / dі = A (E) , arba
Formulė (3.13) išreiškia masės centro judėjimo teoremą: sistemos masės centras juda kaip materialus taškas, turintis sistemos masę, kurią veikia pagrindinis išorinių jėgų vektorius.
Kampinio momento kitimo teorema. Įveskime materialaus taško kampinio momento sampratą kaip jo spindulio vektoriaus ir impulso vektorinę sandaugą:
į oi = bl X kad, (3.14)
Kur į OI - materialaus taško kampinis impulsas fiksuoto taško atžvilgiu APIE(3.6 pav.).

Dabar apibrėžiame mechaninės sistemos kampinį impulsą kaip geometrinę sumą:
К() = X ko, = ШУ, ? O-15>
Diferencijuodami (3.15), gauname:
Ґ sek--- X t i U. + g u X t i
Atsižvelgiant į tai = U G U i X t i u i= 0 ir formulę (3.2), gauname:
сіК а /с1ї - ї 0 .
Remdamiesi antrąja (3.6) išraiška, pagaliau turėsime teoremą apie sistemos kampinio momento pokytį:
Pirmoji mechaninės sistemos impulso momento išvestinė fiksuoto centro O atžvilgiu yra lygi pagrindiniam išorinių jėgų, veikiančių šią sistemą to paties centro atžvilgiu, momentui.
Išvedant ryšį (3.16) buvo daroma prielaida, kad APIE- fiksuotas taškas. Tačiau galima įrodyti, kad daugeliu kitų atvejų santykio forma (3.16) nepasikeis, ypač jei plokštumoje judant momento taškas pasirenkamas masės centre, momentiniame greičių ar pagreičių centre. Be to, jei taškas APIE sutampa su judančiu materialiu tašku, šiam taškui parašyta lygybė (3.16) pavirs tapatybe 0 = 0.
Kinetinės energijos kitimo teorema. Kai mechaninė sistema juda, keičiasi ir „išorinė“, ir vidinė sistemos energija. Jei vidinių jėgų charakteristikos, pagrindinis vektorius ir pagrindinis momentas, neturi įtakos pagrindinio vektoriaus ir pagrindinio pagreičių skaičiaus pokyčiui, tada vidinės jėgos gali būti įtrauktos į sistemos energetinės būklės procesų vertinimą. Todėl, svarstant sistemos energijos pokyčius, reikia atsižvelgti į atskirų taškų judesius, kuriems taip pat taikomos vidinės jėgos.
Materialaus taško kinetinė energija apibrėžiama kaip kiekis
T^tuTsg. (3.17)
Mechaninės sistemos kinetinė energija lygi materialių sistemos taškų kinetinių energijų sumai:
Atkreipkite dėmesį, kad T > 0.
Jėgos galią apibrėžkime kaip jėgos vektoriaus ir greičio vektoriaus skaliarinę sandaugą:

Gana dažnai įmanoma nustatyti svarbias mechaninės sistemos judėjimo ypatybes, neintegruojant judėjimo diferencialinių lygčių sistemos. Tai pasiekiama taikant bendrąsias dinamikos teoremas.
5.1. Pagrindinės sąvokos ir apibrėžimai
Išorinės ir vidinės jėgos. Bet kokia jėga, veikianti tašką mechaninėje sistemoje, būtinai yra aktyvi jėga arba sujungimo reakcija. Visą jėgų rinkinį, veikiančią sistemos taškus, galima skirtingai suskirstyti į dvi klases: išorines jėgas ir vidines jėgas (indeksai e ir i – iš lotyniškų žodžių externus – išorinis ir internus – vidinis). Išorinės jėgos yra tos, kurios veikia sistemos taškus iš taškų ir kūnų, kurie nėra nagrinėjamos sistemos dalis. Nagrinėjamos sistemos taškų ir kūnų sąveikos jėgos vadinamos vidinėmis.
Šis skirstymas priklauso nuo to, kokius materialius taškus ir kūnus tyrėjas įtraukia į nagrinėjamą mechaninę sistemą. Jei išplėsime sistemos sudėtį įtraukdami papildomus taškus ir kūnus, tai kai kurios jėgos, kurios ankstesnėje sistemoje buvo išorinės, gali tapti vidinėmis išplėstoje sistemoje.
Vidinių jėgų savybės. Kadangi šios jėgos yra sąveikos tarp sistemos dalių jėgos, jos į pilną vidinių jėgų sistemą patenka „dveje“, organizuojamos pagal veiksmo-reakcijos aksiomą. Kiekvienas toks „du“ turi stipriąsias puses
pagrindinis vektorius ir pagrindinis momentas apie savavališką centrą yra lygūs nuliui. Kadangi visa vidinių jėgų sistema susideda tik iš „dviejų“, tai
1) pagrindinis vidinių jėgų sistemos vektorius lygus nuliui,
2) pagrindinis vidinių jėgų sistemos momentas savavališko taško atžvilgiu lygus nuliui.
Sistemos masė yra visų sistemą sudarančių taškų ir kūnų masių mk aritmetinė suma:
Masės centras mechaninės sistemos (inercijos centras) yra geometrinis taškas C, kurio spindulio vektorius ir koordinatės nustatomos pagal formules.
kur yra sistemą sudarančių taškų spindulio vektoriai ir koordinatės.
Kietam kūnui, esančiam vienodame gravitaciniame lauke, masės centro ir svorio centro padėtys sutampa kitais atvejais, tai yra skirtingi geometriniai taškai.
Kartu su inercine atskaitos sistema dažnai vienu metu nagrinėjama ir neinercinė atskaitos sistema, judanti transliaciniu būdu. Jo koordinačių ašys (König axes) parenkamos taip, kad pradžia C nuolat sutaptų su mechaninės sistemos masės centru. Pagal apibrėžimą masės centras yra nejudantis Koenig ašyse ir yra koordinačių pradžioje.
Sistemos inercijos momentas ašies atžvilgiu yra skaliarinis dydis, lygus visų sistemos taškų masių mk sandaugų sumai jų atstumo iki ašies kvadratais:
![]()
Jei mechaninė sistema yra standus korpusas, norėdami rasti 12, galite naudoti formulę

kur yra tankis, kūno užimamas tūris.
Masės centro judėjimo teorema. Mechaninės sistemos judėjimo diferencialinės lygtys. Mechaninės sistemos masės centro judėjimo teorema. Masės centro judėjimo išsaugojimo dėsnis.
Impulso kitimo teorema. Materialaus taško judėjimo dydis. Elementarus jėgos impulsas. Jėgos impulsas ribotam laikui ir jo projekcija į koordinačių ašis. Teorema apie materialaus taško impulso kitimo diferencialinėje ir baigtinėje formoje.
Mechaninės sistemos judesio kiekis; jo išraiška per sistemos masę ir jos masės centro greitį. Teorema apie mechaninės sistemos impulsų kitimo diferencialinėje ir baigtinėje formoje. Mechaninio impulso tvermės dėsnis
(Kūno ir kintamos masės taško samprata. Meščerskio lygtis. Ciolkovskio formulė.)
Kampinio momento kitimo teorema. Materialaus taško impulso momentas centro ir ašies atžvilgiu. Materialaus taško kampinio momento kitimo teorema. Centrinė valdžia. Materialaus taško kampinio impulso išsaugojimas centrinės jėgos atveju. (Sektorių greičio samprata. Plytų dėsnis.)
Pagrindinis mechaninės sistemos impulso arba kinetinis momentas centro ir ašies atžvilgiu. Besisukančio standaus kūno kinetinis momentas apie sukimosi ašį. Mechaninės sistemos kinetinio momento kitimo teorema. Mechaninės sistemos kampinio momento išsaugojimo dėsnis. (Teorema apie mechaninės sistemos kinetinio momento kitimą santykiniame judėjime masės centro atžvilgiu.)
Kinetinės energijos kitimo teorema. Materialaus taško kinetinė energija. Elementarus jėgos darbas; elementaraus darbo analitinė raiška. Darbas, kurį atlieka jėga galutinai pasislinkus jo taikymo taškui. Gravitacijos, tamprumo ir gravitacijos jėgos darbas. Teorema apie materialaus taško kinetinės energijos kitimą diferencialinėje ir baigtinėje formoje.
Mechaninės sistemos kinetinė energija. Formulės, skirtos standaus kūno kinetinės energijos apskaičiavimui atliekant transliacinį judėjimą, sukimosi aplink fiksuotą ašį ir bendruoju judėjimo atveju (ypač plokštumai lygiagretaus judėjimo metu). Teorema apie mechaninės sistemos kinetinės energijos kitimą diferencialinėmis ir baigtinėmis formomis. Vidinių jėgų atliekamo darbo kietame kūne suma lygi nuliui. Jėgų, veikiančių aplink fiksuotą ašį besisukantį standųjį kūną, darbas ir galia.
Jėgos lauko samprata. Potencialus jėgos laukas ir jėgos funkcija. Jėgos projekcijų išraiška jėgos funkcija. Vienodo potencialo paviršiai. Jėgos darbas galutiniam taško poslinkiui potencialiame jėgos lauke. Potenciali energija. Potencialių jėgų laukų pavyzdžiai: vienodas gravitacinis laukas ir gravitacinis laukas. Mechaninės energijos tvermės dėsnis.
Tvirta kėbulo dinamika. Standžiojo kūno transliacinio judėjimo diferencialinės lygtys. Standžio kūno sukimosi aplink fiksuotą ašį diferencialinė lygtis. Fizinė švytuoklė. Standžiojo kūno plokštuminio judėjimo diferencialinės lygtys.
D'Alemberto principas. D'Alemberto principas dėl materialaus taško; inercinė jėga. D'Alemberto principas mechaninei sistemai. Standaus kūno taškų inercijos jėgų nukreipimas į centrą; pagrindinis inercijos jėgų vektorius ir pagrindinis momentas.
(Guolių dinaminių reakcijų nustatymas standžiam kūnui sukant aplink fiksuotą ašį. Atvejis, kai sukimosi ašis yra pagrindinė centrinė kėbulo inercijos ašis.)
Galimų judesių principas ir bendroji dinamikos lygtis. Sujungimai ant mechaninės sistemos. Galimi (arba virtualūs) materialaus taško ir mechaninės sistemos judesiai. Sistemos laisvės laipsnių skaičius. Idealios jungtys. Galimų judesių principas. Bendroji dinamikos lygtis.
Sistemos judėjimo apibendrintomis koordinatėmis lygtys (Lagranžo lygtys). Apibendrintos sistemos koordinatės; apibendrintas greitis. Elementaraus darbo raiška apibendrintomis koordinatėmis. Apibendrintos jėgos ir jų skaičiavimas; potencialą turinčių jėgų atveju. Sistemos pusiausvyros apibendrintomis koordinatėmis sąlygos. Sistemos judėjimo diferencialinės lygtys apibendrintomis koordinatėmis arba 2-osios rūšies Lagranžo lygtys. Lagranžo lygtys potencialių jėgų atveju; Lagranžo funkcija (kinetinis potencialas).
Pusiausvyros stabilumo samprata. Vieno laisvės laipsnio mechaninės sistemos mažos laisvosios vibracijos šalia stabilios sistemos pusiausvyros padėties ir jų savybės.
Poveikio teorijos elementai. Poveikio reiškinys. Smūgio jėga ir smūgio impulsas. Smūgio jėgos veikimas materialiame taške. Teorema apie mechaninės sistemos impulso kitimo po smūgio. Tiesioginis centrinis kūno smūgis į nejudantį paviršių; elastiniai ir neelastingi smūgiai. Smūgio atsistatymo koeficientas ir jo eksperimentinis nustatymas. Tiesioginis centrinis dviejų kūnų poveikis. Carnot teorema.
NUORODOS
Pagrindinis
Butenin N.V., Lunts Ya-L., Merkin D.R. Teorinės mechanikos kursas. T. 1, 2. M., 1985 ir ankstesni leidimai.
Dobronravovas V.V., Nikitinas N.N. Teorinės mechanikos kursas. M., 1983 m.
Staržinskis V.M. Teorinė mechanika. M., 1980 m.
Targas S. M. Trumpas teorinės mechanikos kursas. M., 1986 ir ankstesni leidimai.
Yablonsky A. A., Nikiforova V. M. Teorinės mechanikos kursas. 1 dalis. M., 1984 ir ankstesni leidimai.
Yablonsky A. A. Teorinės mechanikos kursas. 2 dalis. M., 1984 ir ankstesni leidimai.
Meščerskis I. V. Teorinės mechanikos uždavinių rinkinys. M., 1986 ir ankstesni leidimai.
Teorinės mechanikos uždavinių rinkinys/Red. K. S. Kolesnikova. M., 1983 m.
Papildomas
Bat M. I., Dzhanelidze G. Yu., Kelzon A. S. Teorinė mechanika pavyzdžiuose ir uždaviniuose. 1, 2 dalys. M., 1984 ir ankstesni leidimai.
Užduočių rinkinys apie teorinę mechaniką/5razhnichen/so N. A., Kan V. L., Mintzberg B. L. ir kiti, 1987 m.
Novožilovas I. V., Zatsepinas M. F. Tipiški kompiuteriniai skaičiavimai teorinėje mechanikoje. M., 1986 m.
Užduočių rinkinys teorinės mechanikos kursiniams darbams / Red. A. A. Yablonsky. M., 1985 ir ankstesni leidimai (yra problemų sprendimo pavyzdžių).








