С суши имеет особенности на всех уровнях, от сотни километров в размере до крошечных долей миллиметра и ниже, нет никаких очевидных ограничений на размер наименьших особенностей, и, следовательно, ни один четко определенный периметр суши не зафиксирован. Различные аппроксимации существуют при определенных допущениях минимального размера.

Примером парадокса служит всем известное побережье Великобритании . Если береговая линия Великобритании измеряется с использованием фрактальной единиц в 100 км (62 мили) в длину, то длина береговой линии составляет около 2800 км (1700 миль). С единицей в 50 км (31 миль), общая протяженность составляет около 3400 км (2100 миль), примерно на 600 км (370 миль) длиннее.

Математические аспекты

Основная концепция длины происходит от Евклидова расстояния . В знакомой евклидовой геометрии , прямая линия представляет кратчайшее расстояние между двумя точками; эта линия имеет только одну конечную длину. Геодезическая длина на поверхности сферы, называемая большой длиной круга, измеряется по поверхности кривой, которая существует в плоскости, в содержащей конечные точки пути и центр сферы. Длина основной кривой является более сложной, но также может быть рассчитана. Измеряя с помощью линейки, человек может аппроксимировать длины кривой добавлением суммы прямых линий, соединяющих точки:

Используя несколько прямых приближенных к длине кривой будет произведена низкая оценка. Использование все более и более коротких линий будет производить сумму длин, которая приближается к истинной длине кривой. Точное значение этой длины можно установить с помощью исчисления, - раздела математики, позволяющим рассчитывать бесконечно малые расстояниях. Следующая анимация иллюстрирует данный пример:

Однако, не все кривые могут быть измерены таким образом. Фрактальной по определению считается кривая , со сложными изменениями шкалы измерения. Принимая во внимание приближение гладкой кривой ближе и ближе к одному значению по мере увеличения точности измерений, измеренное значение фракталов может существенно измениться.

Длина "истинного фрактала " всегда стремится к бесконечности. Однако, эта цифра основана на идее, что пространство может быть подразделено до неопределенности, т.е. быть неограниченным. Это фантастика, которая лежит в основе евклидовой геометрии и служит в качестве полезной модели в повседневных измерениях, почти наверняка не отражает изменяющиеся реалии «пространства» и «расстояния» на атомном уровне. Береговые линии отличаются от математических фракталов, они образуются из многочисленных мелких деталей, которые создают модели только статистически.

Из практических соображений , можно использовать измерение при соответствующем выборе минимального размера порядковой единицы. Если береговая линия измеряется в километрах, то небольшие вариации намного меньше, чем в одном километре и их легко игнорировать. Для измерения береговой линии в сантиметрах, малюсенькие изменения размера должны быть рассмотрены. Использование различных методик измерения для различных единиц также разрушает обычную уверенность, что блоки могут быть преобразованы с помощью простого умножения. Крайние случаи береговой линии включают парадокс фьордов тяжелых побережья Норвегии, Чили и Тихоокеанского побережья Северной Америки.

Незадолго до 1951 года, Льюис Фрай Ричардсон , в исследовании возможного влиянии длины границы на вероятность войны, заметил, что португальцы представили свои измеренные границе с Испанией , длину в 987 км, но Испания сообщила ее как 1214 км. Это было началом проблемы береговой линии, которую математически сложно измерить ввиду нерегулярности самой линии. Преобладающим методом оценки длины границы (или береговой линии) было наложение N количества равных отрезков с длиной ℓ с разделителями на карте или аэрофотоснимков. Каждый конец сегмента должен быть на границе. Исследовав расхождения в оценке границ, Ричардсон обнаружил то, что сейчас называется эффектом Ричардсона: сумма сегментов обратно пропорциональна общей длине сегментов. По сути, тем короче линейка, тем больше измеренной границы; испанскими и португальскими географами граница была просто измерена с помощью разной длины линеек. В результате поразило Ричардсона то, что, при определенных обстоятельствах, когда длина линейки ℓ стремится к нулю, длина береговой линии также стремится к бесконечности. Ричардсон считает, что на основании геометрии Евклида , береговая линия будет подходить к фиксированной длине, как делать подобные оценки правильных геометрических фигур. Например, периметр правильного многоугольника, вписанного в окружность, приближается к окружности с увеличением числа сторон (и уменьшение длины одной стороны). В геометрической теории меры такая гладкая кривая, как круг, к которому могут быть приближены небольшие прямые сегменты с определенным пределом, называется спрямляемой кривой.

Более десяти лет после того, как Ричардсон завершил свою работу, Бенуа Мандельброт разработал новую область математики, - фрактальную геометрию для описания именно таких неспрямляемых комплексов в природе в виде бесконечной береговой линии. Собственное определение новой фигуры, выступающей в качестве основания для его исследования: Я придумал фрактал от латинского прилагательного «фрагментированный » чтобы создать нерегулярные фрагменты. Поэтому целесообразно... что, в дополнение к "фрагментированным" ... разорванные должно также означать "нерегулярные".

Ключевым свойством фрактала есть самоподобие, то есть, в любом масштабе проявляется та же общая конфигурация. Береговая линия воспринимается как заливы, чередующиеся с мысами. В гипотетической ситуации, данное побережье обладает этим свойством самоподобия, независимо от того, как сильно любой небольшого участка побережья проявляется в увеличенном виде, аналогичная картина меньших заливов и мысов накладывается на большие заливы и мысы, вплоть до песчинки. При этом масштабы береговой линии мгновенно меняется в потенциально бесконечно длинную нить со случайным расположением бухт и мысов формируемых из небольших объектов. В таких условиях (в отличие от гладких кривых) Мандельброт утверждает, "длина береговой линии оказывается неуловимым понятием, которая скользит между пальцами тех, кто хочет понять его. "Существуют различные виды фракталов. Береговая линия с указанными параметрами находится в "первой категории фракталов, а именно кривые с фрактальной размерностью больше 1." Это последнее утверждение представляет собой расширение Мандельбротом мысли Ричардсона.

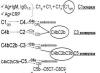
Заявление Мандельброта Эффекта Ричардсона:

где L, длина береговой линии, функция единицы измерения, ε, аппроксимируется выражением. F является постоянной и D это параметр Ричардсона. Он не дал теоретическое объяснение, но Мандельброт определил D с нецелой формой размерности Хаусдорфа , позже - фрактальной размерности. Перегруппировав правую сторону выражения получаем:

где Fε-D должно быть количеством единиц ε, необходимых для получения L. Фрактальная размерность - число размеров фрактала используемых для аппроксимации фрактала: 0 для точки, 1 для линии, 2 для площади. D в выражении находится между 1 и 2, для побережья обычно меньше, чем 1,5. Ломаное измерение побережья не распространяется в одном направлении и не представляют собой область, но является промежуточным. Это можно интерпретировать как толстые линии или полосы шириной 2ε. Более ломаные береговые линии имеют большую D и, следовательно, L больше, за тот же ε. Мандельброт показал, что D не зависит от ε.

Источник : http://en.wikipedia.org/wiki/Coast#Coastline_problem

http://en.wikipedia.org/wiki/Coastline_paradox

Перевод: Дмитрий Шахов

Длина береговой линии

Измерима ли она?
Вправе ли мы приводить в учебниках длину
береговой линии и не оконфузимся ли,
спрашивая эту цифру с учеников?

К.С. ЛАЗАРЕВИЧ

На уроках географии мы оперируем множеством статистических показателей. Большинство из них на вид очень просты и четки: столько-то миллионов человек, столько-то миллионов тонн угля, столько-то километров. Но это если не вдумываться. А стоит только копнуть любую цифру поглубже - и она перестает быть четкой. Иногда же - рассыпается в прах. Вот примеры.
Открываем недавно изданный и только что поступивший в продажу Атлас мира (М.: ФГУП Производственное картосоставительское объединение «Картография», 2003.). В таблице «Государства и территории мира» находим: «Столица Франции - Париж (2 125,2 тыс. жителей). Если ученик приведет на экзамене такую цифру, будет ли экзаменатор удовлетворен? Ведь Париж - один из крупнейших центров Европы и никак не меньше Петербурга. Но в приведенной цифре нет ошибки: это Париж в административных границах города Парижа. А в границах реально сложившегося городского сгустка - это десятимиллионник. Очень многое зависит от того, как считать. Сказанное не значит, что мы можем принять от ученика в качестве ответа любую цифру в диапазоне от 2,2 до 10; приводя то или иное число, учащийся должен понимать, что за ним стоит, что и как измерено.
Миллион тонн высококалорийного угля и угля бурого - разные миллионы.
Но вот, казалось бы, километры. Километр - он и в Африке километр. И что уж измеренное в километрах можно подвергнуть сомнению? Но, оказывается, и приводя длины в километрах, автор учебника должен сначала подумать. Учитель же, пользуясь учебником, также должен подвергнуть цифру критическому анализу, прежде чем транслировать ее ученикам и требовать ее запоминания. Читаем учебник для 10-го класса: «Канада выходит к трем океанам, и общая протяженность ее береговой линии (около 250 тыс. км) не имеет себе равных в мире». Как была измерена береговая линия, что мерили, как мерили, чем мерили? Как вообще можно измерить береговую линию?

Неправильные кривые по карте можно измерять при помощи курвиметра - колесико этого прибора катят по кривой, тщательно выписывая каждую извилину. Однако извилистость береговой линии часто бывает столь велика, что курвиметром по ней не пройти. Приходится вышагивать по кривой циркулем-измерителем. Наиболее удобная длина шага - 2 мм. В разных масштабах этот шаг соответствует, конечно, разным расстояниям, точной длины такое измерение никогда не даст, так как каждый шаг спрямляет кривую на небольшом отрезке, но относительная погрешность более или менее сохраняется.
Давайте, ради примера, попробуем измерить длину береговой линии Чукотского а.о. Возьмем карту из Школьного атласа по географии России (масштаб 1: 22 000 000) и двухмиллиметровым шагом циркуля (44 км) прошагаем все чукотское побережье. Результат будет 4300 км (98 шагов циркуля). Произведем то же измерение по карте масштаба
1: 7 500 000. Здесь мы уже насчитаем 345 двухмиллиметровых (15 км) шажков, то есть
5 200 км. Логично предположить, что если в измерениях будет использована карта еще большего масштаба, измеренная береговая линия станет еще протяженнее.
Поставим еще один эксперимент. Длина береговой линии Ленинградской обл. по карте
1: 22 000 000 - 300 км, по карте 1: 2 500 000 - 555 км, а по топографической карте
1: 500 000 - 670 км. При этом длина береговой линии одного только Выборгского залива (где берега особо изрезаны заливчиками и бухточками), измеренная по топографической карте, составляет 338 км, тогда как по школьному атласу - 65 км (разница более чем в
5 раз!).
Таким образом, наблюдается закономерное увеличение длины измеренной береговой линии с укрупнением масштаба. Причина не только в том, что двухмиллиметровый шаг циркуля соответствует всё меньшей величине на местности, но главным образом в том, что сама линия, даже если ее очень точно измерить и перевести в соответствии с масштабом в километры, действительно становится длиннее (рис. 1). На карте России у берега Ленинградской обл. угадываются лишь Выборгский залив, Невская губа и небольшие изгибы южного берега Финского залива. На карте масштаба 1: 2 500 000 очертания Выборгского залива уже довольно сложные, а на юге ясно видны Копорская и Лужская губы. На полумиллионной карте в пределах Выборгского залива множество других мелких заливов, некоторые из которых имеют собственные имена (зал. Балтиец, бухта Ключевская), и лишь южный берег Финского залива выглядит мало изменившимся по сравнению с предыдущим масштабом, там изрезанность берега гораздо меньше.

Как же установить точную длину береговой линии?
Этой целью задался английский метеоролог Ричардсон, выбрав в качестве полигона свой родной остров - Великобританию. Он и пришел к выводу об увеличении длины береговой линии с увеличением масштаба карты, по которой эту длину измеряют (рис. 2). Есть ли предел такого увеличения? Едва ли. Длину береговой линии увеличивает каждая небольшая песчаная коса, вдающаяся в море, каждая ложбинка, создающая крохотный залив, каждый камешек, который обтекает вода. Даже на самой крупномасштабной карте их не видно, между тем в действительности все эти неровности береговой линии существуют.

Приводят много примеров того, как использование математических методов позволяет сделать географические исследования более убедительными, более достоверными. Здесь же произошло обратное: географическое исследование - изучение длины береговой линии - способствовало возникновению нового математического понятия. Английское название этого понятия - fractal, по-русски же оно еще окончательно не устоялось и встречается в трех вариантах: фрактал (родительный и творительный падежи будут фрактала , фракталом ), фракталь в мужском роде (фракталя , фракталем ) и фракталь в женском роде (фрактали , фракталью ); за последнее время, кажется, склоняются к фракталу .
Фрактал - это линия, каждый фрагмент которой бесконечно усложняется, длина каждого фрагмента и всей линии постоянно увеличивается. В качестве примера можно привести фигуру, обычно называемую снежинкой Коха, хотя название это неверно: построила эту снежинку в начале ХХ в. Хельга фон Кох, и склонять ее фамилию не следует.
Возьмем равносторонний треугольник. Разделим каждую его сторону на три равные части и на среднем отрезке каждой стороны построим равносторонний треугольник. Получится правильная шестиконечная звезда, фигура с шестью выпуклыми углами и шестью входящими. Разделим каждую ее сторону (а этих сторон 12) на три равные части и на среднем отрезке каждой стороны снова построим равносторонний треугольник. Получится фигура уже с 48 сторонами, с 18 выпуклыми и 30 входящими углами. Повторяя эту операцию бесконечное число раз (сделать это можно, конечно, лишь мысленно), мы получим фигуру, площадь которой постоянно увеличивается, но все медленнее, постепенно приближаясь к некоторому пределу (рис. 3). Периметр же этой фигуры увеличивается беспредельно, так как каждый раз, когда мы строим на стороне фигуры новый равносторонний треугольничек, сколь бы мал он ни был, три равных отрезка этой стороны заменяются на четыре таких же и потому длина каждой стороны (и следовательно всего периметра) увеличивается в 4/3 раза, а любое число больше единицы в степени, равной бесконечности (а построение мы делаем бесконечное число раз), стремится к бесконечности.

Граница снежинки будет представлять собой что-то вроде широкой, мохнатой линии, заполняющей собою всю приграничную область этой фигуры. Понятия «широкая линия», «толстая поверхность», казалось бы, абсурдные с точки зрения классической математики (линия там не имеет ширины, а поверхность - толщины), с развитием теории фракталов приобрели права гражданства. Считается, что линия одномерна, она имеет только длину, положение точки на ней определяется одной координатой; поверхность двумерна, она имеет площадь, положение точки на ней определяется двумя координатами; тело трехмерно, оно имеет объем, нужны уже три координаты. А теория фракталов вводит понятие дробной размерности: линия не стала двумерной, но уже перестала быть одномерной. Неподготовленному человеку это довольно трудно понять (нельзя же чихнуть полтора раза), но если мы вспомним, как ведет себя береговая линия - не только на карте, но и в природе, как она меняется, если смотреть на нее, присев на корточки, потом выпрямившись во весь рост, потом поднявшись на гору, потом взлетев на самолете или космическом корабле, мы не столько поймем, сколько почувствуем, какую сложную систему представляет собой эта линия; для нее определенно мало одной характеристики - длины.
И теория фракталов, родившаяся из географических исследований, уже сама приходит на помощь географии. Еще не разработан, но определенно имеет перспективы метод изучения рельефа как фрактала. Рассматривая рельеф в общем виде, рисуя его на мелкомасштабной карте, мы видим горные хребты, плато, глубокие долины. В среднем масштабе вырисовываются уже холмы, небольшие долины, овраги. Еще крупнее - и видны кочки, ветровая рябь на песке. Но и это не предел: есть отдельные камешки, песчинки. В практическом отношении все это важно потому, что нужно научиться правильно отбирать объекты для изображения на картах разных масштабов; одна из главных ошибок составителей карт - несоответствие содержания карты ее масштабу, карта или недогружена, или перегружена.
А что же все-таки делать с длиной береговой линии? Отказаться ее измерять, потому что она неизмерима?
Нет, это не выход. Просто, приводя длину береговой линии, следует всегда указывать, по картам какого масштаба она измерялась, каким способом. И обязательно оговаривать при этом, учитывалась береговая линия островов или нет. Без указания масштаба карт и того, учтены острова или нет, всякие данные о длине береговой линии теряют смысл. К сожалению, даже в источниках, претендующих на сугубую солидность, можно встретить страшные нелепости. Например, известный сайт ЦРУ «The World Factbook». Здесь для каждой страны и океана приведены данные по береговой линии, но способ измерения не указан. В результате береговая линия Канады оказывается больше 200 тыс. км, Северного Ледовитого океана - 45,4 тыс. км, Атлантического - 111,9 тыс. км (данные приведены - не подумайте плохого! - с точностью до километра). Канаду считали с учетом островов, это несомненно; как считали океаны, неизвестно, но береговая линия двух из трех океанов, омывающих Канаду, в сумме меньше береговой линии одной только Канады. Для Норвегии приведена цифра 21 925 км и дано примечание: «Материк 3419 км, большие острова 2413 км, длинные фьорды, многочисленные маленькие острова и мелкие изгибы [в буквальном переводе зазубрины ] береговой линии 16 093 км». В сумме получается как раз указанная общая длина береговой линии. Но вот почему берега фьордов - не часть береговой линии материка, почему длина зазубрин приплюсована к длине береговой линии материка, какие острова считать большими - обо всем этом приходится только догадываться. Совершенно бесспорные данные в этой таблице приведены только для Андорры, Австрии, Ботсваны, Венгрии, Свазиленда и подобных им стран, выхода к морю не имеющих, - написано: «0 км».

Фракталами называются геометрические объекты: линии поверхности, пространственные тела, имеющие сильно изрезанную форму и обладающие свойством самоподобия. Слово фрактал произошло от слова fractus и переводится как дробный, ломаный. Самоподобие, как основная характеристика означает, что он более или менее единообразно устроен в широком диапазоне масштабов. Так, при увеличении маленькие фрагменты фрактала получаются очень похожими на большие. В идеальном случае такое самоподобие приводит к тому, что фрактальный объект оказывается инвариантным относительно растяжений, т.е. ему, как говорят, присуща дилатационная симметрия. Она предполагает неизменность основных геометрических особенностей фрактала при изменении масштаба.

Конечно, для реального природного фрактала существует некоторый минимальный масштаб длины, такой, что на расстояниях его основное свойство - самоподобие - пропадает. Кроме того, на достаточно больших масштабах длин, где - характерный геометрический размер объектов, это свойство самоподобия также нарушается. Поэтому свойства природных фракталов рассматриваются лишь на масштабах l, удовлетворяющих соотношении . Такие ограничения являются довольно естественными, потому что, когда мы приводим в качестве примера фрактала - изломанную, негладкую траекторию броуновской частицы, то мы понимаем, что образ является очевидной идеализацией. Дело в том, что на маленьких масштабах сказывается конечность времени соударения. При учете этих обстоятельств, траектория броуновской частицы становится плавной кривой.

Отметим, что свойство самоподобия характерно лишь для регулярных фракталов. Если вместо детерминированного способы построения включить в алгоритм их создания некоторый элемент случайности (как это бывает, например, во многих процессах диффузионного роста кластеров, электрическом пробое и т.д.), то возникают так называемые случайные фракталы. Основное их отличие от регулярных состоит в том, что свойства самоподобия справедливы только после соответствующего усрединения по всем статистически независимым реализациям объекта. При этом увеличенная часть фрактала не точно идентична исходному фрагменту, однако их статистические характеристики совпадают. Но изучаемый нами фрактал является одним из классических фракталов, а поэтому регулярным.

Длина береговой линии

Первоначально понятие фрактала возникло в физике в связи с задачей о нахождении береговой линии. При ее измерении по имеющейся карте местности выяснилась любопытная деталь - чем более крупномасштабная берется карта, тем более длинной оказывается эта береговая линия.

Рисунок 1 - Карта береговой линии

Пусть, например, расстояние по прямой между расположенными на береговой линии точками A и B равно R (см. рис. 1). Тогда, чтобы измерить длину береговой линии между этими точками, мы расставим по берегу жестко связанные друг с другом вешки так, что расстояние между соседними вешками составляло бы, например, l=10км . Длину береговой линии в километрах между точками A и B мы примем тогда равной чиcле вешек минус одна, помноженному на десять. Следующее измерение этой длины мы произведем подобным же образом, но расстояние между соседними вешками сделаем уже равным l=1км.

Оказывается, что результаты этих измерений будут различными. При уменьшении масштаба l мы будем получать все большие значения длины. В отличие от гладкой кривой, линия морского побережья оказывается зачастую настолько изрезанной (вплоть до самых маленьких масштабов), что с уменьшением звена l величина L - длина береговой линии - не стремится к конечному пределу, а увеличивается по постепенному закону

где D - некоторый показатель степени, который называется фрактальной размерностью береговой линии. Чем больше величина D , тем более изрезанной является эта береговая линия. Происхождение зависимости (1) интуитивно понятно: чем меньший масштаб мы используем, тем меньшие детали побережья будут учтены и дадут вклад в измеряемую длину. Наоборот, увеличивая масштаб, мы спрямляем побережье, уменьшая длину L .

Таким образом, очевидно, что для определения длины береговой линии L с помощью жесткого масштаба l (например, с помощью циркуля с фиксированным раствором), необходимо сделать N=L/l шагов, причем величина L меняется c l так, что N зависит от l по закону. В результате с уменьшением масштаба, длина береговой линии неограниченно возрастает. Это обстоятельство резко отличает фрактальную кривую от обычной гладкой кривой (типа окружности, эллипса), для которой предел длины аппроксимирующей ломаной L при стремлении к нулю длины ее звена l конечен. В результате для гладкой кривой ее фрактальная размерность D=1 , т.е. совпадает с топологической.

Приведем величины фрактальных размерностей D для различных береговых линий. Например, для Британских островов D ? 1. 3 , а для Норвегии D ? 1. 5 . Фрактальная размерность побережья Австралии D ? 1. 1. Близкими к единице оказываются и фрактальные размерности других побережий.

Выше было введено понятие о фрактальной размерности береговой линии. Дадим теперь общее определение этой величины. Пусть d - обычная Евклидова размерность пространства, в котором находится наш фрактальный объект (d=1 - линия, d=2 - плоскость, d=3 - обычное трехмерное пространство). Покроем теперь этот объект целиком d -мерными "шарами" радиуса l . Предположим, что нам потребовалось для этого не менее чем N (l) шаров. Тогда, если при достаточно малых l величина N (l ) меняется по степенному закону:

то D - называется Хаусдорфовой или фрактальной размерностью этого объекта.

Прежде чем познакомиться с первым видом фракталов - а именно, с кривыми, фрактальная размерность которых превышает 1, - рассмотрим типичный участок какого-нибудь берега. Очевидно, что его длина не может быть меньше расстояния по прямой между его начальной и конечной точками. Однако, как правило, береговые линии имеют неправильную форму - они извилисты и изломаны, и их длины, вне всякого сомнения, значительно превышают расстояния между их крайними точками, измеренные по прямой.

Известно много способов оценить длину береговой линии более точно, и в этой главе мы проанализируем некоторые из них. В конце концов мы придем к очень примечательному выводу: длина береговой линии - понятие весьма скользкое, и голыми руками его не ухватишь. Какой бы метод измерения мы ни применяли, результат всегда одинаков: длина типичного побережья очень велика и настолько нечетко определена, что удобнее всего считать ее бесконечной. Следовательно, если кому-нибудь вздумается сравнить различные берега с точки зрения их протяженности, ему придется подыскать что-нибудь взамен понятия длины, которое к данному случаю неприменимо.

В этой главе мы как раз и займемся поисками подходящей замены, причем в процессе поисков нам не избежать знакомства с различными формами фрактальных концепций размерности, меры и кривой.

АЛЬТЕРНАТИВНЫЕ МЕТОДЫ ИЗМЕРЕНИЯ

Метод А . Установим раствор измерительного циркуля на некоторую заданную длину , которую назовем длиной шага, и пройдемся этим циркулем вдоль интересующей нас береговой линии, начиная каждый новый шаг в той точке, где закончился предыдущий. Количество шагов, умноженное на длину е, даст нам приблизительную длину берега . Со школьной скамьи нам известно, что если повторять эту операцию, каждый раз уменьшая раствор циркуля, то можно ожидать, что величина быстро устремится к некоторому вполне определенному значению, называемому истинной длиной. Однако то, что происходит на деле, никак не соответствует нашим ожиданиям. В типичном случае наблюдаемая длина склонна увеличиваться неограниченно.

Причина такого ее поведения очевидна: если рассмотреть какой-нибудь полуостров или бухту на картах масштаба 1/100 000 и 1/10 000, то на последней карте мы ясно различим более мелкие полуострова и бухты, которых не было видно на первой. Карта того же участка, выполненная в масштабе 1/1000, покажет нам еще более мелкие полуостровки и бухточки, и так далее. Каждая новая деталь увеличивает общую длину берега.

Вышеописанная процедура подразумевает, что линия берега имеет слишком неправильную форму, и поэтому ее длина не может быть непосредственно представлена в виде суммы длин простых геометрических кривых, значения длин которых можно найти в справочниках. То есть, Метод А заменяет береговую линию на последовательность ломаных линий, составленных из прямолинейных участков, длину которых мы определять умеем.

Метод В. Такого же «сглаживания» можно добиться и другими способами. Вообразите себе человека, проходящего вдоль берега по кратчайшему пути, траектория которого нигде не отходит от воды далее чем на заданное расстояние . Дойдя до конечной точки, он возвращается назад, несколько уменьшив при этом величину . Затем еще и еще, пока, наконец, величина не достигнет, скажем, 50 см. Уменьшать ее далее не представляется возможным, так как человек слишком велик и неуклюж, чтобы суметь проследить более детализированную траекторию. Мне могут возразить, что эти недостижимые мелкие детали, во-первых, не представляют для человека никакого непосредственного интереса, а во-вторых, подвержены столь значительным изменениям в зависимости от времени года и высоты прилива, что их подробная регистрация вообще теряет всякий смысл. Первое из возражений мы рассмотрим позднее в этой главе. Что касается второго возражения, то его можно нейтрализовать, ограничившись рассмотрением скалистого берега при низком приливе и спокойной воде. В принципе, человек может проследить и более детализированные приближенные кривые, призвав себе на помощь мышь, затем муравья и так далее. И снова, по мере того, как наш ходок следует все более близкой к воде тропой, расстояние, которое ему предстоит пройти, неограниченно возрастает.

Метод С. Метод В подразумевает определенную асимметричность между водой и берегом. Для того, чтобы избежать этой асимметричности, Кантор предложил рассматривать береговую линию словно бы через расфокусированный объектив, вследствие чего каждая точка превращается в круглое пятно радиуса . Другими словами, Кантор рассматривает все точки - как на суше, так и на воде, - расстояние от которых до собственно береговой линии не превышает . Эти точки образуют некое подобие сосиски или ленты шириной (пример такой «сосиски» - правда, в ином контексте - приведен на рис. 56). Измерим площадь полученной ленты и разделим ее на . Если бы береговая линия была прямой, то лента представляла бы собой прямоугольник, а найденная вышеописанным образом величина оказалась бы действительной длиной берега. Имея дело с реальными береговыми линиями, мы получаем приблизительную оценку длины , которая неограниченно возрастает при уменьшении .

Метод D . Вообразите себе карту, выполненную в манере худож- ников-пуантилистов, т. е. такую, где материки и океаны изображены цветными круглыми пятнами радиуса . Вместо того, чтобы считать центрами пятен точки, принадлежащие береговой линии, как в Методе С, потребуем, чтобы количество пятен, полностью скрывающих линию, было наименьшим. В результате у мысов пятна будут по большей части лежать на суше, а у бухт - в море. Оценкой длины береговой линии здесь будет результат деления закрытой пятнами площади на . «Поведение» этой оценки также оставляет желать лучшего.

ПРОИЗВОЛЬНОСТЬ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Резюмируя предыдущий раздел, заметим, что результат применения любого из четырех методов всегда один и тот же. По мере уменьшения е приблизительная длина кривой устремляется в бесконечность.

Для того, чтобы в должной мере уяснить значение этого факта, произведем аналогичное измерение длины какой-либо обыкновенной евклидовой кривой. Например, на отрезке прямой приблизительные оценочные данные измерения в основном совпадают и определяют искомую длину. В случае окружности приблизительное значение длины возрастает, но довольно быстро устремляется к некоторому конкретному пределу. Кривые, длину которых можно определить таким образом, называются спрямляемыми.

Еще более поучительно попробовать измерить длину какой-нибудь из береговых линий, одомашненных человеком, - скажем, побережья вблизи Челси в его сегодняшнем виде. Поскольку очень большие складки местности человек пока оставляет без изменений, установим на нашем циркуле очень большой раствор и будем его постепенно уменьшать. Как и следовало ожидать, длина береговой линии при этом будет расти.

Однако здесь имеется одна интересная особенность: при дальнейшем уменьшении мы неизбежно попадаем в некую промежуточную зону, где длина почти не изменяется. Эта зона простирается приблизительно от 20 м до 20 см (очень приблизительно). Когда становится меньше 20 см, длина снова начинает возрастать - теперь на результат измерения влияют уже отдельные камни. Таким образом, если построить график изменения величины как функции от , то на ней, вне всякого сомнения, обнаружится плоский участок при значениях е в интервале от 20 м до 20 см - на аналогичных графиках для естественных «диких» побережий подобных плоских участков не наблюдается.

Очевидно, что измерения, произведенные в этой плоской зоне, обладают огромной практической ценностью. Поскольку границы между различными научными дисциплинами являются, в основном, результатом договоренности между учеными о разделении труда, мы можем, например, передать все феномены, масштабы которых превышают 20 м, т. е. те, до которых человек еще не дотянулся, в ведомство географии. Такое ограничение даст нам вполне определенную географическую длину. Береговая охрана может с успехом использовать то же значение для работы с «дикими» берегами, а энциклопедии и альманахи сообщат всем желающим соответствующую длину .

С другой стороны, мне трудно представить, что все заинтересованные правительственные учреждения пусть даже какой-либо одной страны договорятся между собой об использовании единого значения , а уж принятие его всеми странами мира совершенно невозможно вообразить. Ричардсон приводит такой пример: в испанских и португальских энциклопедиях приводится различная длина сухопутной границы между этими странами, причем разница составляет 20% (так же обстоит дело с границей между Бельгией и Нидерландами). Это несоответствие, должно быть, частично объясняется различным выбором . Эмпирические данные, которые мы вскоре обсудим, показывают, что для возникновения такой разницы достаточно, чтобы одно значение отличалось от другого всего лишь в два раза; кроме того, нет ничего удивительного в том, что маленькая страна (Португалия) измеряет длину своих границ более тщательно, чем ее большой сосед.

Второй и более значительный довод против выбора произвольного носит философский и общенаучный характер. Природа существует независимо от человека, и всякий, кто приписывает слишком большую важность какому-либо конкретному значению или , предполагает, что определяющим звеном в процессе постижения Природы является человек со своими общепринятыми мерками или весьма переменчивыми техническими средствами. Если береговым линиям суждено когда-нибудь стать объектами научного исследования, вряд ли нам удастся законодательным порядком запретить неопределенность, наблюдаемую в отношении их длин. Как бы то ни было, концепция географической длины вовсе не столь безобидна, как представляется на первый взгляд. Она не является до конца «объективной», так как при определении длины таким образом неизбежно влияние наблюдателя.

ПРИЗНАНИЕ И ЗНАЧЕНИЕ ПРОИЗВОЛЬНОСТИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Несомненно, многие придерживаются мнения, что береговые линии представляют собой неспрямляемые кривые, и я, если уж на то пошло, не могу припомнить, чтобы кто-нибудь считал иначе. Однако мои поиски письменных свидетельств в пользу этого мнения потерпели почти полный провал. Помимо цитат из Перрена, приведенных во второй главе, имеется еще вот такое наблюдение в статье Штейнгауза : «Измеряя длину левого берега Вислы с возрастающей точностью, можно получить значения в десятки, сотни и даже тысячи раз большие, чем то, что дает школьная карта... Весьма близким к реальности представляется следующее заявление: большинство встречающихся в природе дуг не являются спрямляемыми. Это заявление противоречит распространенному мнению, сводящемуся к тому, что неспрямляемые дуги - математическая фикция, а в природе все дуги спрямляемы. Из этих двух противоречивых заявлений верным, по всей видимости, следует считать все же первое». Однако ни Перрен, ни Штейнгауз так и не удосужились разработать свои догадки подробнее и довести их до логического конца.

К. Фадиман рассказывает одну занятную историю. Его друг Эдвард Каснер несколько раз проводил такой эксперимент: он «спрашивал у маленьких детей, какова, по их мнению, общая длина побережья Соединенных Штатов. После того, как кто-то из детей высказывал достаточно «разумное» предположение,... Каснер... предлагал им подумать о том, насколько можно увеличить эту цифру, если очень тщательно измерить периметр всех мысов и бухт, затем так же тщательно проследить меньшие мыски и бухточки в каждом из этих мысов и в каждой из этих бухт, затем измерить каждый камешек и каждую песчинку из тех, что образуют береговую линию, каждую молекулу, каждый атом и т. д. Получалось, что берег может быть каким угодно длинным. Дети понимали это сразу, а вот со взрослыми у Каснера возникали проблемы.» История, конечно, очень мила, однако вряд ли она имеет отношение к моим поискам. Каснер явно не ставил перед собой цель выделить некий аспект реальности, достойный дальнейшего изучения.

Таким образом, можно сказать, что статья и книга, которую вы держите в руках, представляют собой по существу первые работы, посвященные этой теме.

В своей книге «Воля верить»1 Уильям Джеймс пишет: «То, что не укладывается в рамки классификаций... всегда являет собой тучную ниву для великих открытий. В любой науке вокруг общепризнанных и упорядоченных фактов вечно кружит пыльное облако исключений из правил - явлений малозаметных, непостоянных, редко встречающихся, явлений, которые проще игнорировать, нежели рассматривать. Всякая наука стремится к идеальному состоянию замкнутой и строгой системы истин... Феномены, не подлежащие классификации в рамках системы, считаются парадоксальными нелепостями и заведомо не истинны. Ими пренебрегают и их отвергают, исходя из лучших побуждений научной совести... Тот, кто всерьез займется иррегулярными феноменами, окажется способен создать новую науку на фундаменте старой. По завершении же этого процесса правилами обновленной науки по большей части станут вчерашние исключения».

Настоящее эссе, скромной целью которого является полное обновление геометрии Природы, описывает феномены, настолько не вписывающиеся в классификацию, что говорить о них можно лишь с позволения цензуры. С первым из таких феноменов вы встретитесь уже в следующем разделе.

ЭФФЕКТ РИЧАРДСОНА

Эмпирическое исследование изменения приблизительной длины , получаемой с помощью Метода А, описано в статье Ричардсона , ссылка на которую по счастливой (или роковой) случайности попала мне на глаза. Я обратил на нее внимание только потому, что я был наслышан о Льюисе Фрае Ричардсоне как о выдающемся ученом, оригинальность мышления которого была сродни эксцентричности (см. главу 40). Как мы увидим в главе 10, человечество обязано ему некоторыми наиболее глубокими и долговечными идеями относительно природы турбулентности - особого внимания среди них заслуживает та, согласно которой турбулентность предполагает возникновение самоподобного каскада. Он также занимался и другими сложными проблемами - такими, например, как природа вооруженного конфликта между государствами. Его опыты являли собой образец классической простоты, однако он, если возникала такая необходимость, не колеблясь пользовался и более утонченными концепциями.

Приведенные на рис. 57 графики, обнаруженные уже после смерти Ричардсона среди его бумаг, были опубликованы в чуть ли не секретном (и совершенно не подходящем для таких публикаций) «Ежегоднике по общим системам». Рассмотрев эти графики, мы приходим к заключению, что существуют две постоянные (назовем их и ) - такие, что для определения длины береговой линии посредством построения приближенной к ней ломаной необходимо взять примерно интервалов длины и записать следующую формулу:

Значение показателя зависит, по всей видимости, от характера измеряемой береговой линии, причем различные участки этой линии, рассматриваемые по отдельности, могут дать различные . Для Ричардсона величина была просто удобным показателем, не имеющим какого-либо особенного смысла. Однако похоже, что значение этого показателя не зависит от выбранного метода оценки длины береговой линии. А значит, он заслуживает самого пристального внимания.

ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ БЕРЕГОВОЙ ЛИНИИ

Изучив работу Ричардсона, я предположил , что хотя показатель не является целым числом, его можно и нужно понимать как размерность - точнее, как фрактальную размерность. Разумеется, я вполне осознавал, что все вышеперечисленные методы измерения базируются на нестандартных обобщенных определениях размерности, уже применяемых в чистой математике. Определение длины, основанное на покрытии береговой линии наименьшим числом пятен радиуса , используется в для определения размерности покрытия. Определение длины, основанное на покрытии береговой линии лентой шириной , воплощает идею Кантора и Минковского (см. рис. 56), а соответствующей размерностью мы обязаны Булигану. Однако эти два примера лишь намекают на существование многих размерностей (большинство из которых известны лишь немногим специалистам), которые блистают в различных узкоспециализированных областях математики. Некоторые из этих размерностей мы обсудим более подробно в главе 39.

Зачем математикам понадобилось вводить это изобилие различных размерностей? Затем, что в определенных случаях они принимают различные значения. К счастью, с такими случаями вы в этом эссе не встретитесь, поэтому список возможных альтернативных размерностей можно с чистой совестью сократить до двух, о которых я, правда, еще не упоминал. Старейшая и подробнее исследованная размерность из нашего списка восходит еще к Хаусдорфу и служит для определения фрактальной размерности - очень скоро мы ею займемся. Вторая, более простая, размерность называется размерностью подобия: она носит не такой общий характер, как первая размерность, однако оказывается более чем адекватной во многих случаях - ее мы рассмотрим в следующей главе.

Разумеется, я не собираюсь приводить здесь математическое доказательство того, что показатель Ричардсона является размерностью. Честно говоря, я не представляю, как можно провести такое доказательство в рамках какой бы то ни было естественной науки. Я хочу лишь обратить внимание читателя на тот факт, что понятие длины ставит перед нами концептуальную задачу, а показатель предоставляет удобное и изящное решение. Теперь, когда фрактальная размерность заняла свое место в изучении береговых линий, вряд мы захотим, из каких бы то ни было особенных соображений, возвращаться к тем временам, когда мы бездумно и наивно полагали . Тому, кто все еще считает , придется теперь постараться, если он пожелает доказать свою правоту.

Следующий шаг - объяснение формы береговых линий и выведение значения из других, более фундаментальных соображений - я предлагаю отложить до главы 28. На этом этапе достаточно сказать, что в первом приближении . Это значение слишком велико, чтобы верно описывать факты, однако его более чем достаточно для того, чтобы мы могли заявить: можно, должно и естественно полагать, что размерность береговой линии превосходит обычное евклидово значение для кривой .

ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ ХАУСДОРФА

Если согласиться с тем, что различные естественные береговые линии обладают бесконечной длиной, а также с тем, что значение длины, основанное на антропометрической величине , дает лишь частичное представление о реальном положении дел, то каким образом можно сравнить между собой разные берега? Так как бесконечность ничем не отличается от бесконечности, умноженной на четыре, много ли нам будет проку от утверждения, что длина любого берега в четыре раза больше, чем длина любой из его четвертей? Необходим лучший способ для выражения вполне разумной идеи о том, что кривая должна обладать некоторой «мерой», причем эта мера для всей кривой должна быть в четыре раза больше, чем та же мера для любой из ее четвертей.

В высшей степени остроумный метод для достижения этой цели предложил Феликс Хаусдорф. В основе его метода лежит тот факт, что линейная мера многоугольника вычисляется сложением длин его сторон без каких бы то ни было их преобразований. Можно предположить, что эти длины сторон возводятся в степень , равную евклидовой размерности прямой (причина такого предположения вскоре станет очевидной). Аналогичным образом вычисляется мера поверхности внутренней области замкнутого многоугольника - посредством покрытия ее квадратами, нахождения суммы длин сторон этих квадратов и возведения ее в степень (евклидова размерность плоскости). Если же использовать при вычислениях «неверную» степень, то результат этих вычислений не даст нам никакой полезной информации: площадь любого замкнутого многоугольника окажется равной нулю, а длина его внутренней области будет бесконечной.

Рассмотрим с таких позиций полигональную (кусочно-линейную) аппроксимацию береговой линии, составленной из малых интервалов длины . Возведя длину интервала в степень и умножив ее на число интервалов, мы получим некую величину, которую можно предварительно назвать «аппроксимативной протяженностью в размерности ». Так как, согласно Ричардсону, число сторон равно то наша аппроксимативная протяженность принимает значение .. То есть аппроксимативная протяженность береговой линии демонстрирует благоразумное поведение тогда и только тогда, когда .

ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ КРИВОЙ МОЖЕТ БЫТЬ БОЛЬШЕ ЕДИНИЦЫ; ФРАКТАЛЬНЫЕ КРИВЫЕ

Согласно замыслу своего создателя, хаусдорфова размерность сохраняет за собой обязанности обычной размерности и служит показателем степени при определении меры.

Однако с другой стороны, размерность в высшей степени необычна, - она выражается дробным числом! Мало того, она больше единицы, которая представляет собой «естественную» размерность для кривых (можно строго доказать, что единице равна и их топологическая размерность ).

Я предлагаю называть кривые, фрактальная размерность которых превосходит их топологическую размерность 1, фрактальными кривыми. А в качестве краткого резюме для настоящей главы могу предложить следующее утверждение: в географических масштабах береговые линии можно моделировать с помощью фрактальных кривых. Береговые линии по своей структуре фрактальны.

Рис. 55. ОБЕЗЬЯНЬЕ ДЕРЕВО

На данном этапе этот небольшой рисунок следует рассматривать просто как декоративный элемент, он всего лишь заполняет пустое место.

Однако после прочтения главы 14 читатель сможет обнаружить здесь подсказку для распутывания «архитектурной» загадки на рис. 210. Более серьезную подсказку дает нижеприведенный генератор:

Если у математика возникает необходимость «приручить» какую-нибудь особенно нерегулярную кривую, он может воспользоваться следующей стандартной процедурой: выбирается некое значение , и вокруг каждой точки кривой строится круг радиуса . Эта процедура, восходящая, по меньшей мере, к Герману Минковскому, а то и к самому Георгу Кантору, несколько грубовата, но зато весьма эффективна. (Что касается термина сосиска, то его происхождение, согласно непроверенным слухам, как-то связано с применением Норбертом Винером данной процедуры к броуновским кривым.)

На помещенных здесь иллюстрациях вышеописанное сглаживание применяется не к реальным берегам, а к одной теоретической кривой, которую мы построим несколько позже (см. рис. 79) путем постоянного добавления все более мелких деталей. Сравнивая изображенный справа кусок сосиски с правым концом сосиски, помещенной вверху, мы видим, что критический этап в построении кривой наступает, когда кривая начинает включать в себя детали меньшего, чем , размера. На более поздних этапах сосиска существенно не изменяется.

Рис. 57. ЭМПИРИЧЕСКИЕ ДАННЫЕ РИЧАРДСОНА ОТНОСИТЕЛЬНО СКОРОСТИ РОСТА ДЛИН БЕРЕГОВЫХ ЛИНИЙ

На этом рисунке приведены экспериментальные результаты измерения длины кривой, произведенные на различных кривых с использованием равносторонних многоугольников с уменьшающейся длиной стороны . Как и ожидалось, в случае окружности измерения с возрастающей точностью дают величину, которая очень быстро стабилизируется около вполне определенного значения.

В случае береговых линий приближенные значения длины, напротив, не стабилизируются вовсе. По мере того, как длина шага стремится к нулю, аппроксимативные значения длины, отложенные в дважды логарифмической системе координат, образуют прямую с отрицательным наклоном. Так же обстоит дело и с сухопутными границами между странами. Наведенные Ричардсоном в различных энциклопедиях справки вскрыли значительные различия в определении длины общей границы картографами соответствующих стран: например, длина границы между Испанией и Португалией составляет 987 км с точки зрения испанцев и 1214 км с точки зрения португальцев; аналогичным образом пострадала и граница между Нидерландами и Бельгией (380 и 449 км). Так как угловой коэффициент соответствующих прямых равен -0,25, двадцатипроцентная разница между результатами измерений означает двукратную разницу между принятыми для этих измерений значениями - не такое уж невероятное предположение.

Ричардсон не дал никакой теоретической интерпретации различному наклону своих прямых. Мы же с вами намерены интерпретировать береговые линии как приближения к фрактальным кривым и рассматривать угловые коэффициенты соответствующих им прямых как приближенные значения разности , где - фрактальная размерность.

Пример парадокса: если береговая линия Великобритании измеряется отрезками по 100 км, то её длина составляет примерно 2 800 км. Если используются отрезки по 50 км, то длина равна приблизительно 3 400 км, что на 600 км больше.

Длина береговой линии зависит от способа её измерения. Поскольку для участка суши можно выделить изгибы любого размера, от сотен километров до долей миллиметра и меньше, нельзя очевидным образом подобрать размер наименьшего элемента, который должен быть взят для измерения. Следовательно, нельзя однозначно определить и периметр данного участка. Существуют различные математические приближения при решении данной задачи.

Основным методом оценки длины границы или береговой линии было наложение N равных отрезков длиной l на карту или аэрофотоснимок с помощью циркуля. Каждый конец отрезка должен принадлежать измеряемой границе. Исследуя расхождения в оценке границ, Ричардсон обнаружил то, что сейчас называется эффектом Ричардсона : масштаб измерений обратно пропорционален общей длине всех отрезков. То есть чем короче используемая линейка, тем длиннее измеряемая граница. Таким образом, испанские и португальские географы попросту руководствовались измерениями разных масштабов.

Наиболее поразительным для Ричардсона оказалось то, что когда величина l стремится к нулю, длина побережья стремится к бесконечности. Изначально Ричардсон полагал, опираясь на Евклидову геометрию, что эта длина достигнет фиксированной величины, как это происходит в случае с правильными геометрическими фигурами. Например, периметр правильного многоугольника, вписанного в окружность, приближается к длине самой окружности с увеличением числа сторон (и уменьшением длины каждой стороны). В теории геометрических измерений такая гладкая кривая, как окружность, которая может быть приближённо представлена в виде небольших отрезков с заданным пределом, называется спрямляемой кривой.

Спустя более десяти лет после завершения Ричардсоном своей работы Мандельброт разработал новую ветвь математики - фрактальную геометрию - для описания таких неспрямляемых комплексов, существующих в природе, как бесконечная береговая линия . Его собственное определение фрактала как основы его исследования таково :

Я придумал слово фрактал , взяв за основу латинское прилагательное fractus . Соответствующий латинский глагол frangere означает ломать : создавать нерегулярные фрагменты. Поэтому разумно, что, помимо «фрагментный», fractus также должно означать и «нерегулярный».

Ключевым свойством фракталов является самоподобие , заключающееся в проявлении одной и той же общей фигуры на любом масштабе. Береговая линия воспринимается как чередование заливов и мысов. Гипотетически, если данная береговая линия имеет свойство самоподобия, то независимо от того, насколько сильно масштабируется та или иная часть, всё равно проявляется аналогичная картина меньших заливов и мысов, наложенная на бо́льшие заливы и мысы, вплоть до песчинок. На таких масштабах береговая линия оказывается мгновенно изменяющейся, потенциально бесконечной нитью со стохастическим расположением заливов и мысов. В таких условиях (в отличие от гладких кривых) Мандельброт утверждает: «Длина береговой линии оказывается недостижимым понятием, скользящим между пальцами тех, кто пытается его понять» .

где длина береговой линии L является функцией от единицы измерения ε и аппроксимируется выражением из правой части. F - константа, D - параметр Ричардсона, зависящий от самой береговой линии (Ричардсон не дал теоретического объяснения этой величины, однако Мандельброт определил D как нецелочисленную форму размерности Хаусдорфа , позже - фрактальной размерности. Иными словами, D - это практически измеренное значение «неровности»). Перегруппировав правую часть выражения, получаем:

где Fε -D должно быть количеством единиц ε, необходимых для получения L. Фрактальная размерность - это число измерений объекта, используемое для аппроксимации фрактала: 0 - для точки, 1 - для линии, 2 - для площадных фигур. Поскольку ломаная линия, измеряющая длину берега, не распространяется в одном направлении и вместе с тем не представляет собой площадь, значение D в выражении занимает промежуточное положение между 1 и 2 (для побережья обычно менее 1,5). Оно может быть интерпретировано как толстая линия или полоса шириной 2ε. Более «разбитые» побережья имеют большее значение D и тем самым L оказывается длиннее при одинаковых ε. Мандельброт показал, что D не зависит от ε.

В целом береговые линии отличаются от математических фракталов, поскольку они формируются с использованием многочисленных мелких деталей, создающих модели только статистически .

В реальности на береговых линиях отсутствуют детали меньше 1 см [ ] . Это связано с эрозией и другими морскими явлениями. В большинстве мест минимальный размер гораздо больше. Поэтому модель бесконечного фрактала не подходит для береговых линий.

Из практических соображений выбирают минимальный размер деталей равным порядку единиц измерения. Так, если береговая линия измеряется в километрах, то небольшие изменения линий, гораздо меньшие одного километра, просто не принимаются во внимание. Для измерения береговой линии в сантиметрах должны быть рассмотрены все небольшие вариации размером около одного сантиметра. Однако на масштабах порядка сантиметров должны быть сделаны различные произвольные нефрактальные допущения, например, там, где устье присоединяется к морю, или в тех местах, где должны быть проведены измерения на широких ваттах . Кроме того, использование различных методов измерения для разных единиц измерения не позволяет сделать преобразование этих единиц с помощью простого умножения.

Для определения государственных территориальных вод строят так называемые изгибы побережья канадской провинции Британская Колумбия составляют более 10 % длины канадской береговой линии (с учётом всех островов Канадского Арктического архипелага) - 25 725 км из 243 042 км на линейном расстоянии, равном всего 965 км