Treguesit kryesorë përgjithësues të variacionit në statistika janë dispersionet dhe devijimet standarde.
Dispersion kjo mesatare aritmetike devijimet në katror të secilës vlerë karakteristike nga mesatarja e përgjithshme. Varianca zakonisht quhet katrori mesatar i devijimeve dhe shënohet me 2. Në varësi të të dhënave burimore, varianca mund të llogaritet duke përdorur mesataren aritmetike të thjeshtë ose të ponderuar:
variancë e papeshuar (e thjeshtë);
 varianca e ponderuar.
varianca e ponderuar.
Devijimi standard kjo është një karakteristikë përgjithësuese e madhësive absolute variacionet shenjat në agregat. Shprehet në të njëjtat njësi matëse si atributi (në metra, ton, përqindje, hektarë, etj.).
Devijimi standard është rrënja katrore e variancës dhe shënohet me :
 devijimi standard i papeshuar;
devijimi standard i papeshuar;
 devijimi standard i ponderuar.
devijimi standard i ponderuar.
Devijimi standard është një masë e besueshmërisë së mesatares. Sa më i vogël të jetë devijimi standard, aq më mirë mesatarja aritmetike pasqyron të gjithë popullsinë e përfaqësuar.
Llogaritja e devijimit standard paraprihet nga llogaritja e variancës.
Procedura për llogaritjen e variancës së ponderuar është si më poshtë:
1) përcaktoni mesataren aritmetike të ponderuar:
2) llogaritni devijimet e opsioneve nga mesatarja:
3) katrore devijimin e secilit opsion nga mesatarja:
4) shumëzoni katrorët e devijimeve me peshat (frekuencat):
5) përmblidhni produktet që rezultojnë:
![]()
6) shuma që rezulton pjesëtohet me shumën e peshave:

Shembulli 2.1

Le të llogarisim mesataren aritmetike të ponderuar:

Vlerat e devijimeve nga mesatarja dhe katrorët e tyre janë paraqitur në tabelë. Le të përcaktojmë variancën:

Devijimi standard do të jetë i barabartë me:

Nëse të dhënat burimore paraqiten si interval seritë e shpërndarjes , atëherë së pari duhet të përcaktoni vlerën diskrete të atributit dhe më pas të aplikoni metodën e përshkruar.
Shembulli 2.2
Le të tregojmë llogaritjen e variancës për një seri intervali duke përdorur të dhëna për shpërndarjen e sipërfaqes së mbjellë të një ferme kolektive sipas rendimentit të grurit.

Mesatarja aritmetike është:

Le të llogarisim variancën:

6.3. Llogaritja e variancës duke përdorur një formulë të bazuar në të dhëna individuale
Teknika e llogaritjes variancat komplekse, dhe me vlera të mëdha opsionesh dhe frekuencash mund të jetë i rëndë. Llogaritjet mund të thjeshtohen duke përdorur vetitë e dispersionit.
Dispersioni ka vetitë e mëposhtme.
1. Zvogëlimi ose rritja e peshave (frekuencave) të një karakteristike të ndryshueshme me një numër të caktuar herë nuk e ndryshon shpërndarjen.
2. Zvogëloni ose rritni çdo vlerë të një karakteristike me të njëjtën sasi konstante A nuk ndryshon dispersionin.
3. Zvogëloni ose rritni çdo vlerë të një karakteristike me një numër të caktuar herë k respektivisht zvogëlon ose rrit variancën në k 2 herë dhe devijimi standard në k një herë.
4. Shpërndarja e një karakteristike në lidhje me një vlerë arbitrare është gjithmonë më e madhe se shpërndarja në lidhje me mesataren aritmetike për katror të diferencës midis vlerave mesatare dhe arbitrare:
![]()
Nëse A 0, atëherë arrijmë në barazinë e mëposhtme:
domethënë, varianca e karakteristikës është e barabartë me diferencën midis katrorit mesatar të vlerave karakteristike dhe katrorit të mesatares.
Çdo veti mund të përdoret në mënyrë të pavarur ose në kombinim me të tjerat gjatë llogaritjes së variancës.
Procedura për llogaritjen e variancës është e thjeshtë:
1) përcaktoni mesatare aritmetike :
2) katrori i mesatares aritmetike:

3) katrore devijimin e secilit variant të serisë:
X i 2 .
4) gjeni shumën e katrorëve të opsioneve:
5) ndani shumën e katrorëve të opsioneve me numrin e tyre, d.m.th. përcaktoni katrorin mesatar:
6) përcaktoni ndryshimin midis katrorit mesatar të karakteristikës dhe katrorit të mesatares:
Shembulli 3.1 Të dhënat e mëposhtme janë të disponueshme për produktivitetin e punëtorëve:

Le të bëjmë llogaritjet e mëposhtme:
![]()
Hapat
Llogaritja e variancës së mostrës
-
Regjistroni vlerat e mostrës. Në shumicën e rasteve, statisticienët kanë akses vetëm në mostrat e popullatave specifike. Për shembull, si rregull, statisticienët nuk analizojnë koston e ruajtjes së tërësisë së të gjitha makinave në Rusi - ata analizojnë një mostër të rastësishme prej disa mijëra makinash. Një mostër e tillë do të ndihmojë në përcaktimin e kostos mesatare të një makine, por ka shumë të ngjarë që vlera që rezulton do të jetë larg nga ajo reale.
- Për shembull, le të analizojmë numrin e simiteve të shitura në një kafene gjatë 6 ditëve, të marra në mënyrë të rastësishme. Mostra duket kështu: 17, 15, 23, 7, 9, 13. Ky është një mostër, jo një popullsi, sepse ne nuk kemi të dhëna për simitet e shitura për çdo ditë që kafeneja është e hapur.
- Nëse ju jepet një popullatë dhe jo një mostër vlerash, vazhdoni në seksionin tjetër.
-
Shkruani një formulë për të llogaritur variancën e mostrës. Dispersioni është një masë e përhapjes së vlerave të një sasie të caktuar. Sa më afër zeros të jetë vlera e variancës, aq më afër grupohen vlerat së bashku. Kur punoni me një mostër vlerash, përdorni formulën e mëposhtme për të llogaritur variancën:
- s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2))- kjo është dispersion. Dispersioni matet në njësi katrore.
- x i (\displaystyle x_(i))– çdo vlerë në mostër.
- x i (\displaystyle x_(i)) ju duhet të zbrisni x̅, ta vendosni në katror dhe më pas të shtoni rezultatet.
- x̅ – mesatare e mostrës (mesatarja e mostrës).
- n - numri i vlerave në mostër.
-
Llogaritni mesataren e mostrës. Ajo shënohet si x̅. Mesatarja e mostrës llogaritet si një mesatare aritmetike e thjeshtë: mblidhni të gjitha vlerat në mostër dhe më pas ndani rezultatin me numrin e vlerave në mostër.
- Në shembullin tonë, shtoni vlerat në mostër: 15 + 17 + 23 + 7 + 9 + 13 = 84
Tani ndajeni rezultatin me numrin e vlerave në mostër (në shembullin tonë ka 6): 84 ÷ 6 = 14.
Mesatarja e mostrës x̅ = 14. - Mesatarja e mostrës është vlera qendrore rreth së cilës shpërndahen vlerat në mostër. Nëse vlerat në kampion grumbullohen rreth kampionit mesatar, atëherë varianca është e vogël; përndryshe varianca është e madhe.
- Në shembullin tonë, shtoni vlerat në mostër: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
Zbrisni mesataren e mostrës nga çdo vlerë në mostër. Tani llogarisni diferencën x i (\displaystyle x_(i))- x̅, ku x i (\displaystyle x_(i))– çdo vlerë në mostër. Çdo rezultat i marrë tregon shkallën e devijimit të një vlere të caktuar nga mesatarja e mostrës, domethënë sa larg është kjo vlerë nga mesatarja e mostrës.
- Në shembullin tonë:
x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1 - Korrektësia e rezultateve të marra është e lehtë për t'u kontrolluar, pasi shuma e tyre duhet të jetë e barabartë me zero. Kjo lidhet me përcaktimin e mesatares, pasi vlerat negative (distancat nga mesatarja në vlerat më të vogla) kompensohen plotësisht nga vlerat pozitive (distancat nga mesatarja në vlerat më të mëdha).
- Në shembullin tonë:
-
Siç u përmend më lart, shuma e dallimeve x i (\displaystyle x_(i))- x̅ duhet të jetë e barabartë me zero. Kjo do të thotë se varianca mesatare është gjithmonë zero, gjë që nuk jep asnjë ide për përhapjen e vlerave të një sasie të caktuar. Për të zgjidhur këtë problem, katrore çdo ndryshim x i (\displaystyle x_(i))- x̅. Kjo do të rezultojë që të merrni vetëm numra pozitivë, të cilët kurrë nuk do të mblidhen deri në 0.
- Në shembullin tonë:
(x 1 (\displaystyle x_(1))- x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
(x 2 (\displaystyle (x_(2))- x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
9 2 = 81
(-7) 2 = 49
(-5) 2 = 25
(-1) 2 = 1 - Ju gjetët katrorin e diferencës - x̅) 2 (\displaystyle ^(2)) për çdo vlerë në mostër.
- Në shembullin tonë:
-
Llogaritni shumën e katrorëve të diferencave. Domethënë, gjeni atë pjesë të formulës që është shkruar kështu: ∑[( x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))]. Këtu shenja Σ nënkupton shumën e diferencave në katror për secilën vlerë x i (\displaystyle x_(i)) në mostër. Ju keni gjetur tashmë dallimet në katror (x i (\displaystyle (x_(i))- x̅) 2 (\displaystyle ^(2)) për çdo vlerë x i (\displaystyle x_(i)) në mostër; tani thjesht shtoni këto katrorë.
- Në shembullin tonë: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
-
Pjestoni rezultatin me n - 1, ku n është numri i vlerave në mostër. Disa kohë më parë, për të llogaritur variancën e mostrës, statisticienët thjesht e ndanë rezultatin me n; në këtë rast do të merrni mesataren e variancës në katror, e cila është ideale për të përshkruar variancën e një kampioni të caktuar. Por mbani mend se çdo mostër është vetëm një pjesë e vogël e popullsisë së vlerave. Nëse merrni një mostër tjetër dhe kryeni të njëjtat llogaritje, do të merrni një rezultat tjetër. Siç rezulton, pjesëtimi me n - 1 (në vend të vetëm n) jep një vlerësim më të saktë të variancës së popullsisë, e cila është ajo që ju intereson. Pjesëtimi me n – 1 është bërë i zakonshëm, kështu që përfshihet në formulën për llogaritjen e variancës së mostrës.
- Në shembullin tonë, mostra përfshin 6 vlera, domethënë n = 6.
Varianca e mostrës = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
- Në shembullin tonë, mostra përfshin 6 vlera, domethënë n = 6.
-
Dallimi midis variancës dhe devijimit standard. Vini re se formula përmban një eksponent, kështu që dispersioni matet në njësi katrore të vlerës që analizohet. Ndonjëherë një madhësi e tillë është mjaft e vështirë për t'u operuar; në raste të tilla, përdorni devijimin standard, i cili është i barabartë me rrënjën katrore të variancës. Kjo është arsyeja pse varianca e mostrës shënohet si s 2 (\displaystyle s^(2)), dhe devijimi standard i kampionit është si s (\displaystyle s).
- Në shembullin tonë, devijimi standard i mostrës është: s = √33.2 = 5.76.
Llogaritja e variancës së popullsisë
-
Analizoni disa grupe vlerash. Seti përfshin të gjitha vlerat e sasisë në shqyrtim. Për shembull, nëse po studioni moshën e banorëve të rajonit të Leningradit, atëherë tërësia përfshin moshën e të gjithë banorëve të këtij rajoni. Kur punoni me një popullsi, rekomandohet të krijoni një tabelë dhe të vendosni vlerat e popullsisë në të. Merrni parasysh shembullin e mëposhtëm:
- Në një dhomë të caktuar ka 6 akuariume. Çdo akuarium përmban numrin e mëposhtëm të peshqve:
x 1 = 5 (\displaystyle x_(1)=5)
x 2 = 5 (\displaystyle x_(2)=5)
x 3 = 8 (\displaystyle x_(3)=8)
x 4 = 12 (\displaystyle x_(4)=12)
x 5 = 15 (\displaystyle x_(5)=15)
x 6 = 18 (\displaystyle x_(6)=18)
- Në një dhomë të caktuar ka 6 akuariume. Çdo akuarium përmban numrin e mëposhtëm të peshqve:
-
Shkruani një formulë për të llogaritur variancën e popullsisë. Meqenëse popullsia përfshin të gjitha vlerat e një sasie të caktuar, formula e mëposhtme ju lejon të merrni vlerën e saktë të variancës së popullsisë. Për të dalluar variancën e popullsisë nga varianca e mostrës (e cila është vetëm një vlerësim), statisticienët përdorin variabla të ndryshëm:
- σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)))/n
- σ 2 (\displaystyle ^(2))– shpërndarja e popullsisë (lexohet si “sigma në katror”). Dispersioni matet në njësi katrore.
- x i (\displaystyle x_(i))– çdo vlerë në tërësinë e saj.
- Σ – shenjë shumës. Kjo është, nga çdo vlerë x i (\displaystyle x_(i)) ju duhet të zbrisni μ, ta vendosni në katror dhe më pas të shtoni rezultatet.
- μ – mesatarja e popullsisë.
- n - numri i vlerave në popullatë.
-
Llogaritni mesataren e popullsisë. Kur punoni me një popullsi, mesatarja e saj shënohet si μ (mu). Mesatarja e popullsisë llogaritet si një mesatare aritmetike e thjeshtë: mblidhni të gjitha vlerat në popullatë dhe më pas ndani rezultatin me numrin e vlerave në popullatë.
- Mbani në mend se mesataret nuk llogariten gjithmonë si mesatare aritmetike.
- Në shembullin tonë, mesatarja e popullsisë: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\style ekrani (\frac (5+5+8+12+15+18)(6))) = 10,5
-
Zbrisni mesataren e popullsisë nga çdo vlerë në popullatë. Sa më afër zeros të jetë diferenca, aq më afër mesatares së popullsisë është vlera specifike. Gjeni ndryshimin midis secilës vlerë në popullatë dhe mesatares së saj dhe do të merrni një ide të parë të shpërndarjes së vlerave.
- Në shembullin tonë:
x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5
- Në shembullin tonë:
-
Sheshoni çdo rezultat të marrë. Vlerat e diferencës do të jenë pozitive dhe negative; Nëse këto vlera vizatohen në një vijë numerike, ato do të shtrihen në të djathtë dhe në të majtë të mesatares së popullsisë. Kjo nuk është e mirë për llogaritjen e variancës sepse numrat pozitivë dhe negativë anulojnë njëri-tjetrin. Pra katrore çdo ndryshim për të marrë numra ekskluzivisht pozitivë.
- Në shembullin tonë:
(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) për secilën vlerë të popullsisë (nga i = 1 në i = 6):
(-5,5)2 (\displaystyle ^(2)) = 30,25
(-5,5)2 (\displaystyle ^(2)), Ku x n (\displaystyle x_(n))– vlera e fundit në popullatë. - Për të llogaritur vlerën mesatare të rezultateve të marra, duhet të gjeni shumën e tyre dhe ta pjestoni me n:(( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2)))/n
- Tani le të shkruajmë shpjegimin e mësipërm duke përdorur variablat: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n dhe merrni një formulë për llogaritjen e variancës së popullsisë.
- Në shembullin tonë:
Nëse popullsia ndahet në grupe sipas karakteristikës që studiohet, atëherë për këtë popullatë mund të llogariten llojet e mëposhtme të variancës: totali, grupi (brenda grupit), mesatarja e grupit (mesatarja e brenda grupit), ndërgrupi.
Fillimisht, ai llogarit koeficientin e përcaktimit, i cili tregon se cila pjesë e variacionit total të tiparit që studiohet është variacioni ndërgrupor, d.m.th. për shkak të karakteristikave të grupimit:
Marrëdhënia empirike e korrelacionit karakterizon afërsinë e lidhjes midis karakteristikave të grupimit (faktorial) dhe performancës.
Raporti empirik i korrelacionit mund të marrë vlera nga 0 në 1.
Për të vlerësuar afërsinë e lidhjes bazuar në raportin empirik të korrelacionit, mund të përdorni marrëdhëniet Chaddock:
Shembulli 4. Të dhënat e mëposhtme janë të disponueshme për performancën e punës nga organizatat e projektimit dhe anketimit të formave të ndryshme të pronësisë:
Përcaktoni:
1) varianca totale;
2) variancat në grup;
3) mesatarja e variancave të grupit;
4) varianca ndërgrupore;
5) varianca totale në bazë të rregullit për mbledhjen e variancave;
6) koeficienti i përcaktimit dhe raporti empirik i korrelacionit.
Nxirrni përfundime.
Zgjidhja:
1. Le të përcaktojmë vëllimin mesatar të punës së kryer nga ndërmarrjet e dy formave të pronësisë:
Le të llogarisim variancën totale:
![]()
2. Përcaktoni mesataret e grupeve:
![]() milion rubla;
milion rubla;
![]() milion rubla
milion rubla
Ndryshimet në grup:
![]() ;
;
3. Llogaritni mesataren e variancave të grupit:
4. Le të përcaktojmë variancën ndërgrupore:
5. Llogaritni variancën totale bazuar në rregullin për mbledhjen e variancave:
6. Le të përcaktojmë koeficientin e përcaktimit:
![]() .
.
Kështu, vëllimi i punës së kryer nga organizatat e projektimit dhe anketimit varet me 22% nga forma e pronësisë së ndërmarrjeve.
Raporti empirik i korrelacionit llogaritet duke përdorur formulën
![]() .
.
Vlera e treguesit të llogaritur tregon se varësia e vëllimit të punës nga forma e pronësisë së ndërmarrjes është e vogël.
Shembulli 5. Si rezultat i një studimi të disiplinës teknologjike të zonave të prodhimit, u morën të dhënat e mëposhtme:
Përcaktoni koeficientin e përcaktimit
Pritshmëria dhe varianca janë karakteristikat numerike më të përdorura të një ndryshoreje të rastësishme. Ato karakterizojnë tiparet më të rëndësishme të shpërndarjes: pozicionin e saj dhe shkallën e shpërndarjes. Në shumë probleme praktike, një karakteristikë e plotë, shteruese e një ndryshoreje të rastësishme - ligji i shpërndarjes - ose nuk mund të merret fare, ose nuk nevojitet fare. Në këto raste, kufizohet në një përshkrim të përafërt të një ndryshoreje të rastësishme duke përdorur karakteristika numerike.
Vlera e pritur shpesh quhet thjesht vlera mesatare e një ndryshoreje të rastësishme. Shpërndarja e një ndryshoreje të rastësishme është një karakteristikë e dispersionit, përhapja e një ndryshoreje të rastësishme rreth pritshmërisë së saj matematikore.
Pritja e një ndryshoreje të rastësishme diskrete
Le t'i qasemi konceptit të pritjes matematikore, së pari bazuar në interpretimin mekanik të shpërndarjes së një ndryshoreje të rastësishme diskrete. Lëreni masën njësi të shpërndahet ndërmjet pikave të boshtit x x1 , x 2 , ..., x n, dhe çdo pikë materiale ka një masë përkatëse prej fq1 , fq 2 , ..., fq n. Kërkohet të zgjidhet një pikë në boshtin e abshisës, duke karakterizuar pozicionin e të gjithë sistemit të pikave materiale, duke marrë parasysh masat e tyre. Është e natyrshme që qendra e masës së sistemit të pikave materiale të merret si një pikë e tillë. Kjo është mesatarja e ponderuar e ndryshores së rastësishme X, tek e cila abshisa e secilës pikë xi hyn me një “peshë” të barabartë me probabilitetin përkatës. Vlera mesatare e ndryshores së rastësishme është marrë në këtë mënyrë X quhet pritshmëria e saj matematikore.
Pritja matematikore e një ndryshoreje të rastësishme diskrete është shuma e produkteve të të gjitha vlerave të saj të mundshme dhe probabiliteteve të këtyre vlerave:

Shembulli 1.Është organizuar një short fitues. Ka 1000 fitime, nga të cilat 400 janë 10 rubla. 300 - 20 rubla secila. 200 - 100 rubla secila. dhe 100 - 200 rubla secila. Sa janë fitimet mesatare për dikë që blen një biletë?
Zgjidhje. Fitimet mesatare do të gjejmë nëse e ndajmë shumën totale të fitimeve, e cila është 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubla, me 1000 (shuma totale e fitimeve). Pastaj marrim 50000/1000 = 50 rubla. Por shprehja për llogaritjen e fitimeve mesatare mund të paraqitet në formën e mëposhtme:

Nga ana tjetër, në këto kushte, madhësia fituese është një ndryshore e rastësishme, e cila mund të marrë vlerat 10, 20, 100 dhe 200 rubla. me probabilitet të barabartë me 0.4, përkatësisht; 0.3; 0,2; 0.1. Prandaj, fitorja mesatare e pritur është e barabartë me shumën e produkteve të madhësisë së fitimeve dhe probabilitetit të marrjes së tyre.
Shembulli 2. Botuesi vendosi të botojë një libër të ri. Ai planifikon ta shesë librin për 280 rubla, nga të cilat ai vetë do të marrë 200, 50 në librari dhe 30 për autorin. Tabela jep informacion për kostot e botimit të një libri dhe probabilitetin e shitjes së një numri të caktuar kopjesh të librit.
Gjeni fitimin e pritur të botuesit.
Zgjidhje. Variabli i rastësishëm "fitimi" është i barabartë me diferencën midis të ardhurave nga shitjet dhe kostos së kostove. Për shembull, nëse shiten 500 kopje të një libri, atëherë të ardhurat nga shitja janë 200 * 500 = 100,000, dhe kostoja e botimit është 225,000 rubla. Kështu, botuesi përballet me një humbje prej 125,000 rubla. Tabela e mëposhtme përmbledh vlerat e pritura të ndryshores së rastësishme - fitimi:
| Numri | Fitimi xi | Probabiliteti fqi | xi fq i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Gjithsej: | 1,00 | 25000 |
Kështu, marrim pritshmërinë matematikore të fitimit të botuesit:
![]() .
.
Shembulli 3. Mundësia për të goditur me një goditje fq= 0.2. Përcaktoni konsumin e predhave që ofrojnë një pritje matematikore të numrit të goditjeve të barabartë me 5.
Zgjidhje. Nga e njëjta formulë e pritjes matematikore që kemi përdorur deri tani, shprehemi x- konsumi i guaskës:
![]() .
.
Shembulli 4. Përcaktoni pritshmërinë matematikore të një ndryshoreje të rastësishme x numri i goditjeve me tre të shtëna, nëse probabiliteti i një goditjeje me çdo goditje fq = 0,4 .
Këshillë: gjeni probabilitetin e vlerave të ndryshoreve të rastësishme nga formula e Bernulit .
Vetitë e pritjes matematikore
Le të shqyrtojmë vetitë e pritjes matematikore.
Prona 1. Pritja matematikore e një vlere konstante është e barabartë me këtë konstante:
Prona 2. Faktori konstant mund të hiqet nga shenja e pritjes matematikore:
![]()
Prona 3. Pritja matematikore e shumës (diferencës) e variablave të rastit është e barabartë me shumën (diferencën) e pritjeve të tyre matematikore:
Prona 4. Pritshmëria matematikore e një produkti të ndryshoreve të rastësishme është e barabartë me produktin e pritjeve të tyre matematikore:
Prona 5. Nëse të gjitha vlerat e një ndryshoreje të rastësishme X zvogëlohet (shtohet) me të njëjtin numër ME, atëherë pritshmëria e tij matematikore do të ulet (rritet) me të njëjtin numër:
![]()
Kur nuk mund ta kufizosh veten vetëm në pritjet matematikore
Në shumicën e rasteve, vetëm pritshmëria matematikore nuk mund të karakterizojë mjaftueshëm një ndryshore të rastësishme.
Lërini variablat e rastit X Dhe Y jepen nga ligjet e mëposhtme të shpërndarjes:
| Kuptimi X | Probabiliteti |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Kuptimi Y | Probabiliteti |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Pritjet matematikore të këtyre sasive janë të njëjta - të barabarta me zero:


Megjithatë, modelet e shpërndarjes së tyre janë të ndryshme. Ndryshore e rastësishme X mund të marrë vetëm vlera që ndryshojnë pak nga pritshmëria matematikore dhe ndryshorja e rastësishme Y mund të marrë vlera që devijojnë ndjeshëm nga pritshmëria matematikore. Një shembull i ngjashëm: paga mesatare nuk bën të mundur të gjykohet pjesa e punëtorëve me pagë të lartë dhe të ulët. Me fjalë të tjera, nuk mund të gjykohet nga pritshmëria matematikore se cilat devijime prej tij, të paktën mesatarisht, janë të mundshme. Për ta bërë këtë, ju duhet të gjeni variancën e ndryshores së rastësishme.
Varianca e një ndryshoreje të rastësishme diskrete
Varianca ndryshore diskrete e rastësishme X quhet pritshmëria matematikore e katrorit të devijimit të tij nga pritshmëria matematikore:

Devijimi standard i një ndryshoreje të rastësishme X vlera aritmetike e rrënjës katrore të variancës së saj quhet:
![]() .
.
Shembulli 5. Llogaritni variancat dhe devijimet standarde të ndryshoreve të rastit X Dhe Y, ligjet e shpërndarjes së të cilave janë dhënë në tabelat e mësipërme.
Zgjidhje. Pritjet matematikore të ndryshoreve të rastit X Dhe Y, siç u gjet më lart, janë të barabarta me zero. Sipas formulës së dispersionit në E(X)=E(y)=0 marrim:


Pastaj devijimet standarde të variablave të rastit X Dhe Y make up
![]() .
.
Kështu, me të njëjtat pritshmëri matematikore, varianca e ndryshores së rastit X shumë i vogël, por një ndryshore e rastësishme Y- domethënëse. Kjo është pasojë e dallimeve në shpërndarjen e tyre.
Shembulli 6. Investitori ka 4 projekte alternative investimi. Tabela përmbledh fitimin e pritur në këto projekte me probabilitetin përkatës.
| Projekti 1 | Projekti 2 | Projekti 3 | Projekti 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Gjeni për secilën alternativë pritjen matematikore, variancën dhe devijimin standard.
Zgjidhje. Le të tregojmë se si llogariten këto vlera për alternativën e tretë:
Tabela përmbledh vlerat e gjetura për të gjitha alternativat.
Të gjitha alternativat kanë të njëjtat pritshmëri matematikore. Kjo do të thotë që në terma afatgjatë të gjithë kanë të njëjtat të ardhura. Devijimi standard mund të interpretohet si një masë e rrezikut - sa më i lartë të jetë, aq më i madh është rreziku i investimit. Një investitor që nuk dëshiron shumë rrezik do të zgjedhë projektin 1 pasi ka devijimin standard më të vogël (0). Nëse investitori preferon rrezikun dhe fitimet e larta në një periudhë të shkurtër, atëherë ai do të zgjedhë projektin me devijimin standard më të madh - projektin 4.
Vetitë e dispersionit
Le të paraqesim vetitë e dispersionit.
Prona 1. Varianca e një vlere konstante është zero:
Prona 2. Faktori konstant mund të hiqet nga shenja e dispersionit duke e kuadruar atë:
![]() .
.
Prona 3. Varianca e një ndryshoreje të rastësishme është e barabartë me pritjen matematikore të katrorit të kësaj vlere, nga e cila zbritet katrori i pritjes matematikore të vetë vlerës:
![]() ,
,
Ku ![]() .
.
Prona 4. Varianca e shumës (diferencës) e variablave të rastit është e barabartë me shumën (diferencën) e variancave të tyre:
Shembulli 7. Dihet se një ndryshore e rastësishme diskrete X merr vetëm dy vlera: −3 dhe 7. Përveç kësaj, pritja matematikore është e njohur: E(X) = 4. Gjeni variancën e një ndryshoreje të rastësishme diskrete.
Zgjidhje. Le të shënojmë me fq probabiliteti me të cilin një ndryshore e rastësishme merr një vlerë x1 = −3 . Pastaj probabiliteti i vlerës x2 = 7 do të jetë 1 − fq. Le të nxjerrim ekuacionin për pritshmërinë matematikore:
E(X) = x 1 fq + x 2 (1 − fq) = −3fq + 7(1 − fq) = 4 ,
ku marrim probabilitetet: fq= 0,3 dhe 1 − fq = 0,7 .
Ligji i shpërndarjes së një ndryshoreje të rastësishme:
| X | −3 | 7 |
| fq | 0,3 | 0,7 |
Ne llogarisim variancën e kësaj ndryshoreje të rastësishme duke përdorur formulën nga vetia 3 e dispersionit:
D(X) = 2,7 + 34,3 − 16 = 21 .
Gjeni vetë pritshmërinë matematikore të një ndryshoreje të rastësishme dhe më pas shikoni zgjidhjen
Shembulli 8. Ndryshore diskrete e rastësishme X merr vetëm dy vlera. Ai pranon më të madhen nga vlerat 3 me probabilitet 0.4. Përveç kësaj, dihet varianca e ndryshores së rastësishme D(X) = 6. Gjeni pritshmërinë matematikore të një ndryshoreje të rastësishme.
Shembulli 9. Në një urnë ka 6 topa të bardhë dhe 4 të zinj. Nga urna nxirren 3 topa. Numri i topave të bardhë midis topave të vizatuar është një ndryshore e rastësishme diskrete X. Gjeni pritshmërinë matematikore dhe variancën e kësaj ndryshoreje të rastësishme.
Zgjidhje. Ndryshore e rastësishme X mund të marrë vlerat 0, 1, 2, 3. Probabilitetet përkatëse mund të llogariten nga rregulla e shumëzimit të probabilitetit. Ligji i shpërndarjes së një ndryshoreje të rastësishme:
| X | 0 | 1 | 2 | 3 |
| fq | 1/30 | 3/10 | 1/2 | 1/6 |
Prandaj pritshmëria matematikore e kësaj ndryshoreje të rastësishme:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
Varianca e një ndryshoreje të caktuar të rastësishme është:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Pritshmëria dhe varianca e një ndryshoreje të rastësishme të vazhdueshme
Për një ndryshore të rastësishme të vazhdueshme, interpretimi mekanik i pritshmërisë matematikore do të ruajë të njëjtin kuptim: qendra e masës për një masë njësi të shpërndarë vazhdimisht në boshtin x me densitet f(x). Ndryshe nga një ndryshore e rastësishme diskrete, argumenti i funksionit të së cilës xi ndryshon befas për një ndryshore të rastësishme të vazhdueshme, argumenti ndryshon vazhdimisht. Por pritshmëria matematikore e një ndryshoreje të rastësishme të vazhdueshme lidhet gjithashtu me vlerën mesatare të saj.
Për të gjetur pritshmërinë matematikore dhe variancën e një ndryshoreje të rastësishme të vazhdueshme, duhet të gjeni integrale të përcaktuara . Nëse jepet funksioni i densitetit të një ndryshoreje të rastësishme të vazhdueshme, atëherë ai hyn drejtpërdrejt në integrand. Nëse jepet një funksion i shpërndarjes së probabilitetit, atëherë duke e diferencuar atë, duhet të gjeni funksionin e densitetit.
Mesatarja aritmetike e të gjitha vlerave të mundshme të një ndryshoreje të rastësishme të vazhdueshme quhet e saj pritje matematikore, e shënuar me ose .
Për të dhënat e grupuara variancë e mbetur- mesatarja e variancave brenda grupit:Ku σ 2 j është varianca brenda grupit të grupit j.
Për të dhëna të pagrupuara variancë e mbetur– masa e saktësisë së përafrimit, d.m.th. përafrimi i vijës së regresionit me të dhënat origjinale: 
ku y(t) është parashikimi duke përdorur ekuacionin e trendit; y t – seria e dinamikës fillestare; n – numri i pikëve; p – numri i koeficientëve të ekuacionit të regresionit (numri i variablave shpjegues).
Në këtë shembull quhet vlerësues i paanshëm i variancës.
Shembulli nr. 1. Shpërndarja e punëtorëve të tre ndërmarrjeve të një shoqate sipas kategorive tarifore karakterizohet nga të dhënat e mëposhtme:
| Kategoria e tarifës së punëtorëve | Numri i punëtorëve në ndërmarrje | ||
| ndërmarrje 1 | ndërmarrje 2 | ndërmarrje 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Përcaktoni:
1. varianca për çdo ndërmarrje (ndryshimet brenda grupit);
2. mesataren e variancave brenda grupit;
3. shpërndarje ndërgrupore;
4. varianca totale.
Zgjidhje.
Para se të filloni të zgjidhni problemin, është e nevojshme të zbuloni se cila veçori është efektive dhe cila është faktoriale. Në shembullin në shqyrtim, atributi rezultant është “Kategoria tarifore”, dhe atributi faktor është “Numri (emri) i ndërmarrjes”.
Pastaj kemi tre grupe (ndërmarrje), për të cilat është e nevojshme të llogaritet mesatarja e grupit dhe variancat brenda grupit:

| Ndërmarrja | Mesatarja e grupit, | Varianca brenda grupit, |
| 1 | 4 | 1,8 |
Mesatarja e variancave brenda grupit ( variancë e mbetur) do të llogaritet duke përdorur formulën:

ku mund të llogarisni:

ose:

Pastaj:
Varianca totale do të jetë e barabartë me: s 2 = 1.6 + 0 = 1.6.
Varianca totale mund të llogaritet gjithashtu duke përdorur një nga dy formulat e mëposhtme:
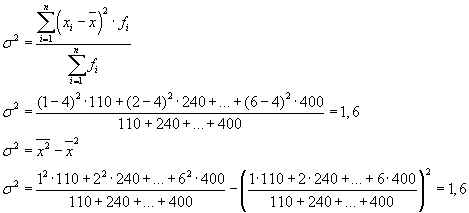
Kur zgjidhen probleme praktike, shpesh duhet të merret me një veçori që merr vetëm dy vlera alternative. Në këtë rast, nuk po flasim për peshën e një vlere të veçantë të një veçorie, por për pjesën e tij në agregat. Nëse përqindja e njësive të popullsisë që zotërojnë karakteristikën që studiohet shënohet me " r", dhe ata që nuk kanë - përmes " q", atëherë varianca mund të llogaritet duke përdorur formulën:
s 2 = p×q
Shembulli nr. 2. Bazuar në të dhënat e prodhimit të gjashtë punëtorëve në një ekip, përcaktoni variancën ndërgrupore dhe vlerësoni ndikimin e ndërrimit të punës në produktivitetin e tyre të punës nëse varianca totale është 12.2.
| Punonjësi i ekipit nr. | Prodhimi i punëtorëve, copë. | |
| në turnin e parë | në turnin e dytë | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Zgjidhje. Të dhënat fillestare
| X | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | Gjithsej |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Gjithsej | 31 | 33 | 37 | 37 | 40 | 38 |
Pastaj kemi 6 grupe për të cilat është e nevojshme të llogaritet mesatarja e grupit dhe variancat brenda grupit.
1. Gjeni vlerat mesatare të secilit grup.
2. Gjeni katrorin mesatar të secilit grup.
Le të përmbledhim rezultatet e llogaritjes në një tabelë:
| Numri i grupit | Mesatarja e grupit | Varianca brenda grupit |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Varianca brenda grupit karakterizon ndryshimin (ndryshimin) e karakteristikës së studiuar (rezultative) brenda një grupi nën ndikimin e të gjithë faktorëve në të, me përjashtim të faktorit që qëndron në themel të grupimit:
Mesatarja e variancave brenda grupit do të llogaritet duke përdorur formulën:
4. Varianca ndërgrupore karakterizon ndryshimin (ndryshimin) e karakteristikës së studiuar (rezultative) nën ndikimin e një faktori (karakteristike faktoriale) që përbën bazën e grupit.
Ne e përkufizojmë variancën ndërgrupore si:
Ku
Pastaj
Varianca totale karakterizon ndryshimin (ndryshimin) e karakteristikës së studiuar (rezultative) nën ndikimin e të gjithë faktorëve (karakteristikave faktoriale) pa përjashtim. Sipas kushteve të problemit është e barabartë me 12.2.
Marrëdhënia empirike e korrelacionit mat se cila pjesë e ndryshueshmërisë totale të karakteristikës që rezulton është shkaktuar nga faktori që studiohet. Ky është raporti i variancës së faktorëve ndaj variancës totale:
Ne përcaktojmë marrëdhënien empirike të korrelacionit:
Lidhjet ndërmjet karakteristikave mund të jenë të dobëta dhe të forta (të afërta). Kriteret e tyre vlerësohen në shkallën Chaddock:
0,1 0,3 0,5 0,7 0,9 Në shembullin tonë, marrëdhënia midis tiparit Y dhe faktorit X është e dobët
Koeficienti i përcaktimit.
Le të përcaktojmë koeficientin e përcaktimit:
Kështu, 0.67% e variacionit është për shkak të dallimeve midis tipareve dhe 99.37% është për shkak të faktorëve të tjerë.
konkluzioni: në këtë rast, prodhimi i punëtorëve nuk varet nga puna në një ndërrim specifik, d.m.th. ndikimi i ndërrimit të punës në produktivitetin e tyre të punës nuk është i rëndësishëm dhe është për shkak të faktorëve të tjerë.
Shembulli nr. 3. Bazuar në të dhënat për pagën mesatare dhe devijimet në katror nga vlera e saj për dy grupe punëtorësh, gjeni variancën totale duke zbatuar rregullin e mbledhjes së variancave:
Zgjidhja:Mesatarja e variancave brenda grupit
Ne e përkufizojmë variancën ndërgrupore si:
Varianca totale do të jetë: 480 + 13824 = 14304








