Endless infinity. Elimination of uncertainty “one to the power of infinity”

Disclosure of uncertainties of the form 0/0 or ∞/∞ and some other uncertainties arising during the calculation limit The relationship between two infinitesimal or infinitely large functions is greatly simplified with the help of L'Hopital's rule (actually two rules and comments to them).

The essence L'Hopital's rules is that in the case when calculating the limit of the ratio of two infinitesimal or infinitely large functions gives uncertainties of the form 0/0 or ∞/∞, the limit of the ratio of two functions can be replaced by the limit of the ratio of their derivatives and thus obtain a certain result.

Let's move on to the formulation of L'Hopital's rules.

L'Hopital's rule for the case of the limit of two infinitesimal quantities. If the functions f(x) And g(x aa, and in this vicinity g"(x a are equal to each other and equal to zero

().

L'Hopital's rule for the case of the limit of two is infinite large quantities . If the functions f(x) And g(x) are differentiable in some neighborhood of the point a, except perhaps for the point itself a, and in this vicinity g"(x)≠0 and if and if the limits of these functions as x tends to the value of the function at the point a equal to each other and equal to infinity

(),

then the limit of the ratio of these functions equal to the limit relations of their derivatives

().

In other words, for uncertainties of the form 0/0 or ∞/∞, the limit of the ratio of two functions is equal to the limit of the ratio of their derivatives, if the latter exists (finite or infinite).

Notes.

1. L'Hopital's rules are also applicable when the functions f(x) And g(x) are not defined when x = a.

2. If, when calculating the limit of the ratio of derivatives of functions f(x) And g(x) we again come to an uncertainty of the form 0/0 or ∞/∞, then L'Hôpital's rules should be applied repeatedly (at least twice).

3. L'Hopital's rules are also applicable when the argument of functions (x) does not tend to a finite number a, and to infinity ( x → ∞).

Uncertainties of other types can also be reduced to uncertainties of the types 0/0 and ∞/∞.

Disclosure of uncertainties of the types “zero divided by zero” and “infinity divided by infinity”

Example 1.

x=2 leads to uncertainty of the form 0/0. Therefore, the derivative of each function is obtained

The derivative of the polynomial was calculated in the numerator, and in the denominator - derivative of a complex logarithmic function. Before the last sign equalities calculated usual limit, substituting a two instead of an X.

Example 2. Calculate the limit of the ratio of two functions using L'Hopital's rule:

Solution. Substitution in given function values x

Example 3. Calculate the limit of the ratio of two functions using L'Hopital's rule:

Solution. Substituting a value into a given function x=0 leads to uncertainty of the form 0/0. Therefore, we calculate the derivatives of the functions in the numerator and denominator and get:

Example 4. Calculate

Solution. Substituting the value x equal to plus infinity into a given function leads to an uncertainty of the form ∞/∞. Therefore, we apply L'Hopital's rule:

Comment. Let's move on to examples in which L'Hopital's rule has to be applied twice, that is, to come to the limit of the ratio of the second derivatives, since the limit of the ratio of the first derivatives is an uncertainty of the form 0/0 or ∞/∞.

Apply L'Hopital's rule yourself and then see the solution

Uncovering uncertainties of the form “zero times infinity”

Example 12. Calculate

.

Solution. We get

This example uses the trigonometric identity.

Disclosure of uncertainties of the types "zero to the power of zero", "infinity to the power of zero" and "one to the power of infinity"

Uncertainties of the form , or are usually reduced to the form 0/0 or ∞/∞ by taking the logarithm of a function of the form

To calculate the limit of an expression, you should use logarithmic identity, a special case of which is the property of the logarithm .

Using the logarithmic identity and the property of continuity of a function (to go beyond the sign of the limit), the limit should be calculated as follows:

Separately, you should find the limit of the expression in the exponent and build e to the found degree.

Example 13.

Solution. We get

.

.

Example 14. Calculate using L'Hopital's rule

Solution. We get

Calculate the limit of an expression in exponent

.

.

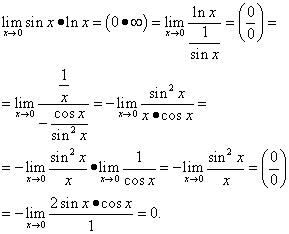Example 15. Calculate using L'Hopital's rule

This uncertainty is “served” second wonderful limit , and in the second part of that lesson we looked in great detail standard examples solutions that are found in practice in most cases. Now the painting with the exhibitors will be completed, in addition, final tasks The lesson will be devoted to “fake” limits, in which it SEEMS that it is necessary to apply the 2nd wonderful limit, although this is not at all the case.

The disadvantage of the two working formulas for the 2nd remarkable limit is that the argument must tend to “plus infinity” or to zero. But what if the argument tends to a different number?

Comes to the rescue universal formula(which is actually a consequence of the second remarkable limit):

Uncertainty can be eliminated using the formula:

Somewhere I think I already explained what they mean square brackets. Nothing special, brackets are just brackets. They are usually used to highlight mathematical notation more clearly.

Let us highlight the essential points of the formula:

1) It's about only about certainty and nothing else.

2) The “x” argument can tend to arbitrary value(and not just to zero or), in particular, to “minus infinity” or to anyone finite number.

Using this formula you can solve all the examples in the lesson. Wonderful Limits, which belong to the 2nd remarkable limit. For example, let's calculate the limit:

IN in this case , and according to the formula :

True, I don’t recommend doing this; the tradition is to still use the “usual” design of the solution, if it can be applied. However using the formula it is very convenient to check"classical" examples to the 2nd remarkable limit.

All this is good and correct, but now there are more interesting shots in the frame:

Example 18

Calculate limit

At the first step, I will not tire of repeating, we substitute the value of “x” into the expression under the limit sign. What if there is no uncertainty at all? It happens! But not this time. Substituting the “three”, we come to the conclusion that there is uncertainty here

We use the formula

In order not to drag the letter “e” around with you and not to make it smaller, the indicator It’s more convenient to calculate separately:

In this case:

Thus:

From the point of view of calculation technology, everything is routine: first we reduce the first term to common denominator, then we take out the constants and make reductions, getting rid of the uncertainty 0:0.

As a result:

Promised gift with logarithm difference and uncertainty:

Example 19

Calculate limit

At first complete solution, then comments:

(1)-(2) In the first two steps we use the formulas . U complex derivatives we “fall apart” logarithms, but here, on the contrary, they need to be “assembled”.

(3) Move the limit icon below the logarithm. This can be done because this logarithm continuous to "minus infinity". In addition, the limit refers to the “filling” of the logarithm.

(4)-(5) Standard technique discussed at basic lesson about wonderful limits, we transform the uncertainty to the form .

(6) We use the formula .

(7) Exponential and logarithmic function– mutually inverse functions, so both “e” and the logarithm can be removed. Indeed, according to the property of the logarithm: . We add the minus before the fraction to the denominator:

(8) No comments =)

The type of limit considered is not so rare; I found 30-40 examples.

Example 20

Calculate limit

This is an example for independent decision. In addition to using the formula, you can represent the limit as and by replacement reduce the solution to the case .

In conclusion, let’s look at the “fake” limits.

Let's return to uncertainty. This uncertainty not always can be reduced to uncertainty and use the second remarkable limit or corollary formula. The transformation is feasible if numerator and denominator of the base - equivalent endlessly great features . For example: .

Let's take a break from the indicator and calculate the limit of the base:

In the limit obtained unit, which means the numerator and denominator not just of the same order of growth, but also equivalent. In class Remarkable limits. Examples of solutions we mixed without any problems this example to uncertainty and received an answer.

You can come up with a lot of similar limits:
etc.

The fractions of these examples are united by the above feature: . In other cases, if there is uncertainty 2nd remarkable limit is not applicable.

Example 21

Find limits

No matter how hard you try, uncertainty cannot be transformed into uncertainty

Here are the numerators and denominators of the bases same order of growth, but not equivalent: .

Thus, the second remarkable limit and, even more so, the formula, CANNOT BE APPLIED.

! Note: Not to be confused with Example #18, in which the numerator and denominator of the base are not equivalent. There is ready-made uncertainty, but here we are talking about uncertainty.

The method for solving “fake” limits is simple and sign: you need a numerator and a denominator grounds divide by “x” to the highest degree (regardless of the exponent):

If the numerator and denominator of the base are of different order of growth, then the solution is exactly the same:

Example 22

Find limits

This short examples For self-study

Sometimes there may be no uncertainty at all:

Such tricks are especially loved by the compilers of Kuznetsov’s collection. That is why it is very important to ALWAYS substitute “x” into the expression under the limit sign in the first step!

Example 2

Major degree of numerator: 2; highest degree of denominator: 3.
:

Example 4

Divide the numerator and denominator by :


Note : the very last action was to multiply the numerator and denominator by to get rid of irrationality in the denominator.

Example 6

Divide the numerator and denominator by :

Example 8

Divide the numerator and denominator by :

Note : term tend to zero slower than , That's why is the “main” zero of the denominator. .

Example 22


Note : endlessly small function tends to zero slower than , so the “larger” zero of the denominator plays a decisive role:

1. In order for the number A to be the limit of f(x) as x->a, it is necessary and sufficient that this function be representable in the form f(x)=A+alpha(x), where alpha(x) is infinitesimal.

2. Limit constant value equal to the constant itself. LimC,x->a=C.

3. Iff(x)>= 0 (f(x)<=0) в некоторой окрестности точки а, кроме самой точки а, и в этой точке имеет предел, то пределlimf(x),x->a>=0 (limf(x)x->a,<=0)

4. If the functions f1(x), f2(x) have limits at point a, then their sum, product and quotient also have limits, and lim(f1(x)+f2(x)),x->a=limf1(x ),x->a+limf2(x),x->a, the same with the product and quotient

5. If f(x) has a limit at point a, then lim(f(x))^n,x->a= (limf(x),x->a)^n, where n is a natural number

6. The constant factor can be taken beyond the sign of the limit. Lim cf(x), x->a = cLim f(x), x->a.

7. If for the functions f(x), f1(x), f2(x) in some neighborhood at point a the inequality f1(x) is satisfied<=f(x)<=f2(x) и пределlimf1(x),x->a=limf2(x),x->a=A, then limf(x),x->a=A.

8. Limc^x,x->b = infinity ifc>1 and 0 if 0

Uncertainty of the form infinity to infinity

Divide everything by x to the highest degree, taking into account the decrease in the degree at the root.

Lim(x->0) sin 5x/sin3x = =lim(x->0) x sin5x/x sin3x = lim(x->0) sin5x/x*lim(x->0) x/sin3x=lim( x->0) 5sin5x/5x*lim 3sin3x/3x)=5/3

Lim(x-unl) (1+1/x) x =e;

1/x=a=>x=1/a, a->0

Lim(a-0) (1+a) 1/2 =e

Lim(x-0) (log a (1+x))/x = lim(x-0) 1/x*log a (1+x)=lim(x-0) log a (1+x) 1 /x =log a lim(x-0)(1+x) 1/x =log a e

Lim(x-0) ln(1+x)/x=ln e=1

Lim(x-0) a x -1/x=|a x -1=t;a x =t+1;ln a x =ln(t+1)

Comparison of infinitesimal functions

Let a(x,b(x) be infinitesimal functions for x->a

1. Lim(x->a)a(x)/b(x)=0 =>a(x) – infinitesimal of higher order than b(x)

2. Lim(x->a)a(x)/b(x) =c<>0=>a and b – infinitesimal functions of the same order

3. Lim(x->a)a(x)/b(x) = 1 =>aub – equivalent infinitesimal functions

4. Lim(x->a)d(x)/b n (x) =c<>0 =>a– infinitesimal function of nth order relative to b(x)

Cos2x=1-2sin 2 x

Theorem: if b.m. a(x) is equivalent to a 1 (x) and b(x) ~b 1 (x) and lim(x->a)a(x)/b(x) =>lim(x->a)a 1 (x) /b 1 (x)

6. A kx ~kx ln a

8. 1-cos kx ~kx 2 /2

23. Limit of a function, limit theorems. Uncertainty of the form 0/0. Infinitely large and infinitely small.

Function f(x) tends to infinity as x striving for a, if for any M> 0, you can specify a value  > 0 such that for all x satisfying the inequality  xa <  имеет место неравенство f(x) > M.

lim x  a =

 Function limited when x a.

 Function limited when x .

 Theorem. If lim x  a f(x)=b, then the function f(x) limited at x a.

 Infinitesimals and their properties. lim x  a (x)=0

Theorem. 1. If f(x)=b+, where  - b.m. at x a, then lim x  a f(x)=b and vice versa if lim x  a f(x)=b, then we can write f(x)=b+(x).

Theorem. 2. If lim x  a (x)=0 and ( x)  0, then 1/ .

Theorem. 3. Amount finite number b.m. there is b.m.

Theorem. 4. Product b.m. for a limited function there is a b.m.

 Limit theorems.

Theorem. 1. The amount limit is the sum of the limits.

Theorem. 2. The limit of a product is the product of limits.

Theorem. 3. The limit of a quotient is the quotient of the limits (if the denominator does not turn to 0).

Theorem. 4. If u(x)  z(x)  v(x), and lim x  a u(x)=lim x  a v(x)=b, then lim x  a z(x)=b. (“The Two Policeman Theorem”).

 The first remarkable limit.

at nhas a limit between 2 and 3. In this work we will consider the uncertainty of the form for the function. To find the limit of a function, we use the transformation method, the substitution method, and the definition of infinitesimal quantities.

Suppose we need to find the limit of a fraction

where P(x) and Q(x) are functions defined in the vicinity of the limiting argument a, but at the very limiting value they vanish.

Theorem 1. Let the number a for a polynomial of the nth degree P(x) = P n (x) be a k multiple solution, and for a polynomial of the mth degree Q(x) = Q n (x) be an r multiple solution, then

(2)

where P n-k (a) and Q m-r (a) are the values ​​of the corresponding polynomials P n-k (x) and Q m-r (x) at point x = a.

Proof. Since the number a is a solution of the polynomials P n (x) and Q m (x), they can be represented at any time in the form:

The binomials (x - a) k and (x - a) r in the neighborhood of the point x = a are infinitesimal, and their equivalent bases are infinitesimal. From here

Relying on the last equality, we can obtain formula (2) from the limit (3). 25. 1st Remarkable limit.

does calico go with every adult dress?

the amount of beads made at the factory in Ust-Ruditsy if its price per pound was 6 rubles less?

more than the first time. How many kilograms of cookies were brought to each store? Problem No. 2 Two athletes simultaneously began to run towards each other. The first athlete ran with average speed 305m/min, second - 312m/min. The athletes met after 4 minutes. What was the distance between them at first? Solve the problem step by step with explanations. Problem No. 3 The train leaves at 19:35. The passenger journey from home to the station takes 45 minutes. At what time does a passenger need to leave home in order to be at the station 15 minutes before the train departs? Problem No. 4 15 identical raincoats were sewn from 60 m of fabric. How many such raincoats can be sewn from 100 m of the same fabric? Problem No. 5 The perimeter of a square is 8 cm. A rectangle is made from two such squares. Find the area of ​​this rectangle. Problem No. 6 Garden area 192a. One tenth of the garden area is occupied by apple trees, and one fifth of the remaining area is occupied by plum trees. What area of ​​the garden is occupied by plum trees? Problem No. 7 The mass of four identical boxes with tangerines is 34 kg. The mass of an empty box is 1 kg 500 g. Find the mass of tangerines in each box.

By the third year of life, most of us can already count. Since we understand the magic of numbers, nothing can stop us. Although the concept of infinity seems harmless enough, just keep counting and the world will appear in a completely different light! Mathematicians managed to identify huge amount infinities, and each subsequent one turns out to be greater than the previous one. If the Universe is truly infinite, the consequences could be even more unpredictable and surprising. IN infinite universe may exist infinite number copies of the Earth and... your copies! It is possible that there are infinite multi-universes that contain our Universe and that are older than our time. This film based on mathematical theories, is an attempt to construct an idea of ​​​​the infinity of all things.

Year of manufacture: 2010
Production: BBC Horizon, UK
Director: Steven Berkoff

In 1980, the Guinness Book of Records repeated Gardner's claims, further fueling public interest in this number. Graham's number is an unimaginable number of times larger than other well-known ones. big numbers, such as googol, googolplex and even more than Skewes number and Moser number. In fact, the entire observable universe is too small to contain an ordinary decimal notation Graham numbers.

Mathematics is the universal language of the Universe, the foundation on which all other sciences are based. How was humanity able to discover the secrets of this universal language? Starting from ancient times, the history of mathematics is traced to the present day and ends with a story about the most important issues modernity. Their solution will allow us to better understand the structure of our world.

IN lately Scientists are increasingly able to study in more detail what the microworld looks like. Microscopes made it possible to magnify objects a hundred times, a thousand, ten thousand times. Finally managed to build electron microscopes, capable of showing individual atoms. But scientists are interested in seeing not only atoms, but also looking inside atoms. The nucleus of an atom is one hundred thousand times smaller than the atom itself. To study matter at this scale, particle accelerators are needed. More and more powerful and more sophisticated. And finally, having reached the deepest level, where it is impossible to look even with the help of the most powerful accelerators, scientists have to take up an unexpected tool - a telescope. The film talks about the methods used to study the structure of our universe at various microscales.

The boundless, vast and complex Universe has been a subject of admiration and an object for several thousand years. scientific research. Its mysteries may seem distant and incomprehensible, but Professor Jim Al-Khalili comes to our aid. It will try to explain everything that is known about the universe and a little more.

Where did our Universe come from? How did it all start? For almost a hundred years, we thought that Big bang was about 14 billion years ago. But now some scientists believe that there wasn't really a "beginning"; our universe may have been destroyed "before." This film will take you into the unknown to explore the dizzying world of space and multiple universes, and you will learn what happened before the Big Bang.

It is impossible to answer this question correctly, because number series doesn't have upper limit. So, to any number you just need to add one to get an even larger number. Although the numbers themselves are infinite, proper names they don't have much, since most of them are content with names made up of smaller numbers. It is clear that in the finite set of numbers that humanity has awarded own name there must be some greatest number. But what is it called and what does it equal? Let's try to figure this out and at the same time find out how large numbers mathematicians came up with.

Mathematician, Professor Marcus du Satele talks in this film about how the laws of mathematics permeate all forms of our world with their strict beauty.