Tarp funkcinių serijų svarbiausią vietą užima galios serijos.

Galios serija yra serija

kurių terminai yra laipsnio funkcijos, išdėstytos didėjančiais neneigiamais sveikųjų skaičių laipsniais x, A c0 , c 1 , c 2 , c n - pastovios vertės. Skaičiai c1 , c 2 , c n - serijos terminų koeficientai, c0 - laisvas narys. Laipsnių eilučių sąlygos apibrėžtos visoje skaičių eilutėje.

Susipažinkime su koncepcija laipsnių eilučių konvergencijos sritis. Tai kintamųjų reikšmių rinkinys x, kurio serija sutampa. Galios eilutės turi gana paprastą konvergencijos sritį. Realioms kintamosioms reikšmėms x konvergencijos sritis susideda arba iš vieno taško, arba yra tam tikras intervalas (konvergencijos intervalas), arba sutampa su visa ašimi Jautis .

Keičiant reikšmes į galios eilutes x= 0 bus skaičių serija

c0 +0+0+...+0+... ,

kuris susilieja.

Todėl kai x= 0 bet kuri laipsnio eilutė suartėja ir todėl jos konvergencijos sritis negali būti tuščias rinkinys. Visų laipsnių eilučių konvergencijos srities struktūra yra vienoda. Jį galima nustatyti naudojant šią teoremą.

1 teorema (Abelio teorema). Jei laipsnio eilutė suartėja ties kokia nors verte x = x 0 , skiriasi nuo nulio, tada jis susilieja ir, be to, absoliučiai visoms reikšmėms |x| < |x 0 | . Atkreipkite dėmesį: ir pradinė reikšmė „X yra nulis“, ir bet kuri „X“ reikšmė, kuri lyginama su pradine reikšme, imama modulo – neatsižvelgiant į ženklą.

Pasekmė. Jeigu galios serijos skiriasi tam tikra verte x = x 1 , tada jis skiriasi visoms vertėms |x| > |x 1 | .

Kaip jau sužinojome anksčiau, bet kuri laipsnio eilutė suartėja su verte x= 0. Yra laipsnių eilučių, kurios susilieja tik tada, kai x= 0 ir kitoms reikšmėms skiriasi X. Neatsižvelgdami į šį atvejį, darome prielaidą, kad laipsnio eilutė suartėja ties tam tikra verte x = x 0 , skiriasi nuo nulio. Tada, pagal Abelio teoremą, jis suartėja visuose intervalo ]-| taškuose x0 |, |x 0 |[ (intervalas, kurio kairioji ir dešinioji ribos yra x reikšmės, kuriose laipsnių eilutė suartėja, atitinkamai paimta su minuso ir pliuso ženklu), simetriškas kilmės atžvilgiu.

Jei galios eilutė skiriasi tam tikra verte x = x 1 , tada, remiantis Abelio teoremos išvadomis, jis skiriasi visuose taškuose, esančiuose už atkarpos ribų [-| x1 |, |x 1 |] . Iš to išplaukia, kad bet kuriai laipsnio eilei yra intervalas, simetriškas pradžios atžvilgiu, vadinamas konvergencijos intervalas , kiekviename taške, kurio eilutė suartėja, ties ribomis ji gali suartėti arba gali skirtis, ir nebūtinai tuo pačiu metu, o už atkarpos ribų serija skiriasi. Skaičius R vadinamas laipsnių eilučių konvergencijos spinduliu.

Ypatingais atvejais laipsnių eilučių konvergencijos intervalas gali išsigimti iki taško (tada serija susilieja tik tada, kai x= 0 ir laikoma, kad R= 0) arba pavaizduoti visą skaičių tiesę (tada serija suartėja visuose skaičių linijos taškuose ir daroma prielaida, kad ).

Taigi laipsnių eilutės konvergencijos srities nustatymas susideda iš jos nustatymo konvergencijos spindulys R ir tiriant eilučių konvergenciją ties konvergencijos intervalo ribomis (prie ).

2 teorema. Jei visi laipsnio eilutės koeficientai, pradedant nuo tam tikro, skiriasi nuo nulio, tada jos konvergencijos spindulys yra lygus ribinei bendrų sekančių serijos narių koeficientų absoliučių verčių santykiui. , t.y.

1 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Čia

Naudodami (28) formulę randame šios eilutės konvergencijos spindulį:

Ištirkime eilučių konvergenciją konvergencijos intervalo galuose. 13 pavyzdys rodo, kad ši eilutė suartėja ties x= 1 ir skiriasi ties x= -1. Vadinasi, konvergencijos sritis yra pusės intervalas.

2 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Serijos koeficientai yra teigiami, ir

Raskime šio santykio ribą, t.y. laipsnių eilučių konvergencijos spindulys:

Išnagrinėkime eilučių konvergenciją intervalo galuose. Vertybių pakeitimas x= -1/5 ir x= 1/5 šioje eilutėje suteikia:

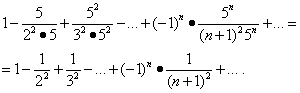
Pirmoji iš šių eilučių suartėja (žr. 5 pavyzdį). Bet tada, remiantis „absoliučios konvergencijos“ skyriaus teorema, antroji eilutė taip pat suartėja, o jos konvergencijos sritis yra segmentas

3 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Čia

Naudodami (28) formulę randame eilučių konvergencijos spindulį:

Išnagrinėkime reikšmių eilučių konvergenciją. Pakeitę juos šioje serijoje, gauname atitinkamai

Abi eilutės skiriasi, nes netenkinama būtina konvergencijos sąlyga (jų bendrieji terminai nelinkę į nulį ties ). Taigi abiejuose konvergencijos intervalo galuose ši eilutė skiriasi, o jos konvergencijos sritis yra intervalas.

5 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Mes randame santykį, kur , ir :

Pagal (28) formulę šios eilutės konvergencijos spindulys

tai yra, serija susilieja tik tada, kai x= 0 ir skiriasi kitoms reikšmėms X.

Pavyzdžiai rodo, kad konvergencijos intervalo pabaigoje eilutės elgiasi skirtingai. 1 pavyzdyje viename konvergencijos intervalo gale konverguoja, o kitame, 2 pavyzdyje, ji suartėja abiejuose galuose;

Laipsnių eilutės konvergencijos spindulio formulė gaunama darant prielaidą, kad visi eilutės narių koeficientai, pradedant nuo tam tikro taško, skiriasi nuo nulio. Todėl (28) formulę galima naudoti tik šiais atvejais. Jei ši sąlyga pažeidžiama, laipsnių eilučių konvergencijos spindulį reikia ieškoti naudojant d'Alemberto ženklas, arba, pakeitus kintamąjį, transformuoti eilutę į formą, kurioje tenkinama nurodyta sąlyga.

6 pavyzdys. Raskite laipsnių eilučių konvergencijos intervalą

Sprendimas. Šioje serijoje nėra terminų su nelyginiais laipsniais X. Todėl transformuojame seriją, nustatymą . Tada gauname seriją

rasti kurio konvergencijos spindulį galime pritaikyti (28) formulę. Kadangi , a , tada šios serijos konvergencijos spindulys

Iš lygybės gauname Todėl ši serija suartėja su intervalu .

Galios eilučių suma. Galios eilučių diferencijavimas ir integravimas

Leiskite galios serijai

konvergencijos spindulys R> 0, t.y. ši serija susilieja į intervalą .

Tada kiekviena vertė X iš konvergencijos intervalo atitinka tam tikrą eilutės sumą. Todėl laipsnių eilučių suma yra funkcija X konvergencijos intervale. Žymėdamas tai f(x), galime parašyti lygybę

suprasti tai ta prasme, kad serijų suma kiekviename taške X iš konvergencijos intervalo yra lygus funkcijos reikšmei f(x) Šiuo atveju. Ta pačia prasme sakysime, kad laipsnio eilutė (29) konverguoja į funkciją f(x) konvergencijos intervale.

Už konvergencijos intervalo ribų lygybė (30) neturi prasmės.

7 pavyzdys. Raskite laipsnių eilučių sumą

Sprendimas. Tai geometrinė serija, kuriai a= 1, a q= x. Todėl jo suma yra funkcija . Serija konverguoja, jei , ir yra jos konvergencijos intervalas. Todėl lygybė

galioja tik reikšmėms, nors funkcija apibrėžtos visoms vertėms X, išskyrus X= 1.

Galima įrodyti, kad laipsnių eilutės suma f(x) yra tęstinis ir diferencijuojamas bet kuriame konvergencijos intervalo intervale, ypač bet kuriame eilutės konvergencijos intervalo taške.

Pateiksime teoremas apie laipsnių eilučių diferencijavimą ir integravimą.

1 teorema. Laipsninės eilutės (30) jos konvergencijos intervale gali būti diferencijuojamos pagal terminą neribotą skaičių kartų, o gautos laipsnių eilutės konvergencijos spindulys yra toks pat kaip ir pradinė eilutė, o jų sumos atitinkamai lygios .

2 teorema. Galios eilutes (30) galima integruoti po termino neribotą skaičių kartų intervale nuo 0 iki X, jei , ir gautos laipsnio eilutės turi tokį patį konvergencijos spindulį kaip ir pradinės eilutės, o jų sumos yra atitinkamai lygios

Funkcijų išplėtimas į galių eilutes

Tegu funkcija duota f(x), kurią reikia išplėsti į galios eilutę, t.y. pavaizduoti formoje (30):

Užduotis – nustatyti koeficientus eilutė (30). Norėdami tai padaryti, diferencijuodami lygybę (30) pagal terminą, nuosekliai randame:

……………………………………………….. (31)

Darant prielaidą, kad lygybės (30) ir (31) X= 0, randame

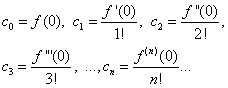
Rastus posakius pakeitę lygybe (30), gauname

(32)

Raskime kai kurių elementarių funkcijų Maclaurin serijos išplėtimą.

8 pavyzdys. Išplėskite funkciją Maclaurin serijoje

Sprendimas. Šios funkcijos išvestiniai sutampa su pačia funkcija:

Todėl kai X= 0 turime

Pakeitę šias reikšmes į (32) formulę, gauname norimą išplėtimą:

(33)

Ši eilutė susilieja į visą skaičių tiesę (jos konvergencijos spindulį).

1 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį:

A) ; b) ;

V) ; G)
;

d)
.

A) Raskime konvergencijos spindulį R. Nes
,
, Tai

x
, tai yra eilučių konvergencijos intervalas
.

At
gauname skaičių seriją . Ši serija susilieja, nes tai apibendrinta harmoninė serija adresu
.

At
gauname skaičių seriją
. Ši serija yra absoliučiai konvergentiška, nes serija sudaryta iš absoliučių jos terminų verčių , konvergentinis.

b) Raskime konvergencijos spindulį R. Nes
, Tai
.

Taigi, eilučių konvergencijos intervalas
.

Nagrinėjame šios eilutės konvergenciją konvergencijos intervalo galuose.

At
turime skaičių seriją

.

At
turime skaičių seriją
. Ši serija skiriasi, nes
neegzistuoja.

Taigi, šios eilutės konvergencijos sritis
.

V) Raskime konvergencijos spindulį R. Nes
,
Tai
.

Taigi, konvergencijos intervalas
. Šios eilutės konvergencijos sritis sutampa su konvergencijos intervalu, tai yra, eilutė konverguoja bet kuriai kintamojo vertei x.

G) Raskime konvergencijos spindulį R. Nes
,
Tai
.

Nes
, tada serija susilieja tik taške
. Tai reiškia, kad šios eilutės konvergencijos sritis yra vienas taškas
.

d) Raskime konvergencijos spindulį R.

Nes
,
, Tai

Taigi, serialas susilieja absoliučiai visiems x, tenkinantis nelygybę
, tai yra
.

Iš čia
- konvergencijos intervalas,
− konvergencijos spindulys.

Panagrinėkime šios eilutės konvergenciją konvergencijos intervalo galuose.

At
gauname skaičių seriją

kuri skiriasi (harmoninės serijos).

At
gauname skaičių seriją
, kuri konverguoja sąlygiškai (serija konverguoja pagal Leibnizo kriterijų, o serija, sudaryta iš jos narių absoliučių verčių, skiriasi, nes yra harmoninga).

Taigi, eilutės konvergencijos sritis
.

2.3. Taylor ir Maclaurin serija.

Funkcijų išplėtimas į galių eilutes.

Galios eilučių taikymas apytiksliems skaičiavimams

Problemų sprendimo pavyzdžiai

1 pavyzdys. Išplėskite funkciją į galios eilutę:

A)
; b)
;

V)
; G)
.

A) Pakeitimas formulėje
xįjungta
, gauname norimą išplėtimą:

Kur

b) Pakeitimas lygybe

Kur
xįjungta
, gauname norimą išplėtimą:

V)Šią funkciją galima parašyti taip:
. Norint rasti norimą seriją, pakanka išplėsti

Kur
pakaitalas
. Tada gauname:

G)Šią funkciją galima perrašyti taip: .

Funkcija
gali būti išplėsta į laipsnio eilutę įtraukiant į dvinarę eilutę
, mes gausime .

Kur
.

Norint gauti norimą išplėtimą, pakanka gautas eilutes padauginti (dėl absoliučios šių eilučių konvergencijos).

Vadinasi,

, Kur
.

2 pavyzdys. Raskite apytiksles šių funkcijų vertes:

A)
0,0001 tikslumu;

b)
0,00001 tikslumu.

A) Nes
, tada į funkcijos išplėtimą, kur
pakeiskime
:

arba

Nes
, tada reikiamas tikslumas bus užtikrintas, jei apsiribosime tik pirmomis dviem gautos plėtimosi sąlygomis.

Mes naudojame dvinarę eilutę

Kur
.

Tikėdamas
Ir
, gauname tokį išplėtimą:

Jei paskutinėje kintamoje serijoje atsižvelgiama tik į pirmuosius du terminus, o likusieji atmetami, tada skaičiavimo klaida
absoliučia verte neviršys 0,000006. Tada skaičiavimo klaida
neviršys skaičiaus. Vadinasi,

3 pavyzdys. Apskaičiuokite 0,001 tikslumu:

A)
; b)
.

A)
.

Išplėskime integrandą į galių eilutę. Norėdami tai padaryti, pakeiskime dvinarę seriją
ir pakeiskite xįjungta :

Nuo integracijos segmento
priklauso gautų eilučių konvergencijos sričiai
, tada integruosime po termino nurodytose ribose:

Gautoje kintamoje eilutėje ketvirtasis narys yra mažesnis nei 0,001 absoliučia verte. Vadinasi, reikiamas tikslumas bus užtikrintas, jei bus atsižvelgta tik į pirmąsias tris serijos sąlygas.

Kadangi pirmasis iš atmestų terminų turi minuso ženklą, gauta apytikslė vertė bus perteklinė. Todėl atsakymas 0,001 tikslumu yra 0,487.

b) Pirmiausia pavaizduokime integrandą kaip laipsnių eilutę. Pakeiskime funkcijos išplėtimą

Kur

xįjungta
, mes gauname:

Tada
.

Gauta kintamoji eilutė atitinka Leibnizo kriterijaus sąlygas. Ketvirtasis eilutės narys yra mažesnis nei 0,001 absoliučia verte. Norint užtikrinti reikiamą tikslumą, pakanka rasti pirmųjų trijų terminų sumą.

Vadinasi,
.

Funkcinė serija. Galios serija.
Eilučių konvergencijos diapazonas

Juokas be priežasties yra d'Alemberto ženklas

Išmušė funkcinių gretų valanda. Norėdami sėkmingai įsisavinti temą, o ypač šią pamoką, turite gerai suprasti įprastas skaičių serijas. Turėtumėte gerai suprasti, kas yra eilutė, ir mokėti taikyti palyginimo kriterijus, kad ištirtumėte serijų konvergenciją. Taigi, jei ką tik pradėjote studijuoti temą arba esate aukštosios matematikos naujokas, būtina iš eilės dirbkite tris pamokas: Eilės manekenams,D'Alemberto ženklas. Koši požymiai Ir Kintamos eilutės. Leibnizo testas. Tikrai visi trys! Jei turite pagrindinių žinių ir įgūdžių sprendžiant su skaičių serijomis susijusias problemas, tada su funkcinėmis serijomis susidoroti bus gana paprasta, nes naujos medžiagos nėra daug.

Šioje pamokoje apžvelgsime funkcinės serijos sampratą (kas tai net yra), susipažinsime su galių eilėmis, kurios randamos 90% praktinių užduočių, ir išmoksime išspręsti dažną tipinę spindulio radimo problemą. laipsnių eilutės konvergencijos, konvergencijos intervalo ir konvergencijos srities. Toliau rekomenduoju apsvarstyti medžiagą apie funkcijų išplėtimas į galių eilutes, o pradedančiajam bus suteikta pirmoji pagalba. Šiek tiek atgavę kvapą pereiname į kitą lygį:

Taip pat funkcinių serijų skyriuje jų yra daug apytikslės skaičiavimo programos, o kai kurios išsiskiria Furjė serijomis, kurioms, kaip taisyklė, skiriamas atskiras skyrius mokomojoje literatūroje. Turiu tik vieną straipsnį, bet jis ilgas ir yra daug, daug papildomų pavyzdžių!

Taigi, orientyrai nustatyti, eikime:

Funkcinių serijų ir galios serijų samprata

Jei riba pasirodo esanti begalybė, tada sprendimo algoritmas taip pat baigia savo darbą, o mes pateikiame galutinį atsakymą į užduotį: „Serija konverguoja ties “ (arba ties bet kuriuo „). Žr. ankstesnės pastraipos bylą Nr. 3.

Jei riba pasirodys nei nulis, nei begalybė, tada turime praktikoje dažniausiai pasitaikantį atvejį Nr. 1 – serija susilieja tam tikru intervalu.

Šiuo atveju riba yra. Kaip rasti eilučių konvergencijos intervalą? Sudarome nelygybę:

IN BET KOKIA tokio tipo užduotis kairėje nelygybės pusėje turėtų būti limito skaičiavimo rezultatas, o dešinėje nelygybės pusėje – griežtai vienetas. Tiksliai nepaaiškinsiu, kodėl yra tokia nelygybė ir kodėl yra dešinėje. Pamokos praktiškai orientuotos, ir jau labai gerai, kad mano pasakojimai neužkabino mokytojų kolektyvo ir kai kurios teoremos tapo aiškesnės.

Pirmaisiais metais straipsnyje buvo išsamiai aptarta darbo su moduliu technika ir dvigubų nelygybių sprendimas Funkcijos domenas, bet patogumo dėlei visus veiksmus pasistengsiu pakomentuoti kuo detaliau. Nelygybės išplėtimas moduliu pagal mokyklos taisyklę . Tokiu atveju:

Pusė kelio baigėsi.

Antrame etape būtina ištirti eilučių konvergenciją rasto intervalo galuose.

Pirmiausia paimame kairįjį intervalo galą ir pakeičiame jį į savo galių eilutę:

Gavome skaičių eilutę ir turime išnagrinėti jos konvergenciją (užduotis, jau pažįstama iš ankstesnių pamokų).

1) Serija yra kintama.
2) – modulio mažėjimo eilutės sąlygos. Be to, kiekvienas kitas serijos narys yra mažesnis už ankstesnį absoliučia verte: , o tai reiškia, kad sumažėjimas yra monotoniškas.
Išvada: serija susilieja.

Naudodami seriją, sudarytą iš modulių, tiksliai išsiaiškinsime, kaip:
– susilieja („standartinės“ serijos iš apibendrintų harmoninių eilučių).

Taigi gautos skaičių eilutės absoliučiai suartėja.

adresu – susilieja.

! primenu tau kad bet kuri konverguojanti teigiama eilutė taip pat yra absoliučiai konverguojanti.

Taigi laipsnio eilutė suartėja ir absoliučiai abiejuose rasto intervalo galuose.

Atsakymas: tiriamų galių eilučių konvergencijos sritis:

Kita atsakymo forma turi teisę į gyvybę: serija susilieja, jei

Kartais problemos teiginyje reikia nurodyti konvergencijos spindulį. Akivaizdu, kad nagrinėjamame pavyzdyje .

2 pavyzdys

Raskite laipsnių eilučių konvergencijos sritį

Sprendimas: randame eilučių konvergencijos intervalą naudojant d'Alemberto ženklas (bet ne BY atributas! – toks atributas funkcinėms serijoms neegzistuoja):

Serija susilieja ties

Kairė mums reikia išvykti tik, todėl abi nelygybės puses padauginame iš 3:

– Serialas kaitaliojasi.
– – modulio mažėjimo eilutės sąlygos. Kiekvienas kitas serijos narys yra mažesnis už ankstesnį absoliučia verte: , o tai reiškia, kad sumažėjimas yra monotoniškas.

Išvada: serija susilieja.

Panagrinėkime konvergencijos pobūdį:

Palyginkime šią seriją su skirtingomis serijomis.
Mes naudojame ribojantį palyginimo kriterijų:

Gaunamas baigtinis skaičius, kuris skiriasi nuo nulio, o tai reiškia, kad serija skiriasi nuo serijos.

Taigi serija konverguoja sąlyginai.

2) Kada – skiriasi (pagal tai, kas įrodyta).

Atsakymas: Tiriamos galios eilučių konvergencijos sritis: . Kai serija suartėja sąlygiškai.

Nagrinėjamame pavyzdyje laipsnių eilutės konvergencijos sritis yra pusės intervalas, o visuose intervalo taškuose laipsnių eilutė absoliučiai susilieja, o taške , kaip paaiškėjo - sąlyginai.

3 pavyzdys

Raskite laipsnių eilutės konvergencijos intervalą ir ištirkite jo konvergenciją rasto intervalo galuose

Tai pavyzdys, kurį galite išspręsti patys.

Pažvelkime į keletą pavyzdžių, kurie yra reti, bet pasitaiko.

4 pavyzdys

Raskite eilučių konvergencijos sritį:

Sprendimas: Naudodami d'Alemberto testą randame šios eilutės konvergencijos intervalą:

(1) Sudarome kito serijos nario ir ankstesnio nario santykį.

(2) Atsikratome keturių aukštų trupmenos.

(3) Pagal operacijų su laipsniais taisyklę, kubus sujungiame į vieną laipsnį. Skaitiklyje sumaniai išplečiame laipsnį, t.y. Ją išdėstome taip, kad kitame žingsnyje trupmeną galėtume sumažinti . Mes išsamiai aprašome faktorines.

(4) Po kubu dalijame skaitiklį iš vardiklio termino pagal terminą, nurodydami, kad . Dalyje sumažiname viską, ką galima sumažinti. Mes paimame veiksnį už ribinio ženklo, jį galima išimti, nes jame nėra nieko, kas priklausytų nuo „dinaminio“ kintamojo „en“. Atkreipkite dėmesį, kad modulio ženklas nenubraižytas – dėl to, kad bet kuriam „x“ jis ima neneigiamas reikšmes.

Riboje gaunamas nulis, o tai reiškia, kad galime pateikti galutinį atsakymą:

Atsakymas: Serija susilieja ties

Tačiau iš pradžių atrodė, kad šią eilutę su „baisiu įdaru“ bus sunku išspręsti. Nulis arba begalybė riboje yra beveik dovana, nes sprendimas pastebimai sumažėjo!

5 pavyzdys

Raskite eilučių konvergencijos sritį

Tai pavyzdys, kurį galite išspręsti patys. Būkite atsargūs;-) Visas sprendimas yra pamokos pabaigoje.

Pažvelkime į dar kelis pavyzdžius, kuriuose yra techninių metodų naudojimo naujumo elementas.

6 pavyzdys

Raskite eilutės konvergencijos intervalą ir ištirkite jos konvergenciją rasto intervalo galuose

Sprendimas: Bendras galios eilės terminas apima koeficientą, užtikrinantį ženklų sukimąsi. Sprendimo algoritmas yra visiškai išsaugotas, tačiau sudarydami ribą ignoruojame (nerašome) šio veiksnio, nes modulis sunaikina visus „minusus“.

Eilučių konvergencijos intervalą randame naudodami d'Alemberto testą:

Sukurkime standartinę nelygybę:
Serija susilieja ties
Kairė mums reikia išvykti tik modulis, todėl abi nelygybės puses padauginame iš 5:

Dabar atidarome modulį pažįstamu būdu:

Dvigubos nelygybės viduryje reikia palikti tik „X“, iš kiekvienos nelygybės dalies atimame 2:

– tiriamų laipsnių eilučių konvergencijos intervalas.

Mes tiriame eilučių konvergenciją rasto intervalo galuose:

1) Pakeiskite vertę į mūsų galių eilutes :

Būkite ypač atsargūs, daugiklis neteikia ženklų kaitos su jokiu natūraliu „en“. Gautą minusą paimame už eilutės ribų ir pamirštame, nes jis (kaip ir bet kuri faktorių konstanta) jokiu būdu neturi įtakos skaičių eilučių konvergencijai ar divergencijai.

Dar kartą atkreipkite dėmesį kad reikšmę pakeičiant į bendrą laipsnių eilutės terminą, mūsų koeficientas buvo sumažintas. Jei taip neatsitiktų, tai reikštų, kad arba neteisingai apskaičiavome limitą, arba neteisingai išplėtėme modulį.

Taigi, turime išnagrinėti skaičių eilutes konvergencijai. Paprasčiausias būdas yra naudoti ribojantį palyginimo kriterijų ir palyginti šią seriją su skirtingomis harmonikų serijomis. Bet, tiesą sakant, aš siaubingai pavargau nuo ribojančio palyginimo ženklo, todėl sprendimą paįvairinsiu.

Taigi, serija susilieja

Abi nelygybės puses padauginame iš 9:

Mes ištraukiame šaknį iš abiejų dalių, prisimindami senosios mokyklos pokštą:

Modulio išplėtimas:

ir pridėkite vieną prie visų dalių:

– tiriamų laipsnių eilučių konvergencijos intervalas.

Ištirkime laipsnių eilučių konvergenciją rasto intervalo galuose:

1) Jei , tada gaunama tokia skaičių serija: