Kaip apskaičiuoti pagreitį. Pradinio greičio nustatymas pagal nuvažiuotą atstumą, laiką ir pagreitį

Visos užduotys, kuriose vyksta daiktų judėjimas, jų judėjimas ar sukimasis, yra kažkaip susijusios su greičiu.

Šis terminas apibūdina objekto judėjimą erdvėje per tam tikrą laikotarpį – atstumo vienetų skaičių per laiko vienetą. Jis yra dažnas abiejų matematikos ir fizikos skyrių „svečias“. Originalus korpusas gali keisti savo vietą tiek tolygiai, tiek su pagreičiu. Pirmuoju atveju greičio reikšmė yra statinė ir judėjimo metu nekinta, antruoju, atvirkščiai, didėja arba mažėja.

Kaip rasti greitį – tolygus judėjimas

Jei kūno judėjimo greitis išliko nepakitęs nuo judėjimo pradžios iki kelio pabaigos, tai mes kalbame apie judėjimą su pastoviu pagreičiu – tolygų judėjimą. Jis gali būti tiesus arba išlenktas. Pirmuoju atveju kūno trajektorija yra tiesi.

Tada V = S/t, kur:

• V – norimas greitis,
• S – nuvažiuotas atstumas (bendras kelias),
• t – bendras judėjimo laikas.

Kaip rasti greitį – pagreitis pastovus

Jei objektas judėjo su pagreičiu, tada judant jo greitis pasikeitė. Tokiu atveju ši išraiška padės rasti norimą reikšmę:

V = V (pradžia) + ties, kur:

• V (start) – pradinis objekto greitis,
• a – kūno pagreitis,
• t – bendras kelionės laikas.

Kaip rasti greitį – netolygus judėjimas

Šiuo atveju yra situacija, kai kūnas skirtingais laikais praėjo skirtingas kelio atkarpas.
S(1) – t(1),
S(2) – t(2) ir kt.

Pirmoje atkarpoje judėjimas vyko „tempu“ V(1), antrajame – V(2) ir t.t.

Norėdami sužinoti objekto judėjimo greitį per visą kelią (jo vidutinę vertę), naudokite išraišką:

Kaip rasti greitį – objekto sukimąsi

Sukimosi atveju kalbame apie kampinį greitį, kuris lemia kampą, kuriuo elementas sukasi per laiko vienetą. Norima reikšmė nurodoma simboliu ω (rad/s).

• ω = Δφ/Δt, kur:

Δφ – praleistas kampas (kampo prieaugis),
Δt – praėjęs laikas (judėjimo laikas – laiko prieaugis).

• Jei sukimasis vienodas, norima reikšmė (ω) siejama su tokia sąvoka kaip sukimosi periodas – kiek laiko užtruks, kol mūsų objektas atliks 1 pilną apsisukimą. Tokiu atveju:

ω = 2π/T, kur:
π – konstanta ≈3,14,
T – taškas.

Arba ω = 2πn, kur:
π – konstanta ≈3,14,
n – cirkuliacijos dažnis.

• Atsižvelgiant į žinomą objekto linijinį greitį kiekviename judėjimo taške ir apskritimo, kuriuo jis juda, spindulį, norint rasti greitį ω, jums reikės šios išraiškos:

ω = V/R, kur:
V – vektoriaus dydžio (tiesinio greičio) skaitinė reikšmė,
R yra kūno trajektorijos spindulys.

Kaip rasti greitį – judantys taškai arčiau ir toliau

Tokio pobūdžio problemose būtų tikslinga vartoti artėjimo greičio ir išvykimo greičio terminus.

Jei objektai yra nukreipti vienas į kitą, artėjimo (pašalinimo) greitis bus toks:
V (arčiau) = V(1) + V(2), čia V(1) ir V(2) yra atitinkamų objektų greičiai.

Jei vienas iš kūnų pasiveja kitą, tai V (arčiau) = V(1) – V(2), V(1) didesnis už V(2).

Kaip rasti greitį – judėjimas vandens telkiniu

Jei įvykiai klostosi vandenyje, tada srovės greitis (t. y. vandens judėjimas nejudančio kranto atžvilgiu) taip pat pridedamas prie paties objekto greičio (kūno judėjimo vandens atžvilgiu). Kaip šios sąvokos yra tarpusavyje susijusios?

Judant su srove, V=V(savas) + V(tėkmė).
Jei prieš srovę – V=V(savo) – V(srovė).

Greitis yra laiko funkcija ir yra nustatomas pagal absoliučią vertę ir kryptį. Dažnai fizikos uždaviniuose reikia rasti pradinį greitį (jo dydį ir kryptį), kurį tiriamas objektas turėjo nuliniu laiko momentu. Pradiniam greičiui apskaičiuoti gali būti naudojamos įvairios lygtys. Remdamiesi problemos teiginyje pateiktais duomenimis, galite pasirinkti tinkamiausią formulę, kuri nesunkiai gaus norimą atsakymą.

Žingsniai

Pradinio greičio nustatymas iš galutinio greičio, pagreičio ir laiko

1. Sprendžiant fizikos uždavinį, reikia žinoti, kokios formulės tau reikės. Norėdami tai padaryti, pirmiausia užsirašykite visus problemos teiginyje pateiktus duomenis. Jei galutinis greitis, pagreitis ir laikas yra žinomi, pradiniam greičiui nustatyti patogu naudoti šį ryšį:

   • V i = V f – (a * t)
   • • V i- pradinis greitis
     • Vf- galutinis greitis
     • a- pagreitis
     • t- laikas
   • Atkreipkite dėmesį, kad tai yra standartinė formulė, naudojama pradiniam greičiui apskaičiuoti.

2. Užrašę visus pradinius duomenis ir užrašę reikiamą lygtį, galite į ją pakeisti žinomus dydžius. Svarbu atidžiai išstudijuoti problemos teiginį ir atidžiai užsirašyti kiekvieną žingsnį ją sprendžiant.

   • Jei kur nors padarėte klaidą, galite lengvai ją rasti peržiūrėję savo užrašus.

3. Išspręskite lygtį. Formulėje pakeisdami žinomas reikšmes, naudokite standartines transformacijas, kad gautumėte norimą rezultatą. Jei įmanoma, naudokite skaičiuotuvą, kad sumažintumėte klaidingų skaičiavimų tikimybę.

   • Tarkime, kad objektas, judantis į rytus 10 metrų per sekundę pagreičiu 12 sekundžių kvadratu, įsibėgėja iki galutinio 200 metrų per sekundę greičio. Būtina rasti pradinį objekto greitį.
     • Užsirašykime pradinius duomenis:
     • V i = ?, Vf= 200 m/s, a= 10 m/s 2, t= 12 s
   • Padauginkime pagreitį iš laiko: a*t = 10 * 12 =120
   • Iš galutinio greičio atimkite gautą vertę: V i = V f – (a * t) = 200 – 120 = 80 V i= 80 m/s į rytus
   • m/s

Pradinio greičio nustatymas pagal nuvažiuotą atstumą, laiką ir pagreitį

1. Naudokite atitinkamą formulę. Sprendžiant bet kokią fizinę problemą, būtina pasirinkti tinkamą lygtį. Norėdami tai padaryti, pirmiausia užsirašykite visus problemos teiginyje pateiktus duomenis. Jei žinomas nuvažiuotas atstumas, laikas ir pagreitis, pradiniam greičiui nustatyti galima naudoti tokį ryšį:

   • Ši formulė apima šiuos kiekius:
     • V i- pradinis greitis
     • d- nuvažiuotas atstumas
     • a- pagreitis
     • t- laikas

2. Į formulę pakeiskite žinomus kiekius.

   • Jei apsisprendžiate suklysti, galite lengvai jį rasti peržvelgę ​​savo užrašus.

3. Išspręskite lygtį. Pakeiskite žinomas reikšmes į formulę ir naudokite standartines transformacijas, kad rastumėte atsakymą. Jei įmanoma, naudokite skaičiuotuvą, kad sumažintumėte klaidingo skaičiavimo tikimybę.

   • Tarkime, objektas juda vakarų kryptimi su 7 metrų per sekundę pagreičiu, kvadratiniu 30 sekundžių, nuvažiuodamas 150 metrų. Būtina apskaičiuoti jo pradinį greitį.
     • Užsirašykime pradinius duomenis:
     • V i = ?, d= 150 m, a= 7 m/s 2, t= 30 s
   • Padauginkime pagreitį iš laiko: a*t = 7 * 30 = 210
   • Padalinkime gaminį į dvi dalis: (a * t) / 2 = 210 / 2 = 105
   • Padalinkime atstumą iš laiko: d/t = 150 / 30 = 5
   • Atimkite pirmąjį kiekį iš antrojo: V i = (d / t) - [(a * t) / 2] = 5 – 105 = -100 V i= -100 m/s į vakarus
   • Parašykite atsakymą tinkama forma. Būtina nurodyti matavimo vienetus, mūsų atveju metrus per sekundę, arba m/s, taip pat objekto judėjimo kryptį. Jei nenurodysite krypties, atsakymas bus neišsamus, jame bus tik greičio reikšmė be informacijos, kuria kryptimi objektas juda.

Pradinio greičio nustatymas iš galutinio greičio, pagreičio ir nuvažiuoto atstumo

1. Naudokite atitinkamą lygtį. Norėdami išspręsti fizinę problemą, turite pasirinkti tinkamą formulę. Pirmiausia užsirašykite visus pradinius duomenis, nurodytus problemos pareiškime. Jei galutinis greitis, pagreitis ir nuvažiuotas atstumas yra žinomi, pradiniam greičiui nustatyti patogu naudoti šį ryšį:

   • V i = √
   • Šioje formulėje yra šie kiekiai:
     • V i- pradinis greitis
     • Vf- galutinis greitis
     • a- pagreitis
     • d- nuvažiuotas atstumas

2. Į formulę pakeiskite žinomus kiekius. Užrašę visus pradinius duomenis ir užrašę reikiamą lygtį, galite į ją pakeisti žinomus dydžius. Svarbu atidžiai išstudijuoti problemos teiginį ir atidžiai užsirašyti kiekvieną žingsnį ją sprendžiant.

   • Jei kur nors padarysite klaidą, ją nesunkiai rasite peržiūrėję sprendimo eigą.

3. Išspręskite lygtį. Pakeisdami žinomas reikšmes į formulę, naudokite reikiamas transformacijas, kad gautumėte atsakymą. Jei įmanoma, naudokite skaičiuotuvą, kad sumažintumėte klaidingų skaičiavimų tikimybę.

   • Tarkime, kad objektas juda šiaurės kryptimi 5 metrų per sekundę kvadratu pagreičiu ir, nuvažiavęs 10 metrų, jo galutinis greitis yra 12 metrų per sekundę. Būtina rasti pradinį jo greitį.
     • Užsirašykime pradinius duomenis:
     • V i = ?, Vf= 12 m/s, a= 5 m/s 2, d= 10 m
   • Padėkime galutinį greitį kvadratu: V f 2= 12 2 = 144
   • Pagreitį padauginkite iš nuvažiuoto atstumo ir iš 2: 2*a*d = 2 * 5 * 10 = 100
   • Iš galutinio greičio kvadrato atimkite daugybos rezultatą: V f 2 – (2 * a * d) = 144 – 100 = 44
   • Paimkime gautos vertės kvadratinę šaknį: = √ = √44 = 6,633 V i= 6,633 m/s į šiaurę
   • Parašykite atsakymą tinkama forma. Turi būti nurodyti matavimo vienetai, t. y. metrai per sekundę arba m/s, taip pat objekto judėjimo kryptį. Jei nenurodysite krypties, atsakymas bus neišsamus, jame bus tik greičio reikšmė be informacijos, kuria kryptimi objektas juda.

Greitis yra fizinis dydis, apibūdinantis materialaus taško judėjimo greitį ir kryptį pasirinktos atskaitos sistemos atžvilgiu; pagal apibrėžimą lygus taško spindulio vektoriaus išvestinei laiko atžvilgiu.

Greitis plačiąja prasme yra bet kokio dydžio (nebūtinai spindulio vektoriaus) kitimo greitis priklausomai nuo kito (dažniau tai reiškia pokyčius laike, bet ir erdvėje ar bet kuriame kitame). Taigi, pavyzdžiui, jie kalba apie kampinį greitį, temperatūros kitimo greitį, cheminės reakcijos greitį, grupės greitį, jungimosi greitį ir kt. Matematiškai „pokyčio greitis“ apibūdinamas išvestine svarstomas kiekis.

Pagreitis žymimas greičio kitimo greičiu, tai yra pirmoji greičio išvestinė laiko atžvilgiu, vektorinis dydis, parodantis, kiek keičiasi kūno greičio vektorius jam judant per laiko vienetą:

pagreitis yra vektorius, tai yra, atsižvelgiama ne tik į greičio dydžio pokytį (vektoriaus kiekio dydį), bet ir į jo krypties pokytį. Visų pirma, kūno, judančio apskritimu pastoviu absoliučiu greičiu, pagreitis nėra lygus nuliui; kūnas patiria pastovaus dydžio (ir kintamo krypties) pagreitį, nukreiptą į apskritimo centrą (centripetalinis pagreitis).

Tarptautinėje vienetų sistemoje (SI) pagreičio vienetas yra metrai per sekundę per sekundę (m/s2, m/s2),

Pagreičio išvestinė laiko atžvilgiu, tai yra dydis, apibūdinantis pagreičio kitimo greitį, vadinamas trūkčiojimu:

Kur yra trūkčiojimo vektorius.

Pagreitis yra dydis, apibūdinantis greičio kitimo greitį.

Vidutinis pagreitis

Vidutinis pagreitis yra greičio pokyčio ir laikotarpio, per kurį šis pokytis įvyko, santykis. Vidutinį pagreitį galima nustatyti pagal formulę:

kur yra pagreičio vektorius.

Pagreičio vektoriaus kryptis sutampa su greičio kitimo kryptimi Δ = - 0 (čia 0 yra pradinis greitis, tai yra greitis, kuriuo kūnas pradėjo greitėti).

Laike t1 (žr. 1.8 pav.) kūno greitis yra 0. Laike t2 kūno greitis . Pagal vektorių atimties taisyklę randame greičio kitimo vektorių Δ = - 0. Tada pagreitį galima nustatyti taip:

SI pagreičio vienetas yra 1 metras per sekundę per sekundę (arba metras per sekundę kvadratu), tai yra

Metras per sekundę kvadratu lygus tiesia linija judančio taško pagreičiui, kuriam esant šio taško greitis per vieną sekundę padidėja 1 m/s. Kitaip tariant, pagreitis lemia, kiek kūno greitis pasikeičia per vieną sekundę. Pavyzdžiui, jei pagreitis yra 5 m/s2, tai reiškia, kad kūno greitis kas sekundę padidėja 5 m/s.

Momentinis pagreitis

Momentinis kūno (materialaus taško) pagreitis tam tikru laiko momentu yra fizinis dydis, lygus ribai, iki kurios vidutinis pagreitis linksta, kai laiko intervalas linkęs į nulį. Kitaip tariant, tai yra pagreitis, kurį kūnas sukuria per labai trumpą laiką:

Pagreičio kryptis taip pat sutampa su greičio kitimo kryptimi Δ labai mažoms laiko intervalo vertėms, per kurias vyksta greičio pokytis. Pagreičio vektorius gali būti nurodytas projekcijomis į atitinkamas koordinačių ašis tam tikroje atskaitos sistemoje (projekcijos aX, aY, aZ).

Esant pagreitėjusiam linijiniam judėjimui, kūno greitis didėja absoliučia verte, tai yra

o pagreičio vektoriaus kryptis sutampa su greičio vektoriumi 2.

Jei kūno greitis sumažėja absoliučia verte, tai yra

tada pagreičio vektoriaus kryptis yra priešinga greičio vektoriaus 2 krypčiai. Kitaip tariant, tokiu atveju judėjimas sulėtėja, o pagreitis bus neigiamas (ir< 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.

Normalus pagreitis yra pagreičio vektoriaus komponentas, nukreiptas išilgai normalės į judėjimo trajektoriją tam tikrame kūno trajektorijos taške. Tai yra, normalaus pagreičio vektorius yra statmenas tiesiniam judėjimo greičiui (žr. 1.10 pav.). Normalus pagreitis apibūdina greičio pokytį kryptimi ir žymimas raide n. Normalus pagreičio vektorius nukreiptas išilgai trajektorijos kreivės spindulį.

O kam to reikia? Mes jau žinome, kas yra atskaitos sistema, judėjimo reliatyvumas ir materialus taškas. Na, laikas judėti toliau! Čia apžvelgsime pagrindines kinematikos sąvokas, sudėliosime naudingiausias kinematikos pagrindų formules ir pateiksime praktinį problemos sprendimo pavyzdį.

Išspręskime šią problemą: taškas juda apskritimu, kurio spindulys yra 4 metrai. Jo judėjimo dėsnis išreiškiamas lygtimi S=A+Bt^2. A=8m, B=-2m/s^2. Kuriuo laiko momentu normalus taško pagreitis yra lygus 9 m/s^2? Raskite taško greitį, tangentinį ir bendrą pagreitį šiuo laiko momentu.

Sprendimas: žinome, kad norint rasti greitį, reikia paimti pirmą kartą judėjimo dėsnio išvestinę, o normalusis pagreitis yra lygus greičio kvadrato ir apskritimo, išilgai kurio taškas, spindulio daliniui. juda. Apsiginklavę šiomis žiniomis, surasime reikiamus kiekius.

Reikia pagalbos sprendžiant problemas? Profesionali studentų paslauga pasiruošusi tai suteikti.

Tačiau kūnas galėjo pradėti tolygiai pagreitintą judėjimą ne iš ramybės būsenos, o jau turėdamas tam tikrą greitį (arba jam buvo suteiktas pradinis greitis). Tarkime, naudodami jėgą mesti akmenį vertikaliai žemyn nuo bokšto. Tokį kūną veikia gravitacinis pagreitis, lygus 9,8 m/s2. Tačiau tavo jėga suteikė akmeniui dar daugiau greičio. Taigi galutinis greitis (liečiant žemę momentu) bus greičio, susidariusio dėl pagreičio, ir pradinio greičio suma. Taigi galutinis greitis bus rastas pagal formulę:

ties = v – v0
a = (v – v0)/t

Stabdymo atveju:

ties = v0 – v
a = (v0 – v)/t

Dabar spausdinkime

s = ½ * (v0 + v) * t

§ 5. Pagreitis

Kitas žingsnis kelyje į judesio lygtis yra dydžio, kuris yra susijęs su judėjimo greičio pasikeitimu, įvedimas. Natūralu klausti: kaip keičiasi judėjimo greitis? Ankstesniuose skyriuose nagrinėjome atvejį, kai veikianti jėga lėmė greičio pasikeitimą. Yra lengvųjų automobilių, kurie greitį padidina iš vietos. Tai žinodami galime nustatyti, kaip keičiasi greitis, bet tik vidutiniškai. Išspręskime kitą sudėtingesnį klausimą: kaip sužinoti greičio kitimo greitį. Kitaip tariant, kiek metrų per sekundę keičiasi greitis . Jau nustatėme, kad krintančio kūno greitis laikui bėgant kinta pagal formulę (žr. 8.4 lentelę), o dabar norime išsiaiškinti, kiek jis kinta . Šis dydis vadinamas pagreičiu.

Taigi pagreitis apibrėžiamas kaip greičio kitimo greitis. Su viskuo, kas pasakyta anksčiau, mes jau esame pakankamai pasiruošę iš karto įrašyti pagreitį kaip greičio išvestinę, kaip greitis rašomas kaip atstumo išvestinė. Jei dabar diferencijuosime formulę, gautume krintančio kūno pagreitį

(Diferencijuodami šią išraišką naudojome anksčiau gautą rezultatą. Pamatėme, kad išvestinė yra lygi tiesiog (konstanta). Jei šią konstantą pasirinksime lygiai 9,8, iškart pamatysime, kad išvestinė yra lygi 9.8.) Tai reiškia, kad krentančio kūno greitis nuolat didėja kas sekundę. Tą patį rezultatą galima gauti iš lentelės. 8.4. Kaip matote, krentančio kūno atveju viskas pasirodo gana paprastai, tačiau pagreitis, paprastai kalbant, nėra pastovus. Ji pasirodė esanti pastovi tik todėl, kad krintantį kūną veikianti jėga yra pastovi, o pagal Niutono dėsnį pagreitis turi būti proporcingas jėgai.

Kaip kitą pavyzdį, suraskime pagreitį problemoje, kurią jau sprendėme tirdami greitį:

.

Dėl greičio gavome formulę

Kadangi pagreitis yra greičio išvestinė laiko atžvilgiu, norint rasti jo vertę, reikia diferencijuoti šią formulę. Dabar prisiminkime vieną iš lentelės taisyklių. 8.3, būtent, kad sumos išvestinė yra lygi jos išvestinių sumai. Norėdami atskirti pirmąjį iš šių terminų, neperžiūrėsime visos ilgos procedūros, kurią darėme anksčiau, o tiesiog prisiminsime, kad diferencijuodami funkciją susidūrėme su tokiu kvadratiniu nariu, todėl koeficientas padvigubėjo ir pavirto į . Patys matote, kad dabar bus tas pats. Taigi išvestinė bus lygi . Dabar pereikime prie antrojo termino diferencijavimo. Pagal vieną iš lentelėje pateiktų taisyklių. 8.3, konstantos išvestinė bus lygi nuliui, todėl šis terminas neturės įtakos pagreičiui. Galutinis rezultatas: .

Išveskime dar dvi naudingas formules, gaunamas integruojant. Jei kūnas juda iš ramybės būsenos pastoviu pagreičiu, tai jo greitis bet kuriuo laiko momentu bus lygus

o iki šio laiko momento jo nuvažiuotas atstumas yra

Taip pat atkreipkime dėmesį, kad kadangi greitis yra , o pagreitis yra greičio išvestinė laiko atžvilgiu, galime rašyti

. (8.10)

Taigi dabar žinome, kaip rašomas antrasis vedinys.

Žinoma, tarp pagreičio ir atstumo yra atvirkštinis ryšys, kuris tiesiog išplaukia iš to, kad . Kadangi atstumas yra greičio integralas, jį galima rasti integruojant pagreitį du kartus. Visa ankstesnė diskusija buvo skirta judėjimui vienoje dimensijoje, o dabar trumpai apsistosime ties judėjimu trijų dimensijų erdvėje. Panagrinėkime dalelės judėjimą trimatėje erdvėje. Šis skyrius prasidėjo aptarimu apie vienmatį lengvojo automobilio judėjimą, ty klausimu, kiek automobilis yra toli nuo judėjimo pradžios įvairiais laiko momentais. Tada aptarėme greičio ir atstumo kitimo laike bei pagreičio ir greičio kitimo santykį. Pažiūrėkime į judėjimą trimis dimensijomis ta pačia seka. Tačiau lengviau pradėti nuo akivaizdesnio dvimačio atvejo ir tik tada apibendrinti iki trimačio atvejo. Nubrėžkime dvi tieses (koordinačių ašis), susikertančias stačiu kampu, ir nustatykime dalelės padėtį bet kuriuo laiko momentu atstumais nuo jos iki kiekvienos ašies. Taigi dalelės padėtis nurodoma dviem skaičiais (koordinatėmis) ir , kurių kiekvienas yra atitinkamai atstumas iki ašies ir iki ašies (8.3 pav.). Dabar galime apibūdinti judesį sukurdami, pavyzdžiui, lentelę, kurioje šios dvi koordinatės pateiktos kaip laiko funkcijos. (Apibendrinant trimačiu atveju reikia įvesti dar vieną ašį, statmeną pirmoms dviem, ir išmatuoti kitą koordinatę. Tačiau dabar atstumai imami ne iki ašių, o iki koordinačių plokštumų.) Kaip nustatyti dalelės greitį ? Norėdami tai padaryti, pirmiausia surandame greičio komponentus kiekviena kryptimi arba jo komponentus. Greičio horizontalioji dedamoji, arba -dedamoji, bus lygi koordinatės laiko išvestinei, t.y.

o vertikalus komponentas arba -komponentas yra lygus

Trijų matmenų atveju taip pat turite pridėti

8.3 pav. Kūno judėjimo plokštumoje aprašymas ir jo greičio skaičiavimas.

Kaip, žinant greičio komponentus, nustatyti bendrą greitį judėjimo kryptimi? Dviejų dimensijų atveju apsvarstykite dvi nuoseklias dalelės padėtis, atskirtas trumpu laiko intervalu ir atstumu . Iš pav. 8.3 aišku, kad

(8.14)

(Simbolis atitinka posakį „apytiksliai lygus“.) Vidutinis greitis per intervalą gaunamas paprastai padalijus: . Norėdami sužinoti tikslų greitį šiuo metu, turite, kaip jau buvo padaryta skyriaus pradžioje, nukreipti į nulį. Dėl to paaiškėja, kad

. (8.15)

Trimačiu atveju lygiai taip pat galima gauti

(8.16)

8.4 pav. Parabolė, kurią apibūdina krentantis kūnas, metamas horizontaliu pradiniu greičiu.

Pagreičius apibrėžiame taip pat, kaip ir greičius: pagreičio dedamoji apibrėžiama kaip greičio komponento išvestinė (t.y. antroji išvestinė laiko atžvilgiu) ir kt.

Pažvelkime į kitą įdomų mišraus judėjimo plokštumoje pavyzdį. Leiskite rutuliui judėti horizontaliai pastoviu greičiu ir tuo pat metu kristi vertikaliai žemyn su pastoviu pagreičiu. Kas tai per judėjimas? Kadangi ir todėl greitis yra pastovus, tada

o kadangi pagreitis žemyn yra pastovus ir lygus - , tai krintančio rutulio koordinatė pateikiama pagal formulę

Kokią kreivę apibūdina mūsų rutulys, t. y. koks ryšys tarp koordinačių ir ? Iš (8.18) lygties pagal (8.17) galime neįtraukti laiko, nes 1=*x/i%, po kurio randame

Tolygiai pagreitintas judėjimas be pradinio greičio

Šis koordinačių ryšys gali būti laikomas rutulio trajektorijos lygtimi. Jei pavaizduotume grafiškai, gautume kreivę, vadinamą parabole (8.4 pav.). Taigi bet koks laisvai krintantis kūnas, mestas tam tikra kryptimi, juda išilgai parabolės.

Tiesiai vienodai pagreitintame judesyje kūnas

1. juda įprasta tiesia linija,
2. jo greitis palaipsniui didėja arba mažėja,
3. per vienodus laiko tarpus greitis pasikeičia vienodai.

Pavyzdžiui, automobilis iš ramybės būsenos pradeda važiuoti tiesiu keliu, o iki, tarkime, 72 km/h greičio, juda tolygiai pagreitintas. Pasiekus nustatytą greitį, automobilis juda nekeisdamas greičio, t.y. tolygiai. Tolygiai paspartinus judesį, jo greitis padidėjo nuo 0 iki 72 km/val. Ir tegul greitis padidėja 3,6 km/h už kiekvieną judesio sekundę. Tada tolygiai pagreitinto automobilio judėjimo laikas bus lygus 20 sekundžių. Kadangi pagreitis SI matuojamas metrais per sekundę kvadratu, 3,6 km/h pagreitis turi būti konvertuojamas į atitinkamus vienetus. Jis bus lygus (3,6 * 1000 m) / (3600 s * 1 s) = 1 m/s2.

Tarkime, po kurio laiko važiuojant pastoviu greičiu automobilis pradėjo sulėtinti greitį, kad sustotų. Judėjimas stabdant taip pat buvo tolygiai pagreitintas (per vienodą laiką greitis sumažėjo tiek pat). Šiuo atveju pagreičio vektorius bus priešingas greičio vektoriui. Galima sakyti, kad pagreitis yra neigiamas.

Taigi, jei pradinis kūno greitis yra lygus nuliui, tada jo greitis po t sekundžių bus lygus pagreičio sandaugai ir šį kartą:

Kai kūnas krenta, gravitacijos pagreitis „veikia“, o kūno greitis pačiame žemės paviršiuje bus nustatytas pagal formulę:

Jei yra žinomas esamas kūno greitis ir laikas, kurio reikia tokiam greičiui išvystyti iš ramybės būsenos, tada pagreitį (t. y. kaip greitai pasikeitė greitis) galima nustatyti greitį padalijus iš laiko:

Tačiau kūnas galėjo pradėti tolygiai pagreitintą judėjimą ne iš ramybės būsenos, o jau turėdamas tam tikrą greitį (arba jam buvo suteiktas pradinis greitis).

Tarkime, naudodami jėgą mesti akmenį vertikaliai žemyn nuo bokšto. Tokį kūną veikia gravitacinis pagreitis, lygus 9,8 m/s2. Tačiau tavo jėga suteikė akmeniui dar daugiau greičio. Taigi galutinis greitis (liečiant žemę momentu) bus greičio, susidariusio dėl pagreičio, ir pradinio greičio suma. Taigi galutinis greitis bus rastas pagal formulę:

Tačiau jei akmuo buvo išmestas aukštyn. Tada jo pradinis greitis nukreipiamas aukštyn, o laisvojo kritimo pagreitis – žemyn. Tai yra, greičio vektoriai yra nukreipti priešingomis kryptimis. Tokiu atveju (taip pat ir stabdant) iš pradinio greičio reikia atimti pagreičio ir laiko sandaugą:

Iš šių formulių gauname pagreičio formules. Pagreičio atveju:

ties = v – v0
a = (v – v0)/t

Stabdymo atveju:

ties = v0 – v
a = (v0 – v)/t

Tuo atveju, kai kūnas sustoja vienodu pagreičiu, tada stabdymo momentu jo greitis yra 0. Tada formulė redukuojama į tokią formą:

Žinant pradinį kėbulo greitį ir stabdymo pagreitį, nustatomas laikas, po kurio kėbulas sustos:

Dabar spausdinkime Kelio, kurį kūnas nukeliauja tiesia linija vienodai pagreitinto judėjimo metu, formulės. Greičio ir laiko grafikas tiesiam tolygiam judėjimui yra atkarpa, lygiagreti laiko ašiai (dažniausiai imama x ašis). Kelias apskaičiuojamas kaip stačiakampio plotas po atkarpa.

Kaip rasti pagreitį žinant kelią ir laiką?

Tai yra, greitį padauginus iš laiko (s = vt). Esant tiesiam tolygiai pagreitintam judėjimui, grafikas yra tiesi linija, bet ne lygiagreti laiko ašiai. Ši tiesi linija arba didėja įsibėgėjant, arba mažėja stabdant. Tačiau kelias taip pat apibrėžiamas kaip paveikslo plotas po grafiku.

Tiesiame tolygiai pagreitintame judėjime ši figūra yra trapecija. Jo pagrindai yra atkarpa y ašyje (greitis) ir atkarpa, jungianti grafiko galinį tašką su jo projekcija x ašyje. Kraštinės yra greičio ir paties laiko ir jo projekcijos į x ašį (laiko ašies) grafikas. Projekcija į x ašį yra ne tik šoninė pusė, bet ir trapecijos aukštis, nes ji yra statmena jos pagrindams.

Kaip žinote, trapecijos plotas yra lygus pusei pagrindų ir aukščio sumos. Pirmosios bazės ilgis lygus pradiniam greičiui (v0), antrojo – galutiniam greičiui (v), o aukštis – laikui. Taip gauname:

s = ½ * (v0 + v) * t

Aukščiau buvo pateikta galutinio greičio priklausomybės nuo pradinio ir pagreičio formulė (v = v0 + at). Todėl kelio formulėje galime pakeisti v:

s = ½ * (v0 + v0 + at) * t = ½ * (2v0 + at) * t = ½ * t * 2v0 + ½ * t * at = v0t + 1/2at2

Taigi, nuvažiuotas atstumas nustatomas pagal formulę:

(Šią formulę galima gauti įvertinus ne trapecijos plotą, o susumavus stačiakampio ir stačiakampio, į kuriuos padalyta trapecija, plotus.)

Jei kūnas pradeda judėti tolygiai pagreitintas iš ramybės būsenos (v0 = 0), tada kelio formulė supaprastėja iki s = at2/2.

Jei pagreičio vektorius buvo priešingas greičiui, tada sandauga ties 2/2 turi būti atimta. Aišku, kad šiuo atveju skirtumas tarp v0t ir at2/2 neturėtų tapti neigiamas. Kai jis taps nuliu, kūnas sustos. Bus rastas stabdymo kelias. Aukščiau buvo formulė, nurodanti laiką iki visiško sustojimo (t = v0/a). Jei trajektorijos formulėje pakeisime reikšmę t, tada stabdymo kelias sumažinamas iki šios formulės:

I. Mechanika

Fizika->Kinematika->vienodai pagreitintas judėjimas->

Testavimas internetu

Tolygiai pagreitintas judesys

Šioje temoje apžvelgsime labai ypatingą netaisyklingo judesio tipą. Remiantis tolygiu judėjimu kontrastu, netolygus judėjimas yra judėjimas nevienodu greičiu bet kuria trajektorija. Koks yra tolygiai pagreitinto judėjimo ypatumas? Tai netolygus judėjimas, bet kuris "vienodai paspartintas". Pagreitį siejame su didėjančiu greičiu. Prisiminkime žodį „lygus“, gauname vienodą greičio padidėjimą. Kaip suprantame „vienodą greičio didėjimą“, kaip galime įvertinti, ar greitis didėja vienodai, ar ne? Norėdami tai padaryti, turime įrašyti laiką ir įvertinti greitį per tą patį laiko intervalą. Pavyzdžiui, automobilis pradeda judėti, per pirmas dvi sekundes išvysto iki 10 m/s greitį, per kitas dvi sekundes pasiekia 20 m/s, o dar po dviejų sekundžių jau juda greičiu 30 m/s. Kas dvi sekundes greitis didėja ir kaskart po 10 m/s. Tai tolygiai pagreitintas judėjimas.

Fizinis dydis, apibūdinantis, kiek kaskart didėja greitis, vadinamas pagreičiu.

Ar dviratininko judėjimas gali būti laikomas tolygiai pagreitėjusiu, jei sustojus jo greitis pirmą minutę yra 7 km/h, antrą – 9 km/h, trečią – 12 km/h? Tai uždrausta! Dviratininkas įsibėgėja, bet ne vienodai, iš pradžių įsibėgėjo 7 km/h (7-0), paskui 2 km/h (9-7), vėliau 3 km/h (12-9).

Paprastai judėjimas didėjant greičiui vadinamas pagreitintu judėjimu. Judėjimas mažėjant greičiui vadinamas sulėtintu. Tačiau fizikai bet kokį judėjimą su besikeičiančiu greičiu vadina pagreitintu judėjimu. Nesvarbu, ar automobilis pradeda judėti (greitis didėja!), ar stabdo (greitis mažėja!), bet kuriuo atveju jis juda su pagreičiu.

Tolygiai pagreitintas judesys- tai kūno judėjimas, kurio greitis bet kurį vienodą laiko tarpą pokyčius(gali padidėti arba mažėti) tas pats

Kūno pagreitis

Pagreitis apibūdina greičio kitimo greitį. Tai skaičius, kuriuo greitis keičiasi kas sekundę. Jei kūno pagreitis yra didelis, tai reiškia, kad kūnas greitai padidina greitį (greitėdamas) arba greitai jį praranda (stabdydamas). Pagreitis yra fizikinis vektorinis dydis, skaitiniu požiūriu lygus greičio pokyčio ir laiko periodo, per kurį šis pokytis įvyko, santykiui.

Kitoje užduotyje nustatykime pagreitį. Pradiniu laiko momentu laivo greitis buvo 3 m/s, pirmosios sekundės pabaigoje laivo greitis tapo 5 m/s, antrosios pabaigoje - 7 m/s, ties trečio pabaiga 9 m/s ir kt. Akivaizdu,. Bet kaip mes nustatėme? Mes žiūrime į greičio skirtumą per vieną sekundę. Pirmą sekundę 5-3=2, antrąją 7-5=2, trečią 9-7=2. Bet ką daryti, jei greičiai duoti ne kiekvienai sekundei? Tokia problema: pradinis laivo greitis 3 m/s, antros sekundės pabaigoje - 7 m/s, ketvirtos pabaigoje 11 m/s Šiuo atveju reikia 11-7 = 4, tada 4/2 = 2. Greičių skirtumą padalijame iš laiko periodo.

Ši formulė dažniausiai naudojama modifikuota forma sprendžiant problemas:

Formulė nėra parašyta vektorine forma, todėl „+“ ženklą rašome, kai kūnas įsibėgėja, ženklą „-“ – kai jis lėtėja.

Pagreičio vektoriaus kryptis

Pagreičio vektoriaus kryptis parodyta paveiksluose

Šiame paveiksle automobilis juda teigiama kryptimi išilgai Ox ašies, greičio vektorius visada sutampa su judėjimo kryptimi (nukreipta į dešinę).

Kaip rasti pagreitį žinant pradinį ir galutinį greitį ir kelią?

Kai pagreičio vektorius sutampa su greičio kryptimi, tai reiškia, kad automobilis greitėja. Pagreitis teigiamas.

Greitėjimo metu pagreičio kryptis sutampa su greičio kryptimi. Pagreitis teigiamas.

Šiame paveikslėlyje automobilis juda teigiama kryptimi išilgai Ox ašies, greičio vektorius sutampa su judėjimo kryptimi (nukreiptas į dešinę), pagreitis NESUTAPA su greičio kryptimi, tai reiškia, kad automobilis stabdo. Pagreitis yra neigiamas.

Stabdant pagreičio kryptis yra priešinga greičio krypčiai. Pagreitis yra neigiamas.

Išsiaiškinkime, kodėl stabdant pagreitis yra neigiamas. Pavyzdžiui, pirmą sekundę motorlaivis savo greitį sumažino nuo 9m/s iki 7m/s, antrąją iki 5m/s, trečią iki 3m/s. Greitis pasikeičia į „-2m/s“. 3-5=-2; 5-7=-2; 7-9=-2m/s. Iš čia atsiranda neigiama pagreičio vertė.

Spręsdamas problemas, jei kūnas sulėtėja, pagreitis keičiamas į formules su minuso ženklu!!!

Judėjimas tolygiai pagreitinto judėjimo metu

Papildoma formulė vadinama nesenstantis

Formulė koordinatėmis

Vidutinio greičio komunikacija

Esant tolygiai pagreitėjusiam judėjimui, vidutinį greitį galima apskaičiuoti kaip pradinio ir galutinio greičių aritmetinį vidurkį

Iš šios taisyklės seka formulė, kurią labai patogu naudoti sprendžiant daugelį problemų

Kelio santykis

Jei kūnas juda tolygiai pagreitintas, pradinis greitis yra lygus nuliui, tada keliai, nueiti vienodais laiko intervalais, yra susieti kaip nuosekli nelyginių skaičių serija.

Svarbiausia prisiminti

1) Kas yra tolygiai pagreitintas judėjimas;
2) Kas apibūdina pagreitį;
3) Pagreitis yra vektorius. Jei kūnas greitėja, pagreitis yra teigiamas, jei jis sulėtėja, pagreitis yra neigiamas;
3) Pagreičio vektoriaus kryptis;
4) Formulės, matavimo vienetai SI

Pratimai

Du traukiniai juda vienas kito link: vienas pagreitintu greičiu važiuoja į šiaurę, kitas lėtai juda į pietus. Kaip nukreipiamas traukinio pagreitis?

Lygiai į šiaurę. Kadangi pirmojo traukinio pagreitis sutampa su judėjimo kryptimi, o antrojo traukinio pagreitis yra priešingas judėjimui (lėtėja).

Traukinys juda tolygiai su pagreičiu a (a>0). Yra žinoma, kad ketvirtos sekundės pabaigoje traukinio greitis siekia 6 m/s. Ką galima pasakyti apie atstumą, įveiktą per ketvirtą sekundę? Ar šis kelias bus didesnis nei 6 m, mažesnis ar lygus?

Kadangi traukinys juda su pagreičiu, jo greitis visą laiką didėja (a>0). Jei ketvirtos sekundės pabaigoje greitis yra 6 m/s, tai ketvirtos sekundės pradžioje buvo mažesnis nei 6 m/s. Todėl ketvirtą sekundę traukinio įveikiamas atstumas nesiekia 6 m.

Kurios iš pateiktų priklausomybių apibūdina tolygiai pagreitintą judėjimą?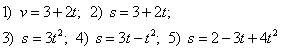

Judančio kūno greičio lygtis. Kokia yra atitinkama kelio lygtis?

* Pirmą sekundę automobilis įveikė 1 m, antrą 2 m, trečią 3 m, ketvirtą 4 m ir t.t. Ar tokį judėjimą galima laikyti tolygiai pagreitintu?

Vienodai pagreitintame judėjime keliai, nueiti vienodais laiko intervalais, yra susieti kaip nuosekli nelyginių skaičių serija. Vadinasi, aprašytas judesys nėra tolygiai pagreitintas.