TRIGONOMETRINIŲ FUNKCIJŲ VERČIŲ LENTELĖ
Trigonometrinių funkcijų verčių lentelė sudaryta 0, 30, 45, 60, 90, 180, 270 ir 360 laipsnių kampams ir atitinkamoms kampų reikšmėms vradianais. Iš trigonometrinių funkcijų lentelėje parodytas sinusas, kosinusas, liestinė, kotangentas, sekantas ir kosekantas. Kad būtų patogiau spręsti mokyklinius pavyzdžius, trigonometrinių funkcijų reikšmės lentelėje rašomos trupmenos pavidalu, išsaugant skaičių kvadratinės šaknies ištraukimo ženklus, o tai labai dažnai padeda sumažinti sudėtingas matematines išraiškas. Tangento ir kotangento atveju kai kurių kampų vertės negali būti nustatytos. Tokių kampų liestinės ir kotangento reikšmėms trigonometrinių funkcijų verčių lentelėje yra brūkšnys. Visuotinai pripažįstama, kad tokių kampų liestinė ir kotangentė yra lygi begalybei. Atskirame puslapyje yra trigonometrinių funkcijų mažinimo formulės.
Trigonometrinės funkcijos sinuso verčių lentelėje pateiktos šių kampų reikšmės: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 laipsniais, kurie atitinka to sin 0 pi, sin pi/6, sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi radianiniu kampų matu. Mokyklinis sinusų lentelė.
Trigonometrinės kosinuso funkcijos lentelėje pateiktos šių kampų vertės: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 laipsniais, o tai atitinka cos 0 pi , cos pi – 6, cos pi – 4, cos pi – 3, cos pi – 2, cos pi, cos 3 pi – 2, cos 2 pi – radianiniu kampų matu. Mokyklinė kosinusų lentelė.
Trigonometrinės liestinės funkcijos trigonometrinėje lentelėje pateikiamos šių kampų vertės: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 laipsniais, kurie atitinka tg 0 pi, tg pi/6, tg pi/4, tg pi/3, tg pi, tg 2 pi radianiniu kampų matu. Šios trigonometrinių liestinių funkcijų reikšmės neapibrėžtos tan 90, tan 270, tan pi/2, tan 3 pi/2 ir laikomos lygiomis begalybei.
Trigonometrinės funkcijos kotangentui trigonometrinėje lentelėje pateikiamos šių kampų reikšmės: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 laipsniais, o tai atitinka ctg pi/6, ctg pi/4 , ctg pi/3, tg pi/ 2, tan 3 pi/2 radianiniu kampų matu. Šios trigonometrinių kotangentų funkcijų reikšmės nėra apibrėžtos ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi ir laikomos lygiomis begalybei.
Trigonometrinių funkcijų sekantas ir kosekantas reikšmės pateikiamos tiems patiems kampams laipsniais ir radianais kaip sinusas, kosinusas, liestinė, kotangentas.

Nestandartinių kampų trigonometrinių funkcijų verčių lentelėje pateiktos sinuso, kosinuso, liestinės ir kotangento reikšmės kampams 15, 18, 22,5, 36, 54, 67,5 72 laipsniais ir radianais pi/12 , pi/10, pi/ 8, pi/5, 3pi/8, 2pi/5 radianai. Trigonometrinių funkcijų reikšmės išreiškiamos trupmenomis ir kvadratinėmis šaknimis, kad mokyklos pavyzdžiuose būtų lengviau sumažinti trupmenas.

Dar trys trigonometrijos monstrai. Pirmasis yra 1,5 pusantro laipsnio liestinė arba pi, padalintas iš 120. Antrasis yra pi kosinusas, padalintas iš 240, pi/240. Ilgiausias yra pi kosinusas, padalintas iš 17, pi/17.

Trigonometrinis sinuso ir kosinuso funkcijų reikšmių ratas vizualiai vaizduoja sinuso ir kosinuso ženklus, priklausomai nuo kampo dydžio. Ypač blondinėms kosinuso reikšmės yra pabrauktos žaliu brūkšneliu, kad būtų išvengta painiavos. Laipsnių perskaičiavimas į radianus taip pat labai aiškiai pateikiamas, kai radianai išreiškiami pi.

Šioje trigonometrinėje lentelėje pateikiamos sinuso, kosinuso, liestinės ir kotangento reikšmės kampams nuo 0 nulio iki 90 devyniasdešimt laipsnių vieno laipsnio intervalais. Pirmųjų keturiasdešimt penkių laipsnių trigonometrinių funkcijų pavadinimus reikia žiūrėti lentelės viršuje. Pirmajame stulpelyje yra laipsniai, sinusų, kosinusų, liestinių ir kotangentų reikšmės rašomos kituose keturiuose stulpeliuose.
Kampams nuo keturiasdešimt penkių laipsnių iki devyniasdešimties laipsnių trigonometrinių funkcijų pavadinimai rašomi lentelės apačioje. Paskutiniame stulpelyje yra laipsniai, kosinusų, sinusų, kotangentų ir liestinių reikšmės parašytos ankstesniuose keturiuose stulpeliuose. Turėtumėte būti atsargūs, nes trigonometrinės lentelės apačioje esančių trigonometrinių funkcijų pavadinimai skiriasi nuo pavadinimų lentelės viršuje. Sinusai ir kosinusai keičiami kaip tangentas ir kotangentas. Taip yra dėl trigonometrinių funkcijų verčių simetrijos.

Trigonometrinių funkcijų ženklai parodyti aukščiau esančiame paveikslėlyje. Sinusas turi teigiamas vertes nuo 0 iki 180 laipsnių arba nuo 0 iki pi. Sinusas turi neigiamas vertes nuo 180 iki 360 laipsnių arba nuo pi iki 2 pi. Kosinuso reikšmės yra teigiamos nuo 0 iki 90 ir 270 iki 360 laipsnių arba nuo 0 iki 1/2 pi ir 3/2 iki 2 pi. Tangentas ir kotangentas turi teigiamas reikšmes nuo 0 iki 90 laipsnių ir nuo 180 iki 270 laipsnių, atitinkančias reikšmes nuo 0 iki 1/2 pi ir pi iki 3/2 pi. Neigiamos tangento ir kotangento reikšmės yra nuo 90 iki 180 laipsnių ir nuo 270 iki 360 laipsnių arba nuo 1/2 pi iki pi ir nuo 3/2 pi iki 2 pi. Nustatydami trigonometrinių funkcijų požymius kampams, didesniems nei 360 laipsnių arba 2 pi, turėtumėte naudoti šių funkcijų periodiškumo savybes.
Trigonometrinės funkcijos sinusas, liestinė ir kotangentas yra nelyginės funkcijos. Šių funkcijų reikšmės neigiamiems kampams bus neigiamos. Kosinusas yra lygi trigonometrinė funkcija – neigiamo kampo kosinuso reikšmė bus teigiama. Dauginant ir dalijant trigonometrines funkcijas, reikia laikytis ženklų taisyklių.
Trigonometrinės sinusinės funkcijos verčių lentelėje pateikiamos šių kampų reikšmės
dokumentasAtskirame puslapyje yra sumažinimo formulės trigonometrinisfunkcijas. IN stalovertybesUžtrigonometrinisfunkcijassinusasduotavertybesUžsekančiąkampus: nuodėmė 0, nuodėmė 30, nuodėmė 45 ...
Siūlomas matematinis aparatas yra pilnas kompleksinio skaičiavimo, skirto n-mačių hiperkompleksiniams skaičiams, turintiems bet kokį laisvės laipsnių skaičių n, analogas ir skirtas matematiniam netiesinių modelių modeliavimui.
dokumentas... funkcijas lygus funkcijas vaizdai. Iš šios teoremos turėtų, Ką Už radus koordinates U, V, užtenka paskaičiuoti funkcija... geometrija; daugianaris funkcijas(daugiamačiai dvimačiai analogai trigonometrinisfunkcijas), jų savybes, lenteles ir taikymas; ...
-
Dėmesio!
Yra papildomų
Specialiajame 555 skyriuje nurodytos medžiagos.
Tiems, kurie labai „nelabai...“
Ir tiems, kurie „labai…“)Pirmiausia leiskite man priminti paprastą, bet labai naudingą pamokos „Kas yra sinusas ir kosinusas?
Tai yra išvestis:
Sinusas, kosinusas, liestinė ir kotangentas yra glaudžiai sujungti su savo kampais. Mes žinome vieną dalyką, vadinasi, žinome kitą.
Kitaip tariant, kiekvienas kampas turi savo pastovų sinusą ir kosinusą. Ir beveik kiekvienas turi savo tangentą ir kotangentą. Kodėl beveik? Daugiau apie tai žemiau.
Šios žinios labai padeda studijuojant! Yra daug užduočių, kai reikia pereiti nuo sinusų prie kampų ir atvirkščiai. Tam yra sinusų lentelė. Panašiai užduotims su kosinusu - kosinuso lentelė. Ir, kaip jau spėjote, yra liestinės lentelė Ir kotangentų lentelė.)
Lentelės yra skirtingos. Ilgieji, kur matai, kam lygus, tarkim, sin37°6’. Atidarome Bradis lenteles, ieškome trisdešimt septynių laipsnių šešių minučių kampo ir matome 0,6032 reikšmę. Akivaizdu, kad šio skaičiaus (ir tūkstančių kitų lentelės reikšmių) atsiminti visiškai nereikia.
Tiesą sakant, mūsų laikais ilgų kosinusų, sinusų, liestinių, kotangentų lentelių tikrai nereikia. Vienas geras skaičiuotuvas juos visiškai pakeičia. Tačiau nepakenks žinoti apie tokių lentelių egzistavimą. Dėl bendros erudicijos.)
Ir kodėl tada ši pamoka?! - klausi tu.
Bet kodėl. Tarp begalinio kampų skaičiaus yra ypatingas, apie kuriuos turėtumėte žinoti Visi. Visa mokyklos geometrija ir trigonometrija yra pastatyta ant šių kampų. Tai savotiška trigonometrijos „daugybos lentelė“. Jei nežinote, kas, pavyzdžiui, yra sin50°, niekas jūsų nesmerks.) Bet jei nežinote, kam yra sin30°, būkite pasirengę gauti užtarnautą du...
Tokie ypatingas Kampai taip pat gana geri. Mokykliniuose vadovėliuose paprastai maloniai siūloma išmokti mintinai sinuso lentelė ir kosinuso lentelė septyniolikai kampų. Ir, žinoma, liestinių lentelė ir kotangentų lentelė tiems patiems septyniolikai kampų... t.y. Siūloma įsiminti 68 reikšmes. Kurie, beje, labai panašūs vienas į kitą, karts nuo karto kartojasi ir keičia ženklus. Žmogui, neturinčiam tobulos regėjimo atminties, tai nemaža užduotis...)
Eisime kitu maršrutu. Įprastą įsiminimą pakeiskime logika ir išradingumu. Tada turėsime įsiminti 3 (tris!) sinusų lentelės ir kosinusų lentelės reikšmes. Ir 3 (trys!) liestinių lentelės ir kotangentų lentelės reikšmės. Tai viskas. Šešias reikšmes lengviau atsiminti nei 68, man atrodo...)
Visas kitas reikalingas vertes iš šių šešių gausime naudodami galingą teisinį kodų lapą - trigonometrinis ratas. Jei nestudijavote šios temos, sekite nuorodą, nepatingėkite. Šis būrelis reikalingas ne tik šiai pamokai. Jis nepakeičiamas visai trigonometrijai iš karto. Nenaudoti tokio įrankio yra tiesiog nuodėmė! Nenori? Tai tavo reikalas. Įsimink sinusų lentelė. Kosinusų lentelė. Tangentų lentelė. Kotangentų lentelė. Visos 68 vertės įvairiems kampams.)
Taigi pradėkime. Pirmiausia visus šiuos specialius kampus padalinkime į tris grupes.
Pirmoji kampų grupė.
Panagrinėkime pirmąją grupę septyniolika kampų ypatingas. Tai yra 5 kampai: 0°, 90°, 180°, 270°, 360°.
Štai kaip atrodo sinusų, kosinusų, liestinių ir kotangentų lentelė šiems kampams:
Kampas x
(laipsniais)0
90
180
270
360
Kampas x
(radianais)0
nuodėmė x
0
1
0
-1
0
cos x
1
0
-1
0
1
tg x
0
daiktavardis
0
daiktavardis
0
ctg x
daiktavardis
0
daiktavardis
0
daiktavardis
Kas nori prisiminti, prisimink. Bet iš karto pasakysiu, kad visi šie vienetai ir nuliai labai susipainioja mano galvoje. Daug stipresnis nei norite.) Todėl įjungiame logiką ir trigonometrinį apskritimą.
Nubrėžiame apskritimą ir pažymime jame tuos pačius kampus: 0°, 90°, 180°, 270°, 360°. Šiuos kampus pažymėjau raudonais taškais:

Iš karto akivaizdu, kuo šie kampai ypatingi. Taip! Tai yra kampai, kurie krenta tiksliai koordinačių ašyje! Tiesą sakant, dėl to žmonės ir susipainioja... Bet mes nesusipainiosime. Išsiaiškinkime, kaip rasti šių kampų trigonometrines funkcijas be didelio įsiminimo.
Beje, kampo padėtis yra 0 laipsnių visiškai sutampa su 360 laipsnių kampo padėtimi. Tai reiškia, kad šių kampų sinusai, kosinusai ir liestinės yra visiškai vienodi. Aš pažymėjau 360 laipsnių kampą, kad užbaigčiau apskritimą.
Tarkime, sunkioje įtemptoje Vieningojo valstybinio egzamino aplinkoje kažkaip suabejojote... Koks yra 0 laipsnių sinusas? Atrodo lyg nulis... O jeigu tai vienas?! Mechaninis įsiminimas yra toks dalykas. Atšiauriomis sąlygomis pradeda kamuoti abejonės...)
Ramiai, tik ramiai!) Pasakysiu praktinę techniką, kuri duos 100% teisingą atsakymą ir visiškai pašalins visas abejones.
Kaip pavyzdį išsiaiškinkime, kaip aiškiai ir patikimai nustatyti, tarkime, 0 laipsnių sinusą. Ir tuo pačiu kosinusas 0. Kaip bebūtų keista, būtent šiose vertybėse žmonės dažnai susipainioja.
Norėdami tai padaryti, pieškite ant apskritimo savavališkas kampe X. Pirmąjį ketvirtį buvo arti 0 laipsnių. Ant ašių pažymėkime šio kampo sinusus ir kosinusus X, viskas gerai. kaip tai:
O dabar – dėmesio! Sumažinkime kampą X, judančiąją pusę priartinkite prie ašies Oi. Užveskite pelės žymeklį ant nuotraukos (arba bakstelėkite paveikslėlį planšetiniame kompiuteryje) ir pamatysite viską.
Dabar įjunkime elementarią logiką! Pažiūrėkime ir pagalvokime: Kaip sinx elgiasi mažėjant kampui x? Kai kampas artėja prie nulio? Tai mažėja! Ir cosx didėja! Belieka išsiaiškinti, kas atsitiks su sinusu, kai kampas visiškai subyrės? Kada judanti kampo pusė (taškas A) nusėda ant OX ašies ir kampas tampa lygus nuliui? Akivaizdu, kad kampo sinusas bus lygus nuliui. O kosinusas padidės iki... iki... Koks yra judančios kampo pusės ilgis (trigonometrinio apskritimo spindulys)? Vienas!
Štai atsakymas. 0 laipsnių sinusas yra lygus 0. 0 laipsnių kosinusas lygus 1. Visiškai geležinis ir be jokių abejonių!) Tiesiog todėl, kad kitaip tai negali būti.
Lygiai taip pat galite sužinoti (arba patikslinti), pavyzdžiui, 270 laipsnių sinusą. Arba kosinusas 180. Nubrėžkite apskritimą, savavališkas kampą per ketvirtį šalia mus dominančios koordinačių ašies, mintyse perkelkite kampo kraštinę ir suvokkite, kuo pavirs sinusas ir kosinusas kampo kraštinei nukritus ant ašies. Tai viskas.
Kaip matote, šiai kampų grupei nieko nereikia įsiminti. Čia nereikia sinusų lentelė... Taip ir kosinuso lentelė- taip pat.) Beje, keletą kartų panaudojus trigonometrinį apskritimą, visos šios reikšmės bus prisimintos pačios. O jei pamiršta, per 5 sekundes nubrėžiau apskritimą ir jį išskaičiau. Daug lengviau nei paskambinti draugui iš tualeto ir rizikuoti savo pažymėjimu, tiesa?)
Kalbant apie tangentą ir kotangentą, viskas yra tas pats. Ant apskritimo nubrėžiame liestinę (kotangentinę) liniją – ir viskas iš karto matosi. Kur jie lygūs nuliui, o kur jų nėra. Ką, jūs nežinote apie liestinės ir kotangentines linijas? Tai liūdna, bet pataisoma.) Mes aplankėme 555 sekciją trigonometrinio apskritimo liestinė ir kotangentas – ir nėra jokių problemų!
Jei sugalvojote, kaip aiškiai apibrėžti sinusą, kosinusą, liestinę ir kotangentą šiems penkiems kampams, sveikiname! Tik tuo atveju informuoju, kad dabar galite apibrėžti funkcijas bet kokie kampai, krintantys ant ašių. Ir tai yra 450°, ir 540°, ir 1800°, ir begalė kitų...) Suskaičiavau (teisingai!) kampą ant apskritimo - ir su funkcijomis problemų nėra.
Bet kaip tik matuojant kampus atsiranda problemų ir klaidų... Kaip jų išvengti, parašyta pamokoje: Kaip nubrėžti (suskaičiuoti) bet kurį trigonometrinio apskritimo kampą laipsniais. Elementaru, bet labai naudinga kovojant su klaidomis.)
Štai pamoka: kaip nubrėžti (išmatuoti) bet kokį kampą trigonometriniame apskritime radianais – bus vėsiau. Kalbant apie galimybes. Tarkime, nustatykite, į kurią iš keturių pusiau ašių patenka kampas
galite tai padaryti per kelias sekundes. Aš nejuokauju! Vos per porą sekundžių. Na, žinoma, ne tik 345 pi...) Ir 121, ir 16, ir -1345. Greitam atsakymui tinka bet koks sveikasis koeficientas.
O jei kampas
Tik pagalvok! Teisingas atsakymas gaunamas per 10 sekundžių. Bet kuri radianų trupmeninė vertė, kurios vardiklyje yra du.
Tiesą sakant, tai yra gerai apie trigonometrinį apskritimą. Kadangi gebėjimas dirbti su kai kurie kampuose jis automatiškai išsiplečia begalinis rinkinys kampus
Taigi, mes sutvarkėme penkis kampus iš septyniolikos.
Antroji kampų grupė.
Kita kampų grupė yra 30°, 45° ir 60° kampai. Kodėl būtent šie, o ne, pavyzdžiui, 20, 50 ir 80? Taip, kažkaip taip išėjo... Istoriškai.) Toliau pažiūrėsime, kodėl šie kampai yra geri.
Šių kampų sinusų kosinusų liestinių kotangentų lentelė atrodo taip:
Kampas x
(laipsniais)0
30
45
60
90
Kampas x
(radianais)0
nuodėmė x
0
1
cos x
1
0
tg x
0
1
daiktavardis
ctg x
daiktavardis
1
0
Palikau 0° ir 90° vertes iš ankstesnės lentelės, kad užbaigčiau paveikslėlį.) Kad matytumėte, kad šie kampai yra pirmajame ketvirtyje ir didėja. Nuo 0 iki 90. Tai mums pravers vėliau.
Reikia atsiminti lentelėje pateiktas 30°, 45° ir 60° kampų vertes. Jei norite, įsiminkite. Tačiau ir čia yra galimybė palengvinti savo gyvenimą.) Atkreipkite dėmesį į sinusinės lentelės reikšmėsšie kampai. Ir palyginkite su kosinusų lentelės reikšmės...
Taip! Jie tie patys! Tiesiog išdėstyta atvirkštine tvarka. Kampai didėja (0, 30, 45, 60, 90) ir sinuso reikšmės padidinti nuo 0 iki 1. Galite patikrinti skaičiuotuvu. O kosinuso reikšmės yra mažėja nuo 1 iki nulio. Be to, pačios vertybės tie patys. 20, 50, 80 kampams tai neveiks...
Tai naudinga išvada. Užteks mokytis trys 30, 45, 60 laipsnių kampų vertės. Ir atminkite, kad dėl sinuso jie didėja, o dėl kosinuso – mažėja. Sinuso link.) Jie susikerta pusiaukelėje (45°), tai yra, 45 laipsnių sinusas yra lygus 45 laipsnių kosinusui. Ir tada jie vėl išsiskiria... Tris reikšmes galima išmokti, tiesa?
Su tangentais – kotangentais vaizdas lygiai toks pat. Vienas prieš vieną. Tik reikšmės skiriasi. Šias vertybes (dar tris!) taip pat reikia išmokti.
Na, beveik visas įsiminimas baigėsi. Jūs (tikiuosi) supratote, kaip nustatyti penkių kampų, kurie patenka į ašį, vertes ir sužinojote 30, 45, 60 laipsnių kampų vertes. Iš viso 8.
Belieka susitvarkyti su paskutine 9 kampų grupe.
Tai yra kampai:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Šiems kampams reikia žinoti sinusų lentelę, kosinusų lentelę ir kt.Košmaras, tiesa?)
O jei čia pridėsite kampų, tokių kaip: 405°, 600° arba 3000° ir daug, daug vienodai gražių?)
Arba kampai radianais? Pavyzdžiui, apie kampus:

ir daugelis kitų, kuriuos turėtumėte žinoti Visi.
Juokingiausia tai žinoti Visi - iš principo neįmanoma. Jei naudojate mechaninę atmintį.
Ir tai labai paprasta, iš tikrųjų elementaru - jei naudojate trigonometrinį apskritimą. Įpratę dirbti su trigonometriniu apskritimu, visi šie baisūs kampai laipsniais gali būti lengvai ir elegantiškai sumažinti iki gerų senamadiškų:
Beje, turiu jums dar keletą įdomių svetainių.)
Galite praktikuotis spręsdami pavyzdžius ir sužinoti savo lygį. Testavimas su momentiniu patvirtinimu. Mokykimės – su susidomėjimu!)
Galite susipažinti su funkcijomis ir išvestinėmis.
Sinuso (), kosinuso (), liestinės (), kotangento () sąvokos yra neatsiejamai susijusios su kampo sąvoka. Norėdami gerai suprasti šias, iš pirmo žvilgsnio, sudėtingas sąvokas (kurios daugeliui moksleivių kelia siaubą) ir įsitikinti, kad „velnias nėra toks baisus, koks jis yra nupieštas“, pradėkime nuo pradžioje ir suprasti kampo sąvoką.
Kampo samprata: radianas, laipsnis
Pažiūrėkime į paveikslėlį. Vektorius tam tikru dydžiu „pasuko“ taško atžvilgiu. Taigi šio sukimosi matas pradinės padėties atžvilgiu bus kampe.
Ką dar reikia žinoti apie kampo sąvoką? Na, kampo vienetai, žinoma!
Kampas tiek geometrijoje, tiek trigonometrijoje gali būti matuojamas laipsniais ir radianais.
Kampas (vienas laipsnis) yra centrinis apskritimo kampas, kurį sudaro apskritimo lankas, lygus apskritimo daliai. Taigi visas apskritimas susideda iš apskritimo lankų „gabalų“ arba apskritimo aprašytas kampas yra lygus.

Tai yra, aukščiau pateiktame paveikslėlyje parodytas kampas, lygus, tai yra, šis kampas remiasi apskritimo lanku, kurio dydis yra apskritimas.
Kampas radianais yra centrinis apskritimo kampas, sudarytas iš apskritimo lanko, kurio ilgis lygus apskritimo spinduliui. Na, ar sugalvojai? Jei ne, tada išsiaiškinkime tai iš piešinio.

Taigi paveiksle parodytas kampas, lygus radianui, tai yra, šis kampas remiasi apskritimo lanku, kurio ilgis lygus apskritimo spinduliui (ilgis lygus ilgiui arba spindulys lygus apskritimo spinduliui). lanko ilgis). Taigi, lanko ilgis apskaičiuojamas pagal formulę:
Kur yra centrinis kampas radianais.
Na, žinodamas tai, ar galite atsakyti, kiek radianų yra apskritimo aprašytame kampe? Taip, tam reikia atsiminti apskritimo formulę. Štai jis:
Na, dabar suderinkime šias dvi formules ir išsiaiškinkime, kad apskritimu aprašytas kampas yra lygus. Tai yra, koreliuodami vertę laipsniais ir radianais, tai gauname. Atitinkamai,. Kaip matote, skirtingai nei "laipsniai", žodis "radianas" yra praleistas, nes matavimo vienetas paprastai yra aiškus iš konteksto.
Kiek ten radianų? Teisingai!
Supratai? Tada eikite į priekį ir pataisykite:
Turite sunkumų? Tada žiūrėk atsakymai:
Statusis trikampis: sinusas, kosinusas, liestinė, kampo kotangentas
Taigi, mes išsiaiškinome kampo sąvoką. Bet kas yra kampo sinusas, kosinusas, tangentas ir kotangentas? Išsiaiškinkime. Norėdami tai padaryti, mums padės stačiakampis trikampis.

Kaip vadinamos stačiojo trikampio kraštinės? Teisingai, hipotenuzė ir kojos: hipotenuzė yra pusė, esanti priešais stačią kampą (mūsų pavyzdyje tai yra pusė); kojos yra dvi likusios pusės ir (tos, esančios greta stačiojo kampo), o jei svarstysime kojas kampo atžvilgiu, tada koja yra gretima koja, o koja yra priešinga. Taigi, dabar atsakykime į klausimą: kas yra kampo sinusas, kosinusas, tangentas ir kotangentas?
Kampo sinusas- tai yra priešingos (tolimos) kojos ir hipotenuzės santykis.
Mūsų trikampyje.
Kampo kosinusas- tai gretimos (artimos) kojos ir hipotenuzės santykis.
Mūsų trikampyje.
Kampo liestinė- tai priešingos (tolimos) pusės ir gretimos (artimos) santykis.
Mūsų trikampyje.
Kampo kotangentas- tai gretimos (artimos) kojos ir priešingos (toli) santykis.
Mūsų trikampyje.
Šie apibrėžimai yra būtini prisiminti! Kad būtų lengviau atsiminti, kurią koją į ką padalinti, turite tai aiškiai suprasti liestinė Ir kotangentas sėdi tik kojos, o hipotenuzė atsiranda tik viduje sinusas Ir kosinusas. Ir tada galite sugalvoti asociacijų grandinę. Pavyzdžiui, šis:
Kosinusas→lietimas→lietimas→gretima;
Kotangentas→lietimas→lietimas→gretima.
Visų pirma, reikia atsiminti, kad sinusas, kosinusas, liestinė ir kotangentas, nes trikampio kraštinių santykiai nepriklauso nuo šių kraštinių ilgių (tuo pačiu kampu). Netikite manimi? Tada įsitikinkite, žiūrėdami į paveikslėlį:

Apsvarstykite, pavyzdžiui, kampo kosinusą. Pagal apibrėžimą iš trikampio: , bet kampo kosinusą galime apskaičiuoti iš trikampio: . Matote, kraštinių ilgiai skirtingi, bet vieno kampo kosinuso reikšmė vienoda. Taigi sinuso, kosinuso, liestinės ir kotangento reikšmės priklauso tik nuo kampo dydžio.
Jei suprantate apibrėžimus, eikite į priekį ir sutvirtinkite juos!
Žemiau esančiame paveikslėlyje parodytam trikampiui randame.

Na, ar gavai? Tada pabandykite patys: apskaičiuokite tą patį kampą.
Vienetinis (trigonometrinis) apskritimas
Suprasdami laipsnio ir radiano sąvokas, laikėme apskritimą, kurio spindulys lygus. Toks ratas vadinamas vienišas. Tai bus labai naudinga studijuojant trigonometriją. Todėl pažvelkime į tai šiek tiek išsamiau.

Kaip matote, šis apskritimas sudarytas Dekarto koordinačių sistemoje. Apskritimo spindulys lygus vienetui, o apskritimo centras yra koordinačių pradžioje, spindulio vektoriaus pradinė padėtis fiksuojama išilgai teigiamos ašies krypties (mūsų pavyzdyje tai yra spindulys).
Kiekvienas apskritimo taškas atitinka du skaičius: ašies koordinatę ir ašies koordinatę. Kas yra šie koordinačių skaičiai? Ir apskritai, ką jie turi bendro su nagrinėjama tema? Norėdami tai padaryti, turime prisiminti apie svarstomą stačiakampį trikampį. Viršuje esančiame paveikslėlyje galite pamatyti du ištisus stačiuosius trikampius. Apsvarstykite trikampį. Jis yra stačiakampis, nes yra statmenas ašiai.
Kam lygus trikampis? tai tiesa. Be to, mes žinome, kad yra vieneto apskritimo spindulys, o tai reiškia . Pakeiskime šią reikšmę kosinuso formulėje. Štai kas nutinka:
Kam lygus trikampis? Na žinoma! Pakeiskite spindulio reikšmę į šią formulę ir gaukite:
Taigi, ar galite pasakyti, kokias koordinates turi apskritimui priklausantis taškas? Na, niekaip? Ką daryti, jei jūs tai suprantate ir esate tik skaičiai? Kurią koordinatę ji atitinka? Na, žinoma, koordinatės! O kokią koordinatę tai atitinka? Teisingai, koordinatės! Taigi, laikotarpis.

Kas tada yra ir kas yra lygūs? Teisingai, naudokime atitinkamus liestinės ir kotangento apibrėžimus ir gaukime, kad a.
O jei kampas didesnis? Pavyzdžiui, kaip šiame paveikslėlyje:

Kas pasikeitė šiame pavyzdyje? Išsiaiškinkime. Norėdami tai padaryti, vėl pasukite į stačiakampį trikampį. Apsvarstykite statųjį trikampį: kampas (kaip greta kampo). Kokios yra kampo sinuso, kosinuso, tangento ir kotangento reikšmės? Taip, mes laikomės atitinkamų trigonometrinių funkcijų apibrėžimų:
Na, kaip matote, kampo sinuso reikšmė vis tiek atitinka koordinatę; kampo kosinuso reikšmė – koordinatė; ir atitinkamų santykių liestinės ir kotangento reikšmės. Taigi šie santykiai taikomi bet kokiam spindulio vektoriaus pasukimui.
Jau buvo minėta, kad pradinė spindulio vektoriaus padėtis yra išilgai teigiamos ašies krypties. Iki šiol mes sukome šį vektorių prieš laikrodžio rodyklę, bet kas atsitiks, jei pasuksime jį pagal laikrodžio rodyklę? Nieko nepaprasto, taip pat gausite tam tikros vertės kampą, bet tik jis bus neigiamas. Taigi, sukdami spindulio vektorių prieš laikrodžio rodyklę, gauname teigiami kampai, o sukant pagal laikrodžio rodyklę - neigiamas.
Taigi, mes žinome, kad visas spindulio vektoriaus apsisukimas aplink apskritimą yra arba. Ar galima pasukti spindulio vektorių į arba į? Na, žinoma, galite! Todėl pirmuoju atveju spindulio vektorius padarys vieną pilną apsisukimą ir sustos padėtyje arba.
Antruoju atveju, tai yra, spindulio vektorius padarys tris pilnus apsisukimus ir sustos padėtyje arba.
Taigi iš aukščiau pateiktų pavyzdžių galime daryti išvadą, kad kampai, kurie skiriasi arba (kur yra bet koks sveikas skaičius), atitinka tą pačią spindulio vektoriaus padėtį.
Žemiau esančiame paveikslėlyje parodytas kampas. Tas pats vaizdas atitinka kampą ir pan. Šį sąrašą galima tęsti neribotą laiką. Visi šie kampai gali būti parašyti pagal bendrą formulę arba (kur yra bet koks sveikasis skaičius)

Dabar, žinodami pagrindinių trigonometrinių funkcijų apibrėžimus ir naudodami vieneto apskritimą, pabandykite atsakyti, kokios yra reikšmės:
Štai vieneto ratas, kuris jums padės:

Turite sunkumų? Tada išsiaiškinkime. Taigi mes žinome, kad:
Iš čia nustatome taškų koordinates, atitinkančias tam tikrus kampo matmenis. Na, pradėkime iš eilės: kampas ties atitinka tašką su koordinatėmis, todėl:
Neegzistuoja;
Be to, laikydamiesi tos pačios logikos, sužinome, kad kampai atitinka atitinkamai taškus su koordinatėmis. Tai žinant, nesunku nustatyti trigonometrinių funkcijų reikšmes atitinkamuose taškuose. Pirmiausia išbandykite patys, o tada patikrinkite atsakymus.
Atsakymai:
Neegzistuoja
Neegzistuoja
Neegzistuoja
Neegzistuoja
Taigi galime sudaryti tokią lentelę:

Nereikia atsiminti visų šių vertybių. Pakanka prisiminti vienetinio apskritimo taškų koordinačių ir trigonometrinių funkcijų verčių atitikimą:
Tačiau kampų trigonometrinių funkcijų reikšmės ir, pateiktos toliau esančioje lentelėje, reikia atsiminti:

Nebijokite, dabar parodysime vieną pavyzdį gana paprasta atsiminti atitinkamas reikšmes:
Norint naudoti šį metodą, labai svarbu atsiminti visų trijų kampo matmenų sinuso reikšmes (), taip pat kampo liestinės reikšmę. Žinant šias vertes, gana paprasta atkurti visą lentelę - kosinuso reikšmės perkeliamos pagal rodykles, tai yra:
Žinodami tai, galite atkurti reikšmes. Skaitiklis „ “ atitiks, o vardiklis „ “. Kotangentinės vertės perkeliamos pagal paveikslėlyje nurodytas rodykles. Jei tai suprasite ir atsimenate diagramą su rodyklėmis, pakaks atsiminti visas lentelės reikšmes.
Apskritimo taško koordinatės
Ar įmanoma apskritime rasti tašką (jo koordinates), žinant apskritimo centro koordinates, jo spindulį ir sukimosi kampą?
Na, žinoma, galite! Išmeskime bendroji taško koordinačių radimo formulė.
Pavyzdžiui, priešais mus yra apskritimas:

Mums duota, kad taškas yra apskritimo centras. Apskritimo spindulys lygus. Reikia rasti taško koordinates, gautas sukant tašką laipsniais.
Kaip matyti iš paveikslo, taško koordinatė atitinka atkarpos ilgį. Atkarpos ilgis atitinka apskritimo centro koordinatę, tai yra lygus. Atkarpos ilgį galima išreikšti naudojant kosinuso apibrėžimą:
Tada mes turime tai taško koordinatei.
Naudodami tą pačią logiką randame taško y koordinatės reikšmę. Taigi,
Taigi, apskritai taškų koordinatės nustatomos pagal formules:
Apskritimo centro koordinatės,
Apskritimo spindulys,
Vektoriaus spindulio sukimosi kampas.
Kaip matote, mūsų svarstomo vieneto apskritimo formulės yra žymiai sumažintos, nes centro koordinatės yra lygios nuliui, o spindulys yra lygus vienetui:
Na, pabandykime šias formules praktikuodami surasti taškus apskritime?
1. Raskite vienetinio apskritimo taško koordinates, gautas sukant tašką į.
2. Raskite vienetinio apskritimo taško koordinates, gautą sukant tašką.
3. Raskite vienetinio apskritimo taško koordinates, gautas sukant tašką į.
4. Taškas yra apskritimo centras. Apskritimo spindulys lygus. Reikia rasti taško, gauto pasukus pradinį spindulio vektorių, koordinates.
5. Taškas yra apskritimo centras. Apskritimo spindulys lygus. Reikia rasti taško, gauto pasukus pradinį spindulio vektorių, koordinates.
Sunku rasti apskritimo taško koordinates?
Išspręskite šiuos penkis pavyzdžius (arba išmokite juos išspręsti) ir išmoksite juos rasti!
1.
Galite tai pastebėti. Bet mes žinome, kas atitinka visišką pradinio taško revoliuciją. Taigi norimas taškas bus toje pačioje padėtyje kaip ir sukant. Tai žinodami randame reikiamas taško koordinates:
2. Vieneto apskritimo centras yra taške, o tai reiškia, kad galime naudoti supaprastintas formules:
Galite tai pastebėti. Mes žinome, kas atitinka du pilnus pradinio taško apsisukimus. Taigi norimas taškas bus toje pačioje padėtyje kaip ir sukant. Tai žinodami randame reikiamas taško koordinates:
Sinusas ir kosinusas yra lentelės reikšmės. Prisimename jų reikšmes ir gauname:
Taigi norimas taškas turi koordinates.
3. Vieneto apskritimo centras yra taške, o tai reiškia, kad galime naudoti supaprastintas formules:
Galite tai pastebėti. Pavaizduokime nagrinėjamą pavyzdį paveikslėlyje:

Spindulys sudaro kampus, lygius ašiai ir su ja. Žinodami, kad kosinuso ir sinuso lentelės reikšmės yra lygios, ir nustatę, kad kosinusas čia turi neigiamą reikšmę, o sinusas – teigiamą, turime:
Tokie pavyzdžiai išsamiau aptariami temoje tiriant trigonometrinių funkcijų mažinimo formules.
Taigi norimas taškas turi koordinates.
4.
Vektoriaus spindulio sukimosi kampas (pagal sąlygą)
Norėdami nustatyti atitinkamus sinuso ir kosinuso ženklus, sudarome vienetinį apskritimą ir kampą:

Kaip matote, vertė, tai yra, yra teigiama, o vertė, tai yra, yra neigiama. Žinodami atitinkamų trigonometrinių funkcijų lentelių reikšmes, gauname, kad:
Pakeiskime gautas reikšmes į savo formulę ir suraskime koordinates:
Taigi norimas taškas turi koordinates.
5. Norėdami išspręsti šią problemą, naudojame formules bendra forma, kur
Apskritimo centro koordinatės (mūsų pavyzdyje
Apskritimo spindulys (pagal sąlygą)
Vektoriaus spindulio sukimosi kampas (pagal sąlygą).
Pakeiskime visas reikšmes į formulę ir gaukime:
ir - lentelės reikšmės. Prisiminkime ir pakeiskime juos į formulę:
Taigi norimas taškas turi koordinates.
SANTRAUKA IR PAGRINDINĖS FORMULĖS
Kampo sinusas yra priešingos (tolimosios) kojos ir hipotenuzės santykis.
Kampo kosinusas yra gretimos (artimos) kojos ir hipotenuzės santykis.
Kampo liestinė yra priešingos (tolimosios) pusės ir gretimos (artimos) pusės santykis.
Kampo kotangentas yra gretimos (artimos) pusės ir priešingos (tolimosios) pusės santykis.
Trigonometrijos tyrimą pradėsime nuo stačiojo trikampio. Apibrėžkime, kas yra sinusas ir kosinusas, taip pat smailiojo kampo liestinė ir kotangentas. Tai yra trigonometrijos pagrindai.
Prisiminkime tai stačiu kampu yra kampas, lygus 90 laipsnių. Kitaip tariant, pusė pasukto kampo.
Aštrus kampas- mažiau nei 90 laipsnių.
Bukas kampas- didesnis nei 90 laipsnių. Kalbant apie tokį kampą, „bukas“ yra ne įžeidimas, o matematinis terminas :-)
Nubrėžkime statųjį trikampį. Status kampas paprastai žymimas . Atkreipkite dėmesį, kad priešinga kampo pusė pažymėta ta pačia raide, tik maža. Taigi, priešinga kampas A yra pažymėtas .
Kampas žymimas atitinkama graikiška raide.

Hipotenuzė stačiojo trikampio kraštinė yra priešinga stačiajam kampui.
Kojos- šonai, esantys priešais smailius kampus.
Priešais kampą esanti koja vadinama priešinga(kampo atžvilgiu). Kita koja, esanti vienoje iš kampo pusių, vadinama gretimas.
Sinusas Stačiakampio trikampio smailusis kampas yra priešingos kraštinės ir hipotenuzės santykis:
Kosinusas smailus kampas stačiakampiame trikampyje - gretimos kojos ir hipotenuzės santykis:
Tangentas smailusis kampas stačiakampiame trikampyje - priešingos kraštinės ir gretimos kraštinės santykis:
Kitas (ekvivalentiškas) apibrėžimas: smailiojo kampo liestinė yra kampo sinuso ir jo kosinuso santykis:
Kotangentas smailusis kampas stačiakampiame trikampyje - gretimos kraštinės ir priešingos pusės santykis (arba, kuris yra tas pats, kosinuso ir sinuso santykis):
Toliau atkreipkite dėmesį į pagrindinius sinuso, kosinuso, liestinės ir kotangento ryšius. Jie mums pravers sprendžiant problemas.

Įrodykime kai kuriuos iš jų.
Gerai, mes pateikėme apibrėžimus ir užrašėme formules. Bet kodėl mums vis dar reikia sinuso, kosinuso, tangento ir kotangento?
Mes tai žinome bet kurio trikampio kampų suma lygi.
Mes žinome ryšį tarp vakarėliams stačiakampis trikampis. Tai Pitagoro teorema: .
Pasirodo, žinodami du trikampio kampus, galite rasti trečiąjį. Žinodami dvi stačiojo trikampio kraštines, galite rasti trečiąją. Tai reiškia, kad kampai turi savo santykį, o šonai - savo. Bet ką daryti, jei stačiakampiame trikampyje žinote vieną kampą (išskyrus stačią) ir vieną kraštinę, bet jums reikia rasti kitas puses?

Su tuo susidurdavo žmonės, kurdami vietovės ir žvaigždėto dangaus žemėlapius. Juk ne visada galima tiesiogiai išmatuoti visas trikampio kraštines.
Sinusas, kosinusas ir tangentas – dar vadinami trigonometrinių kampų funkcijos- suteikti ryšius tarp vakarėliams Ir kampus trikampis. Žinodami kampą, visas jo trigonometrines funkcijas galite rasti naudodami specialias lenteles. O žinodami trikampio ir vienos iš jo kraštinių kampų sinusus, kosinusus ir tangentus, galite rasti likusias dalis.
Taip pat nubraižysime sinuso, kosinuso, liestinės ir kotangento verčių lentelę „geriems“ kampams nuo iki.
Atkreipkite dėmesį į du raudonus brūkšnelius lentelėje. Esant atitinkamoms kampo vertėms, liestinė ir kotangentė neegzistuoja.
Pažvelkime į keletą trigonometrijos problemų iš FIPI užduočių banko.
1. Trikampyje kampas yra , . Rasti.
Problema išspręsta per keturias sekundes.
Nuo ,.
2. Trikampyje kampas yra , , . Rasti.

Raskime jį naudodami Pitagoro teoremą.
Problema išspręsta.
Dažnai problemose yra trikampių su kampais ir arba su kampais ir. Prisiminkite pagrindinius jų santykius mintinai!

Trikampiui su kampais ir kojelė, priešinga kampui ties, yra lygi pusė hipotenuzės.
Trikampis su kampais ir yra lygiašonis. Jame hipotenuzė yra kartų didesnė už koją.
Mes pažvelgėme į uždavinius sprendžiant stačiuosius trikampius – tai yra, kaip rasti nežinomas puses ar kampus. Bet tai dar ne viskas! Vieningame valstybiniame matematikos egzamine yra daug problemų, susijusių su trikampio išorinio kampo sinusu, kosinusu, tangentu arba kotangentu. Daugiau apie tai kitame straipsnyje.
Straipsnyje mes visiškai suprasime, kaip tai atrodo trigonometrinių verčių, sinuso, kosinuso, liestinės ir kotangento lentelė. Panagrinėkime pagrindinę trigonometrinių funkcijų reikšmę 0,30,45,60,90,...,360 laipsnių kampu. Ir pažiūrėkime, kaip naudoti šias lenteles apskaičiuojant trigonometrinių funkcijų reikšmes.
Pirmiausia pažiūrėkime kosinuso, sinuso, liestinės ir kotangento lentelė 0, 30, 45, 60, 90,... laipsnių kampu. Šių dydžių apibrėžimas leidžia nustatyti 0 ir 90 laipsnių kampų funkcijų reikšmę:sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, kotangentas nuo 00 bus neapibrėžtas
sin 90 0 = 1, cos 90 0 = 0, ctg90 0 = 0, liestinė nuo 90 0 bus neapibrėžtaJei imsite stačiuosius trikampius, kurių kampai yra nuo 30 iki 90 laipsnių. Mes gauname:
sin 30 0 = 1/2, cos 30 0 = √3/2, įdegis 30 0 = √3/3, cos 30 0 = √3
sin 45 0 = √ 2/2, cos 45 0 = √ 2/2, tan 45 0 = 1, cos 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, įdegis 60 0 =√3, cos 60 0 = √3/3Visas gautas vertes pateiksime formoje trigonometrinė lentelė:
Sinusų, kosinusų, liestinių ir kotangentų lentelė!
Jei naudosime mažinimo formulę, mūsų lentelė padidės, pridėjus vertes kampams iki 360 laipsnių. Tai atrodys taip:

Taip pat, remiantis periodiškumo savybėmis, lentelę galima padidinti, jei kampus pakeisime 0 0 +360 0 *z .... 330 0 +360 0 *z, kuriame z yra sveikas skaičius. Šioje lentelėje galima apskaičiuoti visų kampų, atitinkančių vieno apskritimo taškus, reikšmę.

Pažiūrėkime, kaip naudoti lentelę sprendime.
Viskas labai paprasta. Kadangi mums reikalinga vertė yra mums reikalingų langelių susikirtimo taške. Pavyzdžiui, paimkite 60 laipsnių kampo koeficientą, lentelėje jis atrodys taip:
Galutinėje pagrindinių trigonometrinių funkcijų verčių lentelėje elgiamės taip pat. Bet šioje lentelėje galima sužinoti, kiek yra liestinė iš 1020 laipsnių kampo, ji = -√3 Patikrinkime 1020 0 = 300 0 +360 0 *2. Raskime jį naudodami lentelę.

Bradis stalas. Sinusui, kosinusui, tangentui ir kotangentui.
Bradis lentelės yra padalintos į keletą dalių, kurias sudaro kosinuso ir sinuso, tangento ir kotangento lentelės, kurios yra padalintos į dvi dalis (kampų tg iki 90 laipsnių ir ctg mažų kampų).
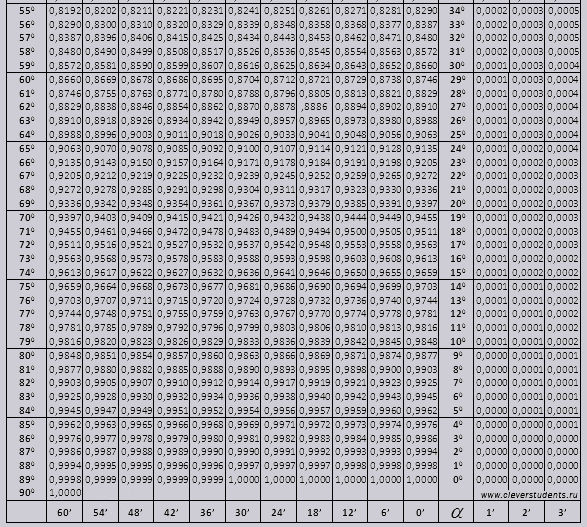
Sinusas ir kosinusas

tg kampo, pradedant nuo 00, baigiant 760, ctg kampo, pradedant nuo 140 ir baigiant 900.


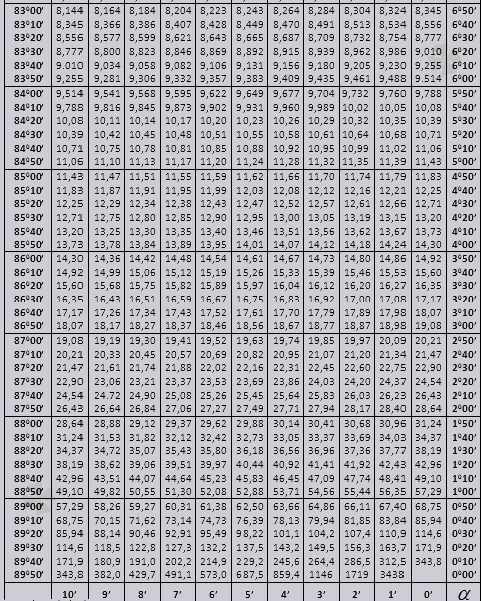
tg iki 900 ir ctg mažų kampų.

Išsiaiškinkime, kaip naudoti Bradis lenteles sprendžiant problemas.
Raskime žymėjimą nuodėmės (pavadinimas stulpelyje kairiajame krašte) 42 minutes (pavadinimas yra viršutinėje eilutėje). Pagal sankryžą ieškome žymėjimo, jis = 0,3040.
Minučių reikšmės nurodomos šešių minučių intervalu, ką daryti, jei mums reikalinga reikšmė patenka būtent į šį intervalą. Paimkime 44 minutes, bet lentelėje yra tik 42 Kaip pagrindą imame 42 ir naudojame papildomus stulpelius dešinėje, paimame 2 pataisą ir pridedame prie 0,3040 + 0,0006 gauname 0,3046.
Kai sin 47 minutės, kaip pagrindą imame 48 minutes ir iš jų atimame 1 pataisą, ty 0,3057 - 0,0003 = 0,3054
Skaičiuodami cos dirbame panašiai kaip nuodėmės, tik kaip pagrindą imame apatinę lentelės eilutę. Pavyzdžiui, cos 20 0 = 0,9397
Tg kampo iki 90 0 ir mažo kampo cot reikšmės yra teisingos ir jose nėra pataisymų. Pavyzdžiui, raskite tg 78 0 37 min = 4,967
ir ctg 20 0 13 min = 25,83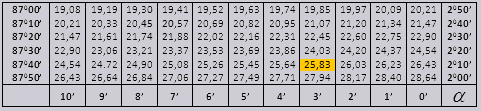
Na, mes pažvelgėme į pagrindines trigonometrines lenteles. Tikimės, kad ši informacija jums buvo labai naudinga. Jei turite klausimų dėl lentelių, būtinai rašykite juos komentaruose!
Pastaba: Sieniniai buferiai yra buferio plokštė, skirta sienoms apsaugoti. Sekite nuorodą berėmiai sieniniai buferiai (http://www.spi-polymer.ru/otboyniki/) ir sužinokite daugiau.








