Тойргийн тойргийн тэгшитгэлээр Delaunay нөхцөлийг шалгах алгоритмын оновчлол ба түүний хэрэглээ

Хоёр гурвалжны хувьд Делауны нөхцөлийг хэрхэн хурдан шалгах тухай нууцыг би танд хэлье.
Үнэн хэрэгтээ оновчлолыг өөрөө арай доогуур тайлбарласан байдаг ("Дэлоны нөхцөлийг тойргийн тэгшитгэлээр шалгах алгоритмыг оновчлох" хэсгийг үзнэ үү), гэхдээ би бүх зүйлийг дарааллаар нь хэлье.

Миний хувьд гурвалжин дүрслэлийг хавтгайг анхдагч секторт (гурвалжин) хуваахын тулд зураг зурахад ашигладаг. Таны мэдэж байгаагаар энэ нь хэд хэдэн үе шатанд хуваагддаг: тохируулах, хил хязгаарыг тодорхойлох, хил хязгаарыг тойрон алхах, контурыг шүүрдэх. Энэ бол хамгийн ерөнхий ойлголт юм. Би хамгийн хэцүү үе шатанд болмоор байна: онгоц шүүрдэх.

Орцонд

Зураг 1

Юу хийх хэрэгтэй

Хайх

Алгоритм

Зураг 2

Зураг 3

Зураг 4

Өөр нэг зүйл бол: дараагийн гурвалжинг хадгалахдаа оройг цагийн зүүний дагуу (зөв координатын системээр) тэмдэглэх шаардлагатай. Энэ нь ирээдүйд тооцоолох нөөцийг багасгахад хэрэгтэй болно.

2) Бид бүхэл бүтэн онгоцыг шүүрч дуустал 1-р алхамыг давтана.

3) Хэрэв хэд хэдэн дараалал байгаа бол, i.e. нэг, дотор нь нэг буюу хэд хэдэн дотоод контур байдаг (Зураг 1). Энд дараалал бүрийг тусад нь авч үзэх шаардлагатай. Өөр нэг дотоод контурыг авч үзье. Нэг гадаад ба нэг дотоод хэлхээнээс бид хоёр нэг хэлхээ хийнэ. Үүнийг хийхийн тулд та нэг хэлхээнээс нөгөө хэлхээ рүү хоёр "порт" олох хэрэгтэй. "Порт"-ын нөхцөл: тэдгээр нь хоорондоо огтлолцох ёсгүй (тэдгээрийн төгсгөлүүд хүртэл хүрч болохгүй), контурын шугамтай огтлолцох ёсгүй (Зураг 5).

Зураг 5

Зураг 6
4) Дараа нь та бүх дотоод дарааллыг бие биенээсээ тусгаарлагдсан аль хэдийн үүссэн дарааллаар нэг нэгээр нь оруулах хэрэгтэй (3-р цэг). Та үүнийг шинийг агуулсан нэгтэй нэгтгэх хэрэгтэй. Тодорхойлолтоор бол ямар ч дотоод дараалал нь бусадтай (нэг гадаад болон бүх боломжит дотоод) хүрч, огтлолцдоггүй тул бүх зүйл жигд явагдах болно.
Портуудыг олсны дараа (Зураг 6) шинэ дарааллыг бий болгож, одоогийн алгоритмын 1 ба 2-р цэгийг ашиглан тэдгээрийг тойрч гарахад хялбар байдаг (Зураг 7).

Зураг 7

5) 4-р шатны дараа бид гурвалжны жагсаалттай байна (Зураг 8). Даалгавар аль хэдийн дууссан мэт боловч зургийг үзэсгэлэнтэй болгох л үлдлээ: Делауны нөхцөл биелсэн эсэхийг шалгана уу (Зураг 9).

Зураг 8

Зураг 9

6) Урагшаа хараад би танд зургаа дахь цэгийн талаар хэлье. Энэ нь 5-р алхамыг ашиглан олж авсан гурвалжны жагсаалтыг дараалан гүйлгэхээс бүрдэнэ. Эхлээд бид бүх гурвалжинг "бохир" гэж тэмдэглэнэ. Цикл бүрт бид гурвалжин бүрийн Делауны нөхцөлийг шалгадаг. Хэрэв нөхцөл хангагдаагүй бол бид хөршүүд болон одоогийн гурвалжинг "бохир" гэж дахин барьж тэмдэглэнэ. Хэрэв нөхцөл хангагдсан бол бид үүнийг цэвэр гэж тэмдэглэнэ. Алгоритмыг хэрэгжүүлэхдээ гурвалжин бүр хөршүүдтэйгээ холбоостой байдаг. Энэ тохиолдолд 6-р цэг хамгийн хурдан ажилладаг.

Тав дахь шатны талаар дэлгэрэнгүй

Тооцоолох чадвар №1: 10 үржүүлэх/хуваах, 13 нэмэх/хасах.
Тооцоолох чадвар №2: 29 үржүүлэх/хуваах үйлдэл, 24 нэмэх/хасах үйлдэл.

Жишээлбэл, номонд тооцоолсон тооцоолох хүчин чадлын үүднээс 1-р сонголт илүү ашигтай байдаг. Би үүнийг хэрэгжүүлэх байсан, үгүй ​​бол ... (Зураг 10). Энэ аргыг "конвейер" дээр тавьсны дараа тодорхойгүй байдал үүссэн. Энэ нь А өнцөг нь өөрөө 180 градусаас их байвал сонголт юм. Энэ нь номонд хувь хүний ​​хувийн аргуудын нэг гэж тооцогддог. Ингэснээр түүний бүх дэгжин байдал, ил тод байдал, гүйцэтгэл алга болно. Мөн хожим нь №2 аргыг маш их оновчтой болгож болох нь тогтоогдсон.

Зураг 10

Тойргийн тэгшитгэлээр Delaunay нөхцөлийг шалгах алгоритмыг оновчтой болгох

Тиймээс бидэнд байна:
M(X, Y) цэгийн нөхцөлийг A(x1, y1), B(x2, y2), C(x3, y3) цэгүүдийг дайран өнгөрөх тойргийн тэгшитгэлээр шалгахдаа дараах байдлаар бичиж болно.

(a ⋅ (X^2 + Y^ 2) − b ⋅ X + c ⋅ Y − d) ⋅ тэмдэг a ≥ 0

Дэлгэрэнгүй мэдээллийг маш сайн номноос олж болно. (Үгүй ээ, би зохиогч биш)
Тэгэхээр, а тэмдэг нь хөндлөн чиглэлийн тэмдэг, би гурвалжингуудыг анхнаасаа цагийн зүүний дагуу барьсан тул үүнийг орхигдуулж болно (энэ нь нэгтэй тэнцүү).

A(x1 - X, y1 - Y), B(x2 - X, y2 - Y), B(x3 - X, y3 - Y);

D>=0

Зураг 11

Энгийн биш гэж үү?

Номын дагуу дахин

(x1^2 + y1^2)*(y2*x3 - x2*y3) + (x2^2 + y2^2)*(x1*y3 - y1*x3) + (x3^2 + y3^2)* (y1*x2 - x1*y2)<= 0

Бидэнд: 15 үржүүлэх/хуваах үйлдэл, 14 нэмэх/хасах үйлдэл байна.

Анхаарал тавьсанд баярлалаа. Би шүүмжлэл хүлээж байна.

Ном зүй

Теплов А.А., Бакалавр, Н.Э. Бауман, Москвагийн Компьютерийн программ хангамж, мэдээллийн технологийн тэнхим, [имэйлээр хамгаалагдсан]

МАЙКОВ К.А., Техникийн шинжлэх ухааны доктор, профессор, Москвагийн Улсын Техникийн Их Сургуулийн Н.Е. Бауман, Москвагийн Компьютерийн программ хангамж, мэдээллийн технологийн тэнхим, [имэйлээр хамгаалагдсан]

Өөрчлөгдсөн алгоритм
Делоны гурвалжин

Өндөр гүйцэтгэлтэй, нөөц бага зарцуулдаг Делонай гурвалжингийн аргуудын харьцуулсан шинжилгээний үр дүнг танилцуулав. Дараачийн шинэчлэлд зориулж прототипийг сонгох нь бодит цаг хугацаанд динамик гурван хэмжээст объектыг практикт шаардлагатай нарийвчлалтайгаар барьж байгуулахтай холбоотой юм. Түгээлтийн нягтралын дагуу гурвалжингийн цэгүүдийн массивыг интервалаар хуваах алгоритмыг санал болгож байгаа бөгөөд энэ нь техник хангамжийг хэрэгжүүлэхэд алдаа гарахаас зайлсхийх боломжийг олгодог. Санал болгож буй өөрчилсөн Delaunay гурвалжингийн алгоритмын шинжилгээг хийж байна

Оршил

Өгөгдсөн түвшний нарийвчлал бүхий динамик 3D объектыг бүтээх нөөцийн эрчмийг тодорхойлдог үе шатуудын нэг бол гурвалжин юм. Практикт өндөр гүйцэтгэлтэй, нөөц багатай байх шаардлагыг хангасан гурвалжингийн аргын загварыг тодорхойлох шаардлагатай бөгөөд дараа нь тодорхой ангиллын асуудалд өөрчлөлт оруулах шаардлагатай байна.

Шийдэх ёстой ажлуудыг тодорхойлох

Хэд хэдэн практик асуудлууд нь үл мэдэгдэх тархалтын хуультай харгалзах багц цэгүүдээр дүрслэгдсэн 3D объектуудыг загварчлах хэрэгцээ шаардлагаар тодорхойлогддог. Ийм асуудлын нэг жишээ бол уулын нуруу эсвэл гадаргуугийн нарийн төвөгтэй, жигд бус байгууламжийг загварчлах явдал бөгөөд өндрийг нь өмнө нь зайнаас тандан судлах замаар олж авдаг. Энэ тохиолдолд гурвалжны анхны багц дээр гурвалжинг хийх шаардлагатай бөгөөд энэ нь гурвалжны хамгийн бага "зөв байдлын зэрэг" -ийг баталгаажуулах бөгөөд энэ нь нийлбэрийн хамгийн бага утгатай "нимгэн" гурвалжны барилгыг хассанаар тодорхойлогддог. хүрээлэгдсэн тойргийн радиусуудын .

Гурвалжны "зохицуулалтын зэрэг"-ийн асуудлыг Делонегийн нөхцөлийг хангасан гурвалжингаар шийддэг.

Мэдэгдэж байгаа Delaunay гурвалжин алгоритмуудыг дараах дөрвөн ангилалд хувааж болно: давталтын алгоритмууд, нэгтгэх алгоритмууд, хоёр дамждаг алгоритмууд, алхам алхмаар; Эдгээр алгоритмын үндсэн шинж чанаруудыг доор авч үзэх болно.

Делонай гурвалжин үүсгэх давталтын алгоритмууд

Давталттай алгоритмууд нь хэсэгчлэн баригдсан Делонай гурвалжинд цэгүүдийг дараалан нэмдэг. Давталтын Delaunay алгоритмуудын нарийн төвөгтэй байдлыг O(N2), цэгүүдийн жигд тархалтын хувьд O(N) гэж тодорхойлдог. Давталтын Delaunay алгоритмын сул тал нь олон тооны давталтын гогцоо, эрэмбэлэх алгоритм нь эх өгөгдлийн бүтцээс хамааралтай, давталт бүрт Делонай нөхцөл байгаа эсэхийг шалгах шаардлагатай байдаг. Давталтын Delaunay алгоритмын давуу тал нь хэрэгжүүлэхэд хялбар, тодорхой оролтын өгөгдөл дээр үндэслэн үр дүнтэй эрэмбэлэх алгоритмыг сонгох өндөр хурд юм.

Нэгтгэх замаар Делонай гурвалжин үүсгэх алгоритмууд

Нэгтгэх алгоритмууд нь анхны багц цэгүүдийг хэд хэдэн дэд бүлэгт хуваахыг хэрэгжүүлдэг бөгөөд үүний дараа хэд хэдэн шийдлүүдийг нэгтгэн гурвалжинг байгуулдаг. Алгоритмуудыг нэгтгэх дундаж төвөгтэй байдал нь O(N). Нэгтгэх алгоритмууд нь "нарийн" судлуудын хувьд гүдгэр хэсгүүдийг бий болгох хэрэгцээ шаардлагаар тодорхойлогддог илүүдэл байдлаар тодорхойлогддог бөгөөд улмаар нэгтгэх явцад дахин бүтээгдсэн урт, "нарийн" гурвалжингууд үүсдэг. Нэгтгэх алгоритмууд нь өндөр гүйцэтгэлтэй байдаг нь тэдний практик давуу талыг тодорхойлдог.

Delaunay гурвалжин үүсгэх хоёр дамжлагын алгоритмууд

Хоёр дамжих алгоритмын давуу тал нь эхний мөчлөгт Делоны нөхцөлийг харгалзахгүйгээр тодорхой гурвалжинг байгуулдаг бөгөөд энэ нь хоёрдугаар шатанд Делоны нөхцлийн дагуу өөрчлөгддөг. Хоёр дамжих алгоритмын нарийн төвөгтэй байдал нь дунджаар O(N), хамгийн бага таатай тохиолдолд O(N2) байна. Хоёр дамжлагатай Delaunay алгоритмын сул тал нь тууз тус бүрт олон тооны сорт хийх хэрэгцээ юм. Үүний зэрэгцээ, энэ алгоритм нь өндөр гүйцэтгэлээр тодорхойлогддог, учир нь гурвалжинд унасан дараагийн гурвалжинг Delaunay нөхцөл хангасан эсэхийг шалгадаггүй бөгөөд энэ нь ихээхэн хэмжээний техник хангамж шаарддаг.

Делонай гурвалжин үүсгэх алхам алхмаар алгоритмууд

Алхам алхмаар бүтээн байгуулалтын алгоритмууд нь эцсийн гурвалжинд Delaunay нөхцөлийг хангасан гурвалжингуудыг л хэрэгжүүлдэг тул сэргээн босгох шаардлагагүй. Их хэмжээний цэгүүдтэй бол алхам алхмаар үүрэн холбооны алгоритмыг ашиглах нь практик биш юм. Энэ алгоритмын нарийн төвөгтэй байдал нь дунджаар O(N), хамгийн муу тохиолдолд O(N2) байна.

Delaunay гурвалжинг өөрчлөх прототипийг сонгох

Бодит цаг хугацаанд динамик 3D объектыг бүтээх асуудлын практик шинж чанарууд нь Delaunay гурвалжны алгоритмд тавигдах шаардлагыг өндөр гүйцэтгэл, бага нөөцийн эрчимтэй тодорхойлдог. Дээрх шинжилгээний үр дүнгээс харахад авч үзсэн алгоритмууд нь эдгээр шаардлагыг бүрэн хангаж чадахгүй байна. Тиймээс гурвалжингийн талбайг гурвалжингийн цэгүүдийг агуулсан командуудад хуваахаас үл хамаарах алгоритмыг бүтээх шаардлагатай бөгөөд одоогийн гурвалжинг анхны гурвалжинд нэмэх давталт бүрт Делоны нөхцөлийг шалгах шаардлагагүй болно. .

Харьцуулсан шинжилгээний дээрх үр дүнгээс үзэхэд хоёр дамжлагатай Делонай гурвалжингийн алгоритмууд, ялангуяа хоёр дамжлагатай сэнсний алгоритм нь өндөр гүйцэтгэл, нөөц бага эрчимтэй байх шалгуурыг зөвхөн хэсэгчлэн хангаж байна.

Гэсэн хэдий ч, энэ төрлийн алгоритмууд нь бодит цагийн асуудлуудтай холбоотой үед гүйцэтгэлийг нэмэгдүүлэхийн тулд өөрчлөлт хийхийг шаарддаг. Хоёр дамжлагатай сэнсний алгоритм нь цэгүүдийн массын төвийг тодорхойлоход илүүдэхгүй. OX эсвэл OY ашиглан массын цэгийн төвийн координатыг тодорхойлохдоо олон тооны цэгүүдтэй бол арифметик дундаж утгыг тооцоолох нь зохисгүй бөгөөд цэгийн координатын их утгатай бол өгөгдлийн халилт үүсч болно. програмын алдаа эсвэл бүтэлгүйтэлд хүргэнэ. Тиймээс гурвалжингийн цэгүүдийн бүх утгыг X тэнхлэгийн дагуу Δx 1, Δx 2, Δx 3 ... Δx n, Y тэнхлэгийн дагуу Δy 1, Δy 2, Δy 3 болгон хуваахыг зөвлөж байна. ... Δy n. Мөн X ба Y тэнхлэгийн дагуух харгалзах интервалд хамаарах цэгүүдийн тоог тодорхойлох шаардлагатай байна.

• x c – массын цэгийн х-координат;
• Δх i – X тэнхлэг дээрх i-р интервал;
• X max – гурвалжингийн бүх цэгүүдийн дундах X тэнхлэгийн дагуух хамгийн их утга;
• X мин – гурвалжингийн бүх цэгүүдийн дундах X тэнхлэгийн дагуух хамгийн бага утга;

• y c – y-массын цэгийн төвийн координат;
• n i – i-р интервал дээрх цэгүүдийн тоо;
• Δy i – Y тэнхлэг дээрх i-р интервал;
• Y max – гурвалжингийн бүх цэгүүдийн дундах Y тэнхлэгийн дагуух хамгийн их утга;
• Y min – бүх гурвалжингийн цэгүүдийн Y тэнхлэгийн дагуух хамгийн бага утга.

Гурвалжингийн дараагийн үе шатуудыг сонгодог сэнсний алгоритмын дагуу хэрэгжүүлдэг. Боловсруулсан сэнс хэлбэртэй Delaunay гурвалжингийн алгоритмын диаграммыг Зураг дээр үзүүлэв. 1.

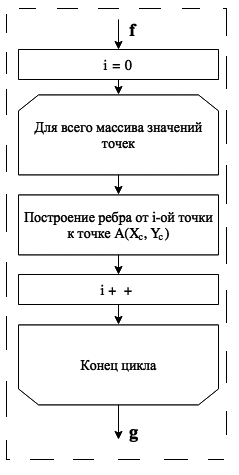Танилцуулсан схемийн хамгийн их хөдөлмөр шаардсан үе шатууд нь гурвалжин хэлбэрийг гүдгэр болгон ангилах, байгуулах үе шатууд юм. Ангилах алгоритмаар нэгтгэх алгоритмыг, гүдгэр гурвалжин байгуулах алгоритмаар Грахам алгоритмыг сонгосон. Аль аль алгоритм нь хүлээн зөвшөөрөгдсөн хугацаанд ажилладаг бөгөөд тэдний төлөөлөгчдийн дунд практикийн хувьд хамгийн их таалагддаг.

Өөрчлөгдсөн сэнс хэлбэртэй Delaunay гурвалжингийн алгоритмын шинжилгээ

Зурагт үзүүлсэн нэгээс. Диаграммын 1-ээс харахад өөрчилсөн сэнсний алгоритмыг ашиглан гурвалжин үүсгэх цаг хугацааны утгыг дараах илэрхийллээр тодорхойлно.

• T 1, T 2 - X ба Y тэнхлэгийн дагуух интервалын оновчтой тоог тооцоолох цаг хугацааны утгууд;
• T 3 , T 4 - тооцооллын хугацаа X мин ба X max тус тус;
• T 5 , T 6 - тооцооллын хугацаа Y min ба Y max тус тус;
• T 7 , T 8 - X ба Y тэнхлэгийн дагуух интервалын утгыг тооцоолох цаг хугацааны утгууд;
• T 9 – массивын цэг бүрийн туйлын өнцгийг A(X c ,Y c) цэгтэй харьцуулах хугацааны утга;
• T 10 – A(X c ,Y c) цэгтэй харьцангуй туйлын өнцгөөр бүх цэгүүдийг нэгтгэх ангилах хугацааны утга;
• T 11 – массивын цэг бүрээс A(X c ,Y c) цэг хүртэл ирмэг байгуулах хугацааны утга;
• T 12 - гурвалжинг гүдгэр болгон дуусгах хугацааны утга;
• T 13 – Делауны нөхцлийг хангасан гурвалжингийн сэргээн босгох хугацааны утга;
• n – цэгийн координатын утгуудын массив.

Цаг хугацааны хамаарал бүрийг тусад нь авч үзье.

X ба Y тэнхлэгийн дагуух интервалын оновчтой тоог тодорхойлохдоо Стержийн дүрмийг ашигладаг бөгөөд үүний дагуу n интервалын тоог дараах байдлаар тодорхойлно.

• N - хэмжигдэхүүний ажиглалтын нийт тоо;
• [x] – х тооны бүхэл хэсэг.

T 1 ба T 2 цаг хугацааны хамаарал нь c 1 ба c 2 тогтмол төлөөлөлтэй байх нь ойлгомжтой.

X min, X max, Y min, Y max утгуудыг тодорхойлох үе шатанд псевдокод дараах байдалтай харагдана.

Xmin ← М

for i ← 1-ээс урт(M) – 1

Хэрэв Xmin › M[i]

Xmin ← M[i]

Xmax ← М

for i ← 1-ээс урт(M) – 1

Хэрэв Xmax< M[i]

Xmax ← M[i]

Ymin ← М

for i ← 1-ээс урт(M) – 1

Хэрэв Ymin › M[i]

Ymin ← M[i]

Ymax ← М

for i ← 1-ээс урт(M) – 1

Хэрэв Ymax< M[i]

Ymax ← M[i]

Дээрх псевдокодоос харахад x эсвэл y-ийн хамгийн их эсвэл хамгийн бага утгыг олох хугацаа нь O(N) шугаман хамааралтай байдаг тул T 3 (n), T 4 (n), T 5 (n) байна. , T 6 (n) нь цаг хугацааны шинж чанартай O(N) тус тус байна.

X тэнхлэгийн дагуух интервалын утгыг тодорхойлох диаграммыг Зураг дээр үзүүлэв. 2.

Дээр үзүүлсэн диаграмаас O(N)-ийн шугаман хугацааны хамаарал бас харагдаж байна, учир нь Цэгийн массивын утгуудын координатын бүх багц нь утгыг тодорхойлоход оролцдог. Y тэнхлэгийн дагуух интервалын утгыг тодорхойлох схем нь ижил төстэй бүтэц, цаг хугацааны шинж чанартай байдаг тул T 7 (n) ба T 8 (n) цаг хугацааны хамаарал нь O (N) хэлбэртэй байна.

Анхны массив цэгийн туйлын өнцгийн утгыг тодорхойлох схемийг Зураг дээр үзүүлэв. 3.

Псевдокодын хэлбэрээр энэ диаграм нь дараах байдлаар харагдах болно.

онооноос оноо авахын тулд

# Хэрэв цэг нь 1-4-р улирлын хоорондох координатын тэнхлэгт оршдог бол

Хэрэв цэг.x ≥ Xc ба цэг.y = Yc бол

Цэг.өнцөг ← 0

# Хэрэв оноо эхний улиралд хатуу оршдог бол

Хэрэв цэг.x > Xc ба point.y > Yc бол өөр

Суурь ← |point.x – Xc|

Point.angle ← arctg(перпендикуляр/суурь)

# Хэрэв цэг нь 1-2-р улирлын хоорондох координатын тэнхлэгт оршдог

Хэрэв цэг.x = Xc ба цэг.y > Yc бол өөр

Цэг.өнцөг ← p/2

# Хэрэв оноо хоёрдугаар улиралд хатуу оршдог бол

Үгүй бол цэг.x< Xc and point.y >Yc

Суурь ← |point.y – Yc|

Цэг.өнцөг ← p/2 + arctg(перпендикуляр/суурь)

# Хэрэв цэг нь II ба III улирлын хоорондох координатын тэнхлэгт оршдог

Хэрэв цэг.x< Xc and point.y = Yc

Цэг.өнцөг ← х

# Хэрэв оноо гуравдугаар улиралд хатуу оршдог бол

Хэрэв цэг.x< Xc and point.y >Yc

Суурь ← |point.x – Xc|

Перпендикуляр ← |point.y – Yc|

Цэг.өнцөг ← p + арктан(перпендикуляр/суурь)

# Хэрэв цэг нь III ба IV улирлын хоорондох координатын тэнхлэгт оршдог бол

Хэрэв цэг.x = Xc ба цэг.y бол< Yc

Цэг.өнцөг ← 3p/2

# Хэрэв цэг нь IV улиралд хатуу оршдог бол

Хэрэв цэг.x > Xc болон цэг.y< Yc

Суурь ← |point.y – Yc|

Перпендикуляр ← |цэг.x – Xc|

Цэг.өнцөг ← 3p/2 + arctg(перпендикуляр/суурь)

Мэдээжийн хэрэг, цэгийн координатын анхны массивын туйлын өнцгийн утгыг тодорхойлох цаг хугацааны шинж чанар нь O (N) хэлбэртэй байдаг тул T 9 (n) = O (N).

-д үзүүлснээр нэгтгэх эрэмбэ нь O(N) хэлбэрийн цаг хугацааны хамааралтай тул T 10 (n) = O(NlnN).

Анхны массивын цэгүүдийг холбосон ирмэгийг барих диаграммыг Зураг дээр үзүүлэв. 4.

Дээрх хэлхээний псевдокод дараах байдлаар харагдах болно.

for i ← 0 хүртэл урт(Цэг) – 1

Зурах(Xc,Yc,Оноо[i].x, Оноо[i].y)

Цаг хугацааны хариу үйлдэл нь мөн шугаман байдаг тул T 11 (n) = O (N).

Гүдгэр гурвалжинг Грахамын алгоритмын дагуу гүйцэтгэнэ. Процедурын оролтын өгөгдөл нь Q цэгүүдийн багц бөгөөд |Q|≥3. Энэ нь S стекийн дээд талд байгаа цэгийг агуулгыг нь өөрчлөхгүйгээр буцаадаг Top(S) функцийг дууддаг. Нэмж дурдахад NextToTop(S) функцийг мөн ашигладаг бөгөөд энэ нь дээд цэгийн доор байрлах S стек дэх цэгийг буцаадаг; S стек өөрчлөгдөөгүй хэвээр байна.

Грахам(Q)

Хамгийн бага координаттай Q олонлогийн цэгийг p 0 гэж үзье.

‹p 1 , p 2 ,...,p N › – Q олонлогийн цэгүүд, эрэмбэлэгдсэн

Туйлын өнцгийг нэмэгдүүлэх дарааллаар.

Түлхэх(p 0,S)

Түлхэх(p 1 ,S)

i=2-оос N хүртэл хийх

NextToTop(S), Top(S) болон pi цэгүүдээс үүссэн өнцөг нь

Зүүн бус эргэлт үүсгэ

# эдгээрээс үүссэн тасархай шугамын дагуу хөдөлж байх үед

# цэгүүд, хөдөлгөөнийг шулуун эсвэл баруун тийш хийдэг

Поп хийх(S)

Түлхэх(pi,S)

буцах С

Graham процедурын ажиллах хугацаа нь O(NlnN) бөгөөд N=length(Q). while давталт нь O(N) цаг, туйлын өнцгийг эрэмбэлэхэд O(NlnN) хугацаа шаардагдах бөгөөд энэ нь Грахамын процедурын ерөнхий асимптотик шинж чанарыг илэрхийлдэг тул T 12 (n) = O болно. (NlnN).

Дэлоны нөхцөлийг хангасан гурвалжинг сэргээх цаг хугацааны онцлог нь O(N) шугаман хамааралтай тул T 13 (n) = O(N).

Хэрэв бид бүх олсон цаг хугацааны шинж чанарыг илэрхийлэлд (3) орлуулбал үүссэн хугацааны хамаарал дараах байдалтай болно.

T(n) = c 1 +c 2 +O(N)+O(N)+O(N)+O(N)+O(N)+O(N)+O(N)+ +O(NlnN) )+O(N)+O(NlnN)+O(N)

T(n) = O(NlnN)

Өөрчлөгдсөн Delaunay гурвалжингийн алгоритмын цаг хугацааны шинж чанарын онолын шинжилгээ нь санал болгож буй алгоритмын үр ашиг, өндөр гүйцэтгэлийг баталж байна.

дүгнэлт

Практикт түгээмэл хэрэглэгддэг Delaunay гурвалжингийн алгоритмуудын харьцуулсан шинжилгээний үр дүнд авч үзсэн аргууд нь бодит цаг хугацаанд динамик гурван хэмжээст объектыг урьдчилан тодорхойлсон нарийвчлалтайгаар бүтээх шаардлагыг хангаагүй болохыг харуулж байна. тэдгээрийг өөрчлөх хэрэгцээ. Сэнс хэлбэртэй хоёр дамжлагатай Delaunay гурвалжингийн алгоритмын өөрчлөлтийг санал болгож байна, функциональ шинж чанар нь цэгүүдийн массивыг дэд олонлогт хуваах замаар гурвалжингийн цэгүүдийн координатын массивын массын төвийн утгыг тооцоолох явдал юм. X ба Y тэнхлэгүүдийг өөрчилсөн Delaunay гурвалжингийн алгоритмын цаг хугацааны шинж чанарыг шинжилэв. Эдгээр тооцоолол нь массын цэгийн төвийн координатыг тодорхойлохдоо олон тооны цэгүүдийн гүйцэтгэлийг мэдэгдэхүйц сайжруулж, мэдээллийн хэт их ачаалал, улмаар програм хангамжийн хэрэгжилтэд алдаа гарахаас зайлсхийх боломжийг олгодог.

1. Кнут Д.Э. Програмчлалын урлаг. Боть 1. Үндсэн алгоритмууд. – М.: Уильямс, 2008. – 680 х.
2. Кнут Д.Э. Програмчлалын урлаг. 3-р боть. Эрэмбэлэх, хайх. – М.: Уильямс, 2008. – 800 х.
3. Mandelbrot B. Байгалийн фрактал геометр. – М.: Компьютерийн судалгааны хүрээлэн, 2002. – 656 х.
4. Skvortsov A.V. Delaunay гурвалжин ба түүний хэрэглээ. – Томск: Томскийн их сургуулийн хэвлэлийн газар, 2002. – 128 х.
5. Скворцов А.В. Шугаман хугацаанд Делонай гурвалжинг байгуулах. – Томск: Томскийн их сургуулийн хэвлэлийн газар, 1999. – С.120-126.
6. Скворцов А.В., Мирза Н.С. Гурвалжин үүсгэх, дүн шинжилгээ хийх алгоритмууд. – Томск: Томскийн их сургуулийн хэвлэлийн газар, 2006. – 168 х.
7. Томас Х.Корман, Чарльз И.Лейзерон, Рональд Л.Ривест, Клиффорд Стейн. Алгоритм: бүтээн байгуулалт, дүн шинжилгээ, 3-р хэвлэл: Орч. англи хэлнээс – М.: Уильямс, 2013. – 1328 х.
8. Шайдуров В.В. Олон сүлжээ хязгаарлагдмал элементийн аргууд. – М.: Наука, 1989. – 288 х.
9. Стержс Х. (1926). Ангийн интервалын сонголт. Ж.Амер. Статист. Асс., 21, 65-66.

Түлхүүр үг:Виртуал бодит байдал, өгөгдсөн массив цэг дээр гурвалжинг хийх, Делонай гурвалжинг хийх, динамик гурван хэмжээст объект бүтээх.

Өөрчлөгдсөн Delaunay-ийн гурвалжингийн алгоритм

Теплов А.А., Бакалавр, MSTU Бауман, "Програм хангамж, мэдээллийн технологийн тэнхим", Москва, [имэйлээр хамгаалагдсан]

Майков К.А., Техникийн шинжлэх ухааны доктор, профессор, MSTU Бауман, "Програм хангамж, мэдээллийн технологийн тэнхим", Москва, [имэйлээр хамгаалагдсан]

Хураангуй:Өндөр гүйцэтгэлтэй, нөөц бага зарцуулдаг Делонай гурвалжны бараг алдартай аргуудын харьцуулсан шинжилгээний үр дүнг энэ нийтлэлд тайлбарласан болно. Динамик 3 хэмжээст объектуудыг бодит цаг хугацаанд тодорхой нарийвчлалтайгаар бүтээх зорилгоор цаашид шинэчлэх аргыг сонгох нь үндэслэлтэй юм. Шилэн кабелийн үндсэн үе шатуудын нэг нь Делонай гурвалжингийн хоёр дамжлагын алгоритмыг өөрчилсөн. Гурвалжингийн эсийн массивыг хуваарилалтын нягтралын дагуу интервалаар хуваах алгоритмын санал байгаа бөгөөд энэ нь техник хангамжийг хэрэгжүүлэхэд алдаа гарахаас зайлсхийх боломжийг олгодог.

Түлхүүр үг:Виртуал бодит байдал, өгөгдсөн эсийн массив дээрх гурвалжинг, Делауны гурвалжин, динамик 3 хэмжээст объект бүтээх.

-тай холбоотой

Хязгаарлагдмал S цэгийн гурвалжин нь S олонлогийн бүх цэгийг хамарсан гүдгэр их биеийг CH(S) гурвалжин болгох асуудал юм. Гурвалжингийн шулуун шугамын хэрчмүүд огтлолцож чадахгүй - тэдгээр нь зөвхөн S олонлогт хамаарах нийтлэг цэгүүдэд таарч болно. шулуун шугамын сегментүүд нь гурвалжингуудыг хаадаг тул бид тэдгээрийг хавирга гэж үзэх болно. Зураг дээр. 1-р зурагт ижил цэгүүдийн гурвалжингийн хоёр өөр хувилбарыг харуулав (бид эдгээр зурагт зурсан тойргийг түр үл тоомсорлох болно).

Цагаан будаа. 1

Өгөгдсөн S цэгүүдийн хувьд бид S олонлогийн бүх цэгүүдийг хилийн цэгүүд - гүдгэр их биений хил дээр байрлах CH(S) цэгүүд болон дотоод цэгүүд - гүдгэр дотор байрлах цэгүүдэд хувааж болохыг харж болно. их бие CH(S). Та мөн S гурвалжингийн үр дүнд олж авсан ирмэгийг ангилж болно бүрхүүлийн хавиргаТэгээд дотоод хавирга. Их биений ирмэгүүд нь гүдгэр их биений CH(S) хилийн дагуу байрлах ирмэгүүд, дотоод ирмэгүүд нь гүдгэр их биений дотор гурвалжингийн сүлжээ үүсгэдэг бусад бүх ирмэгүүд орно. Бүрхүүлийн ирмэг бүр нь хоёр зэргэлдээ хилийн цэгийг холбодог бол дотоод ирмэг нь ямар ч төрлийн хоёр цэгийг холбож болохыг анхаарна уу. Ялангуяа дотоод ирмэг нь хоёр хилийн цэгийг холбодог бол энэ нь гүдгэр их биений хөвч CH(S) юм. Гурвалжингийн ирмэг бүр нь хоёр бүсийн хил гэдгийг анхаарна уу: дотоод ирмэг бүр нь хоёр гурвалжны хооронд, бүрхүүлийн ирмэг бүр нь гурвалжин ба хязгааргүй хавтгайн хооронд байна.

Зарим өчүүхэн тохиолдлоос бусад бүх цэгүүд нь гурвалжингийн нэгээс олон аргыг зөвшөөрдөг. Гэхдээ гайхалтай шинж чанар байдаг: өгөгдсөн олонлогийн гурвалжны аль ч арга нь теоремоос үүдэлтэй ижил тооны гурвалжныг тодорхойлдог.

Цэгүүдийн багцын гурвалжингийн тухай теорем. S цэгүүдийн олонлог нь n>3 цэгийг агуулж байгаа ба тэдгээр нь бүгд хоорондоо уялдаатай биш гэж бодъё. Үүнээс гадна, тэдгээрээс i цэгүүд нь дотоод (өөрөөр хэлбэл, гүдгэр их бие CH(S) дотор хэвтэж байна. Дараа нь S олонлогийн гурвалжингийн аль ч арга нь яг n + i - 2 гурвалжин үүснэ.

Теоремыг батлахын тулд эхлээд n-i хилийн цэгүүдийн гурвалжинг авч үзнэ. Тэд бүгд гүдгэр олон өнцөгтийн орой тул ийм гурвалжингийн үр дүнд (n - i) - 2 гурвалжин үүснэ. (Үүнийг шалгахад хэцүү биш бөгөөд үүнээс гадна ямар ч гурвалжинг харуулж болно дур зоргоорооМ талт олон өнцөгт - гүдгэр эсвэл гүдгэр бус - m - 2 гурвалжин агуулна). Одоо үлдсэн i дотоод цэгүүдийг нэг бүрээр нэмэхэд гурвалжинд юу тохиолдохыг шалгая. Ийм цэг бүрийг нэмбэл гурвалжны тоог хоёроор нэмэгдүүлнэ гэж бид баталж байна. Дотоод цэгийг нэмэхэд хоёр нөхцөл байдал үүсч болзошгүй бөгөөд үүнийг Зураг дээр үзүүлэв. 2. Нэгдүгээрт, цэг нь ямар нэгэн гурвалжин дотор байж болох ба дараа нь ийм гурвалжинг гурван шинэ гурвалжингаар солино. Хоёрдугаарт, хэрэв цэг нь гурвалжингийн ирмэгүүдийн аль нэгтэй давхцаж байвал энэ ирмэгтэй зэргэлдээх хоёр гурвалжин тус бүрийг хоёр шинэ гурвалжингаар солино. Бүх i цэгүүдийг нэмсний дараа гурвалжны нийт тоо (n - i - 2) + (2i) эсвэл зүгээр л n + i - 2 болно.

Цагаан будаа. 2

Энэ хэсэгт бид Delaunay гурвалжин гэгддэг тусгай төрлийн гурвалжин үүсгэх алгоритмыг танилцуулах болно. Үүссэн гурвалжнууд нь тэгш өнцөгт байх хандлагатай байдаг тул энэ гурвалжин нь сайн тэнцвэртэй байдаг. Жишээлбэл, гурвалжинг Зураг дээр үзүүлэв. 1а-г Делонай гурвалжингийн төрөлд хамааруулж болох ба Зураг дээр. 1b гурвалжинг нь хэд хэдэн өндөр сунасан гурвалжныг агуулдаг бөгөөд үүнийг Делонай төрөлд хамааруулах боломжгүй. Зураг дээр. Зураг 3-т олон тооны цэгийн багцад Delaunay гурвалжингийн жишээг үзүүлэв.

Цагаан будаа. 3

Делонай гурвалжин үүсгэхийн тулд бидэнд хэд хэдэн шинэ тодорхойлолт хэрэгтэй. Хэрэв олонлогийн бүх цэгүүд байрлах тойрог байгаа бол олонлог цэгийг дугуй гэж үзнэ. Ийм тойргийг өгөгдсөн багц цэгийн хувьд хязгаарлана. Гурвалжны хүрээлэгдсэн тойрог нь түүний гурвын (конлинеар бус) оройг бүгдийг нь дайран өнгөрдөг. Хэрэв тойрог дотор S олонлогоос ямар ч цэг байхгүй бол тойрог нь өгөгдсөн S цэгийн хувьд цэггүй болно гэж хэлдэг боловч S олонлогийн цэгүүд тухайн тойрог дээр байрлаж болно хамгийн оноогүй.

Хэрэв гурвалжин бүрийн тойрогт цэг байхгүй бол S цэгүүдийн гурвалжин нь Делонай гурвалжин болно. Гурвалжингийн диаграммд Зураг. Зураг 1а-д дотор нь өөр цэг агуулаагүй хоёр тойргийг харуулав (бусад гурвалжнуудын тойрог зурж, тэдгээр нь олонлогийн цэгүүдээс ангид байгаа эсэхийг шалгах боломжтой). Зураг дээрх диаграммд энэ дүрэм ажиглагдаагүй. 16 - өөр гурвалжны нэг цэг нь зурсан тойрог дотор унасан тул энэ грангуляци нь Делонай төрөлд хамаарахгүй.

Гурвалжингийн алгоритмыг хялбарчлахын тулд S багц дахь цэгүүдийн талаар хоёр таамаглал дэвшүүлж болно. Нэгдүгээрт, гурвалжинг огт оршин тогтнохын тулд S олонлог нь дор хаяж гурван цэгийг агуулж байгаа бөгөөд тэдгээр нь хоорондоо уялдаатай биш гэж үзэх ёстой. Хоёрдугаарт, Делонай гурвалжин нь өвөрмөц байхын тулд S олонлогийн дөрвөн цэг нэг тойрог дээр байрлахгүй байх шаардлагатай. Ийм таамаглалгүйгээр Делонай гурвалжин нь өвөрмөц биш байх болно гэдгийг харахад хялбар байдаг, учир нь нэг тойргийн 4 цэг нь хоёр өөр Делонай гурвалжинг хийх боломжийг бидэнд олгодог.

Бидний алгоритм нь одоогийн гурвалжныг нэг нэгээр нь нэг гурвалжинг тасралтгүй өсгөх замаар ажилладаг. Эхний ээлжинд одоогийн гурвалжин нь алгоритмын төгсгөлд байгаа бүрхүүлийн нэг ирмэгээс бүрдэх ба одоогийн гурвалжин нь Делауны гурвалжин болж хувирдаг. Давталт бүрт алгоритм нь холбогдох шинэ гурвалжинг хайдаг хилодоогийн гурвалжин.

Хилийн тодорхойлолт нь одоогийн гурвалжинтай харьцуулахад Делонай гурвалжингийн ирмэгийн дараах ангиллын схемээс хамаарна. Ирмэг бүр байж болно унтаж байна, амьдэсвэл үхсэн:

• унтаж буй хавирга: Алгоритмоор хараахан илрүүлээгүй бол Делонай гурвалжингийн ирмэг идэвхгүй байна;
• амьд хавирга: хавирга нь олдвол амьд, гэхдээ зөвхөн нэг зэргэлдээх хэсэг нь мэдэгддэг;
• үхсэн хавирга: Ирмэг нь олдсон бөгөөд зэргэлдээх хэсгүүд нь хоёулаа мэдэгдэж байвал түүнийг үхсэн гэж үзнэ.

Эхний үед гүдгэр i дэлбээнд хамаарах цорын ганц ирмэг нь амьд байдаг - түүний хажууд хязгааргүй хавтгай байрладаг бөгөөд бусад бүх ирмэгүүд нь унтаа байдаг. Алгоритм ажиллаж байх үед ирмэгүүд нь нойрссоноос амьд руу, үхсэн рүү шилждэг. Үе шат бүрийн хил нь амьд ирмэгүүдийн багцаас бүрдэнэ.

Давталт бүрт хилийн аль нэг ирмэгийг сонгож, хэрэв энэ муж нь f гурвалжин болж хувирвал e ирмэг хамаарах үл мэдэгдэх мужийг хайхаас бүрдэх боловсруулалт хийдэг ирмэгийн төгсгөлийн цэгүүд e ба зарим гурав дахь орой v, дараа нь ирмэг нь үхсэн болно , учир нь түүний зэргэлдээ газар аль аль нь одоо мэдэгдэж байна. Гурвалжны бусад хоёр ирмэг бүр t нь дараах төлөвт шилждэг: унтахаас амьд руу эсвэл амьдаас үхсэн рүү. Энд v оройг дуудах болно коньюгат e ирмэгтэй Үгүй бол үл мэдэгдэх муж нь хязгааргүй хавтгай болж хувирвал e ирмэг зүгээр л үхнэ. Энэ тохиолдолд e ирмэг нь коньюгат оройгүй байна.

Зураг дээр. Зураг 4-т алгоритмын үйлдлийг харуулсан бөгөөд үйлдэл нь дээрээс доошоо, алдар нь баруун тийш явагддаг. Үе шат бүрийн хилийг зузаан шугамаар тодруулсан.

Алгоритм нь delaunayTriangulate программд хэрэгждэг. Програмд ​​n цэгийн массив s өгөгдсөн бөгөөд Делонай гурвалжинг төлөөлөх гурвалжны жагсаалтыг буцаана. Хэрэгжилт нь Геометрийн өгөгдлийн бүтэц хэсгээс дугуй жагсаалтын анги болон ангиудыг ашигладаг. Толь бичгийн анги нь шаардлагатай үйлдлүүдийг дэмждэг ямар ч толь бичиг байж болно. Жишээлбэл, та #define Dictionary RandomizedSearchTree-г дарж болно.

Жагсаалт * (Цэг s, int n) ( Цэг p; Жагсаалт * гурвалжин = шинэ жагсаалт ; Толь бичиг хил хязгаар (edgeCmp); Ирмэг *e = их биеЭдж(s, n); frontier.insert(e); while (!frontier.isEmpty()) ( e = frontier.removeMin(); if (mate(*e, s, n, p)) ( updateFrontier(frontier, p, e->org); updateFrontier(frontier, e) ->dest, p triangles->insert(triangle(e->org, e->dest, p) буцах гурвалжин); )

Цагаан будаа. 4

Гурвалжин үүсгэх гурвалжнуудыг гурвалжны жагсаалтад бичнэ. Хил нь хилийн амьд захуудын толь бичигт дүрслэгдсэн байдаг. Ирмэг бүрийг чиглүүлж, түүний үл мэдэгдэх бүс (тодорхойлох) ирмэгийн баруун талд байрладаг. EdgeCmp харьцуулах функцийг толь бичгийг хайхад ашигладаг. Энэ нь хоёр ирмэгийн эхлэлийн цэгүүдийг харьцуулж, хэрэв тэдгээр нь тэнцүү бол тэдгээрийн төгсгөлийн цэгүүдийг харьцуулна.

Int edgeCmp (Edge *a, Edge *b) ( if (a->org< b->org) буцаах 1; хэрэв (a->org > b->org) 1-ийг буцаана; хэрэв (a->dest< b->dest) буцах -1; хэрэв (a->dest > b->dest) 1-ийг буцаана; буцаах 0; )

Хил нэг алхамаас нөгөө алхам руу хэрхэн өөрчлөгддөг вэ, мөн updateFrontier функц нь эдгээр өөрчлөлтүүдийг тусгахын тулд хилийн захын толь бичгийг хэрхэн өөрчилдөг вэ? Шинэ гурвалжинг t хилтэй холбоход гурвалжны гурван ирмэгийн төлөв өөрчлөгдөнө. Хилийн зэргэлдээх гурвалжны ирмэг t нь амьдаас үхсэн болж өөрчлөгддөг. updateFrontier функц нь энэ ирмэгийг үл тоомсорлож болно, учир нь removeMin функцийг дуудах үед аль хэдийн толь бичгээс хасагдсан байх ёстой. Гурвалжны үлдсэн хоёр ирмэг тус бүр нь толь бичигт бүртгэгдээгүй бол унтаж байгаа байдлаас амьд руу, эсвэл толь бичигт аль хэдийн ирмэг нь байгаа бол амьдаас үхсэн рүү өөрчлөгддөг. Зураг дээр. 5 нь хоёр тохиолдлыг харуулж байна. Зургийн дагуу бид af ирмэгийг боловсруулж, b цэг нь түүний коньюгат болохыг олж мэдсэний дараа одоогийн гурвалжинд afb гурвалжинг нэмнэ. Дараа нь бид толь бичгээс fb ирмэгийг хайж олох бөгөөд энэ нь хараахан байхгүй бөгөөд анх удаа нээгдэж байгаа тул түүний төлөв байдал нь унтаж байгаа байдлаас амьд болж өөрчлөгддөг. Толь бичгийг засахын тулд бид fb ирмэгийг эргүүлж, зэргэлдээх үл мэдэгдэх бүс нь баруун талд байрлах бөгөөд энэ ирмэгийг толь бичигт бичнэ. Дараа нь бид толь бичгээс ба ирмэгийг олох болно - энэ нь түүнд байгаа тул аль хэдийн амьд байна (түүний зэргэлдээх мэдэгдэж буй хэсэг нь abc гурвалжин юм). Түүнд үл мэдэгдэх afb гурвалжин хэсэг саяхан нээгдсэн тул энэ ирмэгийг толь бичгээс хасав.

updateFrontier функц нь a цэгээс b цэг хүртэлх ирмэгийн төлөв өөрчлөгддөг хилийн толь бичгийг засдаг.

Цагаан будаа. 5

Frontier шинэчлэлтийг хүчингүй болгох (Толь бичиг & хил, Цэг &a, Цэг & b) ( Ирмэг *e = шинэ Ирмэг (a, b); хэрэв (хил. олох (д)) хил. арилгах (e); else ( e->flip(); frontier.insert( e);

HullEdge функц нь s массив дахь n цэгийн дундаас их биений ирмэгийг олдог. Энэ функц нь бэлэг боох аргын эхлүүлэх алхам болон эхний давталтыг үнэндээ хэрэгжүүлдэг:

Edge *hullEdge (Point s, int n) ( int m = 0; for (int i = 1; i)< n; i++) if (s[i] < s[m]) m = i; swap(s, s[m]); for (m = 1, i = 2; i < n; i++) { int с = s[i].classify (s, s[m]); if ((c == LEFT) || (C == BETWEEN)) m = i; } return new Edge(s, s[m]); }

Гурвалжин функц нь параметр болгон өөрт нь дамжуулсан гурван цэгийн олон өнцөгтийг үүсгээд буцаана.

Олон өнцөгт *гурвалжин (Цэг &a, Цэг &b, Цэг & в) ( Олон өнцөгт *t = шинэ олон өнцөгт; t->оруулах (a); t->оруулах (б); t->оруулах (в); буцах t; )

Орон зайн Delaunay гурвалжин

Давхардалгүй гурвалжны сүлжээ байгуулах асуудал нь тооцооллын геометрийн үндсэн асуудлын нэг бөгөөд компьютер график, газарзүйн мэдээллийн системд гадаргуугийн загварчлал, орон зайн асуудлыг шийдвэрлэхэд өргөн хэрэглэгддэг.

Давхарддаггүй гурвалжны сүлжээг байгуулах асуудлыг анх 1934 онд Зөвлөлтийн математикч Б.Н.Делонегийн бүтээлд тавьж, холбогдох нөхцлүүдийг томъёолжээ.

Математикийн хувьд өгөгдсөн цэгүүдээс гурвалжин байгуулах даалгавар нь тэдгээрийг огтлолцдоггүй сегментээр хосоор нь холбож гурвалжны сүлжээ үүсгэх даалгавар юм. Үүний гол элементүүд нь (Зураг 5.3): зангилаа (гурвалжны орой), ирмэг (тал) ба нүүр (гурвалжин өөрөө). Баригдсан гурвалжин нь гүдгэр (хэрэв энэ нь загварчлалын талбайг хамарсан хамгийн бага олон өнцөгт бол), гүдгэр бус (хэрэв гурвалжин нь гүдгэр биш бол) болон оновчтой (хэрэв бүх ирмэгийн уртын нийлбэр хамгийн бага бол) байж болно.

Ийм гурвалжнуудын сүлжээг тодорхой нөхцлийг хангасан тохиолдолд Делонай гурвалжин гэж нэрлэдэг.

Анхны цэгүүдийн аль нь ч гурвалжны эргэн тойронд хүрээлэгдсэн тойрог дотор ордоггүй (Зураг 5.3);

Гурвалжин нь гүдгэр бөгөөд дээр дурдсан Делауны нөхцлийг хангадаг;

Бүх гурвалжны хамгийн бага өнцгийн нийлбэр нь бүх боломжит гурвалжны дээд хэмжээ юм;

Гурвалжны эргэн тойронд дүрслэгдсэн тойргийн радиусуудын нийлбэр нь бүх боломжит гурвалжингийн дунд хамгийн бага байна.

Дугуй гэж нэрлэгддэг Делонай гурвалжинг бүтээх дээрх шалгууруудын эхнийх нь гол шалгууруудын нэг бөгөөд нийтлэг нүүртэй гурвалжингуудыг шалгадаг. Шалгуурын математик тайлбарыг Зураг дээр үзүүлэв. 5.3:

(5.2)

Сүүлийн үед гурвалжингийн тор барих хамгийн алдартай аргуудын нэг болох Делонай гурвалжинг бүтээх олон арга бий. Энэ нь олон GIS системд тусламжийн загвар бүтээхэд ашиглагддаг.

Хоёр хэмжээст орон зайд хэрэглэхдээ дараах байдлаар томьёолно: үүссэн гурвалжны эргэн тойронд дүрслэгдсэн тойрог дотор оройнуудын аль нь ч орохгүй бол хоорондоо холбогдсон давхцаагүй гурвалжнуудын систем хамгийн бага периметртэй байна (Зураг 5.4).

Цагаан будаа. 5.4. Делоны гурвалжин

Энэ нь ийм гурвалжин хэлбэртэй гурвалжнууд нь ижил талт гурвалжнуудтай аль болох ойрхон байх ба эсрэг талын оройноос үүссэн гурвалжны тал бүр нь харгалзах хагас хавтгайн бүх боломжит цэгүүдээс хамгийн их өнцгөөр харагдана гэсэн үг юм. Энэ нь яг л хамгийн оновчтой гурвалжингийн ирмэг дээр шугаман интерполяцийг ихэвчлэн изолиныг бүтээхэд хийдэг.

Delaunay гурвалжинг бүтээх олон алгоритмууд дараах теоремыг ашигладаг.

Теорем 1. Дэлоны нөхцөлийг хангахгүй зэргэлдээх ABC болон BCD гурвалжнуудын хосыг ABD ба ACD гурвалжны хос болгон дэс дараалан байрлуулах замаар ижил цэгийн системийг ашиглан бусад дурын гурвалжнаас Делоны гурвалжинг гаргаж болно (Зураг 5.5).

Цагаан будаа. 5.5.. Делоны нөхцөлийг хангаагүй гурвалжныг сэргээн босгох

Энэхүү сэргээн босгох ажиллагааг ихэвчлэн эргүүлэх гэж нэрлэдэг. Энэ теорем нь Делоны гурвалжинг дараалан байгуулах боломжийг олгодог бөгөөд эхлээд зарим гурвалжинг байгуулж, дараа нь Делоны нөхцөлийн утгаараа дараалан сайжруулдаг. Зэргэлдээх гурвалжны хосуудын хувьд Делауны нөхцөлийг шалгахдаа та тодорхойлолтыг шууд ашиглаж болох боловч заримдаа дээр дурдсан нөхцлүүдэд үндэслэн бусад аргуудыг ашигладаг.

Эдгээр нөхцөлд бүх гурвалжингийн нийт шинж чанар (хамгийн бага өнцгийн нийлбэр эсвэл радиусын нийлбэр) гарч ирнэ, аль нь Делонай гурвалжинг олж авах боломжтойг оновчтой болгосноор.

Дээр дурьдсанчлан гурвалжин үүсгэх үед хийгддэг хамгийн чухал үйлдлүүдийн нэг бол өгөгдсөн хос гурвалжны хувьд Делонегийн нөхцөлийг шалгах явдал юм. Делонай гурвалжингийн тодорхойлолт ба холбогдох нөхцлүүдэд үндэслэн практикт баталгаажуулах хэд хэдэн аргыг ихэвчлэн ашигладаг.

– тойргийн тэгшитгэлээр шалгах;

- урьдчилан тооцоолсон тойргийн дагуу шалгах;

– эсрэг талын өнцгүүдийн нийлбэрийг шалгах;

– эсрэг өнцгүүдийн нийлбэрийг өөрчилсөн шалгах.

Олон системүүд туршилтыг урьдчилан тооцоолсон тойрог хэлбэрээр гүйцэтгэдэг. Урьдчилан тооцоолсон тойргоор дамжуулан баталгаажуулах алгоритмын гол санаа нь баригдсан гурвалжин бүрийн хувьд тойргийн төв ба радиусыг урьдчилан тооцоолох явдал бөгөөд үүний дараа Делауны нөхцөлийг шалгах нь төв хүртэлх зайг тооцоолоход багасах болно. Энэ тойргийн үр дүнг радиустай харьцуулах. Эргэн тойронд дүрслэгдсэн тойргийн төв ба радиус r-ийг , , , r 2 = (b 2 + c 2 - 4аd)/4а 2 гэж харж болно. a B C D(5.3) томъёогоор тодорхойлно.

(5.3)

Энэ тойргийн тэгшитгэлийн өөр нэг оруулга нь:

(5.5.)

(5.6)

Дараа нь бусад гурвалжингийн цэгийн хувьд дараах тохиолдолд л Делоны нөхцөл хангагдана.

(x 0 – x C) 2 + (y 0 – y C) 2 ≥ r 2 . (5.7)

Одоогийн байдлаар Delaunay гурвалжинчлалыг бий болгох олон алгоритмууд байдаг. Олон алдартай алгоритмууд нь Delaunay гурвалжингийн тодорхойлолтыг хоёрдогч гурвалжингийн шинж чанар болгон ашигладаг. Тиймээс ийм алгоритмуудад дараахь сул талуудыг тэмдэглэв.

– алгоритмууд нь байнгын тооцоолсон тригонометрийн функцуудыг ашигладаг бөгөөд энэ нь үйл явцыг эрс удаашруулдаг;

- цэгүүд ба үндсэн сегментийн хоорондын хамаарлыг судлахад маш жижиг өнцөгүүд гарч ирдэг бөгөөд тригонометрийн функцийг ашиглах үед компьютерт өгөгдөл дүрслэх нарийвчлал хязгаарлагдмал тул дараалал, 0-д хуваагдах аюул үргэлж байдаг; байнгын нэмэлт боловсруулалт шаарддаг.

Хамгийн алдартай програм хангамжийн бүтээгдэхүүнүүд нь хоосон бөмбөг теоремыг гурвалжин байгуулах үндсэн, үндсэн зарчим болгон ашиглан Делонай гурвалжинг бүтээдэг. Алгоритм нь дараах байдлаар харагдаж байна.

– бүх цэгүүдийг гурвалжинд хуваана, өөрөөр хэлбэл. гурван цэгийн хослолууд үүссэн;

- хослол бүрийн хувьд хүрээлэгдсэн тойрог ба түүний төвийн координатыг олно;

– Хэрэв одоогийн хослолын тойрог дотор үлдсэн ганц цэг байхгүй бол энэ хослол нь гурвалжин болно - Делонай гурвалжингийн нэг хэсэг.

Энэхүү алгоритмын давуу талууд нь:

– барилгын үйл явцыг удаашруулдаггүй тригонометрийн функцийг ашиглахгүй байх;

– Урьдчилсан барилга байгууламжгүйгээр Делонай гурвалжинг шууд барих;

- бүх тооцоо, хувиргалтын энгийн байдал;

– үр дүнд нь гурвалжингийн сүлжээг бие даасан шугамаар бус олон гурвалжингаар төлөөлдөг.

Ийм аргаар хийсэн гурвалжин нь изолиныг барих геометрийн суурь юм.

Delaunay гурвалжинг бүтээх алгоритмыг ашигласан оролтын өгөгдлийн бүтэц, тооцоолох үйлдлүүдийн хэмжээ, анхны байр гэх мэтээр ялгаатай хэд хэдэн бүлэгт хувааж болно. Тэдгээрийн заримыг авч үзье.

Алгоритмуудыг нэгтгэх нь эх үүсвэрийн багцыг дэд олонлогт хувааж, тус бүр дээр гурвалжин үүсгэх, дараа нь тэдгээрийг нэг сүлжээнд нэгтгэх явдал юм. Эдгээр алгоритмуудын аль нэгний мөн чанар нь дараах байдалтай байна.

Анхны цэгүүдийн багцыг босоо шугамаар хоёр ба түүнээс дээш хэсэгт хувааж, дараа нь тус бүрийг хэвтээ ба босоо шугамаар ойролцоогоор тэнцүү хэсгүүдэд хуваана. Үүний үр дүнд эхлэлийн цэгүүдийн бүх талбайг гурваас дөрвөн цэгийн командуудад хуваадаг (Зураг 2.4), тэдгээрийн дагуу нэг эсвэл хоёр гурвалжин баригдсан байна.

Эдгээр гурвалжныг нэг сүлжээнд нэгтгэх нь хоёр үндсэн шугамыг бий болгох замаар хийгддэг (P 0 P 1 ба P 2 P 3, будаа. 5.7.а), суурь шугамын перпендикуляр биссектрист төвлөрсөн хувьсах радиустай тойрог зурах (Зураг 5.7, b), тойрог дээр унах зангилаа хайх (цэг). А, будаа. 5.7. в) шинэ гурвалжин байгуулах (P 0 P 1 A).Энэ тохиолдолд одоо байгаа гурвалжинг устгах шаардлагатай байж магадгүй (жишээлбэл, P 0 AB).

Давталтын алгоритмууд нь хэсэгчилсэн гурвалжинд цэгүүдийг дараалан нэмэх санаан дээр суурилж, Делауны шалгуурын дагуу сайжруулж, сэргээн засварлах ажлыг нэгэн зэрэг хийдэг. Ерөнхийдөө эдгээр нь хэд хэдэн алхмуудыг багтаасан бөгөөд эхний гурван эхлэлийн цэг дээр гурвалжин байгуулж, дараагийн цэгийг байрлуулах хэд хэдэн сонголтыг судлах болно. Ялангуяа загварчлалын талбайн хилээс гадуур, одоо байгаа зангилаа эсвэл ирмэг дээр, баригдсан гурвалжин дотор гэх мэт хувилбаруудыг авч үздэг. Эдгээр сонголт бүр нь тодорхой үйлдлийг гүйцэтгэдэг: ирмэгийг хоёр, нүүрийг хуваах. гурав гэх мэт; Үүний дараа үүссэн гурвалжингууд нь Делауны нөхцөлтэй нийцэж байгаа эсэхийг шалгаж, шаардлагатай сэргээн босголтыг хийнэ.

Хоёр дамжлагын алгоритмууд нь эхлээд Делауны нөхцлийг үл тоомсорлож, зарим гурвалжинг хийж, дараа нь эдгээр нөхцлийн дагуу сэргээн босгохыг хамардаг. Алгоритмыг ашиглах жишээг Зураг дээр үзүүлэв. 5.8.

Бүтээсэн тусламжийн загварыг бодит байдалд ойртуулахын тулд түүний шугаман болон талбайн бүтцийн элементүүдийг харгалзан үзэж, харуулахын тулд нэмэлт элементүүдийг оруулав. Ийм нэмэлт элементүүд нь "тусламжийн араг яс" -ыг тодорхойлдог топографид өргөн хэрэглэгддэг бүтцийн шугамууд юм: усны хагалбар, хавцал, хяр, хад, эрэг, нуур, жалга, эрэг, хиймэл байгууламжийн хил хязгаар гэх мэт. Делонай гурвалжингийн хүрээ. Эдгээр бүтцийн шугамуудыг гурвалжинд гурвалжны ирмэг болгон нэвтрүүлсэн бөгөөд энэ нь дэлхийн гадаргуугийн ерөнхий тэгш бус байдлын дэвсгэр дээр бодит тусламжийн элементүүдийг загварчлахад хүргэдэг. Ийм ирмэгийг бүтцийн (тогтмол, дахин тохируулах боломжгүй) гэж нэрлэдэг бөгөөд бусад гурвалжны ирмэгийг огтолж болохгүй, дараа нь өөрчлөгддөггүй.

Зэргэлдээх гурвалжны аль ч хосын хувьд Делоны нөхцөл хангагдсан тохиолдолд таслалтын шугамаар тусгаарлагдаагүй гадаргуугийн загварыг бий болгох асуудлыг хязгаарлагдмал Делоны гурвалжин гэж нэрлэдэг. Судлаачдын үзэж байгаагаар хамгийн үр дүнтэй арга бол давталтын алгоритмуудыг ашиглан ийм гурвалжин үүсгэх явдал юм.

Delaunay гурвалжин үүсгэх алгоритмууд нь зангилааны координатыг бодит эсвэл бүхэл тоогоор илэрхийлдэг бөгөөд энэ нь боловсруулалтын хурд, нарийвчлалыг мэдэгдэхүйц нэмэгдүүлэх боломжтой боловч тохирох зангилааг хайх, хасах асуудал үүсгэдэг.

TIN загварыг зангилаануудыг хөдөлгөх, шинээр оруулах, байгаа хэсгийг нь устгах, нэг буюу хэд хэдэн ирмэгийн байрлалыг өөрчлөх, бүтцийн шинэ шугам оруулах гэх мэтээр хялбархан засварладаг. Ийм өөрчлөлтүүд нь зэргэлдээх гурвалжны жижиг бүлэгт үргэлж нөлөөлдөг тул дахин барих шаардлагагүй. Сүлжээг бүхэлд нь холбож, курсорыг харгалзах элемент рүү чиглүүлэх замаар онлайнаар гүйцэтгэдэг.

Нарийвчлалын тухай:

Тусламжийн онцлог шинж чанартай элементүүд (жишээлбэл, усны хагалбар ба thalwegs) дээр пикет байрлуулснаар бид цоорхой дахь жижиг элементүүдийг үл тоомсорлодог. Гурвалжны ийм ирмэгийн дагуу контурын шугамыг1 барихад алдаа гардаг бөгөөд энэ нь газрын тэгш бус байдлын хэмжээ, газрын налуу өнцгөөс хамаарна. Жишээлбэл, рельефийн судалгаа хийх дундаж алдаа нь 2-10 градусын налуу өнцгөөр рельефийн хөндлөн огтлолын 1/3-аас хэтрэхгүй байх ёстой. 0.5 м-ийн рельефийн хэсэгтэй бол алдсан тэгш бус байдлын хамгийн их утга (өөрөөр хэлбэл зэргэлдээх пикетээр дамжин өнгөрөх газрын гадаргуугийн шулуун шугамаас хазайх) нь (0.5/3) * cos10 ° -аас хэтрэхгүй байх ёстойг тооцоолж болно. = 0.16 м.

Тээвэрлэсэн хөрсний эзэлхүүнийг үнэн зөв тодорхойлохын тулд тооцоогүй рельефийн хэсгүүдийн эзэлдэг талбай нь бас чухал юм. Хоёр хос пикетийн хоорондох 20х20 м-ийн квадратад хамгийн ихдээ 0.15 м өндөртэй цилиндр хэлбэртэй гүдгэр байна гэж бодъё, энэ гадаргууг зөвхөн хоёр гурвалжингаар дүрслэхдээ үүнийг тооцохгүй байх нь амархан алдаа нь ойролцоогоор 40 м3 байна. Тийм ч их биш, гэхдээ толгод эсвэл налуугийн дээд (ихэвчлэн гүдгэр) хэсэгт байрлах 1 га талбайн хувьд та 40 * 25 = 1000 м3 илүүдэл хөрс авдаг. Хэрэв та хоёр дахин олон удаа пикет авбал (өөрөөр хэлбэл 10 м тутамд) алдаа дөрөв дахин буурч, нэг га талбайд 250 м3 болно. Хавтгай рельефийн эерэг хэлбэрүүд нь ихэвчлэн гүдгэр хэлбэртэй байдаг бол сөрөг хэлбэрүүд нь хотгор хэлбэртэй байдаг тул энэ хүчин зүйлийг урьдчилан анхаарч үзэх боломжтой. Хэрэв судалгаа хийх талбай нь рельефийн талаархи ойролцоо мэдээлэлтэй бол гадаргуугийн муруйлтын радиус ба пикетийн шаардлагатай нягтыг контурын шугам эсвэл бие даасан өндөрлөгүүдийн утгуудаас хялбархан тооцоолж болно.

Лекцийн бүтэц Тодорхойлолт Тодорхойлолт Хэрэглэх талбарууд Хэрэглэх талбарууд Delauny triangulation-ийн шинж чанарууд Delauny triangulation-ийн шинж чанарууд Delaunay triangulation-ийг бий болгох арга замууд Delaunay triangulation-ийг бий болгох арга замууд. -алхам алхмаар түүвэрлэлтийн арга Задрах арга Задрах арга Сканнердах арга Сканнердах арга Хоёр дамжих арга Хоёр дамжих арга

Гурвалжин гурвалжин нь дотоод мужууд нь бүгд гурвалжин байдаг хавтгай график юм. Гурвалжин нь дотоод мужууд нь бүгд гурвалжин хэлбэртэй хавтгай график юм. "Triangulation" гэсэн нэр томъёо нь "Triangulation" гэсэн нэр томъёо нь график юм; график; график бүтээх үйл явц. график бүтээх үйл явц. S цэгийн багцын гурвалжингийн бодлого нь S олонлогийн бүх цэгүүдийг салангид хэрчмүүдтэй холбож гурвалжингийн графикийг олж авах асуудал юм. S цэгийн багцын гурвалжингийн бодлого нь S олонлогийн бүх цэгүүдийг салангид хэрчмүүдтэй холбож гурвалжингийн графикийг олж авах асуудал юм. Гурвалжингийн тодорхойлолт С цэгийн багц

Графикийн бүх ирмэгийн уртын хамгийн бага нийлбэр бүхий гурвалжинг оновчтой гурвалжин гэнэ. Графикийн бүх ирмэгийн уртын хамгийн бага нийлбэр бүхий гурвалжинг оновчтой гурвалжин гэнэ. ! Алдартай, гэхдээ маш их цаг хугацаа шаардсан асуудал O(2 n)! Практикт оновчтой гурвалжингийн ойролцоо (ойролцоогоор) ашигладаг: "Шунам" гурвалжин O(N 2 *logN) "Шунам" гурвалжин O(N 2 *logN) Delaunay triangulation O(N*logN) Delaunay triangulation O(N*logN) ) Оновчтой гурвалжингийн тодорхойлолт

Делоны гурвалжин (DT(S)) нь Делонегийн нөхцөлийг хангасан гүдгэр гурвалжин юм: Делоны гурвалжин (DT(S)) нь Делонегийн нөхцөлийг хангадаг гүдгэр гурвалжин юм: графикийн оройн аль нь ч тойрон хүрээлэгдсэн тойрог дотор орох ёсгүй. түүний аль нэг гурвалжин. Графикийн аль ч орой нь түүний гурвалжны аль нэгийг тойрон хүрээлэгдсэн тойрог дотор орох ёсгүй. Делоны гурвалжингийн тодорхойлолт Делоны нөхцөл хангагдлаа Делоны нөхцөл хангагдаагүй байна B.N. Delaunay()

Delaunay triangulation-ийн хэрэглээ VG-ийн бусад бодлогод VG-ийн бусад бодлогод Цэгүүдийн багцын хамгийн бага хэмжээ Цэгүүдийн багцын хамгийн бага хүрээ Хамгаалалтын бүс байгуулах Орчны бүс байгуулах бүс) Хамгийн их хоосон тойргийг олох Хамгийн их хоосон тойргийг олох г.м. CG, GIS, GM-ийн CAD дахь хэрэглээнд CG, GIS, GM-ийн CAD дахь хэрэглээнд Гадаргуугийн олон өнцөгт загварууд Гадаргуугийн полигональ загварууд ГМС дэх рельефүүд, барималууд , үйлдвэрлэлийн загвар, тоглоом дахь загвар, GIS дахь рельеф, баримал, үйлдвэрлэлийн .загвар, тоглоом дахь загвар, Загварын тоон шинжилгээ Загварын тоон шинжилгээ Isolines, Isoclines, FEM. Isolines, Isoclins, FEM.

Аливаа гүдгэр гурвалжны шинж чанарууд 1. m нь дотоод байх n цэгийн олонлогт Гурвалжин гурвалжны тоо = n + m – 2 Гурвалжин гурвалжны тоо = n + m – 2 Гурвалжингийн ирмэгийн тоо 3n – 6 Гурвалжингийн ирмэгийн тоо 3n – 6 Жишээ: Оноо (n) – 13 Оноо (n) – 13 Дотоод (м) – 4 Дотоод (м) – 4 Гурвалжин – 15 = Гурвалжин – 15 = Ирмэг – 26 3*13-6 = 33 Ирмэг – 26 3 *13-6 = 33

Делонай гурвалжингийн шинж чанарууд 2. Делонай гурвалжин нь бүх гурвалжны боломжит гурвалжны дундах бүх гурвалжны хамгийн бага өнцгийн хамгийн их нийлбэртэй байна. 3. Делонай гурвалжин нь бүх боломжит гурвалжнуудын дунд гурвалжнуудын эргэн тойронд дүрслэгдсэн тойргийн радиусуудын хамгийн бага нийлбэртэй байна. Delaunay гурвалжин БИШ Delaunay гурвалжин

Delaunay triangulation байгуулах арга Алхам алхмаар оруулах аргууд Алхам алхмаар оруулах аргууд Давталтын алгоритмууд () Давталтын алгоритмууд () Алхам алхмаар түүвэрлэлтийн аргууд Алхам алхмаар түүвэрлэлтийн аргууд Шууд (алхам алхмаар) барих алгоритмууд (3) Шууд (алхам алхмаар) бүтээх алгоритмууд (3) Задаргааны аргууд Задаргааны аргууд Нэгтгэх алгоритмууд (2 ) Алгоритмуудыг нэгтгэх (2) Скан хийх аргууд Сканнердах аргууд Цэг нэмэх дарааллыг өөрчилсөн давталттай алгоритмууд (1.4) цэг нэмэх дараалал өөрчлөгдсөн (1.4) Хоёр дамжих алгоритм (4) Хоёр дамжлагын алгоритм (4)

Алхам алхмаар оруулах аргууд Давталтын алгоритмууд () Делоны гурвалжин үүсгэх давтагдах алгоритмын ерөнхий схем 1. Эхний гурван цэг дээр нэг гурвалжин байгуулах 2. S олонлогийн үлдсэн бүх p i цэгийг давталт хийх 3. Цэгтэй хамгийн ойр байрлах t j гурвалжинг ол. Одоогийн гурвалжны p i 4. Хэрэв p i цэг нь t j гурвалжны гадна байвал хамгийн ойрын ирмэг хүртэл гурвалжинг байгуул. 5. Хэрэв p i цэг нь t j гурвалжны дотор байвал гурвалжинг гурав хуваа. 6. Хэрэв p i цэг ирмэг дээр байгаа бол зэргэлдээх гурвалжингуудыг хос болгон хуваа. 7. Хөршүүдийн хувьд Делауны нөхцөлийг зөрчсөн тохиолдолд хөрш гурвалжингуудыг дахин барина. Гурвалжин хайлтыг хурдасгах сонголтууд: Гурвалжин индексжүүлэх (мод) – O(лог n) Гурвалжин индексжүүлэх (мод) – O(лог n) Гурвалжин кэш (тор) – O(s) Гурвалжин кэш (тор) – O(s)

Алхам алхмаар түүвэрлэлтийн аргууд Шууд (алхам алхмаар) барих алгоритмууд (3) Өмнө нь баригдсан зүйлийг дахин бүтээхгүйгээр шаардлагатай гурвалжингуудыг нэн даруй барина. Delaunay гурвалжинг шууд байгуулах алгоритмын ерөнхий схем Боловсруулаагүй ирмэгийн стекийг ашиглах нь тохиромжтой. 1. S цэгүүдийн гүдгэр их биений дурын ирмэг q-г ол. 3. Түүхий ирмэгийн стек хоосон болтол гогцоо. 4. Стекээс ирмэг v-г гарга. 5. v ирмэгийн хувьд Делоны нөхцөлийг хангасан p цэгийг ол (Дэлоны хөрш) 6. Хэрэв Делонай хөрш p олдвол 7. v ирмэгээс p цэг хүртэл гурвалжин байгуул. 8. Шинэ гурвалжны шинэ ирмэгийг түүхий ирмэгийн стек рүү түлхэнэ. Delaunay хөршийн хайлтыг хурдасгах сонголтууд: k-D-модтой цэгүүдийг индексжүүлэх – O(log n) k-D-модтой индексжүүлэх цэгүүд – O(log n) Цэгүүдийн үүрэн индексжүүлэлт – O(c) цэгүүдийн үүрэн индексжүүлэлт – O(c) )

Шунахай Delaunay гурвалжингийн алгоритмын үйл явц

Задаргааны аргууд Нэгтгэх алгоритмууд (2) Дэд олонлогт хуваах, бие даасан боловсруулалт, үр дүнг нэгтгэх. Алгоритмуудыг нэгтгэх ерөнхий схем 0. S олонлогт 3-аас илүүгүй цэг байхгүй бол шууд өөрөөр байгуулна 1. S цэгүүдийн олонлогийг ойролцоогоор тэнцүү дэд олонлогт хуваа. 1. S цэгүүдийн багцыг ойролцоогоор тэнцүү дэд олонлогт хуваа. 2. Дэд олонлогт зориулсан гурвалжин байгуулах. 2. Дэд олонлогт зориулсан гурвалжин байгуулах. 3. Үүссэн гурвалжингуудыг нэгтгэх. 3. Үүссэн гурвалжингуудыг нэгтгэх. Дэд олонлогт хуваах аргууд Ортогональ шулуун шугамууд Ортогональ шулуунууд Гүдгэр их биений голчоор гүдгэр их биений диаметрээр Судал зураасууд

Алгоритмуудыг нэгтгэх (2) Гурвалжинг нэгтгэх арга "Устгах ба барих" (барилга барихаас өмнө шалгах) "Устгах ба барих" (барилга барихаас өмнө шалгах) "Барьж дахин барих" (барилга дууссаны дараа шалгах) "Барьж дахин барих" (барилгын дараа шалгах) " Барилга, сэргээн босгох" (барилгын явцад шалгах) "Барилга, дахин барих" (барилга угсралтын явцад шалгах)

Цэг нэмэх дарааллыг өөрчилсөн давталтын аргын ерөнхий схем 1. Цэгүүдийг цэгцлэх (үйл явдлын цэгүүдийн жагсаалтыг гаргах) 2. Бүх үйл явдлын цэгүүдийг сканнердах 3. p i цэг бүрт өмнөх гурвалжин руу гурвалжин байгуулна. 4. Хөршүүдийн хувьд Делауны нөхцөлийг зөрчсөн тохиолдолд хөрш гурвалжингуудыг дахин барина. Скан хийх аргууд Цэг нэмэх дарааллыг өөрчилсөн давталттай алгоритмууд (1.4)

Сканнердах аргууд Үйл явдлын цэгүүдийг эрэмбэлэх аргууд Шулуун шугаман Туйлт (дугуй, сэнс хэлбэртэй) Туйлт (дугуй, сэнс хэлбэртэй) Судал зураастай дөрвөлжин Гильбертийн муруйгаар Хилбертийн муруйгаар Z кодоор Z кодоор Зорилго: Нэн даруй хамгийн ихдээ барих сайн гурвалжин Хамгийн их сайн гурвалжинг нэн даруй байгуулах Эгнээний өөрчлөлтийн тоог багасгах, эгнээний өөрчлөлтийн тоог багасгах

Делонай гурвалжингийн аргуудын хураангуй шинж чанарууд Гурвалжингийн арга Дундаж хугацаа Хамгийн муу цаг хугацаа сек/т Хэрэгжүүлэхэд хялбар. Алхам алхмаар оруулах аргууд Алхам алхмаар оруулах аргууд Давталтын алгоритмууд () Давталтын алгоритмууд ()O(n)- O(n 3/2) O(n 2) 1.5-9.2 2-5 Алхам алхмаар дээж авах арга Алхам алхмаар түүвэрлэлтийн арга Шууд барих арга (3) Шууд барих арга (3) O(n)- O(n 2) O(n 2) -2 Задрах арга Задрах арга Нэгтгэх арга (2) Нэгтгэх арга ( 2) O(n)- O(nlogn) O (nlogn)- O(n 2) 2.5-4.52-3 Скан хийх аргууд Сканнердах аргууд Цэг нэмэх дарааллын өөрчлөлттэй давталт (1.4) Цэг нэмэх дарааллыг өөрчилсөн давталт ( 1.4)O(n) O(n 2) 1 ,9-5,34-5 Хоёр дамжих аргууд (4) Хоёр дамжих аргууд (4) O(n)- O(n 2) O(nlogn)- O (n 2) 2.2-15.41-5 Скворцов зөвлөж байна: динамик кэштэй давталтын алгоритм

Өнөөдөр юу болж байна вэ? Delaunay гурвалжингийн тухай! Тодорхойлолт Тодорхойлолт Хэрэглэх талбарууд Хэрэглэх талбарууд Delauny triangulation-ийн шинж чанарууд Delaunay triangulation-ийн шинж чанарууд Делонай гурвалжинжуулалтыг бий болгох арга замууд Delaunay triangulation-ийг бий болгох аргууд Алхам алхмаар оруулах аргууд Алхам алхмаар оруулах аргууд -шатлалт түүвэрлэлтийн арга Задрах арга Задрах арга Сканнердах арга Сканнердах арга Хоёр дамжих арга Хоёр дамжих арга