Өсөх, багасгах функцууд

функц y = е(x) интервал дээр нэмэгдэх гэж нэрлэдэг [ а, б], хэрэв ямар нэг хос оноотой бол XТэгээд X", a ≤ x тэгш бус байдал биелнэ е(x) ≤ е (x"), мөн хатуу нэмэгдүүлэх - хэрэв тэгш бус байдал е (x) f(x"). Буурах ба хатуу буурах функцийг ижил төстэй байдлаар тодорхойлдог. Жишээлбэл, функц цагт = X 2 (будаа. , a) сегмент дээр хатуу нэмэгддэг , ба

(будаа. , б) энэ сегмент дээр хатуу буурдаг. Өсөн нэмэгдэж буй функцуудыг тодорхойлсон е (x), буурч байна е (x)↓. е (xДифференциалагдах функцтэй байхын тулд ) сегмент дээр нэмэгдэж байв [, бА е"(x], түүний дериватив нь зайлшгүй бөгөөд хангалттай юм ) сегмент дээр нэмэгдэж байв [, б].

) сөрөг биш байсан [ цагт = е (xХэсэг дээрх функцийн өсөлт, бууралтын зэрэгцээ бид тухайн цэг дэх функцийн өсөлт, бууралтыг авч үздэг. Чиг үүрэг x) цэг дээр нэмэгдэж байгаа гэж нэрлэдэг xХэрэв цэгийг агуулсан интервал (α, β) байвал 0 X 0, аль ч цэгийн хувьд -аас (α, β), x x> е (x 0) ≤ е (x 0, тэгш бус байдал нь биелнэ X 0, аль ч цэгийн хувьд ) болон аль ч цэгийн хувьд е (x) x 0, тэгш бус байдал биелнэ (x≤ f x 0). Цэг дэх функцийн хатуу өсөлтийг ижил төстэй байдлаар тодорхойлно е"(x 0) > 0 . Хэрэв е(x 0, дараа нь функц x 0). Цэг дэх функцийн хатуу өсөлтийг ижил төстэй байдлаар тодорхойлно е (x) цэг дээр хатуу нэмэгддэг а, б) интервалын цэг бүрт нэмэгддэг (

), дараа нь энэ интервалд нэмэгдэнэ.

С.Б.Стечкин.. 1969-1978 .

Зөвлөлтийн агуу нэвтэрхий толь бичиг. - М .: Зөвлөлтийн нэвтэрхий толь бичиг

Бусад толь бичгүүдээс "Өсөх, бууруулах функцүүд" гэж юу болохыг харна уу. Математик анализын тухай ойлголтууд. f(x) функцийг ХҮН АМЫН НАСНЫ БҮТЭЦ сегмент дээр нэмэгдэж буй хүн амын янз бүрийн насны бүлгийн тооны харьцаа гэж нэрлэдэг. Төрөлт, нас баралтын түвшин, хүмүүсийн дундаж насл...

Том нэвтэрхий толь бичиг Математик анализын тухай ойлголтууд. Хэрэв x1 ба x2 хос цэгүүдийн хувьд a≤x1 ... байвал f(x) функц хэрчм дээр нэмэгдэж байна гэж хэлнэ.

Нэвтэрхий толь бичиг<или=х1 <х<или=b, выполняется неравенство f(x1)Математикийн тухай ойлголтууд. шинжилгээ. f(x) функцийг дуудна. [a, b] сегмент дээр нэмэгдэх, хэрэв x1 ба x2 цэгүүдийн аль нэг хосын хувьд, мөн

Байгалийн шинжлэх ухаан. Нэвтэрхий толь бичиг Функцийн дериватив ба дифференциал, тэдгээрийн функцийг судлахад хэрэглэхийг судалдаг математикийн салбар. Дизайн Д. ба. Математикийн бие даасан салбар болох нь И.Ньютон, Г.Лейбниц нарын нэрстэй холбоотой (17 оны хоёрдугаар хагас ...

Дериватив ба дифференциал гэсэн ойлголт, тэдгээрийг функцийг судлахад хэрхэн ашигладаг талаар судалдаг математикийн салбар. D.-ийн хөгжил ба. интеграл тооцооллын хөгжилтэй нягт холбоотой. Тэдний агуулга нь бас салшгүй юм. Тэд хамтдаа үндэс суурийг бүрдүүлдэг ... ... Математик нэвтэрхий толь бичиг

Энэ нэр томъёо нь өөр утгатай, функцийг үзнэ үү. "Дэлгэц" хүсэлтийг энд дахин чиглүүлсэн; бусад утгыг бас үзнэ үү... Википедиа

Аристотель ба перипатетикууд- Аристотелийн асуулт Аристотель Аристотель 384/383 онд төрсөн. МЭӨ д. Македонтой хиллэдэг Стагира хотод. Түүний эцэг Никомахус нь Филипийн эцэг Македонийн хаан Аминтасын үйлчлэлийн эмч байжээ. Залуу Аристотель гэр бүлийнхээ хамт...... Барууны философи үүссэнээс өнөөг хүртэл

- (QCD), квантын дүр төрхөөр бүтээгдсэн кварк ба глюонуудын хүчтэй харилцан үйлчлэлийн квант талбайн онол. "өнгөт" хэмжигч тэгш хэм дээр суурилсан электродинамик (QED). QED-ээс ялгаатай нь QCD дахь фермионууд нэмэлт шинж чанартай байдаг. эрх чөлөөний квант зэрэг тоо, …… Физик нэвтэрхий толь бичиг

Би зүрх Зүрх (Латин кор, Грекийн кардиа) нь шахуургын үүрэг гүйцэтгэдэг, цусны эргэлтийн систем дэх цусны хөдөлгөөнийг хангадаг хөндий фибромускуляр эрхтэн юм. Анатоми Зүрх нь перикардийн урд дунд гэдэсний (Mediastinum) ... хооронд байрладаг. Анагаах ухааны нэвтэрхий толь бичиг

Ургамлын амьдрал нь бусад амьд организмын нэгэн адил харилцан уялдаатай үйл явцын цогц цогц юм; Тэдгээрийн хамгийн чухал нь хүрээлэн буй орчинтой бодис солилцох явдал юм. Хүрээлэн буй орчин нь эх сурвалж юм....... Биологийн нэвтэрхий толь бичиг

Дериватив. Хэрэв функцийн дериватив интервалын аль нэг цэгт эерэг байвал функц нь сөрөг байвал буурна;

Функцийн өсөлт ба бууралтын интервалыг олохын тулд түүний тодорхойлолтын муж, деривативыг олох, F’(x) > 0 ба F’(x) хэлбэрийн тэгш бус байдлыг шийдвэрлэх шаардлагатай.

Шийдэл.

3. y’ > 0 ба y’ 0 тэгш бус байдлыг шийд;
(4 - x)/x³

Шийдэл.
1. Функцийн тодорхойлолтын мужийг олъё. Мэдээжийн хэрэг, хуваагч дахь илэрхийлэл нь үргэлж тэгээс ялгаатай байх ёстой. Иймд 0-ийг тодорхойлолтын мужаас хассан: функц нь x ∈ (-∞; 0)∪(0; +∞)-ийн хувьд тодорхойлогддог.

2. Функцийн деривативыг тооцоол.
y'(x) = ((3 x² + 2 x - 4)' x² – (3 x² + 2 x - 4) (x²)')/x^4 = ((6 x + 2) x² – (3 x²) + 2 x - 4) 2 x)/x^4 = (6 x³ + 2 x² – 6 x³ – 4 x² + 8 x)/x^ 4 = (8 x – 2 x²)/x^4 = 2 (4) - x)/x³.

3. y’ > 0 ба y’ 0 тэгш бус байдлыг шийд;
(4 - x)/x³

4. Тэгш бус байдлын зүүн тал нь нэг бодит x = 4 байх ба x = 0 үед эргэх болно. Иймд x = 4 утгыг интервал болон буурах интервалд хоёуланд нь багтаасан бөгөөд 0 цэгийг оруулаагүй болно.
Тэгэхээр шаардлагатай функц x ∈ (-∞; 0) ∪ интервал дээр нэмэгддэг.

4. Тэгш бус байдлын зүүн тал нь нэг бодит x = 4 байх ба x = 0 үед эргэх болно. Иймд x = 4 утгыг интервал болон буурах интервалд хоёуланд нь багтаасан бөгөөд 0 цэгийг оруулаагүй болно.
Тэгэхээр шаардлагатай функц x ∈ (-∞; 0) ∪ интервал дээр нэмэгддэг.

Эх сурвалжууд:

• Функцийн буурах интервалыг хэрхэн олох

Функц нь нэг тооны нөгөө тооноос хатуу хамааралтай байхыг, эсвэл (y) функцийн утгыг (x) аргументаас илэрхийлдэг. Процесс бүрийг (зөвхөн математикт биш) өөрийн функцээр тодорхойлж болох бөгөөд энэ нь онцлог шинж чанартай байх болно: буурах ба нэмэгдүүлэх интервал, хамгийн бага ба максимум цэг гэх мэт.

Танд хэрэгтэй болно

• - цаас;
• - үзэг.

Заавар

Жишээ 2.
f(x)=sinx +x-ийн бууралтын интервалуудыг ол.
Энэ функцийн дериватив нь f’(x)=cosx+1-тэй тэнцүү байна.
cosx+1 тэгш бус байдлыг шийдвэрлэх

Интервал нэг хэвийн байдалФункц нь зөвхөн өсдөг эсвэл зөвхөн буурдаг интервал гэж функцийг нэрлэж болно. Хэд хэдэн тодорхой үйлдлүүд нь энэ төрлийн алгебрийн бодлогод ихэвчлэн шаардлагатай байдаг функцийн ийм мужийг олоход тусална.

Заавар

Функцийн нэг хэвийн өсөх, буурах интервалыг тодорхойлох асуудлыг шийдэх эхний алхам бол энэ функцийг тооцоолох явдал юм. Үүнийг хийхийн тулд функцийн утгыг олох боломжтой бүх аргументын утгуудыг (x тэнхлэгийн дагуух утгууд) олж мэдээрэй. Тасралт ажиглагдаж буй цэгүүдийг тэмдэглэ. Функцийн деривативыг ол. Деривативыг илэрхийлэх илэрхийлэлийг тодорхойлсны дараа үүнийг тэгтэй тэнцүүл. Үүний дараа та үүссэн үндсийг олох хэрэгтэй. Зөвшөөрөгдсөн талбайн тухай биш.

Функц эсвэл түүний дериватив тэгтэй тэнцүү байх цэгүүд нь интервалуудын хилийг илэрхийлнэ. нэг хэвийн байдал. Эдгээр мужууд болон тэдгээрийг тусгаарлах цэгүүдийг хүснэгтэд дараалан оруулах ёстой. Үүссэн интервал дахь функцийн деривативын тэмдгийг ол. Үүнийг хийхийн тулд интервалаас дурын аргументыг деривативт харгалзах илэрхийлэл болгон орлуулна. Хэрэв үр дүн эерэг байвал энэ муж дахь функц нэмэгдэнэ, өөрөөр хэлбэл энэ нь буурна. Үр дүнг хүснэгтэд оруулсан болно.

f'(x) функцийн деривативыг харуулсан мөрөнд аргументуудын харгалзах утгуудыг бичнэ: "+" - хэрэв дериватив эерэг бол "-" - сөрөг эсвэл "0" - тэгтэй тэнцүү. Дараагийн мөрөнд анхны илэрхийллийн монотон байдлыг тэмдэглэ. Дээш сум нь өсөлттэй, доош сум нь буурсантай тохирч байна. Функцуудыг шалгана уу. Эдгээр нь дериватив нь тэг байх цэгүүд юм. Экстремум нь хамгийн дээд цэг эсвэл хамгийн бага цэг байж болно. Хэрэв функцийн өмнөх хэсэг нэмэгдэж, одоогийнх нь буурсан бол энэ нь хамгийн дээд цэг юм. Тухайн цэгээс өмнө функц буурч байсан бол одоо нэмэгдэж байгаа тохиолдолд энэ нь хамгийн бага цэг юм. Функцийн утгыг экстремум цэгүүдэд хүснэгтэд оруулна уу.

Эх сурвалжууд:

• монотон гэж юу вэ

Аргументаас нийлмэл хамааралтай функцийн зан төлөвийг дериватив ашиглан судалдаг. Деривативын өөрчлөлтийн шинж чанараар та чухал цэгүүд болон функцийн өсөлт, бууралтын хэсгүүдийг олж болно.

Функцийн өсөлт, бууралт, экстремум

Функцийн өсөлт, бууралт, туйлын интервалыг олох нь бие даасан ажил бөгөөд бусад даалгаврын чухал хэсэг юм, ялангуяа бүрэн функциональ судалгаа. Функцийн өсөлт, бууралт, хэт туйлшралын талаархи анхны мэдээллийг энд оруулав деривативын тухай онолын бүлэг, үүнийг би урьдчилсан судалгаанд ашиглахыг зөвлөж байна (эсвэл давталт)– мөн учир нь дараах материал нь маш дээр суурилсан үндсэндээ дериватив,Энэ нийтлэлийн эв нэгдэлтэй үргэлжлэл юм. Хэдийгээр цаг хугацаа бага байгаа бол өнөөдрийн хичээлээс жишээ авах боломжтой.

Өнөөдөр агаарт ховор эв нэгдлийн сүнс байгаа бөгөөд тэнд байгаа бүх хүмүүс хүсэлд шатаж байгааг би шууд мэдэрч байна. функцийг түүний уламжлалыг ашиглан судалж сурах. Тиймээс боломжийн, сайн, мөнхийн нэр томъёо таны дэлгэцийн дэлгэц дээр шууд гарч ирнэ.

Юуны төлөө? Шалтгаануудын нэг нь хамгийн практик юм: Ингэснээр та ямар нэг ажилд ерөнхийдөө юу шаардагдах нь тодорхой болно!

Функцийн монотон байдал. Функцийн экстремум ба экстремум цэгүүд

Зарим функцийг авч үзье. Энгийнээр хэлэхэд бид түүнийг гэж таамаглаж байна тасралтгүйбүх тооны мөрөнд:

Ямар ч тохиолдолд, ялангуяа саяхан танилцсан уншигчдын хувьд болзошгүй хуурмаг байдлаас нэн даруй салцгаая. функцийн тогтмол тэмдгийн интервалууд. Одоо бид СОНИРХОЛГҮЙ, функцийн график тэнхлэгтэй харьцуулахад хэрхэн байрлаж байгааг (дээр, доор, тэнхлэг огтлолцох газар). Итгэл үнэмшилтэй байхын тулд тэнхлэгүүдийг оюун ухаанаараа арчиж, нэг график үлдээгээрэй. Яагаад гэвэл сонирхол энд л байдаг.

Чиг үүрэг нэмэгддэгХэрэв энэ интервалын аль нэг хоёр цэгийн хувьд харьцаагаар холбогдсон бол тэгш бус байдал үнэн байна. Өөрөөр хэлбэл, аргументийн том утга нь функцийн том утгатай тохирч, график нь "доороос дээш" явдаг. Үзүүлэн харуулах функц нь интервалаар нэмэгддэг.

Үүний нэгэн адил функц буурдагөгөгдсөн интервалын аль нэг хоёр цэгийн хувьд тэгш бус байдал нь үнэн бол интервал дээр. Өөрөөр хэлбэл, аргументийн том утга нь функцийн бага утгатай тохирч, график нь "дээрээс доош" явдаг. Бидний функц интервалаар буурдаг .

Хэрэв функц тодорхой хугацааны туршид нэмэгдэж эсвэл буурч байвал түүнийг дуудна хатуу монотонэнэ интервалд. Монотони гэж юу вэ? Үүнийг шууд утгаар нь ойлгоорой - нэг хэвийн байдал.

Та мөн тодорхойлж болно буурдаггүйфункц (эхний тодорхойлолтод тайвширсан нөхцөл) ба өсөхгүйфункц (2-р тодорхойлолтод зөөлрүүлсэн нөхцөл). Интервал дахь буурдаггүй эсвэл өсдөггүй функцийг өгөгдсөн интервал дахь монотон функц гэнэ. (хатуу монотон байдал нь "энгийн" нэгэн хэвийн байдлын онцгой тохиолдол юм).

Онол нь функцын өсөлт/бууралтыг тодорхойлох бусад аргуудыг, түүний дотор хагас интервал, сегментийг авч үздэг боловч таны толгой дээр тос-тос-тос асгахгүйн тулд бид ангиллын тодорхойлолттой нээлттэй интервалтай ажиллахыг зөвшөөрнө. - энэ нь илүү ойлгомжтой бөгөөд олон практик асуудлыг шийдвэрлэхэд хангалттай юм.

Тиймээс, Миний нийтлэлүүдэд "функцийн монотон байдал" гэсэн үг бараг үргэлж нуугдаж байх болно интервалуудхатуу монотон байдал(хатуу нэмэгдүүлэх эсвэл хатуу бууруулах функц).

Нэг цэгийн хөрш. Оюутнууд хаашаа ч хамаагүй зугтаж, булан тохойд айж нуугддаг үгс. ...Хэдийгээр бичлэгийн дараа Коши хязгаарлалтТэд нуугдхаа больсон байх, гэхдээ зүгээр л бага зэрэг чичирч байна =) Санаа зоволтгүй, одоо математик анализын теоремуудын нотолгоо байхгүй болно - тодорхойлолтыг илүү нарийн томъёолохын тулд надад орчин хэрэгтэй байсан экстремум цэгүүд. Санаж үзье:

Нэг цэгийн хөршөгөгдсөн цэгийг агуулсан интервалыг дуудах бөгөөд тохиромжтой байх үүднээс интервалыг ихэвчлэн тэгш хэмтэй гэж үздэг. Жишээлбэл, цэг ба түүний стандарт хөрш:

Үнэндээ тодорхойлолтууд нь:

цэг гэж нэрлэдэг хатуу дээд цэг, Хэрэв байдагтүүний хөрш, хүн бүртцэгээс бусад утгууд нь тэгш бус байдал . Бидний тодорхой жишээнд энэ бол цэг юм.

цэг гэж нэрлэдэг хатуу доод цэг, Хэрэв байдагтүүний хөрш, хүн бүртцэгээс бусад утгууд нь тэгш бус байдал . Зураг дээр "а" цэг байна.

Анхаарна уу : хөршийн тэгш хэмийн шаардлага огт шаардлагагүй. Үүнээс гадна, энэ нь чухал юм оршихуйн үнэн бодит байдалзаасан нөхцлийг хангасан хөрш (жижиг эсвэл бичил харуурын аль нь ч бай).

Цэгүүдийг дууддаг хатуу туйлын цэгүүдэсвэл зүгээр л экстремум цэгүүдфункцууд. Энэ нь хамгийн их оноо, хамгийн бага оноо гэсэн ерөнхий нэр томъёо юм.

"Хэт туйл" гэдэг үгийг бид хэрхэн ойлгох вэ? Тийм ээ, яг л нэг хэвийн байдал шиг. Галзуу хулганы туйлын цэгүүд.

Монотоник байдлын нэгэн адил сул постулатууд байдаг бөгөөд онолын хувьд илүү түгээмэл байдаг (Мэдээжийн хэрэг гэж үзсэн хатуу хэргүүд үүнд хамаарна!):

цэг гэж нэрлэдэг хамгийн дээд цэг, Хэрэв байдагтүүний эргэн тойронд ийм байдаг хүн бүрт
цэг гэж нэрлэдэг хамгийн бага цэг, Хэрэв байдагтүүний эргэн тойронд ийм байдаг хүн бүртЭнэ хөршийн үнэ цэнэ, тэгш бус байдал хэвээр байна.

Сүүлийн хоёр тодорхойлолтын дагуу тогтмол функцийн аль ч цэгийг (эсвэл функцийн "хавтгай хэсэг") хамгийн их ба хамгийн бага цэг гэж үздэг болохыг анхаарна уу! Дашрамд хэлэхэд функц нь өсдөггүй, буурдаггүй, өөрөөр хэлбэл монотон байдаг. Гэсэн хэдий ч практик дээр бид бараг үргэлж уламжлалт "толгод" болон "хонхор" (зураг харна уу) -ийг өвөрмөц "толгойн хаан" эсвэл "намгийн гүнж" гэж үздэг тул бид эдгээр асуудлыг онолчдод үлдээх болно. Төрөл бүрийн хувьд энэ нь тохиолддог зөвлөгөө, дээш эсвэл доош чиглэсэн, жишээлбэл, цэг дээрх функцын хамгийн бага.

Өө, мөн роялтигийн тухай ярихад:
– утгыг гэдэг дээд тал ньфункцууд;
– утгыг гэдэг хамгийн багафункцууд.

Нийтлэг нэр - туйлшралфункцууд.

Үгэндээ болгоомжтой байгаарай!

Экстремум цэгүүд- эдгээр нь "X" утгууд юм.
Хэт их- "тоглоом" гэсэн утгатай.

! Анхаарна уу : заримдаа жагсаасан нэр томьёо нь өөрөө функцийн ГРАФИК дээр шууд байрлах "X-Y" цэгүүдийг хэлдэг.

Функц хэдэн экстремумтай байж болох вэ?

Аль нь ч биш, 1, 2, 3, ... гэх мэт. хязгааргүй. Жишээлбэл, синус хязгааргүй олон минимум, максимумтай.

ЧУХАЛ!"Функцийн дээд хэмжээ" гэсэн нэр томъёо ижил биш"функцийн хамгийн их утга" гэсэн нэр томъёо. Зөвхөн орон нутгийн хороололд л хамгийн их үнэ цэнэтэй гэдгийг анзаарахад хялбар байдаг бөгөөд зүүн дээд талд "илүү сэрүүн нөхдүүд" байдаг. Үүний нэгэн адил "функцийн хамгийн бага утга" нь "функцийн хамгийн бага утгатай" ижил биш бөгөөд зураг дээр бид зөвхөн тодорхой хэсэгт утга нь хамгийн бага болохыг харж байна. Үүнтэй холбогдуулан экстремум цэгүүдийг бас нэрлэдэг орон нутгийн экстремум цэгүүд, ба экстремум - орон нутгийн эрс тэс. Тэд ойролцоо алхаж, тэнүүчилж байна дэлхийнах нар аа. Тэгэхээр аливаа параболын орой нь байдаг дэлхийн хамгийн багаэсвэл дэлхийн дээд хэмжээ. Цаашилбал, би хэт туйлшралын төрлүүдийг ялгахгүй бөгөөд тайлбарыг ерөнхий боловсролын зорилгоор илүү их хэлдэг - "орон нутгийн"/"дэлхийн" нэмэлт нэр үгс таныг гайхшруулж болохгүй.

Онол руу хийсэн богино аялалаа туршилтын зургаар дүгнэж үзье: "Функцийн нэг хэвийн байдлын интервал ба экстремум цэгүүдийг олох" даалгавар нь юу гэсэн үг вэ?

Үг хэллэг нь таныг дараахь зүйлийг олоход уриалж байна.

– Өсөх/буурах функцийн интервал (буурахгүй, нэмэгдэхгүй байх нь хамаагүй бага тохиолддог);

- хамгийн их ба/эсвэл хамгийн бага оноо (хэрэв байгаа бол). За, бүтэлгүйтлээс зайлсхийхийн тулд хамгийн бага/максимумыг өөрсдөө олох нь дээр ;-)

Энэ бүхнийг хэрхэн тодорхойлох вэ?Дериватив функцийг ашиглах!

Өсөх, буурах интервалыг хэрхэн олох,
функцийн экстремум цэг ба экстремум?

Үнэн хэрэгтээ олон дүрмийг аль хэдийн мэддэг, ойлгодог деривативын утгын тухай хичээл.

Тангенсийн дериватив үйл ажиллагаа нэмэгдэж байгаа тухай хөгжилтэй мэдээг хүргэж байна тодорхойлолтын домэйн.

Котангенс ба түүний деривативтай байдал яг эсрэгээрээ байна.

Арксин нь интервалаар нэмэгддэг - энд үүссэн дериватив эерэг байна: .
Функц нь тодорхойлогдсон боловч ялгах боломжгүй үед. Гэсэн хэдий ч эгзэгтэй цэг дээр баруун гарт дериватив ба баруун гарт шүргэгч байдаг бөгөөд нөгөө ирмэг дээр тэдний зүүн гарт байдаг.

Нуман косинус ба түүний деривативын талаархи ижил төстэй үндэслэлийг гаргах нь танд тийм ч хэцүү биш байх болно гэж би бодож байна.

Дээрх бүх тохиолдлууд, тэдгээрийн ихэнх нь хүснэгтийн деривативууд, Би танд сануулж байна, -аас шууд дагаарай дериватив тодорхойлолтууд.

Яагаад функцийг дериватив ашиглан судлах вэ?

Энэ функцийн график ямар харагдахыг илүү сайн ойлгохын тулд: хаана "доошоо дээш", "дээд доош", хамгийн бага ба максимумд хүрэх газар (хэрэв энэ нь огт хүрсэн бол). Бүх функцууд тийм ч энгийн байдаггүй - ихэнх тохиолдолд бид тодорхой функцийн графикийн талаар огт ойлголтгүй байдаг.

Илүү утга учиртай жишээнүүд рүү шилжиж, эргэцүүлэн бодох цаг болжээ Функцийн монотон ба экстремумын интервалыг олох алгоритм:

Жишээ 1

Функцийн өсөлт/бууралтын интервал ба экстремумыг ол

Шийдэл:

1) Эхний алхам бол олох явдал юм функцийн домэйн, мөн таслах цэгүүдийг (хэрэв байгаа бол) тэмдэглэ. Энэ тохиолдолд функц нь бүхэл тооны мөрөнд тасралтгүй үргэлжлэх бөгөөд энэ үйлдэл нь тодорхой хэмжээгээр албан ёсны шинж чанартай байдаг. Гэхдээ хэд хэдэн тохиолдолд ноцтой хүсэл тэмүүлэл энд гарч ирдэг тул догол мөрийг үл тоомсорлон авч үзье.

2) Алгоритмын хоёр дахь цэг нь холбоотой юм

Экстремумын зайлшгүй нөхцөл:

Хэрэв цэг дээр экстремум байвал утга нь байхгүй болно.

Төгсгөлд нь андуурч байна уу? “Модуль x” функцийн экстремум .

Нөхцөл байдал зайлшгүй шаардлагатай, гэхдээ хангалттай биш, мөн эсрэгээрээ үргэлж үнэн байдаггүй. Тэгэхээр функц нь цэг дээр хамгийн их эсвэл хамгийн багадаа хүрдэг гэсэн тэгш байдлаас хараахан гараагүй байна. Сонгодог жишээг дээр аль хэдийн онцолсон - энэ бол куб парабол ба түүний чухал цэг юм.

Гэсэн хэдий ч экстремумын зайлшгүй нөхцөл нь сэжигтэй цэгүүдийг олох хэрэгцээг шаарддаг. Үүнийг хийхийн тулд деривативыг олж, тэгшитгэлийг шийднэ.

Эхний нийтлэлийн эхэнд функцийн графикийн тухайБи жишээн дээр параболыг хэрхэн хурдан бүтээх талаар хэлсэн : “...бид эхний деривативыг аваад тэгтэй тэнцүүлнэ: ...Тэгэхээр бидний тэгшитгэлийн шийдэл: - яг энэ үед параболын орой байрлаж байна...”. Одоо би параболын орой яагаад яг энэ цэг дээр байдгийг хүн бүр ойлгосон байх гэж бодож байна =) Ерөнхийдөө энд ижил төстэй жишээнээс эхлэх хэрэгтэй, гэхдээ энэ нь хэтэрхий энгийн (цайны аяганд ч гэсэн). Нэмж дурдахад хичээлийн төгсгөлд аналог байдаг функцийн дериватив. Тиймээс зэрэглэлийг нэмэгдүүлье:

Жишээ 2

Функцийн монотон ба туйлын интервалыг ол

Энэ бол та өөрөө шийдэх жишээ юм. Хичээлийн төгсгөлд асуудлын бүрэн шийдэл, ойролцоогоор эцсийн түүвэр.

Бутархай-рационал функцуудтай уулзах удаан хүлээсэн мөч ирлээ.

Жишээ 3

Эхний дериватив ашиглан функцийг судлаарай

Нэг ажлыг хэрхэн өөрчлөх боломжтойг анхаарч үзээрэй.

Шийдэл:

1) Функц нь цэгүүдэд хязгааргүй тасалдалтай байдаг.

2) Бид чухал цэгүүдийг илрүүлдэг. Эхний деривативыг олоод тэгтэй тэнцүүлье.

Тэгшитгэлээ шийдье. Бутархай нь тэг байх үед түүний тоологч нь тэг болно:

Тиймээс бид гурван чухал оноо авдаг:

3) Бид илрүүлсэн БҮХ цэгүүдийг тооны шулуун дээр зурдаг интервалын аргаБид ДЕРИВАТИВ-ийн шинж тэмдгийг тодорхойлно:

Та интервал дахь тодорхой цэгийг авч, үүсмэл хэрэгслийн утгыг тооцоолох хэрэгтэй гэдгийг би танд сануулж байна мөн түүний тэмдгийг тодорхойлно. Бүр тоочихгүй, амаар "тооцох" нь илүү ашигтай. Жишээлбэл, интервалд хамаарах цэгийг авч, орлуулалтыг хийцгээе. .

Хоёр "нэмэх", нэг "хасах" нь "хасах" гэсэн утгыг өгдөг бөгөөд энэ нь дериватив нь бүх интервалд сөрөг байна гэсэн үг юм.

Таны ойлгож байгаагаар үйлдлийг зургаан интервал тус бүрээр хийх шаардлагатай. Дашрамд хэлэхэд, тоологч хүчин зүйл болон хуваагч нь ямар ч интервалын аль ч цэгт хатуу эерэг байдаг бөгөөд энэ нь даалгаврыг ихээхэн хөнгөвчилдөг гэдгийг анхаарна уу.

Тэгэхээр, үүсмэл функц нь ӨӨРӨӨ -өөр нэмэгддэг гэж хэлсэн -аар буурдаг. Нэг төрлийн интервалыг нэгдэх дүрсээр холбоход тохиромжтой.

Тухайн үед функц хамгийн дээд хэмжээндээ хүрнэ:
Тухайн үед функц хамгийн багадаа хүрнэ:

Яагаад хоёр дахь утгыг дахин тооцоолох шаардлагагүй гэж бодож үзээрэй ;-)

Цэгээр дамжин өнгөрөхөд дериватив тэмдэг өөрчлөгддөггүй тул функц NO EXTREMUM байхгүй - энэ нь аль аль нь буурч, буурсан хэвээр байна.

! Нэг чухал зүйлийг дахин хэлье: оноо нь чухал гэж тооцогддоггүй - тэдгээр нь функцийг агуулдаг тодорхойлогдоогүй. Үүний дагуу энд Зарчмын хувьд хэт туйлшрал байж болохгүй(үүсмэл шинж тэмдэг өөрчлөгдсөн ч гэсэн).

Хариулах: функцээр нэмэгддэг Функцийн хамгийн дээд хэмжээнд хүрэх үед дараах байдлаар буурна: , мөн цэг дээр – хамгийн бага нь: .

Монотоник байдлын интервал ба экстремын талаархи мэдлэг, тогтсон асимптотуудфункцийн графикийн харагдах байдлын талаар маш сайн санааг аль хэдийн өгдөг. Дундаж боловсролтой хүн функцийн график нь хоёр босоо асимптот ба ташуу асимптоттой болохыг амаар тодорхойлж чаддаг. Энд манай баатар байна:

Судалгааны үр дүнг энэ функцийн графиктай харьцуулахыг дахин оролдоно уу.
Эгзэгтэй цэг дээр экстремум байхгүй, гэхдээ байдаг гулзайлтын цэг(энэ нь дүрмээр бол ижил төстэй тохиолдлуудад тохиолддог).

Жишээ 4

Функцийн экстремумыг ол

Жишээ 5

Функцийн монотон байдлын интервал, максимум, минимумыг ол

…өнөөдөр бараг л “X in a шоо”-гийн баяр шиг байна...
Soooo, галерейд хэн үүний төлөө уухыг санал болгосон бэ? =)

Даалгавар бүр өөрийн гэсэн үндсэн нюанс, техникийн нарийн шинж чанартай байдаг бөгөөд үүнийг хичээлийн төгсгөлд тайлбарласан болно.

Функцийн экстремум

Тодорхойлолт 2

$x_0$ цэгийг $f(x)$ функцийн хамгийн их цэг гэж нэрлэдэг бөгөөд энэ цэгийн хөрш байгаа бөгөөд энэ хөршийн бүх $x$-д $f(x)\le f(x_0) тэгш бус байдал бий болно. доллар хадгалагдана.

Тодорхойлолт 3

$x_0$ цэгийг $f(x)$ функцийн хамгийн их цэг гэж нэрлэнэ. Хэрэв энэ цэгийн хөрш байгаа бөгөөд энэ хөршийн бүх $x$-д $f(x)\ge f(x_0) тэгш бус байдал бий болно. доллар хадгална.

Функцийн экстремумын тухай ойлголт нь функцийн эгзэгтэй цэгийн тухай ойлголттой нягт холбоотой. Түүний тодорхойлолтыг танилцуулъя.

Тодорхойлолт 4

$x_0$-г $f(x)$ функцийн чухал цэг гэж нэрлэдэг, хэрэв:

1) $x_0$ - тодорхойлолтын домэйны дотоод цэг;

2) $f"\left(x_0\right)=0$ эсвэл байхгүй байна.

Экстремумын тухай ойлголтын хувьд бид түүний оршин тогтнох хангалттай, шаардлагатай нөхцлийн талаар теоремуудыг томъёолж болно.

Теорем 2

Экстремум үүсэх хангалттай нөхцөл

$x_0$ цэг нь $y=f(x)$ функцийн хувьд чухал байх ба $(a,b)$ интервалд хэвтэнэ. $\left(a,x_0\right)\ ба \ (x_0,b)$ интервал бүр дээр $f"(x)$ дериватив байгаа бөгөөд тогтмол тэмдэг хадгална. Дараа нь:

1) Хэрэв $(a,x_0)$ интервал дээр дериватив нь $f"\left(x\right)>0$, харин $(x_0,b)$ интервал дээр дериватив нь $f"\left( x\баруун)

2) Хэрэв $(a,x_0)$ интервал дээр $f"\left(x\right)0$ дериватив байвал $x_0$ цэг нь энэ функцийн хамгийн бага цэг болно.

3) Хэрэв $(a,x_0)$ болон $(x_0,b)$ интервал дээр $f"\left(x\right) >0$ дериватив эсвэл $f"\left(x) үүсмэл байвал \баруун)

Энэ теоремыг 1-р зурагт үзүүлэв.

Зураг 1. Экстремум оршин тогтнох хангалттай нөхцөл

Хэт туйлшралын жишээ (Зураг 2).

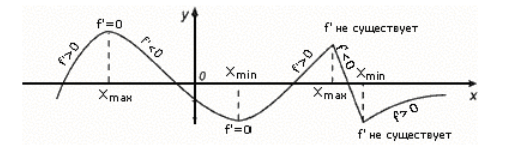
Зураг 2. Хэт туйлын цэгүүдийн жишээ

Экстремумын функцийг судлах дүрэм

2) $f"(x)$ деривативыг ол;

7) Теорем 2-ыг ашиглан интервал бүр дээр максимум ба минимум байгаа эсэх талаар дүгнэлт гарга.

Өсөх, багасгах функцууд

Эхлээд нэмэгдэх ба буурах функцүүдийн тодорхойлолтыг танилцуулъя.

Тодорхойлолт 5

$X$ интервал дээр тодорхойлсон $y=f(x)$ функцийг $x_1-д $x_1,x_2\ X$-ийн аль нэг цэгийн хувьд нэмэгдэж байгаа гэж хэлнэ.

Тодорхойлолт 6

$X$ интервал дээр тодорхойлсон $y=f(x)$ функцийг $x_1f(x_2)$-д $x_1,x_2\ X$-ийн аль нэг цэгийн хувьд буурч байна гэж хэлнэ.

Өсөх, буурах функцийг судлах

Та дериватив ашиглан нэмэгдэж, буурах функцийг судалж болно.

Функцийн өсөлт ба буурах интервалыг шалгахын тулд та дараахь зүйлийг хийх ёстой.

1) $f(x)$ функцийн тодорхойлолтын мужийг ол;

2) $f"(x)$ деривативыг ол;

3) $f"\left(x\right)=0$ тэнцүү байх цэгүүдийг ол;

4) $f"(x)$ байхгүй цэгүүдийг ол;

5) Координатын шугам дээр олсон бүх цэгүүд болон энэ функцийг тодорхойлох мужийг тэмдэглэнэ;

6) Үүссэн интервал бүр дээр $f"(x)$ деривативын тэмдгийг тодорхойлох;

7) Дүгнэлт гарга: $f"\left(x\right)0$ функц нэмэгдэх интервалд.

Өсөлт, бууралт, хэт туйлшралын функцийг судлах асуудлын жишээ

Жишээ 1

Өсөх ба буурах функц, хамгийн их ба хамгийн бага оноо байгаа эсэхийг шалгана уу: $f(x)=(2x)^3-15x^2+36x+1$

Эхний 6 оноо ижил тул эхлээд тэдгээрийг авч үзье.

1) Тодорхойлолтын домэйн - бүх бодит тоо;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $f"\left(x\right)=0$;

\ \ \

4) $f"(x)$ нь тодорхойлолтын домэйны бүх цэгүүдэд байдаг;

5) Координатын шугам:

Зураг 3.

6) Интервал бүр дээр $f"(x)$ деривативын тэмдгийг тодорхойл.

\ \}