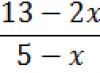In this paragraph we will focus on a special, but important class positive quadratic forms.

Definition 3. A real quadratic form is called non-negative (non-positive) if, for any real values ​​of the variables

. (35)

In this case, the symmetric matrix of coefficients is called positive semidefinite (negative semidefinite).

Definition 4. A real quadratic form is called positive definite (negative definite) if, for any real values ​​of the variables that are not simultaneously zero,

. (36)

In this case, the matrix is ​​also called positive definite (negative definite).

The class of positive definite (negative definite) forms is part of the class of non-negative (resp. non-positive) forms.

Let a non-negative form be given. Let's imagine it as a sum of independent squares:

. (37)

In this representation, all squares must be positive:

. (38)

Indeed, if there were any , then it would be possible to select values ​​such that

But then, with these values ​​of the variables, the form would have a negative value, which is impossible by condition. Obviously, conversely, from (37) and (38) it follows that the form is positive.

Thus, a non-negative quadratic form is characterized by the equalities.

Let it be positive now definite shape. Then it is a non-negative form. Therefore, it can be represented in the form (37), where all are positive. From the positive definiteness of the form it follows that . Indeed, in the case it is possible to select values ​​that are not simultaneously equal to zero, at which all would turn to zero. But then, by virtue of (37), for , which contradicts condition (36).

It is easy to see that conversely, if in (37) and are all positive, then it is a positive definite form.

In other words, a non-negative form is positive definite if and only if it is not singular.

The following theorem gives a criterion for the positive definiteness of a form in the form of inequalities that the form coefficients must satisfy. In this case, the notation already encountered in previous paragraphs for successive principal minors of the matrix is ​​used:

.

Theorem 3. In order for a quadratic form to be positive definite, it is necessary and sufficient that the inequalities be satisfied

Proof. The sufficiency of conditions (39) follows directly from Jacobi formula (28). The necessity of conditions (39) is established as follows. From the positive definiteness of the form follows the positive definiteness of “truncated” forms

.

But then all these forms must be non-singular, i.e.

Now we have the opportunity to use the Jacobi formula (28) (at ). Since on the right side of this formula all squares must be positive, then

This implies inequalities (39). The theorem is proven.

Since any principal minor of a matrix, with proper renumbering of variables, can be placed in the upper left corner, then we have

Consequence. In positive definite quadratic form, all major minors of the coefficient matrix are positive:

Comment. From the non-negativity of successive principal minors

the non-negativity of the form does not follow. Indeed, the form

,

in which , satisfies the conditions , but is not non-negative.

However, the following holds

Theorem 4. In order for a quadratic form to be non-negative, it is necessary and sufficient that all the major minors of its coefficient matrix are non-negative:

Proof. Let's introduce auxiliary form was non-positive, it is necessary and sufficient for inequalities to occur

A homogeneous polynomial of degree 2 in several variables is called a quadratic form.

The quadratic form of variables consists of terms of two types: squares of variables and their pairwise products with certain coefficients. The quadratic form is usually written as the following square diagram:

Couples similar members are written with identical coefficients, so that each of them constitutes half of the coefficient with the corresponding product of the variables. Thus, each quadratic form is naturally associated with its coefficient matrix, which is symmetric.

It is convenient to represent the quadratic form in the following way: matrix notation. Let us denote by X a column of variables through X - a row, i.e., a matrix transposed with X. Then

Quadratic shapes found in many branches of mathematics and its applications.

In number theory and crystallography, quadratic forms are considered under the assumption that the variables take only integer values. IN analytical geometry the quadratic form is part of the equation of a curve (or surface) of order. In mechanics and physics, the quadratic form appears to express kinetic energy systems through the components of generalized velocities, etc. But, in addition, the study of quadratic forms is also necessary in analysis when studying functions of many variables, in questions for the solution of which it is important to find out how this function in the vicinity of a given point deviates from the one approaching it linear function. An example of a problem of this type is the study of a function for its maximum and minimum.

Consider, for example, the problem of studying the maximum and minimum for a function of two variables that has continuous partial derivatives up to order. A necessary condition In order for a point to give a maximum or minimum of a function, the partial derivatives of the order at the point are equal to zero. Let us assume that this condition is met. Let's give the variables x and y small increments and k and consider the corresponding increment of the function. According to Taylor's formula, this increment, up to small higher orders, is equal to the quadratic form where are the values ​​of the second derivatives calculated at the point If this quadratic form is positive for all values ​​of and k (except ), then the function has a minimum at the point; if it is negative, then it has a maximum. Finally, if the form takes both positive and negative values, then there will be neither maximum nor minimum. Functions of more variables.

The study of quadratic forms mainly consists of studying the problem of equivalence of forms with respect to one or another set of linear transformations of variables. Two quadratic forms are said to be equivalent if one of them can be converted into the other by one of the transformations of a given set. Closely related to the problem of equivalence is the problem of reducing the form, i.e. transforming it to some possibly simplest form.

IN various issues associated with quadratic forms, various sets of admissible transformations of variables are also considered.

In questions of analysis, any non-special transformations of variables are used; for the purposes of analytical geometry, the greatest interest is orthogonal transformations, i.e. those that correspond to a transition from one system of variables Cartesian coordinates to another. Finally, in number theory and crystallography linear transformations with integer coefficients and with a determinant equal to unity are considered.

We will consider two of these problems: the question of reducing a quadratic form to its simplest form through any non-singular transformations and the same question for orthogonal transformations. First of all, let's find out how a matrix of quadratic form is transformed during a linear transformation of variables.

Let , where A is a symmetric matrix of form coefficients, X is a column of variables.

Let's do it linear transformation variables, writing it abbreviated as . Here C denotes the matrix of coefficients of this transformation, X is a column of new variables. Then and therefore, so the matrix of the transformed quadratic form is

The matrix automatically turns out to be symmetric, which is easy to check. Thus, the problem of reducing a quadratic form to the simplest form is equivalent to the problem of reducing a symmetric matrix to the simplest form by multiplying it on the left and right by mutually transposed matrices.

Rules for entering functions:

A twice continuously differentiable function f(x) is convex (concave) if and only if Hessian matrix the function f(x) with respect to x is positive (negative) semidefinite for all x (see points of local extrema of a function of several variables).

Function critical points:

• if the Hessian is positive definite, then x 0 is a point local minimum functions f(x) ,
• if the Hessian is negative definite, then x 0 is the local maximum point of the function f(x),
• if the Hessian is not sign-definite (takes both positive and negative values) and is non-degenerate (det G(f) ≠ 0), then x 0 is the saddle point of the function f(x).

Criteria for the definiteness of a matrix (Sylvester's theorem)

• all diagonal elements of the matrix must be positive;
• all leading main qualifiers must be positive.

Positive semi-definiteness:

• all diagonal elements are non-negative;
• all main determinants are non-negative.

Square symmetric matrix of order n, whose elements are partial derivatives objective function second order called the Hessian matrix and is designated:

In order for a symmetric matrix to be positive definite, it is necessary and sufficient that all its diagonal minors are positive, i.e.


for the matrix A = (a ij) are positive.

Negative certainty.
In order for a symmetric matrix to be negative definite, it is necessary and sufficient that the following inequalities take place:
(-1) k D k > 0, k=1,.., n.
In other words, in order for the quadratic form to be negative definite, it is necessary and sufficient that the signs of the angular minors of a matrix of quadratic form alternate, starting with the minus sign. For example, for two variables, D 1< 0, D 2 > 0.

If the Hessian is semidefinite, then this may also be an inflection point. Needed additional research, which can be carried out according to one of the following options:

1. Decreasing order. A change of variables is made. For example, for a function of two variables it is y=x, as a result we get a function of one variable x. Next, we study the behavior of the function on the lines y=x and y=-x. If in the first case the function at the point under study will have a minimum, and in the other case a maximum (or vice versa), then the point under study is a saddle point.
2. Finding the eigenvalues ​​of the Hessian. If all values ​​are positive, the function at the point under study has a minimum; if all values ​​are negative, there is a maximum.
3. Study of the function f(x) in the neighborhood of the point ε. Variables x are replaced by x 0 +ε. Next, it is necessary to prove that the function f(x 0 +ε) of one variable ε, or greater than zero(then x 0 is the minimum point), or less than zero(then x 0 is the maximum point).

Note. To find inverse Hessian it is enough to find the inverse matrix.

Example No. 1. Which of following functions are convex or concave: f(x) = 8x 1 2 +4x 1 x 2 +5x 2 2.
Solution. 1. Let's find partial derivatives.


2. Let's solve the system of equations.
-4x 1 +4x 2 +2 = 0
4x 1 -6x 2 +6 = 0
We get:
a) From the first equation we express x 1 and substitute it into the second equation:
x 2 = x 2 + 1/2
-2x 2 +8 = 0
Where x 2 = 4
We substitute these values ​​x 2 into the expression for x 1. We get: x 1 = 9 / 2
The number of critical points is 1.
M 1 (9 / 2 ;4)
3. Let's find the second order partial derivatives.



4. Let us calculate the value of these second-order partial derivatives in critical points M(x 0 ;y 0).
We calculate the values ​​for point M 1 (9 / 2 ;4)



We build the Hessian matrix:

D 1 = a 11< 0, D 2 = 8 > 0
Since diagonal minors have various signs, then nothing can be said about the convexity or concavity of the function.

Positive definite quadratic forms

Definition. Quadratic form from n unknowns are called positive definite, if its rank is equal to the positive inertia index and equal to the number unknown.

Theorem. A quadratic form is positive definite if and only if, on any nonzero set of variable values, it takes positive values.

Proof. Let the quadratic form be a non-degenerate linear transformation of the unknowns

brought back to normal

.

For any non-zero set of variable values, at least one of the numbers different from zero, i.e. . The necessity of the theorem is proven.

Suppose that the quadratic form takes positive values ​​on any non-zero set of variables, but its positive inertia index is a non-degenerate linear transformation of the unknowns

Let's bring it to normal form. Without loss of generality, we can assume that in this normal form the square of the last variable is either absent or included with a minus sign, i.e. , where or . Let us assume that is a non-zero set of variable values ​​obtained as a result of solving the system linear equations

In this system, the number of equations is equal to the number of variables and the determinant of the system is nonzero. According to Cramer's theorem, the system has the only solution, and it is non-zero. For this set. Contradiction with the condition. We come to a contradiction with the assumption, which proves the sufficiency of the theorem.

Using this criterion, it is impossible to determine from the coefficients whether the quadratic form is positive definite. The answer to this question is given by another theorem, for the formulation of which we introduce another concept. Principal diagonal minors of a matrix are minors located in its left top corner:

, , , … , .

Theorem.A quadratic form is positive definite if and only if all its principal diagonal minors are positive.

Proof we will carry out the method of complete mathematical induction by number n quadratic variables f.

Induction hypothesis. Let us assume that for quadratic forms with fewer variables n the statement is true.

Consider the quadratic form of n variables. Let's put all the terms containing . The remaining terms form a quadratic form of the variables. According to the induction hypothesis, the statement is true for her.

Let us assume that the quadratic form is positive definite. Then the quadratic form is positive definite. If we assume that this is not the case, then there is a non-zero set of variable values , for which and, accordingly, , and this contradicts the fact that the quadratic form is positive definite. By the induction hypothesis, all principal diagonal minors of a quadratic form are positive, i.e. all first principal minors of quadratic form f are positive. Last principal minor of quadratic form – this is the determinant of its matrix. This determinant is positive, since its sign coincides with the sign of its matrix normal looking, i.e. with the sign of the determinant of the identity matrix.

Let all the main diagonal minors of the quadratic form be positive. Then all the main diagonal minors of the quadratic form are positive from the equality . By the induction hypothesis, the quadratic form is positive definite, so there is a non-degenerate linear transformation of the variables that reduces the form to the form of the sum of squares of the new variables. This linear transformation can be extended to a non-degenerate linear transformation of all variables by setting . This transformation reduces the quadratic form to the form

Quadratic shapes

Quadratic shape f(x 1, x 2,...,x n) of n variables is a sum, each term of which is either the square of one of the variables, or the product of two different variables, taken with a certain coefficient: f(x 1, x 2, ...,x n) = (a ij = a ji).

The matrix A composed of these coefficients is called a matrix of quadratic form. It's always symmetrical matrix (i.e. a matrix symmetrical about the main diagonal, a ij = a ji).

In matrix notation, the quadratic form is f(X) = X T AX, where

Indeed

For example, let's write in matrix form quadratic form.

To do this, we find a matrix of quadratic form. Its diagonal elements are equal to the coefficients of the squared variables, and the remaining elements are equal to the halves of the corresponding coefficients of the quadratic form. That's why

Let the matrix-column of variables X be obtained by a non-degenerate linear transformation of the matrix-column Y, i.e. X = CY, where C is a non-singular matrix of nth order. Then the quadratic form
f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Thus, with a non-degenerate linear transformation C, the matrix of quadratic form takes the form: A * = C T AC.

For example, let's find the quadratic form f(y 1, y 2), obtained from the quadratic form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 by linear transformation.

The quadratic form is called canonical(has canonical view), if all its coefficients a ij = 0 for i ≠ j, i.e.
f(x 1, x 2,...,x n) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 = .

Its matrix is ​​diagonal.

Theorem(proof not given here). Any quadratic form can be reduced to canonical form using a non-degenerate linear transformation.

For example, let us reduce the quadratic form to canonical form
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3.

To do this, we first select perfect square with variable x 1:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 – x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 – x 2 x 3.

Now we select a complete square with the variable x 2:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 – 5(x 2 2 – 2* x 2 *(1/10)x 3 + (1/100)x 3 2) - (5/100)x 3 2 =
= 2(x 1 + x 2) 2 – 5(x 2 – (1/10)x 3) 2 - (1/20)x 3 2.

Then the non-degenerate linear transformation y 1 = x 1 + x 2, y 2 = x 2 – (1/10)x 3 and y 3 = x 3 brings this quadratic form to the canonical form f(y 1, y 2, y 3) = 2y 1 2 - 5y 2 2 - (1/20)y 3 2 .

Note that the canonical form of a quadratic form is determined ambiguously (the same quadratic form can be reduced to the canonical form in different ways). However, the received in various ways canonical forms have a number of general properties. In particular, the number of terms with positive (negative) coefficients of a quadratic form does not depend on the method of reducing the form to this form (for example, in the example considered there will always be two negative and one positive coefficient). This property is called law of inertia of quadratic forms.

Let us verify this by bringing the same quadratic form to canonical form in a different way. Let's start the transformation with the variable x 2:
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 – x 2 x 3 = -3x 2 2 – x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 –
- 2* x 2 ((1/6) x 3 + (2/3)x 1) +((1/6) x 3 + (2/3)x 1) 2) – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 – (1/6) x 3 - (2/3)x 1) 2 – 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -
-3y 2 2 + 2y 3 2, where y 1 = - (2/3)x 1 + x 2 – (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 and y 3 = x 1 . Here there is a positive coefficient of 2 at y 3 and two negative coefficients (-3) at y 1 and y 2 (and using another method we got a positive coefficient of 2 at y 1 and two negative coefficients - (-5) at y 2 and (-1 /20) at y 3).

It should also be noted that the rank of a matrix of quadratic form, called rank of quadratic form, is equal to the number of non-zero coefficients canonical form and does not change under linear transformations.

The quadratic form f(X) is called positively (negative) certain, if for all values ​​of the variables that are not simultaneously equal to zero, it is positive, i.e. f(X) > 0 (negative, i.e.
f(X)< 0).

For example, the quadratic form f 1 (X) = x 1 2 + x 2 2 is positive definite, because is a sum of squares, and the quadratic form f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 is negative definite, because represents it can be represented as f 2 (X) = -(x 1 - x 2) 2.

In most practical situations, it is somewhat more difficult to establish the definite sign of a quadratic form, so for this we use one of the following theorems (we will formulate them without proof).

Theorem. A quadratic form is positive (negative) definite if and only if all eigenvalues its matrices are positive (negative).

Theorem (Sylvester criterion). A quadratic form is positive definite if and only if all the leading minors of the matrix of this form are positive.

Main (corner) minor The kth order matrix A of the nth order is called the determinant of the matrix, composed of the first k rows and columns of the matrix A ().

Note that for negative definite quadratic forms the signs of the principal minors alternate, and the first-order minor must be negative.

For example, let us examine the quadratic form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 for sign definiteness.

= (2 - l)*
*(3 - l) – 4 = (6 - 2l - 3l + l 2) – 4 = l 2 - 5l + 2 = 0; D = 25 – 8 = 17;
. Therefore, the quadratic form is positive definite.

Method 2. Principal minor of the first order of matrix A D 1 = a 11 = 2 > 0. Principal minor of the second order D 2 = = 6 – 4 = 2 > 0. Therefore, according to Sylvester’s criterion, the quadratic form is positive definite.

We examine another quadratic form for sign definiteness, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Method 1. Let's construct a matrix of quadratic form A = . Characteristic equation will look like = (-2 - l)*
*(-3 - l) – 4 = (6 + 2l + 3l + l 2) – 4 = l 2 + 5l + 2 = 0; D = 25 – 8 = 17;
. Therefore, the quadratic form is negative definite.