Let there be square matrix nth order
Matrix A -1 is called inverse matrix in relation to the matrix A, if A*A -1 = E, where E is the identity matrix of the nth order.
Identity matrix- such a square matrix in which all elements are along the main diagonal passing from the left top corner to the lower right corner are ones, and the rest are zeros, for example:
Inverse matrix may exist only for square matrices those. for those matrices in which the number of rows and columns coincide.
Theorem for the existence condition of an inverse matrix
In order for a matrix to have an inverse matrix, it is necessary and sufficient that it be non-singular.
The matrix A = (A1, A2,...A n) is called non-degenerate, if the column vectors are linearly independent. The number of linearly independent column vectors of a matrix is called the rank of the matrix. Therefore, we can say that in order for an inverse matrix to exist, it is necessary and sufficient that the rank of the matrix is equal to its dimension, i.e. r = n.
Algorithm for finding the inverse matrix
- Write matrix A into the table for solving systems of equations using the Gaussian method and assign matrix E to it on the right (in place of the right-hand sides of the equations).
- Using Jordan transformations, reduce matrix A to a matrix consisting of unit columns; in this case, it is necessary to simultaneously transform the matrix E.
- If necessary, rearrange the rows (equations) of the last table so that under the matrix A of the original table you get the identity matrix E.
- Write down the inverse matrix A -1, which is in last table under matrix E of the original table.
For matrix A, find the inverse matrix A -1

Solution: We write matrix A and assign the identity matrix E to the right. Using Jordan transformations, we reduce matrix A to the identity matrix E. The calculations are given in Table 31.1.

Let's check the correctness of the calculations by multiplying the original matrix A and inverse matrix A -1.

As a result of matrix multiplication, the identity matrix was obtained. Therefore, the calculations were performed correctly.
Answer: 
Solving matrix equations
Matrix equations can look like:
AX = B, HA = B, AXB = C,
where A, B, C are the specified matrices, X is the desired matrix.
Matrix equations are solved by multiplying the equation by inverse matrices.
For example, to find the matrix from the equation, you need to multiply this equation by on the left.
Therefore, to find a solution to the equation, you need to find the inverse matrix and multiply it by the matrix on the right side of the equation.
Other equations are solved similarly.

Solve the equation AX = B if 
Solution: Since the inverse matrix is equal to (see example 1)
Matrix method in economic analysis
Along with others, they are also used matrix methods . These methods are based on linear and vector-matrix algebra. Such methods are used for the purposes of analyzing complex and multidimensional economic phenomena. Most often, these methods are used when it is necessary to make a comparative assessment of the functioning of organizations and their structural divisions.
In the process of applying matrix analysis methods, several stages can be distinguished.
At the first stage the system is being formed economic indicators and on its basis, a source data matrix is compiled, which is a table in which system numbers are shown in its individual rows (i = 1,2,....,n), and in vertical columns - numbers of indicators (j = 1,2,....,m).
At the second stage For each vertical column, the largest of the available indicator values is identified, which is taken as one.
After this, all amounts reflected in this column are divided by highest value and a matrix of standardized coefficients is formed.
At the third stage all components of the matrix are squared. If they have different significance, then each matrix indicator is assigned a certain weight coefficient k. The value of the latter is determined by expert opinion.
On the last one, fourth stage found quantities ratings Rj are grouped in order of their increase or decrease.
The matrix methods outlined should be used, for example, when comparative analysis various investment projects, as well as when assessing other economic indicators of organizations.
Given methodological manual will help you learn how to perform operations with matrices: addition (subtraction) of matrices, transposition of a matrix, multiplication of matrices, finding the inverse matrix. All material is presented in a simple and accessible form, relevant examples are given, so even an untrained person can learn how to perform operations with matrices. For self-monitoring and self-testing, you can download a matrix calculator for free >>>.
I will try to minimize theoretical calculations, in some places explanations “on the fingers” and the use of non-scientific terms are possible. Lovers of solid theory, please do not engage in criticism, our task is learn to perform operations with matrices.
For SUPER FAST preparation on the topic (who is “on fire”) there is an intensive pdf course Matrix, determinant and test!
The Matrix is rectangular table any elements. As elements we will consider numbers, that is, numerical matrices. ELEMENT is a term. It is advisable to remember the term, it will appear often, it is no coincidence that I used bold font to highlight it.
Designation: matrices are usually denoted in capitals in Latin letters
Example: Consider a two-by-three matrix:
![]()
This matrix consists of six elements:
All numbers (elements) inside the matrix exist on their own, that is, there is no question of any subtraction: ![]()
It's just a table (set) of numbers!
We'll also agree don't rearrange numbers, unless otherwise stated in the explanations. Each number has its own location and cannot be shuffled!
The matrix in question has two rows: 
and three columns: 
STANDARD: when talking about matrix sizes, then at first indicate the number of rows, and only then the number of columns. We have just broken down the two-by-three matrix.
If the number of rows and columns of a matrix is the same, then the matrix is called square, For example:  – a three-by-three matrix.
– a three-by-three matrix.
If a matrix has one column or one row, then such matrices are also called vectors.
In fact, we have known the concept of a matrix since school; consider, for example, a point with coordinates “x” and “y”: . Essentially, the coordinates of a point are written into a one-by-two matrix. By the way, here is an example of why the order of numbers matters: and are two completely different points plane.
Now let's move on to studying operations with matrices:
1) Act one. Removing a minus from the matrix (introducing a minus into the matrix).
Let's return to our matrix  . As you probably noticed, there are too many negative numbers in this matrix. This is very inconvenient from the point of view of performing various actions with the matrix, it is inconvenient to write so many minuses, and it simply looks ugly in design.
. As you probably noticed, there are too many negative numbers in this matrix. This is very inconvenient from the point of view of performing various actions with the matrix, it is inconvenient to write so many minuses, and it simply looks ugly in design.
Let's move the minus outside the matrix by changing the sign of EACH element of the matrix:
At zero, as you understand, the sign does not change; zero is also zero in Africa.
Reverse example:  . It looks ugly.
. It looks ugly.
Let's introduce a minus into the matrix by changing the sign of EACH element of the matrix:

Well, it turned out much nicer. And, most importantly, it will be EASIER to perform any actions with the matrix. Because there is such a mathematical folk sign: the more minuses, the more confusion and errors.
2) Act two. Multiplying a matrix by a number.
Example:
![]()
It's simple, in order to multiply a matrix by a number, you need every matrix element multiplied by given number. IN in this case- for three.
Another useful example:
 – multiplying a matrix by a fraction
– multiplying a matrix by a fraction
First let's look at what to do NO NEED:
There is NO NEED to enter a fraction into the matrix, firstly, it only complicates further actions with a matrix, secondly, it makes it difficult for the teacher to check the solution (especially if  – final answer of the task).
– final answer of the task).
And, moreover, NO NEED divide each element of the matrix by minus seven:

From the article Mathematics for dummies or where to start, we remember that decimals in higher mathematics they try to avoid them in every possible way.
The only thing is preferably What to do in this example is to add a minus to the matrix:
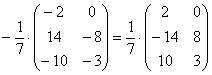
But if only ALL matrix elements were divided by 7 without a trace, then it would be possible (and necessary!) to divide.
Example:

In this case, you can NEED TO multiply all matrix elements by , since all matrix numbers are divisible by 2 without a trace.
Note: in theory higher mathematics school concept"division" no. Instead of saying “this divided by that,” you can always say “this multiplied by a fraction.” That is, division is special case multiplication.
3) Act three. Matrix Transpose.
In order to transpose a matrix, you need to write its rows into the columns of the transposed matrix.
Example:
Transpose matrix
There is only one line here and, according to the rule, it needs to be written in a column:
– transposed matrix.
A transposed matrix is usually indicated by a superscript or a prime at the top right.
Step by step example:
Transpose matrix 
First we rewrite the first row into the first column:

Then we rewrite the second line into the second column: 
And finally, we rewrite the third row into the third column:

Ready. Roughly speaking, transposing means turning the matrix on its side.
4) Act four. Sum (difference) of matrices.
The sum of matrices is a simple operation.
NOT ALL MATRICES CAN BE FOLDED. To perform addition (subtraction) of matrices, it is necessary that they be the SAME SIZE.
For example, if a two-by-two matrix is given, then it can only be added with a two-by-two matrix and no other! 
Example:
Add matrices ![]() And
And ![]()
In order to add matrices, you need to add their corresponding elements:

For the difference of matrices the rule is similar, it is necessary to find the difference of the corresponding elements.
Example:
Find matrix difference ![]() ,
, ![]()

How to decide this example easier so as not to get confused? It is advisable to get rid of unnecessary minuses; to do this, add a minus to the matrix:
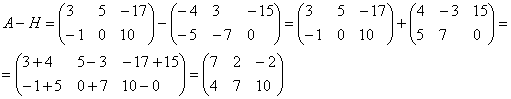
Note: in the theory of higher school mathematics there is no concept of “subtraction”. Instead of saying “subtract this from this,” you can always say “add this to this.” negative number" That is, subtraction is a special case of addition.
5) Act five. Matrix multiplication.
What matrices can be multiplied?
In order for a matrix to be multiplied by a matrix, it is necessary so that the number of matrix columns is equal to the number of matrix rows.
Example:
Is it possible to multiply a matrix by a matrix?

This means that matrix data can be multiplied.
But if the matrices are rearranged, then, in this case, multiplication is no longer possible!

Therefore, multiplication is not possible:

It is not so rare to encounter tasks with a trick, when the student is asked to multiply matrices, the multiplication of which is obviously impossible.
It should be noted that in some cases it is possible to multiply matrices in both ways.
For example, for matrices, and both multiplication and multiplication are possible
Points in space, product Rv gives another vector that determines the position of the point after rotation. If v is a row vector, the same transformation can be obtained using vR T, where R T - transposed to R matrix.
Encyclopedic YouTube
1 / 5
C# - Console - Olympiad - Square Spiral
Matrix: definition and basic concepts
Where to get strength and inspiration Recharging the 4 square matrix
Sum and difference of matrices, multiplication of a matrix by a number
Transposed matrix / Transposed matrix
Subtitles
Main diagonal
Elements a ii (i = 1, ..., n) form the main diagonal of a square matrix. These elements lie on an imaginary straight line running from the upper left corner to the lower right corner of the matrix. For example, the main diagonal of the 4x4 matrix in the figure contains the elements a 11 = 9, a 22 = 11, a 33 = 4, a 44 = 10.
The diagonal of a square matrix passing through the lower left and upper right corners is called side.
Special types
| Name | Example with n = 3 |
|---|---|
| Diagonal matrix | [ a 11 0 0 0 a 22 0 0 0 a 33 ] (\displaystyle (\begin(bmatrix)a_(11)&0&0\\0&a_(22)&0\\0&0&a_(33)\end(bmatrix))) |
| Lower triangular matrix | [ a 11 0 0 a 21 a 22 0 a 31 a 32 a 33 ] (\displaystyle (\begin(bmatrix)a_(11)&0&0\\a_(21)&a_(22)&0\\a_(31)&a_( 32)&a_(33)\end(bmatrix))) |
| Upper triangular matrix | [ a 11 a 12 a 13 0 a 22 a 23 0 0 a 33 ] (\displaystyle (\begin(bmatrix)a_(11)&a_(12)&a_(13)\\0&a_(22)&a_(23)\\ 0&0&a_(33)\end(bmatrix))) |
Diagonal and triangular matrices
If all elements outside the main diagonal are zero, A called diagonal. If all elements above (below) the main diagonal are zero, A called the lower (upper) triangular matrix.
Identity matrix
Q(x) = x T Axaccepts only positive values(respectively, negative values or both). If quadratic form takes only non-negative (respectively, only non-positive) values, a symmetric matrix is called positively semidefinite (respectively, negative semidefinite). A matrix will be indeterminate if it is neither positive nor negative semidefinite.
A symmetric matrix is positive definite if and only if all of its eigenvalues are positive. The table on the right shows two possible cases for 2x2 matrices.
If we use two different vectors, we obtain a bilinear form associated with A:
B A (x, y) = x T Ay.Orthogonal matrix
Orthogonal matrix is a square matrix with real elements whose columns and rows are orthogonal unit vectors (i.e., orthonormal). You can also define orthogonal matrix as a matrix whose inverse is equal to the transposed one:
A T = A − 1 , (\displaystyle A^(\mathrm (T) )=A^(-1),)where does it come from
A T A = A A T = E (\displaystyle A^(T)A=AA^(T)=E),Orthogonal matrix A always reversible ( A −1 = A T), unitary ( A −1 = A*), and normal ( A*A = A.A.*). The determinant of any orthonormal matrix is either +1 or −1. As a linear mapping, any orthonormal matrix with determinant +1 is a simple rotation, while any orthonormal matrix with determinant −1 is either a simple reflection or a composition of reflection and rotation.
Operations
Track
Determinant det( A) or | A| square matrix A is a number that determines some properties of the matrix. A matrix is invertible if and only if its determinant is nonzero.
The matrix is denoted by capital Latin letters ( A, IN, WITH,...).
Definition 1. Rectangular table view,

consisting of m lines and n columns is called matrix.
Matrix element, i – row number, j – column number.
Types of matrices:
elements on the main diagonal:
trA=a 11 +a 22 +a 33 +…+a nn .
§2. Determinants of 2nd, 3rd and nth order
Let two square matrices be given:


Definition 1. Determinant of the second order matrix A 1
is a number denoted by ∆ and equal to  , Where
, Where
Example. Calculate the 2nd order determinant:
![]()
Definition 2. Determinant of the 3rd order of a square matrix A 2 is called a number of the form:


This is one way to calculate the determinant.
Example. Calculate

Definition 3. If a determinant consists of n-rows and n-columns, then it is called an n-th order determinant.
Properties of determinants:
The determinant does not change when transposed (that is, if its rows and columns are swapped while maintaining the order).
If you swap any two rows or two columns in the determinant, then the determinant will only change the sign.
The common factor of any row (column) can be taken beyond the sign of the determinant.
If all elements of any row (column) of the determinant are equal to zero, then the determinant equal to zero.
The determinant is zero if the elements of any two rows are equal or proportional.
The determinant will not change if the corresponding elements of another row (column) are added to the elements of a row (column), multiplied by the same number.
Example.

Definition 4. The determinant obtained from a given one by crossing out a column and a row is called minor the corresponding element. M ij element a ij .
Definition 5. Algebraic complement element a ij is called the expression
![]()
§3. Actions on matrices
Linear operations
1) When adding matrices, their elements of the same name are added.

When subtracting matrices, their elements of the same name are subtracted.
When multiplying a matrix by a number, each element of the matrix is multiplied by that number:

3.2.Matrix multiplication.
![]()

![]()
Work matrices A to the matrix IN there is a new matrix whose elements are equal to the sum of the products of the elements of the i-th row of the matrix A to the corresponding elements of the jth column of the matrix IN. Matrix product A to the matrix IN can be found only if the number of matrix columns A equal to the number of rows of the matrix IN. Otherwise, the work is impossible.

Comment:
(does not obey the commutative property)
§ 4. Inverse matrix
The inverse matrix exists only for a square matrix, and the matrix must be non-singular.
Definition 1. Matrix A called non-degenerate, if the determinant of this matrix is not equal to zero
Definition 2. A-1 is called inverse matrix for a given non-singular square matrix A, if when multiplying this matrix by the given one, both on the right and on the left, the identity matrix is obtained.
![]()
Algorithm for calculating the inverse matrix
1 way (using algebraic additions)
![]()
Example 1:

Definition by Matrix– called a table of numbers containing a certain number of rows and columns
The elements of the matrix are numbers of the form a ij, where i is the row number j is the column number
Example 1 i = 2 j = 3
Designation: A=
Types of matrices:
1. If the number of rows is not equal to the number of columns, then the matrix is called rectangular:
2. If the number of rows is equal to the number of columns, then the matrix is called square:
The number of rows or columns of a square matrix is called its in order. In the example n = 2
Consider a square matrix of order n:

The diagonal containing the elements a 11, a 22......., a nn is called main , and the diagonal containing the elements a 12, a 2 n -1, …….a n 1 – auxiliary.
A matrix in which only the elements on the main diagonal are nonzero is called diagonal:
Example 4  n=3
n=3
3. If a diagonal matrix has elements equal to 1, then the matrix is called single and is designated by the letter E:
Example 6  n=3
n=3
4. A matrix, all elements of which are equal to zero, is called null matrix and is denoted by the letter O
Example 7 ![]()
5. Triangular A matrix of nth order is a square matrix, all of whose elements located below the main diagonal are equal to zero:
Example 8  n=3
n=3
Actions on matrices:
The sum of a matrix A and B is a matrix C whose elements are equal to the sum of the corresponding elements of matrices A and B.
Only matrices that have same number rows and columns.
Product of matrix A and number k such a matrix kA is called, each element of which is equal to ka ij
Example10 
Multiplying a matrix by a number is reduced to multiplying all the elements of the matrix by that number.
Product of matrices To multiply a matrix by a matrix, you need to select the first row of the first matrix and multiply by the corresponding elements of the first column of the second matrix, and add the result. Place this result in the result matrix in the 1st row and 10th column. We perform the same actions with all other elements: 1st line to the second column, to the 3rd, etc., then with the following lines.
Example 11 
Multiplying matrix A by matrix B is possible only if the number of columns of the first matrix is equal to the number of columns of the second matrix.
![]() - the work exists;
- the work exists;
![]() - the work does not exist
- the work does not exist
Examples 12  there is nothing to multiply the last line in matrix II with, i.e. the work does not exist
there is nothing to multiply the last line in matrix II with, i.e. the work does not exist
Matrix Transpose The operation of replacing row elements with column elements is called:
Example13 
By raising to a power is called sequential multiplication of a matrix by itself.









