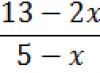Instructions
Given a square pyramid base with a known side length (a) and a given volume (V), replace the area in the calculation formula from the previous step with the squared side length: H = 3*V/a².
The formula from the first step can be transformed to calculate the height (H) of a regular pyramid with a base of any shape. The initial data that should be involved in it are the volume (V) of the polyhedron, the length of the edge at the base (a) and the number of vertices at the base (n). Square regular polygon is determined by a quarter of the product of the number of vertices by the square of the side length and the cotangent of the angle, equal to the ratio of 180° and the number of vertices: ¼*n*a²*ctg(180°/n). Substitute this expression into the formula from the first step: H = 3*V/(¼*n*a²*ctg(180°/n)) = 12*V/(n*a²*ctg(180°/n)).
If the area of the base is unknown from the conditions of the problem, and only the volume (V) and the length of the edge (a) are given, then the missing variable in the formula from the previous step can be replaced by its equivalent, expressed in terms of the length of the edge. The area (it, as you remember, lies at the base of the pyramid of the type in question) is equal to one quarter of the product square root from the three to the squared length of the side. Substitute this expression instead of the area of the base into the formula from the previous step, and get the following result: H = 3*V*4/(a²*√3) = 12*V/(a²*√3).
Since the volume of a tetrahedron can also be expressed through the length of an edge, all variables can be removed from the formula for calculating the height of a figure, leaving only the side of its face. The volume of this pyramid is calculated by dividing by 12 the product of the square root of two by the cubed length of the face. Substitute this expression into the formula from the previous step, and get the result: H = 12*(a³*√2/12)/(a²*√3) = (a³*√2)/(a²*√3) = a* √⅔ = ⅓*a*√6.
The correct prism can be inscribed in a sphere, and knowing only its radius (R) one can calculate the tetrahedron. The length of the edge is equal to four times the ratio of the radius and the square root of six. Replace variable a in the formula from the previous step with this expression and get the equality: H = ⅓*√6*4*R/√6 = 4*r/3.
A similar formula can be obtained by knowing the radius (r) of the circle inscribed in the tetrahedron. In this case, the length of the edge will be equal to twelve ratios between the radius and the square of six. Substitute this expression into the formula from the third step: H = ⅓*a*√6 = ⅓*√6*12*R/√6 = 4*R.
The pyramid is one of the most mystical figures in geometry. Streams are associated with it cosmic energy, many ancient peoples chose this particular form for the construction of their religious buildings. However, from a mathematical point of view, a pyramid is just a polyhedron, with a polygon at the base, and the faces are triangles with common top. Let's look at how to find square edges V pyramid.

You will need
- calculator.
Instructions
Types of pyramids: regular (at the base is a regular polygon, and the vertices at its center), arbitrary (at the base is any polygon, and the projection of the vertex does not necessarily coincide with its center), rectangular (one of the side edges makes a right angle with the base) and . Depending on the sides of the polygon at the base of the pyramid, it is called three-, four-, five- or, for example, decagonal.
For all types of pyramids, except truncated ones: Multiply the lengths of the base of the triangle and the height lowered onto it from the top of the pyramid. Divide the resulting product by 2 - this will be the desired square side edges pyramids.
Truncated pyramidFold both bases of the trapezoid, which is the face of such a pyramid. Divide the resulting amount by two. Multiply the resulting value by the height edges-trapeze. The resulting value is square side edges pyramids of this type.
Video on the topic
The area of the lateral surface and the base, the perimeter of the base of the pyramid and its volume are interconnected certain formulas. This sometimes makes it possible to calculate the values of the missing data necessary to determine the area of a face in the pyramid.
The volume of any non-truncated pyramid is equal to one third of the product of the height of the pyramid and the area of the base. For a regular pyramid, it is true: the area of the lateral surface is equal to half the perimeter of the base multiplied by the height of one of the faces. When calculating the volume of a truncated pyramid, instead of the area of the base, substitute the value equal to the sum areas of the upper and lower bases and the square root of their product.
Sources:
- Stereometry
- how to find the side face of a pyramid
A pyramid is called rectangular if one of its edges is perpendicular to its base, that is, it stands at an angle of 90˚. This edge is also the height rectangular pyramid. The formula for the volume of a pyramid was first derived by Archimedes.

You will need
- - pen;
- - paper;
- - calculator.
Instructions
IN rectangular height there will be its edge, which stands at an angle of 90˚ to the base. As, the area of the rectangular base is denoted as S, and the height, which is also pyramids, − h. Then, to find the volume of this pyramids, it is necessary to multiply the area of its base by its height and divide by 3. Thus, the volume of a rectangular pyramids calculated using the formula: V=(S*h)/3.
Build following given parameters. Label its base with Latin ABCDE, and its top pyramids- S. Since the drawing will be on a plane in projection, in order not to get confused, indicate the data you already know: SE = 30cm; S(ABCDE)=45 cm².
Calculate the volume of a rectangular pyramids, using the formula. Substituting the data and making calculations, it turns out that the volume of a rectangular pyramids will be equal to: V=(45*30)/3=cm³.
If the problem statement does not contain data on and height pyramids, then you need to carry out additional calculations to obtain these values. The area of the base will be calculated depending on whether the polygon lies at its base.
Height pyramids find out if you know the hypotenuse of any of the rectangular EDS or EAS and the angle at which the side face SD or SA is inclined to its base. Calculate the SE leg using the sine theorem. It will be the height of the rectangular pyramids.
Please note
When calculating quantities such as height, volume, area, you should remember that each of them has its own unit of measurement. So, area is measured in cm², height in cm, and volume in cm³.
Cubic centimeter is a unit of volume that is equal to the volume of a cube with edges 1 cm long. If we substitute the data into our formula, we get: cm³= (cm²*cm)/3.
Useful advice
As a rule, if the problem requires finding the volume of a rectangular pyramid, then all the necessary data is known - at least in order to find the area of the base and the height of the figure.
A drawing is the first and very important step in solving geometric problem. What should the drawing of a regular pyramid look like?
First let's remember parallel design properties:
- parallel segments of the figure are depicted parallel segments;
— the ratio of the lengths of segments of parallel lines and segments of one straight line is preserved.
Drawing correct triangular pyramid
First we draw the base. Since when parallel design angles and length ratios are not parallel segments are not saved, the regular triangle at the base of the pyramid is depicted as an arbitrary triangle.
The center of a regular triangle is the point of intersection of the triangle's medians. Since the medians at the intersection point are divided in a ratio of 2:1, counting from the vertex, we mentally connect the vertex of the base with the middle of the opposite side, approximately divide it into three parts, and place a point at a distance of 2 parts from the vertex. From this point upward we draw a perpendicular. This is the height of the pyramid. Draw a perpendicular of such length that side rib did not cover the height image.
Drawing correct quadrangular pyramid

We also start drawing a regular quadrangular pyramid from the base. Since the parallelism of the segments is preserved, but the magnitudes of the angles are not, the square at the base is depicted as a parallelogram. Preferably acute angle make this parallelogram smaller, then the side faces will be larger. The center of a square is the point of intersection of its diagonals. We draw diagonals and restore a perpendicular from the intersection point. This perpendicular is the height of the pyramid. We choose the length of the perpendicular so that the side ribs do not merge with each other.
Drawing correct hexagonal pyramid

Since during parallel design the parallelism of the segments is preserved, the base of a regular hexagonal pyramid - a regular hexagon - is depicted as a hexagon whose opposite sides are parallel and equal. The center of a regular hexagon is the point of intersection of its diagonals. In order not to clutter the drawing, we do not draw diagonals, but find this point approximately. From it we restore the perpendicular - the height of the pyramid - so that the side ribs do not merge with each other.
Pyramids are: triangular, quadrangular, etc., depending on what is the base - triangle, quadrangle, etc.
A pyramid is called regular (Fig. 286, b) if, firstly, its base is a regular polygon, and, secondly, its height passes through the center of this polygon.
Otherwise, the pyramid is called irregular (Fig. 286, c). IN correct pyramid all side ribs are equal to each other (as inclined with equal projections). Therefore, all the lateral faces of a regular pyramid are equal isosceles triangles.
Analysis of the elements of a regular hexagonal pyramid and their depiction in a complex drawing (Fig. 287).

A) Complex drawing regular hexagonal pyramid. The base of the pyramid is located on the plane P 1; two sides of the base of the pyramid are parallel to the projection plane P 2.
b) The base ABCDEF is a hexagon located in the projection plane P 1.
V) Side edge ASF is a triangle located in the general plane.
d) The side face of FSE is a triangle located in the profile-projecting plane.
e) Edge SE is a segment in general position.
f) Rib SA - frontal segment.
g) The top S of the pyramid is a point in space.
Figures 288 and 289 show examples of sequential graphic operations when performing a complex drawing and visual images (axonometry) of the pyramids.

Given:
1. The base is located on the plane P 1.
2. One of the sides of the base is parallel to the x-axis 12.
I. Complex drawing.
I, a. We design the base of the pyramid - a polygon, according to this condition lying in the plane P1.
We design a vertex - a point located in space. The height of point S is equal to the height of the pyramid. The horizontal projection S 1 of point S will be in the center of the projection of the base of the pyramid (by condition).
I, b. We design the edges of the pyramid - segments; To do this, we connect the projections of the vertices of the base ABCDE with the corresponding projections of the vertex of the pyramid S by straight lines. We depict the frontal projections S 2 C 2 and S 2 D 2 of the edges of the pyramid with dashed lines, as invisible, closed by the edges of the pyramid (SА and SAE).
I, c. Given a horizontal projection K 1 of point K on the side face of SBA, you need to find its frontal projection. To do this, we draw an auxiliary straight line S 1 F 1 through points S 1 and K 1, find its frontal projection and on it using vertical line connection, we determine the location of the desired frontal projection K 2 of point K.
II. Development of the surface of the pyramid - flat figure, consisting of side faces - identical isosceles triangles, one side of which is equal to the side of the base, and the other two - to the side edges, and from a regular polygon - the base.
The natural dimensions of the sides of the base are revealed on its horizontal projection. The natural dimensions of the ribs were not revealed on the projections.
Hypotenuse S 2 ¯A 2 (Fig. 288, 1
, b) right triangle S 2 O 2 ¯A 2, which has a large leg equal to height S 2 O 2 of the pyramid, and the small one is the horizontal projection of the edge S 1 A 1 is the natural size of the edge of the pyramid. The construction of the sweep should be performed in the following order:
a) from arbitrary point S (vertices) draw an arc of radius R, equal to the edge pyramids;
b) on the drawn arc we will lay down five chords of size R 1 equal to the side of the base;
c) connect points D, C, B, A, E, D with straight lines in series with each other and with point S, we get five isosceles equal triangles, constituting the development of the lateral surface of this pyramid, cut along the edge SD;
d) we attach the base of the pyramid - a pentagon - to any face using the triangulation method, for example to the DSE face.
The transfer of point K to the scan is carried out by an auxiliary straight line using the dimension B 1 F 1 taken on the horizontal projection and the dimension A 2 K 2 taken on the natural size of the rib.
III. A visual representation of a pyramid in isometry.
III, a. We depict the base of the pyramid using the coordinates according to (Fig. 288, 1
, A).
We depict the top of the pyramid using the coordinates according to (Fig. 288, 1
, A).
III, b. We depict the side edges of the pyramid, connecting the top with the vertices of the base. The edge S"D" and the sides of the base C"D" and D"E" are depicted with dashed lines, as invisible, closed by the edges of the pyramid C"S"B", B"S"A" and A"S"E".
III, e. We determine point K on the surface of the pyramid using the dimensions y F and x K. For a dimetric image of a pyramid, the same sequence should be followed.
Image of an irregular triangular pyramid.

Given:
1. The base is located on the plane P 1.
2. Side BC of the base is perpendicular to the X axis.
I. Complex drawing
I, a. Designing the base of the pyramid - isosceles triangle, lying in the plane P 1, and the vertex S is a point located in space, the height of which is equal to the height of the pyramid.
I, b. We design the edges of the pyramid - segments, for which we connect straight lines of the same-name projections of the base vertices with the same-name projections of the pyramid's apex. We depict the horizontal projection of the side of the base of the aircraft with a dashed line, as invisible, covered by two faces of the pyramid ABS, ACS.
I, c. On the frontal projection A 2 C 2 S 2 of the side face, a projection D 2 of point D is given. You need to find its horizontal projection. To do this, through point D 2 we draw an auxiliary line parallel to the x 12 axis - the frontal projection of the horizontal, then we find its horizontal projection and on it, using a vertical connection line, we determine the location of the desired horizontal projection D 1 of point D.
II. Constructing a pyramid scan.
The natural dimensions of the sides of the base are revealed on the horizontal projection. The natural size of rib AS was revealed on the frontal projection; there are no natural size edges BS and CS in the projections; the size of these edges is revealed by rotating them around the i axis perpendicular to the plane P1 passing through the top of the pyramid S. New frontal projection¯C 2 S 2 is the natural value of the edge CS.
The sequence of constructing the development of the surface of the pyramid:
a) draw an isosceles triangle - face CSB, the base of which is equal to the side of the base of the pyramid CB, and sides- natural size of rib SC;
b) we attach two triangles to the sides SC and SB of the constructed triangle - the faces of the pyramid CSA and BSA, and to the base CB of the constructed triangle - the base CBA of the pyramid, as a result we obtain a complete development of the surface of this pyramid.
Transferring point D to the scan is carried out in the following order: first, on the scan of the side face ASC, draw a horizontal line using size R 1 and then determine the location of point D on the horizontal line using size R 2.
III. A visual representation of the pyramid e frontal dimetric projection
III, a. We depict the base A"B"C and the top S" of the pyramid, using coordinates according to (
Calculating the volumes of spatial figures is one of the important tasks stereometry. In this article we will consider the issue of determining the volume of such a polyhedron as a pyramid, and also give a hexagonal regular one.
Hexagonal pyramid
First, let’s look at what the figure that will be discussed in the article is.
Let us have an arbitrary hexagon, the sides of which are not necessarily equal to each other. Let's also assume that we have chosen a point in space that is not located in the plane of the hexagon. By connecting all the corners of the latter with the selected point, we get a pyramid. Two different pyramids having hexagonal base, are shown in the figure below.
It can be seen that in addition to the hexagon, the figure consists of six triangles, the connecting point of which is called the vertex. The difference between the pyramids depicted is that the height h of the right one does not intersect the hexagonal base at its geometric center, and the height of the left figure falls exactly in this center. Thanks to this criterion, the left pyramid was called straight, and the right pyramid was called inclined.
Since the base of the left figure in the figure is formed by a hexagon with equal sides and angles, it is called regular. Further in the article we will talk only about this pyramid.

To calculate the volume of an arbitrary pyramid, we have following formula:
Here h is the length of the height of the figure, S o is the area of its base. Let's use this expression to determine the volume of a hexagonal regular pyramid.
Since the base of the figure in question is an equilateral hexagon, to calculate its area you can use the following general expression for n-gon:
S n = n/4 * a 2 * ctg(pi/n)
Here n is an integer equal to the number of sides (angles) of the polygon, a is the length of its side, the cotangent function is calculated using the appropriate tables.
Applying the expression for n = 6, we get:
S 6 = 6/4 * a 2 * ctg(pi/6) = √3/2 * a 2
Now all that remains is to substitute this expression into general formula for volume V:
V 6 = S 6 * h = √3/2 * h * a 2
Thus, to calculate the volume of the pyramid in question, it is necessary to know its two linear parameter: length of the side of the base and height of the figure.
Example of problem solution

Let us show how the resulting expression for V 6 can be used to solve the following problem.
It is known that the correct volume is 100 cm 3 . It is necessary to determine the side of the base and the height of the figure if it is known that they are related to each other by the following equality:
Since the formula for volume includes only a and h, you can substitute any of these parameters into it, expressed in terms of the other. For example, substituting a, we get:
V 6 = √3/2*h*(2*h) 2 =>
h = ∛(V 6 /(2*√3))
To find the height of a figure, you need to take the third root of the volume, which corresponds to the dimension of length. We substitute the value of the volume V 6 of the pyramid from the problem conditions, we get the height:
h = ∛(100/(2*√3)) ≈ 3.0676 cm
Since the side of the base, in accordance with the condition of the problem, is twice as large as the found value, we obtain the value for it:
a = 2*h = 2*3.0676 = 6.1352 cm
The volume of a hexagonal pyramid can be found not only through the height of the figure and the value of the side of its base. It is enough to know two different linear parameters of the pyramid to calculate it, for example, the apothem and the length of the side edge.
Problems with pyramids. In this article we will continue to consider problems with pyramids. They cannot be attributed to any class or type of tasks and general (algorithmic) recommendations for solution cannot be given. It’s just that the remaining tasks that were not considered earlier are collected here.
I will list the theory that you need to refresh your memory before solving: pyramids, properties of similarity of figures and bodies, properties of regular pyramids, Pythagorean theorem, formula for the area of a triangle (it’s the second one). Let's consider the tasks:
From a triangular pyramid whose volume is 80, a triangular pyramid is cut off by a plane passing through the top of the pyramid and the midline of the base. Find the volume of the cut-off triangular pyramid.

The volume of a pyramid is equal to one third of the product of the area of its base and its height:

These pyramids (original and cut off) have a common height, so their volumes are related as the areas of their bases. Middle line from the original triangle, cuts off a triangle whose area is four times smaller, that is:

More information about this can be found here.
This means that the volume of the cut-off pyramid will be four times smaller.
So it will be equal to 20.
Answer: 20
* a similar problem, the formula for the area of a triangle is used.
The volume of a triangular pyramid is 15. The plane passes through the side of the base of this pyramid and intersects the opposite side edge at a point dividing it in a ratio of 1: 2, counting from the top of the pyramid. Find the largest volume of the pyramids into which the plane divides the original pyramid.
Let's build a pyramid and mark the vertices.Let's mark point E on edge AS, so that AE is twice as large as ES (the condition says that ES is related to AE as 1 to 2), and construct the indicated plane passing through edge AC and point E:

Let's analyze the volume of which pyramid will be larger: EABC or SEBC?
*The volume of a pyramid is equal to one third of the product of the area of its base and its height:

If we consider the two resulting pyramids and take the face EBC as the base in both, it becomes obvious that the volume of the pyramid AEBS will be greater than the volume of the pyramid SEBC. Why?
The distance from point A to the EBC plane is greater than the distance from point S. And this distance plays the role of height for us.
So, let’s find the volume of the pyramid EABC.
The volume of the original pyramid is given to us; the pyramids SABC and EABC have a common base. If we establish the ratio of heights, we can easily determine the volume.
From the ratio of the segments ES and AE it follows that AE is equal to two thirds ES. The heights of the pyramids SABC and EABC are in the same relationship -the height of the pyramid EABC will be equal to 2/3 of the height of the pyramid SABC.
Thus, if

That
Answer: 10
The volume of a regular hexagonal pyramid is 6. The side of the base is 1. Find the side edge.

In a regular pyramid, the apex is projected into the center of the base.Let's perform additional constructions:

We can find the side edge from the right triangle SOC. To do this you need to know SO and OS.
SO is the height of the pyramid, we can calculate it using the volume formula:

Let's calculate the area of the base. is a regular hexagon with side equal to 1. The area of a regular hexagon is equal to the area of six equilateral triangles with the same side, more about this (item 6), so:

Means

OS = BC = 1, since in a regular hexagon the segment connecting its center with the vertex equal to side this hexagon.
Thus, according to the Pythagorean theorem:

Answer: 7
VolumeThe volume of a tetrahedron is 200. Find the volume of a polyhedron whose vertices are the midpoints of the edges of the given tetrahedron.

Volume of the specified polyhedron equal to the difference volumes of the original tetrahedron V 0 and four equal tetrahedra, each of which is obtained by cutting off a plane passing through the midpoints of the edges having a common vertex:
![]()
Let's determine what equal to volume cut tetrahedron.
Note that the original tetrahedron and the “cut off” tetrahedron are similar bodies. It is known that the ratio of volumes similar bodies equals k 3, where k is the similarity coefficient. IN in this case it is equal to 2 (since all linear dimensions of the original tetrahedron are twice as large as the corresponding dimensions of the cut one):
Let's calculate the volume of the cut tetrahedron:

Thus, the required volume will be equal to:
Answer: 100
The surface area of the tetrahedron is 120. Find the surface area of the polyhedron whose vertices are the midpoints of the edges of the given tetrahedron.

First way:
The required surface consists of 8 equilateral triangles with a side half the size of the edge of the original tetrahedron. The surface of the original tetrahedron consists of 16 such triangles (on each of the 4 faces of the tetrahedron there are 4 triangles), so the required area is equal to half the surface area of the given tetrahedron and is equal to 60.
Second way:
Since the surface area of the tetrahedron is known, we can find its edge, then determine the length of the edge of the polyhedron and then calculate its surface area.
The surface area of a tetrahedron consists of four equal areas regular triangles. Let the side of such a triangle (edge of the tetrahedron) be equal to a, then we can write:

That's all. Good luck to you!
Sincerely, Alexander Krutitskikh.
P.S: I would be grateful if you tell me about the site on social networks.