Empecemos explicando qué es el espacio de cuatro dimensiones.
Este es un espacio unidimensional, es decir, simplemente el eje OX. Cualquier punto sobre él se caracteriza por una coordenada.

Ahora dibujemos el eje OY perpendicular al eje OX. Entonces obtenemos un espacio bidimensional, es decir, el plano XOY. Cualquier punto se caracteriza por dos coordenadas: abscisa y ordenada.

Dibujemos el eje OZ perpendicular a los ejes OX y OY. El resultado es un espacio tridimensional en el que cualquier punto tiene abscisa, ordenada y aplicación.

Es lógico que el cuarto eje, OQ, sea perpendicular a los ejes OX, OY y OZ al mismo tiempo. Pero no podemos construir con precisión tal eje y, por lo tanto, sólo podemos intentar imaginarlo. Cada punto en el espacio de cuatro dimensiones tiene cuatro coordenadas: x, y, z y q.
Ahora veamos cómo apareció el cubo de cuatro dimensiones.

La imagen muestra una figura en un espacio unidimensional: una línea.

Si haces una traslación paralela de esta línea a lo largo del eje OY y luego conectas los extremos correspondientes de las dos líneas resultantes, obtendrás un cuadrado.

De manera similar, si haces una traslación paralela del cuadrado a lo largo del eje OZ y conectas los vértices correspondientes, obtendrás un cubo.

Y si hacemos una traslación paralela del cubo a lo largo del eje OQ y conectamos los vértices de estos dos cubos, obtendremos un cubo de cuatro dimensiones. Por cierto, se llama teseracto.
Para dibujar un cubo en un avión, lo necesitas. proyecto. Visualmente se ve así: 
Imaginemos que está suspendido en el aire sobre la superficie. modelo de estructura alámbrica cubo, es decir, como “hecho de alambre”, y encima hay una bombilla. Si enciende la bombilla, traza la sombra del cubo con un lápiz y luego apaga la bombilla, se representará una proyección del cubo en la superficie.
Pasemos a algo un poco más complejo. Observa de nuevo el dibujo de la bombilla: como puedes ver, todos los rayos convergen en un punto. Se llama punto de fuga y se utiliza para construir proyección en perspectiva(y también ocurre paralelo, cuando todos los rayos son paralelos entre sí. El resultado es que no se crea la sensación de volumen, pero sí más ligero, y además, si el punto de fuga está bastante alejado del objeto proyectado, entonces la diferencia entre estas dos proyecciones es poco perceptible). Para proyectar un punto dado en un plano determinado usando un punto de fuga, es necesario dibujar una línea recta a través del punto de fuga y el punto dado, y luego encontrar el punto de intersección de la línea recta resultante y el plano. Y para proyectar una figura más compleja, digamos, un cubo, es necesario proyectar cada uno de sus vértices y luego conectar los puntos correspondientes. se debe notar que algoritmo para proyectar el espacio sobre el subespacio se puede generalizar al caso de 4D->3D, no solo 3D->2D.
Como dije, no podemos imaginar exactamente cómo se ve el eje OQ, al igual que el teseracto. ¡Pero podemos hacernos una idea limitada si lo proyectamos en un volumen y luego lo dibujamos en la pantalla de una computadora!
Ahora hablemos de la proyección del teseracto.

A la izquierda está la proyección del cubo sobre el plano y a la derecha está el teseracto sobre el volumen. Son bastante similares: la proyección de un cubo parece dos cuadrados, pequeño y grande, uno dentro del otro, y cuyos vértices correspondientes están conectados por líneas. Y la proyección del teseracto parece dos cubos, pequeño y grande, uno dentro del otro, y cuyos vértices correspondientes están conectados. Pero todos hemos visto el cubo, y podemos decir con seguridad que tanto el cuadrado pequeño como el grande, y los cuatro trapecios arriba, abajo, a la derecha e izquierda del cuadrado pequeño, son en realidad cuadrados, y son iguales. . Y el teseracto tiene lo mismo. Y un cubo grande, un cubo pequeño y seis pirámides truncadas en los lados de un cubo pequeño: todos estos son cubos y son iguales.
Mi programa no sólo puede dibujar la proyección de un teseracto sobre un volumen, sino también rotarlo. Veamos cómo se hace esto.
Primero te diré qué es. rotación paralela al plano.
Imagine que el cubo gira alrededor del eje OZ. Luego cada uno de sus vértices describe un círculo alrededor del eje OZ. 
Un círculo es una figura plana. Y los planos de cada uno de estos círculos son paralelos entre sí, y en este caso paralelos al plano XOY. Es decir, podemos hablar no sólo de rotación alrededor del eje OZ, sino también de rotación paralela al plano XOY. Como vemos, para puntos que giran paralelos al eje XOY, solo cambian la abscisa y la ordenada, mientras que la aplicada permanece. sin cambios. Y, de hecho, podemos hablar de rotación alrededor de una línea recta sólo cuando se trata de un espacio tridimensional. En el espacio bidimensional todo gira alrededor de un punto, en el espacio cuatridimensional todo gira alrededor de un plano, en el espacio pentadimensional hablamos de rotación alrededor de un volumen. Y si podemos imaginar la rotación alrededor de un punto, entonces la rotación alrededor de un plano y un volumen es algo impensable. Y si hablamos de rotación paralela al plano, entonces en cualquier espacio n-dimensional un punto puede girar paralelo al plano.
Muchos de ustedes probablemente hayan oído hablar de la matriz de rotación. Multiplicando el punto por él, obtenemos un punto girado paralelo al plano en un ángulo phi. Para un espacio bidimensional se ve así: 
Cómo multiplicar: x de un punto girado por un ángulo phi = coseno del ángulo phi*ix del punto original menos seno del ángulo phi*ig del punto original;
ig de un punto girado por un ángulo phi = seno del ángulo phi * ix del punto original más coseno del ángulo phi * ig del punto original.
Xa`=cosф*Xa - sinф*Ya
Ya`=sinф*Xa + cosф*Ya
, donde Xa y Ya son la abscisa y la ordenada del punto a rotar, Xa` y Ya` son la abscisa y la ordenada del punto ya rotado
Para el espacio tridimensional, esta matriz se generaliza de la siguiente manera: 
Rotación paralela al plano XOY. Como puede ver, la coordenada Z no cambia, solo cambian X e Y.
Xa`=cosф*Xa - sinф*Ya + Za*0
Ya`=sinф*Xa +cosф*Ya + Za*0
Za`=Xa*0 + Ya*0 + Za*1 (esencialmente, Za`=Za)

Rotación paralela al plano XOZ. Nada nuevo,
Xa`=cosф*Xa + Ya*0 - sinф*Za
Ya`=Xa*0 + Ya*1 + Za*0 (esencialmente, Ya`=Ya)
Za`=senф*Xa + Ya*0 + cosф*Za

Y la tercera matriz.
Xa`=Xa*1 + Ya*0 + Za*0 (esencialmente, Xa`=Xa)
Ya`=Xa*0 + cosф*Ya - sinф*Za
Za`=Xa*0 + sinф*Ya + cosф*Za
Y para la cuarta dimensión se ven así: 
Creo que ya entiendes por qué multiplicar, así que no volveré a entrar en detalles. ¡Pero observo que hace lo mismo que una matriz de rotación paralela a un plano en un espacio tridimensional! Ambos cambian solo la ordenada y la aplicación, y no tocan las otras coordenadas, por lo que se puede usar en el caso tridimensional, simplemente sin prestar atención a la cuarta coordenada.
Pero con la fórmula de proyección no todo es tan sencillo. No importa cuántos foros lea, ninguno de los métodos de proyección funcionó para mí. La paralela no me convenía, ya que la proyección no parecería tridimensional. En algunas fórmulas de proyección, para encontrar un punto es necesario resolver un sistema de ecuaciones (y no sé cómo enseñarle a una computadora a resolverlas), otras simplemente no las entendí... En general, decidí idear mi propio camino. Para ello, considere la proyección 2D->1D.

pov significa "Punto de vista", ptp significa "Punto a proyectar" (el punto a proyectar) y ptp` es el punto deseado en el eje OX.
Los ángulos povptpB y ptpptp`A son iguales (la línea de puntos es paralela al eje OX, la línea recta povptp es secante).
La x del punto ptp` es igual a la x del punto ptp menos la longitud del segmento ptp`A. Este segmento se puede encontrar a partir del triángulo ptpptp`A: ptp`A = ptpA/tangente del ángulo ptpptp`A. Esta tangente la podemos encontrar a partir del triángulo povptpB: tangente ptpptp`A = (Ypov-Yptp)(Xpov-Xptp).
Respuesta: Xptp`=Xptp-Yptp/tangente del ángulo ptpptp`A.
No describí este algoritmo en detalle aquí, ya que hay muchos casos especiales en los que la fórmula cambia un poco. Si alguien está interesado, mire el código fuente del programa, allí se describe todo en los comentarios.
Para proyectar un punto en el espacio tridimensional sobre un plano, simplemente consideramos dos planos: XOZ e YOZ, y resolvemos este problema para cada uno de ellos. En el caso del espacio de cuatro dimensiones, es necesario considerar tres planos: XOQ, YOQ y ZOQ.
Y finalmente, sobre el programa. Funciona así: inicializa dieciséis vértices del teseracto -> dependiendo de los comandos ingresados por el usuario, gíralo -> proyéctalo en el volumen -> dependiendo de los comandos ingresados por el usuario, rota su proyección -> proyéctalo en el avión -> dibujar.
Yo mismo escribí las proyecciones y rotaciones. Funcionan según las fórmulas que acabo de describir. La biblioteca OpenGL dibuja líneas y también maneja la mezcla de colores. Y las coordenadas de los vértices del tesseract se calculan de esta forma:
Coordenadas de los vértices de una recta centrada en el origen y longitud 2 - (1) y (-1);
- " - " - cuadrado - " - " - y con una arista de longitud 2:
(1; 1), (-1; 1), (1; -1) y (-1; -1);
- " - " - cubo - " - " -:
(1; 1; 1), (-1; 1; 1), (1; -1; 1), (-1; -1; 1), (1; 1; -1), (-1; 1; -1), (1; -1; -1), (-1; -1; -1);
Como puede ver, un cuadrado está una línea por encima del eje OY y una línea por debajo del eje OY; un cubo está un cuadrado delante del plano XOY y otro detrás de él; El teseracto es un cubo al otro lado del volumen XOYZ y otro a este lado. Pero es mucho más fácil percibir esta alternancia de unos y menos unos si se escriben en una columna.
1; 1; 1
-1; 1; 1
1; -1; 1
-1; -1; 1
1; 1; -1
-1; 1; -1
1; -1; -1
-1; -1; -1
En la primera columna se alternan uno y menos uno. En la segunda columna, primero hay dos ventajas, luego dos desventajas. En el tercero, cuatro más unos y luego cuatro menos unos. Estos eran los vértices del cubo. El tesseract tiene el doble de ellos y, por lo tanto, fue necesario escribir un bucle para declararlos; de lo contrario, es muy fácil confundirse.
Mi programa también puede dibujar anaglifos. Los felices propietarios de gafas 3D pueden observar una imagen estereoscópica. No hay nada complicado en hacer un dibujo; simplemente dibuja dos proyecciones en el plano, para el ojo derecho y el izquierdo. Pero el programa se vuelve mucho más visual e interesante y, lo más importante, da una mejor idea del mundo de cuatro dimensiones.
Funciones menos importantes son la iluminación de uno de los bordes en rojo para que los giros se puedan ver mejor, así como pequeñas comodidades: regulación de las coordenadas de los puntos "ojo", aumento y disminución de la velocidad de giro.
Archivo con el programa, código fuente e instrucciones de uso.
María Bakalyar
Se estudian los métodos para introducir el concepto de cubo de cuatro dimensiones (tesseract), su estructura y algunas propiedades. La cuestión de qué objetos tridimensionales se obtienen cuando un cubo de cuatro dimensiones es intersecado por hiperplanos paralelos a sus caras tridimensionales. , así como hiperplanos perpendiculares a su diagonal principal. Se considera el aparato de geometría analítica multidimensional utilizado para la investigación.
Descargar:
Avance:
Introducción……………………………………………………………………………….2
Parte principal………………………………………………………………..4
Conclusiones………….. ………………………………………………………..12
Referencias…………………………………………………………..13
Introducción
El espacio de cuatro dimensiones ha atraído durante mucho tiempo la atención tanto de matemáticos profesionales como de personas alejadas del estudio de esta ciencia. El interés por la cuarta dimensión puede deberse a la suposición de que nuestro mundo tridimensional está “sumergido” en un espacio de cuatro dimensiones, así como un avión está “sumergido” en un espacio tridimensional, una línea recta está “sumergida” en un espacio tridimensional. plano y un punto está en línea recta. Además, el espacio de cuatro dimensiones juega un papel importante en la teoría moderna de la relatividad (el llamado espacio-tiempo o espacio de Minkowski), y también puede considerarse como un caso especial.espacio euclidiano dimensional (con).
Un cubo de cuatro dimensiones (teseracto) es un objeto en un espacio de cuatro dimensiones que tiene la máxima dimensión posible (así como un cubo ordinario es un objeto en un espacio tridimensional). Tenga en cuenta que también es de interés directo, es decir, puede aparecer en problemas de optimización de programación lineal (como un área en la que se encuentra el mínimo o máximo de una función lineal de cuatro variables), y también se utiliza en microelectrónica digital (cuando programar el funcionamiento de una pantalla de reloj electrónico). Además, el propio proceso de estudiar un cubo de cuatro dimensiones contribuye al desarrollo del pensamiento espacial y la imaginación.
En consecuencia, el estudio de la estructura y propiedades específicas de un cubo de cuatro dimensiones es bastante relevante. Vale la pena señalar que en términos de estructura, el cubo de cuatro dimensiones se ha estudiado bastante bien. De mucho mayor interés es la naturaleza de sus secciones por varios hiperplanos. Así, el objetivo principal de este trabajo es estudiar la estructura del teseracto, así como aclarar la cuestión de qué objetos tridimensionales se obtendrán si un cubo de cuatro dimensiones es disecado por hiperplanos paralelos a uno de sus tres dimensiones. caras dimensionales, o por hiperplanos perpendiculares a su diagonal principal. Un hiperplano en un espacio de cuatro dimensiones se denominará subespacio tridimensional. Podemos decir que una línea recta en un plano es un hiperplano unidimensional, un plano en un espacio tridimensional es un hiperplano bidimensional.
La meta determinó los objetivos del estudio:
1) Estudiar los hechos básicos de la geometría analítica multidimensional;
2) Estudiar las características de la construcción de cubos de dimensiones de 0 a 3;
3) Estudiar la estructura de un cubo de cuatro dimensiones;
4) Describir analítica y geométricamente un cubo de cuatro dimensiones;
5) Realizar maquetas de desarrollos y proyecciones centrales de cubos tridimensionales y cuatridimensionales.
6) Utilizando el aparato de geometría analítica multidimensional, describir objetos tridimensionales resultantes de la intersección de un cubo de cuatro dimensiones con hiperplanos paralelos a una de sus caras tridimensionales, o hiperplanos perpendiculares a su diagonal principal.
La información obtenida de esta manera nos permitirá comprender mejor la estructura del teseracto, así como identificar analogías profundas en la estructura y propiedades de cubos de diferentes dimensiones.
Parte principal
Primero, describimos el aparato matemático que usaremos durante este estudio.
1) Coordenadas vectoriales: si, Eso
2) Ecuación de un hiperplano con un vector normal parece aqui
3) Aviones y son paralelos si y sólo si
4) La distancia entre dos puntos se determina de la siguiente manera: si, Eso
5) Condición de ortogonalidad de vectores:
En primer lugar, descubramos cómo describir un cubo de cuatro dimensiones. Esto se puede hacer de dos formas: geométrica y analítica.
Si hablamos del método geométrico de especificación, entonces es recomendable rastrear el proceso de construcción de cubos, comenzando desde la dimensión cero. Un cubo de dimensión cero es un punto (tenga en cuenta, por cierto, que un punto también puede desempeñar el papel de una bola de dimensión cero). A continuación, introducimos la primera dimensión (el eje x) y en el eje correspondiente marcamos dos puntos (dos cubos de dimensión cero) situados a una distancia de 1 entre sí. El resultado es un segmento: un cubo unidimensional. Observemos inmediatamente un rasgo característico: los límites (extremos) de un cubo (segmento) unidimensional son dos cubos de dimensión cero (dos puntos). A continuación, introducimos la segunda dimensión (eje de ordenadas) y en el planoConstruyamos dos cubos unidimensionales (dos segmentos), cuyos extremos estén a una distancia de 1 entre sí (de hecho, uno de los segmentos es una proyección ortogonal del otro). Al conectar los extremos correspondientes de los segmentos, obtenemos un cuadrado, un cubo bidimensional. Nuevamente, observe que el límite de un cubo bidimensional (cuadrado) son cuatro cubos unidimensionales (cuatro segmentos). Finalmente, introducimos la tercera dimensión (eje de aplicación) y construimos en el espacio.dos cuadrados de tal manera que uno de ellos sea una proyección ortogonal del otro (los vértices correspondientes de los cuadrados están a una distancia de 1 entre sí). Conectemos los vértices correspondientes con segmentos: obtenemos un cubo tridimensional. Vemos que el límite de un cubo tridimensional son seis cubos bidimensionales (seis cuadrados). Las construcciones descritas nos permiten identificar el siguiente patrón: en cada pasoel cubo dimensional “se mueve, dejando un rastro” ene medición a una distancia de 1, mientras que la dirección del movimiento es perpendicular al cubo. Es la continuación formal de este proceso lo que nos permite llegar al concepto de cubo de cuatro dimensiones. Es decir, obligaremos al cubo tridimensional a moverse en dirección a la cuarta dimensión (perpendicular al cubo) a una distancia de 1. Actuando de forma similar al anterior, es decir, conectando los vértices correspondientes de los cubos, obtendremos un cubo de cuatro dimensiones. Cabe señalar que geométricamente tal construcción en nuestro espacio es imposible (ya que es tridimensional), pero aquí no encontramos ninguna contradicción desde un punto de vista lógico. Pasemos ahora a la descripción analítica de un cubo de cuatro dimensiones. También se obtiene formalmente, mediante analogía. Entonces, la especificación analítica de un cubo unitario de dimensión cero tiene la forma:
La tarea analítica de un cubo unitario unidimensional tiene la forma:
La tarea analítica de un cubo unitario bidimensional tiene la forma:
La tarea analítica de un cubo unitario tridimensional tiene la forma:
Ahora es muy fácil dar una representación analítica de un cubo de cuatro dimensiones, a saber:
Como podemos ver, tanto el método geométrico como el analítico para definir un cubo de cuatro dimensiones utilizaron el método de analogías.
Ahora, utilizando el aparato de geometría analítica, descubriremos cuál es la estructura de un cubo de cuatro dimensiones. Primero, averigüemos qué elementos incluye. Aquí también podemos utilizar una analogía (para plantear una hipótesis). Los límites de un cubo unidimensional son puntos (cubos de dimensión cero), de un cubo bidimensional, segmentos (cubos unidimensionales), de un cubo tridimensional, cuadrados (caras bidimensionales). Se puede suponer que los límites del teseracto son cubos tridimensionales. Para demostrarlo, aclaremos qué se entiende por vértices, aristas y caras. Los vértices de un cubo son sus vértices. Es decir, las coordenadas de los vértices pueden ser ceros o unos. Así, se revela una conexión entre la dimensión del cubo y el número de sus vértices. Apliquemos la regla del producto combinatorio - desde el vérticecubo medido tiene exactamentecoordenadas, cada una de las cuales es igual a cero o uno (independiente de todas las demás), entonces en total haypicos Por tanto, para cualquier vértice todas las coordenadas son fijas y pueden ser iguales a o . Si fijamos todas las coordenadas (poniendo cada una de ellas iguales o , independientemente de los demás), excepto uno, obtenemos rectas que contienen las aristas del cubo. Similar al anterior, puedes contar que hay exactamentecosas. Y si ahora fijamos todas las coordenadas (poniendo cada una de ellas iguales o , independientemente de los demás), salvo algunos dos, obtenemos planos que contienen caras bidimensionales del cubo. Usando la regla de la combinatoria, encontramos que hay exactamentecosas. A continuación, de manera similar: arreglando todas las coordenadas (poniendo cada una de ellas iguales o , independientemente de los demás), salvo unos tres, obtenemos hiperplanos que contienen caras tridimensionales del cubo. Usando la misma regla, calculamos su número, exactamenteetc. Esto será suficiente para nuestra investigación. Apliquemos los resultados obtenidos a la estructura de un cubo de cuatro dimensiones, es decir, en todas las fórmulas derivadas ponemos. Por tanto, un cubo de cuatro dimensiones tiene: 16 vértices, 32 aristas, 24 caras bidimensionales y 8 caras tridimensionales. Para mayor claridad, definamos analíticamente todos sus elementos.
Vértices de un cubo de cuatro dimensiones:
Aristas de un cubo de cuatro dimensiones ():
Caras bidimensionales de un cubo de cuatro dimensiones (restricciones similares):
Caras tridimensionales de un cubo de cuatro dimensiones (restricciones similares):
Ahora que la estructura de un cubo de cuatro dimensiones y los métodos para definirlo se han descrito con suficiente detalle, pasemos a la implementación del objetivo principal: aclarar la naturaleza de las distintas secciones del cubo. Empecemos por el caso elemental en el que las secciones de un cubo son paralelas a una de sus caras tridimensionales. Por ejemplo, considere sus secciones con hiperplanos paralelos a la cara.De la geometría analítica se sabe que cualquier sección de este tipo estará dada por la ecuaciónDefinamos analíticamente los apartados correspondientes:
Como podemos ver, hemos obtenido una especificación analítica para un cubo unitario tridimensional que se encuentra en un hiperplano.
Para establecer una analogía, escribamos la sección de un cubo tridimensional por un plano. Obtenemos:
Este es un cuadrado que se encuentra en un avión.. La analogía es obvia.
Secciones de un cubo de cuatro dimensiones por hiperplanos.dar resultados completamente similares. Estos también serán cubos tridimensionales individuales que se encuentran en hiperplanos. respectivamente.
Ahora consideremos secciones de un cubo de cuatro dimensiones con hiperplanos perpendiculares a su diagonal principal. Primero, resolvamos este problema para un cubo tridimensional. Utilizando el método descrito anteriormente para definir un cubo tridimensional unitario, concluye que como diagonal principal se puede tomar, por ejemplo, un segmento con extremos Y . Esto significa que el vector de la diagonal principal tendrá coordenadas. Por tanto, la ecuación de cualquier plano perpendicular a la diagonal principal será:
Determinemos los límites del cambio de parámetros.. Porque , entonces, sumando estas desigualdades término por término, obtenemos:
O .
Si entonces (debido a restricciones). Del mismo modo - si, Eso . Entonces, cuando y cuando el plano de corte y el cubo tienen exactamente un punto común ( Y respectivamente). Ahora observemos lo siguiente. Si(nuevamente debido a limitaciones variables). Los planos correspondientes cortan tres caras a la vez, porque de lo contrario el plano de corte sería paralelo a una de ellas, lo que no es así según la condición. Si, entonces el plano interseca todas las caras del cubo. Si, entonces el plano interseca las caras. Presentemos los cálculos correspondientes.
Dejar Entonces el avióncruza la línea en línea recta, y . El borde, además. Borde el plano se corta en linea recta, y
Dejar Entonces el avióncruza la línea:
borde en línea recta, y .
borde en línea recta, y .
borde en línea recta, y .
borde en línea recta, y .
borde en línea recta, y .
borde en línea recta, y .
Esta vez obtenemos seis segmentos que tienen extremos comunes secuencialmente:
Dejar Entonces el avióncruza la línea en línea recta, y . Borde el plano se corta en linea recta, y . Borde el plano se corta en linea recta, y . Es decir, obtenemos tres segmentos que tienen extremos comunes por pares:Por lo tanto, para los valores de parámetros especificadosel plano cortará el cubo a lo largo de un triángulo regular con vértices
Entonces, aquí hay una descripción completa de las figuras planas que se obtienen cuando un cubo es intersecado por un plano perpendicular a su diagonal principal. La idea principal era la siguiente. Es necesario comprender qué caras cruza el plano, en qué conjuntos las cruza y cómo se relacionan estos conjuntos entre sí. Por ejemplo, si resulta que el plano cruza exactamente tres caras a lo largo de segmentos que tienen extremos comunes por pares, entonces la sección es un triángulo equilátero (lo cual se prueba calculando directamente las longitudes de los segmentos), cuyos vértices son estos extremos. de los segmentos.
Utilizando el mismo aparato y la misma idea de estudiar secciones, se pueden deducir de forma completamente análoga los siguientes hechos:
1) El vector de una de las diagonales principales de un cubo unitario de cuatro dimensiones tiene las coordenadas
2) Cualquier hiperplano perpendicular a la diagonal principal de un cubo de cuatro dimensiones se puede escribir en la forma.
3) En la ecuación de un hiperplano secante, el parámetropuede variar de 0 a 4;
4) Cuando y un hiperplano secante y un cubo de cuatro dimensiones tienen un punto común ( Y respectivamente);
5) cuando la sección transversal producirá un tetraedro regular;
6) cuando en sección transversal el resultado será un octaedro;
7) cuando la sección transversal producirá un tetraedro regular.
En consecuencia, aquí el hiperplano cruza el teseracto a lo largo de un plano en el que, debido a las restricciones de las variables, se distingue una región triangular (una analogía: el plano corta al cubo a lo largo de una línea recta, en la que, debido a las restricciones de la variables, se distinguió un segmento). En el caso 5) el hiperplano interseca exactamente cuatro caras tridimensionales del teseracto, es decir, se obtienen cuatro triángulos que tienen lados comunes por pares, es decir, formando un tetraedro (cómo se puede calcular esto es correcto). En el caso 6), el hiperplano interseca exactamente ocho caras tridimensionales del teseracto, es decir, se obtienen ocho triángulos que tienen lados secuencialmente comunes, es decir, formando un octaedro. El caso 7) es completamente similar al caso 5).
Ilustremos esto con un ejemplo específico. Es decir, estudiamos la sección de un cubo de cuatro dimensiones por un hiperplano.Debido a restricciones variables, este hiperplano intersecta las siguientes caras tridimensionales: Borde se cruza a lo largo de un planoDebido a las limitaciones de las variables, tenemos:Obtenemos un área triangular con vértices.Más,obtenemos un trianguloCuando un hiperplano intersecta una caraobtenemos un trianguloCuando un hiperplano intersecta una caraobtenemos un trianguloAsí, los vértices del tetraedro tienen las siguientes coordenadas. Como es fácil de calcular, este tetraedro es efectivamente regular.
conclusiones
Entonces, en el proceso de esta investigación, se estudiaron los hechos básicos de la geometría analítica multidimensional, se estudiaron las características de la construcción de cubos de dimensiones de 0 a 3, se estudió la estructura de un cubo de cuatro dimensiones, se estudió un cubo de cuatro dimensiones. Se describieron analítica y geométricamente, se realizaron modelos de desarrollos y proyecciones centrales de cubos tridimensionales y cuatridimensionales, se describieron analíticamente cubos tridimensionales, objetos resultantes de la intersección de un cubo cuatridimensional con hiperplanos paralelos a uno de sus tres dimensiones. caras dimensionales, o con hiperplanos perpendiculares a su diagonal principal.
La investigación realizada permitió identificar profundas analogías en la estructura y propiedades de cubos de diferentes dimensiones. La técnica de analogía utilizada se puede aplicar en la investigación, por ejemplo,esfera dimensional osimplex dimensional. A saber,una esfera dimensional se puede definir como un conjunto de puntosespacio dimensional equidistante de un punto dado, que se llama centro de la esfera. Más,un simplex dimensional se puede definir como una parteespacio dimensional limitado por el número mínimohiperplanos dimensionales. Por ejemplo, un simplex unidimensional es un segmento (una parte del espacio unidimensional, limitado por dos puntos), un simplex bidimensional es un triángulo (una parte del espacio bidimensional, limitado por tres líneas rectas), un simplex tridimensional es un tetraedro (una parte del espacio tridimensional, limitada por cuatro planos). Finalmente,definimos el simplex dimensional como la parteespacio dimensional, limitadohiperplano de dimensión.
Tenga en cuenta que, a pesar de las numerosas aplicaciones del teseracto en algunas áreas de la ciencia, esta investigación sigue siendo en gran medida un estudio matemático.
Bibliografía
1) Bugrov Ya.S., Nikolsky S.M.Matemáticas superiores, vol 1 – M.: Avutarda, 2005 – 284 p.
2) Cuántico. Cubo de cuatro dimensiones / Duzhin S., Rubtsov V., No. 6, 1986.
3) Cuántico. Como dibujar cubo dimensional / Demidovich N.B., No. 8, 1974.
En geometría hipercubo- Este norte-analogía dimensional de un cuadrado ( norte= 2) y cubo ( norte= 3). Es una figura convexa cerrada que consta de grupos de líneas paralelas ubicadas en bordes opuestos de la figura y conectadas entre sí en ángulo recto.
Esta figura también se conoce como teseracto(teseracto). El teseracto es al cubo como el cubo es al cuadrado. Más formalmente, un teseracto puede describirse como un politopo (poliedro) convexo regular de cuatro dimensiones cuyo límite consta de ocho celdas cúbicas.
Según el Oxford English Dictionary, la palabra "tesseract" fue acuñada en 1888 por Charles Howard Hinton y utilizada en su libro "A New Era of Thought". La palabra se deriva del griego "τεσσερες ακτινες" ("cuatro rayos"), en forma de cuatro ejes de coordenadas. Además, en algunas fuentes, la misma figura fue denominada tetracubo(tetracubo).
norte El hipercubo dimensional también se llama n-cubo.
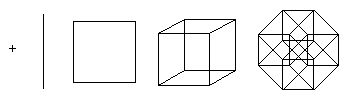
Un punto es un hipercubo de dimensión 0. Si desplaza el punto una unidad de longitud, obtiene un segmento de una unidad de longitud: un hipercubo de dimensión 1. Además, si desplaza el segmento una unidad de longitud en una dirección perpendicular en la dirección del segmento, se obtiene un cubo, un hipercubo de dimensión 2. Al desplazar el cuadrado una unidad de longitud en la dirección perpendicular al plano del cuadrado, se obtiene un cubo, un hipercubo de dimensión 3. Este proceso Se puede generalizar a cualquier número de dimensiones. Por ejemplo, si mueves un cubo una unidad de longitud en la cuarta dimensión, obtienes un teseracto.
La familia de los hipercubos es uno de los pocos poliedros regulares que se puede representar en cualquier dimensión.
Elementos de un hipercubo
Hipercubo de dimensión norte tiene 2 norte“lados” (una línea unidimensional tiene 2 puntos; un cuadrado bidimensional tiene 4 lados; un cubo tridimensional tiene 6 caras; un teseracto de cuatro dimensiones tiene 8 celdas). El número de vértices (puntos) de un hipercubo es 2 norte(por ejemplo, para un cubo - 2 3 vértices).
Cantidad metro-hipercubos dimensionales en el límite norte-cubo es igual
Por ejemplo, en el límite de un hipercubo hay 8 cubos, 24 cuadrados, 32 aristas y 16 vértices.
| n-cubo | Nombre | Vértice (0-cara) |
Borde (1 cara) |
Borde (2 caras) |
Celúla (3 caras) |
(4 caras) | (5 caras) | (6 caras) | (7 caras) | (8 caras) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-cubo | Punto | 1 | ||||||||
| 1-cubo | Segmento de línea | 2 | 1 | |||||||
| 2 cubos | Cuadrado | 4 | 4 | 1 | ||||||
| 3 cubos | Cubo | 8 | 12 | 6 | 1 | |||||
| 4 cubos | Teseracto | 16 | 32 | 24 | 8 | 1 | ||||
| 5 cubos | pentacto | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6 cubos | Hexeract | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7 cubos | hepteracto | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8 cubos | Octeract | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9 cubos | Eneneract | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Proyección sobre un avión.
La formación de un hipercubo se puede representar de la siguiente manera:
- Se pueden conectar dos puntos A y B para formar un segmento de recta AB.
- Dos segmentos paralelos AB y CD se pueden conectar para formar un cuadrado ABCD.
- Se pueden conectar dos cuadrados paralelos ABCD y EFGH para formar un cubo ABCDEFGH.
- Se pueden conectar dos cubos paralelos ABCDEFGH e IJKLMNOP para formar el hipercubo ABCDEFGHIJKLMNOP.
Esta última estructura no es fácil de visualizar, pero es posible representar su proyección en un espacio bidimensional o tridimensional. Además, las proyecciones en un plano bidimensional pueden resultar más útiles al permitir reorganizar las posiciones de los vértices proyectados. En este caso, es posible obtener imágenes que ya no reflejan las relaciones espaciales de los elementos dentro del teseracto, sino que ilustran la estructura de las conexiones de los vértices, como en los ejemplos siguientes.

La primera ilustración muestra cómo, en principio, se forma un teseracto uniendo dos cubos. Este esquema es similar al esquema para crear un cubo a partir de dos cuadrados. El segundo diagrama muestra que todos los bordes del teseracto tienen la misma longitud. Este esquema también te obliga a buscar cubos conectados entre sí. En el tercer diagrama, los vértices del teseracto están ubicados de acuerdo con las distancias a lo largo de las caras con respecto al punto inferior. Este esquema es interesante porque se utiliza como esquema básico para la topología de red de los procesadores de conexión cuando se organiza la computación en paralelo: la distancia entre dos nodos cualesquiera no excede las 4 longitudes de borde y hay muchos caminos diferentes para equilibrar la carga.
Hipercubo en el arte
El hipercubo ha aparecido en la literatura de ciencia ficción desde 1940, cuando Robert Heinlein, en el cuento "Y construyó una casa torcida", describió una casa construida con la forma de un escaneo de teseracto. En la historia de este Next, esta casa se derrumba, convirtiéndose en un teseracto de cuatro dimensiones. Después de esto, el hipercubo aparece en muchos libros y cuentos.
La película Cube 2: Hypercube trata sobre ocho personas atrapadas en una red de hipercubos.
El cuadro de Salvador Dalí "Crucifixión (Corpus Hypercubus)", 1954, representa a Jesús crucificado en un escaneo de teseracto. Esta pintura se puede ver en el Museo Metropolitano de Arte de Nueva York.
Conclusión
Un hipercubo es uno de los objetos de cuatro dimensiones más simples, en cuyo ejemplo se puede ver toda la complejidad y lo inusual de la cuarta dimensión. Y lo que parece imposible en tres dimensiones es posible en cuatro, por ejemplo, figuras imposibles. Así, por ejemplo, las barras de un triángulo imposible en cuatro dimensiones se conectarán formando ángulos rectos. Y esta figura se verá así desde todos los puntos de vista y no estará distorsionada, a diferencia de las implementaciones de un triángulo imposible en el espacio tridimensional (ver.
Cuando era estudiante de primer año, tuve una acalorada discusión con uno de mis compañeros de clase. Dijo que un cubo de cuatro dimensiones no se puede representar de ninguna forma, pero le aseguré que se puede representar con bastante claridad. Luego incluso hice una proyección de un hipercubo en nuestro espacio tridimensional con clips... Pero hablemos de todo en orden.
¿Qué es un hipercubo y un espacio de cuatro dimensiones?
Nuestro espacio habitual tiene tres dimensiones. Desde un punto de vista geométrico, esto significa que en él se pueden indicar tres líneas perpendiculares entre sí. Es decir, para cualquier línea puedes encontrar una segunda línea perpendicular a la primera, y para un par puedes encontrar una tercera línea perpendicular a las dos primeras. Ya no será posible encontrar una cuarta línea perpendicular a las tres existentes.
Espacio de cuatro dimensiones Se diferencia del nuestro sólo en que tiene una dirección adicional más. Si ya tienes tres líneas mutuamente perpendiculares, entonces puedes encontrar una cuarta, de modo que sea perpendicular a las tres.
Hipercubo es sólo un cubo en un espacio de cuatro dimensiones.
¿Es posible imaginar un espacio de cuatro dimensiones y un hipercubo?
Esta pregunta es similar a la pregunta: “¿Es posible imaginar la Última Cena mirando el cuadro del mismo nombre (1495-1498) de Leonardo da Vinci (1452-1519)?”
Por un lado, usted, por supuesto, no imaginará lo que vio Jesús (está sentado frente al espectador), especialmente porque no olerá el jardín fuera de la ventana ni saboreará la comida en la mesa, no escuchará los pájaros. cantando... No obtendrá una imagen completa de lo que sucedió a esa hora de la noche, pero no se puede decir que no aprenderá nada nuevo y que la imagen no tiene ningún interés.
La situación es similar con la cuestión del hipercubo. Es imposible imaginarlo por completo, pero puedes acercarte a comprender cómo es.
Construcción de un hipercubo
cubo de 0 dimensiones
Empecemos desde el principio: con un cubo de dimensión 0. Este cubo contiene 0 caras mutuamente perpendiculares, es decir, es solo un punto.
cubo unidimensional
En el espacio unidimensional, sólo tenemos una dirección. Movemos el punto en esta dirección y obtenemos un segmento.
Este es un cubo unidimensional.
cubo bidimensional
Tenemos una segunda dimensión, desplazamos nuestro cubo unidimensional (segmento) en la dirección de la segunda dimensión y obtenemos un cuadrado.
Es un cubo en un espacio bidimensional.
cubo tridimensional
Con la llegada de la tercera dimensión hacemos lo mismo: movemos el cuadrado y obtenemos un cubo tridimensional normal.

Cubo de 4 dimensiones (hipercubo)
Ahora tenemos una cuarta dimensión. Es decir, tenemos a nuestra disposición una dirección perpendicular a las tres anteriores. Usémoslo exactamente de la misma manera. Un cubo de cuatro dimensiones se verá así.

Naturalmente, los cubos tridimensionales y cuatridimensionales no se pueden representar en un plano de pantalla bidimensional. Lo que dibujé son proyecciones. Hablaremos de proyecciones un poco más adelante, pero por ahora solo algunos datos y cifras.
Número de vértices, aristas, caras.
Tenga en cuenta que la cara de un hipercubo es nuestro cubo tridimensional ordinario. Si miras de cerca el dibujo de un hipercubo, en realidad puedes encontrar ocho cubos.
Proyecciones y visión de un habitante del espacio cuatridimensional.
Algunas palabras sobre la visión.
Vivimos en un mundo tridimensional, pero lo vemos como bidimensional. Esto se debe a que la retina de nuestros ojos se encuentra en un plano que tiene sólo dos dimensiones. Por eso podemos percibir imágenes bidimensionales y encontrarlas similares a la realidad.
(Por supuesto, gracias a la acomodación, el ojo puede estimar la distancia a un objeto, pero este es un efecto secundario asociado con la óptica integrada en nuestros ojos).
Los ojos de un habitante del espacio de cuatro dimensiones deben tener una retina tridimensional. Una criatura así puede ver inmediatamente toda la figura tridimensional: todas sus caras e interiores. (De la misma forma podemos ver una figura bidimensional, todas sus caras e interiores.)
Por lo tanto, con la ayuda de nuestros órganos de visión, no podemos percibir un cubo de cuatro dimensiones como lo percibiría un residente de un espacio de cuatro dimensiones. Pobre de mí. Todo lo que queda es confiar en el ojo de la mente y la imaginación, que, afortunadamente, no tienen limitaciones físicas.
Sin embargo, al representar un hipercubo en un plano, simplemente me veo obligado a proyectarlo en un espacio bidimensional. Tenga en cuenta este hecho al estudiar los dibujos.
Intersecciones de bordes
Naturalmente, los bordes del hipercubo no se cruzan. Las intersecciones aparecen sólo en los dibujos. Sin embargo, esto no debería sorprendernos, porque en las imágenes las aristas de un cubo normal también se cruzan.
Longitudes de borde
Vale la pena señalar que todas las caras y aristas de un cubo de cuatro dimensiones son iguales. En la figura no son iguales sólo porque están ubicados en diferentes ángulos con respecto a la dirección de visión. Sin embargo, es posible rotar un hipercubo para que todas las proyecciones tengan la misma longitud.
Por cierto, en esta figura se ven claramente ocho cubos, que son las caras de un hipercubo.
El hipercubo está vacío por dentro.
Es difícil de creer, pero entre los cubos que delimitan el hipercubo hay algo de espacio (un fragmento de espacio de cuatro dimensiones).
Para entender esto mejor, veamos una proyección bidimensional de un cubo tridimensional ordinario (la hice deliberadamente algo esquemática).

¿Puedes adivinar que hay algo de espacio dentro del cubo? Sí, pero sólo usando tu imaginación. El ojo no ve este espacio.
Esto sucede porque los bordes ubicados en la tercera dimensión (que no se pueden representar en un dibujo plano) ahora se han convertido en segmentos que se encuentran en el plano del dibujo. Ya no aportan volumen.
Los cuadrados que encerraban el espacio del cubo se superponían entre sí. Pero se puede imaginar que en la figura original (un cubo tridimensional) estos cuadrados estaban ubicados en planos diferentes, y no uno encima de otro en el mismo plano, como sucedía en la figura.
La situación es exactamente la misma con un hipercubo. Los cubos-caras de un hipercubo en realidad no se superponen, como nos parece en la proyección, sino que están ubicados en un espacio de cuatro dimensiones.
barridos
Entonces, un residente del espacio de cuatro dimensiones puede ver un objeto tridimensional desde todos los lados al mismo tiempo. ¿Podemos ver un cubo tridimensional desde todos sus lados al mismo tiempo? Con el ojo - no. Pero a la gente se le ocurrió una manera de representar todas las caras de un cubo tridimensional al mismo tiempo en un dibujo plano. Esta imagen se llama escaneo.
Desarrollo de un cubo tridimensional.
Probablemente todo el mundo sepa cómo se forma el desarrollo de un cubo tridimensional. Este proceso se muestra en la animación.

Para mayor claridad, los bordes de las caras del cubo se hacen translúcidos.
Cabe señalar que sólo podemos percibir esta imagen bidimensional gracias a nuestra imaginación. Si consideramos las fases que se desarrollan desde un punto de vista puramente bidimensional, el proceso parecerá extraño y nada claro.

Parece la aparición gradual de primero los contornos de cuadrados distorsionados, y luego su desplazamiento hacia su lugar, al mismo tiempo que toman la forma requerida.
Si miras el cubo desplegado en la dirección de una de sus caras (desde este punto de vista el cubo parece un cuadrado), entonces el proceso de formación del desplegado es aún menos claro. Todo parece cuadrados que salen del cuadrado inicial (no del cubo desplegado).
Pero no visual escanear solo para ojo.
¿Cómo entender el espacio de 4 dimensiones?
Es gracias a tu imaginación que puedes extraer mucha información de ella.
Desarrollo de un cubo de cuatro dimensiones.
Es simplemente imposible hacer que el proceso animado de desplegar un hipercubo sea al menos algo visual. Pero este proceso se puede imaginar. (Para hacer esto, debes mirarlo a través de los ojos de un ser de cuatro dimensiones).
El escaneo se ve así.

Los ocho cubos que delimitan el hipercubo son visibles aquí.
Los bordes que deben alinearse al doblarse están pintados con los mismos colores. Las caras cuyos pares no son visibles se dejan en gris. Después de doblar, la cara superior del cubo superior debe alinearse con el borde inferior del cubo inferior. (El despliegue de un cubo tridimensional se contrae de manera similar.)
Tenga en cuenta que después de la convolución, todas las caras de los ocho cubos entrarán en contacto, cerrando el hipercubo. Y finalmente, al imaginar el proceso de plegado, no olvide que al plegar no se produce la superposición de cubos, sino su envoltura alrededor de un área determinada (hipercúbica) de cuatro dimensiones.
Salvador Dalí (1904-1989) representó la crucifixión muchas veces y aparecen cruces en muchas de sus pinturas. El cuadro “La Crucifixión” (1954) utiliza un escaneo de hipercubo.
Espacio-tiempo y espacio euclidiano de cuatro dimensiones
Espero que hayas podido imaginar el hipercubo. Pero, ¿has conseguido acercarte a comprender cómo funciona el espacio-tiempo cuatridimensional en el que vivimos? Por desgracia, no del todo.
Aquí hablamos del espacio euclidiano de cuatro dimensiones, pero el espacio-tiempo tiene propiedades completamente diferentes. En particular, durante cualquier rotación, los segmentos siempre permanecen inclinados con respecto al eje del tiempo, ya sea en un ángulo inferior a 45 grados o en un ángulo superior a 45 grados.
Dediqué una serie de notas a las propiedades del espacio-tiempo.
Tridimensionalidad de la imagen.
El mundo es tridimensional. Su imagen es bidimensional. Una tarea importante de la pintura y, ahora, de la fotografía es transmitir la tridimensionalidad del espacio. Los romanos ya dominaban algunas técnicas, luego fueron olvidadas y comenzaron a volver a la pintura clásica con el Renacimiento.
 La principal técnica para crear un espacio tridimensional en la pintura es la perspectiva. Los raíles del ferrocarril, al alejarse del espectador, se estrechan visualmente. Al pintar, los carriles se pueden estrechar físicamente. En fotografía, la perspectiva se produce automáticamente: la cámara fotografiará los rieles tan estrechos como los ve el ojo. Sin embargo, no dejes que casi se cierre: ya no parecerá una perspectiva, sino una figura extraña; Debe haber un espacio notable entre los rieles, los lados de la calle y las orillas del río.
La principal técnica para crear un espacio tridimensional en la pintura es la perspectiva. Los raíles del ferrocarril, al alejarse del espectador, se estrechan visualmente. Al pintar, los carriles se pueden estrechar físicamente. En fotografía, la perspectiva se produce automáticamente: la cámara fotografiará los rieles tan estrechos como los ve el ojo. Sin embargo, no dejes que casi se cierre: ya no parecerá una perspectiva, sino una figura extraña; Debe haber un espacio notable entre los rieles, los lados de la calle y las orillas del río.
Es importante comprender que la perspectiva lineal es la forma más primitiva y realista de transmitir el mundo.
Mensaje de navegación
No es casualidad que su apariencia esté asociada con la escenografía teatral (Florensky, “Reverse Perspective”). La convencionalidad y sencillez de transmitir una escena teatral de poca profundidad es muy adecuada para la fotografía, que carece de la variedad de técnicas disponibles en la pintura.
Hay perspectivas mucho más interesantes que la lineal. En las obras de los maestros chinos hay una perspectiva flotante, cuando los objetos se representan simultáneamente desde abajo, arriba y desde adelante. No fue un error técnico de artistas incompetentes: el legendario autor de esta técnica, Guo Xi, escribió que tal exhibición permite realizar el mundo en su totalidad. La técnica de la pintura de iconos rusa es similar, en la que el espectador puede ver la cara y la espalda del personaje al mismo tiempo. Una técnica interesante de pintura de iconos, que también se encuentra entre los artistas de Europa occidental, fue la perspectiva inversa, en la que los objetos distantes, por el contrario, son más grandes que los cercanos, enfatizando la importancia. Sólo hoy se ha demostrado que tal perspectiva es correcta: a diferencia de los objetos lejanos, el primer plano se percibe en realidad en perspectiva inversa (Rauschenbach). Con Photoshop, puede lograr una perspectiva inversa ampliando los objetos del fondo. Para un espectador acostumbrado a las leyes de la fotografía, una imagen así parecerá extraña.
Introducir la esquina de un edificio en el marco, desde donde las paredes divergen en ambas direcciones, crea una apariencia de perspectiva isométrica. El cerebro comprende que las paredes están en ángulo recto y organiza el resto de la imagen en consecuencia. Esta perspectiva es más dinámica que la frontal y más natural para el primer plano. Simplemente introduzca los ángulos finales de los objetos y de los edificios cercanos en el marco.
Debido a la ampliación, la perspectiva isométrica es importante, lo que rara vez es adecuado para un retrato clásico. La perspectiva lineal, debido al estrechamiento, transmite mejor emociones menores.
En la etapa de toma de fotografías, el fotógrafo tiene a su disposición una serie de herramientas para enfatizar la perspectiva. Los objetos de igual ancho que se extienden en la distancia (vías, calles, columnas, surcos) al estrecharse e incluso simplemente al alejarse indican al espectador la tridimensionalidad del espacio. El efecto es más fuerte si dispara desde un ángulo bajo para aumentar la distorsión de la perspectiva. Esto es suficiente para la fotografía de paisajes, pero con una profundidad de imagen reducida para la fotografía de interiores, el efecto apenas se nota. Se puede mejorar un poco en el posprocesamiento reduciendo la parte superior de la imagen (Transformar perspectiva). Sin embargo, incluso en un paisaje, una perspectiva exagerada puede parecer interesante.
La profundidad puede ser obvia en el significado de la imagen: los edificios están separados por una calle o un río. La diagonal enfatiza la tridimensionalidad; por ejemplo, un puente sobre un río.
Los objetos de fondo de un tamaño conocido por el espectador establecen la escala y, en consecuencia, forman la perspectiva. En la fotografía de paisajes, este sujeto podría ser un automóvil, pero en la fotografía de retratos, intente doblar la pierna (lejos de la cámara) debajo de la silla para que parezca más pequeña y al mismo tiempo permanezca visible. Incluso puedes hacer esta pierna un poco más pequeña en el posprocesamiento.
El adorno transmite perspectiva al reducir visualmente los elementos. Un ejemplo serían grandes baldosas en el suelo, que marcan líneas en la carretera.
Existe una técnica llamada primer plano hipertrofiado. Desproporcionadamente grande, crea profundidad en la imagen. Al comparar la escala del primer plano y la del modelo, el ojo llega a la conclusión de que el modelo está mucho más lejos de lo que parece. La exageración debe ser sutil para que la imagen no se perciba como un error. Esta técnica funciona no sólo para el posprocesamiento, sino también para el rodaje: distorsiona las proporciones disparando con un objetivo de 35 o 50 mm. Disparar con un objetivo gran angular estira el espacio, realzando su tridimensionalidad rompiendo las proporciones. El efecto es más fuerte si disparas al modelo a corta distancia, pero ten cuidado con las proporciones grotescas: sólo los autores de imágenes religiosas pueden representar a una persona más grande que un edificio.
La intersección funciona muy bien. Si la manzana cubre parcialmente la pera, entonces el cerebro no se equivocará: la manzana está delante de la pera. El modelo cubre parcialmente los muebles, creando así profundidad en el interior.
La alternancia de puntos claros y oscuros también da profundidad a la imagen. El cerebro sabe por experiencia que los objetos cercanos están iluminados aproximadamente de la misma manera, por lo que interpreta que los objetos iluminados de manera diferente están ubicados a diferentes distancias. Para este efecto, los puntos se alternan en la dirección del eje de perspectiva, profundamente en la imagen y no a través de ella. Por ejemplo, cuando fotografíes a un modelo acostado lejos de la cámara en un marco oscuro, coloca las luces cerca de las nalgas y cerca de las piernas. Puede aclarar/oscurecer áreas en el posprocesamiento.
Se percibe que la secuencia de objetos cada vez más oscuros disminuye. Al sombrear gradualmente los objetos a lo largo de la línea activa, puede obtener una sutil sensación de perspectiva. Asimismo, se transmite profundidad atenuando la luz: proyecta una franja de luz sobre los muebles o sobre el suelo.
Se puede obtener una imagen tridimensional no solo gracias a la luz, sino también al contraste de color. Esta técnica era conocida por los pintores flamencos, que colocaban manchas de colores brillantes en sus naturalezas muertas. Una granada roja y un limón amarillo uno al lado del otro tendrán un aspecto tridimensional incluso con una iluminación frontal plana. Se destacarán especialmente sobre el fondo de las uvas moradas: un color cálido sobre un fondo frío. Las superficies de colores brillantes emergen bien de la oscuridad incluso con una luz débil, típica de la naturaleza muerta. El contraste de color funciona mejor con los colores primarios: rojo, amarillo, azul, en lugar de con sombras.
Sobre un fondo negro, el amarillo avanza, el azul se esconde detrás. Sobre un fondo blanco ocurre lo contrario. La saturación del color realza este efecto. ¿Por qué está pasando esto? El color amarillo nunca es oscuro, por eso el cerebro se niega a creer que un objeto amarillo pueda sumergirse en un fondo oscuro, no iluminarse. El azul, por el contrario, es oscuro.
Mejorar la perspectiva en el posprocesamiento se reduce a simular la percepción atmosférica: los objetos distantes aparecen más claros, más borrosos y con un contraste reducido en brillo, saturación y tono.
Además de las largas distancias, los efectos atmosféricos parecen naturales en la neblina matutina, la niebla o un bar lleno de humo. Considere el clima: en un día nublado o al anochecer, es posible que no haya una diferencia significativa entre el primer plano y el fondo.
El factor más importante es el contraste de brillo. En los entornos este es el contraste habitual. Reduzca el contraste de los objetos distantes, aumente el contraste del primer plano y la imagen se volverá convexa. No estamos hablando del contraste entre el primer plano y el fondo, sino del contraste del fondo, que debe ser menor que el contraste del primer plano. Este método es adecuado no sólo para paisajes y fotografías de género, sino también para retratos de estudio: aumenta el contraste de la parte frontal de la cara, reduce el contraste en el cabello, los pómulos y la ropa. Los filtros de retrato hacen algo similar: difuminan la piel del modelo y dejan los ojos y los labios ásperos.
El ajuste de contraste es la forma más sencilla de realizar el posprocesamiento de imágenes 3D. A diferencia de otros procesos, el espectador apenas notará cambios, lo que permitirá mantener la máxima naturalidad.
El desenfoque es similar a la reducción del contraste, pero son procesos diferentes. La imagen puede tener poco contraste sin dejar de ser nítida. Debido a la profundidad de campo limitada, desenfocar objetos distantes sigue siendo la forma más popular de transmitir tridimensionalidad en la fotografía y se puede mejorar fácilmente desenfocando sujetos distantes en posproducción. Por lo tanto, se deben colocar menos detalles en el fondo: el cerebro no espera objetos distinguibles en la distancia. Mientras tanto, reducir el contraste corresponde mejor a la percepción natural: las montañas distantes se ven con un contraste bajo y no borrosas, porque al explorar el paisaje, el ojo se reenfoca constantemente y el problema de la profundidad de campo le resulta ajeno. Al difuminar el fondo, al mismo tiempo puedes enfocar el primer plano. Además, en primer plano puedes mejorar las líneas de la imagen (Filtro de paso alto o Claridad). Es la gran nitidez del primer plano lo que explica la protuberancia característica en la imagen de las lentes de alta calidad. Cuidado: para aumentar ligeramente el 3D, es posible que la imagen sea demasiado rígida.
Los objetos más claros aparecen más lejos. Esto se debe al hecho de que en la naturaleza vemos objetos distantes a través del espesor del aire que dispersa la luz; las montañas lejanas parecen claras. Por lo tanto, en la fotografía de paisajes se debe tener cuidado con la colocación de los objetos luminosos en primer plano.
Ilumina objetos distantes. Cuanto más lejos están, más se mimetizan con el brillo y el tono del cielo. Tenga en cuenta que los objetos horizontales (tierra, mar) se iluminan mejor que los verticales (paredes, árboles), así que no se exceda al iluminar estos últimos. En cualquier caso, los objetos deberían permanecer notablemente más claros que el cielo.
 Bueno, si notas que esquivar es otra forma de reducir el contraste en el brillo del fondo. Oscurece ligeramente el primer plano para mejorar el efecto de relieve.
Bueno, si notas que esquivar es otra forma de reducir el contraste en el brillo del fondo. Oscurece ligeramente el primer plano para mejorar el efecto de relieve.
Parecería que en el interior todo es al revés. Si en la calle el ojo está acostumbrado a que la distancia sea brillante, entonces en la habitación la luz a menudo se concentra en la persona y el interior se sumerge en la oscuridad; el cerebro está acostumbrado a la iluminación de primer plano, no a la iluminación de fondo.
En imágenes de interiores con poca profundidad de escena, a diferencia de las imágenes de paisajes, el modelo iluminado sobresale de un fondo oscuro. Pero también hay un factor contrario: durante el 99% de su evolución, el hombre observó la perspectiva en espacios abiertos, y con la llegada de las habitaciones, el cerebro aún no había tenido tiempo de reestructurarse. Vermeer prefería un fondo claro para sus retratos, y sus retratos son realmente prominentes. Iluminar un fondo vertical, recomendado en fotografía, no sólo separa al modelo de éste, sino que además, al aclarar el fondo, aporta a la imagen una ligera tridimensionalidad. Aquí nos enfrentamos al hecho de que el cerebro analiza la ubicación de los objetos en función de varios factores, que pueden resultar contradictorios.
Resulta interesante la iluminación del estudio, en la que los puntos de luz se encuentran en áreas del modelo alejadas de la cámara. Por ejemplo, se resalta el seno que está más alejado de la cámara.
Reducir la saturación de color en objetos distantes: debido a la densidad del aire que nos separa, las montañas distantes se desaturan casi hasta el nivel monocromático y se cubren con una neblina azul. Se puede aumentar la saturación del primer plano.
Dado que el amarillo es claro y el azul y el rojo son oscuros, el contraste de color también es un contraste de brillo.
Al desaturar el fondo distante, no permita que desaparezca de la vista. A menudo, por el contrario, es necesario aumentar la saturación del fondo para revelarlo. Esto es más importante que la tridimensionalidad.
Muchos consejos sobre fotografía 3D se centran en el contraste de temperatura. De hecho, este efecto es muy débil y se interrumpe fácilmente por el contraste de brillo. Además, el contraste de temperatura es molesto y notorio.
Los objetos muy distantes parecen de colores más fríos porque el aire absorbe la cálida luz naranja. Al fotografiar un modelo en la playa con barcos en el horizonte de fondo, baje la temperatura de color del mar distante y de los barcos en el posprocesamiento. Una modelo en traje de baño rojo emerge del mar azul, y una modelo a la luz amarilla de una farola emerge del crepúsculo azulado.
Ésta es la esencia de la tonificación separada: hacemos que el modelo sea más cálido y el fondo más frío. El cerebro comprende que no hay diferentes temperaturas de color en un mismo plano y percibe una imagen tridimensional en la que el modelo sobresale del fondo. La división de tonos añade profundidad a los paisajes: hace que el primer plano sea más cálido y el fondo más frío.
Una excepción importante a la separación de tonos: al amanecer y al atardecer, el fondo lejano no es frío en absoluto, sino cálido, con tonos amarillos y rojo anaranjados. La solución obvia, usar una modelo blanca con un traje de baño morado, no funciona porque la luz del atardecer también arroja un tinte cálido en el cuerpo de la modelo.
Resumamos: para darle tridimensionalidad a una foto basada en efectos atmosféricos, es necesario contrastar el primer plano y el fondo. El contraste principal se basa en el contraste habitual: el primer plano tiene un contraste alto, el fondo tiene un contraste bajo. El segundo contraste se da en términos de nitidez: el primer plano es nítido, el fondo está borroso. El tercer contraste se produce en términos de luminosidad: el primer plano es oscuro, el fondo es claro. El cuarto contraste es en términos de saturación: los colores de primer plano están saturados, los colores de fondo están desaturados. El quinto contraste está en la temperatura: el primer plano es cálido, el fondo es frío.
Los factores enumerados suelen ser multidireccionales. El amarillo es más brillante que el azul y los objetos claros aparecen más lejos de los oscuros. Sería natural esperar que el amarillo retrocediera y el azul se acercara al espectador. De hecho, es al revés: un color cálido emerge de un fondo frío. Es decir, el color resulta ser un factor más importante que el brillo. Lo cual, pensándolo bien, no es sorprendente: el amarillo y el rojo sólo se distinguen claramente de cerca, y el espectador no espera encontrarlos a gran distancia.
En pocas palabras: mantenga el fondo con bajo contraste, descolorido, claro, desaturado, azulado. Y prepárate para el hecho de que el espectador, acostumbrado al 3D hipertrofiado de las películas, encontrará que la tridimensionalidad que usted creó apenas se nota o está ausente.
En la fotografía de retratos, es mejor confiar en el probado efecto claroscuro: el juego de luces y sombras en el rostro del modelo, que hará que la imagen sea bastante prominente. En la fotografía de género, la perspectiva proporciona el efecto tridimensional más notable. En una naturaleza muerta, el factor principal será la intersección (superposición) de objetos.
No se deje llevar por la perspectiva; es sólo un fondo para el plano frontal en el que flota tu imagen. En la pintura moderna, alejada del realismo, la perspectiva no se tiene en alta estima.
Descarga el libro completo: pdfepubazw3mobifb2litContenidos
Puntos (±1, ±1, ±1, ±1). En otras palabras, se puede representar como el siguiente conjunto:
El teseracto está limitado por ocho hiperplanos, cuya intersección con el propio teseracto define sus caras tridimensionales (que son cubos ordinarios). Cada par de caras 3D no paralelas se cruzan para formar caras 2D (cuadrados), y así sucesivamente. Finalmente, el teseracto tiene 8 caras 3D, 24 caras 2D, 32 aristas y 16 vértices.
Descripción popular
Intentemos imaginar cómo se verá un hipercubo sin salir del espacio tridimensional.
En un “espacio” unidimensional, en una línea recta, seleccionamos un segmento AB de longitud L. En un plano bidimensional a una distancia L de AB, dibujamos un segmento DC paralelo a él y conectamos sus extremos. El resultado es un CDBA cuadrado. Repitiendo esta operación con el plano obtenemos un cubo tridimensional CDBAGHFE. Y desplazando el cubo en la cuarta dimensión (perpendicular a las tres primeras) una distancia L, obtenemos el hipercubo CDBAGHFEKLJIOPNM.
Construcción de un teseracto en un avión.
El segmento unidimensional AB sirve como lado del cuadrado bidimensional CDBA, el cuadrado, como lado del cubo CDBAGHFE, que, a su vez, será el lado del hipercubo de cuatro dimensiones. Un segmento de recta tiene dos puntos límite, un cuadrado tiene cuatro vértices y un cubo ocho. En un hipercubo de cuatro dimensiones habrá, por tanto, 16 vértices: 8 del cubo original y 8 del desplazado en la cuarta dimensión. Tiene 32 aristas: 12 de cada una dan las posiciones inicial y final del cubo original, y otras 8 aristas "dibujan" sus ocho vértices, que se han movido a la cuarta dimensión. Se puede aplicar el mismo razonamiento a las caras de un hipercubo. En el espacio bidimensional sólo hay uno (el cuadrado en sí), un cubo tiene 6 de ellos (dos caras del cuadrado movido y cuatro más que describen sus lados). Un hipercubo de cuatro dimensiones tiene 24 caras cuadradas: 12 cuadrados del cubo original en dos posiciones y 12 cuadrados de sus doce aristas.
Así como los lados de un cuadrado son 4 segmentos unidimensionales, y los lados (caras) de un cubo son 6 cuadrados bidimensionales, así para un “cubo de cuatro dimensiones” (teseracto) los lados son 8 cubos tridimensionales . Los espacios de pares opuestos de cubos tesseract (es decir, los espacios tridimensionales a los que pertenecen estos cubos) son paralelos. En la figura estos son los cubos: CDBAGHFE y KLJIOPNM, CDBAKLJI y GHFEOPNM, EFBAMNJI y GHDCOPLK, CKIAGOME y DLJBHPNF.
De manera similar, podemos continuar nuestro razonamiento para hipercubos de un mayor número de dimensiones, pero es mucho más interesante ver cómo se verá un hipercubo de cuatro dimensiones para nosotros, residentes del espacio tridimensional. Para ello utilizaremos el ya conocido método de analogías.
Tomemos el cubo de alambre ABCDHEFG y mirémoslo con un ojo desde el lado del borde. Veremos y podremos dibujar dos cuadrados en un plano (sus bordes cercano y lejano), conectados por cuatro líneas: bordes laterales. De manera similar, un hipercubo de cuatro dimensiones en un espacio tridimensional se verá como dos "cajas" cúbicas insertadas entre sí y conectadas por ocho aristas. En este caso, las propias "cajas", caras tridimensionales, se proyectarán en "nuestro" espacio y las líneas que las conectan se extenderán en la dirección del cuarto eje. También puedes intentar imaginar el cubo no en proyección, sino en una imagen espacial.
Así como un cubo tridimensional está formado por un cuadrado desplazado a lo largo de su cara, un cubo desplazado a la cuarta dimensión formará un hipercubo. Está limitado por ocho cubos, que en perspectiva parecerán una figura bastante compleja. El hipercubo de cuatro dimensiones consta de un número infinito de cubos, del mismo modo que un cubo tridimensional se puede “cortar” en un número infinito de cuadrados planos.
Al cortar las seis caras de un cubo tridimensional, puedes descomponerlo en una figura plana: un desarrollo. Tendrá un cuadrado a cada lado de la cara original, más uno más: la cara opuesta. Y el desarrollo tridimensional de un hipercubo de cuatro dimensiones consistirá en el cubo original, seis cubos que "crecen" a partir de él y uno más: la "hipercara" final.
Las propiedades de un teseracto representan una continuación de las propiedades de las figuras geométricas de dimensión inferior en un espacio de cuatro dimensiones.
Proyecciones
Al espacio bidimensional
Esta estructura es difícil de imaginar, pero es posible proyectar un teseracto en espacios bidimensionales o tridimensionales. Además, proyectar sobre un plano facilita comprender la ubicación de los vértices de un hipercubo. De esta manera, es posible obtener imágenes que ya no reflejan las relaciones espaciales dentro del teseracto, sino que ilustran la estructura de conexión de los vértices, como en los siguientes ejemplos:

La tercera imagen muestra el teseracto en isometría, en relación con el punto de construcción. Esta representación es de interés cuando se utiliza un teseract como base para una red topológica para vincular múltiples procesadores en computación paralela.
Al espacio tridimensional
Una de las proyecciones de un teseracto en el espacio tridimensional representa dos cubos tridimensionales anidados, cuyos vértices correspondientes están conectados por segmentos. Los cubos internos y externos tienen diferentes tamaños en el espacio tridimensional, pero en el espacio cuatridimensional son cubos iguales. Para comprender la igualdad de todos los cubos de tesseract, se creó un modelo de tesseract giratorio.
|
|
- Las seis pirámides truncadas a lo largo de los bordes del teseracto son imágenes de seis cubos iguales. Sin embargo, estos cubos son para un teseracto lo que los cuadrados (caras) son para un cubo. Pero, de hecho, el teseracto se puede dividir en un número infinito de cubos, del mismo modo que un cubo se puede dividir en un número infinito de cuadrados, o un cuadrado en un número infinito de segmentos.
Otra proyección interesante del teseracto en el espacio tridimensional es un dodecaedro rómbico con sus cuatro diagonales que conectan pares de vértices opuestos en grandes ángulos de los rombos. En este caso, 14 de los 16 vértices del teseracto se proyectan en 14 vértices del dodecaedro rómbico, y las proyecciones de los 2 restantes coinciden en su centro. En tal proyección sobre el espacio tridimensional, se conserva la igualdad y el paralelismo de todos los lados unidimensionales, bidimensionales y tridimensionales.
par estéreo
Un par estéreo de un teseracto se representa como dos proyecciones en un espacio tridimensional. Esta imagen del teseracto fue desarrollada para representar la profundidad como una cuarta dimensión. El par estéreo se ve de manera que cada ojo ve solo una de estas imágenes, aparece una imagen estereoscópica que reproduce la profundidad del teseracto.
Teseracto desenvolviendo
La superficie de un teseracto se puede desplegar en ocho cubos (similar a cómo la superficie de un cubo se puede desplegar en seis cuadrados). Hay 261 diseños de teseracto diferentes. El desarrollo de un teseracto se puede calcular trazando los ángulos conectados en un gráfico.
Teseracto en el arte
- En "New Abbott Plain" de Edwina A., el hipercubo actúa como narrador.
- En un episodio de Las aventuras de Jimmy Neutron, el "niño genio" Jimmy inventa un hipercubo de cuatro dimensiones idéntico a la caja plegable de la novela Glory Road (1963) de Robert Heinlein.
- Robert E. Heinlein ha mencionado los hipercubos en al menos tres historias de ciencia ficción. En "La casa de las cuatro dimensiones" ("La casa que construyó Teal"), describió una casa construida como un teseract sin envolver, y luego, debido a un terremoto, "doblado" en la cuarta dimensión y se convirtió en un teseract "real". .
- La novela Glory Road de Heinlein describe una caja de gran tamaño que era más grande por dentro que por fuera.
- La historia de Henry Kuttner "All Tenali Borogov" describe un juguete educativo para niños de un futuro lejano, similar en estructura a un teseracto.
- En la novela de Alex Garland (), el término "teseracto" se utiliza para el despliegue tridimensional de un hipercubo de cuatro dimensiones, en lugar del hipercubo en sí. Esta es una metáfora diseñada para mostrar que el sistema cognitivo debe ser más amplio que lo cognoscible.
- La trama de Cube 2: Hypercube se centra en ocho extraños atrapados en un "hipercubo", o red de cubos conectados.
- La serie de televisión Andrómeda utiliza generadores de teseracto como dispositivo argumental. Están diseñados principalmente para manipular el espacio y el tiempo.
- Cuadro “La Crucifixión” (Corpus Hypercubus) de Salvador Dalí ().
- El cómic de Nextwave muestra un vehículo que incluye 5 zonas de teseracto.
- En el álbum Voivod Nothingface una de las composiciones se llama “In my hypercube”.
- En la novela Route Cube de Anthony Pearce, una de las lunas en órbita de la Asociación Internacional de Fomento se llama teseracto y ha sido comprimida en 3 dimensiones.
- En la serie “Black Hole School” en la tercera temporada hay un episodio “Tesseract”. Lucas presiona un botón secreto y la escuela comienza a “tomar forma como un teseracto matemático”.
- El término "tesseract" y su término derivado "tesserate" se encuentran en el cuento "A Wrinkle in Time" de Madeleine L'Engle.
- TesseracT es el nombre de una banda británica de djent.
- En la serie de películas Marvel Cinematic Universe, el Tesseract es un elemento clave de la trama, un artefacto cósmico en forma de hipercubo.
- En el cuento de Robert Sheckley "Miss Mouse y la cuarta dimensión", un escritor esotérico, conocido del autor, intenta ver el teseracto mirando durante horas el dispositivo que diseñó: una bola en una pierna con varillas clavadas en ella, en en el que se montan cubos, cubiertos con todo tipo de símbolos esotéricos. La historia menciona el trabajo de Hinton.
- En las películas El primer vengador, Los Vengadores. Teseracto: la energía del universo entero.
Otros nombres
- hexadecachoron hexadecachoron)
- Octocoron (inglés) octacoron)
- tetracubo
- 4 cubos
- Hipercubo (si no se especifica el número de dimensiones)
Notas
Literatura
- Charles H. Hinton. Cuarta Dimensión, 1904. ISBN 0-405-07953-2
- Martin Gardner, Carnaval matemático, 1977. ISBN 0-394-72349-X
- Ian Stewart, Conceptos de matemáticas modernas, 1995. ISBN 0-486-28424-7
Enlaces
En ruso- Programa Transformator4D. Formación de modelos de proyecciones tridimensionales de objetos cuatridimensionales (incluido el Hipercubo).
- Un programa que implementa la construcción de un teseracto y todas sus transformaciones afines, con código fuente en C++.
En Inglés
- Mushware Limited - programa de salida de tesseract ( Entrenador Teseracto, licencia compatible con GPLv2) y un shooter en primera persona en el espacio de cuatro dimensiones ( Adanaxis; los gráficos son principalmente tridimensionales; Hay una versión GPL en los repositorios del sistema operativo).
| Poliedros | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Correcto (Sólidos platónicos) |
|||||||||
| Dodecaedro estrellado Icosidodecaedro estrellado Icosaedro estrellado Poliedro estrellado Octaedro estrellado | |||||||||
| Convexo |
|
||||||||
| Fórmulas, teoremas, teorías |
|||||||||
| Otro | |||||||||
Fundación Wikimedia. 2010.









