Entre las series funcionales, el lugar más importante lo ocupan las series de potencias.

Una serie de potencias es una serie.

cuyos términos son funciones de potencia dispuestas en potencias enteras crecientes no negativas X, A C0 , C 1 , C 2 , C norte - valores constantes. Números C1 , C 2 , C norte - coeficientes de los términos de la serie, C0 - miembro gratuito. Los términos de la serie de potencias se definen en toda la recta numérica.

Conozcamos el concepto. áreas de convergencia de la serie de potencias. Este es un conjunto de valores variables. X, para lo cual la serie converge. Las series de potencias tienen una región de convergencia bastante simple. Para valores de variables reales X la región de convergencia consta de un punto, o es un cierto intervalo (intervalo de convergencia), o coincide con todo el eje Buey .

Al sustituir los valores en la serie de potencias. X= 0 dará como resultado una serie numérica

C0 +0+0+...+0+... ,

que converge.

Por lo tanto, cuando X= 0 cualquier serie de potencias converge y, por tanto, su área de convergencia no puede ser el conjunto vacío. La estructura de la región de convergencia de todas las series de potencias es la misma. Se puede establecer utilizando el siguiente teorema.

Teorema 1 (teorema de Abel). Si una serie de potencias converge en algún valor X = X 0 , diferente de cero, entonces converge y, además, absolutamente, para todos los valores |X| < |X 0 | . Tenga en cuenta: tanto el valor inicial “X es cero” como cualquier valor de “X” que se compara con el valor inicial se toman módulo, sin tener en cuenta el signo.

Consecuencia. Si la serie de potencias diverge a algún valor X = X 1 , entonces diverge para todos los valores |X| > |X 1 | .

Como ya hemos descubierto anteriormente, cualquier serie de potencias converge en el valor X= 0. Hay series de potencias que convergen sólo cuando X= 0 y divergen para otros valores X. Excluyendo este caso de la consideración, asumimos que la serie de potencias converge en algún valor X = X 0 , diferente de cero. Entonces, según el teorema de Abel, converge en todos los puntos del intervalo ]-| X0 |, |X 0 |[ (un intervalo cuyos límites izquierdo y derecho son los valores de x en los que converge la serie de potencias, tomados con un signo menos y un signo más, respectivamente), simétrico con respecto al origen.

Si la serie de potencias diverge en un cierto valor X = X 1 , entonces, basándose en un corolario del teorema de Abel, diverge en todos los puntos fuera del segmento [-| X1 |, |X 1 |] . De ello se deduce que para cualquier serie de potencias existe un intervalo simétrico con respecto al origen, llamado intervalo de convergencia , en cada punto en el que la serie converge, en los límites puede converger o divergir, y no necesariamente al mismo tiempo, y fuera del segmento la serie diverge. Número R se llama radio de convergencia de la serie de potencias.

En casos especiales intervalo de convergencia de series de potencias puede degenerar a un punto (entonces la serie converge sólo cuando X= 0 y se considera que R= 0) o representar la recta numérica completa (entonces la serie converge en todos los puntos de la recta numérica y se supone que ).

Así, determinar la región de convergencia de una serie de potencias consiste en determinar su radio de convergencia R y estudiar la convergencia de la serie en los límites del intervalo de convergencia (en ).

Teorema 2. Si todos los coeficientes de una serie de potencias, a partir de uno determinado, son diferentes de cero, entonces su radio de convergencia es igual al límite en la relación de los valores absolutos de los coeficientes de los siguientes miembros comunes de la serie. , es decir.

Ejemplo 1. Encuentra la región de convergencia de la serie de potencias.

Solución. Aquí

Usando la fórmula (28), encontramos el radio de convergencia de esta serie:

Estudiemos la convergencia de la serie en los extremos del intervalo de convergencia. El ejemplo 13 muestra que esta serie converge en X= 1 y diverge en X= -1. En consecuencia, la región de convergencia es el medio intervalo.

Ejemplo 2. Encuentra la región de convergencia de la serie de potencias.

Solución. Los coeficientes de la serie son positivos y

Encontremos el límite de esta relación, es decir Radio de convergencia de la serie de potencias:

Estudiemos la convergencia de la serie en los extremos del intervalo. Sustitución de valor X= -1/5 y X= 1/5 en esta fila da:

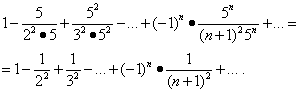
La primera de estas series converge (ver Ejemplo 5). Pero entonces, en virtud del teorema de la sección "Convergencia absoluta", la segunda serie también converge, y la región de su convergencia es el segmento

Ejemplo 3. Encuentra la región de convergencia de la serie de potencias.

Solución. Aquí

Usando la fórmula (28) encontramos el radio de convergencia de la serie:

Estudiemos la convergencia de la serie para valores de . Sustituyéndolos en esta serie, obtenemos respectivamente

Ambas series divergen porque no se cumple la condición necesaria para la convergencia (sus términos comunes no tienden a cero en ). Entonces, en ambos extremos del intervalo de convergencia, esta serie diverge y la región de su convergencia es el intervalo.

Ejemplo 5. Encuentra la región de convergencia de la serie de potencias.

Solución. Encontramos la relación donde , y :

Según la fórmula (28), el radio de convergencia de esta serie

es decir, la serie converge sólo cuando X= 0 y diverge para otros valores X.

Los ejemplos muestran que en los extremos del intervalo de convergencia las series se comportan de manera diferente. En el ejemplo 1, en un extremo del intervalo de convergencia la serie converge, y en el otro diverge; en el ejemplo 2, converge en ambos extremos; en el ejemplo 3, diverge en ambos extremos;

La fórmula para el radio de convergencia de una serie de potencias se obtiene suponiendo que todos los coeficientes de los términos de la serie, a partir de un determinado punto, son distintos de cero. Por tanto, el uso de la fórmula (28) está permitido sólo en estos casos. Si se viola esta condición, entonces el radio de convergencia de la serie de potencias debe buscarse usando signo de d'Alembert, o, reemplazando la variable, transformando la serie a una forma en la que se cumpla la condición especificada.

Ejemplo 6. Encuentra el intervalo de convergencia de la serie de potencias.

Solución. Esta serie no contiene términos con grados impares. X. Por tanto, transformamos la serie, fijando . Luego obtenemos la serie.

para encontrar el radio de convergencia al que podemos aplicar la fórmula (28). Dado que , a , entonces el radio de convergencia de esta serie

De la igualdad obtenemos, por tanto, esta serie converge en el intervalo .

Suma de series de potencias. Diferenciación e integración de series de potencias.

Sea para la serie de potencias

radio de convergencia R> 0, es decir esta serie converge en el intervalo .

Entonces cada valor X del intervalo de convergencia corresponde a una determinada suma de la serie. Por lo tanto, la suma de la serie de potencias es función de X en el intervalo de convergencia. denotándolo por F(X), podemos escribir la igualdad

entendiéndolo en el sentido de que la suma de la serie en cada punto X del intervalo de convergencia es igual al valor de la función F(X) en este punto. En el mismo sentido diremos que la serie de potencias (29) converge a la función F(X) en el intervalo de convergencia.

Fuera del intervalo de convergencia, la igualdad (30) no tiene sentido.

Ejemplo 7. Encuentra la suma de la serie de potencias.

Solución. Esta es una serie geométrica para la cual a= 1, un q= X. Por tanto, su suma es una función. . Una serie converge si , y es su intervalo de convergencia. Por lo tanto igualdad

es válido sólo para valores, aunque la función definido para todos los valores X, excepto X= 1.

Se puede demostrar que la suma de las series de potencias F(X) es continua y diferenciable en cualquier intervalo dentro del intervalo de convergencia, en particular en cualquier punto del intervalo de convergencia de la serie.

Presentemos teoremas sobre la diferenciación término por término y la integración de series de potencias.

Teorema 1. La serie de potencias (30) en el intervalo de su convergencia se puede diferenciar término por término un número ilimitado de veces, y la serie de potencias resultante tiene el mismo radio de convergencia que la serie original, y sus sumas son respectivamente iguales a .

Teorema 2. La serie de potencias (30) se puede integrar término por término un número ilimitado de veces en el rango de 0 a X, si , y la serie de potencias resultante tienen el mismo radio de convergencia que la serie original, y sus sumas son correspondientemente iguales

Expansión de funciones a series de potencias.

Sea dada la función F(X), que debe expandirse a una serie de potencias, es decir representar en la forma (30):

La tarea es determinar los coeficientes. fila (30). Para ello, diferenciando la igualdad (30) término por término, encontramos consistentemente:

……………………………………………….. (31)

Suponiendo en las igualdades (30) y (31) X= 0, encontramos

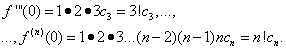
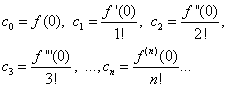
Sustituyendo las expresiones encontradas en la igualdad (30), obtenemos

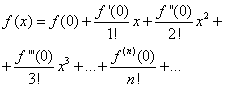(32)

Encontremos el desarrollo en serie de Maclaurin de algunas funciones elementales.

Ejemplo 8. Ampliar la función en una serie de Maclaurin.

Solución. Las derivadas de esta función coinciden con la función misma:

Por lo tanto, cuando X= 0 tenemos

Sustituyendo estos valores en la fórmula (32), obtenemos la expansión deseada:

(33)

Esta serie converge en toda la recta numérica (su radio de convergencia).

Ejemplo 1. Encuentre la región de convergencia de la serie de potencias:

A) ; b) ;

V) ; GRAMO)
;

d)
.

A) Encontremos el radio de convergencia. R. Porque
,
, Eso

X
, es decir, el intervalo de convergencia de la serie
.

En
obtenemos una serie numérica . Esta serie converge porque es una serie armónica generalizada. en
.

En
obtenemos una serie numérica
. Esta serie es absolutamente convergente, ya que una serie compuesta por los valores absolutos de sus términos , convergente.

b) Encontremos el radio de convergencia. R. Porque
, Eso
.

Entonces, el intervalo de convergencia de la serie
.

Examinamos la convergencia de esta serie en los extremos del intervalo de convergencia.

En
tenemos una serie de números

.

En
tenemos una serie de números
. Esta serie es divergente porque
no existe.

Entonces, la región de convergencia de esta serie
.

V) Encontremos el radio de convergencia. R. Porque
,
Eso
.

Entonces, el intervalo de convergencia
. La región de convergencia de esta serie coincide con el intervalo de convergencia, es decir, la serie converge para cualquier valor de la variable. X.

GRAMO) Encontremos el radio de convergencia. R. Porque
,
Eso
.

Porque
, entonces la serie converge solo en el punto
. Esto significa que la región de convergencia de esta serie es un punto
.

d) Encontremos el radio de convergencia. R.

Porque
,
, Eso

Entonces, la serie converge para absolutamente todos. X, satisfaciendo la desigualdad
, eso es
.

De aquí
− intervalo de convergencia,
− radio de convergencia.

Examinemos esta serie para determinar la convergencia en los extremos del intervalo de convergencia.

En
obtenemos una serie numérica

que diverge (serie armónica).

En
obtenemos una serie numérica
, que converge condicionalmente (la serie converge según el criterio de Leibniz, y la serie compuesta por los valores absolutos de sus miembros diverge, ya que es armónica).

Entonces, la región de convergencia de la serie.
.

2.3. Serie de Taylor y Maclaurin.

Expansión de funciones a series de potencias.

Aplicación de series de potencias a cálculos aproximados.

Ejemplos de resolución de problemas

Ejemplo 1. Expanda la función a una serie de potencias:

A)
; b)
;

V)
; GRAMO)
.

A) Reemplazo en la fórmula
X en
, obtenemos la expansión deseada:

Dónde

b) Sustituyendo en igualdad

Dónde
X en
, obtenemos la expansión deseada:

V) Esta función se puede escribir así:
. Para encontrar la serie deseada, basta con expandir

Dónde
sustituto
. Entonces obtenemos:

GRAMO) Esta función se puede reescribir así: .

Función
se puede expandir a una serie de potencias poniendo la serie binomial
, recibiremos .

Dónde
.

Para obtener la expansión deseada, basta con multiplicar las series resultantes (debido a la convergencia absoluta de estas series).

Por eso,

, Dónde
.

Ejemplo 2. Encuentre valores aproximados de estas funciones:

A)
con una precisión de 0,0001;

b)
con una precisión de 0,00001.

A) Porque
, luego a la expansión de la función, donde
sustituyamos
:

Porque
, entonces la precisión requerida estará garantizada si nos limitamos solo a los dos primeros términos de la expansión resultante.

Usamos la serie binomial.

Dónde
.

Creyendo
Y
, obtenemos la siguiente expansión:

Si en la última serie alterna solo se tienen en cuenta los dos primeros términos y se descartan el resto, entonces el error en el cálculo
no excederá 0,000006 en valor absoluto. Entonces el error en el cálculo.
no excederá el número. Por eso,

Ejemplo 3. Calcule al 0,001 más cercano:

A)
; b)
.

A)
.

Expandamos el integrando a una serie de potencias. Para ello sustituimos en la serie binomial
y reemplazar X en :

Desde el segmento de integración
pertenece a la región de convergencia de la serie resultante
, luego integraremos término por término dentro de los límites especificados:

En la serie alterna resultante, el cuarto término es menor que 0,001 en valor absoluto. En consecuencia, se garantizará la precisión requerida si sólo se tienen en cuenta los tres primeros términos de la serie.

Dado que el primero de los términos descartados tiene signo menos, el valor aproximado resultante será excedente. Por lo tanto, la respuesta dentro de 0,001 es 0,487.

b) Primero representemos el integrando como una serie de potencias. Reemplacemos en la expansión de la función.

Dónde

X en
, obtenemos:

Entonces
.

La serie alterna resultante satisface las condiciones del criterio de Leibniz. El cuarto término de la serie es menor que 0,001 en valor absoluto. Para garantizar la precisión requerida, basta con encontrar la suma de los tres primeros términos.

Por eso,
.

Serie funcional. Serie de potencia.
Rango de convergencia de la serie.

La risa sin motivo es señal de d'Alembert

Ha llegado la hora de las filas funcionales. Para dominar con éxito el tema y, en particular, esta lección, es necesario tener un buen conocimiento de las series de números ordinarios. Debe tener una buena comprensión de qué es una serie y poder aplicar criterios de comparación para examinar la convergencia de la serie. Por lo tanto, si acaba de empezar a estudiar el tema o es principiante en matemáticas superiores, necesario trabaje en tres lecciones en secuencia: Filas para tontos,Signo de D'Alembert. signos de cauchy Y Filas alternas. La prueba de Leibniz. ¡Definitivamente los tres! Si tiene conocimientos y habilidades básicos para resolver problemas con series numéricas, afrontar series funcionales será bastante sencillo, ya que no hay mucho material nuevo.

En esta lección, veremos el concepto de serie funcional (lo que es), nos familiarizaremos con las series de potencias, que se encuentran en el 90% de las tareas prácticas, y aprenderemos cómo resolver un problema típico común de encontrar el radio. de convergencia, intervalo de convergencia y región de convergencia de una serie de potencias. A continuación, recomiendo considerar el material sobre expansión de funciones en series de potencias, y se proporcionarán primeros auxilios al principiante. Después de recuperar un poco el aliento, pasamos al siguiente nivel:

También en el apartado de series funcionales hay numerosas de ellas. aplicaciones para aproximar la computación, y en cierto modo se destacan las series de Fourier, que, por regla general, ocupan un capítulo aparte en la literatura educativa. ¡Solo tengo un artículo, pero es largo y hay muchos, muchos ejemplos adicionales!

Entonces, los hitos están establecidos, vamos:

El concepto de serie funcional y serie de potencias.

Si el límite resulta ser infinito, entonces el algoritmo de solución también termina su trabajo y damos la respuesta final a la tarea: "La serie converge en " (o en cualquiera de los dos "). Ver caso No. 3 del párrafo anterior.

Si el límite resulta no ser ni cero ni infinito, entonces tenemos el caso más común en la práctica número 1: la serie converge en un intervalo determinado.

En este caso el límite es . ¿Cómo encontrar el intervalo de convergencia de una serie? Calculamos la desigualdad:

EN CUALQUIER tarea de este tipo en el lado izquierdo de la desigualdad debería estar resultado del cálculo del límite, y en el lado derecho de la desigualdad – estrictamente unidad. No explicaré exactamente por qué existe tal desigualdad y por qué la hay en la derecha. Las lecciones están orientadas a la práctica, y es muy bueno que mis historias no colgaran al profesorado y algunos teoremas se hayan vuelto más claros.

La técnica de trabajar con un módulo y resolver desigualdades dobles se discutió en detalle en el primer año del artículo. Dominio de funciones, pero por comodidad intentaré comentar todas las acciones con el mayor detalle posible. Revelamos la desigualdad con el módulo según la regla escolar. . En este caso:

La mitad del camino ha terminado.

En la segunda etapa, es necesario investigar la convergencia de la serie en los extremos del intervalo encontrado.

Primero, tomamos el extremo izquierdo del intervalo y lo sustituimos en nuestra serie de potencias:

Hemos obtenido una serie numérica y necesitamos examinarla para determinar su convergencia (una tarea que ya conocemos de lecciones anteriores).

1) La serie es alterna.
2) – los términos de la serie disminuyen en módulo. Además, cada miembro siguiente de la serie es menor que el anterior en valor absoluto: , lo que significa que la disminución es monótona.
Conclusión: la serie converge.

A través de una serie compuesta por módulos, descubriremos exactamente cómo:
– converge (serie “estándar” de la familia de series armónicas generalizadas).

Por tanto, la serie numérica resultante converge absolutamente.

en – converge.

! te recuerdo que cualquier serie positiva convergente también es absolutamente convergente.

Por tanto, la serie de potencias converge, y de forma absoluta, en ambos extremos del intervalo encontrado.

Respuesta:área de convergencia de la serie de potencias en estudio:

Otra forma de respuesta tiene derecho a la vida: una serie converge si

A veces, el planteamiento del problema requiere que usted indique el radio de convergencia. Es obvio que en el ejemplo considerado .

Ejemplo 2

Encuentra la región de convergencia de la serie de potencias.

Solución: encontramos el intervalo de convergencia de la serie mediante el uso signo de d'Alembert (¡pero no POR atributo! – tal atributo no existe para series funcionales):

La serie converge en

Izquierda tenemos que irnos solo, entonces multiplicamos ambos lados de la desigualdad por 3:

– La serie es alterna.
– – los términos de la serie disminuyen en módulo. Cada miembro siguiente de la serie es menor que el anterior en valor absoluto: , lo que significa que la disminución es monótona.

Conclusión: la serie converge.

Examinemos la naturaleza de la convergencia:

Comparemos esta serie con una serie divergente.
Utilizamos el criterio de comparación limitante:

Se obtiene un número finito distinto de cero, lo que significa que la serie diverge de la serie.

Por tanto, la serie converge condicionalmente.

2) cuando – diverge (según lo demostrado).

Respuesta:Área de convergencia de la serie de potencias en estudio: . Cuando la serie converge condicionalmente.

En el ejemplo considerado, la región de convergencia de la serie de potencias es un medio intervalo, y en todos los puntos del intervalo la serie de potencias converge absolutamente, y en el punto , como resultó – condicionalmente.

Ejemplo 3

Encuentre el intervalo de convergencia de la serie de potencias e investigue su convergencia en los extremos del intervalo encontrado.

Este es un ejemplo para que lo resuelvas por tu cuenta.

Veamos un par de ejemplos que son raros, pero que ocurren.

Ejemplo 4

Encuentra el área de convergencia de la serie:

Solución: Utilizando la prueba de d'Alembert encontramos el intervalo de convergencia de esta serie:

(1) Componemos la proporción del siguiente miembro de la serie con respecto al anterior.

(2) Nos deshacemos de la fracción de cuatro pisos.

(3) Según la regla de las operaciones con potencias, colocamos los cubos bajo una sola potencia. En el numerador ampliamos hábilmente el grado, es decir Lo organizamos de tal manera que en el siguiente paso podamos reducir la fracción en . Describimos los factoriales en detalle.

(4) Debajo del cubo, dividimos el numerador por el denominador término por término, indicando que . En una fracción reducimos todo lo que se puede reducir. Llevamos el factor más allá del signo límite; se puede eliminar, ya que no hay nada en él que dependa de la variable “dinámica” “en”. Tenga en cuenta que el signo del módulo no se dibuja porque toma valores no negativos para cualquier "x".

En el límite se obtiene cero, lo que significa que podemos dar la respuesta final:

Respuesta: La serie converge en

Pero al principio parecía que esta disputa con el “relleno terrible” sería difícil de resolver. Cero o infinito en el límite es casi un regalo, ¡porque la solución se reduce notablemente!

Ejemplo 5

Encuentra el área de convergencia de la serie.

Este es un ejemplo para que lo resuelvas por tu cuenta. Ten cuidado ;-) La solución completa está al final de la lección.

Veamos algunos ejemplos más que contienen un elemento de novedad en cuanto al uso de técnicas técnicas.

Ejemplo 6

Encuentre el intervalo de convergencia de la serie e investigue su convergencia en los extremos del intervalo encontrado

Solución: El término común de la serie de potencias incluye un factor que asegura la alternancia de signos. El algoritmo de solución se conserva por completo, pero al establecer el límite ignoramos (no escribimos) este factor, ya que el módulo destruye todos los "menos".

Encontramos el intervalo de convergencia de la serie mediante la prueba de d'Alembert:

Creemos una desigualdad estándar:
La serie converge en
Izquierda tenemos que irnos solo módulo, entonces multiplicamos ambos lados de la desigualdad por 5:

Ahora abrimos el módulo de forma familiar:

En medio de la doble desigualdad hay que dejar solo “X” para ello restamos 2 de cada parte de la desigualdad:

– intervalo de convergencia de la serie de potencias en estudio.

Investigamos la convergencia de la serie en los extremos del intervalo encontrado:

1) Sustituir el valor en nuestra serie de potencias. :

Tenga mucho cuidado, el multiplicador no proporciona alternancia de signos para ningún "en" natural. Sacamos el menos resultante de la serie y nos olvidamos de él, ya que (como cualquier constante factorial) no afecta de ninguna manera la convergencia o divergencia de la serie numérica.

Por favor nota de nuevo que al sustituir el valor en el término general de la serie de potencias, nuestro factor se redujo. Si esto no sucediera, significaría que calculamos el límite incorrectamente o expandimos el módulo incorrectamente.

Entonces, necesitamos examinar la serie numérica para determinar la convergencia. Aquí la forma más sencilla es utilizar el criterio de comparación límite y comparar esta serie con una serie armónica divergente. Pero, para ser honesto, estoy terriblemente cansado del signo limitante de comparación, así que agregaré algo de variedad a la solución.

Entonces la serie converge en

Multiplicamos ambos lados de la desigualdad por 9:

Extraemos la raíz de ambas partes, recordando el chiste de la vieja escuela:

Ampliando el módulo:

y agregue uno a todas las partes:

– intervalo de convergencia de la serie de potencias en estudio.

Investiguemos la convergencia de la serie de potencias en los extremos del intervalo encontrado:

1) Si , entonces se obtiene la siguiente serie numérica: