Entre las series funcionales, el lugar más importante lo ocupan las series de potencias.
Una serie de potencias es una serie.
cuyos términos son funciones de potencia dispuestas en potencias enteras crecientes no negativas X, A C 0 , C 1 , C 2 , C norte - valores constantes. Números C 1 , C 2 , C n - coeficientes de términos de la serie, C 0 - miembro gratuito. Los términos de la serie de potencias se definen en toda la recta numérica.
Conozcamos el concepto. áreas de convergencia de la serie de potencias. Este es un conjunto de valores variables. X, para lo cual la serie converge. Las series de potencias tienen una región de convergencia bastante simple. Para valores de variables reales X la región de convergencia consta de un punto, o es un cierto intervalo (intervalo de convergencia), o coincide con todo el eje Buey .
Al sustituir los valores en la serie de potencias. X= 0 dará como resultado una serie numérica
C 0 +0+0+...+0+... ,
que converge.
Por lo tanto, cuando X= 0 cualquier serie de potencias converge y, por tanto, su área de convergencia no puede ser el conjunto vacío. La estructura de la región de convergencia de todas las series de potencias es la misma. Se puede establecer utilizando el siguiente teorema.
Teorema 1 (teorema de Abel). Si una serie de potencias converge en algún valor X = X 0, distinto de cero, entonces converge y, además, absolutamente, para todos los valores de | X| < |X 0 | . Tenga en cuenta: tanto el valor inicial “X es cero” como cualquier valor de “X” que se compara con el valor inicial se toman módulo, sin tener en cuenta el signo.
Consecuencia. Si la serie de potencias diverge a algún valor X = X 1, entonces diverge para todos los valores de | X| > |X 1 | .
Como ya hemos descubierto anteriormente, cualquier serie de potencias converge en el valor X= 0. Hay series de potencias que convergen sólo cuando X= 0 y divergen para otros valores X. Excluyendo este caso de la consideración, asumimos que la serie de potencias converge en algún valor X = X 0, diferente de cero. Entonces, según el teorema de Abel, converge en todos los puntos del intervalo ]-| X 0 |, |X 0 |[ (un intervalo cuyos límites izquierdo y derecho son los valores de x en los que converge la serie de potencias, tomados con un signo menos y un signo más, respectivamente), simétrico con respecto al origen.
Si la serie de potencias diverge en un cierto valor X = X 1, entonces, según el corolario del teorema de Abel, diverge en todos los puntos fuera del segmento [-| X 1 |, |X 1 |] . De ello se deduce que para cualquier serie de potencias existe un intervalo simétrico con respecto al origen, llamado intervalo de convergencia, en cada punto en el que la serie converge, en los límites puede converger o divergir, y no necesariamente al mismo tiempo, y fuera del segmento la serie diverge. Número R se llama radio de convergencia de la serie de potencias.
En casos especiales intervalo de convergencia de series de potencias puede degenerar a un punto (entonces la serie converge sólo cuando X= 0 y se considera que R= 0) o representar la recta numérica completa (entonces la serie converge en todos los puntos de la recta numérica y se supone que ).
Así, determinar la región de convergencia de una serie de potencias consiste en determinar su radio de convergencia R y estudiar la convergencia de la serie en los límites del intervalo de convergencia (en ).
Teorema 2. Si todos los coeficientes de una serie de potencias, a partir de una determinada, son diferentes de cero, entonces su radio de convergencia es igual al límite en la relación de los valores absolutos de los coeficientes de los términos comunes de la serie que le sigue, es decir.
Ejemplo 1. Encuentra la región de convergencia de la serie de potencias.
Solución. Aquí
Usando la fórmula (28), encontramos el radio de convergencia de esta serie:
Estudiemos la convergencia de la serie en los extremos del intervalo de convergencia. El ejemplo 13 muestra que esta serie converge en X= 1 y diverge en X= -1. En consecuencia, la región de convergencia es el medio intervalo.
Ejemplo 2. Encuentra la región de convergencia de la serie de potencias.
Solución. Los coeficientes de la serie son positivos y
Encontremos el límite de esta relación, es decir Radio de convergencia de la serie de potencias:
Estudiemos la convergencia de la serie en los extremos del intervalo. Sustitución de valor X= -1/5 y X= 1/5 en esta fila da:
La primera de estas series converge (ver Ejemplo 5). Pero entonces, en virtud del teorema de la sección "Convergencia absoluta", la segunda serie también converge, y la región de su convergencia es el segmento
Ejemplo 3. Encuentra la región de convergencia de la serie de potencias.
Solución. Aquí
Usando la fórmula (28) encontramos el radio de convergencia de la serie:
Estudiemos la convergencia de la serie para valores de . Sustituyéndolos en esta serie, obtenemos respectivamente
Ambas series divergen porque no se cumple la condición necesaria para la convergencia (sus términos comunes no tienden a cero en ). Entonces, en ambos extremos del intervalo de convergencia, esta serie diverge y la región de su convergencia es el intervalo.
Ejemplo 5. Encuentra la región de convergencia de la serie de potencias.
Solución. Encontramos la relación donde , y 
:
Según la fórmula (28), el radio de convergencia de esta serie
,
es decir, la serie converge sólo cuando X= 0 y diverge para otros valores X.
Los ejemplos muestran que en los extremos del intervalo de convergencia las series se comportan de manera diferente. En el ejemplo 1, en un extremo del intervalo de convergencia la serie converge, y en el otro diverge; en el ejemplo 2, converge en ambos extremos; en el ejemplo 3, diverge en ambos extremos;
La fórmula para el radio de convergencia de una serie de potencias se obtiene suponiendo que todos los coeficientes de los términos de la serie, a partir de un determinado punto, son distintos de cero. Por tanto, el uso de la fórmula (28) está permitido sólo en estos casos. Si se viola esta condición, entonces se debe buscar el radio de convergencia de la serie de potencias utilizando la prueba de d'Alembert o, reemplazando la variable, transformando la serie a una forma en la que se cumpla la condición especificada.
Ejemplo 6. Encuentra el intervalo de convergencia de la serie de potencias.
Solución. Esta serie no contiene términos con grados impares. X. Por tanto, transformamos la serie, fijando . Luego obtenemos la serie.
para encontrar el radio de convergencia al que podemos aplicar la fórmula (28). Dado que , a , entonces el radio de convergencia de esta serie
De la igualdad obtenemos, por tanto, esta serie converge en el intervalo .
Suma de series de potencias. Diferenciación e integración de series de potencias.Sea para la serie de potencias
radio de convergencia R> 0, es decir esta serie converge en el intervalo .
Entonces cada valor X del intervalo de convergencia corresponde a una determinada suma de la serie. Por lo tanto, la suma de la serie de potencias es función de X en el intervalo de convergencia. denotándolo por F(X), podemos escribir la igualdad
entendiéndolo en el sentido de que la suma de la serie en cada punto X del intervalo de convergencia es igual al valor de la función F(X) en este punto. En el mismo sentido diremos que la serie de potencias (29) converge a la función F(X) en el intervalo de convergencia.
Fuera del intervalo de convergencia, la igualdad (30) no tiene sentido.
Ejemplo 7. Encuentra la suma de la serie de potencias.
Solución. Esta es una serie geométrica para la cual a= 1, un q= X. Por tanto, su suma es una función. 
. Una serie converge si , y es su intervalo de convergencia. Por lo tanto igualdad
es válido sólo para valores, aunque la función 
definido para todos los valores X, excepto X= 1.
Se puede demostrar que la suma de las series de potencias F(X) es continua y diferenciable en cualquier intervalo dentro del intervalo de convergencia, en particular en cualquier punto del intervalo de convergencia de la serie.
Presentemos teoremas sobre la diferenciación término por término y la integración de series de potencias.
Teorema 1. Las series de potencias (30) en el intervalo de su convergencia se pueden diferenciar término por término un número ilimitado de veces, y las series de potencias resultantes tienen el mismo radio de convergencia que la serie original, y sus sumas son respectivamente iguales a .
Teorema 2. La serie de potencias (30) se puede integrar término por término un número ilimitado de veces en el rango de 0 a X, si , y la serie de potencias resultante tienen el mismo radio de convergencia que la serie original, y sus sumas son correspondientemente iguales
Sea dada la función F(X), que debe expandirse a una serie de potencias, es decir representar en la forma (30):
La tarea es determinar los coeficientes. 
fila (30). Para ello, diferenciando la igualdad (30) término por término, encontramos consistentemente:
……………………………………………….. (31)
Suponiendo en las igualdades (30) y (31) X= 0, encontramos
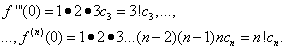
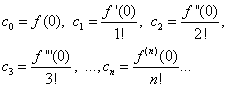
Sustituyendo las expresiones encontradas en la igualdad (30), obtenemos
(32)
Encontremos el desarrollo en serie de Maclaurin de algunas funciones elementales.
Ejemplo 8. Ampliar la función en una serie de Maclaurin
Solución. Las derivadas de esta función coinciden con la función misma:
Por lo tanto, cuando X= 0 tenemos
Sustituyendo estos valores en la fórmula (32), obtenemos la expansión deseada:
(33)
Esta serie converge en toda la recta numérica (su radio de convergencia).
16.1. Expansión de funciones elementales en series de Taylor y Maclaurin.Demostremos que si una función arbitraria se define en un conjunto 
, en las proximidades del punto 
tiene muchas derivadas y es la suma de una serie de potencias:
entonces puedes encontrar los coeficientes de esta serie.
Sustituyamos en una serie de potencias. 
. Entonces 
.
Encontremos la primera derivada de la función. 
:
En 
:
.
Para la segunda derivada obtenemos:
En 
:
.
Continuando con este procedimiento norte una vez que obtenemos: 
.
Así, obtuvimos una serie de potencias de la forma:
,
Lo que es llamado junto a taylor para función 
en las proximidades del punto 
.
Un caso especial de la serie de Taylor es serie maclaurin en 
:
El resto de la serie de Taylor (Maclaurin) se obtiene descartando la serie principal norte primeros miembros y se denota como 
. Entonces la función 
se puede escribir como una suma norte primeros miembros de la serie 
y el resto 
:,
.
El resto suele ser 
expresado en diferentes fórmulas.
Uno de ellos está en forma de Lagrange:
, Dónde 
.
.
Tenga en cuenta que en la práctica se utiliza con mayor frecuencia la serie de Maclaurin. Así, para escribir la función 
en forma de suma de series de potencias es necesario:
1) encuentre los coeficientes de la serie de Maclaurin (Taylor);
2) encontrar la región de convergencia de la serie de potencias resultante;
3) demostrar que esta serie converge a la función 
.
Teorema 1 (condición necesaria y suficiente para la convergencia de la serie de Maclaurin). Sea el radio de convergencia de la serie. 
. Para que esta serie converja en el intervalo 
funcionar 
, es necesario y suficiente que se cumpla la condición: 
en el intervalo especificado.
Teorema 2. Si derivadas de cualquier orden de una función 
en algún intervalo 
limitado en valor absoluto al mismo número METRO, eso es 
, entonces en este intervalo la función 
se puede ampliar a una serie de Maclaurin.
Ejemplo 1. Expandir en una serie de Taylor alrededor del punto. 
función.
Solución.
.
,;
,
;
,
;
,
.......................................................................................................................................
,
;
Región de convergencia 
.
Ejemplo 2. Expandir una función 
en una serie de Taylor alrededor de un punto 
.
Solución:
Encuentre el valor de la función y sus derivadas en 
.
,
;
,
;
...........……………………………
,
.
Pongamos estos valores en una fila. Obtenemos:
o 
.
Encontremos la región de convergencia de esta serie. Según la prueba de d'Alembert, una serie converge si
.
Por lo tanto, para cualquier 
este límite es menor que 1, por lo que el rango de convergencia de la serie será: 
.
Consideremos varios ejemplos de la expansión en serie de Maclaurin de funciones elementales básicas. Recordemos que la serie Maclaurin:
.
converge en el intervalo 
funcionar 
.
Tenga en cuenta que para expandir una función a una serie es necesario:
a) encuentre los coeficientes de la serie de Maclaurin para esta función;
b) calcular el radio de convergencia de la serie resultante;
c) demostrar que la serie resultante converge a la función 
.
Ejemplo 3. Considere la función. 
.
Solución.
Calculemos el valor de la función y sus derivadas en 
.
Entonces los coeficientes numéricos de la serie tienen la forma:
para cualquiera norte. Sustituyamos los coeficientes encontrados en la serie de Maclaurin y obtenemos: 
Encontremos el radio de convergencia de la serie resultante, a saber:
.
Por tanto, la serie converge en el intervalo 
.
Esta serie converge a la función 
para cualquier valor 
, porque en cualquier intervalo 
función 
y sus derivadas de valor absoluto están limitadas en número 
.
Ejemplo 4. Considere la función 
.
Solución.
:
Es fácil ver que las derivadas de orden par 
, y las derivadas son de orden impar. Sustituyamos los coeficientes encontrados en la serie de Maclaurin y obtenemos el desarrollo:
Encontremos el intervalo de convergencia de esta serie. Según el signo de d'Alembert:
para cualquiera 
. Por tanto, la serie converge en el intervalo 
.
Esta serie converge a la función 
, porque todas sus derivadas están limitadas a la unidad.
Ejemplo 5. 
.
Solución.
Encontremos el valor de la función y sus derivadas en 
:
Así, los coeficientes de esta serie: 
Y 
, por eso:
Al igual que en la fila anterior, el área de convergencia 
. La serie converge a la función. 
, porque todas sus derivadas están limitadas a la unidad.
Tenga en cuenta que la función 
expansión impar y en serie en potencias impares, función 
– par y expansión en una serie en potencias pares.
Ejemplo 6. Serie binomial: 
.
Solución.
Encontremos el valor de la función y sus derivadas en 
:
De esto se puede ver que:
Sustituyamos estos valores de coeficientes en la serie de Maclaurin y obtengamos la expansión de esta función en una serie de potencias:
Encontremos el radio de convergencia de esta serie:
Por tanto, la serie converge en el intervalo 
. En los puntos límite de 
Y 
una serie puede converger o no dependiendo del exponente 
.
La serie estudiada converge en el intervalo. 
funcionar 
, es decir, la suma de la serie 
en 
.
Ejemplo 7. Ampliemos la función en la serie de Maclaurin. 
.
Solución.
Para expandir esta función a una serie, usamos la serie binomial en 
. Obtenemos: 
Basándonos en la propiedad de las series de potencias (una serie de potencias se puede integrar en la región de su convergencia), encontramos la integral de los lados izquierdo y derecho de esta serie:
Encontremos el área de convergencia de esta serie: 
,
es decir, el área de convergencia de esta serie es el intervalo 
. Determinemos la convergencia de la serie en los extremos del intervalo. En 
. Esta serie es una serie armoniosa, es decir, diverge. En 
obtenemos una serie numérica con un término común 
.
La serie converge según la prueba de Leibniz. Por tanto, la región de convergencia de esta serie es el intervalo 
.
En los cálculos aproximados, las series de potencias juegan un papel extremadamente importante. Con su ayuda se han elaborado tablas de funciones trigonométricas, tablas de logaritmos, tablas de valores de otras funciones, que se utilizan en diversas áreas del conocimiento, por ejemplo, en teoría de probabilidades y estadística matemática. Además, la expansión de funciones en series de potencias es útil para su estudio teórico. El principal problema al utilizar series de potencias en cálculos aproximados es la cuestión de estimar el error al reemplazar la suma de una serie por la suma de sus primeras norte miembros.
Consideremos dos casos:
la función se expande a una serie de alternancia de signos;
la función se expande en una serie de signo constante.
Cálculo utilizando series alternas.Deja que la función 
expandido en una serie de potencias alternas. Luego, al calcular esta función para un valor específico 
obtenemos una serie numérica a la que podemos aplicar el criterio de Leibniz. De acuerdo con este criterio, si la suma de una serie se sustituye por la suma de sus primeras norte términos, entonces el error absoluto no excede el primer término del resto de esta serie, es decir: 
.
Ejemplo 8. Calcular 
con una precisión de 0,0001.
Solución.
Usaremos la serie Maclaurin para 
, sustituyendo el valor del ángulo en radianes:
Si comparamos el primer y segundo término de la serie con una precisión dada, entonces: .
Tercer plazo de ampliación:
menor que la precisión de cálculo especificada. Por lo tanto, para calcular 
basta con dejar dos términos de la serie, es decir
.
De este modo 
.
Ejemplo 9. Calcular 
con una precisión de 0,001.
Solución.
Usaremos la fórmula de la serie binomial. Para hacer esto, escribamos 
como: 
.
en esta expresión 
,
Comparemos cada uno de los términos de la serie con la precisión que se especifica. Está claro que 
. Por lo tanto, para calcular 
basta con dejar tres términos de la serie.
o 
.
Ejemplo 10. Calcular numero 
con una precisión de 0,001.
Solución.
En una fila para una función 
sustituyamos 
. Obtenemos:
Estimemos el error que surge al sustituir la suma de una serie por la suma de la primera 
miembros. Anotemos la desigualdad obvia:
eso es 2
