Los principales indicadores generalizadores de variación en las estadísticas son las dispersiones y las desviaciones estándar.
Dispersión esto significado aritmetico desviaciones al cuadrado de cada valor característico del promedio general. La varianza generalmente se denomina cuadrado medio de las desviaciones y se denota por 2. Dependiendo de los datos de origen, la varianza se puede calcular utilizando la media aritmética simple o ponderada:
varianza no ponderada (simple);
 varianza ponderada.
varianza ponderada.
Desviación Estándar esta es una característica generalizadora de los tamaños absolutos variaciones signos en conjunto. Se expresa en las mismas unidades de medida que el atributo (en metros, toneladas, porcentaje, hectáreas, etc.).
La desviación estándar es la raíz cuadrada de la varianza y se denota por :
 desviación estándar no ponderada;
desviación estándar no ponderada;
 desviación estándar ponderada.
desviación estándar ponderada.
La desviación estándar es una medida de la confiabilidad de la media. Cuanto menor sea la desviación estándar, mejor refleja la media aritmética a toda la población representada.
El cálculo de la desviación estándar va precedido del cálculo de la varianza.
El procedimiento para calcular la varianza ponderada es el siguiente:
1) determinar la media aritmética ponderada:
2) calcular las desviaciones de las opciones del promedio:
3) eleva al cuadrado la desviación de cada opción del promedio:
4) multiplicar los cuadrados de las desviaciones por pesos (frecuencias):
5) resumir los productos resultantes:
![]()
6) la cantidad resultante se divide por la suma de los pesos:

Ejemplo 2.1

Calculemos la media aritmética ponderada:

Los valores de las desviaciones de la media y sus cuadrados se presentan en la tabla. Definamos la varianza:

La desviación estándar será igual a:

Si los datos de origen se presentan en forma de intervalo serie de distribución , primero debe determinar el valor discreto del atributo y luego aplicar el método descrito.
Ejemplo 2.2
Muestremos el cálculo de la varianza para una serie de intervalos utilizando datos sobre la distribución del área sembrada de una finca colectiva según el rendimiento del trigo.

La media aritmética es:

Calculemos la varianza:

6.3. Cálculo de la varianza mediante una fórmula basada en datos individuales.
Técnica de cálculo variaciones complejo y con grandes valores de opciones y frecuencias puede resultar engorroso. Los cálculos se pueden simplificar utilizando las propiedades de dispersión.
La dispersión tiene las siguientes propiedades.
1. Reducir o aumentar los pesos (frecuencias) de una característica variable un cierto número de veces no cambia la dispersión.
2. Disminuir o aumentar cada valor de una característica en la misma cantidad constante A no cambia la dispersión.
3. Disminuir o aumentar cada valor de una característica un cierto número de veces. k respectivamente reduce o aumenta la varianza en k 2 veces Desviación Estándar en k una vez.
4. La dispersión de una característica con respecto a un valor arbitrario es siempre mayor que la dispersión con respecto a la media aritmética por cuadrado de la diferencia entre los valores promedio y arbitrarios:
![]()
Si A 0, entonces llegamos a la siguiente igualdad:
es decir, la varianza de la característica es igual a la diferencia entre el cuadrado medio de los valores característicos y el cuadrado de la media.
Cada propiedad se puede utilizar de forma independiente o en combinación con otras al calcular la varianza.
El procedimiento para calcular la varianza es simple:
1) determinar significado aritmetico :
2) eleva al cuadrado la media aritmética:

3) eleva al cuadrado la desviación de cada variante de la serie:
X i 2 .
4) encuentra la suma de cuadrados de las opciones:
5) dividir la suma de los cuadrados de las opciones por su número, es decir determinar el cuadrado promedio:
6) determinar la diferencia entre el cuadrado medio de la característica y el cuadrado de la media:
Ejemplo 3.1 Se dispone de los siguientes datos sobre la productividad de los trabajadores:

Hagamos los siguientes cálculos:
![]()
Pasos
Calcular la varianza de la muestra
-
Registre los valores de la muestra. En la mayoría de los casos, los estadísticos sólo tienen acceso a muestras de poblaciones específicas. Por ejemplo, como regla general, los estadísticos no analizan el costo de mantener la totalidad de todos los automóviles en Rusia, sino que analizan una muestra aleatoria de varios miles de automóviles. Esta muestra ayudará a determinar el costo promedio de un automóvil, pero lo más probable es que el valor resultante esté lejos del real.
- Por ejemplo, analicemos la cantidad de bollos vendidos en una cafetería durante 6 días, tomados en orden aleatorio. La muestra se ve así: 17, 15, 23, 7, 9, 13. Esta es una muestra, no una población, porque no tenemos datos sobre los bollos vendidos cada día que la cafetería está abierta.
- Si le dan una población en lugar de una muestra de valores, continúe con la siguiente sección.
-
Escriba una fórmula para calcular la varianza muestral. La dispersión es una medida de la dispersión de valores de una determinada cantidad. Cuanto más cerca esté el valor de la varianza de cero, más cerca se agruparán los valores. Cuando trabaje con una muestra de valores, utilice la siguiente fórmula para calcular la varianza:
- s 2 (\displaystyle s^(2)) = ∑[(x yo (\displaystyle x_(i))- X) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2))– esto es dispersión. La dispersión se mide en unidades cuadradas.
- x yo (\displaystyle x_(i))– cada valor de la muestra.
- x yo (\displaystyle x_(i)) necesitas restar x̅, elevarlo al cuadrado y luego sumar los resultados.
- x̅ – media muestral (media muestral).
- n – número de valores en la muestra.
-
Calcule la media muestral. Se denota como x̅. La media muestral se calcula como una media aritmética simple: sume todos los valores de la muestra y luego divida el resultado por el número de valores de la muestra.
- En nuestro ejemplo, suma los valores de la muestra: 15 + 17 + 23 + 7 + 9 + 13 = 84
Ahora divide el resultado por el número de valores de la muestra (en nuestro ejemplo son 6): 84 ÷ 6 = 14.
Media muestral x̅ = 14. - La media muestral es el valor central alrededor del cual se distribuyen los valores de la muestra. Si los valores de la muestra se agrupan alrededor de la media muestral, entonces la varianza es pequeña; de lo contrario, la variación es grande.
- En nuestro ejemplo, suma los valores de la muestra: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
Reste la media muestral de cada valor de la muestra. Ahora calcula la diferencia x yo (\displaystyle x_(i))- x̅, donde x yo (\displaystyle x_(i))– cada valor de la muestra. Cada resultado obtenido indica el grado de desviación de un valor particular de la media muestral, es decir, qué tan lejos está este valor de la media muestral.
- En nuestro ejemplo:
x 1 (\displaystyle x_(1))- x = 17 - 14 = 3
x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
x 3 (\displaystyle x_(3))- x = 23 - 14 = 9
x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
x6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1 - La exactitud de los resultados obtenidos es fácil de comprobar, ya que su suma debe ser igual a cero. Esto está relacionado con la definición de promedio, ya que los valores negativos (distancias del promedio a valores más pequeños) se compensan completamente con valores positivos (distancias del promedio a valores más grandes).
- En nuestro ejemplo:
-
Como se señaló anteriormente, la suma de las diferencias x yo (\displaystyle x_(i))- x̅ debe ser igual a cero. Esto significa que la varianza media es siempre cero, lo que no da ninguna idea sobre la dispersión de los valores de una determinada cantidad. Para resolver este problema, eleva al cuadrado cada diferencia x yo (\displaystyle x_(i))- X. Esto dará como resultado que solo obtenga números positivos, que nunca sumarán 0.
- En nuestro ejemplo:
(x 1 (\displaystyle x_(1))- X) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
(x 2 (\displaystyle (x_(2))- X) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
9 2 = 81
(-7) 2 = 49
(-5) 2 = 25
(-1) 2 = 1 - Encontraste el cuadrado de la diferencia - x̅) 2 (\displaystyle ^(2)) para cada valor de la muestra.
- En nuestro ejemplo:
-
Calcula la suma de los cuadrados de las diferencias. Es decir, encuentra esa parte de la fórmula que se escribe así: ∑[( x yo (\displaystyle x_(i))- X) 2 (\displaystyle ^(2))]. Aquí el signo Σ significa la suma de diferencias al cuadrado para cada valor x yo (\displaystyle x_(i)) en la muestra. Ya has encontrado las diferencias al cuadrado. (x yo (\displaystyle (x_(i))- X) 2 (\displaystyle ^(2)) para cada valor x yo (\displaystyle x_(i)) en la muestra; ahora solo suma estos cuadrados.
- En nuestro ejemplo: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
-
Divida el resultado por n - 1, donde n es el número de valores de la muestra. Hace algún tiempo, para calcular la varianza muestral, los estadísticos simplemente dividían el resultado entre n; en este caso obtendrás la media de la varianza al cuadrado, que es ideal para describir la varianza de una muestra determinada. Pero recuerde que cualquier muestra es sólo una pequeña parte de la población de valores. Si toma otra muestra y realiza los mismos cálculos, obtendrá un resultado diferente. Resulta que dividir por n - 1 (en lugar de solo n) da una estimación más precisa de la varianza de la población, que es lo que le interesa. La división por n – 1 se ha vuelto común, por lo que se incluye en la fórmula para calcular la varianza muestral.
- En nuestro ejemplo, la muestra incluye 6 valores, es decir, n = 6.
Varianza muestral = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
- En nuestro ejemplo, la muestra incluye 6 valores, es decir, n = 6.
-
La diferencia entre varianza y desviación estándar. Tenga en cuenta que la fórmula contiene un exponente, por lo que la dispersión se mide en unidades cuadradas del valor que se analiza. A veces es bastante difícil operar con tal magnitud; en tales casos, utilice la desviación estándar, que es igual a la raíz cuadrada de la varianza. Es por eso que la varianza muestral se denota como s 2 (\displaystyle s^(2)), y la desviación estándar de la muestra es como s (\displaystyle s).
- En nuestro ejemplo, la desviación estándar de la muestra es: s = √33,2 = 5,76.
Calcular la varianza de la población
-
Analizar algún conjunto de valores. El conjunto incluye todos los valores de la cantidad considerada. Por ejemplo, si estudia la edad de los residentes de la región de Leningrado, entonces la totalidad incluye la edad de todos los residentes de esta región. Cuando se trabaja con una población, se recomienda crear una tabla e ingresar en ella los valores de la población. Considere el siguiente ejemplo:
- En cierta habitación hay 6 acuarios. Cada acuario contiene la siguiente cantidad de peces:
x 1 = 5 (\displaystyle x_(1)=5)
x 2 = 5 (\displaystyle x_(2)=5)
x 3 = 8 (\displaystyle x_(3)=8)
x 4 = 12 (\displaystyle x_(4)=12)
x 5 = 15 (\displaystyle x_(5)=15)
x6 = 18 (\displaystyle x_(6)=18)
- En cierta habitación hay 6 acuarios. Cada acuario contiene la siguiente cantidad de peces:
-
Escribe una fórmula para calcular la varianza poblacional. Dado que la población incluye todos los valores de una determinada cantidad, la siguiente fórmula le permite obtener el valor exacto de la varianza de la población. Para distinguir la varianza de la población de la varianza de la muestra (que es sólo una estimación), los estadísticos utilizan varias variables:
- σ 2 (\displaystyle ^(2)) = (∑(x yo (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)))/norte
- σ 2 (\displaystyle ^(2))– dispersión de la población (léase “sigma cuadrado”). La dispersión se mide en unidades cuadradas.
- x yo (\displaystyle x_(i))– cada valor en su totalidad.
- Σ – signo de suma. Es decir, de cada valor x yo (\displaystyle x_(i)) necesitas restar μ, elevarlo al cuadrado y luego sumar los resultados.
- μ – media poblacional.
- n – número de valores en la población.
-
Calcula la media poblacional. Cuando se trabaja con una población, su media se denota como μ (mu). La media poblacional se calcula como una media aritmética simple: suma todos los valores de la población y luego divide el resultado por el número de valores de la población.
- Tenga en cuenta que los promedios no siempre se calculan como media aritmética.
- En nuestro ejemplo, la media poblacional: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
-
Reste la media poblacional de cada valor de la población. Cuanto más cerca esté el valor de la diferencia de cero, más cerca estará el valor específico de la media poblacional. Encuentra la diferencia entre cada valor de la población y su media y tendrás una primera idea de la distribución de valores.
- En nuestro ejemplo:
x 1 (\displaystyle x_(1))- µ = 5 - 10,5 = -5,5
x 2 (\displaystyle x_(2))- µ = 5 - 10,5 = -5,5
x 3 (\displaystyle x_(3))- µ = 8 - 10,5 = -2,5
x 4 (\displaystyle x_(4))- µ = 12 - 10,5 = 1,5
x 5 (\displaystyle x_(5))- µ = 15 - 10,5 = 4,5
x6 (\displaystyle x_(6))- µ = 18 - 10,5 = 7,5
- En nuestro ejemplo:
-
Cuadra cada resultado obtenido. Los valores de diferencia serán tanto positivos como negativos; Si estos valores se trazan en una recta numérica, estarán a la derecha y a la izquierda de la media poblacional. Esto no es bueno para calcular la varianza porque los números positivos y negativos se cancelan entre sí. Así que eleva al cuadrado cada diferencia para obtener números exclusivamente positivos.
- En nuestro ejemplo:
(x yo (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) para cada valor de población (de i = 1 a i = 6):
(-5,5)2 (\displaystyle ^(2)) = 30,25
(-5,5)2 (\displaystyle ^(2)), Dónde x norte (\displaystyle x_(n))– el último valor de la población. - Para calcular el valor promedio de los resultados obtenidos, es necesario encontrar su suma y dividirla por n:(( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x norte (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2)))/norte
- Ahora escribamos la explicación anterior usando variables: (∑( x yo (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n y obtenga una fórmula para calcular la varianza poblacional.
- En nuestro ejemplo:
Si la población se divide en grupos según la característica que se está estudiando, entonces se pueden calcular los siguientes tipos de varianza para esta población: total, grupo (dentro del grupo), promedio del grupo (promedio dentro del grupo), intergrupo.
Inicialmente, calcula el coeficiente de determinación, que muestra qué parte de la variación total del rasgo en estudio es variación intergrupal, es decir debido a la característica de agrupación:
La relación de correlación empírica caracteriza la estrecha conexión entre la agrupación (factorial) y las características de desempeño.
La relación de correlación empírica puede tomar valores de 0 a 1.
Para evaluar la cercanía de la conexión basándose en la relación de correlación empírica, puede utilizar las relaciones de Chaddock:
Ejemplo 4. Se dispone de los siguientes datos sobre el desempeño del trabajo por parte de organizaciones de diseño y encuesta de diversas formas de propiedad:
Definir:
1) varianza total;
2) variaciones grupales;
3) el promedio de las varianzas del grupo;
4) varianza intergrupal;
5) varianza total basada en la regla para sumar varianzas;
6) coeficiente de determinación y relación de correlación empírica.
Sacar conclusiones.
Solución:
1. Determinemos el volumen medio de trabajo realizado por empresas de dos formas de propiedad:
Calculemos la varianza total:
![]()
2. Determinar los promedios del grupo:
![]() millones de rublos;
millones de rublos;
![]() millones de rublos
millones de rublos
Variaciones de grupo:
![]() ;
;
3. Calcule el promedio de las variaciones del grupo:
4. Determinemos la varianza intergrupal:
5. Calcule la varianza total según la regla para sumar varianzas:
6. Determinemos el coeficiente de determinación:
![]() .
.
Así, el volumen de trabajo realizado por las organizaciones de diseño y encuesta depende en un 22% de la forma de propiedad de las empresas.
El índice de correlación empírica se calcula mediante la fórmula
![]() .
.
El valor del indicador calculado indica que la dependencia del volumen de trabajo de la forma de propiedad de la empresa es pequeña.
Ejemplo 5. Como resultado de un relevamiento de la disciplina tecnológica de las áreas productivas, se obtuvieron los siguientes datos:
Determinar el coeficiente de determinación.
La expectativa y la varianza son las características numéricas más utilizadas de una variable aleatoria. Caracterizan las características más importantes de la distribución: su posición y grado de dispersión. En muchos problemas prácticos, una característica completa y exhaustiva de una variable aleatoria (la ley de distribución) no se puede obtener en absoluto o no es necesaria en absoluto. En estos casos, uno se limita a una descripción aproximada de una variable aleatoria utilizando características numéricas.
El valor esperado a menudo se denomina simplemente valor promedio de una variable aleatoria. La dispersión de una variable aleatoria es una característica de la dispersión, la dispersión de una variable aleatoria alrededor de su expectativa matemática.
Expectativa de una variable aleatoria discreta
Acerquémonos al concepto de expectativa matemática, basándonos primero en la interpretación mecánica de la distribución de una variable aleatoria discreta. Sea la unidad de masa distribuida entre los puntos del eje x. X1 , X 2 , ..., X norte, y cada punto material tiene una masa correspondiente de pag1 , pag 2 , ..., pag norte. Es necesario seleccionar un punto en el eje de abscisas, caracterizando la posición de todo el sistema de puntos materiales, teniendo en cuenta sus masas. Es natural tomar como tal punto el centro de masa de un sistema de puntos materiales. Este es el promedio ponderado de la variable aleatoria. X, a la que la abscisa de cada punto Xi entra con un “peso” igual a la probabilidad correspondiente. El valor medio de la variable aleatoria obtenido de esta forma. X se llama expectativa matemática.
La expectativa matemática de una variable aleatoria discreta es la suma de los productos de todos sus valores posibles y las probabilidades de estos valores:

Ejemplo 1. Se ha organizado una lotería en la que todos ganan. Hay 1000 ganancias, de las cuales 400 son 10 rublos. 300 - 20 rublos cada uno. 200 - 100 rublos cada uno. y 100 - 200 rublos cada uno. ¿Cuál es la ganancia promedio de alguien que compra un boleto?
Solución. Encontraremos las ganancias promedio si dividimos la cantidad total de ganancias, que es 10*400 + 20*300 + 100*200 + 200*100 = 50 000 rublos, por 1000 (cantidad total de ganancias). Entonces obtenemos 50000/1000 = 50 rublos. Pero la expresión para calcular las ganancias promedio se puede presentar de la siguiente forma:

Por otro lado, en estas condiciones, la cantidad ganadora es una variable aleatoria, que puede tomar valores de 10, 20, 100 y 200 rublos. con probabilidades iguales a 0,4, respectivamente; 0,3; 0,2; 0.1. Por lo tanto, la ganancia promedio esperada es igual a la suma de los productos del tamaño de las ganancias y la probabilidad de recibirlas.
Ejemplo 2. El editor decidió publicar un nuevo libro. Planea vender el libro por 280 rublos, de los cuales él mismo recibirá 200, 50 - la librería y 30 - el autor. La tabla proporciona información sobre los costos de publicar un libro y la probabilidad de vender una cierta cantidad de copias del libro.
Encuentre la ganancia esperada del editor.
Solución. La variable aleatoria “beneficio” es igual a la diferencia entre los ingresos por ventas y el costo de los gastos. Por ejemplo, si se venden 500 copias de un libro, los ingresos por la venta son 200 * 500 = 100 000 y el costo de publicación es 225 000 rublos. Por tanto, el editor se enfrenta a una pérdida de 125.000 rublos. La siguiente tabla resume los valores esperados de la variable aleatoria - beneficio:
| Número | Ganancia Xi | Probabilidad pagi | Xi pag i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Así, obtenemos la expectativa matemática del beneficio del editor:
![]() .
.
Ejemplo 3. Probabilidad de acertar de un solo tiro. pag= 0,2. Determinar el consumo de proyectiles que proporcionen una expectativa matemática del número de impactos igual a 5.
Solución. A partir de la misma fórmula matemática de expectativa que hemos usado hasta ahora, expresamos X- consumo de cáscara:
![]() .
.
Ejemplo 4. Determinar la expectativa matemática de una variable aleatoria. X número de aciertos con tres disparos, si la probabilidad de acierto con cada disparo pag = 0,4 .
Sugerencia: encuentre la probabilidad de valores de variables aleatorias por La fórmula de Bernoulli. .
Propiedades de la expectativa matemática
Consideremos las propiedades de la expectativa matemática.
Propiedad 1. La expectativa matemática de un valor constante es igual a esta constante:
Propiedad 2. El factor constante se puede sacar del signo de expectativa matemática:
![]()
Propiedad 3. La expectativa matemática de la suma (diferencia) de variables aleatorias es igual a la suma (diferencia) de sus expectativas matemáticas:
Propiedad 4. La expectativa matemática de un producto de variables aleatorias es igual al producto de sus expectativas matemáticas:
Propiedad 5. Si todos los valores de una variable aleatoria X disminuir (aumentar) en el mismo número CON, entonces su expectativa matemática disminuirá (aumentará) en el mismo número:
![]()
Cuando no puedes limitarte solo a las expectativas matemáticas
En la mayoría de los casos, sólo la expectativa matemática no puede caracterizar suficientemente una variable aleatoria.
Deja que las variables aleatorias X Y Y están dadas por las siguientes leyes de distribución:
| Significado X | Probabilidad |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Significado Y | Probabilidad |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Las expectativas matemáticas de estas cantidades son las mismas: iguales a cero:


Sin embargo, sus patrones de distribución son diferentes. Valor aleatorio X sólo puede tomar valores que difieren poco de la expectativa matemática, y la variable aleatoria Y Puede tomar valores que se desvíen significativamente de la expectativa matemática. Un ejemplo similar: el salario medio no permite juzgar la proporción de trabajadores con salarios altos y bajos. En otras palabras, a partir de la expectativa matemática no se puede juzgar qué desviaciones de ella, al menos en promedio, son posibles. Para hacer esto, necesitas encontrar la varianza de la variable aleatoria.
Varianza de una variable aleatoria discreta
Diferencia variable aleatoria discreta X se llama expectativa matemática del cuadrado de su desviación de la expectativa matemática:

La desviación estándar de una variable aleatoria. X el valor aritmético de la raíz cuadrada de su varianza se llama:
![]() .
.
Ejemplo 5. Calcular varianzas y desviaciones estándar de variables aleatorias. X Y Y, cuyas leyes de distribución se dan en las tablas anteriores.
Solución. Expectativas matemáticas de variables aleatorias. X Y Y, como se encontró arriba, son iguales a cero. Según la fórmula de dispersión en mi(X)=mi(y)=0 obtenemos:


Entonces las desviaciones estándar de variables aleatorias. X Y Y constituir
![]() .
.
Así, con las mismas expectativas matemáticas, la varianza de la variable aleatoria X muy pequeña, pero una variable aleatoria Y- significativo. Esto es consecuencia de diferencias en su distribución.
Ejemplo 6. El inversor tiene 4 proyectos de inversión alternativos. La tabla resume el beneficio esperado en estos proyectos con la probabilidad correspondiente.
| Proyecto 1 | Proyecto 2 | Proyecto 3 | Proyecto 4 |
| 500, PAG=1 | 1000, PAG=0,5 | 500, PAG=0,5 | 500, PAG=0,5 |
| 0, PAG=0,5 | 1000, PAG=0,25 | 10500, PAG=0,25 | |
| 0, PAG=0,25 | 9500, PAG=0,25 |
Encuentre la expectativa matemática, la varianza y la desviación estándar para cada alternativa.
Solución. Muestremos cómo se calculan estos valores para la tercera alternativa:
La tabla resume los valores encontrados para todas las alternativas.
Todas las alternativas tienen las mismas expectativas matemáticas. Esto significa que a la larga todos tienen los mismos ingresos. La desviación estándar se puede interpretar como una medida del riesgo: cuanto mayor es, mayor es el riesgo de la inversión. Un inversor que no quiera correr mucho riesgo elegirá el proyecto 1 ya que tiene la desviación estándar más pequeña (0). Si el inversor prefiere el riesgo y una alta rentabilidad en un período corto, elegirá el proyecto con la mayor desviación estándar: el proyecto 4.
Propiedades de dispersión
Presentemos las propiedades de la dispersión.
Propiedad 1. La varianza de un valor constante es cero:
Propiedad 2. El factor constante se puede sacar del signo de dispersión elevándolo al cuadrado:
![]() .
.
Propiedad 3. La varianza de una variable aleatoria es igual a la expectativa matemática del cuadrado de este valor, del cual se resta el cuadrado de la expectativa matemática del valor mismo:
![]() ,
,
Dónde ![]() .
.
Propiedad 4. La varianza de la suma (diferencia) de variables aleatorias es igual a la suma (diferencia) de sus varianzas:
Ejemplo 7. Se sabe que una variable aleatoria discreta X toma sólo dos valores: −3 y 7. Además, se conoce la expectativa matemática: mi(X) = 4 . Encuentra la varianza de una variable aleatoria discreta.
Solución. Denotemos por pag la probabilidad con la que una variable aleatoria toma un valor X1 = −3 . Entonces la probabilidad del valor X2 = 7 será 1 - pag. Derivemos la ecuación para la expectativa matemática:
mi(X) = X 1 pag + X 2 (1 − pag) = −3pag + 7(1 − pag) = 4 ,
donde obtenemos las probabilidades: pag= 0,3 y 1 − pag = 0,7 .
Ley de distribución de una variable aleatoria:
| X | −3 | 7 |
| pag | 0,3 | 0,7 |
Calculamos la varianza de esta variable aleatoria usando la fórmula de la propiedad 3 de dispersión:
D(X) = 2,7 + 34,3 − 16 = 21 .
Encuentre usted mismo la expectativa matemática de una variable aleatoria y luego observe la solución
Ejemplo 8. Variable aleatoria discreta X toma sólo dos valores. Acepta el mayor de los valores 3 con probabilidad 0,4. Además, se conoce la varianza de la variable aleatoria. D(X) = 6 . Encuentre la expectativa matemática de una variable aleatoria.
Ejemplo 9. En una urna hay 6 bolas blancas y 4 negras. De la urna se extraen 3 bolas. El número de bolas blancas entre las bolas extraídas es una variable aleatoria discreta. X. Encuentre la expectativa matemática y la varianza de esta variable aleatoria.
Solución. Valor aleatorio X puede tomar valores 0, 1, 2, 3. Las probabilidades correspondientes se pueden calcular a partir de regla de multiplicación de probabilidad. Ley de distribución de una variable aleatoria:
| X | 0 | 1 | 2 | 3 |
| pag | 1/30 | 3/10 | 1/2 | 1/6 |
De ahí la expectativa matemática de esta variable aleatoria:
METRO(X) = 3/10 + 1 + 1/2 = 1,8 .
La varianza de una variable aleatoria dada es:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Expectativa y varianza de una variable aleatoria continua.
Para una variable aleatoria continua, la interpretación mecánica de la expectativa matemática conservará el mismo significado: el centro de masa de una unidad de masa distribuida continuamente en el eje x con densidad F(X). A diferencia de una variable aleatoria discreta, cuyo argumento de función Xi cambia abruptamente; para una variable aleatoria continua, el argumento cambia continuamente. Pero la expectativa matemática de una variable aleatoria continua también está relacionada con su valor promedio.
Para encontrar la expectativa matemática y la varianza de una variable aleatoria continua, necesitas encontrar integrales definidas . Si se da la función de densidad de una variable aleatoria continua, entonces entra directamente en el integrando. Si se da una función de distribución de probabilidad, al diferenciarla, es necesario encontrar la función de densidad.
La media aritmética de todos los valores posibles de una variable aleatoria continua se llama expectativa matemática, denotado por o .
Para datos agrupados varianza residual- promedio de variaciones intragrupo:Donde σ 2 j es la varianza intragrupo del jésimo grupo.
Para datos desagrupados varianza residual– medida de la precisión de la aproximación, es decir aproximación de la línea de regresión a los datos originales: 
donde y(t) – pronóstico según la ecuación de tendencia; y t – serie dinámica inicial; n – número de puntos; p – número de coeficientes de la ecuación de regresión (número de variables explicativas).
En este ejemplo se llama estimador de varianza insesgado.
Ejemplo No. 1. La distribución de los trabajadores de tres empresas de una asociación según categorías arancelarias se caracteriza por los siguientes datos:
| Categoría arancelaria del trabajador | Número de trabajadores en la empresa. | ||
| empresa 1 | empresa 2 | empresa 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Definir:
1. variación para cada empresa (variaciones intragrupo);
2. el promedio de las variaciones dentro del grupo;
3. dispersión intergrupal;
4. variación total.
Solución.
Antes de empezar a solucionar el problema, es necesario averiguar qué característica es efectiva y cuál es factorial. En el ejemplo que nos ocupa, el atributo resultante es “Categoría arancelaria” y el atributo del factor es “Número (nombre) de la empresa”.
Luego tenemos tres grupos (empresas), para los cuales es necesario calcular el promedio del grupo y las variaciones intragrupo:

| Compañía | promedio del grupo, | Variación dentro del grupo, |
| 1 | 4 | 1,8 |
El promedio de las varianzas dentro del grupo ( varianza residual) se calculará mediante la fórmula:

donde puedes calcular:

o:

Entonces:
La varianza total será igual a: s 2 = 1,6 + 0 = 1,6.
La varianza total también se puede calcular utilizando una de las dos fórmulas siguientes:
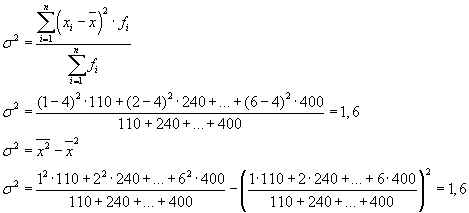
Al resolver problemas prácticos, a menudo uno tiene que lidiar con una característica que toma sólo dos valores alternativos. En este caso, no estamos hablando del peso de un valor particular de una característica, sino de su participación en el agregado. Si la proporción de unidades de población que poseen la característica que se está estudiando se denota por " R", y los que no tienen - a través de " q", entonces la varianza se puede calcular usando la fórmula:
s2 = p×q
Ejemplo No. 2. Con base en los datos de producción de seis trabajadores en un equipo, determine la varianza intergrupal y evalúe el impacto del turno de trabajo en su productividad laboral si la varianza total es 12,2.
| Trabajador del equipo no. | Producción de trabajadores, uds. | |
| en el primer turno | en el segundo turno | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Solución. Datos iniciales
| X | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | Total |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Total | 31 | 33 | 37 | 37 | 40 | 38 |
Luego tenemos 6 grupos para los cuales es necesario calcular la media grupal y las varianzas intragrupo.
1. Encuentra los valores promedio de cada grupo..
2. Encuentra el cuadrado medio de cada grupo..
Resumamos los resultados del cálculo en una tabla:
| Número de grupo | Promedio del grupo | Variación dentro del grupo |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Variación dentro del grupo caracteriza el cambio (variación) de la característica estudiada (resultante) dentro de un grupo bajo la influencia de todos los factores sobre él, excepto el factor subyacente a la agrupación:
El promedio de las variaciones intragrupo se calculará mediante la fórmula:
4. varianza intergrupal caracteriza el cambio (variación) de la característica estudiada (resultante) bajo la influencia de un factor (característica factorial) que forma la base del grupo.
Definimos la varianza intergrupal como:
Dónde
Entonces
varianza total caracteriza el cambio (variación) de la característica estudiada (resultante) bajo la influencia de todos los factores (características factoriales) sin excepción. Según las condiciones del problema, es igual a 12,2.
Relación de correlación empírica Mide qué parte de la variabilidad total de la característica resultante es causada por el factor que se está estudiando. Esta es la relación entre la varianza del factor y la varianza total:
Definimos la relación de correlación empírica:
Las conexiones entre características pueden ser débiles y fuertes (estrechas). Sus criterios se evalúan según la escala de Chaddock:
0,1 0,3 0,5 0,7 0,9 En nuestro ejemplo, la relación entre el rasgo Y y el factor X es débil
Coeficiente de determinación.
Determinemos el coeficiente de determinación:
Así, el 0,67% de la variación se debe a diferencias entre rasgos, y el 99,37% se debe a otros factores.
Conclusión: en este caso, la producción de los trabajadores no depende del trabajo en un turno específico, es decir la influencia del turno de trabajo en su productividad laboral no es significativa y se debe a otros factores.
Ejemplo No. 3. Con base en los datos sobre los salarios promedio y las desviaciones al cuadrado de su valor para dos grupos de trabajadores, encuentre la varianza total aplicando la regla de sumar varianzas:
Solución:Promedio de variaciones dentro del grupo
Definimos la varianza intergrupal como:
La varianza total será: 480 + 13824 = 14304








