Lorsqu'on demande aux gens la différence entre une sphère et une balle, beaucoup haussent simplement les épaules, pensant qu'il s'agit en fait de la même chose (analogie avec un cercle et un cercle). En effet, est-ce que nous connaissons tous bien la géométrie grâce au programme scolaire et pouvons-nous immédiatement répondre à cette question ? Une sphère présente certaines différences par rapport à une balle, que non seulement les écoliers doivent connaître afin d'obtenir une bonne note pour leurs connaissances démontrées, mais aussi de nombreuses autres personnes, par exemple, dont le travail est directement lié aux dessins.

Définition

Balle– l’ensemble de tous les points de l’espace. Tous ces points sont situés du centre du corps géométrique à une distance qui n'est pas supérieure à une distance donnée. Cette distance elle-même est appelée rayon. Une boule, en tant que corps géométrique, est formée comme suit : un demi-cercle tourne près de son diamètre. Quant à la sphère, c'est la surface de la balle (par exemple, une balle fermée l'inclut, une balle ouverte ne l'inclut pas). Le calcul de l’aire ou du volume d’une balle implique des formules géométriques entières très complexes, malgré l’apparente simplicité de la figure géométrique elle-même.

Sphère, comme indiqué ci-dessus, est la surface de la balle, sa coque. Tous les points de l'espace sont équidistants du centre de la sphère. Quant au rayon d'un corps géométrique, on l'appelle tout segment dont un point est directement le centre de la sphère, et l'autre peut être situé en n'importe quel point de la surface. On peut dire qu'une sphère est la coque d'une balle sans aucun contenu (des exemples plus précis seront donnés ci-dessous). Tout comme une balle, une sphère est un corps de révolution. À propos, beaucoup se demandent également quelle est la différence entre un cercle et un cercle d'une sphère et une balle. Tout est simple ici : dans le premier cas, ce sont des figures dans un plan, dans le second, dans l'espace.

Comparaison

On a déjà dit qu'une sphère est la surface d'une balle, ce qui permet déjà de parler d'un signe significatif de différence. La différence entre les deux corps géométriques s’observe sous d’autres aspects :

Toutes les pointes de la balle sont à la même distance du centre, tandis que le corps est limité par la surface (une sphère vide à l'intérieur). Autrement dit, la sphère est creuse. Habituellement, pour faciliter la compréhension, un exemple simple est donné avec un ballon et une boule de billard. Ces deux objets sont appelés boules, mais dans le premier cas, nous avons affaire à une sphère et dans le second à une boule à part entière avec son contenu à l'intérieur.
Une sphère a sa propre aire, mais elle n’a pas de volume. Une sphère est à l’opposé : son volume peut être calculé, alors qu’elle n’a pas d’aire. Certains diront que c'est le principal signe de différence, mais il n'apparaît que s'il est nécessaire de faire quelques calculs (formules géométriques complexes). Par conséquent, la principale différence est que la sphère est creuse et que la balle est un corps avec un contenu à l'intérieur.
Une autre différence réside dans le rayon. Par exemple, le rayon d’une sphère n’est pas seulement la distance des points au centre. Un rayon peut être n'importe quel segment reliant un point d'une sphère à son centre. Tous ces segments sont égaux les uns aux autres. Quant à la balle, les points qui se trouvent à l'intérieur sont éloignés du centre de moins d'un rayon (précisément à cause de la sphère qui la délimite).

Site Web des conclusions

Une sphère est creuse, tandis qu'une boule est un corps rempli à l'intérieur. Par exemple, un ballon est une sphère, une boule de billard est une boule à part entière.
Une sphère a une aire et pas de volume, mais une sphère fait le contraire.
La troisième différence est la mesure du rayon de deux corps géométriques.

Définition.

Sphère (surface du ballon) est l’ensemble de tous les points dans l’espace tridimensionnel qui sont à la même distance d’un point, appelé centre de la sphère(À PROPOS DE).

Une sphère peut être décrite comme une figure tridimensionnelle formée en faisant tourner un cercle autour de son diamètre de 180° ou un demi-cercle autour de son diamètre de 360°.

Définition.

Balle est l'ensemble de tous les points dans l'espace tridimensionnel, dont la distance ne dépasse pas une certaine distance jusqu'à un point appelé centre du ballon(O) (l'ensemble de tous les points de l'espace tridimensionnel limité par une sphère).

Une balle peut être décrite comme une figure tridimensionnelle formée en faisant tourner un cercle autour de son diamètre de 180° ou un demi-cercle autour de son diamètre de 360°.

Définition. Rayon de la sphère (balle)(R) est la distance du centre de la sphère (balle) Ô vers n'importe quel point de la sphère (surface de la balle).

Définition. Diamètre de la sphère (boule)(D) est un segment reliant deux points d'une sphère (la surface d'une balle) et passant par son centre.

Formule. Volume de la sphère:

V=	4	π R 3 =	1	π D 3
	3		6

Formule. Superficie d'une sphèreà travers le rayon ou le diamètre :

S = 4π R 2 = π D 2

Équation de sphère

1. Équation d'une sphère de rayon R et de centre à l'origine du repère cartésien:

x 2 + y 2 + z 2 = R 2

2. Équation d'une sphère de rayon R et de centre en un point de coordonnées (x 0, y 0, z 0) dans le système de coordonnées cartésiennes:

(x - x 0) 2 + (y - y 0) 2 + (z - z 0) 2 = R 2

Définition. Des points diamétralement opposés sont deux points quelconques sur la surface d'une boule (sphère) qui sont reliés par un diamètre.

Propriétés de base d'une sphère et d'une boule

1. Tous les points de la sphère sont à égale distance du centre.

2. Toute section d'une sphère par un plan est un cercle.

3. Toute section d'une balle par un plan est un cercle.

4. La sphère a le plus grand volume parmi toutes les figures spatiales ayant la même superficie.

5. Par deux points diamétralement opposés, vous pouvez tracer plusieurs grands cercles pour une sphère ou des cercles pour une balle.

6. Par deux points quelconques, à l’exception des points diamétralement opposés, vous ne pouvez tracer qu’un seul grand cercle pour une sphère ou un grand cercle pour une boule.

7. Deux grands cercles d'une balle se coupent le long d'une ligne droite passant par le centre de la balle, et les cercles se coupent en deux points diamétralement opposés.

8. Si la distance entre les centres de deux balles est inférieure à la somme de leurs rayons et supérieure au module de la différence de leurs rayons, alors ces balles couper, et un cercle est formé dans le plan d'intersection.

Sécante, corde, plan sécant d'une sphère et leurs propriétés

Définition. Sphère sécante est une ligne droite qui coupe la sphère en deux points. Les points d'intersection sont appelés points de perçage surfaces ou points d’entrée et de sortie sur la surface.

Définition. Accord d'une sphère (boule)- il s'agit d'un segment reliant deux points d'une sphère (la surface d'une balle).

Définition. Plan de coupe est le plan qui coupe la sphère.

Définition. Plan diamétral- il s'agit d'un plan sécant passant par le centre d'une sphère ou d'une boule, la section se forme en conséquence grand cercle Et grand cercle. Le grand cercle et le grand cercle ont un centre qui coïncide avec le centre de la sphère (boule).

Toute corde passant par le centre d'une sphère (boule) est un diamètre.

Une corde est un segment de ligne sécante.

La distance d du centre de la sphère à la sécante est toujours inférieure au rayon de la sphère :

d< R

La distance m entre le plan de coupe et le centre de la sphère est toujours inférieure au rayon R :

m< R

L'emplacement de la section du plan coupant sur la sphère sera toujours petit cercle, et sur le ballon la section sera petit cercle. Le petit cercle et le petit cercle ont leurs propres centres qui ne coïncident pas avec le centre de la sphère (boule). Le rayon r d'un tel cercle peut être trouvé à l'aide de la formule :

r = √R2 - m2,

Où R est le rayon de la sphère (balle), m est la distance entre le centre de la balle et le plan de coupe.

Définition. Hémisphère (hémisphère)- il s'agit de la moitié d'une sphère (boule) qui se forme lorsqu'elle est coupée par un plan diamétral.

Tangente, plan tangent à une sphère et leurs propriétés

Définition. Tangente à une sphère- Il s'agit d'une ligne droite qui touche la sphère en un seul point.

Définition. Plan tangent à une sphère est un plan qui touche la sphère en un seul point.

La ligne tangente (plan) est toujours perpendiculaire au rayon de la sphère tracée jusqu'au point de contact

La distance entre le centre de la sphère et la ligne tangente (plan) est égale au rayon de la sphère.

Définition. Segment de balle- c'est la partie de la balle qui est coupée de la balle par un plan coupant. Base du segment appelé le cercle qui s'est formé sur le site de la section. Hauteur des segments h est la longueur de la perpendiculaire tracée du milieu de la base du segment à la surface du segment.

Formule. Surface extérieure d'un segment de sphère de hauteur h passant par le rayon de la sphère R :

S = 2πRh

La sphère est l'un des premiers corps à haute symétrie dont les propriétés sont étudiées dans un cours de géométrie scolaire. Cet article traite de la formule d'une sphère, de sa différence avec une balle et fournit également un calcul de la superficie de notre planète.

Sphère : concept en géométrie

Pour mieux comprendre la formule de surface donnée ci-dessous, vous devez vous familiariser avec le concept de sphère. En géométrie, c'est un corps tridimensionnel qui contient un certain volume d'espace. La définition mathématique d'une sphère est la suivante : c'est un ensemble de points situés à une certaine distance égale d'un point fixe appelé centre. La distance marquée est le rayon de la sphère, noté r ou R et mesuré en mètres (kilomètres, centimètres et autres unités de longueur).

La figure ci-dessous montre la figure décrite. Les lignes montrent les contours de sa surface. Le point noir est le centre de la sphère.

Vous pouvez obtenir ce chiffre si vous prenez un cercle et commencez à le faire tourner autour de l'un des axes passant par le diamètre.

Sphère et boule : quelle est la différence et quelle est la similitude ?

Souvent, les écoliers confondent ces deux figures, qui se ressemblent, mais ont des propriétés physiques complètement différentes. Une sphère et une boule se distinguent avant tout par leur masse : une sphère est une couche infiniment mince, tandis qu'une boule est un corps volumétrique de densité finie, qui est le même en tous ses points délimité par une surface sphérique. Autrement dit, la balle a une masse finie et constitue un objet tout à fait réel. Une sphère est une figure idéale, sans masse, qui en réalité n'existe pas, mais c'est une idéalisation réussie en géométrie lors de l'étude de ses propriétés.

Des exemples d'objets réels, dont la forme correspond pratiquement à une sphère, sont un jouet du Nouvel An en forme de boule pour décorer un sapin de Noël ou une bulle de savon.

Quant aux similitudes entre les chiffres considérés, on peut citer les caractéristiques suivantes :

ils ont tous deux la même symétrie ;
pour les deux, la formule de la surface est la même, de plus, ils ont la même surface si leurs rayons sont égaux ;
les deux figures à rayons égaux occupent le même volume dans l'espace, seule la boule le remplit complètement, et la sphère ne le limite que par sa surface.

Une sphère et une boule de rayon égal sont représentées dans la figure ci-dessous.

Notez qu'une boule, comme une sphère, est un corps de révolution, elle peut donc être obtenue en faisant tourner un cercle (pas un cercle !) autour de son diamètre.

Éléments de sphère

Ce sont les noms de grandeurs géométriques dont la connaissance nous permet de décrire soit la figure entière, soit ses parties individuelles. Ses principaux éléments sont les suivants :

Rayon r, déjà mentionné plus tôt. C'est la distance entre le centre de la figure et la surface sphérique. En fait, c’est la seule grandeur qui décrit toutes les propriétés d’une sphère.
Diamètre d, ou D. Il s'agit d'un segment dont les extrémités reposent sur une surface sphérique et dont le milieu passe par le point central de la figure. Le diamètre d'une sphère peut être dessiné d'une infinité de façons, mais tous les segments résultants auront la même longueur, qui est égale à deux fois le rayon, c'est-à-dire D = 2*R.
La surface S est une caractéristique bidimensionnelle dont la formule sera donnée ci-dessous.
Les angles tridimensionnels associés à une sphère se mesurent en stéradians. Un stéradian est un angle dont le sommet se trouve au centre de la sphère et qui repose sur une partie de la surface sphérique d'aire R 2.

Propriétés géométriques d'une sphère

À partir de la description donnée de cette figure, vous pouvez deviner indépendamment ces propriétés. Ils sont les suivants :

Toute ligne droite qui coupe la sphère et passe par son centre est l'axe de symétrie de la figure. Faire pivoter la sphère autour de cet axe sous n’importe quel angle la transforme en elle-même.
Le plan qui coupe la figure en question par son centre divise la sphère en deux parties égales, c'est-à-dire qu'il s'agit d'un plan de réflexion.

Superficie d'une figure

Cette valeur est désignée par la lettre latine S. La formule de calcul de l'aire d'une sphère est la suivante :

S = 4*pi*R 2, où pi ≈ 3,1416.

La formule démontre que l'aire S peut être calculée à condition que le rayon de la figure soit connu. Si son diamètre D est connu, alors la formule de la sphère peut s'écrire comme suit :

Le nombre irrationnel pi, pour lequel quatre décimales sont données, peut être utilisé dans un certain nombre de calculs mathématiques avec une précision au centième, soit 3,14.

Il est également intéressant de se poser la question de savoir à combien de stéradians correspond toute la surface de la figure en question. A partir de la définition de cette valeur, on obtient :

Ω = S/R 2 = 4*pi*R 2 /R 2 = 4*pi stéradian.

Pour calculer n'importe quel angle volumétrique, vous devez remplacer la valeur correspondante de la zone S dans l'expression ci-dessus.

Surface de la planète Terre

La formule de la sphère peut être utilisée pour déterminer sur quoi nous vivons. Avant de commencer les calculs, il y a quelques mises en garde :

Premièrement, la Terre n’a pas une surface sphérique parfaite. Ses rayons équatorial et polaire sont respectivement de 6 378 km et 6 357 km. La différence entre ces chiffres ne dépasse pas 0,3%, donc pour le calcul on peut prendre le rayon moyen de 6371 km.
Deuxièmement, le relief est tridimensionnel, c'est-à-dire qu'il comporte des dépressions et des montagnes. Ces traits caractéristiques de la planète entraînent une augmentation de sa superficie, mais nous ne les prendrons pas en compte dans le calcul, puisque même la plus grande montagne, l'Everest, représente 0,1 % du rayon de la Terre (8,848/6371).

En utilisant la formule de la sphère, on obtient :

S = 4*pi*R 2 = 4*3,1416*6371 2 ≈ 510,066 millions de km 2.

La Russie, selon les données officielles, occupe une superficie de 17,125 millions de km 2, soit 3,36 % de la surface de la planète. Si l'on tient compte du fait que seulement 150,387 millions de km 2 sont des terres, alors la superficie de notre pays représentera 11,4% de l'ensemble du territoire non recouvert d'eau.

Une balle est un corps constitué de tous les points de l'espace situés à une distance non supérieure à une distance donnée d'un point donné. Ce point est appelé le centre de la balle et cette distance est appelée le rayon de la balle. La limite d’une balle est appelée surface sphérique ou sphère. Les points de la sphère sont tous les points de la balle qui sont éloignés du centre à une distance égale au rayon. Tout segment qui relie le centre d'une balle à un point de la surface sphérique est également appelé rayon. Le segment passant par le centre de la boule et reliant deux points de la surface sphérique est appelé diamètre. Les extrémités de n'importe quel diamètre sont appelées points diamétralement opposés de la balle.

Une balle est un corps de révolution, tout comme un cône et un cylindre. Une balle est obtenue en faisant tourner un demi-cercle autour de son diamètre comme axe.

La surface de la balle peut être trouvée à l'aide des formules :

où r est le rayon de la balle, d est le diamètre de la balle.

Le volume de la balle est trouvé par la formule :

V = 4/3 πr 3,

où r est le rayon de la balle.

Théorème. Chaque section d'une balle par un plan est un cercle. Le centre de ce cercle est la base de la perpendiculaire tracée du centre de la balle sur le plan de coupe.

Sur la base de ce théorème, si une balle de centre O et de rayon R est coupée par le plan α, alors la section transversale donne un cercle de rayon r de centre K. Le rayon de la section de la balle par le plan peut être trouvé par la formule

D'après la formule, il ressort clairement que des plans équidistants du centre coupent la balle en cercles égaux. Le rayon de section est plus grand, plus le plan de coupe est proche du centre de la boule, c'est-à-dire plus la distance OK est petite. Le plus grand rayon a une section par un plan passant par le centre de la balle. Le rayon de ce cercle est égal au rayon de la balle.

Le plan passant par le centre de la balle est appelé plan central. La section d'une boule par le plan diamétral s'appelle un grand cercle, et la section d'une sphère s'appelle un grand cercle, et la section d'une sphère s'appelle un grand cercle.

Théorème. Tout plan diamétral d'une balle est son plan de symétrie. Le centre de la balle est son centre de symétrie.

Le plan qui passe par le point A de la surface sphérique et est perpendiculaire au rayon tracé vers le point A est appelé plan tangent. Le point A est appelé le point tangent.

Théorème. Le plan tangent n'a qu'un seul point commun avec la balle : le point de contact.

La droite qui passe par le point A de la surface sphérique perpendiculaire au rayon tracé jusqu'à ce point est appelée tangente.

Théorème. Un nombre infini de tangentes passent par n'importe quel point de la surface sphérique et toutes se trouvent dans le plan tangent de la boule.

Un segment sphérique est la partie d'une balle qui en est séparée par un plan. Le cercle ABC est la base du segment sphérique. Le segment perpendiculaire MN tiré du centre N du cercle ABC jusqu'à l'intersection avec la surface sphérique est la hauteur du segment sphérique. Le point M est le sommet du segment sphérique.

La surface d'un segment sphérique peut être calculée à l'aide de la formule :

Le volume d'un segment sphérique peut être trouvé à l'aide de la formule :

V = πh 2 (R – 1/3h),

où R est le rayon du grand cercle, h est la hauteur du segment sphérique.

Un secteur sphérique est obtenu à partir d'un segment sphérique et d'un cône comme suit. Si le segment sphérique est plus petit qu'un hémisphère, alors le segment sphérique est complété par un cône dont le sommet est au centre de la balle et la base est la base du segment. Si le segment est plus grand qu'un hémisphère, le cône spécifié en est supprimé.

Un secteur sphérique est une partie d'une boule délimitée par une surface courbe d'un segment sphérique (sur notre figure, c'est AMCB) et une surface conique (sur notre figure, c'est OABC), dont la base est la base du segment (ABC), et le sommet est le centre de la boule O.

Le volume du secteur sphérique se trouve par la formule :

V = 2/3 πR 2 H.

Une couche sphérique est une partie d'une boule enfermée entre deux plans parallèles (plans ABC et DEF sur la figure) coupant la surface sphérique. La surface incurvée de la couche sphérique est appelée ceinture (zone) sphérique. Les cercles ABC et DEF sont les bases de la ceinture sphérique. La distance NK entre les bases de la ceinture sphérique est sa hauteur.

blog.site, lors de la copie totale ou partielle du matériel, un lien vers la source originale est requis.

‌‌‌V‌ conférence scientifique et pratique régionale de recherche, de conception et de création des étudiants « Premiers pas en science »

Travaux de recherche sur le sujet :

"La sphère et la boule sont des corps géométriques ordinaires."

Réalisé par : élève de 9ème de MBOU

«L'école secondaire Kochetovskaya» Dima Romanov.

Responsable : professeur de mathématiques et de physique Tremaskina V.S.

Introduction _________________________________________________________________3

1. Histoire de l'étude des corps géométriques : boule, sphère_______________________3

2. Sphère et boule.

2.1. Le concept de sphère et de balle_________________________________________________3-4

2.2. Équation de sphère________________________________________________4

2.3. La position relative de la sphère et du plan______________________________4-6

2.4. Plan tangent à la sphère________________________________________________________6-7

2.5. Aire d'une sphère et volume d'une balle________________________________________________________ 7

2.6. Obtenir la sphère_____________________________________________________________ 7-8

2.7. Trouver une sphère et une balle dans la nature______________________________ 9-13

2.8.Sphère et ballon au quotidien_________________________________14-15

2.9.Utilisation de la sphère et de la boule en architecture________________________________________16-22

2.10. Application de la sphère et de la boule en géodésie____________________________23

2.11 Application de la sphère et de la boule en astronomie et géographie_________________24

2.12. Sphère et boule dans l'art___________________________________________________________25

Conclusion_________________________________________________________________25

Littérature_________________________________________________________________26

Pertinence du sujet choisi.

Au fil des siècles, l'humanité n'a cessé d'élargir ses connaissances scientifiques dans l'un ou l'autre domaine scientifique. De nombreux géomètres scientifiques, et même des gens ordinaires, s'intéressaient à une figure telle qu'une boule et sa « coquille », appelée sphère. De nombreux objets réels en physique, astronomie, biologie et autres sciences naturelles sont sphériques. Par conséquent, l’étude des propriétés de la balle a joué un rôle important à diverses époques historiques et joue un rôle important à notre époque.

But de l'étude:étudier les corps géométriques boule et sphère, considérer leur application dans divers domaines scientifiques, dans la vie quotidienne, dans la nature, créer une présentation « Sphère et boule - corps géométriques ordinaires ».

Tâches:

1. Rassemblez du matériel sur le ballon et la sphère en utilisant diverses sources d'information, y compris les ressources Internet.

2. Systématisez le matériel sur le ballon et la sphère.

4. Créez une présentation" La sphère et la boule sont des corps géométriques ordinaires».

5. Présentez le travail dans une leçon de géométrie lors de l'étude du thème « Sphère et boule ».

Objet d'étude : sphère et boule

Sujet d'étude : éléments et propriétés de la sphère et de la boule

Hypothèse: Nous avons besoin de balles pour rendre notre monde plus diversifié et plus volumineux.

Méthodes : partiellement recherche, recherche, analyse comparative, synthèse, pratique.

Résultat de la recherche : Les connaissances acquises sont nécessaires non seulement aux astronomes, aux navigateurs de navires de mer, d'avions, d'engins spatiaux, qui déterminent leurs coordonnées par les étoiles, mais aussi aux constructeurs de mines, de métros, de tunnels, aux architectes, ainsi qu'aux levés géodésiques de vastes zones de la surface de la Terre, lorsqu'il devient nécessaire de prendre en compte sa sphéricité, dans la vie de tous les jours.

Nouveauté scientifique : le matériel théorique est présenté sous une forme compréhensible pour les lycéens.

Importance pratique: ce matériel peut être utilisé comme base pour un cours au choix dans les cours de physique et de mathématiques, dans les cours d'étude des thèmes « Sphère et balle ».

Introduction

Pendant de nombreux siècles, l'humanité n'a cessé d'élargir ses connaissances scientifiques dans l'un ou l'autre domaine scientifique. La stéréométrie, en tant que science des figures dans l’espace, est intégralement liée à de nombreuses disciplines scientifiques. Ces disciplines comprennent : les mathématiques, la physique, l'informatique et la programmation, ainsi que la chimie et la biologie. Cette dernière pose le problème de l’étude du microcosme, qui est une combinaison complexe de diverses particules dans l’espace les unes par rapport aux autres. Les théorèmes et corollaires de la stéréométrie sont constamment utilisés en architecture.

De nombreux géomètres scientifiques, et même des gens ordinaires, s'intéressaient à une figure telle qu'une boule et sa « coquille », appelée sphère. Étonnamment, la balle est le seul corps qui a une plus grande surface avec un volume égal au volume d'autres corps comparables, comme un cube, un prisme ou d'autres polyèdres divers. Nous traitons des balles tous les jours. Par exemple, presque tout le monde utilise un stylo à bille avec une bille métallique montée à l'extrémité de la recharge, qui tourne sous l'influence du frottement entre elle et le papier, et en tournant, la bille « retire » une autre partie d'encre à sa surface. Dans l'industrie automobile, on fabrique des rotules, qui constituent un élément très important dans une voiture et assurent la rotation correcte des roues et la stabilité de la voiture sur la route. Les éléments des voitures, des avions, des fusées, des motos, des projectiles et des navires qui sont constamment exposés à l'eau ou à l'air ont principalement des sortes de surfaces sphériques appelées carénages.

Histoire de l'étude des corps géométriques : boule, sphère

Une balle est généralement appelée un corps délimité par une sphère, c'est-à-dire une boule et une sphère sont des corps géométriques différents. Cependant, les mots balle et sphère viennent du même mot grec sphaira – balle. De plus, le mot « boule » est né de la transition des consonnes sf en sh.

Dans le livre XI des Éléments, Euclide définit une boule comme une figure décrite par un demi-cercle tournant autour d'un diamètre fixe. Dans l’Antiquité, la sphère était tenue en haute estime. Les observations astronomiques du firmament évoquaient invariablement l'image d'une sphère.

La sphère a toujours été largement utilisée dans divers domaines scientifiques et technologiques.

2.1. Concept de sphère et de balle

Une sphère est une surface constituée de tous les points de l'espace situés à une distance donnée d'un point donné.

Un corps délimité par une sphère s’appelle une balle.

Ce point est appelé centre de la sphère et cette distance est appelée rayon de la sphère.

Un segment reliant deux points sur une sphère et passant

par son centre est appelé le diamètre de la sphère.

Le centre, le rayon et le diamètre d'une sphère sont également appelés centre, rayon et diamètre d'une boule.

2.2. Équation de sphère

Définissons un système de coordonnées rectangulaires À PROPOSxyz

Construisons une sphère de centre au point C (x 0;y 0;z 0)

et rayon R

MC = (x – x 0 ) 2 + (y – y 0 ) 2 + (z – z 0 ) 2

MC = R, ou MC2 = R2

d'où l'équation

la sphère a la forme :

(x-x 0 ) 2 + (o - oui 0 ) 2 + (z-z 0 ) 2 = R 2

2.3. La position relative de la sphère et du plan

Donné:

Une sphère de rayon R de centre C (x 0 ; y 0 ; z 0), le point M (x ; y ; z) se trouve sur la sphère.

Quelle est la distance MC ?

Parce que MS = R, alors

Avec

AVEC AVECSS

Étant donné : plan α, sphère (C ; R),

d - distance du centre C au plan α.

Introduisons un système de coordonnées où le point C est (x 0 ;y 0 ;z 0). Composons les équations de la sphère et du plan α.

P.
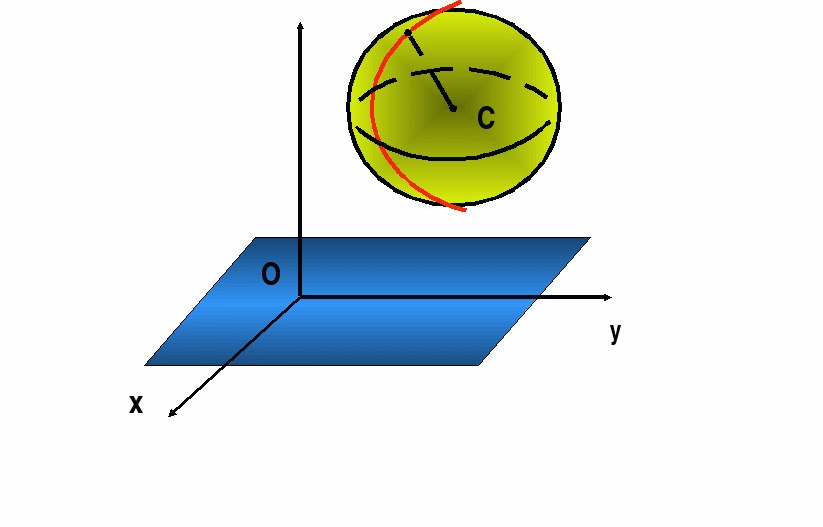
Laissez le point C se situer sur l’axe z. Alors ses coordonnées sont (0 ; 0 ; d).

Équation de sphère :

Équation du plan α : z = 0

Explorons le système d'équations :

z = 0

Alors

Selon le rapport de d et R, 3 cas sont possibles...

1
)d< R .

Alors

équation d'un cercle (O; r)

Section d'une sphère par un plan - cercle

2
) ré = R .

Alors

DANS juste à

x = 0 et y = 0

La sphère et le plan ont un point commun.

3
) ré > R .

Alors

n'a pas de solutions.

La sphère et le plan n'ont pas de points communs.

2.4. Plan tangent à une sphère

Un plan qui n'a qu'un seul point commun avec une sphère est appelé plan tangent à la sphère, et leur point commun est appelé point de tangence entre le plan et la sphère.

Théorème. Le rayon d'une sphère tracée jusqu'au point de contact entre la sphère et le plan est perpendiculaire au plan tangent.

Étant donné : sphère avec centreÀ PROPOS et rayonR. , α - tangent à la sphère en un pointUN avion.

Prouver: O.A. UN .

Preuve : Soit O.A. pas perpendiculaire au plan UN , Alors O.A. est incliné par rapport au plan, ce qui signifie la distance du centre au plan d < R. . Ceux. la sphère doit couper le plan le long du cercle, mais cela ne satisfait pas aux conditions du théorème. Moyens, O.A. UN .

Démontrons le théorème inverse.

Si le rayon d'une sphère est perpendiculaire au plan passant par son extrémité située sur la sphère, alors ce plan est tangent à la sphère.

Étant donné : sphère avec centreÀ PROPOS et rayon O.A. , UN, O.A. UN .

Prouver:UN – plan tangent.

Preuve : parce que O.A. UN , alors la distance du centre de la sphère au plan est égale au rayon. Cela signifie que la sphère et le plan ont un point commun. Par définition, un plan est tangent à une sphère.

2.5. Aire d'une sphère et volume d'une balle

Et rayon de balle sont déterminés par les formules :

Preuve

Prenons un quart de cercle de rayon R de centre au point. L'équation de la circonférence de ce cercle est :, où.

La fonction est continue, croissante, non négative. Lorsqu'un quart de cercle tourne autour de l'axe Buffle, un hémisphère se forme donc :

D'où vient Ch. etc.

Preuve

Etc.

Une partie du ballon, [ ] coupé de lui par un avion s'appelle segment sphérique ou sphérique. La base d'un segment sphérique s'appelle un cercle A B C D. La hauteur d'un segment sphérique est le segment N.M., c'est à dire. longueur de la perpendiculaire restaurée à partir du centre N base jusqu'à ce qu'elle croise la surface de la balle. Point M est appelé le sommet du segment sphérique.

Volume du segment de balle exprimé par la formule :

V = π h 2 ( R. − 1/3 h)

Couche de balle - cela fait partie du ballon [ ], enserré entre deux plans parallèles sécants. Ceinture à billes ou Zone de balle est la surface courbe de la couche sphérique. Cercles abc Et DEF ce sont les bases de la ceinture sphérique. Espacement des bases activé est la hauteur de la couche sphérique.

Volume de la balle exprimé par la formule :

V = 1/6 π h 3 + 1/2 π( r 1 2 + r 2 2 ) h

Secteur de balle- cela fait partie du ballon [ ], délimité par la surface courbe du segment sphérique et la surface conique dont la base est la base du segment, et le sommet est le centre de la boule.

Volume du secteur de balle équivaut à , dont la base a la même aire que la partie de la surface sphérique découpée par le secteur, et la hauteur est égale au rayon

V = 1/3 R.S. = 2/3 π R. 2 h

2.6. Obtenir la sphère

Une sphère peut être obtenue en faisant tourner le demi-cercle ACB autour du diamètre AB

2.7. Trouver une sphère et une balle dans la nature

Z énigmes de la nature - Ballons-messages.Ces mystérieuses formations rocheuses parfaitement rondes ont été découvertes à la fin des années 1940 dans les jungles de la République centraméricaine du Costa Rica. Les boules mesurent entre 10 cm et 3 à 4 mètres de diamètre. Lors de la photographie aérienne, il s'est avéré qu'ils n'étaient pas dispersés au hasard à la surface de la terre, mais formaient des formes géométriques. Il est même possible que les boules ne soient pas dispersées, mais disposées sous la forme d'une immense carte d'étoiles ; chaque boule est une étoile avec une description correspondante.

Parmi les hypothèses sur l'origine des boules, il n'y a que des versions exotiques : des extraterrestres aux sculpteurs de l'Atlantide. Il existe également une version selon laquelle les ballons ont été découpés (en comptant sur les futurs dividendes du tourisme) par des migrants nazis ennuyés qui ont inondé l'Amérique latine après l'effondrement du « Troisième Reich ». Il n’était pas possible d’expliquer l’abondance des balles et leurs motifs étranges par des causes naturelles. Au Kazakhstan, lors de l'aménagement d'une carrière de sable à une assez grande profondeur, plusieurs gros spécimens de tels rochers ont également été découverts... Cette découverte a été rapportée par la commission « Phénomène » ; hélas, aucune photographie des découvertes n'a survécu.

Boule de cristal. Macrophotographie. Il y a une boule de verre posée sur une branche d’arbre ; la nature qui l’entoure s’y reflète. Très jolies fleurs jaunes et herbe verte luxuriante.

AVEC boules flottantes

sur la photo dans les lieux de pouvoir - le résultat de la désintégration de l'uranium ou d'une forme de vie plasmoïde ?

Église du Saint-Sépulcre et autres lieux en Israël

ET
phénomène naturel intéressant Des milliers de boules de glace régulières se sont formées sur les rives d'un lac du Michigan

Algues sous forme de boules insolites

Des boules étranges est apparu sur la côte de Hampton, sur la côte est des États-Unis, en juin 2002. Le raz-de-marée a commencé à emporter un nombre incalculable de ces balles verdâtres - douces, rappelant vaguement une éponge et de la taille d'une balle de tennis ou de golf. À une distance d'environ 300 mètres ou plus, toute la plage de sable était littéralement jonchée de telles balles. Les différends ont immédiatement commencé : qu'est-ce que c'est et d'où vient-il ? Des biologistes marins, des vacanciers sur la plage et des passants aléatoires ont été impliqués dans le débat. Personne n’avait jamais vu quelque chose de pareil ici auparavant.

La nature a peur de la symétrie ; elle ne connaît pas les formes géométriques idéales. Mais l'homme peut forcer la nature à acquérir ces formes qui lui sont étrangères. Un exemple clair en est le travail de l'artiste coréen Lee Jae-Hyo, qui crée à partir deles troncs d'arbres sont des sphères parfaites

T

Des milliers de petites boules violettes se sont étrangement retrouvées au centre du désert de l'Arizona, aux États-Unis. Les habitants de Tucson, Geraldine Vargas et son mari ont découvert il y a quelques semaines un amas inexpliqué d'orbes étranges alors qu'ils se promenaient dans le quartier. "Nous photographions la nature du désert lorsque nous sommes tombés sur cet endroit étrange... Je ne comprends pas comment nous ne l'avons pas remarqué tout de suite ?", a déclaré Géraldine aux journalistes. "Il brillait au soleil." Les photographes ont envoyé des photos d’objets étranges à leur amie zoologiste, mais elle ne pouvait pas dire de quoi il s’agissait, elle n’avait même aucune hypothèse à ce sujet.

Boules faites de minéraux.

Améthyste.Brésil.

Cristal de roche. Région du Sud.

Amazonite. Péninsule de Kola.

2.8 Sphère et boule au quotidien

N
et la boule géométrique est similaire globe, ballon de football, jouets du Nouvel An.

Boule en mousse bricolage

Zorbing – c’est l’un des divertissements extrêmes les plus en vogue aujourd’hui. Le Zorbing vous permettra d'éprouver des sensations nouvelles, inhabituellement lumineuses et puissantes et de vous sortir de l'ordinaire du quotidien.

Qu'est-ce qu'une balle Zorb

Z orbe (ZORB) est une sphère transparente (boule) d'un diamètre de 3,2 mètres à l'intérieur de laquelle se trouve une sphère d'un diamètre de 1,8 mètres, dans laquelle se trouve zorbonaute (passager zorba). L'espace entre ces sphères est rempli d'air dont la pression écarte les sphères et est au contraire maintenue en place par les élingues. Ce système absorbe très bien, lisse les irrégularités du terrain et sécurise le ski.

2.9.Application de la sphère et de la boule en architecture

Cette maison s'appelle WIGWAM. De telles maisons sont construites INDIENS.

Billes et hémisphères en acier inoxydable

Fontaine "Tournante"balle "à St.

Saint-Pétersbourg -

Maisons modernes

Et simaison non seulement sur un arbre, mais aussi sous la forme d'une boule.

C'est un vrai villagemaisons rondes .

AVEC
maisons rondes modernes

Biosphère de Montréal - Pavillon d'exposition américain à l'Expo 67 au Canada,

conçu par l'architecte Richard Fuller.

Hôtel sous forme de boules transparentes

DANS
À propos de la ville française de Roubaix, des chambres d'hôtel portables, l'Hôtel Bolha, ont été ouvertes dans l'un des parcs. Nous l'avons fait spécialement pour les personnes qui, même au cœur de la jungle urbaine, souhaitent se rapprocher de la nature.Le concept de la bulle a été inventé par le designer Pierre Stéphane Dumas. Cette conception avancée a été créée dans le but de connecter temporairement les invités à l'inconnu. Après tout, peu de gens peuvent se permettre de dormir sous un plafond rond.

Robe ballon.

Bureau de pays Le printemps arrive bientôt (puis l'été) et beaucoup commenceront à se rendre dans leur datcha pour se détendre.
Mais parfois, il faut travailler à la datcha (bon sang !). Vous n'avez pas d'endroit où prendre votre retraite ?
Vous pouvez créer un « Archipode » dans une petite structure sphérique comme ceci :

EFFICACITÉ ÉNERGÉTIQUE enarchitecture . Smart Home est une molécule.

Dans le parc scientifique et technologique de La Vilette, construit sur le site d'un abattoir à l'est de Paris, une boule géante, dont la surface miroir reflète le ciel parisien et le paysage environnant, attire le regard. Aujourd'hui, ce bâtiment est considéré comme la structure sphérique la plus parfaite au monde. Les Parisiens l'appellent « Géode ». C'est panoramique

cinéma avec le plus grand écran d'Europe. miroir de la maison de balle

Ces pelotes de fil peuvent être simplement suspendues aux branches d'arbres si vos vacances se déroulent en extérieur, ou au plafond. Ils peuvent également être utilisés pour décorer une table de banquet, en complétant la composition avec des bougies et des fleurs.

2.10. Application de la sphère et de la boule en géodésie.

Projections cartographiques

affichant toute la surface de l’ellipsoïde terrestre (Voir. ) ou n'importe quelle partie de celui-ci sur un plan, obtenu principalement dans le but de construire une carte.

Échelle.Les stations de contrôle sont construites à une certaine échelle. Réduire mentalement l'ellipsoïde terrestre àMfois, par exemple 10 000 000 de fois, on obtient son modèle géométrique - , dont l'image grandeur nature sur plan donne une carte de la surface de cet ellipsoïde. Valeur 1 :M(dans l'exemple 1 : 10 000 000) détermine l'échelle principale ou générale de la carte. Parce que les surfaces d'un ellipsoïde et d'une boule ne peuvent pas être développées sur un plan sans cassures et plis (elles n'appartiennent pas à la classe des surfaces développables (Voir. )), toute carte est caractérisée par des distorsions dans les longueurs de lignes, les angles, etc., caractéristiques de toute carte. La principale caractéristique d'un système spatial en tout point est l'échelle partielle μ. C'est l'inverse du rapport du segment infinitésimaldssur l'ellipsoïde terrestre à son imagedσ en surface : μ min ≤ μ ≤ μ maximum, et l'égalité ici n'est possible qu'en certains points ou le long de certaines lignes de la carte. Ainsi, l'échelle principale de la carte ne la caractérise qu'en termes généraux, sous une forme moyenne. Attitude μ/M est appelé l'échelle relative, ou augmentation de longueur, la différence M = 1.

1. Réseaux de lignes de coordonnées sphériques.

2.11. Application de la sphère et de la sphère en astronomie et géographie.

AVEC la sphère et la boule, ainsi que le cercle et le cercle, étaient considérés dans l'Antiquité. La découverte de la forme sphérique de la Terre et l'émergence d'idées sur la sphère céleste ont donné une impulsion au développement d'une science spéciale - la SPHERE, qui étudie les figures situées sur la sphère.

En parcourant le monde, les marins ont remarqué qu'en revenant au même endroit, ils perdaient ou gagnaient une journée entière, ce qui serait totalement impossible si la Terre avait la forme d'un disque.

Ainsi, la preuve de la sphéricité de la Terre à l’heure actuelle est :

Toujours une figure circulaire de l'horizon dans l'océan et dans les basses terres ou plateaux ouverts ;

Voyager autour du monde.

Approche ou retrait progressif des objets ;

ET
En étudiant diverses cartes géographiques, nous avons découvert qu’en géographie il existe des noms de lieux associés au ballon. Par exemple, entre les îles du nord et du sud de Novaya Zemlya, il existe un détroit qui relie les mers de Barents et de Kara, appelé Matochkin Shar, ou un détroit entre les rives de l'île de Vaigach et le continent de l'Eurasie - Yugorsky Shar. Nous pensons que ces détroits sont appelés boules en raison du fait que leur taille et leur forme de fond ressemblent à une surface sphérique.

2.12. Sphère et boule dans l'art

Les mathématiques d'Escher

De plus, les peintures d’Escher, qui représentent diverses « figures impossibles », « jouent » avec la logique de l’espace ; Escher les a représentés séparément et dans des lithographies et des gravures.

Trois sphères. 1946

Main avec sphère réfléchissante. 1935

Conclusion

Je pense que le matériel que j'ai collecté et les connaissances acquises au cours du travail effectué peuvent être utilisés dans les cours de géométrie, les cours de travail, dans la vie quotidienne, comme base d'un cours au choix dans les cours de physique et de mathématiques, ainsi que dans les cours extrascolaires. activités pour élargir les horizons des étudiants.