Parmi les séries fonctionnelles, la place la plus importante est occupée par les séries de puissance.

Une série entière est une série

dont les termes sont des fonctions puissance disposées en puissances entières croissantes non négatives X, UN c0 , c 1 , c 2 , c n - des valeurs constantes. Nombres c1 , c 2 , c n - les coefficients des termes de la série, c0 - Membre gratuit. Les termes de la série entière sont définis sur toute la droite numérique.

Faisons connaissance avec le concept zones de convergence des séries entières. C'est l'ensemble des valeurs d'une variable X, pour lequel la série converge. Les séries entières ont une région de convergence assez simple. Pour les valeurs variables réelles X la région de convergence est constituée soit d'un point, soit d'un certain intervalle (intervalle de convergence), soit elle coïncide avec l'ensemble de l'axe Bœuf .

Lors de la substitution des valeurs dans la série entière X= 0 donnera une série de nombres

c0 +0+0+...+0+... ,

qui converge.

Par conséquent, quand X= 0 toute série entière converge et, par conséquent, sa zone de convergence ne peut pas être l’ensemble vide. La structure de la région de convergence de toutes les séries de puissances est la même. Il peut être établi à l’aide du théorème suivant.

Théorème 1 (théorème d'Abel). Si une série de puissances converge vers une certaine valeur X = X 0 , différent de zéro, alors il converge, et, de plus, absolument, pour toutes les valeurs |X| < |X 0 | . Attention : tant la valeur de départ « X est zéro » que toute valeur de « X » comparée à la valeur de départ sont prises modulo - sans tenir compte du signe.

Conséquence. Si les séries de puissances divergent à une certaine valeur X = X 1 , alors il diverge pour toutes les valeurs |X| > |X 1 | .

Comme nous l'avons déjà découvert précédemment, toute série de puissances converge vers la valeur X= 0. Il existe des séries entières qui convergent uniquement lorsque X= 0 et divergent pour d'autres valeurs X. En excluant ce cas de considération, nous supposons que la série de puissances converge vers une certaine valeur X = X 0 , différent de zéro. Alors, selon le théorème d'Abel, il converge en tous points de l'intervalle ]-| X0 |, |X 0 |[ (un intervalle dont les limites gauche et droite sont les valeurs x auxquelles converge la série entière, prises respectivement avec un signe moins et un signe plus), symétrique par rapport à l'origine.

Si la série de puissances diverge à une certaine valeur X = X 1 , alors, d’après le corollaire du théorème d’Abel, il diverge en tout point en dehors du segment [-| X1 |, |X 1 |] . Il s'ensuit que pour toute série entière, il existe un intervalle symétrique par rapport à l'origine, appelé intervalle de convergence , en chaque point duquel la série converge, aux frontières elle peut converger, ou elle peut diverger, et pas nécessairement en même temps, et en dehors du segment la série diverge. Nombre R. est appelé le rayon de convergence de la série entière.

Dans des cas particuliers intervalle de convergence des séries entières peut dégénérer jusqu'à un point (alors la série ne converge que lorsque X= 0 et on considère que R.= 0) ou représentent la droite numérique entière (alors la série converge en tous les points de la droite numérique et on suppose que ).

Ainsi, déterminer la région de convergence d’une série entière consiste à déterminer sa rayon de convergence R. et étudier la convergence des séries aux limites de l'intervalle de convergence (en ).

Théorème 2. Si tous les coefficients d'une série entière, à partir d'un certain, sont différents de zéro, alors son rayon de convergence est égal à la limite au rapport des valeurs absolues des coefficients des membres communs suivants de la série , c'est à dire.

Exemple 1. Trouver la région de convergence de la série entière

Solution. Ici

A l'aide de la formule (28), on trouve le rayon de convergence de cette série :

Etudions la convergence des séries aux extrémités de l'intervalle de convergence. L'exemple 13 montre que cette série converge en X= 1 et diverge en X= -1. Par conséquent, la région de convergence est le demi-intervalle.

Exemple 2. Trouver la région de convergence de la série entière

Solution. Les coefficients de la série sont positifs, et

Trouvons la limite de ce rapport, c'est-à-dire rayon de convergence de la série entière :

Etudions la convergence des séries aux extrémités de l'intervalle. Substitution de valeur X= -1/5 et X= 1/5 dans cette ligne donne :

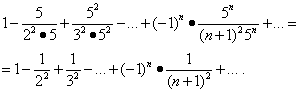
La première de ces séries converge (voir exemple 5). Mais alors, en vertu du théorème de la section « Convergence absolue », la deuxième série converge également, et la région de sa convergence est le segment

Exemple 3. Trouver la région de convergence de la série entière

Solution. Ici

A l'aide de la formule (28) on trouve le rayon de convergence de la série :

Etudions la convergence des séries pour les valeurs de . En les substituant dans cette série, on obtient respectivement

Les deux séries divergent parce que la condition nécessaire à la convergence n'est pas satisfaite (leurs termes communs ne tendent pas vers zéro en ). Ainsi, aux deux extrémités de l’intervalle de convergence, cette série diverge et la région de sa convergence est l’intervalle.

Exemple 5. Trouver la région de convergence de la série entière

Solution. On trouve la relation où , et :

D'après la formule (28), le rayon de convergence de cette série

c'est-à-dire que la série ne converge que lorsque X= 0 et diverge pour les autres valeurs X.

Des exemples montrent qu’aux extrémités de l’intervalle de convergence, les séries se comportent différemment. Dans l’exemple 1, à une extrémité de l’intervalle de convergence la série converge, et à l’autre, elle diverge ; dans l’exemple 2, elle converge aux deux extrémités ; dans l’exemple 3, elle diverge aux deux extrémités.

La formule du rayon de convergence d'une série entière est obtenue en supposant que tous les coefficients des termes de la série, à partir d'un certain point, sont différents de zéro. Par conséquent, l'utilisation de la formule (28) n'est autorisée que dans ces cas. Si cette condition n’est pas respectée, alors le rayon de convergence de la série entière doit être recherché en utilisant signe de d'Alembert, ou, en remplaçant la variable, en transformant la série en une forme dans laquelle la condition spécifiée est satisfaite.

Exemple 6. Trouver l'intervalle de convergence de la série entière

Solution. Cette série ne contient pas de termes avec des degrés impairs X. Par conséquent, nous transformons la série en définissant . On obtient alors la série

pour trouver le rayon de convergence duquel on peut appliquer la formule (28). Puisque , a , alors le rayon de convergence de cette série

De l'égalité que nous obtenons, cette série converge donc vers l'intervalle.

Somme des séries de puissances. Différenciation et intégration des séries de puissance

Supposons la série entière

rayon de convergence R.> 0, c'est-à-dire cette série converge sur l'intervalle .

Alors chaque valeur X de l'intervalle de convergence correspond à une certaine somme de la série. Par conséquent, la somme des séries de puissances est fonction de X sur l'intervalle de convergence. Le désignant par F(X), on peut écrire l'égalité

comprendre dans le sens où la somme des séries en chaque point X de l'intervalle de convergence est égal à la valeur de la fonction F(X) à ce point. Dans le même sens, on dira que la série entière (29) converge vers la fonction F(X) sur l'intervalle de convergence.

En dehors de l’intervalle de convergence, l’égalité (30) n’a aucun sens.

Exemple 7. Trouver la somme de la série de puissances

Solution. Il s'agit d'une série géométrique pour laquelle un= 1, une q= X. Sa somme est donc une fonction . Une série converge si , et est son intervalle de convergence. Donc l'égalité

n'est valable que pour les valeurs, bien que la fonction défini pour toutes les valeurs X, sauf X= 1.

On peut prouver que la somme des séries de puissances F(X) est continue et différentiable sur n'importe quel intervalle de l'intervalle de convergence, en particulier en tout point de l'intervalle de convergence de la série.

Présentons des théorèmes sur la différenciation terme par terme et l'intégration des séries de puissances.

Théorème 1. Les séries de puissances (30) dans l'intervalle de leur convergence peuvent être différenciées terme par terme un nombre illimité de fois, et les séries de puissances résultantes ont le même rayon de convergence que la série d'origine, et leurs sommes sont respectivement égales à .

Théorème 2. Les séries de puissances (30) peuvent être intégrées terme par terme un nombre illimité de fois dans la plage de 0 à X, si , et la série de puissances résultante ont le même rayon de convergence que la série d'origine, et leurs sommes sont par conséquent égales

Extension des fonctions aux séries de puissance

Soit la fonction donnée F(X), qui doit être développé en une série entière, c'est-à-dire représenter sous la forme (30) :

La tâche est de déterminer les coefficients rangée (30). Pour ce faire, en différenciant l'égalité (30) terme par terme, on trouve systématiquement :

……………………………………………….. (31)

En supposant les égalités (30) et (31) X= 0, on trouve

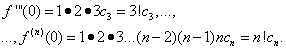
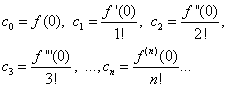
En substituant les expressions trouvées dans l'égalité (30), on obtient

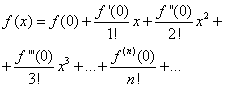(32)

Retrouvons le développement en série de Maclaurin de quelques fonctions élémentaires.

Exemple 8.Étendez la fonction dans une série Maclaurin

Solution. Les dérivées de cette fonction coïncident avec la fonction elle-même :

Par conséquent, quand X= 0 nous avons

En substituant ces valeurs dans la formule (32), on obtient le développement souhaité :

(33)

Cette série converge sur toute la droite numérique (son rayon de convergence).

Exemple 1. Trouvez la région de convergence de la série entière :

UN) ; b) ;

V) ; G)
;

d)
.

UN) Trouvons le rayon de convergence R.. Parce que
,
, Que

X
, c'est-à-dire l'intervalle de convergence de la série
.

À
nous obtenons une série de nombres . Cette série converge car c'est une série harmonique généralisée à
.

À
nous obtenons une série de nombres
. Cette série est absolument convergente, puisqu'une série composée des valeurs absolues de ses termes , convergent.

b) Trouvons le rayon de convergence R.. Parce que
, Que
.

Donc, l'intervalle de convergence de la série
.

Nous examinons la convergence de cette série aux extrémités de l'intervalle de convergence.

À
nous avons une série de nombres

.

À
nous avons une série de nombres
. Cette série est divergente car
n'existe pas.

Donc, la région de convergence de cette série
.

V) Trouvons le rayon de convergence R.. Parce que
,
Que
.

Donc l'intervalle de convergence
. La région de convergence de cette série coïncide avec l'intervalle de convergence, c'est-à-dire que la série converge pour toute valeur de la variable X.

G) Trouvons le rayon de convergence R.. Parce que
,
Que
.

Parce que
, alors la série ne converge qu'au point
. Cela signifie que la région de convergence de cette série est d'un point
.

d) Trouvons le rayon de convergence R..

Parce que
,
, Que

Ainsi, la série converge pour absolument tout le monde X, satisfaisant l'inégalité
, c'est
.

D'ici
− intervalle de convergence,
− rayon de convergence.

Examinons cette série pour la convergence aux extrémités de l'intervalle de convergence.

À
nous obtenons une série de nombres

qui diverge (série harmonique).

À
nous obtenons une série de nombres
, qui converge conditionnellement (la série converge selon le critère de Leibniz, et la série composée des valeurs absolues de ses membres diverge, puisqu'elle est harmonique).

Donc, la région de convergence de la série
.

2.3. Série Taylor et Maclaurin.

Extension des fonctions aux séries de puissance.

Application des séries de puissances aux calculs approximatifs

Exemples de résolution de problèmes

Exemple 1. Développez la fonction en une série entière :

UN)
; b)
;

V)
; G)
.

UN) Remplacer dans la formule
X sur
, on obtient le développement souhaité :

Où

b) Substituer dans l’égalité

Où
X sur
, on obtient le développement souhaité :

V) Cette fonction peut s'écrire ainsi :
. Pour trouver la série souhaitée, il suffit de développer

Où
remplaçant
. On obtient alors :

G) Cette fonction peut être réécrite comme ceci : .

Fonction
peut être étendu en une série entière en insérant la série binomiale
, nous allons recevoir .

Où
.

Pour obtenir le développement souhaité, il suffit de multiplier les séries résultantes (du fait de la convergence absolue de ces séries).

Ainsi,

, Où
.

Exemple 2. Trouvez les valeurs approximatives de ces fonctions :

UN)
avec une précision de 0,0001 ;

b)
avec une précision de 0,00001.

UN) Parce que
, puis dans le développement de la fonction, où
substituons
:

Parce que
, alors la précision requise sera assurée si l'on se limite aux deux premiers termes du développement résultant.

Nous utilisons la série binomiale

Où
.

Croire
Et
, on obtient le développement suivant :

Si dans la dernière série alternée seuls les deux premiers termes sont pris en compte et les autres sont écartés, alors l'erreur de calcul
ne dépassera pas 0,000006 en valeur absolue. Alors l'erreur dans le calcul
ne dépassera pas le nombre. Ainsi,

Exemple 3. Calculez à 0,001 près :

UN)
; b)
.

UN)
.

Développons l'intégrande en une série entière. Pour ce faire, substituons dans la série binomiale
et remplacer X sur :

Depuis le segment d'intégration
appartient à la région de convergence de la série résultante
, alors nous intégrerons terme par terme dans les limites précisées :

Dans la série alternée résultante, le quatrième terme est inférieur à 0,001 en valeur absolue. Par conséquent, la précision requise sera assurée si seuls les trois premiers termes de la série sont pris en compte.

Étant donné que le premier des termes rejetés a un signe moins, la valeur approximative résultante sera excessive. Par conséquent, la réponse à 0,001 près est 0,487.

b) Représentons d’abord l’intégrande comme une série entière. Remplaçons dans le développement de la fonction

Où

X sur
, on a:

Alors
.

La série alternée résultante satisfait aux conditions du critère de Leibniz. Le quatrième terme de la série est inférieur à 0,001 en valeur absolue. Pour assurer la précision requise, il suffit de trouver la somme des trois premiers termes.

Ainsi,
.

Série fonctionnelle. Série de puissance.
Plage de convergence de la série

Le rire sans raison est un signe de d'Alembert

L’heure des grades fonctionnels a sonné. Pour maîtriser avec succès le sujet, et en particulier cette leçon, vous devez avoir une bonne compréhension des séries de nombres ordinaires. Vous devez avoir une bonne compréhension de ce qu'est une série et être capable d'appliquer des critères de comparaison pour examiner la convergence de la série. Ainsi, si vous venez de commencer à étudier le sujet ou si vous êtes débutant en mathématiques supérieures, nécessaire travaillez sur trois leçons en séquence : Des lignes pour les nuls,Le signe de D'Alembert. Les signes de Cauchy Et Rangées alternées. Le test de Leibniz. Certainement les trois ! Si vous possédez des connaissances et des compétences de base pour résoudre des problèmes avec des séries de nombres, alors gérer les séries fonctionnelles sera assez simple, car il n'y a pas beaucoup de nouveau matériel.

Dans cette leçon, nous examinerons le concept de série fonctionnelle (ce qu'elle est), nous familiariserons avec les séries de puissances, que l'on retrouve dans 90 % des tâches pratiques, et apprendrons à résoudre un problème typique courant de recherche du rayon. de convergence, d'intervalle de convergence et de région de convergence d'une série de puissances. Ensuite, je recommande de considérer le matériel sur extension des fonctions en séries entières, et les premiers secours seront prodigués au débutant. Après avoir repris un peu notre souffle, on passe au niveau suivant :

Également dans la section des séries fonctionnelles, il y en a de nombreuses applications au calcul approximatif, et se démarquent à certains égards des séries de Fourier, qui, en règle générale, font l'objet d'un chapitre distinct dans la littérature pédagogique. Je n’ai qu’un seul article, mais il est long et il y a de très nombreux exemples supplémentaires !

Voilà, les repères sont posés, c'est parti :

Le concept de série fonctionnelle et de série de puissance

Si la limite s'avère être l'infini, alors l'algorithme de solution termine également son travail, et nous donnons la réponse finale à la tâche : « La série converge vers » (ou vers l'un ou l'autre « ). Voir cas n°3 du paragraphe précédent.

Si la limite s'avère n'être ni zéro ni l'infini, nous avons alors le cas le plus courant dans la pratique n°1 - la série converge sur un certain intervalle.

Dans ce cas, la limite est . Comment trouver l’intervalle de convergence d’une série ? On compense l'inégalité :

DANS TOUTE tâche de ce type du côté gauche de l’inégalité devrait être résultat du calcul de la limite, et du côté droit de l’inégalité – strictement unité. Je n’expliquerai pas exactement pourquoi il y a une telle inégalité et pourquoi il y en a une à droite. Les cours sont orientés vers la pratique, et c'est très bien que mes histoires n'aient pas accroché le personnel enseignant et que certains théorèmes soient devenus plus clairs.

La technique consistant à travailler avec un module et à résoudre les doubles inégalités a été discutée en détail au cours de la première année dans l'article Domaine de fonction, mais pour plus de commodité, j'essaierai de commenter toutes les actions de manière aussi détaillée que possible. On révèle l'inégalité avec le module selon la règle de l'école . Dans ce cas:

La moitié du chemin est parcourue.

Dans un deuxième temps, il faut étudier la convergence des séries aux extrémités de l'intervalle trouvé.

Tout d’abord, nous prenons l’extrémité gauche de l’intervalle et la substituons dans notre série entière :

Nous avons obtenu une série de nombres et nous devons en examiner la convergence (une tâche déjà familière dans les leçons précédentes).

1) La série est en alternance.
2) – les termes de la série diminuent en module. De plus, chaque membre suivant de la série est inférieur au précédent en valeur absolue : , ce qui signifie que la diminution est monotone.
Conclusion : la série converge.

À l’aide d’une série composée de modules, nous découvrirons exactement comment :
– converge (séries « standards » de la famille des séries harmoniques généralisées).

Ainsi, la série de nombres résultante converge absolument.

à – converge.

! Je vous rappelle que toute série positive convergente est aussi absolument convergente.

Ainsi, la série de puissances converge, et de manière absolue, aux deux extrémités de l’intervalle trouvé.

Répondre: zone de convergence de la série de puissances étudiée :

Une autre forme de réponse a droit à la vie : Une série converge si

Parfois, l'énoncé du problème vous demande d'indiquer le rayon de convergence. Il est évident que dans l'exemple considéré .

Exemple 2

Trouver la région de convergence de la série entière

Solution: on trouve l'intervalle de convergence de la série en utilisant signe de d'Alembert (mais pas l'attribut BY ! – un tel attribut n'existe pas pour les séries fonctionnelles):

La série converge vers

Gauche nous devons partir seulement, on multiplie donc les deux côtés de l'inégalité par 3 :

– La série est en alternance.
– – les termes de la série diminuent en module. Chaque membre suivant de la série est inférieur au précédent en valeur absolue : , ce qui signifie que la diminution est monotone.

Conclusion : la série converge.

Examinons-le pour la nature de la convergence :

Comparons cette série avec une série divergente.
Nous utilisons le critère de comparaison limite :

On obtient un nombre fini différent de zéro, ce qui signifie que la série diverge de la série.

Ainsi, la série converge conditionnellement.

2) Quand – diverge (d’après ce qui a été prouvé).

Répondre: Aire de convergence de la série de puissances étudiée : . Lorsque la série converge conditionnellement.

Dans l'exemple considéré, la région de convergence de la série entière est un demi-intervalle, et en tout point de l'intervalle la série entière converge absolument, et au point , comme il s'est avéré – conditionnellement.

Exemple 3

Trouver l'intervalle de convergence de la série entière et étudier sa convergence aux extrémités de l'intervalle trouvé

Ceci est un exemple à résoudre par vous-même.

Examinons quelques exemples rares, mais qui surviennent.

Exemple 4

Trouver l'aire de convergence de la série :

Solution: A l'aide du test de d'Alembert on trouve l'intervalle de convergence de cette série :

(1) Nous composons le rapport du membre suivant de la série au précédent.

(2) On se débarrasse de la fraction de quatre étages.

(3) Selon la règle des opérations avec puissances, on place les cubes sous une seule puissance. Au numérateur, nous développons intelligemment le degré, c'est-à-dire Nous l'arrangeons de telle manière qu'à l'étape suivante, nous puissions réduire la fraction de . Nous décrivons les factorielles en détail.

(4) Sous le cube, on divise le numérateur par le dénominateur terme par terme, indiquant que . En une fraction on réduit tout ce qui peut l'être. Nous prenons le facteur au-delà du signe limite ; il peut être retiré, puisqu'il n'y a rien qui dépend de la variable « dynamique » « en ». Veuillez noter que le signe du module n'est pas dessiné - car il prend des valeurs non négatives pour tout « x ».

A la limite, on obtient zéro, ce qui signifie que l'on peut donner la réponse finale :

Répondre: La série converge vers

Mais au début, il semblait que cette dispute avec le « terrible remplissage » serait difficile à résoudre. Zéro ou l'infini dans la limite est presque un cadeau, car la solution est sensiblement réduite !

Exemple 5

Trouver l'aire de convergence de la série

Ceci est un exemple à résoudre par vous-même. Soyez prudent ;-) La solution complète se trouve à la fin de la leçon.

Regardons quelques exemples supplémentaires qui contiennent un élément de nouveauté en termes d'utilisation de techniques techniques.

Exemple 6

Trouver l'intervalle de convergence de la série et étudier sa convergence aux extrémités de l'intervalle trouvé

Solution: Le terme commun de série de puissances inclut un facteur qui assure l'alternance des signes. L'algorithme de solution est entièrement conservé, mais lors de l'établissement de la limite, nous ignorons (n'écrivons pas) ce facteur, puisque le module détruit tous les « moins ».

On trouve l'intervalle de convergence de la série à l'aide du test de d'Alembert :

Créons une inégalité standard :
La série converge vers
Gauche nous devons partir module uniquement, on multiplie donc les deux côtés de l'inégalité par 5 :

Maintenant, nous ouvrons le module de manière familière :

Au milieu de la double inégalité, il ne faut laisser que « X » ; pour cela, on soustrait 2 à chaque partie de l'inégalité :

– intervalle de convergence de la série de puissances étudiée.

Nous étudions la convergence des séries aux extrémités de l'intervalle trouvé :

1) Remplacez la valeur dans notre série entière :

Soyez extrêmement prudent, le multiplicateur ne permet pas d'alternance de signe pour un « en » naturel. Nous prenons le moins résultant en dehors de la série et l'oublions, car il (comme toute constante factorielle) n'affecte en rien la convergence ou la divergence de la série de nombres.

Veuillez noter à nouveau qu'au cours de la substitution de la valeur dans le terme général de la série entière, notre facteur a été réduit. Si cela ne se produisait pas, cela signifierait que nous avons mal calculé la limite ou que nous avons mal étendu le module.

Nous devons donc examiner la convergence des séries de nombres. Ici, le plus simple est d'utiliser le critère de comparaison limite et de comparer cette série avec une série harmonique divergente. Mais, pour être honnête, je suis terriblement fatigué du signe limitatif de comparaison, je vais donc ajouter un peu de variété à la solution.

La série converge donc vers

On multiplie les deux côtés de l'inégalité par 9 :

On extrait la racine des deux parties, tout en se souvenant de la blague de la vieille école :

Extension du module :

et ajoutez-en un à toutes les parties :

– intervalle de convergence de la série de puissances étudiée.

Etudions la convergence des séries de puissances aux extrémités de l'intervalle trouvé :

1) Si , alors la série de nombres suivante est obtenue :