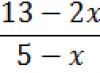Équations linéaires : formules et exemples. Les inégalités et leur solution

Les équations linéaires sont un sujet assez inoffensif et compréhensible en mathématiques scolaires. Mais, curieusement, le nombre d'erreurs inattendues lors de la résolution d'équations linéaires n'est que légèrement inférieur à celui d'autres sujets - équations quadratiques, logarithmes, trigonométrie et autres. Les causes de la plupart des erreurs sont des transformations identiques et banales d'équations. Tout d'abord, il s'agit d'une confusion des signes lors du transfert de termes d'une partie de l'équation à une autre, ainsi que d'erreurs lors du travail avec des fractions et des coefficients fractionnaires. Oui, oui ! Les fractions apparaissent également dans les équations linéaires ! Tout autour. Ci-dessous, nous analyserons certainement ces équations maléfiques.)

Eh bien, ne tirons pas le chat par la queue et commençons à le comprendre, d'accord ? Ensuite, nous le lisons et l'examinons.)

Qu'est-ce qu'une équation linéaire ? Exemples.

Généralement, l'équation linéaire ressemble à ceci :

hache + b = 0,

Où a et b sont des nombres quelconques. N'importe quel type : entiers, fractions, négatifs, irrationnels - toutes sortes de choses peuvent arriver !

Par exemple:

7x + 1 = 0 (ici a = 7, b = 1)

x – 3 = 0 (ici a = 1, b = -3)

x/2 – 1,1 = 0 (ici a = 1/2, b = -1,1)

En général, vous comprenez, j'espère.) Tout est simple, comme dans un conte de fées. Pour le moment... Et si vous regardiez de plus près la notation générale ax+b=0, et réfléchissiez un peu ? Après tout, a et b sont des chiffres! Et si nous avons, disons, a = 0 et b = 0 (n'importe quel nombre peut être pris !), alors qu'obtiendrons-nous ?

0 = 0

Mais ce n'est pas tout le plaisir ! Et si, disons, a = 0, b = -10 ? Ensuite, il s'avère que c'est une sorte d'absurdité :

0 = 10.

Ce qui est très, très ennuyeux et met à mal la confiance dans les mathématiques que nous avons acquise à force de sueur et de sang... Surtout lors des contrôles et des examens. Mais parmi ces égalités incompréhensibles et étranges, il faut aussi trouver X ! Ce qui n’existe pas du tout ! Et ici, même les étudiants bien préparés peuvent parfois tomber dans ce qu’on appelle la stupeur… Mais ne vous inquiétez pas ! Dans cette leçon, nous examinerons également toutes ces surprises. Et nous trouverons aussi certainement un X à partir de telles égalités.) De plus, ce même X peut être trouvé très, très simplement. Oui, oui ! Surprenant mais vrai.)

D'accord, c'est compréhensible. Mais comment pouvez-vous savoir, d’après l’apparence de la tâche, qu’il s’agit d’une équation linéaire et non d’une autre équation ? Malheureusement, il n’est pas toujours possible de reconnaître le type d’équation simplement par son apparence. Le fait est que non seulement les équations de la forme ax+b=0 sont dites linéaires, mais aussi toutes les autres équations qui, par des transformations identiques, sont, d'une manière ou d'une autre, réduites à cette forme. Comment savoir si cela s'additionne ou non ? Jusqu'à ce que vous puissiez difficilement résoudre l'exemple - presque pas du tout. C'est bouleversant. Mais pour certains types d’équations, vous pouvez immédiatement savoir en toute confiance si elles sont linéaires ou non, d’un simple coup d’œil.

Pour ce faire, regardons à nouveau la structure générale de toute équation linéaire :

hache + b = 0

Attention : dans l'équation linéaire Toujours seule la variable x est présente au premier degré et quelques chiffres ! C'est tout ! Rien de plus. En même temps, il n’y a pas de X dans le carré, dans le cube, sous la racine, sous le logarithme et autres choses exotiques. Et (surtout !) il n’y a pas de fractions avec X au dénominateur ! Mais les fractions avec des nombres au dénominateur ou une division par numéro- facilement!

Par exemple:

Il s'agit d'une équation linéaire. L'équation ne contient que des X à la première puissance et des nombres. Et il n’y a pas de X dans les puissances supérieures – au carré, au cube, etc. Oui, il y a des fractions ici, mais en même temps les dénominateurs des fractions contiennent seulement des chiffres. A savoir - deux et trois. En d'autres termes, il n'y a pas division par x.

Et voici l'équation

On ne peut plus l’appeler linéaire, même si ici aussi il n’y a que des nombres et des X à la puissance première. Parce que, entre autres, il existe aussi des fractions avec des X dans les dénominateurs. Et après simplifications et transformations, une telle équation peut devenir n'importe quoi : linéaire, quadratique - n'importe quoi.

Comment résoudre des équations linéaires ? Exemples.

Alors, comment résoudre des équations linéaires ? Continuez à lire et soyez surpris.) La solution entière des équations linéaires est basée sur seulement deux éléments principaux. Listons-les.

1) Un ensemble d'actions élémentaires et de règles mathématiques.

Il s'agit d'utiliser des parenthèses, d'ouvrir des parenthèses, de travailler avec des fractions, de travailler avec des nombres négatifs, des tables de multiplication, etc. Ces connaissances et compétences sont nécessaires non seulement pour résoudre des équations linéaires, mais pour toutes les mathématiques en général. Et si cela vous pose des problèmes, n'oubliez pas les notes inférieures. Sinon tu vas avoir du mal...

2)

Il n'y en a que deux. Oui, oui ! De plus, ces transformations d’identité très basiques sont à la base de la solution non seulement d’équations linéaires, mais généralement de toutes équations mathématiques ! En un mot, la solution de toute autre équation - quadratique, logarithmique, trigonométrique, irrationnelle, etc. – en règle générale, cela commence par ces transformations très fondamentales. Mais la solution des équations linéaires, en fait, se termine par elles (transformations). Réponse toute prête.) Alors ne soyez pas paresseux et jetez un œil au lien.) De plus, les équations linéaires y sont également analysées en détail.

Eh bien, je pense qu'il est temps de commencer à regarder des exemples.

Pour commencer, en guise d’échauffement, examinons quelques éléments de base. Sans aucune fraction ni autre cloche et sifflet. Par exemple, cette équation :

x – 2 = 4 – 5x

Il s'agit d'une équation linéaire classique. Tous les X sont au plus à la première puissance et il n’y a de division par X nulle part. Le schéma de solution dans de telles équations est toujours le même et terriblement simple : tous les termes avec X doivent être rassemblés à gauche, et tous les termes sans X (c'est-à-dire les nombres) doivent être rassemblés à droite. Alors commençons à collectionner.

Pour ce faire, nous lançons la première transformation identitaire. Nous devons déplacer -5x vers la gauche et déplacer -2 vers la droite. Avec un changement de signe, bien sûr.) On transfère donc :

x + 5x = 4 + 2

Voici. La moitié de la bataille est terminée : les X ont été rassemblés en pile, tout comme les chiffres. Maintenant, nous en présentons des similaires à gauche, et nous les comptons à droite. On obtient :

6x = 6

Que nous manque-t-il désormais pour être pleinement heureux ? Oui, pour que le X pur reste à gauche ! Et le six gêne. Comment s'en débarrasser ? Maintenant, nous effectuons la deuxième transformation identique : divisons les deux côtés de l'équation par 6. Et voilà ! La réponse est prête.)

x = 1

Bien entendu, l’exemple est complètement primitif. Pour avoir une idée générale. Eh bien, décidons de quelque chose de plus important. Par exemple, regardons cette équation :

Regardons cela en détail.) Il s'agit également d'une équation linéaire, même s'il semblerait qu'il y ait ici des fractions. Mais dans les fractions il y a division par deux et il y a division par trois, mais il n'y a pas de division par une expression avec un X ! Alors décidons. En utilisant les mêmes transformations identiques, oui.)

Que devons-nous faire en premier ? Avec des X - à gauche, sans X - à droite ? En principe, c'est possible. Envolez-vous vers Sotchi via Vladivostok.) Ou vous pouvez emprunter l'itinéraire le plus court, en utilisant immédiatement une méthode universelle et puissante. Si vous connaissez les transformations identitaires, bien sûr.)

Tout d’abord, je pose une question clé : qu’est-ce qui vous frappe le plus et ce qui vous déplaît le plus dans cette équation ? 99 personnes sur 100 diront : fractions ! Et ils auront raison.) Alors débarrassons-nous-en d’abord. Sans danger pour l'équation elle-même.) Par conséquent, commençons tout de suite par deuxième transformation identitaire- de la multiplication. Par quoi devrions-nous multiplier le côté gauche pour que le dénominateur soit réduit avec succès ? C'est vrai, un deux. Et le côté droit ? Pour trois ! Mais... Les mathématiques sont une femme capricieuse. Elle, voyez-vous, nécessite seulement de multiplier les deux côtés pour le même numéro ! Multiplier chaque partie par son propre nombre ne fonctionne pas... Qu'allons-nous faire ? Quelque chose... Cherchez un compromis. Afin de satisfaire nos envies (se débarrasser des fractions) et de ne pas offenser les mathématiques.) Multiplions les deux parties par six !) C'est-à-dire par le dénominateur commun de toutes les fractions incluses dans l'équation. Ensuite, d’un seul coup, les deux et les trois seront réduits !)

Alors multiplions. Tout le côté gauche et tout le côté droit ! Nous utilisons donc des parenthèses. Voici à quoi ressemble la procédure elle-même :

Maintenant, nous ouvrons ces mêmes parenthèses :

Maintenant, représentant 6 par 6/1, multiplions six par chacune des fractions de gauche et de droite. C'est la multiplication habituelle des fractions, mais qu'il en soit ainsi, je vais la décrire en détail :

Et ici, attention ! Je mets le numérateur (x-3) entre parenthèses ! Tout cela parce que lors de la multiplication de fractions, le numérateur est multiplié entièrement, entièrement ! Et l’expression x-3 doit être travaillée comme une seule structure intégrale. Mais si vous écrivez le numérateur comme ceci :

6x – 3,

Mais tout est parfait et nous devons le finaliser. Que faire ensuite ? Ouvrir les parenthèses au numérateur de gauche ? Certainement pas! Vous et moi avons multiplié les deux côtés par 6 pour nous débarrasser des fractions et ne pas nous soucier d'ouvrir les parenthèses. A ce stade, nous avons besoin réduire nos fractions. Avec un sentiment de profonde satisfaction, nous réduisons tous les dénominateurs et obtenons une équation sans aucune fraction, en ligne :

3(x-3) + 6x = 30 – 4x

Et maintenant les parenthèses restantes peuvent être ouvertes :

3x – 9 + 6x = 30 – 4x

L’équation ne cesse de s’améliorer ! Rappelons maintenant à nouveau la première transformation identique. Avec un visage impassible, nous répétons le sort des classes juniors : avec X - à gauche, sans X - à droite. Et appliquez cette transformation :

3x + 6x + 4x = 30 + 9

Nous en présentons des similaires à gauche et comptons à droite :

13x = 39

Il reste à diviser les deux parties par 13. C'est-à-dire à appliquer à nouveau la deuxième transformation. Nous divisons et obtenons la réponse :

x = 3

Le travail est terminé. Comme vous pouvez le voir, dans cette équation nous avons dû appliquer la première transformation (transfert de termes) une fois et la seconde deux fois : au début de la solution nous avons utilisé la multiplication (par 6) afin de nous débarrasser des fractions, et à la fin de la solution nous avons utilisé la division (par 13), pour supprimer le coefficient devant le X. Et la solution de n’importe quelle (oui, n’importe quelle !) équation linéaire consiste en une combinaison de ces mêmes transformations dans une séquence ou une autre. Par où commencer exactement dépend de l’équation spécifique. Dans certains endroits, il est plus rentable de commencer par le transfert, et dans d'autres (comme dans cet exemple) par la multiplication (ou la division).

Nous travaillons du simple au complexe. Considérons maintenant la cruauté pure et simple. Avec un tas de fractions et de parenthèses. Et je vais vous dire comment ne pas vous surmener.)

Par exemple, voici l'équation :

Nous regardons l'équation pendant une minute, sommes horrifiés, mais nous nous ressaisissons quand même ! Le principal problème est de savoir par où commencer ? Vous pouvez ajouter des fractions sur le côté droit. Vous pouvez soustraire des fractions entre parenthèses. Vous pouvez multiplier les deux parties par quelque chose. Ou diviser... Alors, qu'est-ce qui est encore possible ? Réponse : tout est possible ! Les mathématiques n'interdisent aucune des actions répertoriées. Et quelle que soit la séquence d'actions et de transformations que vous choisissez, la réponse sera toujours la même : la bonne. À moins, bien sûr, qu’à un moment donné vous ne violiez l’identité de vos transformations et que vous créiez ainsi des erreurs…

Et, afin de ne pas commettre d'erreurs, dans des exemples aussi sophistiqués que celui-ci, il est toujours très utile d'évaluer son apparence et de comprendre dans son esprit : que peut-on faire dans l'exemple pour que maximum le simplifier en une seule étape ?

Alors découvrons-le. À gauche, les six au dénominateur. Personnellement, je ne les aime pas et ils sont très faciles à retirer. Permettez-moi de multiplier les deux côtés de l’équation par 6 ! Ensuite, les six à gauche seront réduits avec succès, les fractions entre parenthèses n'iront encore nulle part. Eh bien, ça va. Nous y reviendrons un peu plus tard.) Mais à droite, nous ferons annuler les dénominateurs 2 et 3. C'est avec cette action (en multipliant par 6) qu'on obtient un maximum de simplifications en une seule étape !

Après multiplication, toute notre mauvaise équation devient comme ceci :

Si vous ne comprenez pas exactement comment cette équation est née, c’est que vous n’avez pas bien compris l’analyse de l’exemple précédent. Et j'ai essayé, d'ailleurs...

Alors, révélons :

Maintenant, l’étape la plus logique serait d’isoler les fractions de gauche et d’envoyer 5x vers la droite. En même temps, nous en présenterons des similaires sur le côté droit. On obtient :

Beaucoup mieux déjà. Désormais, le côté gauche s’est préparé à la multiplication. Par quoi devrions-nous multiplier le côté gauche pour que le cinq et le quatre soient réduits à la fois ? Le 20 ! Mais nous avons également des désavantages des deux côtés de l’équation. Par conséquent, il sera plus pratique de multiplier les deux côtés de l'équation non pas par 20, mais par -20. Ensuite, d’un seul coup, les moins et les fractions disparaîtront.

On multiplie donc :

Quiconque ne comprend toujours pas cette étape signifie que le problème ne réside pas dans les équations. Les problèmes sont à la base ! Rappelons encore la règle d'or des parenthèses ouvrantes :

Si un nombre est multiplié par une expression entre parenthèses, alors ce nombre doit être multiplié séquentiellement par chaque terme de cette même expression. De plus, si le nombre est positif, alors les signes des expressions sont conservés après développement. Si négatif, remplacez par le contraire :

a(b+c) = ab+ac

-a(b+c) = -ab-ac

Nos inconvénients ont disparu après avoir multiplié les deux côtés par -20. Et maintenant, nous multiplions les parenthèses avec les fractions à gauche par tout à fait nombre positif 20. Ainsi, lorsque ces parenthèses sont ouvertes, tous les signes qui se trouvaient à l'intérieur sont conservés. Mais d'où viennent les parenthèses dans les numérateurs des fractions, je l'ai déjà expliqué en détail dans l'exemple précédent.

Vous pouvez maintenant réduire des fractions :

4(3-5x)-5(3x-2) = 20

Ouvrez les supports restants. Encore une fois, nous le révélons correctement. Les premières parenthèses sont multipliées par le nombre positif 4 et, par conséquent, tous les signes sont conservés lors de leur ouverture. Mais les secondes parenthèses sont multipliées par négatif le nombre est -5 et, par conséquent, tous les signes sont inversés :

12 - 20x - 15x + 10 = 20

Il ne reste que des bagatelles. Avec les X à gauche, sans les X à droite :

-20x – 15x = 20 – 10 – 12

-35x = -2

C'est presque tout. Sur la gauche, vous avez besoin d'un X pur, mais le nombre -35 vous gêne. On divise donc les deux côtés par (-35). Permettez-moi de vous rappeler que la deuxième transformation identitaire nous permet de multiplier et de diviser les deux côtés par peu importe nombre. Y compris les négatifs.) Pourvu que ce ne soit pas zéro ! N'hésitez pas à diviser et à obtenir la réponse :

X = 2/35

Cette fois, le X s'est avéré être fractionnaire. C'est bon. Un tel exemple.)

Comme on peut le voir, le principe de résolution d'équations linéaires (même les plus compliquées) est assez simple : on prend l'équation d'origine et, en utilisant des transformations identiques, on la simplifie successivement jusqu'à obtenir la réponse. Avec les bases, bien sûr ! Les principaux problèmes ici sont précisément le non-respect des bases (par exemple, il y a un moins devant les parenthèses, et ils ont oublié de changer les signes lors de l'expansion), ainsi que l'arithmétique banale. Alors ne négligez pas les bases ! Ils sont le fondement de toutes les autres mathématiques !

Quelques choses amusantes à faire lors de la résolution d’équations linéaires. Ou des occasions spéciales.

Tout irait bien. Cependant... Parmi les équations linéaires, il y a aussi des joyaux tellement amusants qu'en les résolvant, ils peuvent vous plonger dans une forte stupeur. Même un excellent élève.)

Par exemple, voici une équation qui semble anodine :

7x + 3 = 4x + 5 + 3x - 2

En bâillant largement et légèrement ennuyés, nous rassemblons tous les X à gauche et tous les chiffres à droite :

7x-4x-3x = 5-2-3

Nous en présentons des similaires, comptons et obtenons :

0 = 0

C'est ça! J'ai donné un exemple d'astuce ! Cette égalité en elle-même ne soulève aucune objection : zéro est bien égal à zéro. Mais X manque ! Sans laisser de trace ! Et nous devons écrire dans la réponse, à quoi x est égal. Sinon, la décision ne compte pas, oui.) Que faire ?

Ne pas paniquer! Dans de tels cas non standard, les concepts et principes mathématiques les plus généraux viennent à la rescousse. Qu'est-ce qu'une équation ? Comment résoudre des équations ? Que signifie résoudre une équation ?

Résoudre une équation signifie trouver Tous valeurs de la variable x, qui, lorsqu'elle est substituée dans original l'équation nous donnera la bonne égalité (identité) !

Mais nous avons une vraie égalité c'est déjà arrivé! 0=0, ou plutôt nulle part !) Nous ne pouvons que deviner à quels X nous obtenons cette égalité. Quel genre de X peut être remplacé dans originaléquation si, lors de la substitution, tous seront-ils encore réduits à zéro ? Vous ne l'avez pas encore compris ?

Eh bien, bien sûr ! Les X peuvent être remplacés n'importe lequel!!! Absolument n'importe lequel. Soumettez ce que vous voulez. Au moins 1, au moins -23, au moins 2,7 - peu importe ! Ils seront encore réduits et, par conséquent, la pure vérité demeurera. Essayez-le, remplacez-le et voyez par vous-même.)

Voici votre réponse :

x – n'importe quel nombre.

En notation scientifique, cette égalité s’écrit comme suit :

Cette entrée se lit comme ceci : "X est n'importe quel nombre réel."

Ou sous une autre forme, à intervalles réguliers :

Concevez-le comme vous préférez. C'est une réponse correcte et complètement complète !

Maintenant, je vais changer un seul nombre dans notre équation d'origine. Résolvons maintenant cette équation :

7x + 2 = 4x + 5 + 3x – 2

Encore une fois, nous transférons les termes, comptons et obtenons :

7x – 4x – 3x = 5 – 2 – 2

0 = 1

Et que pensez-vous de cette blague ? Il existait une équation linéaire ordinaire, mais elle est devenue une égalité incompréhensible

0 = 1…

Scientifiquement parlant, nous avons fausse égalité. Mais en russe, ce n’est pas vrai. Connerie. C’est absurde.) Parce que zéro n’est en aucun cas égal à un !

Et maintenant, voyons à nouveau quel type de X, lorsqu'ils sont remplacés dans l'équation d'origine, nous donneront une vraie égalité ? Lequel? Mais aucun ! Peu importe le X que vous remplacez, tout sera toujours raccourci et tout restera de la merde.)

Voici la réponse : aucune solution.

En notation mathématique, cette réponse s'écrit ainsi :

On y lit : « X appartient à l’ensemble vide. »

De telles réponses se produisent également assez souvent en mathématiques : les équations n’ont pas toujours de racines de principe. Certaines équations peuvent ne pas avoir de racine du tout. Du tout.

Voici deux surprises. J'espère que la disparition soudaine des X de l'équation ne vous laissera pas éternellement perplexe. C'est assez familier.)

Et puis j'entends une question logique : seront-ils à l'OGE ou à l'examen d'État unifié ? Sur l'examen d'État unifié en soi en tant que tâche - non. Trop simple. Mais dans l'OGE ou dans les problèmes de mots - facilement ! Alors maintenant, entraînons-nous et décidons :

Réponses (en désarroi) : -2 ; -1 ; n'importe quel nombre ; 2 ; aucune solution ; 7/13.

Est-ce que tout s'est bien passé ? Super! Vous avez de bonnes chances à l'examen.

Quelque chose ne colle pas ? Hm... Tristesse, bien sûr. Cela signifie qu’il y a encore des lacunes quelque part. Soit dans les bases, soit dans des transformations identiques. Ou alors c’est juste une simple question d’inattention. Relisez la leçon. Parce que ce n’est pas un sujet dont on peut se passer si facilement en mathématiques…

Bonne chance! Elle vous sourira certainement, croyez-moi !)

Un système d'équations linéaires est une union de n équations linéaires, chacune contenant k variables. C'est écrit ainsi :

Beaucoup, rencontrant pour la première fois l'algèbre supérieure, croient à tort que le nombre d'équations doit nécessairement coïncider avec le nombre de variables. En algèbre scolaire, cela se produit généralement, mais pour l’algèbre supérieure, ce n’est généralement pas vrai.

La solution d'un système d'équations est une séquence de nombres (k 1, k 2, ..., k n), qui est la solution de chaque équation du système, c'est-à-dire lors de la substitution dans cette équation au lieu des variables x 1, x 2, ..., x n donne l'égalité numérique correcte.

Ainsi, résoudre un système d’équations signifie trouver l’ensemble de toutes ses solutions ou prouver que cet ensemble est vide. Le nombre d'équations et le nombre d'inconnues pouvant ne pas coïncider, trois cas sont possibles :

1. Le système est incohérent, c'est-à-dire l'ensemble de toutes les solutions est vide. Un cas assez rare et facilement détectable quelle que soit la méthode utilisée pour résoudre le système.
2. Le système est cohérent et déterminé, c'est-à-dire a exactement une solution. La version classique, bien connue depuis l'école.
3. Le système est cohérent et indéfini, c'est-à-dire a une infinité de solutions. C'est l'option la plus difficile. Il ne suffit pas d'indiquer que « le système possède un ensemble infini de solutions », il faut décrire comment cet ensemble est structuré.

Une variable x i est dite autorisée si elle est incluse dans une seule équation du système, et avec un coefficient de 1. En d'autres termes, dans d'autres équations, le coefficient de la variable x i doit être égal à zéro.

Si nous sélectionnons une variable autorisée dans chaque équation, nous obtenons un ensemble de variables autorisées pour l'ensemble du système d'équations. Le système lui-même, écrit sous cette forme, sera également appelé résolu. D'une manière générale, un même système original peut être réduit à différents systèmes autorisés, mais pour l'instant cela ne nous préoccupe pas. Voici des exemples de systèmes autorisés :

Les deux systèmes sont résolus par rapport aux variables x 1 , x 3 et x 4 . Cependant, avec le même succès, on peut affirmer que le deuxième système est résolu par rapport à x 1, x 3 et x 5. Il suffit de réécrire la toute dernière équation sous la forme x 5 = x 4.

Considérons maintenant un cas plus général. Disons k variables au total, dont r sont autorisées. Deux cas sont alors possibles :

1. Le nombre de variables autorisées r est égal au nombre total de variables k : r = k. Nous obtenons un système de k équations dans lesquelles r = k variables autorisées. Un tel système est conjoint et définitif, car x 1 = b 1, x 2 = b 2, ..., x k = b k ;
2. Le nombre de variables autorisées r est inférieur au nombre total de variables k : r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Ainsi, dans les systèmes ci-dessus, les variables x 2, x 5, x 6 (pour le premier système) et x 2, x 5 (pour le second) sont libres. Le cas où il existe des variables libres est mieux formulé sous forme de théorème :

Attention : c’est un point très important ! Selon la façon dont vous écrivez le système résultant, la même variable peut être autorisée ou libre. La plupart des professeurs de mathématiques supérieures recommandent d'écrire les variables par ordre lexicographique, c'est-à-dire indice ascendant. Cependant, vous n’êtes pas obligé de suivre ces conseils.

Théorème. Si dans un système de n équations les variables x 1, x 2, ..., x r sont autorisées, et x r + 1, x r + 2, ..., x k sont libres, alors :

1. Si nous définissons les valeurs des variables libres (x r + 1 = t r + 1, x r + 2 = t r + 2, ..., x k = t k), puis trouvons les valeurs x 1, x 2, ..., x r, nous obtenons une des décisions.
2. Si dans deux solutions les valeurs des variables libres coïncident, alors les valeurs des variables autorisées coïncident également, c'est-à-dire les solutions sont égales.

Quelle est la signification de ce théorème ? Pour obtenir toutes les solutions d’un système d’équations résolu, il suffit d’isoler les variables libres. Ensuite, en attribuant différentes valeurs aux variables libres, nous obtiendrons des solutions toutes faites. C'est tout - de cette façon, vous pouvez obtenir toutes les solutions du système. Il n'y a pas d'autres solutions.

Conclusion : le système d'équations résolu est toujours cohérent. Si le nombre d'équations dans un système résolu est égal au nombre de variables, le système sera défini ; s'il est inférieur, il sera indéfini ;

Et tout irait bien, mais la question se pose : comment en obtenir une résolue à partir du système d'équations d'origine ? Pour cela il y a

Une équation linéaire à inconnues x 1, x 2, ..., x n est une équation de la forme

A 1 x 1 + a 2 x 2 + …+ a n x n = b ;

les nombres a et a 2 , a 2 , ..., an sont appelés coefficients des inconnues, le nombre b est le terme libre de l'équation.

Des équations linéaires à une inconnue ont pu être résolues dans l'ancienne Babylone et en Égypte il y a plus de 4 000 ans. Citons par exemple un problème du papyrus Rhind (appelé aussi papyrus Ahmes), conservé au British Museum et datant de la période 2000-1700. Colombie-Britannique e.: "Trouver un nombre si l'on sait qu'en y ajoutant les 2/3 et en soustrayant son tiers de la somme résultante, on obtient le nombre 10." La solution à ce problème revient à résoudre l’équation linéaire

x + (2/3)x − (1/3)(x + (2/3)x) = 10, d'où x = 9.

Présentons également le problème de Metrodorus, dont on ne sait rien de la vie, sinon qu'il fut l'auteur d'intéressants problèmes composés en vers.

Ici Diophante est enterré, et la pierre tombale
Avec un comptage habile, il nous dira
Quelle était la durée de sa vie.
Par décret de Dieu, il fut un garçon pendant un sixième de sa vie ;
Dans la douzième partie, sa brillante jeunesse passe alors.
Ajoutons la septième partie de la vie - devant nous se trouve le foyer de l'Hymen.
Cinq ans se sont écoulés ; et Hymen lui envoya un fils.
Mais malheur à l'enfant ! Il a à peine vécu la moitié
Ces années où le père est mort, le malheureux.
Diophante a souffert pendant quatre ans de la perte d'une telle tombe
Et il est mort après avoir vécu pour la science. Dites-moi,
Quel âge avait Diophante lorsqu’il mourut ?

Résoudre une équation linéaire

(1/6)x + (1/12)x +(1/7)x + 5 + (1/2)x + 4 = x,

nous constatons que x = 84 - c'est le nombre d'années que Diophante a vécu.

Diophante lui-même a accordé beaucoup d'attention aux équations indéfinies (c'est le nom donné aux équations algébriques ou aux systèmes de telles équations à deux ou plusieurs inconnues à coefficients entiers, pour lesquelles des solutions entières ou rationnelles sont recherchées ; le nombre d'inconnues doit être supérieur à le nombre d'équations). Ces équations sont appelées équations diophantiennes. Certes, Diophante, qui vécut au tournant des IIe et IIIe siècles, s'intéressait principalement aux équations indéfinies des degrés supérieurs.

Un système d'équations algébriques, dont chacune a la forme (1), est appelé système linéaire. Les coefficients des équations incluses dans le système sont généralement numérotés avec deux indices, dont le premier est le numéro de l'équation et le second (comme dans (1)) est le numéro de l'inconnue. Par exemple, un système de m équations à n inconnues s’écrit sous la forme

$\gauche. \begin(aligned) ((a)_(11))((x)_(1))+((a)_(12))((x)_(2))+\ldots+((a)_ (1n))((x)_(n))=((b)_(1)), \\ ((a)_(21))((x)_(1))+((a)_ (22))((x)_(2))+\ldots+((a)_(2n))((x)_(n))=((b)_(2)), \\ ((a )_(m1))((x)_(1))+((a)_(m2))((x)_(2))+\ldots+((a)_(mn))((x) _(n))=((b)_(m)). \\ \end(aligné) \right\)(2)$

Considérons un système de deux équations linéaires à deux inconnues :

$\gauche. \begin(aligned) ((a)_(11))((x)_(1))+((a)_(12))((x)_(2))=((b)_(1 )), \\ ((a)_(21))((x)_(1))+((a)_(22))((x)_(2))=((b)_(2 )), \\ \end(aligné) \right\)(3)$

Multiplions la première équation du système (3) par un 22 et soustrayons de l'équation résultante la seconde, multipliée par un 12 ; de même, nous multiplions la deuxième équation du système (3) par un 11 et soustrayons la première, multipliée par un 21, de l'équation résultante. Après cela, nous obtenons le système :

$\gauche. \begin(aligned) (a 11 a 22 - a 12 a 21)x 2 = a 11 b 2 -b 1 a 21 , (a 11 a 22 - a 12 a 21)x 1 = b 1 a 22 - a 12 b 2 , \end(aligné) \right\)(4)$

$\gauche. \begin(aligned) (a_(11)a_(22)−a_(12)a_(21))x_2 = a_(11)b_2−b_1a_(21), \\ (a_(11)a_(22)−a_ (12)a_(21))x_1 = b_1a_(22)−a_(12)b_2, \\ \end(aligned) \right\)(4)$

ce qui est une conséquence du système (3). Le système (4) peut s’écrire sous la forme

$\gauche. \begin(aligned) Δ⋅x_1=Δ_1, \\ Δ⋅x_2=Δ_2, \\ \end(aligned) \right\)(5)$

où ∆ est le déterminant d'une matrice composée des coefficients du système (voir Déterminant), ∆ i sont les déterminants des matrices obtenues à partir du remplacement précédent de la i-ème colonne par une colonne de termes libres, i = 1,2 . De plus, si ∆ ≠ 0, alors le système (5) a une solution unique :

x 1 = ∆ 1 /∆, x 2 = ∆ 2 /∆.

La substitution directe vérifie que cette paire de nombres est également une solution au système (3). En utilisant la même règle, on cherche une solution à un système de n équations linéaires à n inconnues : si le déterminant du système ∆ est non nul, alors le système a une solution unique, et

x je = ∆ je /∆

où ∆ i est le déterminant de la matrice obtenue à partir d'une matrice composée des coefficients du système en remplaçant la i-ème colonne par une colonne de termes libres. La règle décrite pour résoudre des systèmes linéaires est appelée règle de Cramer. (G. Cramer - mathématicien suisse, 1704-1752).

Si ∆ = 0, alors ∆ 1 et ∆ 2 doivent disparaître (sinon (5), et surtout (3) n'ont pas de solutions). Si la condition ∆ = ∆ 1 = ∆ 2 = 0 est satisfaite, si les coefficients correspondants pour les inconnues et les termes libres de l'équation du système (3) sont proportionnels, alors le système aura une infinité de solutions ; si au moins un des coefficients des inconnues est différent de zéro (par exemple, si a 12 ≠ 0), alors x 1 peut être considéré comme n'importe lequel, alors

x 2 = b 1 /une 12 − une 11 x 1 /une 12

Reste à analyser le cas où le système a la forme

$\gauche. \begin(aligned) 0⋅x_1+,0⋅x_2=b_, \\ 0⋅x_1+,0⋅x_2=b_, \\ \end(aligned) \right\)$

pour lequel la réponse est évidente : si b 1 = b 2 = 0, alors la solution est n'importe quelle paire de nombres, sinon il n'y a pas de solutions.

Dans le cas général, pour un système de n équations à n inconnues pour ∆ ≠ 0, le système a une solution unique qui, comme déjà mentionné, peut être trouvée à l’aide de la règle de Cramer. Si ∆ = 0 et qu'au moins un des déterminants ∆ i est différent de zéro, le système est incohérent (c'est-à-dire qu'il n'a pas de solutions). Dans le cas où ∆ = ∆ 1 = ∆ 2 = ... = ∆ n = 0, le système peut soit être incohérent, soit avoir une infinité de solutions. Il est assez difficile d'établir lequel de ces deux cas est réalisé à l'aide de déterminants, et nous n'aborderons pas ce sujet. En pratique, la règle de Cramer n'est généralement pas utilisée pour résoudre des systèmes linéaires. Le plus souvent, la méthode gaussienne est utilisée à ces fins (voir Exception inconnue).

Comme on le sait, l'équation linéaire a 1 x 1 + a 2 x 2 = b définit une droite sur le plan (x 1 ; x 2) dans le cas où au moins un des coefficients a 1 et a 2 est différent de zéro. Si l'on prend deux droites sur un plan, alors les cas suivants sont possibles (voir figure) : 1) les droites sont parallèles et n'ont pas de points communs, et alors le système n'a pas de solutions ; 2) les lignes se croisent, et le système a alors une solution ; 3) les droites coïncident, et alors le système a une infinité de solutions. Mais deux droites prises « au hasard » se croiseront « en règle générale », c'est-à-dire qu'en règle générale, un système de deux équations linéaires à deux variables aura une solution. Tout point sur une certaine ligne du plan correspond à la solution d'un « système » (constitué d'une équation), c'est-à-dire qu'en règle générale, le cas 3 se produit (le cas 2 est impossible, et le cas 1 est réalisé si l'on prend l'équation 0 x 1 + 0 x 2 = b, où b ≠ 0, ce qui ne définit pas de ligne sur le plan). Si nous prenons 3 lignes ou plus sur un plan, alors, d'une manière générale, elles peuvent toutes coïncider ou passer par un point, mais, en règle générale, le premier cas se produit - les lignes n'ont pas de point commun.

Vous devez d’abord comprendre de quoi il s’agit.

Il existe une définition simple équation linéaire, qui est donnée dans une école ordinaire : « une équation dans laquelle la variable n’apparaît qu’à la première puissance ». Mais ce n’est pas tout à fait exact : l’équation n’est pas linéaire, elle ne se réduit même pas à cela, elle se réduit au quadratique.

Une définition plus précise est : équation linéaire est une équation qui, en utilisant transformations équivalentes peut être réduit à la forme , où title="a,b in bbR, ~a0">. На деле мы будем приводить это уравнение к виду путём переноса в правую часть и деления обеих частей уравнения на . Осталось разъяснить, какие уравнения и как мы можем привести к такому виду, и, самое главное, что дальше делать с ними, чтобы решить его.!}

En fait, pour comprendre si une équation est linéaire ou non, il faut d'abord la simplifier, c'est-à-dire la mettre sous une forme où sa classification sera sans ambiguïté. N'oubliez pas que vous pouvez faire ce que vous voulez avec une équation tant qu'elle ne change pas ses racines - c'est ce que c'est. conversion équivalente. Les transformations équivalentes les plus simples incluent :

1. parenthèses ouvrantes
2. apportant des choses similaires
3. multiplier et/ou diviser les deux côtés d'une équation par un nombre non nul
4. ajouter et/ou soustraire des deux côtés du même nombre ou de la même expression*

Exemple 1 :
(ouvrons les parenthèses)
(ajouter aux deux parties et soustraire/transférer en changeant le signe du nombre à gauche et les variables à droite)
(donnons-en des similaires)
(divisez les deux côtés de l'équation par 3)

Nous obtenons donc une équation qui a les mêmes racines que celle d’origine. Rappelons au lecteur que "résoudre l'équation"- c'est retrouver toutes ses racines et prouver qu'il n'y en a pas d'autres, et "racine de l'équation"- c'est un nombre qui, substitué à l'inconnu, transformera l'équation en une véritable égalité. Eh bien, dans la dernière équation, trouver un nombre qui transforme l'équation en une véritable égalité est très simple : c'est le nombre. Aucun autre nombre ne fera une identité à partir de cette équation. Répondre:

Exemple 2 :
(multipliez les deux côtés de l'équation par , après s'être assuré qu'on ne multiplie pas par : title="x3/2"> и title="x3">. То есть если такие корни получатся, то мы их обязаны будем выкинуть.)!}
(ouvrons les parenthèses)
(déplaçons les termes)
(donnons-en des similaires)
(on divise les deux parties par )

C’est à peu près ainsi que toutes les équations linéaires sont résolues. Pour les jeunes lecteurs, cette explication semblait très probablement compliquée, nous proposons donc une version "équations linéaires pour la 5e année"

Équations linéaires à deux variables

Un écolier dispose de 200 roubles pour déjeuner à l’école. Un gâteau coûte 25 roubles et une tasse de café 10 roubles. Combien de gâteaux et de tasses de café pouvez-vous acheter pour 200 roubles ?

Notons le nombre de gâteaux par x, et le nombre de tasses de café à travers oui. Ensuite, le coût des gâteaux sera désigné par l'expression 25 x, et le coût des tasses de café en 10 oui .

25x— prix x gâteaux
10oui — prix oui tasses de café

Le montant total devrait être de 200 roubles. On obtient alors une équation à deux variables x Et oui

25x+ 10oui= 200

Combien de racines cette équation a-t-elle ?

Tout dépend de l’appétit de l’élève. S’il achète 6 gâteaux et 5 tasses de café, alors les racines de l’équation seront les nombres 6 et 5.

La paire de valeurs 6 et 5 serait les racines de l'équation 25 x+ 10oui= 200 . Écrit comme (6 ; 5), le premier nombre étant la valeur de la variable x, et le second - la valeur de la variable oui .

6 et 5 ne sont pas les seules racines qui inversent l’équation 25 x+ 10oui= 200 à l'identité. S'il le souhaite, pour les mêmes 200 roubles, un étudiant peut acheter 4 gâteaux et 10 tasses de café :

Dans ce cas, les racines de l'équation 25 x+ 10oui= 200 est une paire de valeurs (4 ; 10).

De plus, un écolier ne peut pas acheter de café du tout, mais acheter des gâteaux pour la totalité de 200 roubles. Alors les racines de l’équation 25 x+ 10oui= 200 seront les valeurs 8 et 0

Ou vice versa, n'achetez pas de gâteaux, mais achetez du café pour la totalité de 200 roubles. Alors les racines de l’équation 25 x+ 10oui= 200 les valeurs seront 0 et 20

Essayons de lister toutes les racines possibles de l'équation 25 x+ 10oui= 200 . Admettons que les valeurs x Et oui appartiennent à l’ensemble des entiers. Et que ces valeurs soient supérieures ou égales à zéro :

x∈Z, oui∈ Z ;
x ≥ 0, y ≥ 0

Cela conviendra à l'étudiant lui-même. Il est plus pratique d'acheter des gâteaux entiers que, par exemple, plusieurs gâteaux entiers et un demi-gâteau. Il est également plus pratique de prendre du café en tasses entières que, par exemple, plusieurs tasses entières et une demi-tasse.

Notez que pour les impairs x il est impossible d’atteindre l’égalité sous aucun prétexte oui. Alors les valeurs x les nombres suivants seront 0, 2, 4, 6, 8. Et sachant x peut être facilement déterminé oui

Ainsi, nous avons reçu les paires de valeurs suivantes (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Ces paires sont des solutions ou des racines de l'équation 25 x+ 10oui= 200. Ils transforment cette équation en une identité.

Équation de la forme hache + par = c appelé équation linéaire à deux variables. La solution ou les racines de cette équation sont une paire de valeurs ( X ; oui), ce qui en fait une identité.

Notez également que si une équation linéaire à deux variables s'écrit sous la forme hache + b y = c , alors ils disent que c'est écrit en canonique forme (normale).

Certaines équations linéaires à deux variables peuvent être réduites à une forme canonique.

Par exemple, l'équation 2(16x+ 3oui - 4) = 2(12 + 8x − oui) peut être rappelé hache + par = c. Ouvrons les parenthèses des deux côtés de cette équation et obtenons 32x + 6oui − 8 = 24 + 16x − 2oui . Nous regroupons les termes contenant des inconnues sur le côté gauche de l'équation et les termes sans inconnues sur le côté droit. Ensuite, nous obtenons 32x− 16x+ 6oui+ 2oui = 24 + 8 . Nous présentons des termes similaires des deux côtés, nous obtenons l'équation 16 x+ 8oui= 32. Cette équation se réduit à la forme hache + par = c et est canonique.

Équation 25 discutée plus tôt x+ 10oui= 200 est aussi une équation linéaire à deux variables sous forme canonique. Dans cette équation les paramètres un , b Et c sont égaux respectivement aux valeurs 25, 10 et 200.

En fait, l'équation hache + par = c a d'innombrables solutions. Résoudre l'équation 25x+ 10oui= 200, nous avons recherché ses racines uniquement sur l'ensemble des entiers. En conséquence, nous avons obtenu plusieurs paires de valeurs qui ont transformé cette équation en identité. Mais sur l’ensemble des nombres rationnels, l’équation 25 x+ 10oui= 200 aura une infinité de solutions.

Pour obtenir de nouvelles paires de valeurs, vous devez prendre une valeur arbitraire pour x, puis exprimez oui. Par exemple, prenons pour la variable x valeur 7. Ensuite, nous obtenons une équation avec une variable 25×7 + 10oui= 200 dans lequel on peut exprimer oui

Laisser x= 15. Alors l'équation 25x+ 10oui= 200 devient 25 × 15 + 10oui= 200. De là, nous constatons que oui = −17,5

Laisser x= −3 . Alors l'équation 25x+ 10oui= 200 devient 25 × (−3) + 10oui= 200. De là, nous constatons que oui = −27,5

Système de deux équations linéaires à deux variables

Pour l'équation hache + par = c vous pouvez prendre des valeurs arbitraires autant de fois que vous le souhaitez x et trouver des valeurs pour oui. Prise séparément, une telle équation aura d’innombrables solutions.

Mais il arrive aussi que les variables x Et oui relié non pas par une, mais par deux équations. Dans ce cas, ils forment ce qu'on appelle système d'équations linéaires à deux variables. Un tel système d'équations peut avoir une paire de valeurs (ou en d'autres termes : « une solution »).

Il peut également arriver que le système n’ait aucune solution. Un système d'équations linéaires peut avoir d'innombrables solutions dans des cas rares et exceptionnels.

Deux équations linéaires forment un système lorsque les valeurs x Et oui entrer dans chacune de ces équations.

Revenons à la toute première équation 25 x+ 10oui= 200 . L'une des paires de valeurs de cette équation était la paire (6 ; 5) . C'est le cas où pour 200 roubles, vous pourriez acheter 6 gâteaux et 5 tasses de café.

Formulons le problème pour que la paire (6 ; 5) devienne la seule solution de l'équation 25 x+ 10oui= 200 . Pour ce faire, créons une autre équation qui relierait la même x des gâteaux et oui tasses de café.

Énonçons le texte du problème comme suit :

« L'étudiant a acheté plusieurs gâteaux et plusieurs tasses de café pour 200 roubles. Un gâteau coûte 25 roubles et une tasse de café 10 roubles. Combien de gâteaux et de tasses de café l'élève a-t-il acheté si l'on sait que le nombre de gâteaux est supérieur d'une unité au nombre de tasses de café ?

Nous avons déjà la première équation. C'est l'équation 25 x+ 10oui= 200 . Créons maintenant une équation pour la condition "le nombre de gâteaux est supérieur d'une unité au nombre de tasses de café" .

Le nombre de gâteaux est x, et le nombre de tasses de café est oui. Vous pouvez écrire cette phrase en utilisant l'équation x−y= 1. Cette équation signifie que la différence entre les gâteaux et le café est de 1.

x = oui+1. Cette équation signifie que le nombre de gâteaux est supérieur d’un au nombre de tasses de café. Par conséquent, pour obtenir l’égalité, on ajoute un au nombre de tasses de café. Cela peut être facilement compris si l'on utilise le modèle d'échelles que nous avons considéré lors de l'étude des problèmes les plus simples :

Nous avons deux équations : 25 x+ 10oui= 200 et x = oui+ 1. Puisque les valeurs x Et oui, à savoir 6 et 5 sont inclus dans chacune de ces équations, alors ensemble ils forment un système. Écrivons ce système. Si les équations forment un système, elles sont alors encadrées par le signe du système. Le symbole système est une accolade :

Résolvons ce système. Cela nous permettra de voir comment on arrive aux valeurs 6 et 5. Il existe de nombreuses méthodes pour résoudre de tels systèmes. Regardons les plus populaires d'entre eux.

Méthode de substitution

Le nom de cette méthode parle de lui-même. Son essence est de substituer une équation à une autre, après avoir exprimé au préalable l'une des variables.

Dans notre système, rien n'a besoin d'être exprimé. Dans la deuxième équation x = oui+ 1 variable x déjà exprimé. Cette variable est égale à l'expression oui+1. Ensuite, vous pouvez remplacer cette expression dans la première équation au lieu de la variable x

Après avoir remplacé l'expression oui+ 1 dans la première équation à la place x, on obtient l'équation 25(oui+ 1) + 10oui= 200 . Il s'agit d'une équation linéaire à une variable. Cette équation est assez simple à résoudre :

Nous avons trouvé la valeur de la variable oui. Remplaçons maintenant cette valeur dans l'une des équations et trouvons la valeur x. Pour cela, il est pratique d'utiliser la deuxième équation x = oui+1. Remplaçons-y la valeur oui

Cela signifie que la paire (6 ; 5) est une solution du système d’équations, comme nous le souhaitions. On vérifie et s'assure que le couple (6 ; 5) satisfait le système :

Exemple 2

Remplaçons la première équation x= 2 + oui dans la deuxième équation 3 x− 2oui= 9. Dans la première équation, la variable xégal à l'expression 2 + oui. Remplaçons cette expression dans la deuxième équation au lieu de x

Trouvons maintenant la valeur x. Pour ce faire, substituons la valeur oui dans la première équation x= 2 + oui

Cela signifie que la solution du système est la valeur de paire (5 ; 3)

Exemple 3. Résolvez le système d'équations suivant en utilisant la méthode de substitution :

Ici, contrairement aux exemples précédents, l’une des variables n’est pas exprimée explicitement.

Pour remplacer une équation par une autre, vous avez d'abord besoin de .

Il est conseillé d'exprimer la variable qui a un coefficient de un. La variable a un coefficient de un x, qui est contenu dans la première équation x+ 2oui= 11. Exprimons cette variable.

Après expression variable x, notre système prendra la forme suivante :

Remplaçons maintenant la première équation par la seconde et trouvons la valeur oui

Remplaçons oui x

Cela signifie que la solution du système est une paire de valeurs (3 ; 4)

Bien entendu, vous pouvez également exprimer une variable oui. Cela ne changera pas les racines. Mais si vous exprimez oui, Le résultat n’est pas une équation très simple, dont la résolution prendra plus de temps. Cela ressemblera à ceci :

On voit que dans cet exemple on exprime x beaucoup plus pratique que d'exprimer oui .

Exemple 4. Résolvez le système d'équations suivant en utilisant la méthode de substitution :

Exprimons dans la première équation x. Le système prendra alors la forme :

oui

Remplaçons oui dans la première équation et trouvez x. Vous pouvez utiliser l'équation originale 7 x+ 9oui= 8, ou utiliser l'équation dans laquelle la variable est exprimée x. Nous utiliserons cette équation car elle est pratique :

Cela signifie que la solution du système est une paire de valeurs (5 ; −3)

Méthode d'addition

La méthode d’addition consiste à additionner terme par terme les équations incluses dans le système. Cet ajout aboutit à une nouvelle équation à une variable. Et résoudre une telle équation est assez simple.

Résolvons le système d'équations suivant :

Ajoutons le côté gauche de la première équation avec le côté gauche de la deuxième équation. Et le côté droit de la première équation avec le côté droit de la deuxième équation. On obtient l'égalité suivante :

Regardons des termes similaires :

En conséquence, nous avons obtenu l'équation la plus simple 3 x= 27 dont la racine est 9. Connaître la valeur x tu peux trouver la valeur oui. Remplaçons la valeur x dans la deuxième équation x−y= 3 . Nous obtenons 9 − oui= 3 . D'ici oui= 6 .

Cela signifie que la solution du système est une paire de valeurs (9 ; 6)

Exemple 2

Ajoutons le côté gauche de la première équation avec le côté gauche de la deuxième équation. Et le côté droit de la première équation avec le côté droit de la deuxième équation. Dans l’égalité résultante, nous présentons des termes similaires :

En conséquence, nous avons obtenu l'équation la plus simple 5 x= 20, dont la racine est 4. Connaître la valeur x tu peux trouver la valeur oui. Remplaçons la valeur x dans la première équation 2 x+y= 11. Prenons 8+ oui= 11. D'ici oui= 3 .

Cela signifie que la solution du système est une paire de valeurs (4;3)

Le processus d'ajout n'est pas décrit en détail. Cela doit être fait mentalement. Lors de l'addition, les deux équations doivent être réduites à la forme canonique. C'est à dire ac + par = c .

D'après les exemples considérés, il ressort clairement que l'objectif principal de l'ajout d'équations est de se débarrasser de l'une des variables. Mais il n'est pas toujours possible de résoudre immédiatement un système d'équations en utilisant la méthode d'addition. Le plus souvent, le système est d'abord amené sous une forme dans laquelle les équations incluses dans ce système peuvent être ajoutées.

Par exemple, le système peut être résolu immédiatement par addition. Lors de l'addition des deux équations, les termes oui Et −oui disparaîtront car leur somme est nulle. En conséquence, l'équation la plus simple 11 est formée x= 22, dont la racine est 2. Il sera alors possible de déterminer ouiégal à 5.

Et le système d'équations La méthode d'addition ne peut pas être résolue immédiatement, car elle n'entraînera pas la disparition d'une des variables. L'addition donnera l'équation 8 x+ oui= 28, qui a un nombre infini de solutions.

Si les deux côtés de l’équation sont multipliés ou divisés par le même nombre, non égal à zéro, vous obtenez une équation équivalente à celle donnée. Cette règle est également vraie pour un système d'équations linéaires à deux variables. L'une des équations (ou les deux équations) peut être multipliée par n'importe quel nombre. Le résultat sera un système équivalent dont les racines coïncideront avec le précédent.

Revenons au tout premier système, qui décrivait le nombre de gâteaux et de tasses de café qu'un écolier achetait. La solution à ce système était une paire de valeurs (6 ; 5).

Multiplions les deux équations incluses dans ce système par quelques nombres. Disons que l'on multiplie la première équation par 2 et la seconde par 3

En conséquence, nous avons obtenu un système
La solution à ce système est toujours le couple de valeurs (6 ; 5)

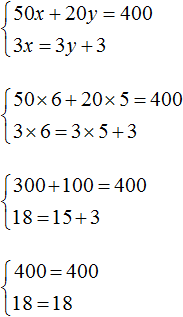
Cela signifie que les équations incluses dans le système peuvent être réduites à une forme adaptée à l'application de la méthode d'addition.

Revenons au système , que nous n’avons pas pu résoudre en utilisant la méthode d’addition.

Multipliez la première équation par 6 et la seconde par −2

On obtient alors le système suivant :

Additionnons les équations incluses dans ce système. Ajout de composants 12 x et −12 x donnera 0, addition 18 oui et 4 oui donnera 22 oui, et ajouter 108 et −20 donne 88. On obtient alors l'équation 22 oui= 88, à partir d'ici oui = 4 .

Si au début il est difficile d'ajouter des équations dans votre tête, vous pouvez alors écrire comment le côté gauche de la première équation s'additionne avec le côté gauche de la deuxième équation, et le côté droit de la première équation avec le côté droit de la deuxième équation :

Sachant que la valeur de la variable oui est égal à 4, vous pouvez trouver la valeur x. Remplaçons oui dans l'une des équations, par exemple dans la première équation 2 x+ 3oui= 18. On obtient alors une équation à une variable 2 x+ 12 = 18. Déplaçons 12 vers la droite, en changeant le signe, nous obtenons 2 x= 6, à partir d'ici x = 3 .

Exemple 4. Résolvez le système d'équations suivant en utilisant la méthode d'addition :

Multiplions la deuxième équation par −1. Le système prendra alors la forme suivante :

Ajoutons les deux équations. Ajout de composants x Et −x donnera 0, addition 5 oui et 3 oui donnera 8 oui, et ajouter 7 et 1 donne 8. Le résultat est l'équation 8 oui= 8 dont la racine est 1. Sachant que la valeur oui est égal à 1, vous pouvez trouver la valeur x .

Remplaçons oui dans la première équation, on obtient x+ 5 = 7, donc x= 2

Exemple 5. Résolvez le système d'équations suivant en utilisant la méthode d'addition :

Il est souhaitable que les termes contenant les mêmes variables soient situés les uns en dessous des autres. Par conséquent, dans la deuxième équation, les termes 5 oui et −2 xÉchangons nos places. En conséquence, le système prendra la forme :

Multiplions la deuxième équation par 3. Le système prendra alors la forme :

Ajoutons maintenant les deux équations. À la suite de l'addition, nous obtenons l'équation 8 oui= 16, dont la racine est 2.

Remplaçons oui dans la première équation, nous obtenons 6 x− 14 = 40. Déplaçons le terme −14 vers la droite, en changeant le signe, et obtenons 6 x= 54 . D'ici x= 9.

Exemple 6. Résolvez le système d'équations suivant en utilisant la méthode d'addition :

Débarrassons-nous des fractions. Multipliez la première équation par 36 et la seconde par 12

Dans le système résultant la première équation peut être multipliée par −5 et la seconde par 8

Additionnons les équations du système résultant. On obtient alors l'équation la plus simple −13 oui= −156 . D'ici oui= 12. Remplaçons oui dans la première équation et trouvez x

Exemple 7. Résolvez le système d'équations suivant en utilisant la méthode d'addition :

Ramenons les deux équations sous forme normale. Ici, il convient d’appliquer la règle de proportion dans les deux équations. Si dans la première équation le côté droit est représenté par , et le côté droit de la deuxième équation par , alors le système prendra la forme :

Nous avons une proportion. Multiplions ses termes extrêmes et moyens. Le système prendra alors la forme :

Multiplions la première équation par −3 et ouvrons les parenthèses dans la seconde :

Ajoutons maintenant les deux équations. En additionnant ces équations, nous obtenons une égalité nulle des deux côtés :

Il s’avère que le système propose d’innombrables solutions.

Mais nous ne pouvons pas simplement prendre des valeurs arbitraires du ciel pour x Et oui. Nous pouvons spécifier l'une des valeurs, et l'autre sera déterminée en fonction de la valeur que nous spécifions. Par exemple, laissez x= 2 . Remplaçons cette valeur dans le système :

Suite à la résolution de l’une des équations, la valeur de oui, qui satisfera les deux équations :

La paire de valeurs résultante (2 ; −2) satisfera le système :

Trouvons une autre paire de valeurs. Laisser x= 4. Remplaçons cette valeur dans le système :

Vous pouvez voir à l'œil nu que la valeur oui est égal à zéro. Nous obtenons alors une paire de valeurs (4 ; 0) qui satisfont notre système :

Exemple 8. Résolvez le système d'équations suivant en utilisant la méthode d'addition :

Multipliez la première équation par 6 et la seconde par 12

Réécrivons ce qui reste :

Multiplions la première équation par −1. Le système prendra alors la forme :

Ajoutons maintenant les deux équations. À la suite de l'addition, l'équation 6 est formée b= 48, dont la racine est 8. Remplacer b dans la première équation et trouvez un

Système d'équations linéaires à trois variables

Une équation linéaire à trois variables comprend trois variables avec des coefficients, ainsi qu'un terme à l'origine. Sous forme canonique, il peut s'écrire ainsi :

hache + par + cz = d

Cette équation a d'innombrables solutions. En donnant des valeurs différentes à deux variables, on peut trouver une troisième valeur. La solution dans ce cas est un triplet de valeurs ( X ; oui ; z) qui transforme l'équation en une identité.

Si les variables x, y, z sont interconnectés par trois équations, alors un système de trois équations linéaires à trois variables est formé. Pour résoudre un tel système, vous pouvez utiliser les mêmes méthodes qui s'appliquent aux équations linéaires à deux variables : la méthode de substitution et la méthode d'addition.

Exemple 1. Résolvez le système d'équations suivant en utilisant la méthode de substitution :

Exprimons dans la troisième équation x. Le système prendra alors la forme :

Faisons maintenant la substitution. Variable x est égal à l'expression 3 − 2oui − 2z . Remplaçons cette expression dans les première et deuxième équations :

Ouvrons les parenthèses dans les deux équations et présentons des termes similaires :

Nous sommes arrivés à un système d'équations linéaires à deux variables. Dans ce cas, il est pratique d’utiliser la méthode d’addition. En conséquence, la variable oui disparaîtra et on pourra retrouver la valeur de la variable z

Trouvons maintenant la valeur oui. Pour ce faire, il est pratique d'utiliser l'équation - oui+ z= 4. Remplacez-y la valeur z

Trouvons maintenant la valeur x. Pour ce faire, il est pratique d'utiliser l'équation x= 3 − 2oui − 2z . Remplaçons-y les valeurs oui Et z

Ainsi, le triple de valeurs (3 ; −2 ; 2) est une solution de notre système. En vérifiant on s'assure que ces valeurs satisfont le système :

Exemple 2. Résoudre le système en utilisant la méthode d'addition

Additionnons la première équation avec la seconde, multipliée par −2.

Si la deuxième équation est multipliée par −2, elle prend la forme −6x+ 6oui - 4z = −4 . Ajoutons-le maintenant à la première équation :

On voit qu'à la suite de transformations élémentaires, la valeur de la variable a été déterminée x. C'est égal à un.

Revenons au système principal. Ajoutons la deuxième équation à la troisième, multipliée par −1. Si la troisième équation est multipliée par −1, elle prend la forme −4x + 5oui − 2z = −1 . Ajoutons-le maintenant à la deuxième équation :

Nous avons l'équation x− 2oui= −1 . Remplaçons-y la valeur x que nous avons trouvé plus tôt. On peut alors déterminer la valeur oui

Maintenant nous connaissons les significations x Et oui. Cela vous permet de déterminer la valeur z. Utilisons l'une des équations incluses dans le système :

Ainsi, le triple de valeurs (1 ; 1 ; 1) est la solution de notre système. En vérifiant on s'assure que ces valeurs satisfont le système :

Problèmes de composition de systèmes d'équations linéaires

La tâche de composer des systèmes d'équations est résolue en entrant plusieurs variables. Ensuite, les équations sont compilées en fonction des conditions du problème. A partir des équations compilées, ils forment un système et le résolvent. Après avoir résolu le système, il faut vérifier si sa solution satisfait aux conditions du problème.

Problème 1. Une voiture Volga a quitté la ville pour se rendre à la ferme collective. Elle est revenue par une autre route, 5 km plus courte que la première. Au total, la voiture a parcouru 35 km aller-retour. Quelle est la longueur de chaque route en kilomètres ?

Solution

Laisser x— longueur de la première route, oui- durée de la seconde. Si la voiture a parcouru 35 km aller-retour, alors la première équation peut s'écrire x+ oui= 35. Cette équation décrit la somme des longueurs des deux routes.

On raconte que la voiture est revenue par une route plus courte de 5 km que la première. Alors la deuxième équation peut s’écrire x− oui= 5. Cette équation montre que la différence entre les longueurs de route est de 5 km.

Ou la deuxième équation peut s’écrire x= oui+5. Nous utiliserons cette équation.

Parce que les variables x Et oui dans les deux équations désignent le même nombre, alors nous pouvons former un système à partir d'elles :

Résolvons ce système en utilisant certaines des méthodes étudiées précédemment. Dans ce cas, il est pratique d'utiliser la méthode de substitution, puisque dans la deuxième équation la variable x déjà exprimé.

Remplacez la deuxième équation par la première et trouvez oui

Remplaçons la valeur trouvée oui dans la deuxième équation x= oui+ 5 et on trouvera x

La longueur de la première route était indiquée via la variable x. Nous avons maintenant trouvé sa signification. Variable x est égal à 20. Cela signifie que la longueur de la première route est de 20 km.

Et la longueur de la deuxième route était indiquée par oui. La valeur de cette variable est 15. Cela signifie que la longueur de la deuxième route est de 15 km.

Vérifions. Tout d'abord, assurons-nous que le système est résolu correctement :

Vérifions maintenant si la solution (20 ; 15) satisfait aux conditions du problème.

On raconte que la voiture a parcouru au total 35 km aller-retour. On additionne les longueurs des deux routes et on s'assure que la solution (20 ; 15) satisfait à cette condition : 20 km + 15 km = 35 km

La condition suivante : la voiture est revenue par une autre route, 5 km plus courte que la première . On voit que la solution (20 ; 15) satisfait également à cette condition, puisque 15 km est plus court que 20 km par 5 km : 20 km − 15 km = 5 km

Lors de la composition d'un système, il est important que les variables représentent les mêmes nombres dans toutes les équations incluses dans ce système.

Notre système contient donc deux équations. Ces équations contiennent à leur tour des variables x Et oui, qui représentent les mêmes nombres dans les deux équations, à savoir des longueurs de route de 20 km et 15 km.

Problème 2. Des traverses en chêne et en pin ont été chargées sur la plateforme, soit 300 traverses au total. On sait que toutes les traverses en chêne pesaient 1 tonne de moins que toutes les traverses en pin. Déterminez combien il y avait de traverses en chêne et en pin séparément, si chaque traverse en chêne pesait 46 kg et chaque traverse en pin 28 kg.

Solution

Laisser x chêne et oui des traverses en pin ont été chargées sur la plate-forme. S’il y avait 300 dormeurs au total, alors la première équation peut s’écrire x+y = 300 .

Toutes les traverses en chêne pesaient 46 x kg, et ceux en pin pesaient 28 oui kg. Puisque les traverses en chêne pesaient 1 tonne de moins que les traverses en pin, la deuxième équation peut s'écrire sous la forme 28oui - 46x= 1000 . Cette équation montre que la différence de masse entre les traverses en chêne et en pin est de 1 000 kg.

Les tonnes étaient converties en kilogrammes puisque la masse des traverses de chêne et de pin était mesurée en kilogrammes.

En conséquence, nous obtenons deux équations qui forment le système

Résolvons ce système. Exprimons dans la première équation x. Le système prendra alors la forme :

Remplacez la première équation par la seconde et trouvez oui

Remplaçons oui dans l'équation x= 300 − oui et découvrez ce que c'est x

Cela signifie que 100 traverses en chêne et 200 traverses en pin ont été chargées sur la plate-forme.

Vérifions si la solution (100 ; 200) satisfait aux conditions du problème. Tout d'abord, assurons-nous que le système est correctement résolu :

On disait qu'il y avait 300 dormeurs au total. On additionne le nombre de traverses en chêne et en pin et on s'assure que la solution (100 ; 200) satisfait à cette condition : 100 + 200 = 300.

La condition suivante : toutes les traverses en chêne pesaient 1 tonne de moins que toutes les traverses en pin . On voit que la solution (100 ; 200) satisfait également à cette condition, puisque 46 × 100 kg de traverses en chêne sont plus légères que 28 × 200 kg de traverses en pin : 5 600 kg − 4 600 kg = 1 000 kg.

Problème 3. Nous avons pris trois morceaux d'alliage cuivre-nickel dans des rapports de 2 : 1, 3 : 1 et 5 : 1 en poids. Une pièce pesant 12 kg en a été fondue avec un rapport de teneur en cuivre et nickel de 4 : 1. Trouvez la masse de chaque pièce originale si la masse de la première est le double de la masse de la seconde.