Intégrale définie et ses propriétés.

Théorème de la valeur moyenne. Si f(x) est continue sur l'intervalle, alors il existe un point tel que . Doc. Une fonction continue sur un intervalle prend ses plus petites valeurs m et ses plus grandes valeurs M sur ce segment. Alors . Nombre est conclu entre les valeurs minimales et maximales de la fonction sur le segment. Une des propriétés d'une fonction continue sur un intervalle est que cette fonction prend toute valeur située entre m et M. Ainsi, il existe un point tel que . Cette propriété a une interprétation géométrique simple : si continue sur le segment , alors il existe un point tel que l'aire du trapèze curviligne ABCD est égale à l'aire du rectangle de base et de hauteur f(c) (mis en surbrillance sur la figure).

7. Intégrale avec limite supérieure variable. Sa continuité et sa différentiabilité.

Considérons une fonction f (x) intégrable de Riemann sur l'intervalle . Puisqu'il est intégrable sur , alors il est également intégrable sur ∀x ∈ . Alors pour chaque x ∈ l'expression a un sens, et pour chaque x elle est égale à un certain nombre.

Ainsi, chaque x ∈ est associé à un certain nombre,

ceux. la fonction est donnée :

(3.1)

Définition:

La fonction F (x) définie en (3.1), ainsi que l'expression elle-même, sont appelées

intégrale avec une limite supérieure variable. Il est défini sur l'ensemble du segment

intégrabilité de la fonction f (x).

Condition : f (t) est continue sur , et la fonction F (x) est donnée par la formule (3.1).

Énoncé : La fonction F(x) est différentiable sur , et F (x) = f (x).

(Au point a, il est différentiable à droite et au point b, il est différentiable à gauche.)

Preuve:

Puisque pour une fonction d'une variable F (x) la dérivabilité équivaut à l'existence d'une dérivée en tous points (au point a à droite, et au point b à gauche), on trouvera la dérivée de F (x) . Considérons la différence

Ainsi,

dans ce cas, le point ξ se situe sur le segment (ou si ∆x< 0).

Rappelons maintenant que la dérivée de la fonction F(x) en un point donné x ∈ est égale à la limite du rapport de différence : . De l’égalité nous avons :

,

En dirigeant maintenant ∆x → 0, du côté gauche de cette égalité on obtient F’(x), et du côté droit

Rappelons la définition de continuité de la fonction f (t) au point x :

Soit x1 dans cette définition égal à ξ. Puisque ξ ∈ (ξ ∈ ), et

∆x → 0, alors |x − ξ| → 0, et par la définition de continuité, f (ξ) → f (x). De là, nous avons :

F'(x) = f (x).

Conséquence:

Condition : f (x) est continu sur .

Énoncé : Toute primitive de la fonction f (x) a la forme

où C ∈ R est une constante.

Preuve. D'après le théorème 3.1 la fonction est une primitive de f(x). Supposons que G(x) soit une autre primitive de f (x). Alors G’(x) = f(x) et pour la fonction F(x) − G(x) on a : (F (x) + G(x))' = F'(x)−G'(x) = f (x)−f(x) ≡ 0. D'où la dérivée de la fonction F (x)−G (X)

est égal à zéro, donc cette fonction est constante : F(x) − G(x) = const.

8. Formule de Newton-Leibniz pour une intégrale définie.

Théorème:

Condition: f(t) est continue sur , et F(x) en est une primitive.

Déclaration:

Preuve: Considérons une primitive F (x) de la fonction f (x). D'après le corollaire du théorème « Sur la différentiabilité d'une intégrale avec une limite supérieure variable » (voir la question précédente), il a la forme . D'ici

=> c= F(un) , Et

Déplaçons F(a) dans la dernière égalité vers la gauche, désignons à nouveau la variable d'intégration par x et obtenons la formule de Newton – Leibniz :

Théorème. Si la fonction f(x) intégrable sur l'intervalle [ un B], Où un< b , et pour tout le monde x ∈ l’inégalité persiste

En utilisant les inégalités du théorème, on peut estimer l'intégrale définie, c'est-à-dire indiquer les limites entre lesquelles sa signification est contenue. Ces inégalités expriment une estimation de l'intégrale définie.

Théorème [Théorème de la moyenne]. Si la fonction f(x) intégrable sur l'intervalle [ un B] et pour tout le monde x ∈ les inégalités sont satisfaites m ≤ f(x) ≤ M, Que

Où m ≤ µ ≤ M.

Commentaire. Dans le cas où la fonction f(x) est continue sur l'intervalle [ un B], l'égalité du théorème prend la forme

Où c ∈. Nombre µ=f(c), défini par cette formule, est appelé valeur moyenne les fonctions f(x) sur le segment [ un B]. Cette égalité a la suivante signification géométrique: aire d'un trapèze courbe délimitée par une ligne continue y=f(x) (f(x) ≤ 0), est égale à l'aire d'un rectangle de même base et de même hauteur égale à l'ordonnée d'un point sur cette ligne.

Existence d'une primitive pour une fonction continue

Tout d’abord, nous introduisons le concept d’intégrale avec une limite supérieure variable.

Laissez la fonction f(x) intégrable sur l'intervalle [ un B]. Alors quel que soit le numéro X depuis [ un B], fonction f(x) intégrable sur l'intervalle [ un B]. Par conséquent, sur l’intervalle [ un B] fonction définie

qui est appelée une intégrale avec une limite supérieure variable.

Théorème. Si l'intégrande est continue sur l'intervalle [ un B], alors la dérivée d'une intégrale définie avec une limite supérieure variable existe et est égale à la valeur de l'intégrande pour cette limite, c'est-à-dire

Conséquence. Une intégrale définie avec une limite supérieure variable est l'une des primitives d'un intégral continu. En d’autres termes, pour toute fonction continue sur un intervalle il existe une primitive.

Note 1. Notez que si la fonction f(x) intégrable sur l'intervalle [ un B], alors l'intégrale à limite supérieure variable est fonction de la limite supérieure, continue sur ce segment. En effet, à partir de St.2 et du théorème de la valeur moyenne, nous avons

Note 2. L'intégrale avec une limite supérieure d'intégration variable est utilisée dans la définition de nombreuses nouvelles fonctions, par exemple, . Ces fonctions ne sont pas basiques ; comme déjà noté, les primitives des intégrandes indiquées ne sont pas exprimées par des fonctions élémentaires.

Règles de base de l'intégration

Formule de Newton-Leibniz

Puisque deux fonctions primitives quelconques f(x) diffèrent par une constante, alors selon le théorème précédent, on peut affirmer que toute primitive Φ(x) continu sur le segment [ un B] les fonctions f(x) ressemble à

Où C- une constante.

En supposant dans cette formule x=une Et x=b, en utilisant les intégrales définies St.1, on trouve

Ces égalités impliquent la relation

qui est appelée Formule de Newton-Leibniz.

Nous avons ainsi démontré le théorème suivant :

Théorème. L'intégrale définie d'une fonction continue est égale à la différence entre les valeurs de l'une de ses primitives pour les limites supérieure et inférieure d'intégration.

La formule de Newton-Leibniz peut être réécrite comme suit

Changer une variable dans une intégrale définie

Théorème. Si

• fonction f(x) est continue sur l'intervalle [ un B];
• segment de ligne [ un B] est l'ensemble des valeurs de fonction φ(t), défini sur le segment α ≤ t ≤ β et ayant une dérivée continue dessus ;
• φ(α)=une, φ(β)=b

alors la formule est correcte

Formule d'intégration par parties

Théorème. Si les fonctions u=u(x), v=v(x) avoir des dérivées continues sur l'intervalle [ un B], alors la formule est valide

Valeur de l'application théorèmes de la valeur moyenne réside dans la possibilité d'obtenir une estimation qualitative de la valeur d'une certaine intégrale sans la calculer. Formulons : si une fonction est continue sur un intervalle, alors à l'intérieur de cet intervalle il y a un point tel que .

Cette formule est tout à fait adaptée pour estimer grossièrement l’intégrale d’une fonction complexe ou lourde. Le seul point qui fait la formule approximatif , est une nécessité choix indépendant points Si nous prenons le chemin le plus simple - le milieu de l'intervalle d'intégration (comme suggéré dans un certain nombre de manuels), alors l'erreur peut être assez importante. Pour obtenir un résultat plus précis nous recommandons effectuez le calcul dans l'ordre suivant :

Construire un graphique d'une fonction sur l'intervalle ;

Tracez la limite supérieure du rectangle de sorte que les parties coupées du graphique de fonction soient superficie à peu près égale (c'est exactement ce qui est montré sur la figure ci-dessus - deux triangles curvilignes sont presque identiques) ;

Déterminer à partir de la figure ;

Utilisez le théorème de la valeur moyenne.

A titre d'exemple, calculons une intégrale simple :

Valeur exacte ;

Pour le milieu de l'intervalle on obtient également une valeur approximative, c'est-à-dire résultat clairement inexact ;

En construisant un graphique avec le côté supérieur du rectangle dessiné conformément aux recommandations, on obtient , d'où la valeur approximative . Un résultat tout à fait satisfaisant, l'erreur est de 0,75%.

Formule trapézoïdale

La précision des calculs utilisant le théorème de la valeur moyenne dépend de manière significative, comme cela a été montré, de objectif visuel selon le planning des points. En effet, en choisissant, dans le même exemple, points ou , on peut obtenir d'autres valeurs de l'intégrale, et l'erreur peut augmenter. Les facteurs subjectifs, l'échelle du graphique et la qualité du dessin influencent grandement le résultat. Ce inacceptable dans les calculs critiques, le théorème de la valeur moyenne ne s'applique donc qu'aux calculs rapides qualité estimations intégrales.

Dans cette section, nous examinerons l'une des méthodes d'intégration approximative les plus populaires - formule trapézoïdale . L'idée principale de la construction de cette formule repose sur le fait que la courbe peut être approximativement remplacée par une ligne brisée, comme le montre la figure.

Supposons, pour être précis (et conformément à la figure), que l'intervalle d'intégration soit divisé en égal (c'est facultatif, mais très pratique) pièces. La longueur de chacune de ces parties est calculée par la formule et est appelée étape . Les abscisses des points de partition, si elles sont données, sont déterminées par la formule où . En utilisant des abscisses connues, il est facile de calculer les ordonnées. Ainsi,

C'est la formule trapézoïdale du cas. A noter que le premier terme entre parenthèses est la demi-somme des ordonnées initiales et finales, à laquelle s'ajoutent toutes les ordonnées intermédiaires. Pour un nombre arbitraire de partitions de l'intervalle d'intégration formule générale pour les trapèzes a la forme : formules de quadrature: rectangles, Simpson, Gaussien, etc. Ils sont basés sur la même idée de représenter un trapèze curviligne par des zones élémentaires de formes diverses, donc, après avoir maîtrisé la formule du trapèze, comprendre des formules similaires ne sera pas difficile. De nombreuses formules ne sont pas aussi simples que la formule trapézoïdale, mais elles permettent d'obtenir des résultats de haute précision avec un petit nombre de partitions.

En utilisant la formule trapézoïdale (ou similaire), il est possible de calculer, avec la précision requise en pratique, aussi bien des intégrales « non exécutables » que des intégrales de fonctions complexes ou lourdes.

Par une intégrale définie à partir d'une fonction continue F(X) sur le segment final [ un, b] (où ) est l'incrément de certaines de ses primitives sur ce segment. (En général, la compréhension sera sensiblement plus facile si vous répétez le sujet de l'intégrale indéfinie) Dans ce cas, la notation est utilisée

Comme on peut le voir dans les graphiques ci-dessous (l'incrément de la fonction primitive est indiqué par ), une intégrale définie peut être un nombre positif ou négatif(Il est calculé comme la différence entre la valeur de la primitive dans la limite supérieure et sa valeur dans la limite inférieure, c'est-à-dire comme F(b) - F(un)).

Nombres un Et b sont appelés respectivement limites inférieure et supérieure d'intégration et le segment [ un, b] – segment d’intégration.

Ainsi, si F(X) – une fonction primitive pour F(X), alors, selon la définition,

(38)

L'égalité (38) s'appelle Formule de Newton-Leibniz . Différence F(b) – F(un) s'écrit brièvement comme suit :

Nous écrirons donc la formule de Newton-Leibniz comme ceci :

(39)

Montrons que l'intégrale définie ne dépend pas de la primitive de l'intégrande prise lors de son calcul. Laisser F(X) et F( X) sont des primitives arbitraires de l'intégrande. Puisqu’il s’agit de primitives de même fonction, elles diffèrent par un terme constant : Ф( X) = F(X) + C. C'est pourquoi

Cela établit que sur le segment [ un, b] incréments de toutes les primitives de la fonction F(X) correspondre.

Ainsi, pour calculer une intégrale définie, il est nécessaire de trouver n'importe quelle primitive de l'intégrande, c'est-à-dire Vous devez d’abord trouver l’intégrale indéfinie. Constante AVEC exclus des calculs ultérieurs. Ensuite, la formule de Newton-Leibniz est appliquée : la valeur de la limite supérieure est substituée dans la fonction primitive b , plus loin - la valeur de la limite inférieure un et la différence est calculée F(b) - F(a) . Le nombre résultant sera une intégrale définie..

À un = b par définition accepté

Exemple 1.

Solution. Tout d'abord, trouvons l'intégrale indéfinie :

Application de la formule de Newton-Leibniz à la primitive

(à AVEC= 0), on obtient

Cependant, lors du calcul d'une intégrale définie, il est préférable de ne pas trouver la primitive séparément, mais d'écrire immédiatement l'intégrale sous la forme (39).

Exemple 2. Calculer l'intégrale définie

Solution. Utiliser la formule

Propriétés d'une intégrale définie

Théorème 2.La valeur de l'intégrale définie ne dépend pas de la désignation de la variable d'intégration, c'est à dire.

(40)

Laisser F(X) – primitive pour F(X). Pour F(t) la primitive est la même fonction F(t), dans lequel la variable indépendante est uniquement désignée différemment. Ainsi,

Basé sur la formule (39), la dernière égalité signifie l'égalité des intégrales

Théorème 3.Le facteur constant peut être soustrait du signe de l'intégrale définie, c'est à dire.

(41)

Théorème 4.L'intégrale définie d'une somme algébrique d'un nombre fini de fonctions est égale à la somme algébrique des intégrales définies de ces fonctions, c'est à dire.

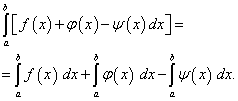(42)

Théorème 5.Si un segment d'intégration est divisé en parties, alors l'intégrale définie sur tout le segment est égale à la somme des intégrales définies sur ses parties, c'est à dire. Si

(43)

Théorème 6.Lors du réaménagement des limites d'intégration, la valeur absolue de l'intégrale définie ne change pas, mais seul son signe change, c'est à dire.

(44)

Théorème 7(théorème de la valeur moyenne). Une intégrale définie est égale au produit de la longueur du segment d'intégration et de la valeur de l'intégrande à un moment donné à l'intérieur de celui-ci., c'est à dire.

(45)

Théorème 8.Si la limite supérieure de l'intégration est supérieure à la limite inférieure et que l'intégrande est non négative (positive), alors l'intégrale définie est également non négative (positive), c'est-à-dire Si

Théorème 9.Si la limite supérieure de l'intégration est supérieure à la limite inférieure et que les fonctions sont continues, alors l'inégalité

peut être intégré terme par terme, c'est à dire.

(46)

Les propriétés de l'intégrale définie permettent de simplifier le calcul direct des intégrales.

Exemple 5. Calculer l'intégrale définie

En utilisant les théorèmes 4 et 3, et en trouvant les primitives - intégrales de table (7) et (6), on obtient

Intégrale définie avec limite supérieure variable

Laisser F(X) – continu sur le segment [ un, b] fonction, et F(X) est sa primitive. Considérons l'intégrale définie

(47)

et à travers t la variable d'intégration est désignée pour ne pas la confondre avec la borne supérieure. Quand ça change X l'intégrale définie (47) change également, c'est-à-dire c'est fonction de la limite supérieure d'intégration X, que nous désignons par F(X), c'est à dire.

(48)

Montrons que la fonction F(X) est une primitive de F(X) = F(t). En effet, différencier F(X), on a

parce que F(X) – primitive pour F(X), UN F(un) est une valeur constante.

Fonction F(X) – l’une des primitives infinies de F(X), à savoir celui qui X = un va à zéro. Cet énoncé est obtenu si dans l'égalité (48) on met X = un et utilisez le théorème 1 du paragraphe précédent.

Calcul d'intégrales définies par la méthode d'intégration par parties et la méthode de changement de variable

où, par définition, F(X) – primitive pour F(X). Si on change la variable dans l'intégrande

alors, d'après la formule (16), on peut écrire

Dans cette expression

fonction primitive pour

En fait, son dérivé, selon règle de différenciation des fonctions complexes, est égal

Soient α et β les valeurs de la variable t, pour lequel la fonction

prend les valeurs en conséquence un Et b, c'est à dire.

Mais, selon la formule de Newton-Leibniz, la différence F(b) – F(un) Il y a

Méthode trapézoïdale

Article principal :Méthode trapézoïdale

Si la fonction sur chacun des segments partiels est approchée par une droite passant par les valeurs finies, alors on obtient la méthode trapézoïdale.

Aire du trapèze sur chaque segment :

Erreur d'approximation sur chaque segment :

Où

La formule complète des trapèzes dans le cas de la division de tout l'intervalle d'intégration en segments d'égale longueur :

Où

Erreur de formule trapézoïdale :

Où

La méthode Simpson.

Intégrande f(x) est remplacé par un polynôme d'interpolation du deuxième degré P(x)– une parabole passant par trois nœuds, par exemple, comme le montre la figure ((1) – fonction, (2) – polynôme).

Considérons deux étapes d'intégration ( h= const = x je + 1 – x je), soit trois nœuds x 0 , x 1 , x 2, à travers laquelle on trace une parabole en utilisant l’équation de Newton :

Laisser z = x - x 0,
Alors

Maintenant, en utilisant la relation obtenue, on calcule l'intégrale sur cet intervalle :

.
Pour maille uniforme Et nombre pair d'étapes m La formule de Simpson prend la forme :

Ici , UN sous l'hypothèse de continuité de la dérivée quatrième de l'intégrande.

[modifier] Précision accrue

L'approximation d'une fonction par un seul polynôme sur tout l'intervalle d'intégration conduit, en règle générale, à une erreur importante dans l'estimation de la valeur de l'intégrale.

Pour réduire l'erreur, le segment d'intégration est divisé en parties et une méthode numérique est utilisée pour évaluer l'intégrale sur chacune d'elles.

Comme le nombre de partitions tend vers l'infini, l'estimation de l'intégrale tend vers sa vraie valeur pour les fonctions analytiques de toute méthode numérique.

Les méthodes ci-dessus permettent une procédure simple consistant à réduire de moitié l'étape, chaque étape nécessitant que les valeurs de fonction soient calculées uniquement au niveau des nœuds nouvellement ajoutés. Pour estimer l'erreur de calcul, la règle de Runge est utilisée.

Application de la règle de Runge

modifier]Évaluer l'exactitude du calcul d'une certaine intégrale

L'intégrale est calculée à l'aide de la formule choisie (rectangles, trapèzes, paraboles de Simpson) avec un nombre de pas égal à n, puis avec un nombre de pas égal à 2n. L'erreur de calcul de la valeur de l'intégrale avec un nombre de pas égal à 2n est déterminée par la formule de Runge :
, pour les formules de rectangles et de trapèzes, et pour la formule de Simpson.
Ainsi, l'intégrale est calculée pour des valeurs successives du nombre de pas, où n 0 est le nombre de pas initial. Le processus de calcul se termine lorsque la condition est satisfaite pour la valeur N suivante, où ε est la précision spécifiée.

Caractéristiques du comportement d'erreur.

Il semblerait pourquoi analyser différentes méthodes d'intégration si nous pouvons obtenir une grande précision simplement en réduisant la taille du pas d'intégration. Cependant, considérons le graphique du comportement de l'erreur a posteriori R. résultats du calcul numérique en fonction de et du numéro n partitions d'intervalles (c'est-à-dire à l'étape . Dans la section (1), l'erreur diminue en raison d'une diminution de l'étape h. Mais dans la section (2), l'erreur de calcul commence à dominer, s'accumulant à la suite de nombreuses opérations arithmétiques. Ainsi, chaque la méthode a la sienne Rmin, qui dépend de nombreux facteurs, mais principalement de la valeur a priori de l'erreur de méthode R..

La formule clarifiante de Romberg.

La méthode de Romberg consiste à affiner séquentiellement la valeur de l'intégrale avec une augmentation multiple du nombre de partitions. La formule des trapèzes à pas uniformes peut être prise comme base h.
Notons l'intégrale avec le nombre de partitions n= 1 comme .
En réduisant le pas de moitié, on obtient .
Si l'on réduit successivement le pas de 2 n fois, on obtient une relation de récurrence pour calculer .