Équation tangente et équation normale au graphique d'une fonction.

Ministère de l'Éducation et de la Politique de la jeunesse de la République de Tchouvachie

BOU DPO (PC) C "Institut républicain d'éducation de Tchouvachie"

Ministère de l'Éducation de Tchouvachie

Département de mathématiques et technologies de l'information

Cours sur le sujet :

«Équations fonctionnelles. Méthodes pour les résoudre"

Complété par : professeur de mathématiques MBOU « Lycée N°60 »

Tcheboksary

Flegentova A.A.

Tcheboksary, 2014

Introduction…………………………………………………….……………..……3

Chapitre 1. Le concept d'équation fonctionnelle……………………………...5

Chapitre 2. Partie pratique. Méthodes de résolution d’une équation fonctionnelle.9

Conclusion………………………………………………………………………………….24

Références……………………………………………………………25

Candidatures………………………………………………………………………………...26

Introduction

L'une des compétences mathématiques les plus importantes que les écoliers doivent maîtriser est la capacité de résoudre des équations. La racine d'une équation se trouve dans une ou plusieurs actions, de nombreux problèmes verbaux sont résolus algébriquement, l'équation peut impliquer des nombres entiers, des rationnels et d'autres nombres, c'est-à-dire que les équations elles-mêmes sont simultanément des tâches et des méthodes de résolution de problèmes, la capacité de résoudre ce qui est nécessaire pour tous les élèves de l'école. Mais en résolvant des tâches de formation, je suis tombé sur une équation que je ne pouvais pas résoudre. Comme je l’ai appris plus tard du professeur, il s’agissait d’une équation fonctionnelle.

Que sont les équations fonctionnelles ? Et quels sont les moyens de les résoudre ? Ces questions m'ont intéressé et j'ai décidé de mener des recherches.équation de Cauchy fonctionnelle

Les équations fonctionnelles sont étudiées depuis très longtemps ; ce cours n'a jamais trouvé sa place dans les programmes mathématiques. C'est dommage. Après tout, résoudre des équations fonctionnelles individuelles nécessite une compréhension assez approfondie du sujet et inculque l'amour du travail créatif indépendant. Étant donné que ce sujet n'est pas étudié dans le cursus scolaire en raison de sa complexité, de tels problèmes se posent lors de l'entrée dans des universités prestigieuses, aux Olympiades et dans la partie C de l'examen d'État unifié.

Actuellement, il n'existe pratiquement aucun manuel expliquant comment résoudre des équations fonctionnelles.

Par conséquent, il existe un besoin pour un manuel qui, à l'aide d'exemples simples et spécifiques, puisse montrer au lecteur ayant une formation mathématique modeste tout l'arsenal des méthodes modernes de résolution d'équations fonctionnelles.

Le but du travail est de découvrir ce qu'est une équation fonctionnelle dans leurs systèmes, de trouver des moyens de la résoudre et de compiler une collection de problèmes destinés aux cours de mathématiques.

Objectifs de recherche:

1. étude et analyse de la littérature ;

2. rechercher des moyens de résoudre des équations fonctionnelles et leurs systèmes ;

3. résoudre des équations fonctionnelles

4. compilation d'une collection

Objet d'étude : équations fonctionnelles

Sujet de recherche : étudier les propriétés et les méthodes de résolution d'équations fonctionnelles.

Structure : introduction, notion d'équation fonctionnelle, ensemble de problèmes, conclusion.

Chapitre 1. Le concept d'équation fonctionnelle

Une équation fonctionnelle est une équation qui contient une ou plusieurs fonctions inconnues (avec des domaines de définition et de valeurs donnés). Résoudre une équation fonctionnelle signifie trouver toutes les fonctions qui la satisfont de manière identique. Les équations fonctionnelles apparaissent dans une grande variété de domaines mathématiques, généralement dans les cas où il est nécessaire de décrire toutes les fonctions ayant des propriétés données. Le terme équation fonctionnelle est généralement utilisé pour les équations qui ne sont pas réductibles par des moyens simples aux équations algébriques. Cette irréductibilité est le plus souvent due au fait que les arguments de la fonction inconnue dans l'équation ne sont pas les variables indépendantes elles-mêmes, mais certaines fonctions données de celles-ci. Souvent trouvé lors de divers concours de mathématiques.

Certaines équations fonctionnelles nous sont familières depuis l'école :

f(x) = f(-x), f(-x) = - f(x), f(x+T) = f(x),

qui définissent des propriétés de fonctions telles que la régularité, l'impair et la périodicité.

Le problème de la résolution d’équations fonctionnelles est l’un des plus anciens de l’analyse mathématique. Ils sont apparus presque simultanément avec les débuts de la théorie des fonctions. Le premier véritable épanouissement de cette discipline est associé au problème du parallélogramme des forces. En 1769, d'Alembert réduisait la logique de la loi de l'addition des forces à la solution d'une équation fonctionnelle

La même équation et dans le même but a été considérée par Poisson en 1804 sous une certaine hypothèse d'analyticité, tandis qu'en 1821 Cauchy (1789 - 1857) a trouvé des solutions générales

de cette équation, en supposant uniquement la continuité de f(x).

Même la formule bien connue de la géométrie non euclidienne pour l'angle de parallélisme

a été obtenu par N. I. Lobatchevski (1792 – 1856) à partir de l'équation fonctionnelle

, (2)

qu'il a résolu en utilisant une méthode similaire à celle de Cauchy. Cette équation peut être réduite à l'équation

.

Un certain nombre de problèmes géométriques conduisant à des équations fonctionnelles ont été étudiés par le mathématicien anglais Charles Babbage (1792-1871). Il a étudié par exemple des courbes périodiques du second ordre, définies par la propriété suivante pour tout couple de points de la courbe : si l'abscisse du deuxième point est égale à l'ordonnée du premier, alors l'ordonnée du deuxième point est égale à l'abscisse du premier. Soit une telle courbe le graphique d'une fonctiony = f(x) ; (x, f(x)) - son point arbitraire. Puis, selon la condition, le point en abscissef(x) a une ordonnée x. Ainsi,

L'équation fonctionnelle (3) est satisfaite notamment par les fonctions suivantes :

Certaines des équations fonctionnelles les plus simples sont les équations de Cauchy

f(x+y) = f(x)+f(y), (4)

f(x+y) = f(x) f(y), (5)

f(xy) = f(x)+f(y), (6)

f(xy) = f(x) f(y), (7)

Cauchy a étudié ces équations en détail dans son (Cours d'analyse), publié en 1821. Les solutions continues de ces quatre équations de base sont respectivement de la forme

, , ,

Il peut y avoir d'autres solutions dans la classe des fonctions discontinues. L'équation (4) a déjà été prise en compte par Legendre et Gauss dans leur dérivation du théorème fondamental de la géométrie projective et dans leur étude de la loi de distribution de probabilité gaussienne.

L'équation fonctionnelle (4) a été encore appliquée par G. Darboux au problème du parallélogramme des forces et au théorème fondamental de la géométrie projective ; sa principale réalisation est un assouplissement significatif des hypothèses. On sait que l'équation fonctionnelle de Cauchy (4) caractérise une fonction linéaire homogène dans la classe des fonctions continuesf(x) = hache . Darboux a montré que toute solution continue au moins en un point ou bornée par le haut (ou par le bas) dans un intervalle arbitrairement petit doit également avoir la formef(x) = hache. D'autres résultats sur l'assouplissement des hypothèses se succèdent rapidement (intégrabilité, mesurabilité sur un ensemble de mesures positives, et même majorisabilité par une fonction mesurable). La question se pose : existe-t-il au moins une fonction additive (c'est-à-dire satisfaisant (4)) autre qu'une fonction linéaire homogène. C'est vraiment difficile de trouver une telle fonctionnalité ! Au cours de ce travail, nous montrerons que pour rationnel x les valeurs de toute fonction additive doivent coïncider avec les valeurs d'une fonction homogène linéaire, c'est-à-diref(x) = hache pour x Q. Il semblerait alors quef(x) = hache pour tout réel x. Sif(x) - est continue, alors c'est effectivement le cas, mais si cette hypothèse est écartée, alors ce n'est pas le cas. Le premier exemple de quelque chose de différent def(x) = hache Une solution discontinue de l'équation fonctionnelle (4) a été construite en 1905 par le mathématicien allemand G. Hamel en utilisant la base des nombres réels qu'il a introduit.

De nombreuses équations fonctionnelles ne définissent pas une fonction spécifique, mais définissent une large classe de fonctions, c'est-à-dire qu'elles expriment une propriété qui caractérise une classe particulière de fonctions. Par exemple, l'équation fonctionnellef(x+1) = f(x) caractérise la classe de fonctions ayant la période 1, et l'équationf(1+x) = f(1-x) - classe de fonctions symétriques par rapport à une droitex = 1, etc.

Chapitre 2. Partie pratique. Méthodes de résolution d'une équation fonctionnelle

Les équations fonctionnelles les plus simples

1. Soit la fonction y =f(x) croissante sur R. Résoudre :

a) équation f(3x + 2) = f(4x 2 + x);

b) inégalité f(3х – 48) ≤ f(-х 2 + x).

Solution:

une) f(3x + 2) = f(4x 2 + x)

Il existe un théorème : si une fonction augmente sur un intervalle X, alors elle prend chacune de ses valeurs en un seul point. C'est pourquoi,

3x+2 = 4x2 + x ;

4x2 -2x-2=0;

2x2 –x-1=0 ;

x 1 = 1 et x 2 = -0,5

Réponse : x 1 = 1 et x 2 = -0,5.

b) f(3x – 48) ≤ f(-x 2 + x);

3x-48 ≤ -x 2 + x;

x 2 + 2x – 48 ≤ 0 ;

x 1 =6 et x 2 = -8 :

Réponse : [-8;6].

2. Soit la fonction y =f(x) décroissante sur R. Résoudre l'inégalité f(2x-3)>f(x+2)

Solution:

Nous résolvons la même chose que dans la tâche précédente, seulement nous changeons le signe de l'inégalité, puisque la fonction diminue de R.

2x-3

Réponse : (-∞ ; 5).

Résolution d'équations fonctionnelles à l'aide de la méthode de substitution

En remplaçant certaines variables de l'équation fonctionnelle soit par des valeurs spécifiques, soit par d'autres expressions, nous essayons soit de simplifier cette équation, soit de la mettre sous une forme telle que la solution ultérieure deviendra évidente. La particularité de la méthode utilisée est précisément que dans un certain nombre de cas elle permet de trouver des solutions dans la classe de toutes les fonctions possibles.

1. Retrouver toutes les fonctions définies sur le plateau , satisfaisant la relation

Solution

Donnons une valeur à x. On a

D'ici

.

Prenons le système

À partir de l’équation (1), nous exprimons et remplacez-le dans l'équation (2).

; ;

D'ici

; ; .

Vérifions si la fonction f(x) satisfait vraiment l'équation

.

x=x - correct.

Répondre: .

Solution:

1) Laissez

2) En remplaçant dans l'équation d'origine, nous obtenons

3) Remplacez z par on obtient ou après transformations du côté droit de l'équation :

4) Nous avons donc deux équations :

5) Multipliez les deux côtés de la 1ère équation par (-2) et ajoutez-les à la 2ème équation, nous obtenons :

3. Laisser - un vrai nombre. Rechercher une fonctionf(x) , défini pour tout x ≠ 1 et satisfaisant l'équation

,

où g est une fonction donnée définie àx ≠ 1 .

Solution : lors du remplacement

nous obtenons un système

.

dont la solution àun 2 ≠ 1 est une fonction

Répondre:

4. Trouver une solution à un système d'équations fonctionnelles pour des fonctions inconnuesf(x) Etg(x) :

Solution : Faisons une substitution dans la première équation2x = 1/z .

Où

et la première équation prend la forme :

Ou

En conséquence, nous obtenons un système d'équations :

dont la solution est g(x) = 1/x, f(x) = x+1.

Réponse : g(x) = 1/x, f(x) = x+1.

5. Trouver toutes les fonctions f : R  R qui, pour tout x, y € R, satisfont à l'équation

f(x+y)=x+yf(x)+(1-x)y. (1)

Solution : Soit f une fonction satisfaisant (1). Puisque (1) est vrai pour toutes les valeurs des variables x et y, il sera également vrai pour des valeurs spécifiques de ces variables. En substituant, par exemple, y égal à 0 dans l'équation d'origine, nous obtenons f(x)=x. Cette égalité doit être vraie pour tout réel x. Ainsi, (1) => f(х)≡х est une solution de l'équation fonctionnelle (1). La vérification directe montre que la fonction trouvée satisfait bien l'équation pour tout x,y € R.

6. Trouver toutes les fonctions f : R  R qui, pour tout x, y € R, satisfont à l'équation

f(x+y)=x+yf(x)+(1-sin x)y (1)

Solution : tout comme dans le problème précédent, nous établissons que pour une fonction f qui satisfait (2), l'identité f(x)≡х doit être satisfaite. Cependant, en substituant la fonction f(x) = x dans (1), nous n'obtenons pas d'identité. Puisqu’aucune autre fonction ne peut également être solution à (1), cette équation n’a pas de solution.

7. Trouver toutes les fonctions f : R  R qui, pour tout x, y € R, satisfont à l'équation

f(x+y 2 +2y+1) = y 4 +4y 3 +2xy 2 +5y 2 +4xy+2y+x 2 +x+1 (1)

Solution : puisque nous voulons obtenir la valeur de f(x), essayons de nous débarrasser du terme y 2 +2y+1 sous le signe fonction. Équation y 2 +2y+1=0 a une solution y=-1. En remplaçant y= -1 dans (1), nous obtenons f(x)= x 2 -x+1 .

Réponse : f(x)= x 2 -x+1

8. Trouver toutes les fonctions f : R  R qui, pour tout x, y € R, satisfont à l'équation

f((x 2 +6x+6)y)=y 2 x 4 +12y 2 x 3 +48y 2 x 2 -4yx 2 +72y 2 x-24yx+36y 2 -24 (1)

Solution : Comme dans le problème précédent, nous souhaitons obtenir une variable libre (x ou y) sous le signe de la fonction. Dans ce cas, il est évidemment plus facile d'obtenir y. Résoudre l'équation x 2 +6x+6)y=0 par rapport à x on obtient x 1 = -1,x2 = -5. La substitution de l'une de ces valeurs dans (1) nous donne f(y)=y 2 à 4 heures.

Résolution d'équations fonctionnelles par la méthode de Cauchy

1. Trouvez la fonction , défini sur l'ensemble des nombres naturels, satisfaisant la condition

Où d est un nombre réel.

Solution:

Nous allons résoudre cette équation en utilisant un schéma appelé en mathématiques la méthode de Cauchy.

1. Trouvons des expressions pour On a

, .

2. Cette « expérience » suggère que, Où .

3. Vérifions si l'égalité est réellement vraie

Où . Utilisons la méthode d’induction mathématique pour preuve.

1. Vérifions si l’égalité est vraie à x=1 :- droite.

2. Supposons que l'égalité soit vraie pour, où, c'est-à-dire

Droite.

3. Montrons que cela implique l'égalité pour x=n. Parce que , alors pour x=n on obtient ou

; .

Cela signifie que l’égalité est vraie pour tout nombre naturel n. Ainsi, la solution de l’équation fonctionnelle donnée sera la fonction , où f(1) est un nombre arbitraire.

2. Trouver toutes les fonctions continues satisfaisant la condition

Solution:

Nous trouverons la solution de l'équation fonctionnelle progressivement, c'est-à-dire Nous trouvons d'abord sa solution s'il s'agit d'un nombre naturel, puis - un entier, puis rationnel et, enfin, - réel.

1. Soit y=x. Alors .

2. Quand, on obtient

, , …

3. Prouvons par induction mathématique que pour les valeurs naturelles (prouvez-le vous-même). (1)

4. Pour x=1 nous obtenons . - nombre constant. Notons-le par. Donc pour , nous avons .

5. Mettons en égalité

(1) , où , on obtient

. D'ici

ou

.

Ayant désigné

à travers, on obtient

Cela signifie que pour x positif et rationnel on obtient

En supposant la fonction - est continu, on obtient

À

, .

6. Prenons l'égalité. On a

D'ici.

Prenons cette égalité

On a

ou

Parce que

Que

ceux. .

Ainsi, pour toute solution réelle de l’équation, il y aura une fonction

Répondre:

L'équation s'appelle l'équation de Cauchy.

3. Trouver des fonctions continues , satisfaisant la condition

. (1)

Solution:

Essayons de réduire cette équation à l'équation fonctionnelle de Cauchy

avec solution continue

Soit y=0, alors

.

Parce que est un nombre constant, notons-le par et nous obtenons

.

Maintenant, donnons une valeur à x .

On a

.

De l'équation (1)

on a

ou

(2).

La solution de l'équation (1) est la fonction

Cela signifie que la solution de l'équation (2) sera la fonction

Répondre:

4. Trouvez toutes les solutions continues des équations de Cauchy :

un)F ( X oui) = F( X) + F( oui) ( x, y€ R.\ { 0 } );

b ) F( X+ oui) = F( xy) ( x, y€ R.);

V ) F( X+ oui) = F( X) F( oui) ( x, y€. R.) .

Solution:

Soit x > 0 en premier.

g (x) = f (e x).

Alors

g (x + y) = f (e x+y) = f (e x e y) = f (e x) + f (e y) = g (x) + g (y), c'est-à-dire g (x)

satisfait l'équation additive de Cauchy. Parce que e x et f (x ) sont continus, alors g(x ) est continue et a la forme cx, où c est une constante. Alors f (x) a la forme c ln x.

En particulier,

f(1) = 0.

En mettant

x = y = - 1,

on a

f (1) = 2 f (- 1),

où

f (- 1) = 0.

Pour arbitraire X< 0 получаем

f (x) = f (- x) + f (- 1) = f (- x).

D'ici

f (x) = c ln | X |

pour arbitraire

x ≠ 0.

b) Mettre

y = 0,

on a

f (x) = f (0), c'est-à-dire f(x) ≡ const.

Évidemment, n’importe quelle constante convient.

c) Si

f(x) = 0

pour certains x,

Que

f (z) = f (x) f (z - x) = 0

pour tout z . Sinon, la fonction, étant continue, a partout le même signe. Parce que

f (2 x ) = (f (x )) 2 ,

alors ce signe est positif et on peut considérer un

fonction

g (x) := ln f (x). On a g (x + y) = ln(f (x) f (y)) = ln f (x)+ln f (y) = g (x)+ g (y),

ceux. l'équation additive de Cauchy est satisfaite. D'ici g(x) = cx pour certains c, et

f (x) = e сх.

Ainsi, soit

f (x)≡ 0, ou f (x) ≡е сх.

Utiliser les valeurs de fonction à certains moments

Parfois, il est impossible de trouver une substitution qui simplifierait considérablement la forme de l’équation. Cependant, si l’une des variables libres est fixe, certains termes de l’équation peuvent également le devenir. Vous pouvez leur introduire des notations pratiques et les utiliser dans votre solution comme constantes ordinaires. Si ces constantes sont incluses dans la réponse, la vérification indiquera quelles valeurs sont valides.

Résous l'équation

f(x+f(y))=xy

Solution : remplacement

y=0

donne

f(x+f(0))=0.

À première vue, il y a peu d’avantages, puisque nous ne savons pas à quoi f(0) est égal. Notons f(0)=c, alors nous obtenons f(x+c)=0. En remplaçant la variable t=x+c (substitution x=t-c), on obtient f(e)=0, mais une telle fonction ne satisfait évidemment pas l'équation d'origine, donc il n'y a pas de solutions.

Résous l'équation

f(x+f(y))=x+y

Solution : Faisons à nouveau la substitution y=0 et notons c=f(0), nous obtenons f(x+c)=x. La substitution de t=x+c donne f(t)=t-c. Bien que nous connaissions la valeur exacte de c, nous savons déjà que seule une fonction de la forme f(x) = x-c, où c = const, peut satisfaire l'équation pour tout x, y. pour trouver c, on substitue la fonction trouvée dans l'équation d'origine (en même temps on vérifiera de cette manière) :

f(x+f(y))=f(x+(y-c))=(x+(y-c))-c= x+y-2c.

De là, nous voyons que l'égalité

f(x+f(y))=x+y

pour tout x,y avec c égal à 0 et seulement avec lui. La réponse est donc f(x)=x.

Réponse : f(x)=x.

L'équation est relative

Trouver tout f : R  R tel que (f(x))2 = 1

Solution : En considérant cela comme une équation pour l’inconnue f(x), on obtient

F( X) = 1 ;

F( X) = -1

Il pourrait sembler que la réponse serait deux fonctions,

f(x)=1, f(x)=-1.

Cependant, ce n’est pas le cas. Prenons par exemple la fonction

1 fois<0

1, x ≥ 0

Il est facile de voir que cette fonction satisfait l’équation. Quel sens est donné à la totalité ? Puisque l’égalité originale doit être satisfaite pour tout x € R, c’est-à-dire pour chacun x une des égalités est vraie. Cependant, l’hypothèse selon laquelle l’une des égalités est immédiatement satisfaite pour tout x sera incorrecte. Comme nous l'avons vu dans l'exemple, pour certains x, une des égalités peut être satisfaite, et pour d'autres, une autre. Essayons de caractériser l'ensemble des fonctions spécifiées par l'équation. Soit A l'ensemble des x pour lesquels la première égalité est vraie. Alors pour tous les autres x, la seconde doit être satisfaite. On voit que l’ensemble A définit de manière unique la fonction f :

Répondre:

E( F) = {+-1} , où E(f)

désigne l'ensemble des valeurs de f.

Solution graphique de l'équation fonctionnelle. A quoi a et b pour la fonction

f(x)=a|x-b| +3a|x-b |

la condition est satisfaite pour tout réel

x : f(x)=f(f(x)) ?

Solution:

Lorsque a=0, la fonction f(x)=0, et l'équation est évidemment satisfaite.

soit a>0, puis pour un grand x>0 la fonction

f(x)=a(x-b)+3a(x-b)=4ax-a(b+3b)>0

À partir de la figure 1, nous déterminons que seule l'égalité f(x)=x est possible si les valeurs de x sont suffisamment grandes et x>0. Plus précisément, x>max(b;b).

Par conséquent, les valeurs possibles pour les paramètres a et b sont déterminées à partir du système :

Qui a deux solutions :

Pour a=1/4, b=-1/3 on obtient la fonction

Son graphique (Fig. 2) est une solution graphique de l'équation

f(x)=f(f(x))

Supposons maintenant qu'un<0, тогда при больших по абсолютной величине и х<0. Конкретно, х

Par conséquent, les valeurs possibles des paramètres a et b sont déterminées à partir du système

Qui a deux solutions

Si

a=-1/4, b=0,

alors la fonction

f(x)=-|x|

satisfait l'équation

f(x)=f(f(x))

Si a=-1/4, b=-1/3, alors on obtient la fonction

Mais son graphique (Fig. 3) n'est pas une solution graphique à l'équation f(x)=f(f(x)).

Répondre: , , ,

Conclusion

Dans ce travail, des équations fonctionnelles et certaines méthodes pour les résoudre ont été considérées. Au cours de nos travaux, nous sommes devenus convaincus que les équations fonctionnelles sont une classe générale d'équations dans lesquelles la fonction recherchée est une certaine fonction. Les équations fonctionnelles comprennent essentiellement les équations différentielles, les équations intégrales et les équations aux différences finies. Par équation fonctionnelle au sens étroit du terme, on entend des équations dans lesquelles les fonctions souhaitées sont liées à des fonctions connues d'une ou plusieurs variables en utilisant l'opération de formation d'une fonction complexe. Une équation fonctionnelle peut également être considérée comme l’expression d’une propriété qui caractérise une classe particulière de fonctions.

Bibliographie

Publié sur Allbest.ru

APPLICATIONS

Fig. 1

Figure 2

Figure 3

Publié sur Allbest.ru

Une tangente est une ligne droite , qui touche le graphique de la fonction en un point et dont tous les points sont à la distance la plus courte du graphique de la fonction. Par conséquent, la tangente passe tangentiellement au graphique de la fonction sous un certain angle, et plusieurs tangentes sous des angles différents ne peuvent pas passer par le point de tangence. Les équations tangentes et les équations normales au graphique d'une fonction sont construites à l'aide de la dérivée.

L'équation de la tangente est dérivée de l'équation de la droite .

Dérivons l'équation de la tangente, puis l'équation de la normale au graphique de la fonction.

oui = kx + b .

En lui k- coefficient angulaire.

De là, nous obtenons l'entrée suivante :

oui - oui 0 = k(X - X 0 ) .

Valeur dérivée F "(X 0 ) les fonctions oui = F(X) à ce point X0 égale à la pente k= tg φ tangente au graphique d'une fonction tracée par un point M0 (X 0 , oui 0 ) , Où oui0 = F(X 0 ) . C'est signification géométrique de la dérivée .

Ainsi, nous pouvons remplacer k sur F "(X 0 ) et obtenez ce qui suit équation de la tangente au graphique d'une fonction :

oui - oui 0 = F "(X 0 )(X - X 0 ) .

Dans les problèmes impliquant la composition de l'équation d'une tangente au graphique d'une fonction (et nous y reviendrons bientôt), il est nécessaire de réduire l'équation obtenue à partir de la formule ci-dessus à équation d'une droite sous forme générale. Pour ce faire, vous devez déplacer toutes les lettres et tous les chiffres vers la gauche de l'équation et laisser zéro sur le côté droit.

Parlons maintenant de l’équation normale. Normale - il s'agit d'une droite passant par le point de tangence au graphique de la fonction perpendiculaire à la tangente. Équation normale :

(X - X 0 ) + F "(X 0 )(oui - oui 0 ) = 0

Pour vous échauffer, il vous est demandé de résoudre vous-même le premier exemple, puis d’examiner la solution. Il y a tout lieu d’espérer que cette tâche ne sera pas une « douche froide » pour nos lecteurs.

Exemple 0. Créer une équation tangente et une équation normale pour le graphique d'une fonction en un point M (1, 1) .

Exemple 1.Écrire une équation tangente et une équation normale au graphique d'une fonction , si l'abscisse est tangente .

Trouvons la dérivée de la fonction :

Nous avons maintenant tout ce qui doit être substitué dans l’entrée donnée dans l’aide théorique pour obtenir l’équation tangente. On a

Dans cet exemple, nous avons eu de la chance : la pente s'est avérée être nulle, il n'était donc pas nécessaire de réduire séparément l'équation à sa forme générale. Nous pouvons maintenant créer l'équation normale :

Dans la figure ci-dessous : le graphique de la fonction est bordeaux, la tangente est verte, la normale est orange.

L'exemple suivant n'est pas non plus compliqué : la fonction, comme dans le précédent, est également un polynôme, mais la pente ne sera pas égale à zéro, donc une étape supplémentaire sera ajoutée - amenant l'équation à une forme générale.

Exemple 2.

Solution. Trouvons l'ordonnée du point tangent :

Trouvons la dérivée de la fonction :

.

Trouvons la valeur de la dérivée au point de tangence, c'est-à-dire la pente de la tangente :

Nous remplaçons toutes les données obtenues dans la « formule vierge » et obtenons l'équation tangente :

On ramène l'équation à sa forme générale (on rassemble toutes les lettres et chiffres autres que zéro sur le côté gauche, et on laisse zéro à droite) :

On compose l'équation normale :

Exemple 3.Écrivez l'équation de la tangente et l'équation de la normale au graphique de la fonction si l'abscisse est le point de tangence.

Solution. Trouvons l'ordonnée du point tangent :

Trouvons la dérivée de la fonction :

.

Trouvons la valeur de la dérivée au point de tangence, c'est-à-dire la pente de la tangente :

.

On retrouve l'équation tangente :

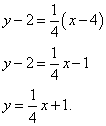
Avant de ramener l'équation à sa forme générale, il faut la « peigner » un peu : multiplier terme par terme par 4. On fait cela et amener l'équation à sa forme générale :

On compose l'équation normale :

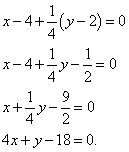
Exemple 4.Écrivez l'équation de la tangente et l'équation de la normale au graphique de la fonction si l'abscisse est le point de tangence.

Solution. Trouvons l'ordonnée du point tangent :

.

Trouvons la dérivée de la fonction :

Trouvons la valeur de la dérivée au point de tangence, c'est-à-dire la pente de la tangente :

.

On obtient l'équation tangente :

On ramène l'équation à sa forme générale :

On compose l'équation normale :

Une erreur courante lors de l'écriture d'équations tangentes et normales est de ne pas remarquer que la fonction donnée dans l'exemple est complexe et de calculer sa dérivée comme la dérivée d'une fonction simple. Les exemples suivants proviennent déjà de fonctions complexes(la leçon correspondante s'ouvrira dans une nouvelle fenêtre).

Exemple 5.Écrivez l'équation de la tangente et l'équation de la normale au graphique de la fonction si l'abscisse est le point de tangence.

Solution. Trouvons l'ordonnée du point tangent :

Attention! Cette fonction est complexe, puisque l'argument tangent (2 X) est elle-même une fonction. On trouve donc la dérivée d’une fonction comme la dérivée d’une fonction complexe.

Equations différentielles non résolues par rapport à la dérivée.

F(x,y,y")=0

1. De l’équation. F(x,y,y")=0 exprimer oui"à travers X Et oui. Vous obtiendrez une ou plusieurs équations de la forme y"=f(x,y), dont chacun doit être résolu.

Exemple.

y" 2 -y 2 =0

y"=y et y"=-y

dy/y=dx et dy/y=-dx

ln|y|=x+lnC et ln|y|=-xlnD

y=Ce x et y=De -x

2. Méthode paramétrique (la version la plus simple de la méthode).

Laissez l'équation F(x,y,y")=0 oui.

y=f(x,y").

Entrons le paramètre p=y"=dy/dx

Alors y=f(x,p)

Prenons le différentiel total des deux parties, en remplaçant mourirà travers pdx, on a

pdx=f x "dx+f y "dy

Si la solution de cette équation se trouve sous la forme x=φ(p), alors on obtient une solution de l'équation originale sous forme paramétrique :

Exemple

y=ln(1+y" 2)

p=y"=dy/dx, y=ln(1+p 2)

Lorsqu'il est divisé par R. perdu la décision y=0

3. Si l'équation F(x,y,y")=0 peut être résolu relativement X:

x=f(y,y"), puis comme en 2 on rentre le paramètre p=y"=dy/dx

4. Équation de Lagrange

y=xφy"+Ψ(y")

et l'équation de Clairaut

y=xy"+Ψ(y")

sont des cas particuliers évoqués au paragraphe 2.

5) Un peu sur les solutions spéciales. Solution y=φ(x)équations F(x,y,y")=0 est dit spécial si par chacun de ses points, en plus de cette solution, passe une autre solution, qui en ce point a la même tangente que la solution φ(x), mais ne coïncide pas avec lui dans un voisinage arbitrairement petit de ce point. Laisser F(x,y,y"), δF/δy et δF/δy" continu. Alors toute solution spéciale de l’équation F(x,y,y")=0 satisfait également l'équation δ F(x,y,y")/δy"=0.

Pour trouver des solutions spéciales, il faut partir du système

exclure oui". L'équation résultante s'appelle courbe discriminante. Pour chaque branche de la courbe discriminante, il faut vérifier si cette branche est une solution et, si oui, si elle sera spéciale (c'est-à-dire si l'unicité est violée en chacun de ses points).

Exemple.

y=xy"-y 2- Équation de Clairaut

p=y"=dy/dx, y=xp-p 2

pdx=pdx+xdp-2pdp

(x-2p)dp=0

dp=0, p=c, ainsi

x=2p, y=xp-p 2

y=Cx-C2 ou y=(x 2 /2)-(x 2 /4)

y = x 2 /4-solution spéciale

y = x 2 /4 solution de l’équation originale. Prouvons que c'est spécial.

On prend un point arbitraire sur la solution y = x 2 /4, Par exemple ( x o ,x 2 o /4). nous trouverons AVEC, pour lequel la droite y=Cx-C2 est également passé par ce point x2o/4=Cx o -C 2, ainsi C=x o /2, ceux. y=(x o /2)x-(x 2 o /4).

2.2 Méthodologie de résolution d'équations et d'inégalités

Les équations et les inégalités sont un sujet traditionnel dans le cours de mathématiques scolaire, occupant une place importante, depuis les classes inférieures, où les équations et inégalités les plus simples sont introduites jusqu'à l'introduction d'une théorie basée sur les propriétés des opérations arithmétiques, et se terminant par le niveau supérieur. niveaux, où les équations transcendantales sont résolues.

Les équations et les inégalités représentent l'appareil algébrique, le langage dans lequel divers types de problèmes sont traduits, y compris les problèmes appliqués, et leurs modèles mathématiques sont construits.

Utiliser la monotonie des fonctions pour résoudre des équations et des inégalités. L’une des idées les plus fréquemment rencontrées est bien illustrée par la résolution de l’inégalité simple suivante :

1. Résoudre les inégalités :.

Solution. Il existe deux solutions standards : la quadrature (fournie
; si
, l'inégalité est satisfaite) et remplacement de l'inconnue
.

Considérons une autre méthode - non standard. La fonction située sur le côté gauche augmente de façon monotone, tandis que la fonction de la première partie diminue. D'après des considérations graphiques évidentes, il s'ensuit que l'équation
X 0 est la solution de cette équation, alors quand
sera, et la solution à cette inégalité sera
. Signification X 0 est facile à sélectionner : X 0 = 1.

Répondre.
.

2. Résous l'équation:
.

Solution. Cette équation a une solution évidente X= 1. Montrons qu'il n'y a pas d'autres solutions. Divisons les deux parties par , on a
. Le côté gauche est une fonction décroissante de façon monotone. Par conséquent, il prend chacune de ses valeurs une fois, c'est-à-dire cette équation a une solution unique.

Répondre. X = 1.

Ainsi, l’idée de base sur laquelle reposaient les solutions de ces deux exemples est assez simple : si F(X) augmente de façon monotone, et φ (X) diminue de façon monotone, alors l'équation F(X) = φ (X) a au plus une solution, et si X = X 0 est la solution de cette équation, alors quand X > X 0 (X est dans le cadre des deux fonctions F(X) Et φ (X) ) volonté F(X) > φ (X) , et quand X X 0 sera

F(X) φ (X) .

Il convient de prêter attention à une modification de cette idée, à savoir : si F(X) est une fonction monotone, alors de l'égalité F(X) = F(oui) il s'ensuit que X = oui .

3.Résous l'équation:.

Solution . Transformons l'équation :

.

Considérez la fonction
.

Prouvons que lorsque t > 1 cette fonction diminue de façon monotone. Cela peut être fait, par exemple, de manière standard : trouver la dérivée

et prouver que lorsque t > 1
. Montrons une autre manière :

.

La fonction résultante est évidemment décroissante (la base augmente, sous le signe du logarithme la fonction diminue).

Notre équation a la forme : , ce qui signifie
. A gauche se trouve une fonction croissante, donc la solution est unique, elle se trouve facilement par sélection : X = 4.

Répondre. X = 4 .

Équations de la formeF ( F ( X )) = X . Lors de la résolution d’équations de ce type, le théorème suivant est utile :

Si y = f(x) est une fonction croissante de façon monotone, alors les équations

F(X) = X(UN)

F (F (X)) = X (B)

équivalent.

Preuve. Le fait que l’équation (B) soit une conséquence de l’équation (A) est évident : toute racine (A) satisfait (B). (Si

F (X 0 ) = X 0 , Que F (F (X 0 )) = F (X 0 ) = X 0.). Montrons que toute racine de l'équation (B) satisfait l'équation (A). Laisser X 0 tel que F (F (X 0 )) = X 0 .Supposons que F (X 0 ) ≠ X 0 et pour plus de précision F (X 0 ) > X 0 . Alors F (F (X 0 )) > F (X 0 ) > X 0, ce qui contredit l'hypothèse ( F (F (X 0 )) = X 0). Le théorème a été prouvé.

Le théorème est-il vrai pour une fonction décroissante monotone ?

Commentaire. Si oui = F (X) augmente de façon monotone, alors pour tout kéquations
Et F (X) = X sont équivalents.

Donnons quelques exemples d'utilisation de ce théorème.

1. Résous l'équation:
.

Solution. Réécrivons l'équation.
. Considérez la fonction
. Cette fonction augmente de façon monotone. Nous avons l'équation

F (F (X)) = X. Conformément au théorème, nous le remplaçons par l'équation équivalente F (X) = X ou .

Répondre.

.

2. Résous l'équation:

.

Solution. Transformons l'équation :
.

Cette équation ressemble à : F (F (X)) = X, Où
.

D'après le théorème, nous avons une équation équivalente :
,

Répondre.
.

3. Résoudre un système d'équations:
.

Solution. Considérons la fonction. Parce que le

Devant tout le monde t, Que F (t) augmente.

Le système a la forme oui = F (X), z = F (oui), X = F (z), ceux. X = F (F (F (X))).

D'après le théorème X satisfait l'équation F (X) = X ou

Répondre.(0, 0, 0), (-1, -1, -1).

Utilisation des propriétés extrêmes des fonctions considérées. Notes. Les idées principales de ce point sont assez clairement visibles à partir des exemples :

1. Résous l'équation:
.

Solution. Le côté gauche de cette équation ne dépasse pas 2 et le côté droit ne dépasse pas 2. Par conséquent, l'égalité ne peut se produire que si les côtés gauche et droit sont égaux à 2, c'est-à-dire X = 0.

Commentaire. Cette situation, où la plus petite valeur d'une fonction située dans une partie de l'équation est égale à la plus grande valeur d'une fonction située dans l'autre partie, peut être généralisée. Un cas plus général est celui des équations de la forme F (X) = φ (X) , Pour qui
acceptable pour tous X(formellement, nous pouvons réécrire cette équation comme

F (X) = φ (X) = 0, nous arrivons donc à la situation déjà considérée, puisque la plus grande valeur du membre de droite est zéro).

2. Résous l'équation:.

Montrons que cette équation n'a pas de solutions. Passons à la conséquence (potentialiser) :
.

Estimons le membre de gauche en fonction de l'inégalité entre la moyenne géométrique et la moyenne arithmétique

:

ceux. le côté gauche est plus petit que le droit. L'équation n'a pas de solutions.

Répondre. Il n'y a pas de décision.

3. Résolvez le système d'équations :

Solution. Prouvons-le.

Laissez pour certitude X 5 > X 4, puis à partir des deux premières équations on obtient, à partir desquelles
et particulièrement
. Ensuite, à partir du troisième et du quatrième, nous obtenons
et particulièrement
. De la dernière paire nous trouvons
. Le résultat est une contradiction (et
, c'est à dire.
, mais c'était supposé cela).

Moyens,
, d'ici
etc., toutes les inconnues sont égales les unes aux autres.

Répondre.(0, 0, 0, 0,0);
.

Problèmes dont la formulation est non standard et qui impliquent des équations ou des inégalités. Cette catégorie comprend notamment des problèmes dans lesquels il faut déterminer le nombre de racines d'une équation donnée, prouver l'existence d'une racine sur un certain intervalle et résoudre une équation ou une inégalité sur un intervalle donné. Regardons quelques exemples.

1. Montrer que l'équation
a un positif décision et une décision négative. méthodes d'enseignement des mathématiques en moyenne école: Cahier de texte. manuel de l'élève....