Kuliah 3. Teorema umum dinamika
Dinamika sistem poin material merupakan cabang penting dari mekanika teoritis. Di sini kita terutama mempertimbangkan masalah tentang gerak sistem mekanis (sistem titik material) dengan jumlah derajat kebebasan yang terbatas - jumlah maksimum parameter independen yang menentukan posisi sistem. Tugas utama dinamika sistem adalah mempelajari hukum gerak benda tegar dan sistem mekanis.
Pendekatan paling sederhana untuk mempelajari gerak suatu sistem, terdiri dari N poin material, dilakukan dengan mempertimbangkan pergerakan masing-masing titik dalam sistem. Dalam hal ini, semua gaya yang bekerja pada setiap titik sistem, termasuk gaya interaksi antar titik, harus ditentukan.
Menentukan percepatan setiap titik sesuai dengan hukum kedua Newton (1.2), kita peroleh untuk setiap titik tiga hukum diferensial skalar gerak orde kedua, yaitu. 3 N hukum diferensial gerak untuk keseluruhan sistem.
Untuk mencari persamaan gerak suatu sistem mekanik berdasarkan gaya-gaya tertentu dan kondisi awal untuk setiap titik sistem, hukum-hukum diferensial yang dihasilkan harus diintegrasikan. Masalah ini sulit bahkan dalam kasus dua titik material yang bergerak hanya di bawah pengaruh gaya interaksi menurut hukum tarik-menarik universal (masalah dua benda), dan sangat sulit dalam kasus tiga titik yang berinteraksi (masalah tiga benda ).
Oleh karena itu, perlu dicari metode penyelesaian masalah yang dapat menghasilkan persamaan yang dapat diselesaikan dan memberikan gambaran tentang gerak suatu sistem mekanik. Teorema umum dinamika, sebagai konsekuensi dari hukum gerak diferensial, memungkinkan kita menghindari kompleksitas yang timbul selama integrasi dan memperoleh hasil yang diperlukan.
3. 1. Catatan umum
Kami akan memberi nomor pada titik-titik sistem mekanis dengan indeks Saya, J, k dll., yang dijalankan melalui semua nilai 1, 2, 3… N, Di mana N – jumlah poin sistem. Besaran fisis berhubungan dengan k titik ke-ditunjuk oleh indeks yang sama dengan titik tersebut. Misalnya, nyatakan vektor jari-jari dan kecepatan masing-masing k poin ke-.
Setiap titik dalam sistem dipengaruhi oleh gaya-gaya yang mempunyai dua asal: pertama, gaya-gaya yang sumbernya terletak di luar sistem, disebut luar pasukan dan ditunjuk; kedua, gaya-gaya dari titik-titik lain pada suatu sistem tertentu, disebut intern pasukan dan ditunjuk. Gaya dalam memenuhi hukum ketiga Newton. Mari kita perhatikan sifat paling sederhana dari gaya dalam yang bekerja pada seluruh sistem mekanik dalam keadaan apa pun.
Properti pertama. Jumlah geometri semua gaya dalam sistem (vektor utama gaya dalam) sama dengan nol.
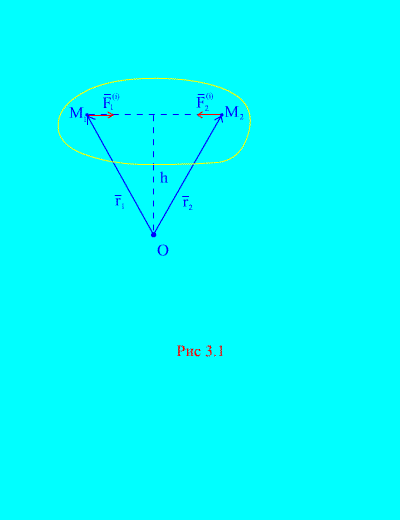
Memang, jika kita mempertimbangkan dua titik sembarang dari sistem, misalnya dan (Gbr. 3.1), lalu untuk mereka ![]() , Karena gaya aksi dan reaksi selalu sama besarnya, bekerja sepanjang satu garis aksi dalam arah berlawanan, yang menghubungkan titik-titik yang berinteraksi. Oleh karena itu, vektor utama gaya dalam terdiri dari pasangan gaya titik-titik yang berinteraksi
, Karena gaya aksi dan reaksi selalu sama besarnya, bekerja sepanjang satu garis aksi dalam arah berlawanan, yang menghubungkan titik-titik yang berinteraksi. Oleh karena itu, vektor utama gaya dalam terdiri dari pasangan gaya titik-titik yang berinteraksi
![]() (3.1)
(3.1)
Properti kedua. Jumlah geometrik momen semua gaya dalam relatif terhadap suatu titik sembarang dalam ruang adalah nol.
Mari kita perhatikan sistem momen gaya dan relatif terhadap suatu titik TENTANG(Gbr. 3.1). Dari (Gbr. 3.1). sudah jelas itu
![]() ,
,
Karena kedua gaya mempunyai lengan yang sama dan arah vektor momen yang berlawanan. Momen utama gaya dalam relatif terhadap suatu titik TENTANG terdiri dari jumlah vektor ekspresi tersebut dan sama dengan nol. Karena itu,
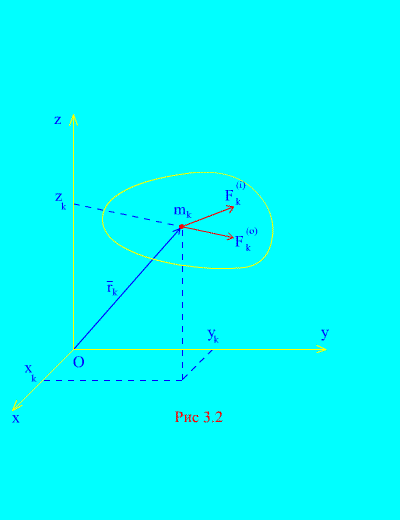
Biarkan gaya eksternal dan internal bekerja pada sistem mekanis yang terdiri dari N poin (Gbr. 3.2). Jika resultan gaya-gaya luar dan resultan semua gaya-gaya dalam diterapkan pada setiap titik dalam sistem, maka untuk sembarang k titik sistem, persamaan diferensial gerak dapat dibuat. Akan ada total persamaan seperti itu N:
dan dalam proyeksi ke sumbu koordinat tetap 3 N:
![]() (3.4)
(3.4)
Persamaan vektor (3.3) atau persamaan skalar yang setara (3.4) mewakili hukum diferensial gerak titik-titik material dari keseluruhan sistem. Jika semua titik bergerak sejajar pada satu bidang atau satu garis lurus, maka banyaknya persamaan (3.4) pada kasus pertama adalah 2 N, di detik N.

Contoh 1. Dua massa dihubungkan satu sama lain melalui kabel yang tidak dapat diperpanjang yang dipasang pada sebuah balok (Gbr. 3.3). Mengabaikan gaya gesekan, serta massa balok dan kabel, menentukan hukum pergerakan beban dan tegangan kabel.
Larutan. Sistem ini terdiri dari dua benda material (dihubungkan dengan kabel yang tidak dapat diperpanjang) yang bergerak sejajar dengan sumbu yang sama X. Mari kita tuliskan hukum diferensial gerak dalam proyeksi pada sumbu X untuk semuanya.
Biarkan beban kanan turun dengan percepatan, maka beban kiri akan naik dengan percepatan. Kita secara mental membebaskan diri dari koneksi (kabel) dan menggantinya dengan reaksi dan (Gbr. 3.3). Mengingat benda bebas, mari kita buat hukum diferensial gerak dalam proyeksi ke sumbu X(artinya tegangan benang adalah gaya dalam, dan berat beban adalah gaya luar):
Karena dan (benda-benda dihubungkan dengan kabel yang tidak dapat diperpanjang), kita peroleh
Memecahkan persamaan percepatan dan tegangan kabel ini T, kita mendapatkan
 .
.
Perhatikan bahwa tegangan pada kabel tidak sama dengan gaya gravitasi beban yang bersangkutan.
3. 2. Teorema gerak pusat massa
Diketahui bahwa benda tegar dan sistem mekanik pada suatu bidang dapat bergerak cukup kompleks. Teorema pertama tentang gerak suatu benda dan sistem mekanik dapat diperoleh sebagai berikut: lempar a k.-l. sebuah benda yang terdiri dari banyak benda padat yang diikat menjadi satu. Jelas dia akan terbang dengan parabola. Hal ini terungkap saat mempelajari pergerakan titik. Namun, kini benda tersebut bukan sebuah titik. Ia berputar dan berayun selama penerbangannya mengelilingi suatu pusat efektif yang bergerak dalam parabola. Teorema pertama tentang gerak benda kompleks mengatakan bahwa pusat efektif tertentu adalah pusat massa suatu benda yang bergerak. Pusat massa tidak harus terletak di dalam benda itu sendiri; ia bisa terletak di suatu tempat di luarnya.
Dalil. Pusat massa suatu sistem mekanis bergerak sebagai suatu titik material yang massanya sama dengan massa keseluruhan sistem, di mana semua gaya luar yang bekerja pada sistem diterapkan.
Untuk membuktikan teorema tersebut, kita tulis ulang hukum diferensial gerak (3.3) dalam bentuk berikut:
![]() (3.5)
(3.5)
Di mana N – jumlah poin sistem.
Mari kita jumlahkan persamaan-persamaan tersebut suku demi suku:
 (A)
(A)
Posisi pusat massa sistem mekanik relatif terhadap sistem koordinat yang dipilih ditentukan oleh rumus (2.1):  Di mana M– massa sistem. Maka ruas kiri persamaan (a) akan ditulis
Di mana M– massa sistem. Maka ruas kiri persamaan (a) akan ditulis
Jumlah pertama di ruas kanan persamaan (a) sama dengan vektor utama gaya luar, dan jumlah terakhir, berdasarkan sifat gaya dalam, sama dengan nol. Kemudian persamaan (a), dengan memperhatikan (b), akan ditulis ulang
![]() , (3.6)
, (3.6)
itu. hasil kali massa sistem dan percepatan pusat massanya sama dengan jumlah geometri semua gaya luar yang bekerja pada sistem.
Dari persamaan (3.6) dapat disimpulkan bahwa gaya-gaya dalam tidak secara langsung mempengaruhi pergerakan pusat massa. Namun, dalam beberapa kasus, hal tersebut menjadi penyebab munculnya gaya eksternal yang diterapkan pada sistem. Jadi, gaya dalam yang menggerakkan roda penggerak mobil ke dalam putaran menyebabkan gaya adhesi eksternal yang diterapkan pada pelek roda bekerja padanya.
Contoh 2. Mekanismenya, yang terletak pada bidang vertikal, dipasang pada bidang datar horizontal dan dipasang padanya dengan palang yang dipasang secara kaku pada permukaan. KE Dan L (Gbr. 3.4).
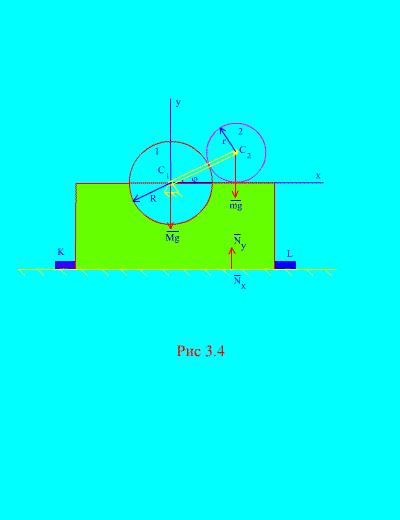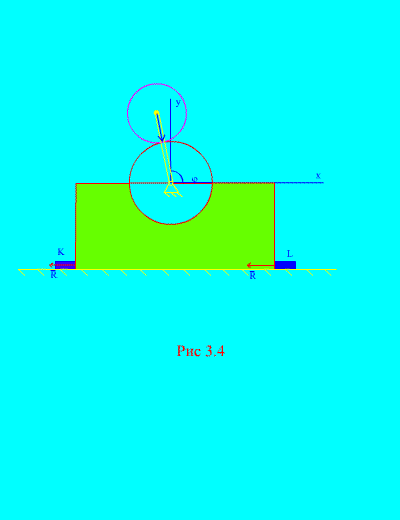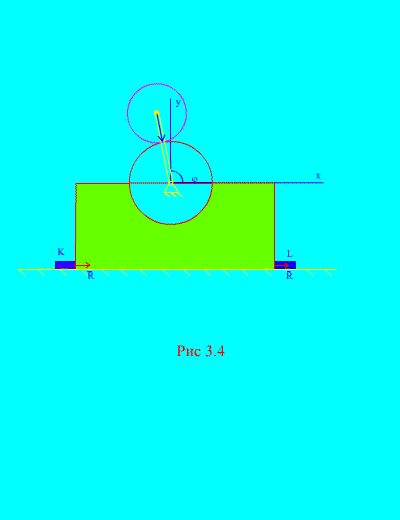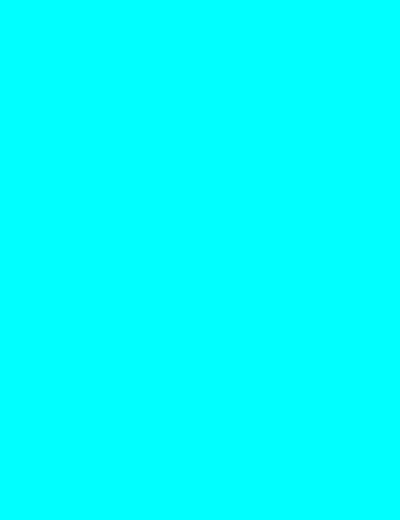
Jari-jari cakram 1 R diam. Disk 2 massa M dan radius R melekat pada engkol, panjang R+ R pada intinya dari 2. Engkol berputar secara konstan
kecepatan sudut. Pada saat awal, engkol menempati posisi horizontal kanan. Dengan mengabaikan massa engkol, tentukan gaya horizontal dan vertikal maksimum yang bekerja pada batang jika massa total rangka dan roda 1 sama dengan M. Pertimbangkan juga perilaku mekanisme tanpa adanya jeruji.
Larutan. Sistem terdiri dari dua massa ( N=2 ): disk tetap 1 dengan bingkai dan disk bergerak 2. Arahkan sumbunya pada melalui pusat gravitasi piringan stasioner secara vertikal ke atas, sumbu X– sepanjang bidang horizontal.
Mari kita tuliskan teorema gerak pusat massa (3.6) dalam bentuk koordinat
Kekuatan eksternal dari sistem ini adalah: berat frame dan disk tetap - mg, memindahkan berat disk – mg, - reaksi total horizontal baut, - reaksi total normal bidang. Karena itu,
Maka hukum gerak (b) akan ditulis ulang
Mari kita hitung koordinat pusat massa sistem mekanik:
 ; (G)
; (G)
seperti yang bisa dilihat dari (Gbr. 3.4), , , ![]() (sudut engkol),
(sudut engkol), ![]() . Substitusikan ekspresi ini ke dalam (d) dan hitung turunan kedua terhadap waktu T dari , , kita mendapatkannya
. Substitusikan ekspresi ini ke dalam (d) dan hitung turunan kedua terhadap waktu T dari , , kita mendapatkannya
 (D)
(D)
Substitusikan (c) dan (e) ke dalam (b), kita temukan

Tekanan horizontal yang bekerja pada batang adalah yang terbesar dan terkecil ketika karena = 1 karenanya, yaitu
![]()
![]()
Tekanan mekanisme pada bidang horizontal mempunyai nilai tertinggi dan terendah ketika dosa karenanya, yaitu
![]()
![]()
Faktanya, masalah pertama dinamika telah terpecahkan: menurut persamaan gerak yang diketahui dari pusat massa sistem (d), gaya-gaya yang terlibat dalam gerak dipulihkan.
Dengan tidak adanya jeruji K Dan L (Gbr. 3.4), mekanismenya mungkin mulai memantul di atas bidang horizontal. Ini akan terjadi ketika, mis. ketika , maka kecepatan sudut putaran engkol, saat mekanisme memantul, harus memenuhi persamaan
 .
.
3. 3. Hukum kekekalan gerak pusat massa
Jika vektor utama gaya luar yang bekerja pada sistem sama dengan nol, mis. , lalu dari(3.6)maka percepatan pusat massa adalah nol, oleh karena itu kecepatan pusat massa adalah konstan besar dan arahnya. Jika, khususnya, pada saat awal pusat massa diam, maka pusat massa diam sepanjang waktu selama vektor utama gaya luar sama dengan nol.
Beberapa akibat wajar mengikuti teorema ini.
· Kekuatan internal saja tidak dapat mengubah sifat pergerakan pusat massa sistem.
· Jika vektor utama gaya luar yang bekerja pada sistem adalah nol, maka pusat massa berada dalam keadaan diam atau bergerak beraturan dan lurus.
· Jika proyeksi vektor utama gaya-gaya luar sistem pada suatu sumbu tetap sama dengan nol, maka proyeksi kecepatan pusat massa sistem pada sumbu tersebut tidak berubah.
· Sepasang gaya yang diterapkan pada benda tegar tidak dapat mengubah pergerakan pusat massanya (hanya dapat menyebabkan benda berputar mengelilingi pusat massa).
Mari kita perhatikan contoh yang menggambarkan hukum kekekalan gerak pusat massa.

Contoh 3. Dua buah massa dihubungkan dengan seutas benang yang tidak dapat diperpanjang dan dilemparkan melalui sebuah balok (Gbr. 3.5), dipasang pada irisan yang bermassa M. Baji tersebut bertumpu pada bidang horizontal licin. Pada saat awal sistem dalam keadaan diam. Temukan perpindahan baji sepanjang bidang ketika beban pertama diturunkan ke ketinggian N. Abaikan massa balok dan benang.
Larutan. Gaya luar yang bekerja pada baji bersama dengan beban adalah gravitasi, dan mg, serta reaksi normal permukaan horizontal halus N. Oleh karena itu,
Karena pada saat awal sistem dalam keadaan diam, kita mempunyai .
Mari kita hitung koordinat pusat massa sistem pada saat dan saat ini T 1 ketika bebannya berat G akan turun ke ketinggian H.
Untuk saat ini:
 ,
,
Di mana , , X– masing-masing koordinat pusat massa beban berbobot g, g dan baji berbobot MG.
Mari kita asumsikan bahwa irisan pada saat tertentu bergerak ke arah sumbu positif Sapi berdasarkan jumlah L, jika berat beban turun ke ketinggian N. Lalu, untuk saat ini
Karena beban bersama-sama dengan baji akan berpindah ke L ke kanan, dan beban akan bergerak ke atas sepanjang baji. Sejak , maka setelah perhitungan kita dapatkan
 .
.
3.4. Kuantitas pergerakan sistem
3.4.1. Perhitungan momentum sistem
Momentum suatu titik material adalah besaran vektor yang sama dengan hasil kali massa suatu titik dan vektor kecepatannya
Satuan pengukuran momentum -
Momentum suatu sistem mekanik adalah jumlah vektor momentum titik-titik individual sistem, yaitu.
Di mana N – jumlah poin sistem.
Momentum suatu sistem mekanik dapat dinyatakan dalam massa sistem M dan kecepatan pusat massa. Benar-benar,
itu. Momentum sistem sama dengan hasil kali massa seluruh sistem dan kecepatan pusat massanya. Arahnya sama dengan arah (Gbr. 3.6)

Dalam proyeksi ke sumbu persegi panjang yang kita miliki
dimana , , adalah proyeksi kecepatan pusat massa sistem.
Di Sini M– massa sistem mekanis; tidak berubah ketika sistem bergerak.
Hasil ini sangat berguna untuk digunakan ketika menghitung besaran gerak benda tegar.
Dari rumus (3.7) jelas bahwa jika suatu sistem mekanik bergerak sedemikian rupa sehingga pusat massanya tetap diam, maka momentum sistem tersebut tetap sama dengan nol.
3.4.2. Impuls kekuatan dasar dan penuh
Aksi suatu gaya pada suatu titik material seiring waktu dt dapat dicirikan oleh dorongan dasar. Dorongan kekuatan total dari waktu ke waktu T, atau impuls gaya, ditentukan oleh rumus
atau dalam proyeksi ke koordinat sumbu
 (3.8a)
(3.8a)
Satuan gaya impuls adalah .
3.4.3. Teorema perubahan momentum suatu sistem
Biarkan gaya eksternal dan internal diterapkan pada titik-titik sistem. Kemudian untuk setiap titik dalam sistem kita dapat menerapkan hukum diferensial gerak (3.3), dengan mengingat hal itu ![]() :
:
 .
.
Menjumlahkan semua poin dari sistem, kita memperoleh
Berdasarkan sifat kekuatan internal dan menurut definisi ![]() kita punya
kita punya
 (3.9)
(3.9)
Mengalikan kedua ruas persamaan ini dengan dt, kita memperoleh teorema tentang perubahan momentum dalam bentuk diferensial:
![]() , (3.10)
, (3.10)
itu. momentum diferensial suatu sistem mekanik sama dengan jumlah vektor impuls elementer dari semua gaya luar yang bekerja pada titik-titik sistem mekanik.
Menghitung integral kedua ruas (3.10) dalam waktu dari 0 sampai T, kita memperoleh teorema dalam bentuk berhingga atau integral
 (3.11)
(3.11)
Dalam proyeksi ke sumbu koordinat yang akan kita miliki
Perubahan momentum sistem mekanik dari waktu ke waktuT, sama dengan jumlah vektor semua impuls gaya luar yang bekerja pada titik-titik sistem mekanik selama waktu yang sama.
Contoh 4. Beban berat M turun dari keadaan diam pada bidang miring karena pengaruh suatu gaya F, sebanding dengan waktu: , dimana (Gbr. 3.7). Berapa kecepatan yang diperoleh tubuh setelahnya T detik setelah dimulainya gerakan, jika koefisien gesekan geser beban pada bidang miring sama dengan F.
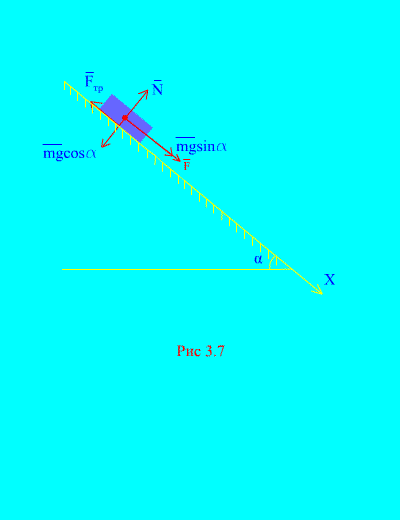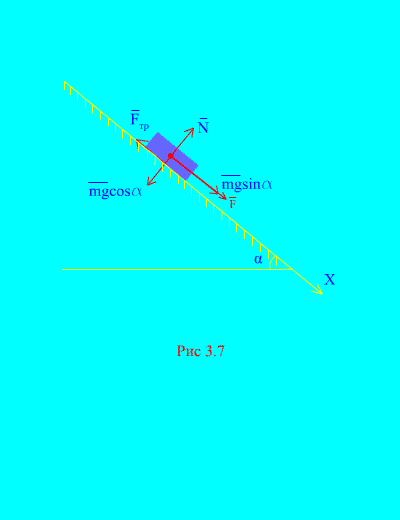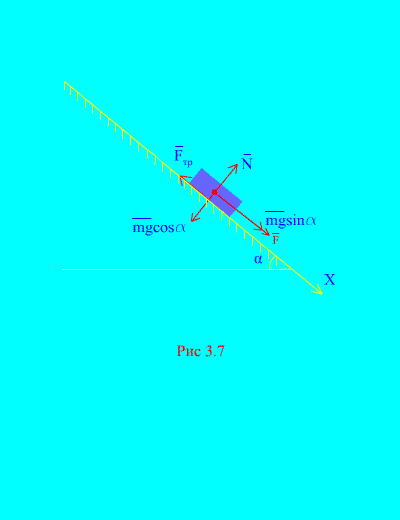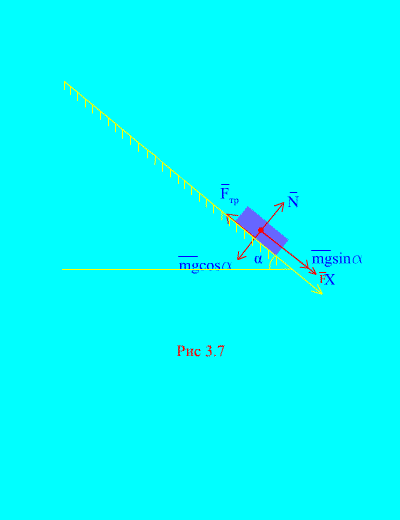
Larutan. Mari kita gambarkan gaya-gaya yang diterapkan pada beban: mg – memuat gaya gravitasi, N adalah reaksi normal bidang, adalah gaya gesek geser beban pada bidang, dan . Arah semua gaya ditunjukkan pada (Gbr. 3.7).
Mari kita arahkan porosnya X sepanjang bidang miring ke bawah. Mari kita tuliskan teorema tentang perubahan momentum (3.11) pada proyeksi ke sumbu X:
 (A)
(A)
Sesuai dengan kondisi, karena pada saat awal beban dalam keadaan diam. Jumlah proyeksi impuls semua gaya pada sumbu x adalah sama dengan

Karena itu,
 ,
,
 .
.
3.4.4. Hukum kekekalan momentum
Hukum kekekalan diperoleh sebagai kasus khusus dari teorema perubahan momentum. Dua kasus khusus mungkin terjadi.
· Jika jumlah vektor semua gaya luar yang diterapkan pada sistem sama dengan nol, mis. , maka dari teorema berikut (3.9) , Apa ,
itu. jika vektor utama gaya luar sistem adalah nol, maka besar dan arah gerak sistem adalah konstan.
· Jika proyeksi vektor utama gaya luar pada sembarang sumbu koordinat sama dengan nol, misalnya Sapi, yaitu. , maka proyeksi momentum pada sumbu tersebut bernilai konstan.
Mari kita perhatikan contoh penerapan hukum kekekalan momentum.

Contoh 5. Pendulum balistik adalah suatu benda yang massanya digantungkan pada seutas benang panjang (Gbr. 3.8).
Peluru bermassa, bergerak dengan kecepatan V dan membentur benda yang tidak bergerak, tersangkut di dalamnya, dan benda tersebut menyimpang. Berapa kecepatan peluru jika benda tersebut diangkat ke ketinggian H ?
Larutan. Biarkan tubuh yang tertancap peluru memperoleh kecepatan. Kemudian, dengan menggunakan hukum kekekalan momentum selama interaksi dua benda, kita dapat menulis ![]() .
.
Kecepatan dapat dihitung dengan menggunakan hukum kekekalan energi mekanik  . Kemudian . Hasilnya kami temukan
. Kemudian . Hasilnya kami temukan
 .
.
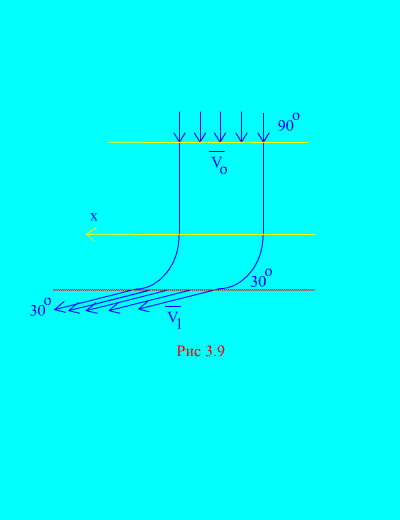
Contoh 6. Air memasuki saluran stasioner (Gbr. 3.9) penampang variabel dengan kecepatan pada sudut horizontal; luas penampang saluran di pintu masuk; kecepatan air di pintu keluar saluran membentuk sudut dengan cakrawala.
Tentukan komponen horizontal reaksi air terhadap dinding saluran. Kepadatan air  .
.
Larutan. Kita akan menentukan komponen horizontal dari reaksi yang dilakukan oleh dinding saluran terhadap air. Gaya ini besarnya sama dan berlawanan tanda dengan gaya yang diinginkan. Kita punya, menurut (3.11a),
 . (A)
. (A)
Kami menghitung massa volume cairan yang memasuki saluran selama waktu t:
Kuantitas rAV 0 disebut massa kedua - massa cairan yang mengalir melalui setiap bagian pipa per satuan waktu.
Jumlah air yang sama keluar dari saluran dalam waktu yang sama. Kecepatan awal dan akhir diberikan dalam kondisi.
Mari kita hitung sisi kanan persamaan (a), yang menentukan jumlah proyeksi ke sumbu horizontal gaya luar yang diterapkan pada sistem (air). Satu-satunya gaya horizontal adalah komponen horizontal dari reaksi dinding yang dihasilkan Rx. Gaya ini konstan selama pergerakan air yang stabil. Itu sebabnya
 . (V)
. (V)
Substitusikan (b) dan (c) ke dalam (a), kita peroleh
3.5. Momen kinetik sistem
3.5.1. Momen utama momentum sistem

Misalkan vektor jari-jari suatu titik dengan massa sistem relatif terhadap suatu titik A, yang disebut pusat (Gbr. 3.10).
Momentum momentum (momen kinetik) suatu titik relatif terhadap pusat A disebut vektor , ditentukan oleh rumus
![]() . (3.12)
. (3.12)
Dalam hal ini, vektor diarahkan tegak lurus terhadap bidang yang melalui pusat A dan vektor .
Momentum momentum (momen kinetik) suatu titik terhadap sumbunya disebut proyeksi ke sumbu momen momentum suatu titik relatif terhadap pusat mana pun yang dipilih pada sumbu ini.
Momen momentum utama (momen kinetik) sistem relatif terhadap pusat A disebut kuantitas
 (3.13)
(3.13)
Momen momentum utama (momen kinetik) sistem relatif terhadap sumbu disebut proyeksi ke sumbu ini dari momen momentum utama sistem relatif terhadap setiap yang dipilih pada sumbu ini poros tengah.
3.5.2. Momen kinetik benda tegar yang berputar terhadap sumbu rotasi
Mari kita sejajarkan titik tetapnya TENTANG benda yang terletak pada sumbu rotasi TENTANGz, dengan asal sistem koordinat Ohoz, yang sumbunya akan berputar bersama tubuh (Gbr. 3.11). Misalkan vektor jari-jari suatu titik pada benda relatif terhadap titik asal koordinat; proyeksinya pada sumbu akan dilambangkan dengan , , . Mari kita nyatakan proyeksi vektor kecepatan sudut suatu benda pada sumbu yang sama dengan 0, 0, ().
Mari kita perhatikan pergerakan suatu sistem benda material relatif terhadap sistem koordinat tetap. Jika sistem tidak bebas, maka sistem tersebut dapat dianggap bebas jika kita membuang hubungan yang dikenakan pada sistem dan mengganti aksinya dengan reaksi yang sesuai.
Mari kita bagi semua gaya yang diterapkan pada sistem menjadi eksternal dan internal; keduanya mungkin termasuk reaksi orang yang dibuang
koneksi. Misalkan dan nyatakan vektor utama dan momen utama gaya luar terhadap titik A.
1. Teorema perubahan momentum. Jika adalah besarnya gerak sistem, maka (lihat)
artinya, teorema ini valid: turunan waktu dari momentum sistem sama dengan vektor utama semua gaya luar.
Dengan mengganti vektor melalui ekspresinya dimana adalah massa sistem, adalah kecepatan pusat massa, persamaan (4.1) dapat diberikan bentuk yang berbeda:
Persamaan ini berarti bahwa pusat massa sistem bergerak seperti suatu titik material yang massanya sama dengan massa sistem dan yang diberikan gaya yang secara geometri sama dengan vektor utama semua gaya luar sistem. Pernyataan terakhir disebut teorema gerak pusat massa (pusat inersia) sistem.
Jika maka dari (4.1) maka vektor momentum adalah konstan besar dan arahnya. Memproyeksikan pada sumbu koordinat, kita memperoleh tiga integral skalar pertama, persamaan diferensial dari topi ganda sistem:
Integral ini disebut integral momentum. Jika kecepatan pusat massa konstan, maka ia bergerak secara beraturan dan lurus.
Jika proyeksi vektor utama gaya luar pada suatu sumbu, misalnya pada suatu sumbu, sama dengan nol, maka kita mempunyai satu integral pertama, atau jika dua proyeksi vektor utama sama dengan nol, maka ada dua integral momentum.
2. Teorema perubahan momentum sudut. Misalkan A adalah suatu titik sembarang dalam ruang (bergerak atau diam), yang tidak harus bertepatan dengan titik material tertentu dalam sistem selama seluruh waktu pergerakan. Kami menyatakan kecepatannya dalam sistem koordinat tetap dengan Teorema perubahan momen kinetik suatu sistem material relatif terhadap titik A berbentuk
![]()
Jika titik A tetap, maka persamaan (4.3) berbentuk lebih sederhana:
Persamaan ini menyatakan teorema tentang variasi momentum sudut suatu sistem relatif terhadap suatu titik tetap: turunan waktu dari momentum sudut sistem, dihitung relatif terhadap suatu titik tetap, sama dengan momen utama semua gaya eksternal relatif sampai pada titik ini.
Jika maka menurut (4.4) vektor momentum sudut tetap besar dan arahnya. Memproyeksikan pada sumbu koordinat, kita memperoleh integral skalar pertama dari persamaan diferensial sistem ganda:
Integral ini disebut integral momentum atau integral luas.
Jika titik A berimpit dengan pusat massa sistem, maka suku pertama pada ruas kanan persamaan (4.3) hilang dan teorema perubahan momentum sudut mempunyai bentuk penulisan yang sama (4.4) seperti pada kasus titik tetap A. Catatan (lihat hal. 4 § 3), bahwa dalam kasus yang dipertimbangkan, momentum sudut absolut sistem di sisi kiri persamaan (4.4) dapat digantikan oleh momentum sudut yang sama dari sistem dalam geraknya relatif terhadap pusat massa.
Misalkan suatu sumbu konstan atau sumbu dengan arah konstan yang melalui pusat massa sistem, dan misalkan momen kinetik sistem relatif terhadap sumbu tersebut. Dari (4.4) berikut ini
dimana adalah momen gaya luar terhadap sumbu. Jika selama keseluruhan gerakan kita mempunyai integral pertama
Dalam karya S.A. Chaplygin diperoleh beberapa generalisasi teorema perubahan momentum kinetik, yang kemudian diterapkan untuk menyelesaikan sejumlah permasalahan pada bola yang menggelinding. Generalisasi lebih lanjut dari teorema tentang perubahan momen mekanis dan penerapannya dalam masalah dinamika benda tegar terdapat dalam karya ini. Hasil utama dari pekerjaan ini berkaitan dengan teorema tentang perubahan momentum kinetik relatif terhadap benda yang bergerak, yang terus-menerus melewati suatu titik bergerak A. Misalkan vektor satuan diarahkan sepanjang sumbu ini. Mengalikan secara skalar dengan kedua ruas persamaan (4.3) dan menjumlahkan suku pada kedua bagiannya, kita peroleh
Ketika kondisi kinematik terpenuhi
Persamaan (4.5) mengikuti dari (4.7). Dan jika kondisi (4.8) terpenuhi selama seluruh gerakan, maka integral pertama (4.6) ada.
Jika hubungan sistem ideal dan memungkinkan, di antara perpindahan maya, rotasi sistem sebagai benda tegar di sekitar sumbu dan, maka momen utama reaksi terhadap sumbu dan sama dengan nol, dan kemudian nilai pada ruas kanan persamaan (4.5) mewakili momen utama dari semua gaya aktif eksternal relatif terhadap sumbu dan . Persamaan dengan nol momen ini dan validitas relasi (4.8) akan berada dalam kondisi yang cukup untuk keberadaan integral (4.6).
Jika arah sumbu dan konstan, maka kondisi (4.8) dituliskan dalam bentuk
![]()
Persamaan ini berarti bahwa proyeksi kecepatan pusat massa dan kecepatan titik A pada sumbu dan pada bidang yang tegak lurus adalah sejajar. Dalam karya S.A. Chaplygin, alih-alih (4.9), kondisi yang kurang umum harus dipenuhi, di mana X adalah nilai konstanta yang berubah-ubah.
Perhatikan bahwa kondisi (4.8) tidak bergantung pada pilihan titik di . Misalkan P adalah titik sembarang pada sumbu. Kemudian
dan maka dari itu
Sebagai kesimpulan, kami mencatat interpretasi geometris Rézal terhadap persamaan (4.1) dan (4.4): vektor kecepatan absolut dari ujung-ujung vektor dan masing-masing sama dengan vektor utama dan momen utama semua gaya eksternal relatif terhadap titik A .
Penggunaan asuransi kesehatan dalam memecahkan masalah memang penuh dengan kesulitan-kesulitan tertentu. Oleh karena itu, hubungan tambahan biasanya dibuat antara karakteristik gerak dan gaya, yang lebih nyaman untuk penerapan praktis. Hubungan seperti itu adalah teorema umum dinamika. Mereka, sebagai konsekuensi dari OMS, membangun hubungan antara kecepatan perubahan beberapa ukuran pergerakan yang diperkenalkan secara khusus dan karakteristik kekuatan eksternal.
Teorema perubahan momentum. Mari kita perkenalkan konsep vektor momentum (R. Descartes) dari suatu titik material (Gbr. 3.4):
saya saya = t V G (3.9)
Beras. 3.4.
Untuk sistem kami memperkenalkan konsepnya vektor utama momentum sistem sebagai jumlah geometri:
Q = Y, m " V r
Sesuai dengan OZMS: Xu, -^=i) , atau X
ULANG) .
Dengan memperhitungkan bahwa /w, = const kita mendapatkan: -Ym,!" = ULANG) ,
atau dalam bentuk akhir
lakukan/di = A (E (3.11)
itu. turunan pertama terhadap waktu dari vektor utama momentum sistem sama dengan vektor utama gaya luar.
Teorema gerak pusat massa. Pusat massa sistem disebut titik geometris yang posisinya bergantung pada T, dll. dari distribusi massa /g/, dalam sistem dan ditentukan oleh ekspresi vektor jari-jari pusat massa (Gbr. 3.5):

Di mana g s - vektor radius pusat massa.

Beras. 3.5.
Sebut saja = t dengan massa sistem. Setelah mengalikan ekspresi
menerapkan (3.12) pada penyebut dan membedakan kedua ruas hasil
kita akan memiliki kesetaraan yang berharga: g s t s = ^t.U. = 0, atau 0 = Ini kamu.
Jadi, vektor momentum utama sistem sama dengan hasil kali massa sistem dan kecepatan pusat massa. Dengan menggunakan teorema perubahan momentum (3.11), kita peroleh:
t s dU s / dі = A (E) , atau
Rumus (3.13) menyatakan teorema pergerakan pusat massa: pusat massa sistem bergerak sebagai titik material yang mempunyai massa sistem, yang dipengaruhi oleh vektor utama gaya luar.
Teorema perubahan momentum sudut. Mari kita perkenalkan konsep momentum sudut suatu titik material sebagai hasil kali vektor dari vektor jari-jari dan momentumnya:
untuk oh = hal X itu, (3.14)
Di mana ke OI - momen momentum suatu titik material relatif terhadap suatu titik tetap TENTANG(Gbr. 3.6).

Sekarang kita mendefinisikan momentum sudut suatu sistem mekanik sebagai jumlah geometri:
К() = X ko, = ШУ, ? O-15>
Membedakan (3.15), kita memperoleh:
Ґ detik--- X itu kamu. + kamu X itu aku
Mengingat bahwa = UGU saya X aku kamu aku= 0, dan rumus (3.2), kita peroleh:
сіК а /с1ї - ї 0 .
Berdasarkan ekspresi kedua pada (3.6), kita akhirnya mempunyai teorema tentang perubahan momentum sudut sistem:
Turunan pertama kali momen momentum suatu sistem mekanik terhadap pusat tetap O sama dengan momen utama gaya luar yang bekerja pada sistem tersebut relatif terhadap pusat yang sama.
Saat menurunkan relasi (3.16), diasumsikan bahwa TENTANG- titik pasti. Namun dapat ditunjukkan bahwa dalam beberapa kasus lain bentuk hubungan (3.16) tidak akan berubah, khususnya jika dalam gerak bidang titik momen dipilih pada pusat massa, pusat kecepatan atau percepatan sesaat. Apalagi jika intinya TENTANG bertepatan dengan titik material yang bergerak, persamaan (3.16) yang ditulis untuk titik tersebut akan berubah menjadi identitas 0 = 0.
Teorema perubahan energi kinetik. Ketika sistem mekanis bergerak, baik energi “eksternal” maupun energi internal sistem berubah. Jika ciri-ciri gaya dalam, vektor utama dan momen utama tidak mempengaruhi perubahan vektor utama dan momen utama terhadap jumlah percepatan, maka kekuatan internal dapat dimasukkan dalam penilaian proses keadaan energi sistem. Oleh karena itu, ketika mempertimbangkan perubahan energi suatu sistem, perlu untuk mempertimbangkan pergerakan titik-titik individual, yang juga dipengaruhi oleh gaya-gaya dalam.
Energi kinetik suatu titik material didefinisikan sebagai kuantitas
T^tuTsg. (3.17)
Energi kinetik suatu sistem mekanik sama dengan jumlah energi kinetik titik-titik material sistem:
perhatikan itu T> 0.
Mari kita definisikan kekuatan gaya sebagai hasil kali skalar vektor gaya dan vektor kecepatan:

Seringkali dimungkinkan untuk mengidentifikasi ciri-ciri penting gerak suatu sistem mekanis tanpa harus mengintegrasikan sistem persamaan gerak diferensial. Hal ini dicapai dengan menerapkan teorema umum dinamika.
5.1. Konsep dasar dan definisi
Kekuatan eksternal dan internal. Setiap gaya yang bekerja pada suatu titik dalam sistem mekanis harus merupakan gaya aktif atau reaksi kopling. Seluruh rangkaian gaya yang bekerja pada titik-titik sistem dapat dibagi menjadi dua kelas dengan cara yang berbeda: gaya eksternal dan gaya internal (indeks e dan i - dari kata Latin externus - eksternal dan internus - internal). Gaya luar adalah gaya yang bekerja pada titik-titik suatu sistem dari titik-titik dan benda-benda yang bukan merupakan bagian dari sistem yang ditinjau. Kekuatan interaksi antara titik dan benda dari sistem yang dipertimbangkan disebut internal.
Pembagian ini bergantung pada titik dan benda material mana yang dimasukkan oleh peneliti ke dalam sistem mekanis yang sedang dipertimbangkan. Jika kita memperluas komposisi sistem dengan memasukkan titik dan benda tambahan, maka beberapa gaya yang bersifat eksternal pada sistem sebelumnya dapat menjadi gaya internal pada sistem yang diperluas.
Sifat-sifat kekuatan internal. Karena gaya-gaya ini adalah gaya-gaya interaksi antar bagian-bagian sistem, gaya-gaya tersebut memasuki sistem gaya-gaya internal yang lengkap dalam bentuk “berdua”, yang disusun sesuai dengan aksioma aksi-reaksi. Masing-masing “dua” tersebut memiliki kekuatan
vektor utama dan momen utama terhadap suatu pusat sembarang sama dengan nol. Karena sistem gaya internal yang lengkap hanya terdiri dari “dua”, maka
1) vektor utama sistem gaya dalam adalah nol,
2) momen utama sistem gaya dalam relatif terhadap suatu titik sembarang sama dengan nol.
Massa sistem adalah jumlah aritmatika dari massa mk semua titik dan benda yang membentuk sistem:
Pusat massa(pusat inersia) suatu sistem mekanik adalah titik geometri C, vektor jari-jari dan koordinatnya ditentukan oleh rumus
dimana adalah vektor jari-jari dan koordinat titik-titik yang membentuk sistem.
Untuk benda tegar yang terletak pada medan gravitasi seragam, posisi pusat massa dan pusat gravitasi bertepatan; dalam kasus lain, ini adalah titik geometri yang berbeda.
Bersama dengan kerangka acuan inersia, kerangka acuan non-inersia yang bergerak secara translasi sering dianggap secara bersamaan. Sumbu koordinatnya (sumbu König) dipilih sehingga titik asal C selalu bertepatan dengan pusat massa sistem mekanis. Sesuai dengan definisinya, pusat massa tidak bergerak pada sumbu Koenig dan terletak pada titik asal koordinat.
Momen inersia sistem relatif terhadap suatu sumbu adalah besaran skalar yang sama dengan jumlah hasil kali massa mk semua titik sistem dengan kuadrat jaraknya ke sumbu:
![]()
Jika sistem mekaniknya adalah benda tegar, untuk mencari 12 dapat menggunakan rumus

dimana adalah massa jenis, volume yang ditempati oleh benda.
Teorema gerak pusat massa. Persamaan diferensial gerak sistem mekanik. Teorema gerak pusat massa sistem mekanik. Hukum kekekalan gerak pusat massa.
Teorema perubahan momentum. Besarnya gerak suatu titik material. Dorongan kekuatan dasar. Impuls gaya untuk jangka waktu tertentu dan proyeksinya pada sumbu koordinat. Teorema perubahan momentum suatu titik material dalam bentuk diferensial dan terbatas.
Besarnya gerak suatu sistem mekanis; ekspresinya melalui massa sistem dan kecepatan pusat massanya. Teorema perubahan momentum sistem mekanik dalam bentuk diferensial dan terbatas. Hukum kekekalan momentum mekanik
(Konsep benda dan titik bermassa variabel. Persamaan Meshchersky. Rumus Tsiolkovsky.)
Teorema perubahan momentum sudut. Momen momentum suatu titik material terhadap pusat dan terhadap sumbu. Teorema perubahan momentum sudut suatu titik material. Kekuatan pusat. Kekekalan momentum sudut suatu titik material jika terdapat gaya pusat. (Konsep kecepatan sektor. Hukum luas.)
Momen utama momentum atau momen kinetik suatu sistem mekanik relatif terhadap pusat dan relatif terhadap sumbu. Momen kinetik benda tegar yang berputar terhadap sumbu rotasi. Teorema perubahan momen kinetik suatu sistem mekanik. Hukum kekekalan momentum sudut suatu sistem mekanik. (Teorema tentang perubahan momen kinetik suatu sistem mekanik dalam gerak relatif terhadap pusat massa.)
Teorema perubahan energi kinetik. Energi kinetik suatu titik material. Kerja kekuatan dasar; ekspresi analitis dari pekerjaan dasar. Usaha yang dilakukan suatu gaya pada perpindahan akhir titik penerapannya. Usaha gravitasi, gaya elastis, dan gaya gravitasi. Teorema perubahan energi kinetik suatu titik material dalam bentuk diferensial dan terbatas.
Energi kinetik suatu sistem mekanik. Rumus untuk menghitung energi kinetik benda tegar selama gerak translasi, selama rotasi pada sumbu tetap dan dalam kasus gerak umum (khususnya, selama gerak sejajar bidang). Teorema perubahan energi kinetik suatu sistem mekanik dalam bentuk diferensial dan terbatas. Jumlah usaha yang dilakukan oleh gaya-gaya dalam pada benda padat sama dengan nol. Kerja dan gaya gaya yang diterapkan pada benda tegar yang berputar pada sumbu tetap.
Konsep medan gaya. Medan gaya potensial dan fungsi gaya. Ekspresi proyeksi gaya melalui fungsi gaya. Permukaan dengan potensi yang sama. Kerja suatu gaya pada perpindahan akhir suatu titik dalam medan gaya potensial. Energi potensial. Contoh medan gaya potensial: medan gravitasi seragam dan medan gravitasi. Hukum kekekalan energi mekanik.
Dinamika tubuh yang kaku. Persamaan diferensial gerak translasi benda tegar. Persamaan diferensial rotasi benda tegar pada sumbu tetap. pendulum fisik. Persamaan diferensial gerak bidang benda tegar.
Prinsip D'Alembert. Prinsip D'Alembert untuk suatu hal material; kekuatan inersia. Prinsip D'Alembert untuk sistem mekanik. Membawa gaya inersia titik-titik benda tegar ke pusat; vektor utama dan momen utama gaya inersia.
(Penentuan reaksi dinamis bantalan selama rotasi benda tegar di sekitar sumbu tetap. Kasus ketika sumbu rotasi adalah sumbu pusat utama inersia benda.)
Prinsip kemungkinan pergerakan dan persamaan umum dinamika. Koneksi dikenakan pada sistem mekanis. Kemungkinan pergerakan (atau virtual) dari suatu titik material dan sistem mekanis. Jumlah derajat kebebasan sistem. Koneksi yang ideal. Prinsip kemungkinan gerakan. Persamaan umum dinamika.
Persamaan gerak suatu sistem dalam koordinat umum (persamaan Lagrange). Koordinat umum dari sistem; kecepatan umum. Ekspresi pekerjaan dasar dalam koordinat umum. Kekuatan umum dan perhitungannya; kasus kekuatan dengan potensi. Kondisi keseimbangan suatu sistem dalam koordinat umum. Persamaan diferensial gerak suatu sistem dalam koordinat umum atau persamaan Lagrange jenis ke-2. Persamaan Lagrange dalam hal gaya potensial; Fungsi Lagrange (potensi kinetik).
Konsep stabilitas keseimbangan. Getaran bebas kecil suatu sistem mekanis dengan satu derajat kebebasan mendekati posisi kesetimbangan stabil sistem dan sifat-sifatnya.
Elemen teori dampak. Fenomena dampak. Kekuatan tumbukan dan impuls tumbukan. Aksi gaya tumbukan pada suatu titik material. Teorema tentang perubahan momentum sistem mekanik saat tumbukan. Dampak sentral langsung dari tubuh pada permukaan yang tidak bergerak; dampak elastis dan inelastis. Koefisien pemulihan dampak dan penentuan eksperimentalnya. Dampak sentral langsung dari dua benda. teorema Carnot.
BIBLIOGRAFI
Dasar
Butenin N.V., Lunts Ya-L., Merkin D.R. Kursus mekanika teoritis. T. 1, 2. M., 1985 dan edisi sebelumnya.
Dobronravov V.V., Nikitin N.N. Kursus mekanika teoritis. M., 1983.
Starzhinsky V.M. Mekanika teoretis. M., 1980.
Targ S.M. Kursus singkat mekanika teoretis. M., 1986 dan edisi sebelumnya.
Yablonsky A.A., Nikiforova V.M. Kursus mekanika teoritis. Bagian 1. M., 1984 dan edisi sebelumnya.
Yablonsky A.A. Kursus mekanika teoritis. Bagian 2. M., 1984 dan edisi sebelumnya.
Meshchersky I.V. Kumpulan soal mekanika teoritis. M., 1986 dan edisi sebelumnya.
Kumpulan Soal Mekanika Teoritis/Ed. K. S. Kolesnikova. M., 1983.
Tambahan
Bat M.I., Dzhanelidze G.Yu., Kelzon A.S. Mekanika teoretis dalam contoh dan masalah. Bagian 1, 2. M., 1984 dan edisi sebelumnya.
Kumpulan Soal Mekanika Teoritis/5razhnichen/so N.A., Kan V.L., Mintzberg B.L. dan lain-lain.
Novozhilov I.V., Zatsepin M.F. Perhitungan berbasis komputer yang khas dalam mekanika teoretis. M., 1986,
Kumpulan tugas mata kuliah mekanika teori / Ed. A.A.Yablonsky. M., 1985 dan edisi sebelumnya (berisi contoh pemecahan masalah).








