Taylor serijos atvirkštinių trigonometrinių funkcijų išplėtimas. Taylor serijos išplėtimas

„Find the Maclaurin serijos funkcijos f(x) plėtinį“– būtent taip skamba aukštosios matematikos užduotis, kurią vieni mokiniai gali atlikti, o kiti nesusidoroja su pavyzdžiais. Yra keletas būdų, kaip išplėsti seriją galiomis, čia pateiksime techniką, kaip išplėsti funkcijas į Maclaurin seriją. Kurdami funkciją serijoje, turite gerai mokėti išvestines.

4.7 pavyzdys Išplėskite funkciją x laipsniais

Skaičiavimai: Atliekame funkcijos išplėtimą pagal Maclaurin formulę. Pirmiausia išplėskime funkcijos vardiklį į seriją

Galiausiai išplėtimą padauginkite iš skaitiklio.
Pirmasis narys yra funkcijos reikšmė nuliui f (0) = 1/3.
Raskime pirmosios ir aukštesnės eilės funkcijos išvestines f (x) ir šių išvestinių reikšmę taške x=0




Toliau, remdamiesi išvestinių išvestinių vertės pokyčių modeliu, kai yra 0, parašome n-osios išvestinės formulę

Taigi, vardiklį atstovaujame Maclaurin serijos išplėtimo forma

Padauginame iš skaitiklio ir gauname norimą funkcijos išplėtimą eilėje x laipsniais

Kaip matote, čia nėra nieko sudėtingo.
Visi pagrindiniai punktai pagrįsti galimybe apskaičiuoti išvestines ir greitai apibendrinti aukštesnės eilės išvestinės finansinės priemonės vertę ties nuliu. Šie pavyzdžiai padės jums sužinoti, kaip greitai išdėstyti funkciją serijoje.

4.10 pavyzdys Raskite funkcijos Maclaurin serijos išplėtimą

Skaičiavimai: Kaip jau spėjote, kosinusą į skaitiklį įdėsime iš eilės. Norėdami tai padaryti, galite naudoti be galo mažų dydžių formules arba išvesti kosinuso plėtrą iš išvestinių. Dėl to gauname sekančią seką x laipsniais

Kaip matote, turime mažiausiai skaičiavimų ir kompaktišką serijos išplėtimo vaizdą.

4.16 pavyzdys Išplėskite funkciją x laipsniais:
7/(12-x-x^2)
Skaičiavimai: tokio tipo pavyzdžiuose trupmeną reikia išplėsti per paprastųjų trupmenų sumą.
Dabar neparodysime, kaip tai padaryti, bet su neapibrėžtųjų koeficientų pagalba gausime trupmenų sumą.
Toliau vardiklius rašome eksponentine forma

Belieka išplėsti terminus naudojant Maclaurin formulę. Susumavus terminus tais pačiais „x“ laipsniais, sudarome formulę, skirtą bendros funkcijos išplėtimo eilėje terminui.



Paskutinę perėjimo prie serijos dalį pradžioje sunku įgyvendinti, nes sunku derinti suporuotų ir nesuporuotų indeksų (laipsnių) formules, tačiau praktikuojantis tai seksis geriau.

4.18 pavyzdys Raskite funkcijos Maclaurin serijos išplėtimą

Skaičiavimai: Raskime šios funkcijos išvestinę:

Išplėskime funkciją į seriją naudodami vieną iš McLaren formulių:

Mes apibendriname serijas pagal terminą, remdamiesi tuo, kad abu yra visiškai identiški. Integravę visą seriją po termino, gauname funkcijos išplėtimą į seriją x laipsniais

Yra perėjimas tarp dviejų paskutinių išplėtimo eilučių, o tai pradžioje užims daug jūsų laiko. Apibendrinti serijos formulę nėra lengva visiems, todėl nesijaudinkite, kad nepavyks gauti gražios, kompaktiškos formulės.

4.28 pavyzdys Raskite funkcijos Maclaurin serijos išplėtimą:

Parašykime logaritmą taip

Naudodami Maclaurin formulę išplečiame logaritmo funkciją eilėmis x laipsniais

Galutinė konvoliucija iš pirmo žvilgsnio sudėtinga, tačiau kaitaliodami ženklus visada gausite kažką panašaus. Baigta įvesties pamoka planavimo funkcijų iš eilės tema. Kitos ne mažiau įdomios skaidymo schemos bus išsamiai aptariamos tolesnėje medžiagoje.

16.1. Elementariųjų funkcijų išplėtimas į Taylor seriją ir

Maklaurinas

Parodykime, kad jei aibėje yra apibrėžta savavališka funkcija
, netoli taško
turi daug išvestinių ir yra laipsnių eilutės suma:

tada galite rasti šios serijos koeficientus.

Pakeiskime galios seriją
. Tada
.

Raskime pirmąją funkcijos išvestinę
:

At
:
.

Dėl antrosios išvestinės gauname:

At
:
.

Tęsiant šią procedūrą n kai tik gausime:
.

Taigi, mes gavome tokios formos galių eilutę:

,

kuris vadinamas šalia Teiloro už funkciją
taško apylinkėse
.

Ypatingas Taylor serijos atvejis yra Maclaurin serija adresu
:

Likusi Taylor (Maclaurin) serijos dalis gaunama išmetus pagrindinę seriją n pirmieji nariai ir žymimas kaip
. Tada funkcija
galima parašyti kaip sumą n pirmieji serijos nariai
o likusią dalį
:,

.

Likusi dalis paprastai yra
išreikštas skirtingomis formulėmis.

Vienas iš jų yra Lagrange formos:

, Kur
.
.

Atkreipkite dėmesį, kad praktikoje Maclaurin serija naudojama dažniau. Taigi, norint parašyti funkciją
laipsnio eilutės sumos pavidalu būtina:

1) rasti Maclaurin (Taylor) serijos koeficientus;

2) rasti gautų laipsnių eilučių konvergencijos sritį;

3) įrodyti, kad ši eilutė suartėja su funkcija
.

Teorema1 (būtina ir pakankama Maclaurino eilučių konvergencijos sąlyga). Tegul serijos konvergencijos spindulys
. Kad ši serija suartėtų intervale
funkcionuoti
, būtina ir pakanka, kad sąlyga būtų įvykdyta:
nurodytu intervalu.

2 teorema. Jei bet kokios eilės funkcijos išvestinės
tam tikru intervalu
absoliučia verte apribota iki to paties skaičiaus M, tai yra
, tada šiame intervale funkcija
gali būti išplėsta į Maclaurin seriją.

Pavyzdys1 . Išplėskite Taylor seriją aplink tašką
funkcija.

Sprendimas.

.

,;

,
;

,
;

,

.......................................................................................................................................

,
;

Konvergencijos regionas
.

Pavyzdys2 . Išplėskite funkciją Taylor serijoje aplink tašką
.

Sprendimas:

Raskite funkcijos ir jos išvestinių reikšmę ties
.

,
;

,
;

...........……………………………

,
.

Sudėkime šias vertes iš eilės. Mes gauname:

arba
.

Raskime šios eilutės konvergencijos sritį. Pagal d'Alemberto testą, serija suartėja, jei

.

Todėl bet kokiam ši riba yra mažesnė nei 1, todėl eilučių konvergencijos diapazonas bus toks:
.

Panagrinėkime keletą pagrindinių elementariųjų funkcijų išplėtimo iš Maclaurin serijos pavyzdžių. Prisiminkite, kad Maclaurin serija:

.

susilieja į intervalą
funkcionuoti
.

Atminkite, kad norint išplėsti funkciją į seriją, būtina:

a) raskite šios funkcijos Maklaurino eilučių koeficientus;

b) apskaičiuokite gautų eilučių konvergencijos spindulį;

c) įrodyti, kad gauta eilutė konverguoja į funkciją
.

3 pavyzdys. Apsvarstykite funkciją
.

Sprendimas.

Apskaičiuokime funkcijos ir jos išvestinių reikšmę ties
.

Tada serijos skaitiniai koeficientai yra tokios formos:

bet kam n. Pakeiskime rastus koeficientus į Maclaurin seriją ir gaukime:

Raskime gautų eilučių konvergencijos spindulį, būtent:

.

Todėl serija susilieja į intervalą
.

Ši serija susilieja su funkcija bet kokioms vertybėms , nes bet kuriuo intervalu
funkcija o jo absoliučios vertės išvestinių priemonių skaičius yra ribotas .

Pavyzdys4 . Apsvarstykite funkciją
.

Sprendimas.

:

Nesunku pastebėti, kad tolygios eilės dariniai
, o išvestinės yra nelyginės eilės. Pakeiskime rastus koeficientus į Maclaurin seriją ir gaukime išplėtimą:

Raskime šios eilutės konvergencijos intervalą. Pagal d'Alemberto ženklą:

bet kam . Todėl serija susilieja į intervalą
.

Ši serija susilieja su funkcija
, nes visi jo vediniai apsiriboja vienybe.

Pavyzdys5 .
.

Sprendimas.

Raskime funkcijos ir jos išvestinių reikšmę ties
:

Taigi šios serijos koeficientai:
Ir
, taigi:

Panašiai kaip ir ankstesnėje eilutėje, konvergencijos sritis
. Serija susilieja su funkcija
, nes visi jo vediniai apsiriboja vienybe.

Atkreipkite dėmesį, kad funkcija
nelyginis ir serijos plėtimas nelyginėmis galiomis, funkcija
– tolygus ir išsiplėtimas į seriją lygiomis galiomis.

Pavyzdys6 . Dvejetainė serija:
.

Sprendimas.

Raskime funkcijos ir jos išvestinių reikšmę ties
:

Iš to matyti, kad:

Pakeiskime šias koeficientų reikšmes į Maclaurin seriją ir gaukime šios funkcijos išplėtimą į galios eilutę:

Raskime šios serijos konvergencijos spindulį:

Todėl serija susilieja į intervalą
. Ribiniuose taškuose ties
Ir
eilutė gali suartėti arba nekonverguoti priklausomai nuo eksponento
.

Ištirtos eilutės susilieja į intervalą
funkcionuoti
, tai yra serijos suma
adresu
.

Pavyzdys7 . Išplėskime funkciją Maclaurin serijoje
.

Sprendimas.

Norėdami išplėsti šią funkciją į seriją, naudojame dvinarę eilutę at
. Mes gauname:

Remdamiesi laipsnių eilučių savybe (laipsnių eilutę galima integruoti jos konvergencijos srityje), randame šios eilutės kairiosios ir dešinės pusės integralą:

Raskime šios serijos konvergencijos sritį:
,

tai yra, šios serijos konvergencijos sritis yra intervalas
.

Nustatykime eilučių konvergenciją intervalo galuose. At
. Ši serija yra harmoninga serija, tai yra, ji skiriasi. At
.

gauname skaičių eilutę su bendru terminu
.

Serija konverguoja pagal Leibnizo testą. Taigi šios eilutės konvergencijos sritis yra intervalas

16.2. Galios eilučių taikymas apytiksliuose skaičiavimuose n Apytiksliuose skaičiavimuose galios eilutės vaidina labai svarbų vaidmenį. Jų pagalba buvo sudarytos trigonometrinių funkcijų lentelės, logaritmų lentelės, kitų funkcijų reikšmių lentelės, kurios naudojamos įvairiose žinių srityse, pavyzdžiui, tikimybių teorijoje ir matematinėje statistikoje. Be to, funkcijų išplėtimas į laipsnių eilutes yra naudingas jų teoriniam tyrimui. Apytiksliuose skaičiavimuose naudojant laipsnio eilutes pagrindinė problema yra klaidos įvertinimas, kai serijos suma pakeičiama jos pirmosios suma.

narių.

Panagrinėkime du atvejus:

funkcija išplečiama į kintamą seriją;

funkcija išplečiama į pastovaus ženklo seką.

Skaičiavimas naudojant kintamąsias eilutes
Tegul funkcija išplėsta į kintamos galios eilutę. Tada apskaičiuojant šią funkciją konkrečiai vertei n gauname skaičių eilutę, kuriai galime pritaikyti Leibnizo kriterijų. Pagal šį kriterijų, jei serijos suma pakeičiama jos pirmosios suma
.

Pavyzdys8 . tada absoliuti paklaida neviršija pirmo likusios šios serijos dalies, ty:
Apskaičiuokite

Sprendimas.

0,0001 tikslumu.
Tam naudosime Maclaurin seriją

, pakeičiant kampo reikšmę radianais:

Jei palyginsime pirmąją ir antrąją eilutės narius tam tikru tikslumu, tada: .

Trečias išplėtimo terminas:
mažesnis už nurodytą skaičiavimo tikslumą. Todėl norint apskaičiuoti

.

pakanka palikti dvi serijos kadencijas, t
.

Pavyzdys9 . tada absoliuti paklaida neviršija pirmo likusios šios serijos dalies, ty:
Taigi

Sprendimas.

0,001 tikslumu.
Naudosime dvinario eilutės formulę. Norėdami tai padaryti, parašykite
.

formoje:
,

Šioje išraiškoje
Palyginkime kiekvieną iš serijos sąlygų nurodytu tikslumu. Tai aišku
. Todėl norint apskaičiuoti

arba
.

pakanka palikti tris serijos terminus.

Pavyzdys10 . Skaičiavimas naudojant teigiamas eilutes Apskaičiuokite skaičių

Sprendimas.

0,001 tikslumu.
Iš eilės funkcijai
pakeiskime

Įvertinkime paklaidą, kuri atsiranda pakeičiant serijos sumą pirmosios suma narių. Užrašykime akivaizdžią nelygybę:

tai yra 2<<3. Используем формулу остаточного члена ряда в форме Лагранжа:
,
.

Pagal problemą reikia rasti n kad galiotų ši nelygybė:
arba
.

Nesunku patikrinti, kada n= 6:
.

Vadinasi,
.

Pavyzdys11 . tada absoliuti paklaida neviršija pirmo likusios šios serijos dalies, ty:
0,0001 tikslumu.

Sprendimas.

Atminkite, kad logaritmams apskaičiuoti galime naudoti funkcijos seriją
, tačiau ši serija konverguoja labai lėtai ir norint pasiekti nurodytą tikslumą reikėtų paimti 9999 terminus! Todėl, norint apskaičiuoti logaritmus, paprastai naudojama funkcijos serija
, kuris susilieja į intervalą
.

Paskaičiuokime
naudojant šią seriją. Leiskite
, Tada .

Vadinasi,
,

Norint apskaičiuoti
su nurodytu tikslumu paimkite pirmųjų keturių terminų sumą:
.

Likusi serija
išmeskime. Įvertinkime klaidą. Tai akivaizdu

arba
.

Taigi, eilėje, kuri buvo naudojama skaičiuojant, užteko paimti tik pirmuosius keturis funkcijos eilės narius, o ne 9999
.

Savidiagnostikos klausimai

1. Kas yra Taylor serija?

2. kokia forma buvo Maclaurin serija?

3. Suformuluokite funkcijos išplėtimo teoremą Teiloro eilutėje.

4. Užrašykite pagrindinių funkcijų Maclaurin serijos išplėtimą.

5. Nurodykite nagrinėjamų eilučių konvergencijos sritis.

6. Kaip įvertinti apytikslių skaičiavimų paklaidą naudojant galių eilutes?

Aukštosios matematikos studentai turėtų žinoti, kad tam tikros laipsnių eilutės, priklausančios mums duotam eilučių konvergencijos intervalui, suma pasirodo esanti ištisinė ir neribotą skaičių kartų diferencijuota funkcija. Kyla klausimas: ar galima sakyti, kad duota savavališka funkcija f(x) yra tam tikros laipsnių eilutės suma? Tai yra, kokiomis sąlygomis funkcija f(x) gali būti pavaizduota laipsnių eilute? Šio klausimo svarba slypi tame, kad funkciją f(x) galima apytiksliai pakeisti kelių pirmųjų laipsnių eilutės narių suma, tai yra daugianario. Toks funkcijos pakeitimas gana paprasta išraiška – daugianario – taip pat patogus sprendžiant tam tikras problemas, būtent: sprendžiant integralus, skaičiuojant ir pan.

Įrodyta, kad tam tikrai funkcijai f(x), kurioje galima apskaičiuoti išvestines iki (n+1) eilės, įskaitant paskutinę, šalia (α - R; x 0 + R ) tam tikras taškas x = α, tiesa, kad formulė:

Ši formulė pavadinta garsaus mokslininko Brooke Taylor vardu. Serija, gauta iš ankstesnės, vadinama Maclaurin serija:

Taisyklė, leidžianti išplėsti Maclaurin seriją:

1. Nustatykite pirmosios, antrosios, trečiosios... eilės vedinius.
2. Apskaičiuokite, kam lygios išvestinės, kai x=0.
3. Užrašykite šios funkcijos Maclaurin eilutes ir nustatykite jos konvergencijos intervalą.
4. Nustatykite intervalą (-R;R), kur lieka Maklaurino formulės dalis

R n (x) -> 0 ties n -> begalybė. Jei tokia yra, joje esanti funkcija f(x) turi sutapti su Maklaurino eilutės suma.

Dabar panagrinėkime Maclaurin seriją atskiroms funkcijoms.

1. Taigi pirmasis bus f(x) = e x. Žinoma, pagal savo charakteristikas tokia funkcija turi labai skirtingų eilių išvestines, o f (k) (x) = e x , kur k yra lygus visiems. Gauname f (k) (0) = e 0 =1, k = 1,2... Remiantis tuo, kas išdėstyta aukščiau, serija e x atrodys taip:

2. Maklaurino eilutė funkcijai f(x) = sin x. Iš karto išsiaiškinkime, kad funkcija visiems nežinomiesiems turės išvestines, be to, f "(x) = cos x = sin(x+n/2), f "" (x) = -sin x = sin(x + 2*n/2)..., f (k) (x) = sin(x+k*n/2), kur k lygus bet kuriam natūraliam skaičiui Tai yra, atlikę paprastus skaičiavimus, galime prieiti išvada, kad f(x) = sin x serija atrodys taip:

3. Dabar pabandykime nagrinėti funkciją f(x) = cos x. Visiems nežinomiesiems jis turi savavališkos eilės išvestinius ir |f (k) (x)| = |cos(x+k*n/2)|<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

Taigi, mes išvardijome svarbiausias funkcijas, kurias galima išplėsti Maclaurin serijoje, tačiau kai kurioms funkcijoms jas papildo Taylor serija. Dabar mes juos išvardinsime. Taip pat verta paminėti, kad Taylor ir Maclaurin serijos yra svarbi praktinio darbo dalis sprendžiant eilutes aukštojoje matematikoje. Taigi, Taylor serija.

1. Pirmoji bus funkcijos f(x) = ln(1+x) eilutė. Kaip ir ankstesniuose pavyzdžiuose, esant nurodytam f(x) = ln(1+x), eilutes galime pridėti naudodami bendrą Maclaurin serijos formą. tačiau šiai funkcijai Maclaurin seriją galima gauti daug paprasčiau. Integravę tam tikrą geometrinę eilutę, gauname tokios imties f(x) = ln(1+x) eilutę:

2. O antrasis, kuris mūsų straipsnyje bus galutinis, bus f(x) = arctan x serija. Jei x priklauso intervalui [-1;1], galioja išplėtimas:

Tai viskas. Šiame straipsnyje buvo nagrinėjamos dažniausiai naudojamos Taylor ir Maclaurin serijos aukštojoje matematikoje, ypač ekonomikos ir technikos universitetuose.

Tarp funkcinių serijų svarbiausią vietą užima galios serijos.

Galios serija yra serija

kurių terminai yra laipsnio funkcijos, išdėstytos didėjančiais neneigiamais sveikųjų skaičių laipsniais x, A c0 , c 1 , c 2 , c n - pastovios vertės. Skaičiai c1 , c 2 , c n - serijos terminų koeficientai, c0 - laisvas narys. Laipsnių eilučių sąlygos apibrėžtos visoje skaičių eilutėje.

Susipažinkime su koncepcija laipsnių eilučių konvergencijos sritis. Tai kintamųjų reikšmių rinkinys x, kurio serija sutampa. Galios eilutės turi gana paprastą konvergencijos sritį. Realioms kintamosioms reikšmėms x konvergencijos sritis susideda arba iš vieno taško, arba yra tam tikras intervalas (konvergencijos intervalas), arba sutampa su visa ašimi Jautis .

Keičiant reikšmes į galios eilutes x= 0 bus skaičių serija

c0 +0+0+...+0+... ,

kuris susilieja.

Todėl kai x= 0 bet kuri laipsnio eilutė suartėja ir todėl jos konvergencijos sritis negali būti tuščias rinkinys. Visų laipsnių eilučių konvergencijos srities struktūra yra vienoda. Jį galima nustatyti naudojant šią teoremą.

1 teorema (Abelio teorema). Jei laipsnio eilutė suartėja ties kokia nors verte x = x 0 , skiriasi nuo nulio, tada jis susilieja ir, be to, absoliučiai visoms reikšmėms |x| < |x 0 | . Atkreipkite dėmesį: ir pradinė reikšmė „X yra nulis“, ir bet kuri „X“ reikšmė, kuri lyginama su pradine reikšme, imama modulo – neatsižvelgiant į ženklą.

Pasekmė. Jeigu galios serijos skiriasi tam tikra verte x = x 1 , tada jis skiriasi visoms vertėms |x| > |x 1 | .

Kaip jau sužinojome anksčiau, bet kuri laipsnio eilutė suartėja su verte x= 0. Yra laipsnių eilučių, kurios susilieja tik tada, kai x= 0 ir kitoms reikšmėms skiriasi X. Neatsižvelgdami į šį atvejį, darome prielaidą, kad laipsnio eilutė suartėja ties tam tikra verte x = x 0 , skiriasi nuo nulio. Tada, pagal Abelio teoremą, jis suartėja visuose intervalo ]-| taškuose x0 |, |x 0 |[ (intervalas, kurio kairioji ir dešinioji ribos yra x reikšmės, kuriose laipsnių eilutė suartėja, atitinkamai paimta su minuso ir pliuso ženklu), simetriškas kilmės atžvilgiu.

Jei galios eilutė skiriasi tam tikra verte x = x 1 , tada, remiantis Abelio teoremos išvadomis, jis skiriasi visuose taškuose, esančiuose už atkarpos ribų [-| x1 |, |x 1 |] . Iš to išplaukia, kad bet kuriai laipsnio eilutei yra intervalas, simetriškas pradžios atžvilgiu, vadinamas konvergencijos intervalas , kiekviename taške, kurio eilutė suartėja, ties ribomis ji gali suartėti arba gali skirtis, ir nebūtinai tuo pačiu metu, o už atkarpos ribų serija skiriasi. Skaičius R vadinamas laipsnių eilučių konvergencijos spinduliu.

Ypatingais atvejais laipsnių eilučių konvergencijos intervalas gali išsigimti iki taško (tada serija susilieja tik tada, kai x= 0 ir laikoma, kad R= 0) arba vaizduoti visą skaičių tiesę (tada serija suartėja visuose skaičių linijos taškuose ir daroma prielaida, kad ).

Taigi, laipsnio eilutės konvergencijos srities nustatymas susideda iš jos nustatymo konvergencijos spindulys R ir tiriant eilučių konvergenciją ties konvergencijos intervalo ribomis (prie ).

2 teorema. Jei visi laipsnio eilutės koeficientai, pradedant nuo tam tikro, skiriasi nuo nulio, tada jos konvergencijos spindulys yra lygus ribinei bendrų sekančių serijos narių koeficientų absoliučių verčių santykiui. , t.y.

1 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Čia

Naudodami (28) formulę randame šios eilutės konvergencijos spindulį:

Ištirkime eilučių konvergenciją konvergencijos intervalo galuose. 13 pavyzdys rodo, kad ši eilutė suartėja ties x= 1 ir skiriasi ties x= -1. Vadinasi, konvergencijos sritis yra pusės intervalas.

2 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Serijos koeficientai yra teigiami, ir

Raskime šio santykio ribą, t.y. laipsnių eilučių konvergencijos spindulys:

Išnagrinėkime eilučių konvergenciją intervalo galuose. Vertės pakeitimas x= -1/5 ir x= 1/5 šioje eilutėje suteikia:

Pirmoji iš šių eilučių suartėja (žr. 5 pavyzdį). Bet tada, remiantis „absoliučios konvergencijos“ skyriaus teorema, antroji eilutė taip pat suartėja, o jos konvergencijos sritis yra segmentas

3 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Čia

Naudodami (28) formulę randame eilučių konvergencijos spindulį:

Išnagrinėkime reikšmių eilučių konvergenciją. Pakeitę juos šioje serijoje, gauname atitinkamai

Abi eilutės skiriasi, nes netenkinama būtina konvergencijos sąlyga (jų bendrieji terminai nelinkę į nulį ties ). Taigi abiejuose konvergencijos intervalo galuose ši eilutė skiriasi, o jos konvergencijos sritis yra intervalas.

5 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Mes randame santykį, kur , ir :

Pagal (28) formulę šios eilutės konvergencijos spindulys

,

tai yra, serija susilieja tik tada, kai x= 0, o kitoms reikšmėms skiriasi X.

Pavyzdžiai rodo, kad konvergencijos intervalo pabaigoje eilutės elgiasi skirtingai. 1 pavyzdyje viename konvergencijos intervalo gale konverguoja, o kitame, 2 pavyzdyje, ji suartėja abiejuose galuose;

Laipsnių eilutės konvergencijos spindulio formulė gaunama darant prielaidą, kad visi eilutės narių koeficientai, pradedant nuo tam tikro taško, skiriasi nuo nulio. Todėl (28) formulę galima naudoti tik šiais atvejais. Jei ši sąlyga pažeidžiama, laipsnių eilučių konvergencijos spindulį reikia ieškoti naudojant d'Alemberto ženklas, arba, pakeitus kintamąjį, transformuoti eilutę į formą, kurioje tenkinama nurodyta sąlyga.

6 pavyzdys. Raskite laipsnių eilučių konvergencijos intervalą

Sprendimas. Šioje serijoje nėra terminų su nelyginiais laipsniais X. Todėl transformuojame seriją, nustatymą . Tada gauname seriją

rasti kurio konvergencijos spindulį galime pritaikyti (28) formulę. Kadangi , a , tada šios serijos konvergencijos spindulys

Iš lygybės gauname Todėl ši serija suartėja su intervalu .

Galios eilučių suma. Galios eilučių diferencijavimas ir integravimas

Leiskite galios serijai

konvergencijos spindulys R> 0, t.y. ši serija susilieja į intervalą .

Tada kiekviena vertė X iš konvergencijos intervalo atitinka tam tikrą eilutės sumą. Todėl laipsnių eilučių suma yra funkcija X konvergencijos intervale. Žymėdamas tai f(x), galime parašyti lygybę

suprasti tai ta prasme, kad serijų suma kiekviename taške X iš konvergencijos intervalo yra lygus funkcijos reikšmei f(x) šiuo metu. Ta pačia prasme sakysime, kad laipsnio eilutė (29) konverguoja į funkciją f(x) konvergencijos intervale.

Už konvergencijos intervalo ribų lygybė (30) neturi prasmės.

7 pavyzdys. Raskite laipsnių eilučių sumą

Sprendimas. Tai geometrinė serija, kuriai a= 1, a q= x. Todėl jo suma yra funkcija . Serija konverguoja, jei , ir yra jos konvergencijos intervalas. Todėl lygybė

galioja tik reikšmėms, nors funkcija apibrėžtos visoms vertėms X, išskyrus X= 1.

Galima įrodyti, kad laipsnių eilutės suma f(x) yra tęstinis ir diferencijuojamas bet kuriame konvergencijos intervalo intervale, ypač bet kuriame eilutės konvergencijos intervalo taške.

Pateiksime teoremas apie laipsnių eilučių diferencijavimą ir integravimą.

1 teorema. Laipsninės eilutės (30) jos konvergencijos intervale gali būti diferencijuojamos pagal terminą neribotą skaičių kartų, o gautos laipsnių eilutės konvergencijos spindulys yra toks pat kaip ir pradinė eilutė, o jų sumos atitinkamai lygios .

2 teorema. Galios eilutes (30) galima integruoti po termino neribotą skaičių kartų intervale nuo 0 iki X, jei , ir gautos laipsnio eilutės turi tokį patį konvergencijos spindulį kaip ir pradinės eilutės, o jų sumos yra atitinkamai lygios

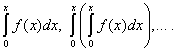
Funkcijų išplėtimas į galių eilutes

Tegu funkcija duota f(x), kurią reikia išplėsti į galios eilutę, t.y. pavaizduoti formoje (30):

Užduotis – nustatyti koeficientus eilutė (30). Norėdami tai padaryti, diferencijuodami lygybę (30) pagal terminą, nuosekliai randame:

……………………………………………….. (31)

Darant prielaidą, kad lygybės (30) ir (31) X= 0, randame

Rastus posakius pakeitę lygybe (30), gauname

(32)

Raskime kai kurių elementarių funkcijų Maclaurin serijos išplėtimą.

8 pavyzdys. Išplėskite funkciją Maclaurin serijoje

Sprendimas. Šios funkcijos išvestiniai sutampa su pačia funkcija:

Todėl kai X= 0 turime

Pakeitę šias reikšmes į (32) formulę, gauname norimą išplėtimą:

(33)

Ši eilutė susilieja į visą skaičių tiesę (jos konvergencijos spindulį).

Jei funkcija f(x) turi visų eilių išvestines tam tikrame intervale, kuriame yra taškas a, tada jai galima pritaikyti Teiloro formulę:
,
Kur r n– vadinamasis liekanos narys arba eilutės liekana, ją galima įvertinti naudojant Lagranžo formulę:
, kur skaičius x yra tarp x ir a.

Funkcijų įvedimo taisyklės:

Jei už kokią nors vertę X r n→0 at n→∞, tada riboje Teiloro formulė tampa konvergentiška šiai reikšmei Taylor serija:
,
Taigi, funkcija f(x) gali būti išplėsta į Taylor seriją nagrinėjamame taške x, jei:
1) turi visų eilučių išvestines;
2) sudarytos eilutės konverguoja šioje vietoje.

Kai a = 0, gauname seriją, vadinamą netoli Maclaurino:
,
Paprasčiausių (elementarių) funkcijų išplėtimas Maclaurin serijoje:
Eksponentinės funkcijos
, R=∞
Trigonometrinės funkcijos
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funkcija actgx nesiplečia x laipsniais, nes ctg0=∞
Hiperbolinės funkcijos


Logaritminės funkcijos
, -1
Dvejetainė serija
.

1 pavyzdys. Išplėskite funkciją į galios eilutę f(x)= 2x.
Sprendimas. Raskime funkcijos ir jos išvestinių reikšmes X=0
f(x) = 2x, f( 0) = 2 0 =1;
f"(x) = 2x ln2, f"( 0) = 2 0 ln2= ln2;
f""(x) = 2x 2 2, f""( 0) = 2 0 ln 2 2 = ln 2 2;
…
f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.
Pakeisdami gautas išvestinių vertes į Taylor serijos formulę, gauname:

Šios eilutės konvergencijos spindulys lygus begalybei, todėl ši plėtra galioja -∞<x<+∞.

2 pavyzdys. Parašykite Taylor seriją galiomis ( X+4) funkcijai f(x)= e x.
Sprendimas. Funkcijos e išvestinių radimas x ir jų vertės taške X=-4.
f(x)= e x, f(-4) = e -4 ;
f"(x)= e x, f"(-4) = e -4 ;
f""(x)= e x, f""(-4) = e -4 ;
…
f(n)(x)= e x, f(n)( -4) = e -4 .
Todėl reikiama funkcijos Taylor serija turi tokią formą:

Šis išplėtimas taip pat galioja -∞<x<+∞.

3 pavyzdys. Išplėskite funkciją f(x)=ln x galių serijoje ( X- 1),
(t. y. Taylor serijoje netoli taško X=1).
Sprendimas. Raskite šios funkcijos išvestinius.
f(x)=lnx , , , ,

f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Pakeitę šias reikšmes į formulę, gauname norimą Taylor seriją:

Naudodami d'Alembert testą, galite patikrinti, ar serijos konverguoja ties ½x-1½<1 . Действительно,

Serija susilieja, jei ½ X- 1½<1, т.е. при 0<x<2. При X=2 gauname kintamąją eilutę, kuri tenkina Leibnizo kriterijaus sąlygas. Kai x=0, funkcija neapibrėžta. Taigi Teiloro eilutės konvergencijos sritis yra pusiau atviras intervalas (0;2]).

4 pavyzdys. Išplėskite funkciją į galios eilutę.
Sprendimas. Išplėtime (1) pakeičiame x į -x 2, gauname:
, -∞

5 pavyzdys. Išplėskite funkciją į Maclaurin seriją.
Sprendimas. Turime
Naudodami (4) formulę galime parašyti:

formulėje vietoj x pakeitę –x, gauname:

Iš čia randame: ln(1+x)-ln(1-x) = -
Atidarę skliaustus, pertvarkydami serijos sąlygas ir atvesdami panašius terminus, gauname
. Ši eilutė konverguoja intervale (-1;1), nes ji gaunama iš dviejų eilučių, kurių kiekviena suartėja šiame intervale.

komentuoti .
Formulės (1)-(5) taip pat gali būti naudojamos atitinkamoms funkcijoms išplėsti į Taylor seriją, t.y. funkcijoms plėsti teigiamais sveikaisiais skaičiais ( Ha). Norėdami tai padaryti, būtina atlikti tokias identiškas tam tikros funkcijos transformacijas, kad būtų gauta viena iš funkcijų (1)–5, kurioje vietoj X kainuoja k( Ha) m , kur k yra pastovus skaičius, m yra teigiamas sveikasis skaičius. Dažnai patogu pakeisti kintamąjį t=Ha ir išplėsti gautą funkciją t atžvilgiu Maclaurino serijoje.

Šis metodas pagrįstas teorema apie funkcijos plėtimosi laipsnių eilutėje unikalumą. Šios teoremos esmė yra ta, kad to paties taško kaimynystėje negalima gauti dviejų skirtingų laipsnių eilučių, kurios suartėtų į tą pačią funkciją, nesvarbu, kaip jos išplėtimas būtų atliktas.

Pavyzdys Nr. 5a. Išplėskite funkciją Maclaurin eilutėje ir nurodykite konvergencijos sritį.
Sprendimas. Pirmiausia randame 1-x-6x 2 =(1-3x)(1+2x) , .
į pradinę:

Trupmeną 3/(1-3x) galima laikyti be galo mažėjančios geometrinės progresijos, kurios vardiklis 3x, suma, jei |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

su konvergencijos regionu |x|< 1/3.

6 pavyzdys. Išplėskite funkciją į Teiloro eilutę šalia taško x = 3.
Sprendimas. Šią problemą, kaip ir anksčiau, galima išspręsti naudojant Taylor serijos apibrėžimą, kuriai turime rasti funkcijos išvestinius ir jų reikšmes X=3. Tačiau bus lengviau naudoti esamą išplėtimą (5):
=
Gautos eilutės konverguoja ties arba –3

7 pavyzdys. Funkcijos ln(x+2) laipsniais (x -1) parašykite Teiloro eilutę.
Sprendimas.


Serija suartėja ties , arba -2< x < 5.

Pavyzdys Nr.8. Išplėskite funkciją f(x)=sin(πx/4) į Teiloro eilutę šalia taško x =2.
Sprendimas. Padarykime pakeitimą t=x-2:

Naudodami išplėtimą (3), kuriame vietoj x pakeičiame π / 4 t, gauname:

Gauta eilutė konverguoja į nurodytą funkciją ties -∞< π / 4 t<+∞, т.е. при (-∞Taigi,
, (-∞

Apytiksliai skaičiavimai naudojant galių eilutes

• jei gauta serija yra kintamoji, naudojama ši savybė: kintamajai serijai, atitinkančiai Leibnizo sąlygas, likusi absoliučios vertės eilutės dalis neviršija pirmojo atmesto nario.
• jei duotoji eilutė yra pastovaus ženklo, tada iš atmestų terminų sudaryta serija lyginama su be galo mažėjančia geometrine progresija.
• bendruoju atveju, norėdami įvertinti likusią Teiloro serijos dalį, galite naudoti Lagranžo formulę: a x ).

1 pavyzdys. Apskaičiuokite ln(3) 0,01 tikslumu.
Sprendimas. Naudokime plėtinį, kur x=1/2 (žr. 5 pavyzdį ankstesnėje temoje):

Patikrinkime, ar galime atmesti likutį po pirmųjų trijų išplėtimo narių, įvertinsime tai naudodami be galo mažėjančios geometrinės progresijos sumą:

Taigi galime išmesti šią likutį ir gauti

2 pavyzdys. Apskaičiuokite 0,0001 tikslumu.
Sprendimas. Naudokime dvinarę eilutę. Kadangi 5 3 yra sveikojo skaičiaus, artimiausio 130, kubas, skaičių 130 patartina pavaizduoti kaip 130 = 5 3 +5.



kadangi jau ketvirtasis gautos kintamos serijos narys, atitinkantis Leibnizo kriterijų, yra mažesnis už reikalaujamą tikslumą:
, todėl jo ir po jo esančių terminų galima atmesti.
Daugelio praktiškai reikalingų apibrėžtųjų arba netinkamų integralų negalima apskaičiuoti naudojant Niutono-Leibnizo formulę, nes jos taikymas yra susijęs su antidarinės suradimu, kuris elementariose funkcijose dažnai neturi išraiškos. Būna ir taip, kad rasti antidarinį įmanoma, tačiau tai be reikalo reikalauja darbo jėgos. Tačiau, jei integrando funkcija išplečiama į laipsnių eilutę, o integravimo ribos priklauso šios serijos konvergencijos intervalui, tada galimas apytikslis integralo apskaičiavimas iš anksto nustatytu tikslumu.

3 pavyzdys. Apskaičiuokite integralą ∫ 0 1 4 sin (x) x 10 -5 tikslumu.
Sprendimas. Atitinkamas neapibrėžtas integralas negali būti išreikštas elementariomis funkcijomis, t.y. reiškia „nenuolatinį integralą“. Niutono-Leibnizo formulė čia negali būti taikoma. Apskaičiuokime integralą apytiksliai.
Nuodėmės serijos dalijimas terminu xįjungta x, gauname:

Integruodami šią eilutę po termino (tai įmanoma, nes integravimo ribos priklauso šios eilutės konvergencijos intervalui), gauname:

Kadangi gauta serija atitinka Leibnizo sąlygas ir pakanka paimti pirmųjų dviejų terminų sumą, kad būtų gauta norima reikšmė nurodytu tikslumu.
Taigi, mes randame
.

4 pavyzdys. Apskaičiuokite integralą ∫ 0 1 4 e x 2 0,001 tikslumu.
Sprendimas.
. Patikrinkime, ar galime atmesti likutį po antrojo gautos serijos termino.
0,0001<0.001. Следовательно, .