Урвуу матрицын тооцоо. Матрицын алгебр - урвуу матриц

Урвуу матрицыг олох- ихэвчлэн хоёр аргаар шийдэгддэг асуудал:

• тодорхойлогчийг олох, матрицыг шилжүүлэх шаардлагатай алгебрийн нэмэлтүүдийн арга;
• матрицын анхан шатны хувиргалт хийхийг шаарддаг үл мэдэгдэх зүйлийг арилгах Гауссын арга (мөр нэмэх, мөрийг ижил тоогоор үржүүлэх гэх мэт).

Ялангуяа сониуч хүмүүсийн хувьд бусад аргууд байдаг, жишээлбэл, шугаман хувиргалтын арга. Энэ хичээлээр бид эдгээр аргуудыг ашиглан урвуу матрицыг олох гурван арга, алгоритмд дүн шинжилгээ хийх болно.

Урвуу матриц А, ийм матриц гэж нэрлэдэг

А
. (1)

Урвуу матриц , үүнийг өгөгдсөн квадрат матрицын хувьд олох шаардлагатай А, ийм матриц гэж нэрлэдэг

матрицуудын үржвэр Абаруун талд нь таних матриц, i.e.
. (1)

Таних матриц нь бүх диагональ элементүүд нь нэгтэй тэнцүү диагональ матриц юм.

Теорем.Ганц бус (мууддаггүй, ганц бие биш) квадрат матриц бүрийн хувьд урвуу матрицыг олох боломжтой бөгөөд зөвхөн нэгийг нь олж болно. Тусгай (муудсан, ганц бие) квадрат матрицын хувьд урвуу матриц байхгүй.

Квадрат матриц гэж нэрлэдэг онцгой биш(эсвэл доройтдоггүй, дан бус), хэрэв түүний тодорхойлогч нь тэг биш бол ба онцгой(эсвэл доройтох, ганц бие) хэрэв түүний тодорхойлогч нь тэг байвал.

Матрицын урвуу талыг зөвхөн квадрат матрицад л олж болно. Мэдээжийн хэрэг урвуу матриц нь өгөгдсөн матрицтай ижил дарааллаар дөрвөлжин байх болно. Урвуу матрицыг олж болох матрицыг урвуу матриц гэнэ.

Учир нь урвуу матриц Тооны урвуутай холбогдох зүйрлэл байдаг. Тоо бүрийн хувьд а, тэгтэй тэнцүү биш, ийм тоо байдаг бтэр ажил аТэгээд бнэгтэй тэнцүү: ab= 1. Тоо бтооны урвуу гэж нэрлэдэг б. Жишээлбэл, 7-ын тооны хувьд 7*1/7=1 тул эсрэг тал нь 1/7 байна.

Алгебрийн нэмэлтүүдийн аргыг ашиглан урвуу матрицыг олох (холбоотой матриц)

Ганц бус квадрат матрицын хувьд Аурвуу нь матриц юм

матрицын тодорхойлогч хаана байна А, a нь матрицтай холбоотой матриц юм А.

Квадрат матрицтай холбоотой Ань ижил эрэмбийн матриц бөгөөд түүний элементүүд нь А матрицад шилжүүлсэн матрицын тодорхойлогчийн харгалзах элементүүдийн алгебрийн нэмэлтүүд юм.Иймээс хэрэв

Тэр

Тэгээд

Алгебрийн нэмэгдлийн аргыг ашиглан урвуу матрицыг олох алгоритм

1. Энэ матрицын тодорхойлогчийг ол А. Хэрэв тодорхойлогч нь тэгтэй тэнцүү бол урвуу матрицыг олох нь зогсдог, учир нь матриц нь ганц бие бөгөөд урвуу нь байхгүй.

2. Харьцуулан шилжүүлсэн матрицыг ол А.

3. Нэгдлийн матрицын элементүүдийг 2-р алхамд олдсон марицын алгебрийн нэмэлт болгон тооцоол.

4. Томъёо (2) хэрэглэнэ: матриц тодорхойлогчийн урвуу тоог үржүүлнэ А, 4-р алхамаас олдсон нэгдлийн матриц руу.

5. Энэ матрицыг үржүүлэх замаар 4-р алхамд олж авсан үр дүнг шалгана уу Аурвуу матриц руу. Хэрэв эдгээр матрицын үржвэр нь таних матрицтай тэнцүү бол урвуу матриц зөв олдсон байна. Үгүй бол шийдлийн процессыг дахин эхлүүлнэ үү.

Жишээ 1.Матрицын хувьд

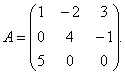
урвуу матрицыг ол.

Шийдэл. Урвуу матрицыг олохын тулд та матрицын тодорхойлогчийг олох хэрэгтэй А. Бид гурвалжны дүрмээр олдог:

Тиймээс матриц А– дан бус (муудсан бус, ганц бие биш) ба үүний урвуу тал бий.

Энэ матрицтай холбоотой матрицыг олъё А.

Матрицын хувьд шилжүүлсэн матрицыг олъё А:

Бид холбоот матрицын элементүүдийг матрицад шилжүүлсэн матрицын алгебрийн нэмэлтүүд гэж тооцдог. А:

Тиймээс матриц нь матрицтай холбоотой А, хэлбэртэй байна

Сэтгэгдэл.Элементүүдийг тооцоолох, матрицыг шилжүүлэх дараалал өөр байж болно. Та эхлээд матрицын алгебрийн нэмэлтүүдийг тооцоолж болно А, дараа нь алгебрийн комплемент матрицыг шилжүүлнэ. Үр дүн нь нэгдлийн матрицын ижил элементүүд байх ёстой.

(2) томъёог ашигласнаар бид матрицын урвуу матрицыг олно А:

Гауссын үл мэдэгдэх арилгах аргыг ашиглан урвуу матрицыг олох

Гауссын арилгах аргыг ашиглан урвуу матрицыг олох эхний алхам бол матрицад оноох явдал юм. Аижил эрэмбийн таних матриц, тэдгээрийг босоо зураасаар тусгаарлана. Бид давхар матриц авах болно. Энэ матрицын хоёр талыг үржүүлье, тэгвэл бид гарна

,

Гауссын үл мэдэгдэх арилгах аргыг ашиглан урвуу матрицыг олох алгоритм

1. Матриц руу Аижил эрэмбийн таних матрицыг оноох.

2. Үүссэн давхар матрицыг хувиргаснаар зүүн талд нь нэгж матриц, дараа нь баруун талд нь таних матрицын оронд автоматаар урвуу матриц гарч ирнэ. Матриц Азүүн талд нь энгийн матрицын хувиргалтаар таних матриц болж хувирдаг.

2. Хэрэв матрицыг хувиргах явцад Атаних матрицад аль ч мөрөнд эсвэл аль ч баганад зөвхөн тэг байх болно, дараа нь матрицын тодорхойлогч нь тэгтэй тэнцүү бөгөөд улмаар матриц болно. Ань ганц бие байх ба урвуу матрицгүй. Энэ тохиолдолд урвуу матрицыг цаашид тодорхойлох нь зогсдог.

Жишээ 2.Матрицын хувьд

урвуу матрицыг ол.

мөн бид үүнийг хувиргаж, зүүн талд нь таних матрицыг авах болно. Бид өөрчлөлтийг эхлүүлнэ.

Зүүн ба баруун матрицын эхний мөрийг (-3)-аар үржүүлж, хоёр дахь эгнээнд нэмээд, дараа нь эхний мөрийг (-4) үржүүлж, гурав дахь эгнээнд нэмбэл бид гарна.

.

Дараагийн хувиргалтуудад бутархай тоо байхгүй эсэхийг баталгаажуулахын тулд эхлээд давхар матрицын зүүн талд хоёр дахь эгнээнд нэгж байгуулъя. Үүнийг хийхийн тулд хоёр дахь мөрийг 2-оор үржүүлж, түүнээс гурав дахь мөрийг хасвал бид авна

.

Эхний мөрийг хоёр дахь мөрөнд нэмээд дараа нь хоёр дахь мөрийг (-9)-оор үржүүлж, гурав дахь мөрөнд нэмье. Дараа нь бид авна

.

Гурав дахь мөрийг 8-д хуваа

.

Гурав дахь мөрийг 2-оор үржүүлж, хоёр дахь мөрөнд нэмнэ. Энэ нь харагдаж байна:

.

Хоёр ба гурав дахь мөрүүдийг сольж, эцэст нь бид дараах зүйлийг авна.

.

Зүүн талд нь таних матриц байгаа тул баруун талд урвуу матриц байгааг бид харж байна. Тиймээс:

.

Та анхны матрицыг олсон урвуу матрицаар үржүүлэх замаар тооцооллын зөв эсэхийг шалгаж болно.

Үр дүн нь урвуу матриц байх ёстой.

Жишээ 3.Матрицын хувьд

урвуу матрицыг ол.

Шийдэл. Хос матрицыг эмхэтгэх

мөн бид үүнийг өөрчлөх болно.

Бид эхний мөрийг 3-аар, хоёр дахь мөрийг 2-оор үржүүлж, хоёр дахь мөрийг хасаад дараа нь эхний мөрийг 5-аар, гурав дахь мөрийг 2-оор үржүүлж, гурав дахь мөрийг хасаад дараа нь бид авна.

.

Бид эхний мөрийг 2-оор үржүүлж, хоёр дахь мөрөнд нэмээд гурав дахь мөрөөс хоёр дахь мөрийг хасаад дараа нь бид гарна.

.

Зүүн талын гурав дахь мөрөнд бүх элементүүд тэгтэй тэнцүү байгааг бид харж байна. Тиймээс матриц нь ганц бие бөгөөд урвуу матрицгүй. Бид урвуу марицыг цаашид олохоо больсон.

Хэрэв $A^(-1)\cdot A=A\cdot A^(-1)=E$ нөхцөл хангагдсан бол $A^(-1)$ матрицыг $A$ квадрат матрицын урвуу гэж нэрлэдэг. Энд $E $ нь таних матриц бөгөөд дараалал нь $A$ матрицын дараалалтай тэнцүү байна.

Ганц бус матриц гэдэг нь тодорхойлогч нь тэгтэй тэнцүү биш матриц юм. Үүний дагуу тодорхойлогч нь тэгтэй тэнцүү байх нэг матрицыг ганцаарчилсан матриц гэнэ.

Урвуу матриц $A^(-1)$ нь зөвхөн $A$ матриц нь дан биш байх тохиолдолд л оршино. Хэрэв урвуу матриц $A^(-1)$ байгаа бол энэ нь өвөрмөц байна.

Матрицын урвуу утгыг олох хэд хэдэн арга байдаг бөгөөд бид хоёрыг нь авч үзэх болно. Энэ хуудсанд ихэнх дээд математикийн хичээлүүдэд стандарт гэж тооцогддог нэмэлт матрицын аргыг хэлэлцэх болно. Гауссын арга эсвэл Гаусс-Жорданы аргыг ашиглах урвуу матрицыг олох хоёр дахь аргыг (элементийн хувиргалт хийх арга) хоёрдугаар хэсэгт авч үзнэ.

Хавсарсан матрицын арга

$A_(n\times n)$ матрицыг өгье. $A^(-1)$ урвуу матрицыг олохын тулд гурван алхам хийх шаардлагатай:

1. $A$ матрицын тодорхойлогчийг олоод $\Delta A\neq 0$, i.e. А матриц нь ганц бие биш юм.
2. $A$ матрицын элемент бүрийн $A_(ij)$ алгебрийн нэмэлтүүдийг зохиож, олдсон алгебраас $A_(n\times n)^(*)=\left(A_(ij) \right)$ матрицыг бичнэ үү. нэмэлт.
3. $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ томьёог харгалзан урвуу матрицыг бич.

$(A^(*))^T$ матрицыг ихэвчлэн $A$ матрицтай залгаа (харилцан, холбоот) гэж нэрлэдэг.

Хэрэв шийдлийг гараар хийсэн бол эхний арга нь зөвхөн харьцангуй бага эрэмбийн матрицуудад тохиромжтой: хоёр дахь (), гурав дахь (), дөрөв дэх (). Өндөр эрэмбийн матрицын урвуу утгыг олохын тулд бусад аргуудыг ашигладаг. Жишээлбэл, хоёр дахь хэсэгт авч үзсэн Гауссын арга.

Жишээ №1

$A=\left(\begin(массив) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 матрицын урвууг ол. & -9 & 0 \end(массив) \right)$.

Дөрөв дэх баганын бүх элементүүд тэгтэй тэнцүү тул $\Delta A=0$ (өөрөөр хэлбэл $A$ матриц нь ганц тоо) болно. $\Delta A=0$ тул $A$ матрицын урвуу матриц байхгүй.

Жишээ №2

$A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$ матрицын урвууг ол.

Бид нэмэлт матрицын аргыг ашигладаг. Эхлээд $A$ матрицын тодорхойлогчийг олъё:

$$ \Дельта А=\зүүн| \begin(массив) (cc) -5 & 7\\ 9 & 8 \end(массив)\right|=-5\cdot 8-7\cdot 9=-103. $$

$\Delta A \neq 0$ тул урвуу матриц байгаа тул бид шийдлийг үргэлжлүүлнэ. Алгебрийн нэмэлтүүдийг олох

\эхлэх(зэрэгцүүлсэн) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \төгсгөл(зэрэгцүүлсэн)

Бид алгебрийн нэмэлтүүдийн матрицыг бүрдүүлдэг: $A^(*)=\left(\begin(массив) (cc) 8 & -9\\ -7 & -5 \end(массив)\баруун)$.

Бид үүссэн матрицыг шилжүүлнэ: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(массив)\right)$ (the Үр дүнд нь матрицыг ихэвчлэн $A$ матрицтай хавсарсан эсвэл холбоот матриц гэж нэрлэдэг. $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ томьёог ашиглан бид:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\эхлэх(массив) (cc) 8 & -7\\ -9 & -5 \төгсгөл(массив)\баруун) =\left(\begin(массив) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \төгсгөл(массив)\баруун) $$

Тиймээс урвуу матриц олддог: $A^(-1)=\left(\begin(массив) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \төгсгөл(массив) )\баруун) $. Үр дүнгийн үнэнийг шалгахын тулд $A^(-1)\cdot A=E$ эсвэл $A\cdot A^(-1)=E$ гэсэн тэгшитгэлүүдийн аль нэгийн үнэнийг шалгахад хангалттай. $A^(-1)\cdot A=E$ тэгш байдлыг шалгая. Бутархайтай бага ажиллахын тулд бид $A^(-1)$ матрицыг $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 хэлбэрээр орлуулах болно. & 5/103 \ end(array)\right)$, мөн хэлбэрээр $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \төгсгөл(массив)\баруун)$:

Хариулах: $A^(-1)=\left(\эхлэх(массив) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \төгсгөл(массив)\баруун)$.

Жишээ №3

$A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(массив) \right)$ матрицын урвуу матрицыг ол. .

$A$ матрицын тодорхойлогчийг тооцоолж эхэлцгээе. Тэгэхээр $A$ матрицын тодорхойлогч нь:

$$ \Дельта А=\зүүн| \begin(массив) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(массив) \баруун| = 18-36+56-12=26. $$

$\Delta A\neq 0$ тул урвуу матриц байгаа тул бид шийдлийг үргэлжлүүлнэ. Өгөгдсөн матрицын элемент бүрийн алгебрийн нэмэлтүүдийг олно:

Бид алгебрийн нэмэлтүүдийн матрицыг бүрдүүлж, шилжүүлнэ:

$$ A^*=\left(\begin(массив) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(массив) \баруун); \; (A^*)^T=\left(\эхлэх(массив) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ төгсгөл(массив) \баруун) $$

$A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ томьёог ашиглан бид дараахийг авна:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(массив) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\төгсгөл(массив) \баруун)= \зүүн(\эхлэх(массив) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \төгсгөл(массив) \баруун) $$

Тэгэхээр $A^(-1)=\left(\begin(массив) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(массив) \right)$. Үр дүнгийн үнэнийг шалгахын тулд $A^(-1)\cdot A=E$ эсвэл $A\cdot A^(-1)=E$ гэсэн тэгшитгэлүүдийн аль нэгийн үнэнийг шалгахад хангалттай. $A\cdot A^(-1)=E$ тэгш байдлыг шалгая. Бутархайтай бага ажиллахын тулд бид $A^(-1)$ матрицыг $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ хэлбэрээр орлуулах болно. \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(массив) \баруун)$, $\frac(1)(26) хэлбэрээр )\cdot \left( \begin(массив) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(массив) \баруун)$:

Шалгалт амжилттай болсон тул урвуу матриц $A^(-1)$ зөв олдсон.

Хариулах: $A^(-1)=\left(\begin(массив) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(массив) \right)$.

Жишээ № 4

$A=\left(\begin(массив) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 матрицын урвуу матрицыг ол. & 8 & -8 & -3 \end(array) \right)$.

Дөрөвдүгээр эрэмбийн матрицын хувьд алгебрийн нэмэлтийг ашиглан урвуу матрицыг олох нь зарим талаараа хэцүү байдаг. Гэсэн хэдий ч ийм жишээ туршилтын баримт бичигт гардаг.

Матрицын урвуу утгыг олохын тулд эхлээд $A$ матрицын тодорхойлогчийг тооцоолох хэрэгтэй. Ийм нөхцөлд үүнийг хийх хамгийн сайн арга бол тодорхойлогчийг эгнээ (багана) дагуу задлах явдал юм. Бид дурын мөр, баганыг сонгож, сонгосон мөр, баганын элемент бүрийн алгебрийн нэмэлтүүдийг олдог.

Тодорхойлолт 1:Хэрэв тодорхойлогч нь тэг байвал матрицыг ганц бие гэж нэрлэдэг.

Тодорхойлолт 2:Хэрэв тодорхойлогч нь 0-тэй тэнцүү биш бол матрицыг ганц биш гэж нэрлэдэг.

Матрицыг "А" гэж нэрлэдэг урвуу матриц, хэрэв A*A-1 = A-1 *A = E (нэгж матриц) нөхцөл хангагдсан бол.

Дөрвөлжин матриц нь зөвхөн ганц биш байвал урвуу болно.

Урвуу матрицыг тооцоолох схем:

1) Хэрэв "А" матрицын тодорхойлогчийг тооцоол ∆ A = 0, тэгвэл урвуу матриц байхгүй болно.

2) "А" матрицын бүх алгебрийн нэмэлтүүдийг ол.

3) Алгебрийн нэмэлтүүдийн матриц үүсгэх (Aij)

4) Алгебрийн нэмэлтүүдийн матрицыг шилжүүл (Aij )T

5) Шилжүүлсэн матрицыг энэ матрицын тодорхойлогчийн урвуугаар үржүүлнэ.

6) Шалгах:

Эхлээд харахад энэ нь төвөгтэй мэт санагдаж болох ч үнэн хэрэгтээ бүх зүйл маш энгийн байдаг. Бүх шийдлүүд нь энгийн арифметик үйлдлүүд дээр суурилдаг. Шийдвэр гаргахдаа гол зүйл бол "-" ба "+" тэмдгээр андуурч, тэдгээрийг алдахгүй байх явдал юм.

Одоо урвуу матрицыг тооцоолох замаар практик даалгаврыг хамтдаа шийдье.

Даалгавар: доорх зурагт үзүүлсэн урвуу матриц "А"-г ​​ол.

1. Хамгийн түрүүнд хийх зүйл бол "А" матрицын тодорхойлогчийг олох явдал юм.

Тайлбар:

Бид тодорхойлогчийн үндсэн функцийг ашиглан хялбаршуулсан. Эхлээд бид 2, 3-р мөрөнд эхний мөрийн элементүүдийг нэг тоогоор үржүүлсэн.

Хоёрдугаарт, тодорхойлогчийн 2, 3-р баганыг өөрчилсөн, шинж чанарын дагуу бид урд талын тэмдгийг өөрчилсөн.

Гуравдугаарт, бид хоёр дахь мөрний нийтлэг хүчин зүйлийг (-1) гаргаж, тэмдгийг дахин өөрчилсөн бөгөөд энэ нь эерэг болсон. Бид мөн 3-р мөрийг жишээний эхэн үеийнхтэй адил хялбаршуулсан.

Бид диагональ доорхи элементүүд нь тэгтэй тэнцүү гурвалжин тодорхойлогчтой бөгөөд 7-р шинж чанараар диагональ элементүүдийн үржвэртэй тэнцүү байна. Эцэст нь бид авсан ∆ A = 26, тиймээс урвуу матриц байна.

A11 = 1*(3+1) = 4

A12 = -1*(9+2) = -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. Дараагийн алхам бол үүссэн нэмэлтүүдээс матрицыг эмхэтгэх явдал юм.

5. Энэ матрицыг тодорхойлогчийн урвуугаар, өөрөөр хэлбэл 1/26-аар үржүүл.

6. Одоо бид шалгах хэрэгтэй:

Туршилтын явцад бид таних матрицыг хүлээн авсан тул шийдлийг үнэхээр зөв хийсэн.

Урвуу матрицыг тооцоолох 2 арга.

1. Элементар матрицын хувиргалт

2. Элементар хөрвүүлэгчээр урвуу матриц.

Элементар матрицын хувиргалт нь:

1. Мөрийг тэгтэй тэнцүү биш тоогоор үржүүлэх.

2. Дурын мөрөнд тоогоор үржүүлсэн өөр мөрийг нэмэх.

3. Матрицын мөрүүдийг соль.

4. Элемент хувиргалтуудын гинжийг ашигласнаар бид өөр матрицыг олж авна.

А -1 = ?

1. (A|E) ~ (E|A -1 )

2.А -1 * A = E

Үүнийг бодит тоогоор практик жишээ ашиглан харцгаая.

Дасгал:Урвуу матрицыг ол.

Шийдэл:

Шалгацгаая:

Шийдлийн талаар бага зэрэг тодруулга:

Эхлээд бид матрицын 1 ба 2-р мөрүүдийг дахин байрлуулж, дараа нь эхний мөрийг (-1) үржүүлэв.

Үүний дараа бид эхний мөрийг (-2) үржүүлж, матрицын хоёр дахь эгнээнд нэмсэн. Дараа нь бид 2-р мөрийг 1/4-ээр үржүүлсэн.

Өөрчлөлтийн эцсийн шат нь хоёр дахь мөрийг 2-оор үржүүлж, эхнийхтэй нь нэмэх явдал байв. Үүний үр дүнд бид зүүн талд таних матрицтай тул урвуу матриц нь баруун талд байгаа матриц юм.

Шалгаж үзээд шийдвэр зөв гэдэгт итгэлтэй байсан.

Таны харж байгаагаар урвуу матрицыг тооцоолох нь маш энгийн.

Энэ лекцийн төгсгөлд би ийм матрицын шинж чанаруудын талаар бага зэрэг цаг зарцуулахыг хүсч байна.

Матрицтай үйлдлийн тухай яриагаа үргэлжлүүлье. Тухайлбал, энэ лекцийг судлах явцад та урвуу матрицыг хэрхэн олохыг сурах болно. Сурах. Хэдийгээр математик хэцүү байсан ч гэсэн.

Урвуу матриц гэж юу вэ? Энд бид урвуу тоонуудтай зүйрлэж болно: жишээлбэл, өөдрөг тоо 5 ба түүний урвуу тоог авч үзье. Эдгээр тоонуудын үржвэр нь нэгтэй тэнцүү байна: . Бүх зүйл матрицтай төстэй! Матриц ба түүний урвуу матрицын үржвэр нь -тэй тэнцүү байна. таних матриц, энэ нь тоон нэгжийн матрицын аналог юм. Гэсэн хэдий ч эхлээд хамгийн түрүүнд чухал практик асуудлыг шийдье, тухайлбал энэ урвуу матрицыг хэрхэн олохыг сурцгаая.

Урвуу матрицыг олохын тулд та юу мэдэж, хийх чадвартай байх хэрэгтэй вэ? Та шийдвэр гаргах чадвартай байх ёстой шалгуур хангагчид. Энэ нь юу болохыг та ойлгох ёстой матрицмөн тэдэнтэй зарим үйлдлийг гүйцэтгэх чадвартай байх.

Урвуу матрицыг олох хоёр үндсэн арга байдаг.
ашиглан алгебрийн нэмэлтүүдТэгээд энгийн хувиргалтыг ашиглан.

Өнөөдөр бид хамгийн анхны энгийн аргыг судлах болно.

Хамгийн аймшигтай, ойлгомжгүй зүйлээс эхэлье. Ингээд авч үзье дөрвөлжинматриц. Урвуу матрицыг дараах томъёогоор олж болно:

Матрицын тодорхойлогч хаана байна, матрицын харгалзах элементүүдийн алгебрийн нэмэлтүүдийн шилжүүлсэн матриц байна.

Урвуу матрицын тухай ойлголт зөвхөн квадрат матрицад л байдаг, матрицууд “хоёр хоёр”, “гурваас гурав” гэх мэт.

Тэмдэглэл: Та аль хэдийн анзаарсан байх, урвуу матрицыг дээд үсгээр тэмдэглэсэн

Хамгийн энгийн тохиолдлоос эхэлцгээе - хоёроос хоёр матриц. Ихэнх тохиолдолд мэдээжийн хэрэг "гурваас гурваар" шаардлагатай байдаг, гэхдээ шийдлийн ерөнхий зарчмыг ойлгохын тулд илүү энгийн ажлыг судлахыг зөвлөж байна.

Жишээ:

Матрицын урвуу утгыг ол

Ингээд шийдье. Үйлдлүүдийн дарааллыг цэг болгон задлах нь тохиромжтой.

1) Эхлээд бид матрицын тодорхойлогчийг олно.

Хэрэв таны энэ үйлдлийн талаарх ойлголт муу байвал материалыг уншина уу Тодорхойлогчийг хэрхэн тооцоолох вэ?

Чухал!Хэрэв матрицын тодорхойлогч нь тэнцүү бол ТЭГ- урвуу матриц БАЙХГҮЙ БАЙНА.

Харж байгаа жишээн дээр бүх зүйл эмх цэгцтэй байгаа гэсэн үг юм.

2) Насанд хүрээгүй хүмүүсийн матрицыг ол.

Бидний асуудлыг шийдэхийн тулд насанд хүрээгүй хүн гэж юу болохыг мэдэх шаардлагагүй, гэхдээ нийтлэлийг уншихыг зөвлөж байна. Тодорхойлогчийг хэрхэн тооцоолох вэ.

Насанд хүрээгүй хүмүүсийн матриц нь матрицтай ижил хэмжээтэй байна, өөрөөр хэлбэл энэ тохиолдолд.
Дөрвөн тоог олж оддын оронд тавих л үлдлээ.

Матриц руугаа буцаж орцгооё
Эхлээд зүүн дээд талын элементийг харцгаая:

Үүнийг яаж олох вэ бага?
Үүнийг дараах байдлаар гүйцэтгэнэ: Энэ элемент байрлах мөр, баганыг СЭТГЭЛЭЭР тайрч ав.

Үлдсэн тоо нь энэ элементийн өчүүхэн, үүнийг бид насанд хүрээгүй хүүхдүүдийн матрицад бичдэг:

Дараах матрицын элементийг авч үзье.

Энэ элемент гарч ирэх мөр, баганыг оюун ухаанаар хөндлөн зур.

Үлдсэн зүйл бол энэ элементийн багахан хэсэг бөгөөд бид матрицдаа бичдэг.

Үүний нэгэн адил бид хоёр дахь эгнээний элементүүдийг авч үзээд тэдний насанд хүрээгүй хүмүүсийг олно.


Бэлэн.

Энэ бол энгийн. Насанд хүрээгүй хүмүүсийн матрицад танд хэрэгтэй Тэмдгүүдийг өөрчлөххоёр тоо:

Эдгээр нь миний дугуйлсан тоонууд юм!

– матрицын харгалзах элементүүдийн алгебрийн нэмэлтүүдийн матриц.

Тэгээд зүгээр л...

4) Алгебрийн нэмэлтүүдийн шилжүүлсэн матрицыг ол.

– матрицын харгалзах элементүүдийн алгебрийн нэмэлтүүдийн шилжүүлсэн матриц.

5) Хариулт.

Томьёогоо санацгаая
Бүх зүйл олдсон!

Тэгэхээр урвуу матриц нь:

Хариултыг байгаагаар нь үлдээсэн нь дээр. ХЭРЭГГҮЙүр дүн нь бутархай тоо байх тул матрицын элемент бүрийг 2-т хуваа. Энэ нюансыг ижил нийтлэлд илүү нарийвчлан авч үзсэн болно. Матрицтай үйлдлүүд.

Шийдлийг хэрхэн шалгах вэ?

Та матрицын үржүүлэлтийг хийх хэрэгтэй эсвэл

Шалгалт:

Өмнө дурдсаныг хүлээн авсан таних матрицнь нэгийг агуулсан матриц юм үндсэн диагональбусад газруудад тэг.

Тиймээс урвуу матриц зөв олддог.

Хэрэв та үйлдлийг хийвэл үр дүн нь мөн адил таних матриц болно. Энэ нь матрицын үржвэрийг солих боломжтой цөөн тохиолдлын нэг бөгөөд дэлгэрэнгүй мэдээллийг нийтлэлээс олж болно. Матриц дээрх үйлдлүүдийн шинж чанарууд. Матрицын илэрхийлэл. Шалгах явцад тогтмол (бутархай) хэсгийг урагшлуулж, хамгийн төгсгөлд нь - матрицыг үржүүлсний дараа боловсруулдаг болохыг анхаарна уу. Энэ бол стандарт техник юм.

Практикт илүү нийтлэг тохиолдол болох гурваас гурван матриц руу шилжье.

Жишээ:

Матрицын урвуу утгыг ол

Алгоритм нь "хоёр хоёр" тохиолдолтой яг ижил байна.

Бид урвуу матрицыг томъёогоор олно: , энд матрицын харгалзах элементүүдийн алгебрийн нэмэлтүүдийн шилжүүлсэн матриц байна.

1) Матрицын тодорхойлогчийг ол.

Энд тодорхойлогч тодорхойлогдоно эхний мөрөнд.

Үүнийг бүү мартаарай, энэ нь бүх зүйл сайхан байна гэсэн үг юм - урвуу матриц байдаг.

2) Насанд хүрээгүй хүмүүсийн матрицыг ол.

Насанд хүрээгүй хүмүүсийн матриц нь "гурваас гурав" гэсэн хэмжээтэй байна. , мөн бид есөн тоог олох хэрэгтэй.

Би насанд хүрээгүй хэд хэдэн хүүхдийг нарийвчлан авч үзэх болно:

Дараах матрицын элементийг авч үзье.

Энэ элементийн байрлаж буй мөр, баганыг СЭТГЭЛЭЭР тайруулна уу:

Бид үлдсэн дөрвөн тоог "хоёр хоёр" тодорхойлогчд бичнэ.

Энэ нь хоёроос хоёр тодорхойлогч ба нь энэ элементийн жижиг хэсэг юм. Үүнийг тооцоолох шаардлагатай:


Ингээд л, насанд хүрээгүй хүн олдсон, бид үүнийг насанд хүрээгүй хүмүүсийн матрицад бичдэг.

Таны таамаглаж байсанчлан есөн хоёрыг хоёр тодорхойлогчийг тооцоолох хэрэгтэй. Энэ үйл явц нь мэдээжийн хэрэг уйтгартай, гэхдээ энэ нь хамгийн ноцтой биш, үүнээс ч дор байж болно.

За, нэгтгэхийн тулд - зургуудаас өөр нэг насанд хүрээгүй хүнийг олоорой:

Үлдсэн насанд хүрээгүй хүүхдүүдийг өөрөө тооцоолохыг хичээ.

Эцсийн үр дүн:
– матрицын харгалзах элементүүдийн багачуудын матриц.

Насанд хүрээгүй хүүхдүүд бүгд сөрөг болж гарсан нь зүгээр л осол юм.

3) Алгебрийн нэмэгдлийн матрицыг ол.

Насанд хүрээгүй хүмүүсийн матрицад энэ нь зайлшгүй шаардлагатай Тэмдгүүдийг өөрчлөхдараах элементүүдийн хувьд хатуу:

Энэ тохиолдолд:

Зөвхөн садист багш л ийм даалгавар өгч чаддаг тул бид "дөрөвөөс дөрөв" матрицын урвуу матрицыг олох талаар бодохгүй байна (Оюутан нэг "дөрөвөөс дөрөв" тодорхойлогч, 16 "гурваас гурав" тодорхойлогчийг тооцоолох). Миний практикт ийм тохиолдол ганц л байсан бөгөөд туршилтын үйлчлүүлэгч миний тарчлалыг маш их төлсөн =).

Хэд хэдэн сурах бичиг, гарын авлагаас та урвуу матрицыг олох арай өөр аргыг олж болно, гэхдээ би дээр дурдсан шийдлийн алгоритмыг ашиглахыг зөвлөж байна. Яагаад? Учир нь тооцоолол, тэмдгүүдэд төөрөлдөх магадлал хамаагүй бага байдаг.

Олон шинж чанараараа урвуутай төстэй.

Нэвтэрхий толь бичиг YouTube

1 / 5

✪ Матрицын урвуу утгыг хэрхэн олох вэ - bezbotvy

✪ Урвуу матриц (олох 2 арга)

✪ Урвуу матриц №1

✪ 2015-01-28. Урвуу 3х3 матриц

✪ 2015-01-27. Урвуу матриц 2х2

Хадмал орчуулга

Урвуу матрицын шинж чанарууд

• det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), Хаана det (\displaystyle \\det)тодорхойлогчийг илэрхийлнэ.
• (A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1))хоёр квадрат урвуу матрицын хувьд A (\displaystyle A)Тэгээд B (\displaystyle B).
• (A T) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), Хаана (... .) T (\displaystyle (...)^(T))шилжүүлсэн матрицыг илэрхийлнэ.
• (k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1))аливаа коэффициентийн хувьд k ≠ 0 (\displaystyle k\ =0 биш).
• E − 1 = E (\displaystyle \E^(-1)=E).
• Шугаман тэгшитгэлийн системийг шийдэх шаардлагатай бол (b нь тэг биш вектор) энд x (\displaystyle x)нь хүссэн вектор бөгөөд хэрэв A − 1 (\displaystyle A^(-1))байдаг, тэгвэл x = A − 1 b (\displaystyle x=A^(-1)b). Үгүй бол шийдлийн орон зайн хэмжээ тэгээс их байна, эсвэл шийдэл огт байхгүй.

Урвуу матрицыг олох аргууд

Хэрэв матриц урвуу бол урвуу матрицыг олохын тулд дараах аргуудын аль нэгийг ашиглаж болно.

Яг (шууд) аргууд

Гаусс-Жорданы арга

Хоёр матрицыг авч үзье: the Аба ганц бие Э. Матрицыг танилцуулъя АГаусс-Жорданы аргыг ашиглан мөрийн дагуу хувиргалтуудыг ашиглан таних матриц руу оруулна (та мөн баганын дагуу хувиргалтыг хийж болно, гэхдээ хоорондоо холилдохгүй). Эхний матрицад үйлдэл бүрийг хэрэглэсний дараа хоёр дахь матрицад ижил үйлдлийг хийнэ. Эхний матрицыг нэгж хэлбэрт буулгаж дуусахад хоёр дахь матриц нь тэнцүү болно A−1.

Гауссын аргыг ашиглах үед эхний матрицыг зүүн талд нь энгийн матрицуудын аль нэгээр үржүүлнэ. Λ i (\displaystyle \Lambda _(i))(нэг байрлалаас бусад нь үндсэн диагональ дээр байгаа хөндлөн огтлол эсвэл диагональ матриц):

Бүх үйлдлийг хэрэгжүүлсний дараа хоёр дахь матриц нь тэнцүү байх болно Λ (\displaystyle \Lambda), энэ нь хүссэн зүйл байх болно. Алгоритмын нарийн төвөгтэй байдал - O (n 3) (\displaystyle O(n^(3))).

Алгебрийн нэмэлт матрицыг ашиглах

Матрицын урвуу матриц A (\displaystyle A), хэлбэрээр төлөөлж болно

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

Хаана adj (A) (\displaystyle (\mbox(adj))(A))- хавсарсан матриц;

Алгоритмын нарийн төвөгтэй байдал нь тодорхойлогч O det-ийг тооцоолох алгоритмын нарийн төвөгтэй байдлаас хамаарах ба O(n²)·O det-тэй тэнцүү байна.

LU/LUP задралыг ашиглах

Матрицын тэгшитгэл A X = I n (\displaystyle AX=I_(n))урвуу матрицын хувьд X (\displaystyle X)цуглуулга гэж үзэж болно n (\displaystyle n)хэлбэрийн системүүд A x = b (\displaystyle Ax=b). гэж тэмдэглэе би (\displaystyle i)матрицын багана X (\displaystyle X)дамжуулан X i (\displaystyle X_(i)); Дараа нь A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\displaystyle i=1,\ldots ,n), учир нь би (\displaystyle i)матрицын багана I n (\displaystyle I_(n))нэгж вектор юм e i (\displaystyle e_(i)). өөрөөр хэлбэл урвуу матрицыг олох нь ижил матрицтай, баруун тал нь өөр өөр n тэгшитгэлийг шийдэхэд хүрдэг. LUP задралыг (O(n³) хугацаа) хийсний дараа n тэгшитгэл бүрийг шийдвэрлэхэд O(n²) хугацаа шаардагдах тул ажлын энэ хэсэгт мөн O(n³) хугацаа шаардагдана.

Хэрэв А матриц нь ганц бие биш бол түүнд зориулж LUP задралыг тооцоолж болно P A = L U (\displaystyle PA=LU). Болъё P A = B (\displaystyle PA=B), B − 1 = D (\displaystyle B^(-1)=D). Дараа нь урвуу матрицын шинж чанаруудаас бид дараахь зүйлийг бичиж болно. D = U − 1 L − 1 (\displaystyle D=U^(-1)L^(-1)). Хэрэв та энэ тэгшитгэлийг U ба L-ээр үржүүлбэл та хэлбэрийн хоёр тэгшитгэлийг авч болно U D = L − 1 (\displaystyle UD=L^(-1))Тэгээд D L = U − 1 (\displaystyle DL=U^(-1)). Эдгээр тэгшитгэлүүдийн эхнийх нь n² шугаман тэгшитгэлийн систем юм n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2)))баруун талууд нь мэдэгдэж байгаа (гурвалжин матрицын шинж чанараас). Хоёр дахь нь мөн n² шугаман тэгшитгэлийн системийг төлөөлдөг n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2)))баруун тал нь мэдэгдэж байгаа (мөн гурвалжин матрицын шинж чанараас). Тэд хамтдаа n² тэгш байдлын системийг төлөөлдөг. Эдгээр тэгш байдлыг ашиглан бид D матрицын бүх n² элементийг рекурсив аргаар тодорхойлж болно. Дараа нь тэгшитгэлээс (PA) −1 = A −1 P −1 = B −1 = D. тэгш байдлыг олж авна. A − 1 = D P (\displaystyle A^(-1)=DP).

LU задралыг ашиглах тохиолдолд D матрицын багануудыг солих шаардлагагүй, гэхдээ А матриц ганц биш байсан ч шийдэл нь зөрөөтэй байж болно.

Алгоритмын нарийн төвөгтэй байдал нь O(n³) юм.

Давталтын аргууд

Шульцын аргууд

( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\эхлэх(тохиолдлууд)\Psi _(k)=E-AU_(k),\\U_() k+1)=U_(k)\нийлбэр _(i=0)^(n)\Psi _(k)^(i)\төгсгөл(тохиолдлууд)))

Алдааны тооцоо

Анхны ойролцооллыг сонгох

Энд авч үзсэн давталттай матрицын урвуу процессын анхны ойролцооллыг сонгох асуудал нь тэдгээрийг жишээлбэл матрицын LU задралд суурилсан шууд инверцийн аргуудтай өрсөлдөх бие даасан бүх нийтийн арга гэж үзэх боломжийг бидэнд олгодоггүй. Сонгох зарим зөвлөмжүүд байдаг U 0 (\displaystyle U_(0)), нөхцөлийн биелэлтийг хангах ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (матрицын спектрийн радиус нь нэгдлээс бага) бөгөөд энэ нь процессыг нэгтгэхэд шаардлагатай бөгөөд хангалттай юм. Гэсэн хэдий ч, энэ тохиолдолд, нэгдүгээрт, урвуу матрицын спектрийн тооцооллыг дээрээс мэдэх шаардлагатай. A A T (\displaystyle AA^(T))(өөрөөр хэлбэл, хэрэв А нь тэгш хэмт эерэг тодорхой матриц ба ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), дараа нь та авч болно U 0 = α E (\displaystyle U_(0)=(\альфа )E), Хаана; хэрэв А нь дурын ганц биш матриц ба ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), дараа нь тэд итгэдэг U 0 = α A T (\displaystyle U_(0)=(\альфа )A^(T)), бас хаана α ∈ (0 , 2 β) (\displaystyle \alpha \left(0,(\frac (2)(\бета ))\баруун)); Мэдээжийн хэрэг та нөхцөл байдлыг хялбаршуулж, давуу талыг ашиглаж болно ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\маткал (k))AA^(T)(\маткал (k))), тавих U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). Хоёрдугаарт, анхны матрицыг ийм байдлаар зааж өгөхөд баталгаа байхгүй ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|)жижиг байх болно (магадгүй энэ нь бүр болж хувирах болно ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), мөн нийлэх хурдны өндөр дарааллыг тэр даруй илрүүлэхгүй.

Жишээ

Матриц 2х2

(\ displaystyle \ mathbf (A) ^ (-1) = (\ эхлэх (бматриц) a&b \\ c & d \\\ төгсгөл (бматриц)) ^ (-1) = (\ frac (1) (\ det (\ mathbf) (A)))))(\эхлэх(бматриц)\,\,\,d&\!\!-b\\-c&\,a\\\төгсгөл(бматриц))=(\frac (1)(ad- bc))(\эхлэх(бматриц)\,\,\,d&\!\!-b\\-c&\,a\\\төгсгөл(бматриц)).) 2х2 матрицыг хөрвүүлэх нь зөвхөн дараах тохиолдолд л боломжтой.