Эрчим хүчний цувралыг онлайнаар өргөжүүлэх. Эрчим хүчний цуваа, тэдгээрийн нэгдэл, функцийг чадлын цуваа болгон өргөжүүлэх

Функциональ цувралуудын дунд хамгийн чухал байрыг цахилгаан цуваа эзэлдэг.

Хүчтэй цуврал нь цуврал юм

Нөхцөлүүд нь сөрөг бус бүхэл тоог нэмэгдүүлэх замаар зохион байгуулагдсан чадлын функцууд юм x, А в 0 , в 1 , в 2 , в n - тогтмол утгууд. Тоонууд в 1 , в 2 , в n - цуврал нөхцлийн коэффициентүүд, в 0 - үнэгүй гишүүн. Эрчим хүчний цувааны нөхцлүүд нь бүх тооны шугам дээр тодорхойлогддог.

Ингээд ойлголттой танилцацгаая хүчний цувааны ойртох талбарууд.Энэ нь хувьсах утгуудын багц юм x, үүний төлөө цуврал нийлдэг. Эрчим хүчний цувралууд нь нэлээн энгийн нэгдэх мужтай байдаг. Бодит хувьсагчийн утгуудын хувьд xнийлэх муж нь нэг цэгээс бүрдэх, эсвэл тодорхой интервал (нэгдэх интервал) эсвэл бүх тэнхлэгтэй давхцах Үхэр .

Утгыг чадлын цувралд орлуулах үед x= 0 нь тооны цуваа үүснэ

в 0 +0+0+...+0+... ,

нийлдэг.

Тиймээс, хэзээ x= 0 аливаа чадлын цуваа нийлдэг тул түүний нэгдэх талбархоосон багц байж болохгүй. Бүх чадлын цувааг нэгтгэх бүсийн бүтэц ижил байна. Үүнийг дараах теоремыг ашиглан тогтоож болно.

Теорем 1 (Абелийн теорем). Хэрэв чадлын цуваа ямар нэг утгаар нийлбэл x = x 0, тэгээс ялгаатай, дараа нь энэ нь нийлдэг бөгөөд үүнээс гадна, бүх утгуудын хувьд | x| < |x 0 |

. Анхаарна уу: "X нь тэг" эхлэлийн утга ба эхлэлийн утгатай харьцуулсан "X" утгыг хоёуланг нь модулиар авна - тэмдгийг харгалзахгүйгээр. Үр дагавар. Хэрэвхүчний цуваа зөрүүтэй байна x = xямар нэг үнэ цэнээр x| > |x 1 | .

1, дараа нь энэ нь |-ийн бүх утгын хувьд ялгаатай байна xӨмнө нь олж мэдсэнээр аливаа цахилгаан цуваа утгаараа нийлдэг x= 0. Зөвхөн үед нийлдэг хүчний цуваа байдаг = 0 ба бусад утгуудын хувьд ялгаатай X x = x. Энэ тохиолдлыг авч үзэхээс хассанаар бид чадлын цуваа ямар нэг утгаар нийлдэг гэж таамаглаж байна x 0 |, |x 0, тэгээс ялгаатай. Дараа нь Абелийн теоремын дагуу ]-| интервалын бүх цэгүүдэд нийлдэг

0 |[ (зүүн ба баруун хил хязгаар нь хасах тэмдэг болон нэмэх тэмдгээр авсан хүчний цуваа нийлэх x утгууд болох интервал), гарал үүслийн хувьд тэгш хэмтэй. x = x 1, тэгвэл Абелийн теоремын үр дүнд үндэслэн энэ нь хэрчмээс гадуурх бүх цэгүүдэд хуваагдана [-| x 1 |, |x 1 |] . Үүнээс үзэхэд аливаа чадлын цувааны хувьд гарал үүсэлтэй холбоотой тэгш хэмтэй интервал гэж нэрлэгддэг нийлэх интервал, цуваа нийлдэг цэг бүрд, хил хязгаарт нь нийлж, эсвэл салж болох ба энэ нь заавал нэгэн зэрэг байх албагүй, сегментээс гадуур цуваа нь хуваагддаг. Тоо Рхүчийг цуваа нийлэх радиус гэнэ.

Онцгой тохиолдолд чадлын цувааны нэгдэх интервалцэг хүртэл доройтож болно (дараа нь цуваа зөвхөн нийлдэг x= 0 бөгөөд энэ нь гэж тооцогддог Р= 0) эсвэл бүхэл тооны шулууныг төлөөлнө (дараа нь тоон шулууны бүх цэгүүдэд цуваа нийлдэг бөгөөд ).

Тиймээс, чадлын цувааны нийлэх мужийг тодорхойлох нь түүнийг тодорхойлоход оршино нэгдэх радиус Рба нийлэх интервалын зааг дахь цувааны нийлэлтийг судлах ( at ).

Теорем 2. Хэрэв тодорхой нэгээс эхлэн чадлын цувааны бүх коэффициентүүд тэгээс ялгаатай бол түүний нэгдэх радиус нь нийтлэг нөхцлийн коэффициентүүдийн үнэмлэхүй утгуудын харьцааны хязгаартай тэнцүү байна. түүнийг дагасан цувралууд, i.e.

Жишээ 1. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Энд

(28) томъёог ашиглан бид энэ цувралын нэгдэх радиусыг олно.

Нэгдэх интервалын төгсгөлд цувааны нийлэлтийг судалъя. Жишээ 13-аас харахад энэ цуврал нь нийлдэг x= 1 ба зөрүүтэй байна x= -1. Иймээс нэгдэх бүс нь хагас интервал юм.

Жишээ 2. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Цувралын коэффициентүүд эерэг, ба

Энэ харьцааны хязгаарыг олъё, өөрөөр хэлбэл. Хүчний цувааны ойртох радиус:

Интервалын төгсгөлд цувааны нийлэлтийг судалцгаая. Үнэ цэнийг орлуулах x= -1/5 ба xЭнэ эгнээний = 1/5 нь:

Эдгээр цувралын эхнийх нь нийлдэг (Жишээ 5-ыг үз). Харин дараа нь “Үнэмлэхүй нийлэх” хэсгийн теоремын дагуу хоёр дахь цуваа бас нийлж, түүний нийлэх муж нь хэрчм болно.

Жишээ 3. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Энд

(28) томъёог ашиглан бид цувралын нэгдэх радиусыг олно.

-ийн утгуудын цувааны нийлэлтийг судалцгаая. Эдгээрийг энэ цувралд орлуулж, бид тус тусад нь авна

Нийцэх шаардлагатай нөхцөл хангагдаагүй учир хоёр цуваа зөрөөд байна (тэдгээрийн нийтлэг нөхцөл нь -д тэг байх хандлагатай байдаггүй). Тэгэхээр нийлбэрийн интервалын хоёр төгсгөлд энэ цуваа нь салж, нийлэх муж нь интервал болно.

Жишээ 5. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Бид хаана, ба гэсэн хамаарлыг олдог :

Томъёоны дагуу (28) энэ цувралын нэгдэх радиус

тэр үед л цуваа нийлдэг x= 0 ба бусад утгуудын хувьд ялгаатай = 0 ба бусад утгуудын хувьд ялгаатай.

Жишээ нь нийлэх интервалын төгсгөлд цуваа өөр өөрөөр ажилладаг болохыг харуулж байна. 1-р жишээнд нийлэх интервалын нэг төгсгөлд цуваа нийлж, нөгөө талд 2-р жишээнд хоёр төгсгөлд нийлдэг;

Тодорхой цэгээс эхлэн цуваа гишүүний бүх коэффициентүүд тэгээс өөр байна гэсэн таамаглалаар чадлын цувааны нийлэх радиусын томъёог олж авна. Тиймээс (28) томъёог зөвхөн эдгээр тохиолдолд ашиглахыг зөвшөөрнө. Хэрэв энэ нөхцөл зөрчигдсөн бол д'Аламбертийн тест ашиглан хүчнүүдийн цуваа нийлэх радиусыг хайж олох эсвэл хувьсагчийг орлуулах замаар цувааг заасан нөхцөл хангагдсан хэлбэрт шилжүүлэх хэрэгтэй.

Жишээ 6. Хүчний цувааны нийлэх интервалыг ол

Шийдэл. Энэ цувралд сондгой зэрэгтэй нэр томъёо агуулаагүй болно = 0 ба бусад утгуудын хувьд ялгаатай. Тиймээс бид цувралыг хувиргаж, тохиргоо . Дараа нь бид цувралыг авна

нийлэх радиусыг олохын тулд бид (28) томъёог хэрэглэж болно. , a , дараа нь энэ цувааны нийлэх радиус

Бидний олж авсан тэгш байдлаас харахад энэ цуваа интервал дээр нийлдэг.

Хүч чадлын цувааны нийлбэр. Эрчим хүчний цувааг ялгах, нэгтгэх

Эрчим хүчний цувралд орцгооё

нэгдэх радиус Р> 0, өөрөөр хэлбэл. энэ цуваа интервал дээр нийлдэг.

Дараа нь утга бүр = 0 ба бусад утгуудын хувьд ялгаатайнийлэх интервалаас цувааны тодорхой нийлбэртэй тохирч байна. Тиймээс чадлын цувааны нийлбэр нь функц юм = 0 ба бусад утгуудын хувьд ялгаатайнийлэх интервал дээр. Үүнийг тэмдэглэж байна е(x), бид тэгш байдлыг бичиж болно

цэг бүр дэх цувааны нийлбэр гэсэн утгаар ойлгох = 0 ба бусад утгуудын хувьд ялгаатайнийлэх интервалаас функцийн утгатай тэнцүү байна е(x) энэ үед. Үүнтэй ижил утгаараа бид чадлын цуваа (29) функцэд нийлдэг гэж хэлэх болно е(x) нэгдэх интервал дээр.

Нэгдэх интервалаас гадуур тэгш байдал (30) утгагүй болно.

Жишээ 7. Хүчний цувааны нийлбэрийг ол

Шийдэл. Энэ бол геометрийн цуврал юм а= 1, a q= x. Тиймээс түүний нийлбэр нь функц юм . Цуврал нийлдэг бол , ба түүний нийлэх интервал юм. Тиймээс тэгш байдал

функц хэдий ч зөвхөн утгуудад хүчинтэй бүх утгын хувьд тодорхойлогдсон = 0 ба бусад утгуудын хувьд ялгаатай, бусад = 0 ба бусад утгуудын хувьд ялгаатай= 1.

Хүчний цувааны нийлбэр гэдгийг баталж болно е(x) нь нийлэх интервалын аль ч интервалд, ялангуяа цувааны нийлэх интервалын аль ч цэгт тасралтгүй ба дифференциал болно.

Хүчний цувааг гишүүнээр нь ялгах, интегралчлах тухай теоремуудыг танилцуулъя.

Теорем 1. (30) нийлбэрийн интервал дахь хүчнүүдийн цувааг гишүүнээр хязгааргүй олон удаа ялгаж болох ба үр дүнд бий болсон зэрэглэлийн цуваа нь анхны цуваатай ижил нийлэх радиустай байх ба тэдгээрийн нийлбэрүүд нь тус тус тэнцүү байна.

Теорем 2. (30) чадлын цувааг 0-ээс хязгааргүй олон удаа гишүүнээр нэгтгэж болно. = 0 ба бусад утгуудын хувьд ялгаатай, хэрэв , ба үр дүнгийн зэрэглэлийн цуваа нь анхны цуваатай ижил нийлэх радиустай бөгөөд тэдгээрийн нийлбэрүүд нь харгалзах тэнцүү байна.

Функцуудыг чадлын цуврал болгон өргөжүүлэх

Функцийг өгье е(x), эрчим хүчний цуврал болгон өргөжүүлэх шаардлагатай, i.e. (30) хэлбэрээр илэрхийлнэ:

Даалгавар бол коэффициентийг тодорхойлох явдал юм эгнээ (30). Үүнийг хийхийн тулд тэгш байдлын (30) нэр томъёог нэр томъёогоор нь ялгаж үзвэл бид дараахь зүйлийг байнга олж авдаг.

……………………………………………….. (31)

(30) ба (31) тэнцүү гэж үзвэл = 0 ба бусад утгуудын хувьд ялгаатай= 0, бид олдог

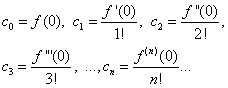
Олдсон илэрхийллийг тэгш байдал (30) болгон орлуулснаар бид олж авна

(32)

Зарим энгийн функцүүдийн Маклаурин цувралын өргөтгөлийг олцгооё.

Жишээ 8. Маклаурин цувралын функцийг өргөжүүл

Шийдэл. Энэ функцийн деривативууд нь функцтэй давхцдаг:

Тиймээс, хэзээ = 0 ба бусад утгуудын хувьд ялгаатай= 0 бидэнд байна

Эдгээр утгыг томъёогоор (32) орлуулснаар бид хүссэн өргөтгөлийг олж авна.

(33)

Энэ цуваа нь бүх тооны шулуун дээр нийлдэг (түүний нэгдэх радиус).

16.1. Тейлор ба Маклаурин цувралын энгийн функцүүдийн өргөтгөл

Олонлог дээр дурын функц тодорхойлогдсон бол гэдгийг харуулъя
, цэгийн ойролцоо
нь олон деривативтай ба зэрэглэлийн цувааны нийлбэр юм:

Дараа нь та энэ цувралын коэффициентүүдийг олох боломжтой.

Хүчний цуваагаар орлуулъя
. Дараа нь
.

Функцийн эхний деривативыг олъё
:

At
:
.

Хоёр дахь деривативын хувьд бид дараахь зүйлийг авна.

At
:
.

Энэ процедурыг үргэлжлүүлнэ nнэг удаа бид:
.

Тиймээс бид дараах хэлбэрийн чадлын цувралыг олж авлаа.

гэж нэрлэдэг Тейлорын хажуудфункцийн хувьд
цэгийн ойролцоо
.

Тейлорын цувралын онцгой тохиолдол бол Маклаурин цувралцагт
:

Тейлор (Маклаурин) цувралын үлдсэн хэсгийг үндсэн цувралыг хаяснаар олж авна nэхний гишүүд ба гэж тэмдэглэнэ
. Дараа нь функц
нийлбэр хэлбэрээр бичиж болно nцувралын анхны гишүүд
болон үлдсэн
:,

Үлдсэн хэсэг нь ихэвчлэн байдаг
янз бүрийн томъёогоор илэрхийлэгддэг.

Тэдний нэг нь Лагранж хэлбэрээр:

, Хаана
.
.

Практикт Maclaurin цувралыг илүү их ашигладаг болохыг анхаарна уу. Тиймээс функцийг бичихийн тулд
Эрчим хүчний цувралын нийлбэр хэлбэрээр дараахь зүйлийг хийх шаардлагатай.

1) Маклаурин (Тейлор) цувралын коэффициентийг олох;

2) үүссэн чадлын цувааны нийлэх мужийг олох;

3) энэ цуваа нь функцэд нийлж байгааг нотол
.

Теорем 1 (Маклаурины цувааг нэгтгэх зайлшгүй ба хангалттай нөхцөл). Цувралын нэгдэх радиусыг үзье
. Энэ цуваа интервалд нийлэхийн тулд
ажиллах
нөхцөлийг хангахад шаардлагатай бөгөөд хангалттай:
заасан интервалд.

Теорем 2. Хэрэв функцийн аль нэг эрэмбийн дериватив
тодорхой интервалд
үнэмлэхүй утгаараа ижил тоогоор хязгаарлагдана М, тэр нь
, дараа нь энэ интервалд функц
Маклаурин цуврал болгон өргөжүүлж болно.

Жишээ 1. Цэгийн эргэн тойронд Тейлорын цувралыг дэлгэнэ үү
функц.

Шийдэл.

,
;

.......................................................................................................................................

,
;

Конвергенцийн бүс
.

Жишээ 2. Функцийг өргөжүүлэх цэгийн эргэн тойронд Тейлорын цувралд
.

Шийдэл:

Функцийн утга ба түүний деривативын утгыг ол
.

,
;

...........……………………………

,
.

Эдгээр утгыг дараалан оруулъя. Бид авах:

эсвэл
.

Энэ цувралын нийлэх мужийг олцгооё. d'Alembert-ийн тестийн дагуу хэрэв цуврал нийлдэг

Тиймээс, аливаад Энэ хязгаар нь 1-ээс бага тул цувралын нэгдэх хүрээ нь:
.

Үндсэн энгийн функцүүдийн Маклаурины цуврал өргөтгөлийн хэд хэдэн жишээг авч үзье. Маклаурин цувралыг санаарай:

интервал дээр нийлдэг
ажиллах
.

Функцийг цуврал болгон өргөжүүлэхийн тулд дараахь зүйлийг хийх шаардлагатайг анхаарна уу.

a) энэ функцийн Маклаурин цувралын коэффициентийг олох;

б) үүссэн цувралын нэгдэх радиусыг тооцоолох;

в) гарсан цуваа нь функцэд нийлдэг болохыг нотол
.

Жишээ 3. Функцийг авч үзье
.

Шийдэл.

Функцийн утга ба түүний деривативыг тооцоолъё
.

Дараа нь цувралын тоон коэффициентүүд дараах хэлбэртэй байна.

хэний ч төлөө n.Олдсон коэффициентүүдийг Маклаурины цувралд орлуулж дараахийг олж авцгаая.

Үүссэн цувааны нэгдэх радиусыг олъё, тухайлбал:

Тиймээс цувралууд интервал дээр нийлдэг
.

Энэ цуврал функцэд нийлдэг аливаа үнэт зүйлсийн хувьд , учир нь дурын интервал дээр
функц мөн үнэмлэхүй утга дахь түүний деривативууд нь тоогоор хязгаарлагддаг .

Жишээ 4. Функцийг авч үзье
.

Шийдэл.

Тэгш эрэмбийн дериватив гэдгийг харахад хялбар байдаг
, мөн деривативууд нь сондгой дараалалтай. Олдсон коэффициентүүдийг Маклаурин цувралд орлуулж, өргөтгөлийг олъё.

Энэ цувралын нэгдэх интервалыг олцгооё. Д'Аламберын тэмдгийн дагуу:

хэний ч төлөө . Тиймээс цувралууд интервал дээр нийлдэг
.

Энэ цуврал функцэд нийлдэг
, учир нь түүний бүх деривативууд нь нэгдмэл байдлаар хязгаарлагддаг.

Жишээ 5.
.

Шийдэл.

Функцийн утга ба түүний деривативын утгыг олъё
:

Тиймээс энэ цувралын коэффициентүүд:
Тэгээд
, иймээс:

Өмнөх эгнээтэй төстэй, нэгдэх талбар
. Цуврал нь функцэд нийлдэг
, учир нь түүний бүх деривативууд нь нэгдмэл байдлаар хязгаарлагддаг.

функц гэдгийг анхаарна уу
сондгой ба цувралын өргөтгөл, функц
– тэгш болон тэгш эрх бүхий цуврал болгон өргөжүүлэх.

Жишээ 6. бином цуврал:
.

Шийдэл.

Функцийн утга ба түүний деривативын утгыг олъё
:

Үүнээс үзэхэд:

Эдгээр коэффициент утгыг Маклаурин цувралд орлуулж, энэ функцийг хүчирхэг цуврал болгон өргөжүүлье.

Энэ цувралын нэгдэх радиусыг олъё.

Тиймээс цувралууд интервал дээр нийлдэг
. Хязгаарлалтын цэгүүд дээр
Тэгээд
Цуврал нь илтгэгчээс хамаарч нийлэх эсвэл нийлэхгүй байж болно
.

Судалгаанд хамрагдсан цувралууд интервал дээр нийлдэг
ажиллах
, өөрөөр хэлбэл цувралын нийлбэр
цагт
.

Жишээ 7. Маклаурин цувралын функцийг өргөжүүлье
.

Шийдэл.

Энэ функцийг цуврал болгон өргөжүүлэхийн тулд бид at binomial цувралыг ашигладаг
. Бид авах:

Эрчим хүчний цувралын шинж чанарт үндэслэн (цахилгаан цувааг нийлэх бүсэд нэгтгэж болно) бид энэ цувралын зүүн ба баруун талуудын салшгүй хэсгийг олно.

Энэ цувралын нэгдэх талбарыг олъё:
,

өөрөөр хэлбэл энэ цувралын нэгдэх талбар нь интервал юм
.

Интервалын төгсгөлд цувааны нийлэлтийг тодорхойлъё. At
. Энэ цуврал нь эв нэгдэлтэй цуврал, өөрөөр хэлбэл ялгаатай. At
.

Бид нийтлэг нэр томъёо бүхий тооны цувралыг авдаг
.

Цуврал нь Лейбницийн шалгуурын дагуу нийлдэг. Тиймээс энэ цувралын нэгдэх муж нь интервал юм

16.2. Ойролцоогоор тооцоололд чадлын цуваа хэрэглэх nОйролцоогоор тооцоололд эрчим хүчний цуваа нь маш чухал үүрэг гүйцэтгэдэг. Тэдгээрийн тусламжтайгаар тригонометрийн функцүүдийн хүснэгтүүд, логарифмын хүснэгтүүд, бусад функцүүдийн утгын хүснэгтүүдийг эмхэтгэсэн бөгөөд эдгээрийг мэдлэгийн янз бүрийн салбарт, жишээлбэл, магадлалын онол, математик статистикт ашигладаг. Нэмж дурдахад функцуудыг хүчирхэг цуврал болгон өргөжүүлэх нь тэдний онолын судалгаанд тустай. Ойролцоогоор тооцоололд чадлын цуваа ашиглах гол асуудал бол цувралын нийлбэрийг эхнийх нь нийлбэрээр солих үед гарсан алдааг тооцоолох асуудал юм.

гишүүд.

Хоёр тохиолдлыг авч үзье:

функцийг тэмдгийн ээлжлэн цуврал болгон өргөжүүлсэн;

функцийг тогтмол тэмдгийн цуврал болгон өргөжүүлсэн.

Ээлжит цуваа ашиглан тооцоолох
Функцийг зөвшөөр ээлжлэн эрчим хүчний цуврал болгон өргөжүүлсэн. Дараа нь энэ функцийг тодорхой утгыг тооцоолохдоо nБид Лейбницийн шалгуурыг хэрэглэж болох тооны цувралыг олж авдаг. Энэ шалгуурын дагуу цувралын нийлбэрийг эхнийх нь нийлбэрээр сольсон бол
.