Optimizimi i algoritmit për kontrollimin e gjendjes Delaunay përmes ekuacionit të rrethit dhe aplikimit të tij

Unë do t'ju tregoj një sekret se si të kontrolloni shpejt gjendjen Delaunay për dy trekëndësha.
Në fakt, vetë optimizimi përshkruhet pak më poshtë (shiko "Optimizimi i algoritmit për kontrollimin e gjendjes Delaunay përmes ekuacionit të rrethit"), por unë do t'ju tregoj për gjithçka në rregull.

Në rastin tim, trekëndëshi përdoret në gjurmimin e imazhit për të ndarë rrafshin në sektorë primitivë (trekëndësha). Siç e dini, ajo ndahet gjithashtu në disa faza: rregullimi, identifikimi i kufijve, ecja rreth kufijve, fshirja e kontureve. Kjo është në termat më të përgjithshëm. Do të doja të ndaloja, mendoj, në fazën më të vështirë: fshirjen e avionit.

Në hyrje

Foto 1

Çfarë duhet bërë

Kërko

Algoritmi

Figura 2

Figura 3

Figura 4

Edhe një gjë: kur ruani trekëndëshin tjetër, është e nevojshme të regjistroni kulmet në një kalim në drejtim të akrepave të orës (në sistemin e duhur të koordinatave). Kjo do të jetë e dobishme në të ardhmen për të reduktuar burimet kompjuterike.

2) Përsëriteni hapin 1 derisa të kemi fshirë të gjithë aeroplanin.

3) Nëse ka disa sekuenca, d.m.th. një, dhe brenda tij ka një tjetër ose më shumë konture të brendshme (Figura 1). Këtu është e nevojshme të merret parasysh çdo sekuencë veç e veç. Le të marrim një kontur tjetër të brendshëm. Nga një i jashtëm dhe një i brendshëm do të bëjmë dy qarqe të vetme. Për ta bërë këtë, ju duhet të gjeni dy "porte" nga një qark në tjetrin. Kushti për "portet": ato nuk duhet të kryqëzohen me njëra-tjetrën (edhe skajet e tyre nuk duhet të preken), dhe ato nuk duhet të kryqëzohen me vija konturore (Figura 5).

Figura 5

Figura 6
4) Më pas, duhet të futni një nga një të gjitha sekuencat e brendshme në sekuencat e formuara tashmë, të ndara nga njëra-tjetra (pika 3). Duhet ta bashkoni me atë që përmban të renë. Sipas definicionit, asnjë sekuencë e brendshme nuk prek apo kryqëzohet me të tjerat (si një e jashtme ashtu edhe të gjitha të brendshmet e mundshme), kështu që gjithçka do të shkojë pa probleme.
Pasi të keni gjetur portat (Figura 6), është e lehtë të ndërtoni sekuenca të reja dhe t'i anashkaloni ato duke përdorur pikat 1 dhe 2 të algoritmit aktual (Figura 7).

Figura 7

5) Pas fazës së 4-të kemi një listë të trekëndëshave (Figura 8). Duket sikur detyra të jetë përfunduar tashmë, por gjithçka që mbetet është ta bëni fotografinë të bukur: kontrolloni nëse kushti Delaunay është përmbushur (Figura 9).

Figura 8

Figura 9

6) Duke parë përpara, do t'ju tregoj për pikën e gjashtë. Ai konsiston në kalimin vijues nëpër listën e trekëndëshave të fituar duke përdorur hapin nr. 5. Së pari, ne i shënojmë të gjithë trekëndëshat si "të pista". Në çdo cikël kontrollojmë kushtin Delaunay për çdo trekëndësh. Nëse kushti nuk plotësohet, atëherë rindërtojmë dhe shënojmë fqinjët dhe trekëndëshin aktual si "të pista". Nëse plotësohet kushti, atëherë e shënojmë të pastër. Në zbatimin tim të algoritmit, çdo trekëndësh ka një lidhje me fqinjët e tij. Në këtë rast, pika 6 funksionon më shpejt.

Më shumë rreth fazës së pestë

Fuqia llogaritëse #1: 10 shumëzoni/pjestoni dhe 13 shtoni/zbrisni.
Fuqia llogaritëse #2: 29 shumëzoj/pjesto dhe 24 shto/zbris.

Nga pikëpamja e fuqisë llogaritëse, e cila llogaritet për shembull në libër, opsioni nr. 1 është më fitimprurës. Do ta kisha zbatuar, nëse jo... (Figura 10). Siç doli, pas vendosjes së kësaj metode në "transportues", rezultoi pasiguri. Ky është një opsion kur vetë këndi A është më shumë se 180 gradë. Ajo konsiderohet në libër si një nga metodat individuale private. Dhe me këtë zhduket e gjithë eleganca, transparenca dhe performanca e saj. Dhe gjithashtu më vonë doli se metoda nr. 2 mund të optimizohet shumë ndjeshëm.

Figura 10

Optimizimi i algoritmit për kontrollimin e gjendjes Delaunay përmes ekuacionit të rrethit

Pra kemi:
Kontrollimi i kushtit për pikën M(X, Y) me ekuacionin e një rrethi që kalon nëpër pikat A(x1, y1), B(x2, y2), C(x3, y3) mund të shkruhet si:

(a ⋅ (X^2 + Y^ 2) − b ⋅ X + c ⋅ Y − d) ⋅ shenjë a ≥ 0

Detajet mund të gjenden në librin e shkëlqyer. (Jo, nuk jam autori)
Pra, shenja a është shenja e drejtimit të kalimit, që në fillim i kam ndërtuar trekëndëshat në drejtim të akrepave të orës, kështu që mund të hiqet (është e barabartë me një).

A(x1 - X, y1 - Y), B(x2 - X, y2 - Y), B(x3 - X, y3 - Y);

D>=0

Figura 11

E thjeshtë apo jo?

Sipas librit, përsëri,

(x1^2 + y1^2)*(y2*x3 - x2*y3) + (x2^2 + y2^2)*(x1*y3 - y1*x3) + (x3^2 + y3^2)* (y1*x2 - x1*y2)<= 0

Kemi: 15 veprime shumëzim/pjestim dhe 14 veprime mbledhje/zbritje.

Faleminderit per vemendjen. Pres kritika.

Bibliografi

Teplov A.A., Bachelor, MSTU me emrin N.E. Bauman, Departamenti i Softuerit Kompjuterik dhe Teknologjive të Informacionit, Moskë, [email i mbrojtur]

MAYKOV K.A., Doktor i Shkencave Teknike, Profesor, Universiteti Teknik Shtetëror i Moskës me emrin N.E. Bauman, Departamenti i Softuerit Kompjuterik dhe Teknologjive të Informacionit, Moskë, [email i mbrojtur]

Algoritmi i modifikuar
Trekëndëshimi i Delaunay

Janë paraqitur rezultatet e një analize krahasuese të metodave të trekëndëshimit të Delaunay me performancë të lartë dhe konsum të ulët të burimeve. Zgjedhja e një prototipi për modernizimin e mëvonshëm është vërtetuar në lidhje me ndërtimin e objekteve dinamike tre-dimensionale në kohë reale me një shkallë praktikisht të nevojshme detajesh. Propozohet një algoritëm për ndarjen intervale të një grupi pikash trekëndëshi në përputhje me densitetin e shpërndarjes, i cili lejon shmangien e gabimeve në zbatimin e harduerit. Është kryer analiza e algoritmit të modifikuar të trekëndëshit Delaunay të propozuar

Prezantimi

Një nga fazat që përcakton intensitetin e burimit të ndërtimit të objekteve dinamike 3D me një nivel të caktuar detajesh është trekëndëshimi. Në praktikë, ekziston nevoja për të përcaktuar një prototip të një metode trekëndëshi që plotëson kërkesat e performancës së lartë dhe intensitetit të ulët të burimeve, me modifikim të mëvonshëm për një klasë specifike problemesh.

Vendosja e detyrave për t'u zgjidhur

Një numër problemesh praktike karakterizohen nga nevoja për të modeluar objekte 3D të përshkruara nga një grup përkatës pikash me një ligj të panjohur shpërndarjeje. Një shembull i problemeve të tilla është modelimi i një vargu malor ose strukturave komplekse dhe të parregullta sipërfaqësore, lartësitë e të cilave më parë janë marrë me sensorë në distancë. Në këtë rast, është e nevojshme të kryhet trekëndëshi në grupin origjinal të pikave, duke siguruar "shkallën e korrektësisë" më të lartë të trekëndëshave, e cila karakterizohet nga përjashtimi i ndërtimit të trekëndëshave "të hollë" me një vlerë minimale të shumës. të rrezeve të rrathëve të rrethuar.

Problemi i "shkallës së rregullsisë" së trekëndëshave zgjidhet me anë të trekëndëshit që plotëson kushtin Delaunay.

Algoritmet e njohura të trekëndëshimit të Delaunay mund të ndahen në katër kategoritë e mëposhtme: algoritme përsëritëse, algoritme të bashkimit, algoritme me dy kalime dhe hap pas hapi; Karakteristikat kryesore të këtyre algoritmeve diskutohen më poshtë.

Algoritme përsëritëse për ndërtimin e trekëndëshit të Delaunay

Algoritmet përsëritëse zbatojnë shtimin sekuencial të pikave në një trekëndëshim Delaunay të ndërtuar pjesërisht. Kompleksiteti i algoritmeve iterative Delaunay përkufizohet si O(N2), dhe për rastin e shpërndarjes uniforme të pikave - O(N). Disavantazhet e algoritmeve iterative Delaunay janë numri i madh i sytheve përsëritëse, varësia e algoritmit të renditjes nga struktura e të dhënave burimore dhe nevoja për të kontrolluar gjendjen Delaunay në çdo lak. Përparësitë e algoritmeve iterative Delaunay janë lehtësia e zbatimit dhe shpejtësia e lartë e zgjedhjes së një algoritmi efektiv të renditjes bazuar në një grup specifik të dhënash hyrëse.

Algoritme për ndërtimin e trekëndëshit të Delaunay me bashkim

Algoritmet e bashkimit zbatojnë ndarjen e grupit origjinal të pikave në një numër nënbashkësish, në të cilat ndërtohen trekëndëshat me bashkimin e mëvonshëm të një numri zgjidhjesh. Kompleksiteti mesatar i algoritmeve të bashkimit është O(N) . Algoritmet e bashkimit karakterizohen nga teprica, e përcaktuar nga nevoja për të ndërtuar zona konvekse për vija "të ngushta" dhe, rrjedhimisht, formimi i trekëndëshave të gjatë, "të ngushtë", të rindërtuar gjatë bashkimit. Algoritmet e bashkimit kanë performancë të lartë, gjë që përcakton avantazhin e tyre praktik.

Algoritme me dy kalime për ndërtimin e trekëndëshit të Delaunay

Karakteristika e favorshme e algoritmeve me dy kalime është se në ciklin e parë ndërtohet një trekëndësh i caktuar pa marrë parasysh kushtin Delaunay, i cili modifikohet në fazën e dytë sipas kushtit Delaunay. Kompleksiteti i algoritmeve me dy kalime është mesatarisht O(N), dhe në rastin më pak të favorshëm – O(N 2). Disavantazhi i algoritmeve Delaunay me dy kalime është nevoja për një numër të madh llojesh për çdo shirit. Në të njëjtën kohë, ky algoritëm karakterizohet me performancë të lartë, sepse trekëndëshi tjetër që bie në trekëndësh nuk kontrollohet për përmbushjen e kushtit Delaunay, i cili kërkon burime të konsiderueshme harduerike.

Algoritme hap pas hapi për ndërtimin e trekëndëshit të Delaunay

Algoritmet e ndërtimit hap pas hapi zbatojnë vetëm trekëndëshat që plotësojnë kushtin Delaunay në trekëndëshimin përfundimtar dhe për këtë arsye nuk kërkojnë rindërtim. Me një përqendrim të madh pikash, përdorimi i një algoritmi qelizor hap pas hapi është jopraktik. Kompleksiteti i këtij algoritmi është mesatarisht O(N), dhe në rastin më të keq – O(N 2).

Zgjedhja e një prototipi për modifikimin e trekëndëshit Delaunay

Karakteristikat praktike të problemit të ndërtimit të objekteve dinamike 3D në kohë reale përcaktojnë kërkesa të tilla për algoritmet e trekëndëshimit Delaunay si performanca e lartë dhe intensiteti i ulët i burimeve. Siç rezulton nga rezultatet e analizës së mësipërme, algoritmet e konsideruara nuk i plotësojnë plotësisht këto kërkesa. Prandaj, ekziston nevoja për të ndërtuar një algoritëm që nuk varet nga ndarja e zonës së trekëndëshit në primitivë që përmbajnë pika të vetë trekëndëshit dhe nuk kërkon kontrollimin e kushtit Delaunay në çdo përsëritje të shtimit të trekëndëshit aktual në trekëndëshin origjinal. .

Nga rezultatet e mësipërme të analizës krahasuese rezulton se algoritmet e trekëndimit Delaunay me dy kalime, në veçanti algoritmi i ventilatorit me dy kalime, plotësojnë vetëm pjesërisht kriteret e performancës së lartë dhe intensitetit të ulët të burimit.

Megjithatë, algoritmet e këtij lloji kërkojnë modifikim në mënyrë që të rrisin performancën kur zbatohen për problemet në kohë reale. Algoritmi i ventilatorit me dy kalime është i tepërt në përcaktimin e qendrës së masës së pikave. Kur përcaktohet koordinata e një qendre të pikës së masës duke përdorur OX ose OY, me një numër të madh pikash është e papërshtatshme të llogaritet vlera e mesatares aritmetike, dhe me vlera të mëdha të koordinatave të pikës, mund të ndodhë tejmbushja e të dhënave, e cila do të çojë në një gabim ose dështim të programit. Prandaj, këshillohet që të gjitha vlerat e pikave të trekëndëshit të ndahen në intervale përgjatë boshtit X në Δx 1, Δx 2, Δx 3 ... Δx n dhe përgjatë boshtit Y në Δy 1, Δy 2, Δy 3 ... Δy n. Është gjithashtu e nevojshme të përcaktohet numri i pikave që i përkasin intervaleve përkatëse përgjatë boshteve X dhe Y. Formulat që rezultojnë për marrjen e qendrës së masës së pikave kanë formën e mëposhtme:

• x c – x-koordinata e qendrës së pikës së masës;
• Δх i – intervali i i-të në boshtin X;
• X max – vlera maksimale përgjatë boshtit X midis të gjitha pikave të trekëndëshit;
• X min – vlera minimale përgjatë boshtit X midis të gjitha pikave të trekëndëshit;

• y c – y-koordinata e qendrës së pikës së masës;
• n i – numri i pikave në intervalin i-të;
• Δy i – intervali i i-të në boshtin Y;
• Y max – vlera maksimale përgjatë boshtit Y midis të gjitha pikave të trekëndëshit;
• Y min – vlera minimale përgjatë boshtit Y midis të gjitha pikave të trekëndëshit.

Fazat pasuese të trekëndëshimit zbatohen sipas algoritmit klasik të ventilatorit. Diagrami i algoritmit të trekëndëshimit Delaunay të modifikuar të modifikuar në formë ventilatori është paraqitur në Fig. 1.

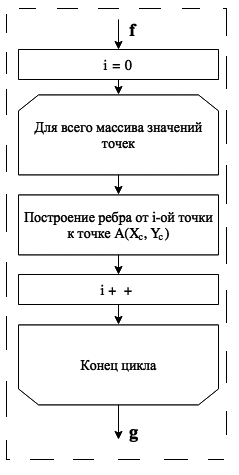Fazat më intensive të punës në skemën e paraqitur janë fazat e renditjes dhe ndërtimit të trekëndëshit në konveks. Algoritmi i bashkimit u zgjodh si algoritmi i renditjes dhe algoritmi Graham u zgjodh si algoritmi për ndërtimin e trekëndëshit konveks. Të dy algoritmet funksionojnë në një kohë të pranueshme dhe janë më të preferuarit në aspektin praktik midis përfaqësuesve të tyre.

Analiza e algoritmit të modifikuar të trekëndëshit Delaunay në formë ventilatori

Nga ai i paraqitur në Fig. 1 i diagramit tregon se vlera kohore për ndërtimin e trekëndëshit duke përdorur algoritmin e modifikuar të ventilatorit përcaktohet nga shprehja:

• T 1, T 2 - vlerat kohore për llogaritjen e numrit optimal të intervaleve përgjatë boshteve X dhe Y, përkatësisht;
• T 3 , T 4 - vlerat e kohës së llogaritjes përkatësisht X min dhe X max;
• T 5 , T 6 - respektivisht vlerat e kohës së llogaritjes Y min dhe Y max;
• T 7, T 8 - vlerat kohore për llogaritjen e vlerave të intervalit përgjatë boshteve X dhe Y, përkatësisht;
• T 9 – vlera kohore për llogaritjen e këndit polar të secilës pikë të vargut në lidhje me pikën A(X c ,Y c);
• T 10 – vlera e kohës së renditjes duke bashkuar të gjitha pikat sipas këndit polar në raport me pikën A(X c ,Y c);
• T 11 – vlera kohore për ndërtimin e një skaji nga çdo pikë e vargut në pikën A(X c ,Y c);
• T 12 - vlera kohore për plotësimin e trekëndëshit në një konveks;
• T 13 – vlera e kohës së rindërtimit të trekëndëshit që plotëson kushtin Delaunay;
• n – vargu i vlerave të koordinatave të pikës.

Le të shqyrtojmë varësinë çdo herë veç e veç.

Kur përcaktojmë numrin optimal të intervaleve përgjatë boshtit X dhe Y, ne përdorim rregullin e Sturges, sipas të cilit numri i intervaleve n përcaktohet si:

• N është numri i përgjithshëm i vëzhgimeve të sasisë;
• [x] – pjesë e plotë e numrit x.

Është e qartë se varësitë kohore T 1 dhe T 2 kanë paraqitje konstante c 1 dhe c 2.

Në fazat e përcaktimit të vlerave X min, X max, Y min, Y max pseudokodi do të duket kështu:

Xmin ← M

për i ← 1 në gjatësi (M) – 1

Nëse Xmin › M[i]

Xmin ← M[i]

Xmax ← M

për i ← 1 në gjatësi (M) – 1

Nëse Xmax< M[i]

Xmax ← M[i]

Ymin ← M

për i ← 1 në gjatësi (M) – 1

Nëse Ymin › M[i]

Ymin ← M[i]

Ymax ← M

për i ← 1 në gjatësi (M) – 1

Nëse Ymax< M[i]

Ymax ← M[i]

Nga pseudokodi i mësipërm është qartë e dukshme se koha për të gjetur vlerën maksimale ose minimale të x ose y ka një varësi lineare O(N), prandaj, T 3 (n), T 4 (n), T 5 (n) , T 6 (n) , kanë një karakteristikë kohore O(N), përkatësisht.

Diagrami për përcaktimin e vlerave të intervaleve përgjatë boshtit X është paraqitur në Fig. 2.

Nga diagrami i paraqitur më sipër është e dukshme edhe varësia kohore lineare e O(N), sepse I gjithë grupi i koordinatave të vlerave të grupit të pikave është i përfshirë në përcaktimin e vlerave. Skema për përcaktimin e vlerave të intervaleve përgjatë boshtit Y ka një strukturë të ngjashme dhe karakteristika kohore, prandaj, varësia kohore për T 7 (n) dhe T 8 (n) ka formën O(N).

Skema për përcaktimin e vlerave të këndit polar për grupin origjinal të pikave është paraqitur në Fig. 3.

Në formën e pseudokodit, ky diagram do të duket si ky:

për pikë në pikë

# Nëse pika shtrihet në boshtin koordinativ midis tremujorit të 1-të dhe të 4-të

Nëse pika.x ≥ Xc dhe pika.y = Yc

Pika.këndi ← 0

# Nëse pika qëndron rreptësisht në tremujorin e parë

Përndryshe nëse pika.x > Xc dhe pika.y > Yc

Themeli ← |pika.x – Xc|

Pika.këndi ← arctg (pingule/themeli)

# Nëse pika shtrihet në boshtin koordinativ midis tremujorit të 1-të dhe të dytë

Përndryshe nëse pika.x = Xc dhe pika.y > Yc

Pika.këndi ← p/2

# Nëse pika qëndron rreptësisht në tremujorin e dytë

Përndryshe nëse pika.x< Xc and point.y >Yc

Themeli ← |pika.y – Yc|

Pika.këndi ← p/2 + arctg (pingule/themeli)

# Nëse pika shtrihet në boshtin koordinativ midis tremujorit II dhe III

Nëse pika.x< Xc and point.y = Yc

Pika.këndi ← f

# Nëse pika qëndron rreptësisht në tremujorin e tretë

Nëse pika.x< Xc and point.y >Yc

Themeli ← |pika.x – Xc|

Perpendikulare ← |pika.y – Yc|

Pika.këndi ← p + arctan (pingule/themeli)

# Nëse pika shtrihet në boshtin koordinativ midis tremujorit III dhe IV

Nëse pika.x = Xc dhe pika.y< Yc

Pika.kënd ← 3p/2

# Nëse pika qëndron rreptësisht në tremujorin e IV

Nëse pika.x > Xc dhe pika.y< Yc

Themeli ← |pika.y – Yc|

Perpendikulare ← |pika.x – Xc|

Pika.këndi ← 3p/2 + arctg(pingule/themeli)

Natyrisht, karakteristika kohore për përcaktimin e vlerave të këndit polar për grupin origjinal të koordinatave të pikave ka formën O(N), pra, T 9 (n) = O(N).

Siç tregohet në , renditja e bashkimit ka një varësi kohore të formës O(N), prandaj T 10 (n) = O(NlnN).

Diagrami për ndërtimin e një skaji që lidh pikat e grupit origjinal është paraqitur në Fig. 4.

Pseudokodi i qarkut të mësipërm do të duket si ky:

për i ← 0 në gjatësi (Pikë) – 1

Barazim (Xc, Yc, Pikat[i].x, Pikat[i].y)

Përgjigja kohore është gjithashtu lineare, prandaj T 11 (n) = O (N).

Përfundimi i trekëndëshit që rezulton në një konveks kryhet sipas algoritmit të Graham. Të dhënat hyrëse të procedurës janë bashkësia e pikave Q, ku |Q|≥3. Ai e quan funksionin Top(S), i cili kthen pikën në krye të pirgut S pa ndryshuar përmbajtjen e tij. Përveç kësaj, përdoret edhe funksioni NextToTop(S), i cili kthen një pikë të vendosur në stivën S, një pozicion poshtë pikës së sipërme; Skema S mbetet e pandryshuar.

Graham (Q)

Le të jetë p 0 një pikë nga bashkësia Q me një koordinatë minimale.

Le të ‹p 1 , p 2 ,...,p N › – pikat e bashkësisë Q, të renditura

Në mënyrë të rritjes së këndit polar.

Push (p 0 ,S)

Push (p 1 ,S)

për i=2 deri në N bëj

Ndërsa këndi i formuar nga pikat NextToTop(S), Top(S) dhe pi,

Formoni një kthesë jo majtas

# kur lëvizni përgjatë një linje të thyer të formuar nga këto

# pika, lëvizja kryhet drejt ose djathtas

Bëj Pop(S)

Push(pi,S)

ktheje S

Koha e ekzekutimit të procedurës Graham është O(NlnN), ku N=gjatësia (Q). Është e lehtë të tregohet se cikli while do të marrë kohë O(N) dhe renditja e këndeve polare do të marrë kohë O(NlnN), që nënkupton asimptotikën e përgjithshme të procedurës Graham, prandaj, T 12 (n) = O( NlnN).

Karakteristika kohore e rindërtimit të një trekëndëshi që plotëson kushtin Delaunay, siç tregohet në , ka një varësi lineare O(N), pra T 13 (n) = O(N).

Nëse i zëvendësojmë të gjitha karakteristikat e gjetura kohore në shprehjen (3), atëherë varësia kohore që rezulton do të duket si:

T(n) = c 1 +c 2 +O(N)+O(N)+O(N)+O(N)+O(N)+O(N)+O(N)+ +O(NlnN )+O(N)+O(NlnN)+O(N)

T(n) = O(NlnN)

Analiza teorike e karakteristikave kohore të algoritmit të modifikuar të trekëndimit Delaunay konfirmon efikasitetin dhe performancën e lartë të algoritmit të propozuar.

konkluzionet

Si rezultat i analizës krahasuese të algoritmeve praktikisht të njohura të trekëndëshimit Delaunay, tregohet se metodat e konsideruara nuk plotësojnë kërkesat për ndërtimin e objekteve dinamike tredimensionale në kohë reale me një shkallë të paracaktuar detajesh, dhe për këtë arsye, ekziston një praktikë praktike. nevoja për modifikimin e tyre. Propozohet një modifikim i algoritmit të trekëndëshimit Delaunay me dy kalime në formë ventilatori, tipari funksional i të cilit është llogaritja e vlerave të qendrës së masës së grupit koordinativ të pikave të trekëndimit duke e ndarë grupin e pikave në nënbashkësi përgjatë Akset X dhe Y janë analizuar karakteristikat kohore të algoritmit të modifikuar të trekëndëshit Delaunay. Këto llogaritje bëjnë të mundur përmirësimin e ndjeshëm të performancës në një grup të madh pikash gjatë përcaktimit të koordinatave të pikës së qendrës së masës dhe shmangin tejmbushjen e të dhënave, dhe për rrjedhojë gabimet në zbatimin e softuerit.

1. Knut D.E. Arti i programimit. Vëllimi 1. Algoritmet bazë. – M.: Williams, 2008. – 680 f.
2. Knut D.E. Arti i programimit. Vëllimi 3. Renditja dhe kërkimi. – M.: Williams, 2008. – 800 f.
3. Mandelbrot B. Gjeometria fraktale e natyrës. – M.: Instituti i Kërkimeve Kompjuterike, 2002. – 656 f.
4. Skvortsov A.V. Trekëndëshimi i Delaunay dhe aplikimi i tij. – Tomsk: Shtëpia Botuese e Universitetit Tomsk, 2002. – 128 f.
5. Skvortsov A.V. Ndërtimi i trekëndëshit Delaunay në kohë lineare. – Tomsk: Shtëpia Botuese e Universitetit Tomsk, 1999. – F.120-126.
6. Skvortsov A.V., Mirza N.S. Algoritme për ndërtimin dhe analizimin e trekëndëshit. – Tomsk: Shtëpia Botuese e Universitetit Tomsk, 2006. – 168 f.
7. Thomas H. Corman, Charles I. Leiseron, Ronald L. Rivest, Clifford Stein. Algoritmet: ndërtim dhe analizë, botimi i 3-të: Përkth. nga anglishtja – M.: Williams, 2013. – 1328 f.
8. Shaidurov V.V. Metodat e elementeve të fundme me shumë rrjete. – M.: Nauka, 1989. – 288 f.
9. Sturges H. (1926). Zgjedhja e një intervali klase. J. Amer. Statist. Asoc., 21, 65-66.

Fjalë kyçe: realiteti virtual, trekëndëshimi në një grup të caktuar pikash, trekëndëshimi i Delaunay, ndërtimi i objekteve dinamike tredimensionale.

Algoritmi i modifikuar i trekëndëshit të Delaunay

Teplov A.A., Bachelor, MSTU Bauman, Departamenti i "Software dhe Teknologjive të Informacionit", Moskë, [email i mbrojtur]

Maikov K.A., Doktor i Shkencave Teknike, Profesor, MSTU Bauman, Departamenti i "Softuerëve dhe Teknologjive të Informacionit", Moskë, [email i mbrojtur]

Abstrakt: Rezultatet e analizës krahasuese të metodave praktikisht të njohura të trekëndëshit të Delaunay me performancë të lartë dhe konsum të ulët të burimeve janë përshkruar në këtë artikull. Zgjedhja e metodës për modernizim të mëtejshëm me qëllim të ndërtimit të objekteve dinamike 3-D në kohë reale me një shkallë të caktuar detajesh është e justifikuar. Një nga fazat kryesore të një fibrash, algoritmi me dy kalime të trekëndëshit të Delaunay është modifikuar. Ekziston propozimi i algoritmit për ndarjen intervale të grupit të qelizave të trekëndëshit në përputhje me densitetin e shpërndarjes, duke lejuar që të shmangen gabimet në zbatimin e harduerit.

Fjalë kyçe: realiteti virtual, trekëndëshimi në një grup të caktuar qelizash, trekëndëshimi i Delaunay, ndërtimi i objekteve dinamike 3-D.

Në kontakt me

Trekëndëshimi për një grup të fundëm pikash S është problemi i trekëndëshimit të trupit konveks CH(S) që përfshin të gjitha pikat e grupit S. Segmentet e drejtëza në trekëndësh nuk mund të kryqëzohen - ato mund të takohen vetëm në pika të përbashkëta që i përkasin grupit S. segmentet e vijës së drejtë mbyllin trekëndëshat, ne do t'i konsiderojmë ato brinjë. Në Fig. Figura 1 tregon dy versione të ndryshme të trekëndëshit për të njëjtin grup pikash (do të injorojmë përkohësisht rrathët e vizatuar në këto figura).

Oriz. 1

Për një grup të caktuar pikash S, mund të shohim se të gjitha pikat nga grupi S mund të ndahen në pika kufitare - ato pika që shtrihen në kufirin e bykut konveks CH(S), dhe pika të brendshme - ato që shtrihen brenda konveksit. byk CH(S). Ju gjithashtu mund t'i klasifikoni skajet e marra si rezultat i trekëndëshimit S si brinjë guaskë Dhe brinjët e brendshme. Skajet e bykut përfshijnë skajet e vendosura përgjatë kufirit të bykut konveks CH(S), dhe skajet e brendshme përfshijnë të gjitha skajet e tjera që formojnë një rrjet trekëndëshash brenda bykut konveks. Vini re se çdo skaj i guaskës lidh dy pika kufitare ngjitur, ndërsa skajet e brendshme mund të lidhin dy pika të çdo lloji. Në veçanti, nëse një skaj i brendshëm lidh dy pika kufitare, atëherë ai është një akord i bykut konveks CH(S). Vini re gjithashtu se çdo skaj i trekëndëshit është kufiri i dy rajoneve: çdo skaj i brendshëm është midis dy trekëndëshave dhe çdo skaj i guaskës është midis një trekëndëshi dhe një rrafshi të pafund.

Çdo grup pikash, me përjashtim të disa rasteve të parëndësishme, lejon më shumë se një metodë trekëndëshimi. Por ekziston një veti e jashtëzakonshme: çdo metodë e trekëndëshimit për një grup të caktuar përcakton të njëjtin numër trekëndëshash, i cili rrjedh nga teorema:

Një teoremë mbi trekëndëshimin e një grupi pikash. Supozojmë se bashkësia e pikave S përmban n>3 pika dhe jo të gjitha janë kolineare. Për më tepër, pikat i prej tyre janë të brendshme (d.m.th., të shtrira brenda bykut konveks CH(S). Pastaj, çdo metodë e trekëndëshimit të grupit S do të rezultojë në saktësisht n + i - 2 trekëndësha.

Për të vërtetuar teoremën, së pari shqyrtojmë trekëndëshimin e pikave kufitare n-i. Meqenëse të gjitha janë kulme të një shumëkëndëshi konveks, një trekëndësh i tillë do të rezultojë në (n - i) - 2 trekëndësha. (Kjo nuk është e vështirë të verifikohet dhe, për më tepër, mund të tregohet se çdo trekëndësh arbitrare Një shumëkëndësh me anë m - konveks ose jo konveks - përmban m - 2 trekëndësha). Tani le të kontrollojmë se çfarë do të ndodhë me trekëndëshin kur shtojmë pikat e mbetura të brendshme i, një çdo herë. Ne pretendojmë se duke shtuar çdo pikë të tillë, numri i trekëndëshave rritet me dy. Kur shtoni një pikë të brendshme, mund të lindin dy situata, të paraqitura në Fig. 2. Së pari, pika mund të jetë brenda ndonjë trekëndëshi dhe më pas një trekëndësh i tillë zëvendësohet me tre trekëndësha të rinj. Së dyti, nëse një pikë përkon me një nga skajet e trekëndëshit, atëherë secili nga dy trekëndëshat ngjitur me këtë skaj zëvendësohet nga dy trekëndësha të rinj. Nga kjo rrjedh se pas mbledhjes së të gjitha pikave i, numri i përgjithshëm i trekëndëshave do të jetë (n - i - 2) + (2i), ose thjesht n + i - 2.

Oriz. 2

Në këtë seksion, ne do të paraqesim një algoritëm për gjenerimin e një lloji të veçantë të trekëndëshit të njohur si trekëndëshimi Delaunay. Ky trekëndësh është i balancuar mirë në kuptimin që trekëndëshat e formuar priren të jenë njëkëndësh. Për shembull, trekëndëshi i paraqitur në Fig. 1a mund t'i atribuohet tipit të trekëndëshit Delaunay, dhe në Fig. Trekëndëshi 1b përmban disa trekëndësha shumë të zgjatur dhe nuk mund t'i atribuohet tipit Delaunay. Në Fig. Figura 3 tregon një shembull të trekëndëshimit të Delaunay për një grup prej një numri të madh pikash.

Oriz. 3

Për të formuar një trekëndëshim Delaunay, na duhen disa përkufizime të reja. Një grup pikash konsiderohet rrethore nëse ka një rreth në të cilin shtrihen të gjitha pikat në grup. Një rreth i tillë do të jetë i rrethuar për një grup të caktuar pikash. Rrethi i rrethuar i një trekëndëshi kalon nëpër të tre kulmet e tij (jokolineare). Thuhet se një rreth do të jetë pa pikë në lidhje me një grup të caktuar pikash S nëse nuk ka pika nga bashkësia S brenda rrethit, por, megjithatë, pikat nga bashkësia S mund të vendosen në rrethin që është më pa pikë.

Një trekëndësh i një grupi pikash S do të jetë një trekëndësh Delaunay nëse rrethi për çdo trekëndësh është i lirë nga pika. Në diagramin e trekëndëshit Fig. Figura 1a tregon dy rrathë që qartësisht nuk përmbajnë pika të tjera brenda tyre (mund të vizatoni rrathë për trekëndëshat e tjerë për t'u siguruar që ata janë gjithashtu të lirë nga pikat e grupit). Ky rregull nuk respektohet në diagramin në Fig. 16 - një pikë e një trekëndëshi tjetër bie brenda rrethit të vizatuar, prandaj, ky griangulim nuk i përket llojit Delaunay.

Mund të bëhen dy supozime për pikat në grupin S për të thjeshtuar algoritmin e trekëndëshit. Së pari, që trekëndëshimi të ekzistojë fare, duhet të supozojmë se bashkësia S përmban të paktën tre pika dhe se ato nuk janë kolineare. Së dyti, që një trekëndëshim Delaunay të jetë unik, është e nevojshme që katër pika nga grupi S të mos qëndrojnë në të njëjtin rreth. Është e lehtë të shihet se pa një supozim të tillë, trekëndëshimi i Delaunay nuk do të jetë unik, sepse 4 pika në një rreth të kufizuar na lejojnë të realizojmë dy trekëndësha të ndryshëm Delaunay.

Algoritmi ynë funksionon duke rritur vazhdimisht trekëndëshin aktual një trekëndësh në të njëjtën kohë. Fillimisht, trekëndëshimi aktual përbëhet nga një skaj i vetëm i guaskës në fund të algoritmit, trekëndëshimi aktual bëhet një trekëndëshim Delaunay. Në çdo përsëritje, algoritmi kërkon një trekëndësh të ri që lidhet me kufiri trekëndëshimi aktual.

Përcaktimi i kufirit varet nga skema e mëposhtme e klasifikimit për skajet e trekëndëshit Delaunay në lidhje me trekëndëshin aktual. Çdo skaj mund të jetë duke fjetur, të gjallë ose i vdekur:

• brinjët e gjumit: një skaj i një trekëndëshi Delaunay është i fjetur nëse nuk është zbuluar ende nga algoritmi;
• brinjë të gjalla: brinja është e gjallë nëse gjendet, por dihet vetëm një zonë ngjitur;
• brinjë të vdekur: Një skaj konsiderohet i vdekur nëse gjendet dhe dihen të dy zonat ngjitur.

Fillimisht, skaji i vetëm që i përket lobit konveks i është i gjallë - një aeroplan i pakufizuar është ngjitur me të, dhe të gjitha skajet e tjera janë të fjetura. Ndërsa algoritmi funksionon, skajet shkojnë nga gjumi në të gjallë në të vdekur. Kufiri në çdo fazë përbëhet nga një grup skajesh të gjalla.

Në çdo përsëritje, zgjidhet cilido nga skajet e kufirit dhe ai i nënshtrohet përpunimit, i cili konsiston në kërkimin e një rajoni të panjohur të cilit i përket skaji e nëse ky rajon rezulton të jetë një trekëndësh f, i përcaktuar nga pikat fundore të skajit e dhe një kulm të tretë v, atëherë skaji e bëhet i vdekur , pasi të dy zonat ngjitur me të tani janë të njohura. Secila nga dy skajet e tjera të trekëndëshit t transferohet në gjendjen e mëposhtme: nga gjumi në i gjallë ose nga i gjallë në të vdekur. Këtu do të thirret kulmi v konjuguar me skajin e Përndryshe, nëse rajoni i panjohur rezulton të jetë një rrafsh i pafund, atëherë skaji e thjesht vdes. Në këtë rast, skaji e nuk ka një kulm të konjuguar.

Në Fig. Figura 4 tregon funksionimin e algoritmit, ku veprimi ndodh nga lart poshtë dhe lavdia në të djathtë. Kufiri në çdo fazë theksohet me një vijë të trashë.

Algoritmi zbatohet në programin delaunayTriangulate. Programit i jepet një grup s me n pika dhe kthen një listë trekëndëshash që përfaqësojnë trekëndëshin Delaunay. Zbatimi përdor klasën e listës së unazave dhe klasat nga seksioni Struktura e të dhënave gjeometrike. Klasa Dictionary mund të jetë çdo fjalor që mbështet operacionet e kërkuara. Për shembull, mund të anashkaloni #define Dictionary RandomizedSearchTree .

Listë * (Pika s, int n) ( Pika p; Lista *trekëndëshat = Lista e re ; Fjalor

kufiri (edgeCmp);

Buzë *e = bykEdge(s, n);

Int edgeCmp (Edge *a, Edge *b) ( if (a->org< b->org) kthimi 1;< b->nëse (a->org > b->org) kthen 1;

nëse (a->dest

dest) kthim -1;

nëse (a->dest > b->dest) kthen 1;

kthimi 0; ) Si ndryshon kufiri nga një hap në tjetrin dhe si e modifikon funksioni updateFrontier fjalorin e skajit të kufirit për të pasqyruar këto ndryshime? Kur një trekëndësh i ri t lidhet me kufirin, gjendjet e tre skajeve të trekëndëshit ndryshojnë. Buza e trekëndëshit t ngjitur me kufirin ndryshon nga i gjallë në i vdekur. Funksioni updateFrontier mund ta injorojë këtë skaj sepse duhet hequr tashmë nga fjalori kur thirret funksioni removeMin. Secila nga dy skajet e mbetura të trekëndëshit t ndryshon gjendjen e saj nga gjumi në i gjallë, nëse nuk janë regjistruar më parë në fjalor, ose nga i gjallë në i vdekur, nëse skaji është tashmë në fjalor. Në Fig. 5 tregon të dyja rastet. Sipas figurës, ne përpunojmë skajin e gjallë af dhe, pasi kemi gjetur se pika b është konjugati i saj, shtojmë trekëndëshin afb në trekëndëshin aktual. Më pas kërkojmë skajin fb në fjalor dhe, meqenëse nuk është ende dhe zbulohet për herë të parë, gjendja e tij ndryshon nga gjumi në i gjallë. Për të redaktuar fjalorin, ne do të rrotullojmë skajin fb në mënyrë që rajoni i panjohur ngjitur me të të shtrihet në të djathtë të tij dhe ta shkruajmë këtë skaj në fjalor. Pastaj do të gjejmë skajin ba në fjalor - meqenëse është në të, ai tashmë është i gjallë (zona e njohur ngjitur me të është trekëndëshi abc). Meqenëse rajoni i panjohur për të, trekëndëshi afb, sapo është zbuluar, ky skaj është hequr nga fjalori.

Funksioni updateFrontier modifikon fjalorin kufitar, në të cilin gjendja e skajit nga pika a në pikën b ndryshon:

Oriz. 5< n; i++) if (s[i] < s[m]) m = i; swap(s, s[m]); for (m = 1, i = 2; i < n; i++) { int с = s[i].classify (s, s[m]); if ((c == LEFT) || (C == BETWEEN)) m = i; } return new Edge(s, s[m]); }

Përditësimi i pavlefshëmFrontier (Fjalori

&kufi, Pika &a, Pika &b) (Buza *e = Buzë e re (a, b); nëse (frontier.find (e)) frontier.remove(e); tjetër ( e->flip(); frontier.insert( e) )

Funksioni trekëndësh thjesht gjeneron dhe kthen një shumëkëndësh për tre pikat që i kalohen si parametra:

Problemi i ndërtimit të një rrjeti të trekëndëshave jo të mbivendosur është një nga ato themelore në gjeometrinë llogaritëse dhe përdoret gjerësisht në grafikën kompjuterike dhe në sistemet e informacionit gjeografik për modelimin e sipërfaqeve dhe zgjidhjen e problemeve hapësinore.

Problemi i ndërtimit të një rrjeti trekëndëshash jo të mbivendosur u shtrua për herë të parë në vitin 1934 në veprën e matematikanit sovjetik B. N. Delone, i cili formuloi kushtet përkatëse.

Në matematikë, detyra e ndërtimit të një trekëndëshi nga pikat e dhëna është detyra e lidhjes së tyre në çift me segmente që nuk kryqëzohen në mënyrë që të formohet një rrjet trekëndëshash. Elementet kryesore të tij janë (Fig. 5.3): nyjet (kulmet e trekëndëshave), skajet (anët) dhe faqet (vetë trekëndëshat). Trekëndëshi i ndërtuar mund të jetë konveks (nëse është një shumëkëndësh minimal që mbulon zonën e modelimit), jo konveks (nëse trekëndëshi nuk është konveks) dhe optimal (nëse shuma e gjatësive të të gjitha skajeve është minimale).

Një rrjet trekëndëshash të tillë quhet trekëndësh Delaunay nëse plotëson disa kushte:

Asnjë nga pikat origjinale nuk bie brenda rrethit të rrethuar rreth ndonjë trekëndëshi (Fig. 5.3);

Trekëndëshi është konveks dhe plotëson kushtin Delaunay të formuluar më sipër;

Shuma e këndeve minimale të të gjithë trekëndëshave është maksimumi i të gjithë trekëndëshave të mundshëm;

Shuma e rrezeve të rrathëve të përshkruar rreth trekëndëshave është minimale midis të gjithë trekëndëshave të mundshëm.

I pari nga kriteret e mësipërme për ndërtimin e një trekëndëshi Delaunay, i quajtur rrethor, është një nga më kryesorët dhe kontrollohet për çdo çift trekëndëshash me faqe të përbashkëta. Interpretimi matematik i kriterit rrjedh nga Fig. 5.3:

(5.2)

Ka shumë mënyra për të ndërtuar trekëndëshimin Delaunay, i cili është një nga metodat më të njohura të ndërtimit të një rrjetë trekëndëshi kohët e fundit. Përdoret në shumë sisteme GIS për të ndërtuar modele lehtësimi.

Kur aplikohet në hapësirën dydimensionale, ai formulohet si vijon: një sistem trekëndëshash të ndërlidhur jo të mbivendosur ka perimetrin më të vogël nëse asnjë nga kulmet nuk bie brenda asnjë prej rrathëve të përshkruar rreth trekëndëshave të formuar (Fig. 5.4).

Oriz. 5.4. Trekëndëshimi i Delaunay

Kjo do të thotë që trekëndëshat që rezultojnë me një trekëndësh të tillë janë sa më afër që të jetë e mundur me ato barabrinjës, dhe secila nga anët e trekëndëshave rezultues nga kulmi i kundërt është i dukshëm në këndin maksimal nga të gjitha pikat e mundshme të gjysmëplanit përkatës. Ky është pikërisht trekëndëshi optimal përgjatë skajeve të të cilit zakonisht bëhet interpolimi linear për të ndërtuar izolina.

Shumë algoritme për ndërtimin e trekëndëshit të Delaunay përdorin teoremën e mëposhtme.

Teorema 1. Trekëndëshi Delaunay mund të merret nga çdo trekëndësh tjetër duke përdorur të njëjtin sistem pikash duke rirregulluar në mënyrë sekuenciale çifte trekëndëshash ngjitur ABC dhe BCD që nuk plotësojnë kushtin Delaunay në çifte trekëndëshash ABD dhe ACD (Fig. 5.5).

Oriz. 5.5.. Rindërtimi i trekëndëshave që nuk plotësojnë kushtin Delaunay

Ky operacion rindërtimi shpesh quhet rrokullisje. Kjo teoremë lejon që dikush të ndërtojë trekëndëshin e Delaunay-t në mënyrë sekuenciale, së pari duke ndërtuar një trekëndëshim, dhe më pas duke e përmirësuar atë në mënyrë të njëpasnjëshme në kuptimin e kushtit të Delaunay. Kur kontrolloni kushtin Delaunay për çiftet e trekëndëshave ngjitur, mund ta përdorni drejtpërdrejt përkufizimin, por ndonjëherë përdoren metoda të tjera bazuar në kushtet e listuara më sipër.

Në këto kushte, shfaqet karakteristika totale e të gjithë trekëndëshit (shuma e këndeve minimale ose shuma e rrezeve), duke optimizuar se cilat mund të merret një trekëndësh Delaunay.

Siç u përmend më lart, një nga operacionet më të rëndësishme të kryera gjatë ndërtimit të trekëndëshit është kontrollimi i gjendjes Delaunay për çifte të dhëna trekëndëshash. Bazuar në përkufizimin e trekëndëshit të Delaunay dhe kushtet përkatëse, zakonisht përdoren disa metoda verifikimi në praktikë:

– kontrollimi përmes ekuacionit rrethor;

– kontrolloni me një rreth të përcaktuar paraprakisht;

– kontrollimi i shumës së këndeve të kundërta;

– kontroll i modifikuar i shumës së këndeve të kundërta.

Shumë sisteme e kryejnë testin me një rreth të llogaritur paraprakisht. Ideja kryesore e algoritmit të verifikimit përmes rrathëve të llogaritur paraprakisht është të parallogarisë për çdo trekëndësh të ndërtuar qendrën dhe rrezen e rrethit të përshkruar rreth tij, pas së cilës kontrollimi i gjendjes Delaunay do të reduktohet në llogaritjen e distancës deri në qendër. të këtij rrethi dhe duke krahasuar rezultatin me rrezen. Qendra dhe rrezja r e rrethit të përshkruar rreth mund të gjenden si , , , r 2 = (b 2 + c 2 - 4аd)/4а 2, ku vlerat a, b, c, d përcaktuar nga formula (5.3)

(5.3)

Një tjetër hyrje për ekuacionin e këtij rrethi është:

(5.5.)

(5.6)

Atëherë kushti Delaunay për do të plotësohet vetëm kur për çdo pikë tjetër trekëndëshimi është:

(x 0 – x C) 2 + (y 0 – y C) 2 ≥ r 2 . (5.7)

Aktualisht, ka shumë algoritme për ndërtimin e trekëndëshit të Delaunay. Shumë nga algoritmet e mirënjohura përdorin përkufizimin e trekëndëshit Delaunay si një veçori dytësore të trekëndimit. Prandaj, dobësitë e mëposhtme vërehen në algoritme të tilla:

– algoritmet përdorin funksione trigonometrike të llogaritura vazhdimisht, gjë që ngadalëson në mënyrë dramatike procesin;

– kur studiohet marrëdhënia midis pikave dhe segmentit bazë, lindin kënde shumë të vogla, dhe kur përdoren funksionet trigonometrike, ekziston gjithmonë rreziku i zhdukjes së rendit dhe ndarjes me 0 për shkak të saktësisë së kufizuar të paraqitjes së të dhënave në një kompjuter; kërkon përpunim të vazhdueshëm shtesë.

Produktet më të njohura softuerike ndërtojnë trekëndëshimin e Delaunay duke përdorur teoremën e topit të zbrazët si parimin kryesor, primar për ndërtimin e trekëndëshave. Algoritmi duket si ky:

– i gjithë grupi i pikave ndahet në trekëndësha, d.m.th. krijohen kombinime të tre pikave;

– për çdo kombinim gjendet rrethi i rrethuar dhe koordinatat e qendrës së tij;

– nëse nuk ka mbetur asnjë pikë e vetme brenda rrethit të kombinimit aktual, atëherë ky kombinim është një trekëndësh - pjesë e trekëndëshit Delaunay.

Përparësitë e këtij algoritmi përfshijnë:

– mungesa e përdorimit të funksioneve trigonometrike, e cila nuk e ngadalëson procesin e ndërtimit;

– ndërtimi i drejtpërdrejtë i trekëndëshit Delaunay, pa asnjë ndërtim paraprak;

– thjeshtësia e të gjitha llogaritjeve dhe transformimeve;

– si rezultat, rrjeti i trekëndëshit përfaqësohet nga shumë trekëndësha, në vend të vijave individuale.

Trekëndëshi i ndërtuar në këtë mënyrë është baza gjeometrike për ndërtimin e izolinave.

Algoritmet për ndërtimin e trekëndëshit Delaunay mund të ndahen në një sërë grupesh, që ndryshojnë në strukturën e të dhënave hyrëse të përdorura, vëllimin e operacioneve llogaritëse, premisat fillestare, etj. Le të shqyrtojmë disa prej tyre.

Algoritmet e bashkimit përfshijnë ndarjen e një grupi pikash burimore në nënbashkësi, ndërtimin e një trekëndëshi në secilën prej tyre dhe më pas kombinimin e tyre në një rrjet të vetëm. Thelbi i njërit prej këtyre algoritmeve zbret në sa vijon.

Një grup pikash fillestare ndahet me vija vertikale në dy ose më shumë pjesë, pas së cilës secila prej tyre ndahet me vija horizontale dhe vertikale në pjesë afërsisht të barabarta. Si rezultat, e gjithë zona e pikave të fillimit ndahet në primitivë me tre ose katër pika (Fig. 2.4), përgjatë të cilave ndërtohen një ose dy trekëndësha.

Bashkimi i këtyre trekëndëshave në një rrjet të vetëm bëhet duke ndërtuar dy vija bazë (P 0 P 1 dhe P 2 P 3, oriz. 5.7.a), duke vizatuar rrathë me rreze të ndryshueshme të përqendruar në përgjysmuesin pingul me vijën bazë (Fig. 5.7, b), duke kërkuar për një nyje që bie mbi rreth (pika A, oriz. 5.7. c) dhe ndërtimi i një trekëndëshi të ri (P 0 P 1 A). Në këtë rast, mund të jetë e nevojshme të fshihet një trekëndësh ekzistues (për shembull, P 0 AB).

Algoritmet përsëritëse bazohen në idenë e shtimit të pikave në mënyrë sekuenciale në një trekëndëshim të ndërtuar pjesërisht me përmirësimin dhe rindërtimin e tij të njëkohshëm në përputhje me kriteret e Delaunay. Në përgjithësi, ato përfshijnë disa hapa dhe përfundojnë në ndërtimin e një trekëndëshi në tre pikat e para të fillimit dhe eksplorimin e disa opsioneve për vendosjen e pikës tjetër. Në veçanti, konsiderohen opsionet që ai të bjerë jashtë kufirit të zonës së modelimit, në një nyje ose skaj ekzistues, brenda një trekëndëshi të ndërtuar, etj. Secili prej këtyre opsioneve përfshin kryerjen e një operacioni të caktuar: ndarjen e një skaji në dysh, fytyrat në tre etj.; pas së cilës trekëndëshat që rezultojnë kontrollohen për pajtueshmëri me kushtin Delaunay dhe rindërtimet e nevojshme.

Algoritmet me dy kalime fillimisht përfshijnë ndërtimin e disa trekëndëshave, duke injoruar kushtet e Delaunay, dhe më pas rindërtimin e tij në përputhje me këto kushte. Një shembull i aplikimit të algoritmit është paraqitur në Fig. 5.8.

Për të afruar modelin e krijuar të relievit me atë real, futen elementë shtesë në të për të siguruar që të merren parasysh dhe të shfaqen elementët strukturorë të tij linearë dhe zonalë. Elementë të tillë shtesë janë linja strukturore të përdorura gjerësisht në topografi që përcaktojnë "skeletin e relievit": pellgjet ujëmbledhëse, thalvegë, kreshta, shkëmbinj, parvaz, liqene, lugina, vija bregdetare, kufijtë e strukturave artificiale etj., tërësia e të cilave krijon një lloj kornizë për trekëndëshin Delaunay. Këto vija strukturore futen në trekëndësh si skajet e trekëndëshave, gjë që arrin modelimin e elementeve reale të relievit në sfondin e pabarazisë së përgjithshme të sipërfaqes së tokës. Skajet e tilla quhen strukturore (të fiksuara, jo të rikonfigurueshme), nuk kryqëzojnë skajet e trekëndëshave të tjerë dhe nuk ndryshojnë më pas.

Problemi i ndërtimit të një modeli sipërfaqësor duke marrë parasysh vijat e shkëputjes quhet trekëndëshim i kufizuar i Delaunay nëse kushtet e Delaunay janë të kënaqura për çdo çift trekëndëshash ngjitur që nuk ndahen me vija shkëputëse. Mënyra më efektive, besojnë studiuesit, është ndërtimi i një trekëndëshi të tillë duke përdorur algoritme iterative.

Algoritmet për ndërtimin e trekëndëshit të Delaunay zbatohen me një paraqitje reale ose të plotë të koordinatave të nyjeve, gjë që mund të rrisë ndjeshëm shpejtësinë dhe saktësinë e përpunimit, por krijon probleme të kërkimit dhe përjashtimit të nyjeve përputhëse.

Modeli TIN modifikohet lehtësisht duke lëvizur nyjet, duke futur të reja, duke fshirë ato ekzistuese, duke ndryshuar pozicionin e një ose disa skajeve, duke futur linja të reja strukturore, etj. Ndryshime të tilla prekin gjithmonë një grup të vogël trekëndëshash ngjitur, nuk kërkojnë rindërtimin e të gjithë rrjetin dhe kryhen on-line, duke e drejtuar kursorin në elementin përkatës.

Rreth saktësisë:

Duke vendosur kunja në elementë karakteristikë të relievit (për shembull, pellgje ujëmbledhëse dhe thalvegë), ne injorojmë elementë më të vegjël në boshllëqe. Kur ndërtohen vija konturore1 përgjatë skajeve të tilla të trekëndëshave, ndodh një gabim, i cili varet nga sasia e pabarazisë së terrenit dhe këndi i pjerrësisë së terrenit. Për shembull, gabimi mesatar në rilevimin e relievit nuk duhet të kalojë 1/3 e prerjes tërthore të relievit në këndet e pjerrësisë së sipërfaqes nga 2 në 10 gradë. Mund të llogaritet se me një seksion reliev prej 0,5 m, vlera maksimale e pabarazisë së humbur (d.m.th., devijimi i sipërfaqes së tokës nga një vijë e drejtë që kalon nëpër kunjat ngjitur) nuk duhet të kalojë (0,5/3)*cos10° =0,16 m.

Për saktësinë e përcaktimit të vëllimit të tokës së transportuar, zona e zënë nga detaji i relievit të pa llogaritur është gjithashtu i rëndësishëm. Le të themi se në një katror 20x20 m ndërmjet dy palëve ka një konveksitet cilindrik me lartësi maksimale 0,15 m Është e lehtë të llogaritet se mos marrja parasysh kur paraqitet kjo sipërfaqe vetëm me dy trekëndësha do të çojë në një gabim afërsisht 40 m3. Jo aq shumë, por për një ngastër prej 1 hektari, të vendosur në një kodër ose në pjesën e sipërme (zakonisht konveks) të shpatit, ju merrni 40 * 25 = 1000 m3 tokë të tepërt. Nëse merrni piketa dy herë më shpesh (d.m.th., çdo 10 m), gabimi do të ulet katërfish dhe do të arrijë në 250 m3 për hektar. Ky faktor mund të merret parasysh paraprakisht, pasi format pozitive të relievit të sheshtë zakonisht kanë një formë konveks, ndërsa format negative kanë një formë konkave. Nëse zona që do të vrojtohet ka të dhëna të përafërta për relievin, atëherë rrezja e lakimit të sipërfaqes dhe dendësia e kërkuar e kutive mund të llogariten lehtësisht nga vlerat e vijave konturore ose lartësive individuale.

Struktura e leksionit Përkufizimet Përkufizimet Fushat e aplikimit Fushat e aplikimit Vetitë e trekëndëshimit të Delaunay Karakteristikat e trekëndëshimit të Delaunay Metodat për ndërtimin e trekëndëshimit të Delaunay Metodat për ndërtimin e trekëndëshimit të Delaunay Metodat e hyrjes hap pas hapi Metodat e hyrjes hap pas hapi Metodat e hyrjes hap pas hapi -metodat e kampionimit me hapa Metodat e zbërthimit Metodat e zbërthimit Metodat e skanimit Metodat e skanimit Metodat me dy kalime Metodat me dy kalime

Trekëndëshi Trekëndëshi është një graf planar, rajonet e brendshme të të cilit janë të gjitha trekëndësha. Trekëndëshi është një graf planar, rajonet e brendshme të të cilit janë të gjitha trekëndësha. Termi "Triangulation" është Termi "Triangulation" është një grafik; grafiku; procesi i ndërtimit të grafikut. procesi i ndërtimit të grafikut. Problemi i trekëndëshit për një grup pikash S është problemi i lidhjes së të gjitha pikave të një bashkësie S me segmente të shkëputura për të marrë një grafik trekëndëshi. Problemi i trekëndëshit për një grup pikash S është problemi i lidhjes së të gjitha pikave të një bashkësie S me segmente të shkëputura për të marrë një grafik trekëndëshi. Përkufizimi i trekëndëshit Bashkësia e pikave S

Trekëndëshimi optimal është një trekëndësh me shumën minimale të gjatësive të të gjitha skajeve të grafikut. Trekëndëshimi optimal është një trekëndësh me shumën minimale të gjatësive të të gjitha skajeve të grafikut. ! Një problem popullor, por që kërkon shumë kohë O(2 n)! Në praktikë përdoren përafrimet (përafrimet me) trekëndëshimin optimal: Trekëndëshi “Greedy” O(N 2 *logN) Trekëndëshi “Greedy” O(N 2 *logN) Trekëndëshi Delaunay O(N*logN) Trekëndëshi Delaunay O(N*logN ) Përkufizimi i trekëndëshit optimal

Trekëndëshimi i Delaunay (DT(S)) është një trekëndësh konveks që plotëson kushtin Delaunay: Trekëndëshi i Delaunay (DT(S)) është një trekëndësh konveks që plotëson kushtin Delaunay: asnjë nga kulmet e grafikut nuk duhet të bjerë brenda rrethit të rrethuar rreth ndonjë nga trekëndëshat e tij. asnjë nga kulmet e grafikut nuk duhet të bjerë brenda rrethit të rrethuar rreth ndonjë prej trekëndëshave të tij. Përkufizimi i trekëndëshit të Delaunay Kushti i Delaunay është i kënaqur Kushti i Delaunay nuk është i kënaqur B.N. Delaunay ()

Zbatimi i trekëndëshit të Delaunay në problemet e tjera VG Në problemet e tjera VG Përfshirja minimale e një grupi pikash Hapësira minimale e një grupi pikash Ndërtimi i zonave tampon Ndërtimi i zonave tampon Ndërtimi i një diagrami Voronoi (zonat e afërsisë) Ndërtimi i një diagrami Voronoi (afërsia Zonat) Gjetja e rrethit maksimal të zbrazët Gjetja e rrethit maksimal bosh, etj etj. Në aplikime në CG, GIS, GM në CAD Në aplikime në CG, GIS, GM në CAD Modele poligonale të sipërfaqeve Modele poligonale të sipërfaqeve Relieve në GIS, skulptura , modele industriale, modele në lojëra, Relieve në GIS, skulptura, .modele industriale, modele në lojëra, Analiza numerike e modeleve Analiza numerike e modeleve Izolines, Isoclines, FEM. Izolinat, Izoklinat, FEM.

Vetitë e çdo trekëndëshi konveks 1. Për një grup prej n pikash nga të cilat m janë të brendshme Numri i trekëndëshave të trekëndëshit = n + m – 2 Numri i trekëndëshave të trekëndëshit = n + m – 2 Numri i skajeve të trekëndëshit 3n – 6 Numri i skajeve të trekëndëshit 3n – 6 Shembull: Pika (n) – 13 Pika (n) – 13 e brendshme (m) – 4 e brendshme (m) – 4 trekëndësha – 15 = trekëndësha – 15 = skaje – 26 3*13-6 = 33 skaje – 26 3 *13-6 = 33

Vetitë e trekëndëshit Delaunay 2. Trekëndëshi Delaunay ka shumën maksimale të këndeve minimale të të gjithë trekëndëshave midis të gjithë trekëndëshave të mundshëm. 3. Trekëndëshi Delaunay ka shumën minimale të rrezeve të rrathëve të përshkruar rreth trekëndëshave midis të gjithë trekëndëshave të mundshëm. Trekëndëshimi i Delaunay JO trekëndëshimi i Delaunay

Metodat për ndërtimin e trekëndëshit të Delaunay Metodat e hyrjes hap pas hapi Metodat e hyrjes hap pas hapi Algoritmet përsëritëse () Algoritmet përsëritëse () Metodat e kampionimit hap pas hapi Metodat e kampionimit hap pas hapi Ndërtimi i drejtpërdrejtë (hap pas hapi) algoritme (3) Algoritme ndërtimi direkt (hap pas hapi) (3) Metodat e zbërthimit Metodat e zbërthimit Algoritmet e bashkimit (2 ) Algoritmet e bashkimit (2) Metodat e skanimit Metodat e skanimit Algoritmet përsëritëse me një rend të ndryshuar të shtimit të pikave (1.4) Algoritmet përsëritëse me një renditje e ndryshuar e shtimit të pikëve (1.4) Algoritme me dy kalime (4) Algoritme me dy kalime (4)

Metodat e hyrjes hap pas hapi Algoritme përsëritëse () Skema e përgjithshme e algoritmeve përsëritëse për ndërtimin e trekëndëshit të Delaunay 1. Ndërtoni një trekëndësh në tre pikat e para 2. Kaloni nëpër të gjitha pikat e mbetura p i të grupit S 3. Gjeni trekëndëshin t j më afër pikës p i i trekëndëshit aktual 4. Nëse pika p i është jashtë trekëndëshit t j, atëherë ndërtoni trekëndësha në skajin më të afërt. 5. Nëse pika p i është brenda trekëndëshit t j, atëherë ndajeni trekëndëshin në tre. 6. Nëse pika p i është në një skaj, atëherë trekëndëshat ngjitur ndajini në çifte. 7. Nëse kushti Delaunay për fqinjët është shkelur, atëherë rindërtoni trekëndëshat fqinjë. Opsionet për përshpejtimin e kërkimit të trekëndëshit: Indeksimi i trekëndëshit (pemë) – O(log n) Indeksimi i trekëndëshit (pemë) – O(log n) Memoria e kujtesës së trekëndëshit (rrjetë) – O(s) Memoria e trekëndëshit (rrjetë) – O(s)

Metodat e kampionimit hap pas hapi Algoritme për ndërtimin e drejtpërdrejtë (hap pas hapi) (3) Ndërtoni menjëherë trekëndëshat e nevojshëm, pa rindërtuar atë që tashmë është ndërtuar. Skema e përgjithshme e algoritmeve për ndërtimin e drejtpërdrejtë të trekëndëshit Delaunay Është i përshtatshëm për të përdorur një pirg skajesh të papërpunuara. 1. Gjeni çdo skaj q të bykut konveks të një grupi pikash S. 2. Shtyjeni skajin q në pirgun e skajeve të papërpunuara. 3. Llokojeni derisa grumbulli i skajeve të papërpunuara të jetë bosh. 4. Nxirrni skajin v nga pirgu. 5. Për skajin v, gjeni një pikë p që plotëson kushtin Delaunay (fqinjë Delaunay) 6. Nëse gjendet fqinji i Delaunay p, atëherë 7. Ndërtoni një trekëndësh nga buza v në pikën p. 8. Shtyni skajet e reja të trekëndëshit të ri në pirgun e skajeve të papërpunuara. Opsionet për përshpejtimin e kërkimit të fqinjëve të Delaunay: Indeksimi i pikave me një pemë k-D – O(log n) Indeksimi i pikave me një pemë k-D – O(log n) Indeksimi celular i pikave – O(c) Indeksimi celular i pikave – O(c )

Procesi i algoritmit të trekëndëshit të babëzitur Delaunay

Metodat e zbërthimit Algoritmet e bashkimit (2) Ndarja në nënbashkësi, përpunimi i pavarur, bashkimi i rezultateve. Skema e përgjithshme e bashkimit të algoritmeve 0. Nëse në bashkësinë S nuk ka më shumë se 3 pika, ndërtoni drejtpërdrejt ndryshe 1. Ndajeni bashkësinë e pikave S në nënbashkësi afërsisht të barabarta. 1. Ndajeni bashkësinë e pikave S në nënbashkësi afërsisht të barabarta. 2. Ndërtimi i trekëndëshit për nënbashkësi. 2. Ndërtimi i trekëndëshit për nënbashkësi. 3. Bashkimi i trekëndëshave që rezultojnë në një. 3. Bashkimi i trekëndëshave që rezultojnë në një. Metodat e ndarjes në nëngrupe Vijat e drejta ortogonale Drejtëza ortogonale Sipas diametrit të bykut konveks Sipas diametrit të një byke konvekse Shirita vija

Algoritmet e bashkimit (2) Metodat për bashkimin e trekëndëshave "Fshi dhe ndërto" (kontrollo përpara ndërtimit) "Fshi dhe ndërto" (kontrollo përpara ndërtimit) "Ndërto dhe rindërto" (kontrollo pas ndërtimit) "Ndërto dhe rindërto" (kontrollo pas ndërtimit) " Ndërtimi, rindërtimi" (kontrolli gjatë ndërtimit) "Ndërtimi, rindërtimi" (kontrolli gjatë ndërtimit)

Skema e përgjithshme e metodave përsëritëse me një rend të modifikuar të mbledhjes së pikave 1. Rregulloni pikat (ndërtoni një listë pikash ngjarjesh) 2. Skanoni ciklin nëpër të gjitha pikat e ngjarjes 3. Për secilën pikë p i, ndërtoni trekëndësha në trekëndëshin e mëparshëm. 4. Nëse kushti Delaunay për fqinjët është shkelur, atëherë rindërtoni trekëndëshat fqinjë. Metodat e skanimit Algoritme përsëritëse me një rend të modifikuar të shtimit të pikave (1.4)

Metodat e skanimit Metodat për renditjen e pikave të ngjarjeve Drejtvizore Drejtvizore Polare (rrethore, në formë ventilatori) Polare (rrethore, në formë ventilatori) Shirit me shirit katror Sheshi Nga kurba Hilbert Nga kurba e Hilbertit Sipas kodit Z Sipas kodit Z Qëllimet: Ndërtoni menjëherë një maksimum prej trekëndëshat e mirë Ndërtoni menjëherë një maksimum trekëndëshash të mirë Minimizo numrin e ndryshimeve të korsisë Minimizo numrin e ndryshimeve të korsisë

Karakteristikat përmbledhëse të metodave të trekëndëshimit të Delaunay Metoda e trekëndëzimit Koha mesatare Koha në më të keqen Koha sek / t Lehtësia e zbatimit. Metodat e hyrjes hap pas hapi Metodat e hyrjes hap pas hapi Algoritmet përsëritëse () Algoritmet përsëritëse ()O(n)- O(n 3/2) O(n 2) 1.5-9.2 2-5 Hap pas hapi metodat e kampionimit Metodat e kampionimit hap pas hapi Metoda e ndërtimit të drejtpërdrejtë (3) Metoda e ndërtimit të drejtpërdrejtë (3) O(n)- O(n 2) O(n 2) -2 Metodat e dekompozimit Metodat e zbërthimit Metodat e bashkimit (2) Metodat e bashkimit ( 2) O(n)- O(nlogn) O (nlogn)- O(n 2) 2.5-4.52-3 Metodat e skanimit Metodat e skanimit Përsëritës me një rend të ndryshuar të shtimit të pikëve (1.4) Përsëritës me një renditje të ndryshuar të shtimit të pikëve ( 1.4) O(n) O(n 2) 1 ,9-5,34-5 Metoda me dy kalime (4) Metoda me dy kalime (4) O(n)- O(n 2) O(nlogn)- O (n 2) 2.2-15.41-5 Skvortsov rekomandon: algoritëm iterativ me memorie dinamike

Për çfarë bëhet fjalë sot? Rreth trekëndëshit të Delaunay! Përkufizimi Përkufizimi Zonat e aplikimit Vetitë e trekëndëshimit të Delaunay Karakteristikat e trekëndëshimit të Delaunay Metodat për ndërtimin e trekëndëshimit të Delaunay Metodat për ndërtimin e trekëndëshimit të Delaunay Metodat e hyrjes hap pas hapi Metodat e hyrjes hap pas hapi Metodat e kampionimit hap pas hapi -metodat e kampionimit me hapa Metodat e zbërthimit Metodat e zbërthimit Metodat e skanimit Metodat e skanimit Metodat me dy kalime Metodat me dy kalime