Aplikacion

Seritë e fuqisë në sit për ushtrime praktike për të konsoliduar materialin e mbuluar. Dhe duke përmirësuar aftësitë e studentëve në mënyrë që të mësojnë se si të përcaktojnë në mënyrë unike konvergjencën e një serie fuqie. Ushtrimet praktike japin plotësisht rezultatin e dëshiruar nëse ndahen një numër i mjaftueshëm mësimesh gjatë studimit. Kjo do të sigurojë plotësisht trajnim me cilësi të lartë për studentët. Por çfarë të bëni kur nuk janë aty? Në këtë rast, faqja jonë e internetit ose një burim i ngjashëm do t'ju ndihmojë të zgjidhni seritë e energjisë në internet. Sidoqoftë, kalkulatorë të tillë nuk do të jenë gjithmonë në gjendje të japin përgjigjen e saktë për problemin. Vetëm për këtë, duke përdorur shembullin e një kushti, duhet të krahasoni përgjigjet e marra midis zgjidhjeve të vendeve të ngjashme. Mund të vëreni se rajoni i konvergjencës së një serie nganjëherë llogaritet duke përdorur teorema të ndryshme dhe përgjigja, megjithëse e saktë, mund të shprehet në forma të ndryshme shënimi. Natyrisht, kjo nuk do të konsiderohet si gabim; Me pak fjalë, ju takon juve të gjeni konvergjencën e një serie fuqie duke përdorur një faqe ose një tjetër, domethënë se si do të jetë e përshtatshme për ju për aplikime të mëtejshme të përgjigjes. Ndonjëherë vetë zgjidhja e një serie fuqie shprehet përmes shënimeve me shenja të pabarazisë, dhe më shpesh përmes shenjës së modulit. Kjo nuk është e rastësishme, pasi në praktikë metodat më të zakonshme të përdorura janë krahasimet e anëtarëve të zakonshëm të një serie duke përdorur module. Nëpërmjet një sërë transformimesh, një ndryshore e mbyllur në një modul izolohet dhe mbetet një shënim i shkurtër që normalisht perceptohet për të kuptuar zgjidhjen. Për një paraqitje vizuale, rrezja e konvergjencës së një serie mund të përfaqësohet në boshtin numerik që tregon pikat kufitare, nga rruga, është gjithashtu e mirëpritur në një numër rastesh. Nuk ka nevojë ta detyroni veten në ndonjë kornizë specifike që do t'ju ngushtojë horizontet. Në përgjithësi, seritë e fuqisë janë një temë e rëndësishme në matematikë, sepse është komplekse dhe do t'ju duhet të kaloni disa kurse për ta kuptuar atë. Për shembull, teoria e kalimit në kufi dhe llogaritja integrale, pasi për të vërtetuar konvergjencën e një serie fuqie ata shpesh përdorin pikërisht teknika të tilla në të cilat këto veprime janë të pranishme. Ne ju ofrojmë të merrni klasa praktike dhe të testoni njohuritë tuaja për studimin e serive të energjisë në internet direkt në sit, pasi garantojmë që të gjitha problemet e zgjidhura të jepen me një përgjigje të saktë, brenda pak sekondash dhe absolutisht falas në kohë reale. Përveç diapazonit të konvergjencës së serisë, ose siç quhet edhe rrezja e konvergjencës së serisë, ne ju ofrojmë shumë kalkulatorë të tjerë të lidhur, të cilët sigurisht që do t'i vlerësoni në nivelin më të lartë. Nëse keni nevojë të gjeni konvergjencën e një serie fuqie, atëherë na lejoni ta bëjmë atë për ju, pasi faqja është një garanci e saktësisë dhe një garanci e një përgjigjeje cilësore të patëmetë. Shumë studentë shpesh bëjnë një pyetje të tillë si të përgatiten shpejt për zgjidhjen e një serie fuqie, por jo vetëm një zgjidhje, por një cilësi të lartë dhe korrekte. Në çdo kohë, seritë e fuqisë kanë pasur një kuptim më të gjerë sesa u mësohet tani studentëve. Kjo është e kuptueshme, sepse kjo shpjegohet me faktin se nuk ka kohë për shkak të nevojës për studim të thelluar të temave më të rëndësishme. Nga njëra anë - PO, por atëherë a do të thotë kjo se ne mund të neglizhojmë konvergjencën e serisë së fuqisë? Me shumë mundësi jo, sepse pa studiuar siç duhet seritë e energjisë në internet, thjesht nuk do të jeni në gjendje t'u përgjigjeni me kompetencë pyetjeve të dukshme në mbrojtjen e kursit ose të disertacionit tuaj. Le të themi se fusha juaj e lëndës përfshin një disiplinë të tillë si mekanika e vazhdueshme ose mekanika strukturore. Është e qartë se stabiliteti i sistemeve është i rëndësishëm gjatë projektimit të objekteve strategjike, veçanërisht nëse ka të bëjë drejtpërdrejt me mbrojtjen e jetës njerëzore. Do të duket se cilat gjëra të dobishme mund të mësohen nëse mësoni ose të paktën kuptoni thelbin se si të gjeni zonën e konvergjencës së një serie? Është e vështirë të përcillet rëndësia e këtij përkufizimi me një fjali. Por prano fjalën time për të, gjetja e konvergjencës së një serie fuqie është një procedurë po aq e rëndësishme dhe e nevojshme sa, për shembull, njohja e teoremës së Pitagorës. Nëse zgjidhja e një serie fuqie kryhet me një gabim, atëherë në llogaritjet e mëtejshme kjo patjetër do të luajë një shaka mizore me studentin. Ndonjëherë ndodh që, për shkak të një pasaktësie të bezdisshme në një gabim, avioni rrëzohet gjatë testeve të para. Dakord, ky është një turp pas punës së bërë dhe investimit të madh të kohës. Prandaj, mësoni dhe mësoni përsëri të gjeni rrezen e konvergjencës së një serie, duke futur kështu korrektësinë dhe ashpërsinë në zgjidhjen e problemeve që në fillim. Le të kthehemi te tema e serive të energjisë dhe t'ju tregojmë pak më shumë rreth këtij seksioni. Në praktikë, shumë seri fuqie fillojnë me termin e parë, megjithëse ka seri në të cilat termi i parë mund të fillojë me termat e dytë dhe të tretë. Kjo është kryesisht për faktin se, për shembull, duke filluar nga termi i parë, e gjithë shuma e serisë shkon menjëherë në pafundësi, e cila natyrisht është e parëndësishme, në thelb. Konvergjenca e një serie fuqie, si lëndë për studimin e fushës së konvergjencës së saj, nuk përdoret shpesh në praktikë, veçanërisht nga studentët, nëse nuk e studiojnë atë në departamentin e analizës matematikore. Thelbi është i qartë dhe detyrat janë të vendosura. Llogaritësi ynë llogarit seritë e fuqisë në internet, dhe gjithashtu flet për konvergjencën e serisë, me çfarë kriteresh konvergojnë një seri numrash, me pak fjalë, mund të përcaktojë konvergjencën e serive të fuqisë. Një variabël mund të bjerë në rajonin e konvergjencës së një serie nëse plotëson një kusht të vetëm specifik, domethënë që seria numerike rezultuese përkatëse konvergjon në një vlerë të fundme reale numerike. Ndoshta ky nuk është vetëm një kusht, është gjithashtu e nevojshme që të gjitha termat e serisë për çdo vlerë natyrore rendore të parametrit n të ekzistojnë dhe të përcaktohen në mënyrë unike. Gjetja e konvergjencës së një serie fuqie nënkupton përcaktimin e rajonit të konvergjencës së saj në boshtin x nëse flasim për një sistem koordinativ kartezian. Duket e mundur për ta bërë këtë duke përdorur parimin e D'Alembert, megjithatë, duhet të kuptoni se ai bazohet vetëm në kriterin, pasi vetë parimi përcakton vetëm intervalin në të cilin do të bjerë ndryshorja. Mos harroni, testi i d'Alembert nuk është i zbatueshëm për seritë funksionale, është vetëm për seritë e numrave. Zgjidhja e një serie fuqie lidhet drejtpërdrejt me gjetjen e rrezes së konvergjencës së kësaj serie, por për shkurtim ajo shprehet në këtë mënyrë. Ne gjithashtu do ta përdorim këtë term për të vazhduar me trendin në botën shkencore. Seritë e fuqisë në pikat kufitare studiohen veçmas. Sigurisht, kjo është pjesë e problemit të përgjithshëm të studimit të konvergjencës së një serie fuqie. Në këto pika kufitare, seria shqyrtohet si një seri numerike - shenjë konstante ose shenjë alternative, në varësi të llojit të termit të përgjithshëm të serisë. Seritë, anëtarët e të cilave janë funksione të fuqisë quhen seri të fuqisë, dhe kalkulatori mund t'i zgjidhë ato në internet. Kur ata thonë këtë, supozimi i mëposhtëm vjen menjëherë në mendje, dhe nëse anëtarët e serisë janë funksione periodike, atëherë një seri e tillë ndoshta duhet të quhet seri periodike funksionale! Është një gjë qesharake, por e gjitha është shumë serioze. Kur të kemi përcaktuar zonën e konvergjencës së serisë, atëherë është e nevojshme të kryhen llogaritjet përfundimtare, përkatësisht, të ekzaminohen seritë numerike për konvergjencë, të cilat fitohen duke zëvendësuar kufijtë e një intervali të caktuar në vend të ndryshores x të seri fuqie. Pastaj mund të shkruani një përgjigje të plotë me një zgjidhje. Le të shqyrtojmë një shembull se si mund të gjeni konvergjencën e një serie fuqie pa përdorur teoremat kryesore, por vetëm në mënyrë krahasuese. Në këtë rast, duhet të bëjmë krahasime me kompetencë të dy serive funksionale derisa të thjeshtojmë serinë origjinale me atë elementare që është studiuar për një kohë të gjatë. Sipas këtij parimi, ne do të marrim si përgjigje rezultatin që prej kohësh është i njohur për të gjithë paraprakisht. Bazuar në zgjidhjen e një serie fuqie, nuk është ende e mundur të merret me mend në mënyrë të qartë se cila do të jetë saktësisht rrezja e konvergjencës së serisë, pasi para kësaj është ende e nevojshme të studiohen të paktën dy seri numrash në secilin prej kufijve të Intervali në dukje, të gjitha seritë e fuqisë janë të njëjta në atë që termi i tyre i përbashkët përfaqëson një funksion të rregullt të argumentit. Thelbi i studimit është pikërisht përcaktimi i vlerave të pranueshme të këtij argumenti për konvergjencën e serisë (të kushtëzuar ose të pakushtëzuar), si dhe në cilat intervale do të ndryshojnë seritë numerike përkatëse. Studimi i serive të fuqisë për konvergjencë kërkon shumë kohë dhe ju rekomandojmë të përdorni një kalkulator të gatshëm në faqen e internetit. Është e nevojshme të ekzaminohen edhe kufijtë e intervalit, përndryshe detyra nuk do të përfundojë plotësisht, që do të thotë se dy pikë janë të garantuara për t'u zbritur. Në faqen tonë të internetit mund të llogarisni shumën e serive të fuqisë në internet. Gjithmonë i shpejtë, i besueshëm dhe më e rëndësishmja falas! Ndërfaqja e përshtatshme dhe kërkesa e qartë e të dhënave Me të drejtë, zona e konvergjencës së një serie është një kusht specifik për ekzistencën e shumës së një serie numerike. Nëse vlera në kufirin e intervalit jep një divergjencë të serisë alternative që rezulton. pastaj thonë se seria konvergjon me kusht, pra sigurisht që konvergon në këtë rajon, por në kushte të caktuara, që është e rëndësishme në çdo rast. Nëse abstragojmë nga koncepti i një serie fuqie dhe për një moment thjesht imagjinojmë shumën e një serie fuqie si një funksion të caktuar në ndryshoren x, atëherë nuk po flasim më për gjetjen e konvergjencës së një serie fuqie, por për përcaktimin kushtet në të cilat vlera e funksionit do të ekzistojë në vlera të ndryshme të argumentit të tij x. Shkurtimisht, ne e reduktojmë problemin në gjetjen më të thjeshtë të fushës së përkufizimit të një funksioni. E vërteta është shumë e thjeshtë dhe e qartë! Çdo zgjidhje për një seri fuqie flet gjithmonë për rrezen e konvergjencës së një serie të tillë fuqie dhe zakonisht përcaktohet përmes kriterit D'Alembert, por jo drejtpërdrejt, por vetëm me një kusht. Pas kësaj, zbulohet moduli i pabarazisë që rezulton dhe seritë numerike shqyrtohen për konvergjencë absolute ose të kushtëzuar. Pastaj nxjerrin një përfundim. Është shumë interesante kur seritë e fuqisë në formën e tyre origjinale integrohen ose diferencohen, dhe më pas llogaritet shuma e serive nga seritë e reja të fuqisë. Kjo çon në shumë opsione për mënyrën sesi një seri sillet në kushte të caktuara. Shuma e gjetur e serisë së fuqisë nga termat e integruar të serisë origjinale është, në fakt, shuma e integruar e serisë origjinale të fuqisë. Interesante dhe informuese, apo jo? Nëse e formuloni saktë tekstin e problemit, duket diçka si kjo: gjeni intervalin e konvergjencës së serisë së fuqisë dhe studiojeni atë në kufijtë e intervalit të gjetur. Nga këtu seritë mund të konvergojnë ose ndryshojnë absolutisht, gjë që nuk kërkon kërkime shtesë. Konvergjenca uniforme tregon seritë e fuqisë në llogaritjen online, duke shtuar një nga një të gjitha termat e serisë origjinale, të shkruara në formë klasike, si në universitet. Duke u mbështetur vetëm në instinktet e tij, një student rrezikon të bjerë në grackën e vetëbesimit të tij për shkak të papërvojës, kur është po aq e lehtë sa të vrasësh dardha vetëm të marrësh dhe të përdorësh një kalkulator faqe interneti që në fillim të studimeve. Nga zona e konvergjencës së serisë, nxirren përfundime në lidhje me konvergjencën e serisë funksionale, ose më saktë, të fuqisë, përkatësisht, konstatohet se ajo konvergon ose me kusht ose absolutisht. E gjithë kjo është e nevojshme për regjistrimin përfundimtar të përgjigjes përfundimtare. Pa e komplikuar situatën dhe pa përdorur emrat e teoremave komplekse, le të themi se gjetja e konvergjencës së një serie fuqie do të jetë më e lehtë për t'u kuptuar nëse imagjinoni një funksion të caktuar si shumën e serisë dhe e studioni atë. Dhe kjo ka qenë prej kohësh e qartë për të gjithë dhe e kupton se si ta bëjë këtë! Rrezja e konvergjencës së një serie dhe zgjidhja e një serie fuqie janë koncepte identike, pasi nënkuptojnë të njëjtën gjë, ato përcaktojnë në mënyrë unike rajonin nga i cili jepen vlerat e ndryshores nga konvergjenca e korrespondencës; seri numrash.

Ndër seritë funksionale, vendin më të rëndësishëm e zënë seritë e fuqisë.

Një seri fuqie është një seri

termat e të cilëve janë funksione të fuqisë të renditura në rritje të fuqive të plota jo negative x, A c0 , c 1 , c 2 , c n - vlera konstante. Numrat c1 , c 2 , c n - koeficientët e termave të serisë, c0 - anëtar i lirë. Termat e serisë së fuqisë përcaktohen në të gjithë vijën numerike.

Le të njihemi me konceptin zonat e konvergjencës së serisë së fuqisë. Ky është një grup vlerash të ndryshueshme x, për të cilën seria konvergon. Seritë e fuqisë kanë një rajon konvergjence mjaft të thjeshtë. Për vlerat reale të ndryshoreve x rajoni i konvergjencës përbëhet ose nga një pikë, ose është një interval i caktuar (intervali i konvergjencës), ose përkon me të gjithë boshtin kau .

Kur zëvendësoni vlerat në serinë e fuqisë x= 0 do të rezultojë në një seri numrash

c0 +0+0+...+0+... ,

e cila konvergon.

Prandaj, kur x= 0 çdo seri fuqie konvergon dhe, për rrjedhojë, zona e saj e konvergjencës nuk mund të jetë grupi bosh. Struktura e rajonit të konvergjencës së të gjitha serive të fuqisë është e njëjtë. Mund të përcaktohet duke përdorur teoremën e mëposhtme.

Teorema 1 (teorema e Abelit). Nëse një seri fuqie konvergon në një vlerë x = x 0 , ndryshe nga zero, atëherë ajo konvergon, dhe, për më tepër, absolutisht, për të gjitha vlerat |x| < |x 0 | . Ju lutemi vini re: si vlera fillestare "X është zero" dhe çdo vlerë e "X" që krahasohet me vlerën fillestare merren modul - pa marrë parasysh shenjën.

Pasoja. Nëse seritë e fuqisë ndryshojnë në një farë vlere x = x 1 , atëherë ai divergjent për të gjitha vlerat |x| > |x 1 | .

Siç e kemi zbuluar tashmë më herët, çdo seri e fuqisë konvergon në vlerë x= 0. Ka seri fuqie që konvergojnë vetëm kur x= 0 dhe divergojnë për vlera të tjera X. Duke e përjashtuar këtë rast nga shqyrtimi, supozojmë se seria e fuqisë konvergon në një vlerë x = x 0 , të ndryshme nga zero. Pastaj, sipas teoremës së Abelit, ajo konvergon në të gjitha pikat e intervalit ]-| x0 |, |x 0 |[ (një interval, kufijtë e majtë dhe të djathtë të të cilit janë vlerat x në të cilat konvergjon seria e fuqisë, e marrë me një shenjë minus dhe një shenjë plus, përkatësisht), simetrike në lidhje me origjinën.

Nëse seria e fuqisë divergon në një vlerë të caktuar x = x 1 , pastaj, bazuar në një konkluzion të teoremës së Abelit, ajo ndryshon në të gjitha pikat jashtë segmentit [-| x1 |, |x 1 |] . Nga kjo rrjedh se për çdo seri fuqie ekziston një interval simetrik në lidhje me origjinën, i quajtur intervali i konvergjencës , në çdo pikë të së cilës seria konvergjon, në kufijtë mund të konvergojë, ose mund të devijojë, dhe jo domosdoshmërisht në të njëjtën kohë, dhe jashtë segmentit seria divergjente. Numri R quhet rrezja e konvergjencës së serisë së fuqisë.

Në raste të veçanta intervali i konvergjencës së serisë së fuqisë mund të degjenerojë deri në një pikë (atëherë seria konvergjon vetëm kur x= 0 dhe konsiderohet se R= 0) ose përfaqësojnë të gjithë vijën numerike (atëherë seria konvergon në të gjitha pikat e drejtëzës numerike dhe supozohet se ).

Kështu, përcaktimi i rajonit të konvergjencës së një serie fuqie konsiston në përcaktimin e tij rrezja e konvergjencës R dhe studimi i konvergjencës së serisë në kufijtë e intervalit të konvergjencës (në ).

Teorema 2. Nëse të gjithë koeficientët e një serie fuqie, duke filluar nga një e caktuar, janë të ndryshëm nga zero, atëherë rrezja e saj e konvergjencës është e barabartë me kufirin në raportin e vlerave absolute të koeficientëve të anëtarëve të zakonshëm vijues të serisë. , d.m.th.

Shembulli 1. Gjeni rajonin e konvergjencës së serisë së fuqisë

Zgjidhje. Këtu

Duke përdorur formulën (28), gjejmë rrezen e konvergjencës së kësaj serie:

Le të studiojmë konvergjencën e serisë në skajet e intervalit të konvergjencës. Shembulli 13 tregon se kjo seri konvergon në x= 1 dhe ndryshon në x= -1. Rrjedhimisht, rajoni i konvergjencës është gjysmë-intervali.

Shembulli 2. Gjeni rajonin e konvergjencës së serisë së fuqisë

Zgjidhje. Koeficientët e serisë janë pozitivë, dhe

Le të gjejmë kufirin e këtij raporti, d.m.th. rrezja e konvergjencës së serisë së fuqisë:

Le të studiojmë konvergjencën e serisë në skajet e intervalit. Zëvendësimi i vlerave x= -1/5 dhe x= 1/5 në këtë rresht jep:

E para nga këto seri konvergon (shih Shembullin 5). Por më pas, në bazë të teoremës në seksionin "Konvergjenca absolute", seria e dytë gjithashtu konvergjon, dhe rajoni i konvergjencës së saj është segmenti

Shembulli 3. Gjeni rajonin e konvergjencës së serisë së fuqisë

Zgjidhje. Këtu

Duke përdorur formulën (28) gjejmë rrezen e konvergjencës së serisë:

Le të studiojmë konvergjencën e serisë për vlerat e . Duke i zëvendësuar ato në këtë seri, ne përkatësisht marrim

Të dyja seritë ndryshojnë sepse kushti i nevojshëm për konvergjencë nuk plotësohet (termat e tyre të përbashkët nuk priren në zero në ). Pra, në të dy skajet e intervalit të konvergjencës, kjo seri divergjent, dhe rajoni i konvergjencës së saj është intervali.

Shembulli 5. Gjeni rajonin e konvergjencës së serisë së fuqisë

Zgjidhje. Gjejmë relacionin ku , dhe :

Sipas formulës (28), rrezja e konvergjencës së kësaj serie

domethënë, seria konvergjon vetëm kur x= 0 dhe divergjent për vlera të tjera X.

Shembujt tregojnë se në skajet e intervalit të konvergjencës seritë sillen ndryshe. Në shembullin 1, në njërin skaj të intervalit të konvergjencës, seria konvergjon, në shembullin 2, ajo konvergjon në të dy skajet;

Formula për rrezen e konvergjencës së një serie fuqie merret me supozimin se të gjithë koeficientët e termave të serisë, duke filluar nga një pikë e caktuar, janë të ndryshëm nga zero. Prandaj, përdorimi i formulës (28) lejohet vetëm në këto raste. Nëse ky kusht shkelet, atëherë rrezja e konvergjencës së serisë së fuqisë duhet të kërkohet duke përdorur Shenja e d'Alembert, ose, duke zëvendësuar variablin, duke e transformuar serinë në një formë në të cilën plotësohet kushti i specifikuar.

Shembulli 6. Gjeni intervalin e konvergjencës së serisë së fuqisë

Zgjidhje. Kjo seri nuk përmban terma me shkallë tek X. Prandaj, ne transformojmë serinë, duke vendosur . Pastaj marrim serinë

për të gjetur rrezen e konvergjencës së së cilës mund të zbatojmë formulën (28). Meqenëse , a , atëherë rrezja e konvergjencës së kësaj serie

Nga barazia që marrim, pra, kjo seri konvergon në intervalin .

Shuma e serive të fuqisë. Diferencimi dhe integrimi i serive të fuqisë

Le për serinë e fuqisë

rrezja e konvergjencës R> 0, d.m.th. kjo seri konvergon në intervalin .

Pastaj çdo vlerë X nga intervali i konvergjencës korrespondon një shumë e caktuar e serisë. Prandaj, shuma e serisë së fuqisë është një funksion i X në intervalin e konvergjencës. Duke e shënuar me f(x), mund të shkruajmë barazinë

duke e kuptuar në kuptimin që shuma e serisë në çdo pikë X nga intervali i konvergjencës është i barabartë me vlerën e funksionit f(x) në këtë pikë. Në të njëjtin kuptim, do të themi se seria e fuqisë (29) konvergon me funksionin f(x) në intervalin e konvergjencës.

Jashtë intervalit të konvergjencës, barazia (30) nuk ka kuptim.

Shembulli 7. Gjeni shumën e serisë së fuqisë

Zgjidhje. Kjo është një seri gjeometrike për të cilën a= 1, a q= x. Prandaj, shuma e tij është një funksion . Një seri konvergjon nëse , dhe është intervali i saj i konvergjencës. Prandaj barazia

është e vlefshme vetëm për vlerat, edhe pse funksioni të përcaktuara për të gjitha vlerat X, përveç X= 1.

Mund të vërtetohet se shuma e serisë së fuqisë f(x) është i vazhdueshëm dhe i diferencueshëm në çdo interval brenda intervalit të konvergjencës, veçanërisht në çdo pikë të intervalit të konvergjencës së serisë.

Le të paraqesim teorema mbi diferencimin term pas termi dhe integrimin e serive të fuqisë.

Teorema 1. Seritë e fuqisë (30) në intervalin e konvergjencës së saj mund të diferencohen term pas termi një numër të pakufizuar herë, dhe seritë e fuqisë që rezultojnë kanë të njëjtën rreze konvergjence si seria origjinale, dhe shumat e tyre janë përkatësisht të barabarta me .

Teorema 2. Seritë e fuqisë (30) mund të integrohen term pas termi një numër të pakufizuar herë në intervalin nga 0 në X, nëse , dhe seria e fuqisë që rezulton ka të njëjtën rreze konvergjence si seria origjinale, dhe shumat e tyre janë përkatësisht të barabarta

Zgjerimi i funksioneve në seritë e fuqisë

Le të jepet funksioni f(x), e cila duhet të zgjerohet në një seri fuqie, d.m.th. përfaqësojnë në formën (30):

Detyra është të përcaktohen koeficientët rreshti (30). Për ta bërë këtë, duke diferencuar barazinë (30) term pas termi, gjejmë vazhdimisht:

……………………………………………….. (31)

Duke supozuar në barazitë (30) dhe (31) X= 0, gjejmë

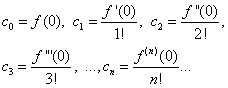
Duke zëvendësuar shprehjet e gjetura në barazi (30), marrim

(32)

Le të gjejmë zgjerimin e serisë Maclaurin të disa funksioneve elementare.

Shembulli 8. Zgjero funksionin në një seri Maclaurin

Zgjidhje. Derivatet e këtij funksioni përkojnë me vetë funksionin:

Prandaj, kur X= 0 kemi

Duke zëvendësuar këto vlera në formulën (32), marrim zgjerimin e dëshiruar:

(33)

Kjo seri konvergon në të gjithë vijën numerike (rrezja e saj e konvergjencës).

Shembulli 1. Gjeni rajonin e konvergjencës së serisë së fuqisë:

A) ; b) ;

V) ; G)
;

d)
.

A) Le të gjejmë rrezen e konvergjencës R. Sepse
,
, Kjo

x
, pra intervali i konvergjencës së serisë
.

Në
marrim një seri numrash . Kjo seri konvergon sepse është një seri harmonike e përgjithësuar në
.

Në
marrim një seri numrash
. Kjo seri është absolutisht konvergjente, pasi një seri e përbërë nga vlerat absolute të termave të saj , konvergjente.

b) Le të gjejmë rrezen e konvergjencës R. Sepse
, Kjo
.

Pra, intervali i konvergjencës së serisë
.

Ne shqyrtojmë konvergjencën e kësaj serie në skajet e intervalit të konvergjencës.

Në
kemi një seri numrash

.

Në
kemi një seri numrash
. Kjo seri është divergjente sepse
nuk ekziston.

Pra, rajoni i konvergjencës së kësaj serie
.

V) Le të gjejmë rrezen e konvergjencës R. Sepse
,
Se
.

Pra, intervali i konvergjencës
. Rajoni i konvergjencës së kësaj serie përkon me intervalin e konvergjencës, domethënë, seria konvergjon për çdo vlerë të ndryshores x.

G) Le të gjejmë rrezen e konvergjencës R. Sepse
,
Se
.

Sepse
, atëherë seria konvergon vetëm në pikën
. Kjo do të thotë se rajoni i konvergjencës së kësaj serie është një pikë
.

d) Le të gjejmë rrezen e konvergjencës R.

Sepse
,
, Kjo

Pra, seriali konvergon për absolutisht të gjithë x, duke kënaqur pabarazinë
, kjo eshte
.

Nga këtu
- intervali i konvergjencës,
− rrezja e konvergjencës.

Le të shqyrtojmë këtë seri për konvergjencë në skajet e intervalit të konvergjencës.

Në
marrim një seri numrash

e cila divergon (seri harmonike).

Në
marrim një seri numrash
, e cila konvergon me kusht (seri konvergon sipas kriterit të Leibniz-it dhe seria e përbërë nga vlerat absolute të anëtarëve të saj divergon, pasi është harmonike).

Pra, rajoni i konvergjencës së serisë
.

2.3. Seritë Taylor dhe Maclaurin.

Zgjerimi i funksioneve në seritë e fuqisë.

Zbatimi i serive të fuqisë për llogaritjet e përafërta

Shembuj të zgjidhjes së problemeve

Shembulli 1. Zgjero funksionin në një seri fuqie:

A)
; b)
;

V)
; G)
.

A) Zëvendësimi në formulë
x në
, marrim zgjerimin e dëshiruar:

b) Zëvendësimi në barazi

Ku
x në
, marrim zgjerimin e dëshiruar:

V) Ky funksion mund të shkruhet kështu:
. Për të gjetur serinë e dëshiruar, mjafton të zgjerohet

Ku
zëvendësues
. Pastaj marrim:

G) Ky funksion mund të rishkruhet kështu: .

Funksioni
mund të zgjerohet në një seri fuqie duke vendosur serinë binomiale
, do të marrim .

Ku
.

Për të marrë zgjerimin e dëshiruar, mjafton të shumëzoni serinë që rezulton (për shkak të konvergjencës absolute të këtyre serive).

Prandaj,

, Ku
.

Shembulli 2. Gjeni vlerat e përafërta të këtyre funksioneve:

A)
me një saktësi prej 0.0001;

b)
me një saktësi prej 0.00001.

A) Sepse
, pastaj në zgjerimin e funksionit, ku
le të zëvendësojmë
:

ose

Sepse
, atëherë saktësia e kërkuar do të sigurohet nëse kufizohemi vetëm në dy termat e parë të zgjerimit që rezulton.

Ne përdorim serinë binomiale

Ku
.

Duke besuar
Dhe
, marrim zgjerimin e mëposhtëm:

Nëse në serinë e fundit alternative merren parasysh vetëm dy termat e parë dhe pjesa tjetër hidhet poshtë, atëherë gabimi në llogaritje
nuk do të kalojë 0.000006 në vlerë absolute. Pastaj gabimi në llogaritje
nuk do ta kalojë numrin. Prandaj,

Shembulli 3. Llogaritni me 0,001 më të afërt:

A)
; b)
.

A)
.

Le ta zgjerojmë integrimin në një seri fuqie. Për ta bërë këtë, le të zëvendësojmë në serinë binomiale
dhe zëvendësoni x në :

Që nga segmenti i integrimit
i përket rajonit të konvergjencës së serisë që rezulton
, atëherë ne do të integrojmë term pas termi brenda kufijve të specifikuar:

Në serinë rezultuese të shenjave alternative, termi i katërt është më pak se 0,001 në vlerë absolute. Rrjedhimisht, saktësia e kërkuar do të sigurohet nëse merren parasysh vetëm tre termat e parë të serisë.

Meqenëse i pari nga termat e hedhur ka një shenjë minus, vlera e përafërt që rezulton do të jetë e tepërt. Prandaj, përgjigja për brenda 0.001 është 0.487.

b) Le të paraqesim së pari integrandin si një seri fuqie. Le të zëvendësojmë në zgjerimin e funksionit

x në
, marrim:

Pastaj
.

Seria e alternuar që rezulton plotëson kushtet e kriterit të Leibniz-it. Termi i katërt i serisë është më pak se 0,001 në vlerë absolute. Për të siguruar saktësinë e kërkuar, mjafton të gjesh shumën e tre termave të parë.

Prandaj,
.

Seri funksionale. Seritë e fuqisë.
Gama e konvergjencës së serisë

E qeshura pa asnjë arsye është një shenjë e d'Alembert

Ka rënë ora e gradave funksionale. Për të zotëruar me sukses temën, dhe, veçanërisht, këtë mësim, duhet të keni një kuptim të mirë të serive të numrave të zakonshëm. Ju duhet të kuptoni mirë se çfarë është një seri dhe të jeni në gjendje të aplikoni kritere krahasimi për të ekzaminuar seritë për konvergjencë. Kështu, nëse sapo keni filluar të studioni temën ose jeni fillestar në matematikën e lartë, e nevojshme Punoni tre mësime me radhë: Rreshtat për dummies,Shenja e D'Alembert. Shenjat e Cauchy Dhe Rreshta të alternuara. Testi i Leibniz-it. Patjetër që të tre! Nëse keni njohuri dhe aftësi themelore në zgjidhjen e problemeve me seritë e numrave, atëherë përballja me seritë funksionale do të jetë mjaft e thjeshtë, pasi nuk ka shumë materiale të reja.

Në këtë mësim, ne do të shikojmë konceptin e një serie funksionale (çfarë është ajo), do të njihemi me seritë e fuqisë, të cilat gjenden në 90% të detyrave praktike dhe do të mësojmë se si të zgjidhim një problem tipik të zakonshëm të gjetjes së rrezes. e konvergjencës, intervalit të konvergjencës dhe rajonit të konvergjencës së një serie fuqie. Tjetra, unë rekomandoj të shqyrtoni materialin rreth zgjerimi i funksioneve në seritë e fuqisë, dhe ndihma e parë do t'i jepet fillestarit. Pasi marrim pak frymë, kalojmë në nivelin tjetër:

Gjithashtu në seksionin e serive funksionale ka shumë prej tyre aplikacione për llogaritjen e përafërt, dhe në një farë mënyre dallohen Seritë Fourier, të cilave, si rregull, u jepet një kapitull i veçantë në literaturën arsimore. Unë kam vetëm një artikull, por është i gjatë dhe ka shumë, shumë shembuj shtesë!

Pra, pikat e referimit janë vendosur, le të shkojmë:

Koncepti i serive funksionale dhe serive të fuqisë

Nëse kufiri rezulton të jetë pafundësi, atëherë edhe algoritmi i zgjidhjes përfundon punën e tij dhe ne i japim përgjigjen përfundimtare detyrës: "Seria konvergjon në " (ose në njërën "). Shih rastin nr. 3 të paragrafit të mëparshëm.

Nëse kufiri rezulton të jetë as zero dhe as pafundësi, atëherë kemi rastin më të zakonshëm në praktikën nr.1 - seria konvergon në një interval të caktuar.

Në këtë rast, kufiri është. Si të gjeni intervalin e konvergjencës së një serie? Ne përcaktojmë pabarazinë:

NË CDO detyre te ketij lloji në anën e majtë të pabarazisë duhet të jetë rezultat i llogaritjes së kufirit, dhe në anën e djathtë të pabarazisë - në mënyrë rigoroze njësi. Unë nuk do të shpjegoj saktësisht pse ekziston një pabarazi e tillë dhe pse ekziston një në të djathtë. Mësimet janë të orientuara praktikisht, dhe tashmë është shumë mirë që historitë e mia nuk e varën stafin mësimdhënës dhe disa teorema u bënë më të qarta.

Teknika e punës me një modul dhe zgjidhjes së pabarazive të dyfishta u diskutua në detaje në vitin e parë në artikull Funksioni Domain, por për lehtësi, do të përpiqem t'i komentoj të gjitha veprimet sa më hollësisht të jetë e mundur. Zgjerimi i pabarazisë me modulin sipas rregullës së shkollës . Në këtë rast:

Gjysma e rrugës ka përfunduar.

Në fazën e dytë, është e nevojshme të hetohet konvergjenca e serisë në skajet e intervalit të gjetur.

Së pari, marrim skajin e majtë të intervalit dhe e zëvendësojmë atë në serinë tonë të fuqisë:

Në

Ne kemi marrë një seri numrash dhe duhet ta shqyrtojmë për konvergjencë (një detyrë tashmë e njohur nga mësimet e mëparshme).

1) Seria është e alternuar.
2) – termat e serisë ulen në modul. Për më tepër, çdo anëtar tjetër i serisë është më i vogël se ai i mëparshmi në vlerë absolute: , që do të thotë se rënia është monotone.
Përfundim: seria konvergon.

Duke përdorur një seri të përbërë nga module, ne do të zbulojmë saktësisht se si:
– konvergon (seri “standarde” nga familja e serive harmonike të përgjithësuara).

Kështu, seria e numrave që rezulton konvergon absolutisht.

në – konvergon.

! po ju kujtoj se çdo seri pozitive konvergjente është gjithashtu absolutisht konvergjente.

Kështu, seria e fuqisë konvergon, dhe absolutisht, në të dy skajet e intervalit të gjetur.

Përgjigje: zona e konvergjencës së serisë së fuqisë në studim:

Një formë tjetër përgjigjeje ka të drejtën e jetës: Një seri konvergjon nëse

Ndonjëherë deklarata e problemit kërkon që ju të tregoni rrezen e konvergjencës. Është e qartë se në shembullin e konsideruar.

Shembulli 2

Gjeni rajonin e konvergjencës së serisë së fuqisë

Zgjidhja: gjejmë intervalin e konvergjencës së serisë duke përdorur Shenja e d'Alembert (por jo BY atribut! – një atribut i tillë nuk ekziston për seritë funksionale):

Seriali konvergon në

Majtas ne duhet të largohemi vetëm, kështu që ne i shumëzojmë të dyja anët e pabarazisë me 3:

– Seriali është i alternuar.
– – termat e serisë ulen në modul. Çdo anëtar tjetër i serisë është më i vogël se ai i mëparshmi në vlerë absolute: , që do të thotë se rënia është monotone.

Përfundim: seria konvergon.

Le ta shqyrtojmë atë për natyrën e konvergjencës:

Le ta krahasojmë këtë seri me një seri divergjente.
Ne përdorim kriterin e krahasimit kufizues:

Përftohet një numër i fundëm që është i ndryshëm nga zero, që do të thotë se seria divergon nga seria.

Kështu, seria konvergon me kusht.

2) Kur – divergjent (sipas asaj që është vërtetuar).

Përgjigje: Zona e konvergjencës së serisë së fuqisë në studim: . Kur seria konvergjon me kusht.

Në shembullin e konsideruar, rajoni i konvergjencës së serisë së fuqisë është një gjysmë interval, dhe në të gjitha pikat e intervalit seria e fuqisë konvergon absolutisht, dhe në atë pikë, siç doli - me kusht.

Shembulli 3

Gjeni intervalin e konvergjencës së serisë së fuqisë dhe hulumtoni konvergjencën e tij në skajet e intervalit të gjetur

Ky është një shembull që ju duhet ta zgjidhni vetë.

Le të shohim disa shembuj që janë të rrallë, por që ndodhin.

Shembulli 4

Gjeni zonën e konvergjencës së serisë:

Zgjidhja: Duke përdorur testin e d'Alembert gjejmë intervalin e konvergjencës së kësaj serie:

(1) Ne hartojmë raportin e anëtarit tjetër të serisë me atë të mëparshëm.

(2) Ne heqim qafe thyesën katërkatëshe.

(3) Sipas rregullit të veprimeve me fuqi, ne i vendosim kubet nën një fuqi të vetme. Në numërues zgjerojmë me zgjuarsi shkallën, d.m.th. E rregullojmë në atë mënyrë që në hapin tjetër të mund ta zvogëlojmë thyesën me . Ne i përshkruajmë faktorët në detaje.

(4) Nën kub, ne e ndajmë numëruesin me emëruesin term me term, duke treguar se . Në një pjesë zvogëlojmë gjithçka që mund të reduktohet. Ne e marrim faktorin përtej shenjës kufitare, ai mund të hiqet, pasi nuk ka asgjë në të që varet nga ndryshorja "dinamike" "en". Ju lutemi vini re se shenja e modulit nuk është tërhequr - për arsye se merr vlera jo negative për çdo "x".

Në kufi, fitohet zero, që do të thotë se mund të japim përgjigjen përfundimtare:

Përgjigje: Seriali konvergon në

Por në fillim u duk se kjo rresht me "mbushjen e tmerrshme" do të ishte e vështirë për t'u zgjidhur. Zero ose pafundësia në kufi është pothuajse një dhuratë, sepse zgjidhja është zvogëluar dukshëm!

Shembulli 5

Gjeni zonën e konvergjencës së serisë

Ky është një shembull që ju duhet ta zgjidhni vetë. Kujdes;-) Zgjidhja e plotë është në fund të mësimit.

Le të shohim disa shembuj të tjerë që përmbajnë një element risie për sa i përket përdorimit të teknikave teknike.

Shembulli 6

Gjeni intervalin e konvergjencës së serisë dhe hulumtoni konvergjencën e saj në skajet e intervalit të gjetur

Zgjidhja: Termi i zakonshëm i serisë së fuqisë përfshin një faktor që siguron alternimin e shenjave. Algoritmi i zgjidhjes ruhet plotësisht, por kur hartojmë kufirin, ne e injorojmë (nuk e shkruajmë) këtë faktor, pasi moduli shkatërron të gjitha "minuset".

Ne gjejmë intervalin e konvergjencës së serisë duke përdorur testin e d'Alembert:

Le të krijojmë një pabarazi standarde:
Seriali konvergon në
Majtas ne duhet të largohemi vetëm modul, kështu që ne i shumëzojmë të dyja anët e pabarazisë me 5:

Tani e hapim modulin në një mënyrë të njohur:

Në mes të pabarazisë së dyfishtë, ju duhet të lini vetëm "X" për këtë qëllim, ne zbresim 2 nga secila pjesë e pabarazisë:

– intervali i konvergjencës së serisë së fuqisë në studim.

Ne hetojmë konvergjencën e serisë në skajet e intervalit të gjetur:

1) Zëvendësoni vlerën në serinë tonë të fuqisë :

Jini jashtëzakonisht të kujdesshëm, shumëzuesi nuk ofron alternim të shenjave për asnjë "en" natyral. Ne e marrim minusin që rezulton jashtë serisë dhe e harrojmë atë, pasi ai (si çdo konstante faktori) nuk ndikon në asnjë mënyrë në konvergjencën ose divergjencën e serisë së numrave.

Ju lutemi vini re përsëri që gjatë zëvendësimit të vlerës në termin e përgjithshëm të serisë së fuqisë, faktori ynë u zvogëlua. Nëse kjo nuk do të ndodhte, do të thoshte që ne ose e kemi llogaritur gabim kufirin ose e kemi zgjeruar gabim modulin.

Pra, duhet të shqyrtojmë seritë e numrave për konvergjencë. Këtu mënyra më e lehtë është përdorimi i kriterit të krahasimit kufizues dhe krahasimi i kësaj serie me një seri harmonike divergjente. Por, të jem i sinqertë, jam tmerrësisht i lodhur nga shenja kufizuese e krahasimit, kështu që do t'i shtoj një larmi zgjidhjes.

Pra, seria konvergon në

Ne i shumëzojmë të dyja anët e pabarazisë me 9:

Ne nxjerrim rrënjën nga të dy pjesët, duke kujtuar shakanë e shkollës së vjetër:

Zgjerimi i modulit:

dhe shtoni një në të gjitha pjesët:

– intervali i konvergjencës së serisë së fuqisë në studim.

Le të hetojmë konvergjencën e serisë së fuqisë në skajet e intervalit të gjetur:

1) Nëse , atëherë fitohet seria e mëposhtme e numrave: