Leksioni 3. Teorema të përgjithshme të dinamikës
Dinamika e një sistemi pikash materialeështë një degë e rëndësishme e mekanikës teorike. Këtu kryesisht shqyrtojmë problemet në lidhje me lëvizjen e sistemeve mekanike (sistemet e pikave materiale) me një numër të kufizuar të shkallëve të lirisë - numri maksimal i parametrave të pavarur që përcaktojnë pozicionin e sistemit. Detyra kryesore e dinamikës së sistemit është studimi i ligjeve të lëvizjes së një trupi të ngurtë dhe sistemeve mekanike.
Qasja më e thjeshtë për të studiuar lëvizjen e një sistemi, që përbëhet nga N pikat materiale, zbret në marrjen në konsideratë të lëvizjeve të çdo pike individuale të sistemit. Në këtë rast, duhet të përcaktohen të gjitha forcat që veprojnë në secilën pikë të sistemit, duke përfshirë forcat e ndërveprimit midis pikave.
Duke përcaktuar nxitimin e secilës pikë në përputhje me ligjin e dytë të Njutonit (1.2), marrim për secilën pikë tre ligje diferenciale skalare të lëvizjes të rendit të dytë, d.m.th. 3 N ligjet diferenciale të lëvizjes për të gjithë sistemin.
Për të gjetur ekuacionet e lëvizjes së një sistemi mekanik bazuar në forcat e dhëna dhe kushtet fillestare për secilën pikë të sistemit, ligjet diferenciale që rezultojnë duhet të integrohen. Ky problem është i vështirë edhe në rastin e dy pikave materiale që lëvizin vetëm nën ndikimin e forcave të ndërveprimit sipas ligjit të tërheqjes universale (problemi me dy trupa), dhe jashtëzakonisht i vështirë në rastin e tre pikave ndërvepruese (problemi me tre trupa ).
Prandaj, është e nevojshme të gjenden metoda për zgjidhjen e problemeve që do të çonin në ekuacione të zgjidhshme dhe do të jepnin një ide të lëvizjes së një sistemi mekanik. Teoremat e përgjithshme të dinamikës, duke qenë pasojë e ligjeve diferenciale të lëvizjes, na lejojnë të shmangim kompleksitetin që lind gjatë integrimit dhe të marrim rezultatet e nevojshme.
3. 1. Shënime të përgjithshme
Pikat e sistemit mekanik do t'i numërojmë me indekse i, j, k etj., të cilat përshkojnë të gjitha vlerat 1, 2, 3… N, Ku N – numri i pikave të sistemit. Sasitë fizike që lidhen me k pikat përcaktohen me të njëjtin indeks si pika. Për shembull, shprehni vektorin e rrezes dhe shpejtësinë, përkatësisht k pika e th.
Mbi çdo pikë të sistemit veprojnë forca me dy origjinë: së pari, forcat burimet e të cilave ndodhen jashtë sistemit, të quajtura e jashtme forcat dhe të caktuar ; së dyti, forcat nga pika të tjera të një sistemi të caktuar, të quajtura e brendshme forcat dhe të caktuar . Forcat e brendshme plotësojnë ligjin e tretë të Njutonit. Le të shqyrtojmë vetitë më të thjeshta të forcave të brendshme që veprojnë në të gjithë sistemin mekanik në çdo gjendje.
Prona e parë. Shuma gjeometrike e të gjitha forcave të brendshme të sistemit (vektori kryesor i forcave të brendshme) është e barabartë me zero.
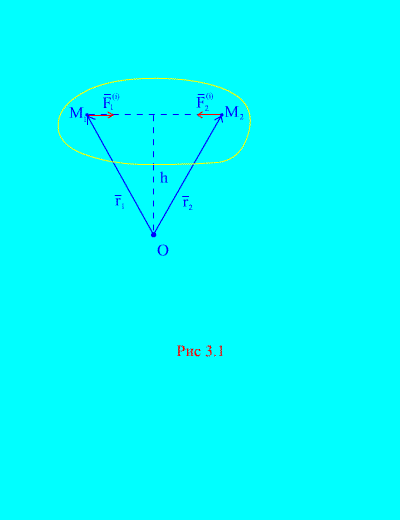
Në të vërtetë, nëse marrim parasysh dy pika arbitrare të sistemit, për shembull dhe (Fig. 3.1), pastaj për ta ![]() , sepse forcat e veprimit dhe të reagimit janë gjithmonë të barabarta në madhësi, duke vepruar përgjatë një linje veprimi në drejtim të kundërt, i cili lidh pikat ndërvepruese. Prandaj, vektori kryesor i forcave të brendshme përbëhet nga çifte forcash të pikave ndërvepruese
, sepse forcat e veprimit dhe të reagimit janë gjithmonë të barabarta në madhësi, duke vepruar përgjatë një linje veprimi në drejtim të kundërt, i cili lidh pikat ndërvepruese. Prandaj, vektori kryesor i forcave të brendshme përbëhet nga çifte forcash të pikave ndërvepruese
![]() (3.1)
(3.1)
Prona e dytë. Shuma gjeometrike e momenteve të të gjitha forcave të brendshme në lidhje me një pikë arbitrare në hapësirë është e barabartë me zero.
Le të shqyrtojmë një sistem momentesh forcash dhe në lidhje me pikën RRETH(Fig. 3.1). Nga (Fig. 3.1). është e qartë se
![]() ,
,
sepse të dyja forcat kanë krahë të njëjtë dhe drejtime të kundërta të momenteve vektoriale. Momenti kryesor i forcave të brendshme në lidhje me një pikë RRETH përbëhet nga shuma vektoriale e shprehjeve të tilla dhe është e barabartë me zero. Prandaj,
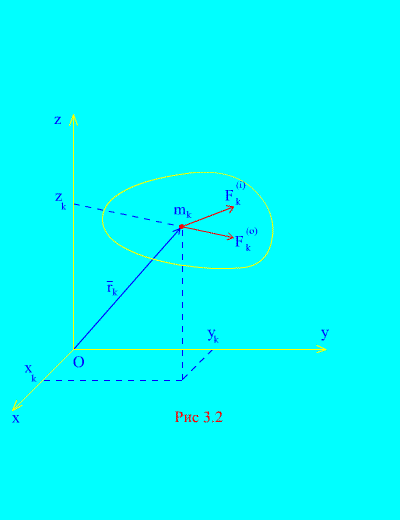
Lërini forcat e jashtme dhe të brendshme që veprojnë në një sistem mekanik të përbërë nga N pikë (Fig. 3.2). Nëse rezultanta e forcave të jashtme dhe rezultanta e të gjitha forcave të brendshme zbatohen në secilën pikë të sistemit, atëherë për çdo k Në pikën e sistemit, mund të hartohen ekuacione diferenciale të lëvizjes. Do të ketë një total të ekuacioneve të tilla N:
dhe në projeksione në akset e koordinatave fikse 3 N:
![]() (3.4)
(3.4)
Ekuacionet vektoriale (3.3) ose ekuacionet skalare ekuivalente (3.4) paraqesin ligjet diferenciale të lëvizjes së pikave materiale të të gjithë sistemit. Nëse të gjitha pikat lëvizin paralelisht me një rrafsh ose një drejtëz, atëherë numri i ekuacioneve (3.4) në rastin e parë do të jetë 2 N, në të dytën N.

Shembulli 1. Dy masa janë të lidhura me njëra-tjetrën nga një kabllo e pazgjatur e hedhur mbi një bllok (Fig. 3.3). Neglizhimi i forcave të fërkimit, si dhe masa e bllokut dhe kabllit, përcaktojnë ligjin e lëvizjes së ngarkesave dhe tensionin e kabllit.
Zgjidhje. Sistemi përbëhet nga dy trupa materialë (të lidhur me një kabllo të pazgjatur) që lëvizin paralelisht me të njëjtin bosht. X. Le të shkruajmë ligjet diferenciale të lëvizjes në projeksione në bosht X për çdo trup.
Lëreni peshën e duhur të bjerë me nxitim, atëherë pesha e majtë do të rritet me nxitim. Ne çlirohemi mendërisht nga lidhja (kabllo) dhe e zëvendësojmë atë me reagime dhe (Fig. 3.3). Duke i konsideruar trupat si të lirë, le të hartojmë ligjet diferenciale të lëvizjes në projeksion mbi bosht X(që do të thotë se tensionet e fillit janë forca të brendshme, dhe pesha e ngarkesave janë të jashtme):
Meqenëse dhe (trupat janë të lidhur me një kabllo të pazgjatur), marrim
Zgjidhja e këtyre ekuacioneve për nxitimin dhe tensionin e kabllit T, marrim
 .
.
Vini re se tensioni në kabllo nuk është i barabartë me forcën e gravitetit të ngarkesës përkatëse.
3. 2. Teorema mbi lëvizjen e qendrës së masës
Dihet se një trup i ngurtë dhe një sistem mekanik në një aeroplan mund të lëvizin mjaft komplekse. Teorema e parë mbi lëvizjen e një trupi dhe një sistemi mekanik mund të arrihet si më poshtë: hidhni një k.-l. një objekt i përbërë nga shumë trupa të ngurtë të lidhur së bashku. Është e qartë se ai do të fluturojë në një parabolë. Kjo u zbulua gjatë studimit të lëvizjes së pikës. Megjithatë, tani objekti nuk është një pikë. Ai kthehet dhe lëkundet gjatë fluturimit të tij rreth një qendre efektive që lëviz në një parabolë. Teorema e parë për lëvizjen e objekteve komplekse thotë se një qendër e caktuar efektive është qendra e masës së një objekti në lëvizje. Qendra e masës nuk është domosdoshmërisht e vendosur në vetë trupin, ajo mund të shtrihet diku jashtë tij.
Teorema. Qendra e masës së një sistemi mekanik lëviz si një pikë materiale me një masë të barabartë me masën e të gjithë sistemit, në të cilën zbatohen të gjitha forcat e jashtme që veprojnë në sistem.
Për të vërtetuar teoremën, ne rishkruajmë ligjet diferenciale të lëvizjes (3.3) në formën e mëposhtme:
![]() (3.5)
(3.5)
Ku N – numri i pikave të sistemit.
Le të mbledhim ekuacionet së bashku term pas termi:
 (A)
(A)
Pozicioni i qendrës së masës së sistemit mekanik në lidhje me sistemin e zgjedhur të koordinatave përcaktohet me formulën (2.1):  Ku M– masa e sistemit. Atëherë do të shkruhet ana e majtë e barazisë (a).
Ku M– masa e sistemit. Atëherë do të shkruhet ana e majtë e barazisë (a).
Shuma e parë në anën e djathtë të barazisë (a) është e barabartë me vektorin kryesor të forcave të jashtme, dhe e fundit, nga vetia e forcave të brendshme, është e barabartë me zero. Pastaj barazia (a), duke marrë parasysh (b), do të rishkruhet
![]() , (3.6)
, (3.6)
ato. produkti i masës së sistemit dhe nxitimi i qendrës së masës së tij është i barabartë me shumën gjeometrike të të gjitha forcave të jashtme që veprojnë në sistem.
Nga ekuacioni (3.6) rezulton se forcat e brendshme nuk ndikojnë drejtpërdrejt në lëvizjen e qendrës së masës. Megjithatë, në disa raste ato janë shkaku i shfaqjes së forcave të jashtme të aplikuara në sistem. Kështu, forcat e brendshme që lëvizin rrotat lëvizëse të një makine në rrotullim bëjnë që një forcë ngjitëse e jashtme e aplikuar në buzën e rrotës të veprojë mbi të.
Shembulli 2. Mekanizmi, i vendosur në një plan vertikal, është instaluar në një plan horizontal të lëmuar dhe i bashkangjitur me shufra të fiksuara fort në sipërfaqe TE Dhe L (Fig. 3.4).
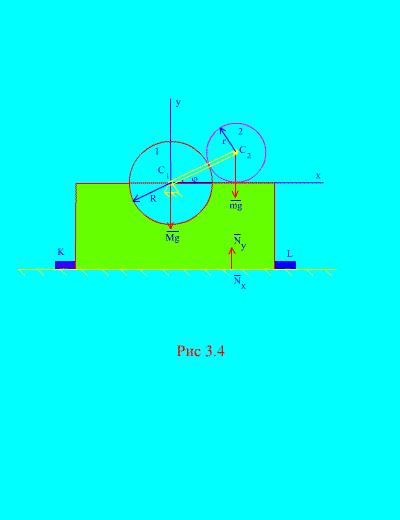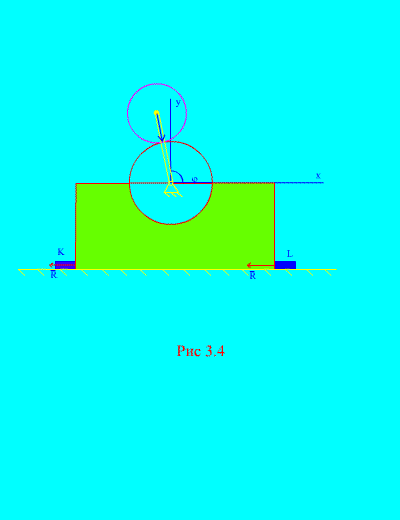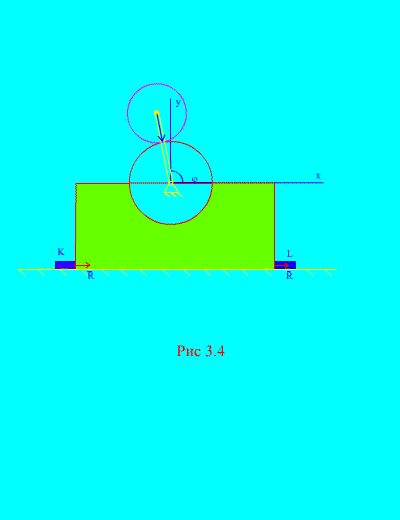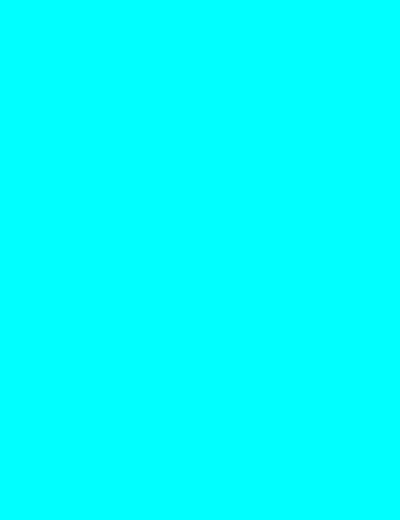
Rrezja e diskut 1 R i palëvizshëm. Masa e diskut 2 m dhe rreze r ngjitur në një manivë, gjatësi R+ r në pikën C 2. Manivari rrotullohet në një konstante
shpejtësi këndore. Në momentin fillestar, fiksimi zinte pozicionin e duhur horizontal. Duke neglizhuar masën e manivelit, përcaktoni forcat maksimale horizontale dhe vertikale që veprojnë në shufra nëse masa totale e kornizës dhe rrotës 1 është e barabartë me M. Konsideroni gjithashtu sjelljen e mekanizmit në mungesë të shufrave.
Zgjidhje. Sistemi përbëhet nga dy masa ( N=2 ): disku fiks 1 me kornizë dhe disku i lëvizshëm 2. Drejtoni boshtin në përmes qendrës së gravitetit të diskut të palëvizshëm vertikalisht lart, boshti X– përgjatë rrafshit horizontal.
Le të shkruajmë teoremën mbi lëvizjen e qendrës së masës (3.6) në formë koordinative
Forcat e jashtme të këtij sistemi janë: pesha e kornizës dhe disku fiks - Mg, pesha lëvizëse e diskut - mg, - reagimi total horizontal i bulonave, - reagimi total normal i avionit. Prandaj,
Më pas ligjet e lëvizjes (b) do të rishkruhen
Le të llogarisim koordinatat e qendrës së masës së sistemit mekanik:
 ; (G)
; (G)
siç shihet nga (Fig. 3.4), , , ![]() (këndi i fiksimit),
(këndi i fiksimit), ![]() . Zëvendësimi i këtyre shprehjeve në (d) dhe llogaritja e derivateve të dytë në lidhje me kohën t nga , , ne e marrim atë
. Zëvendësimi i këtyre shprehjeve në (d) dhe llogaritja e derivateve të dytë në lidhje me kohën t nga , , ne e marrim atë
 (d)
(d)
Duke zëvendësuar (c) dhe (e) në (b), gjejmë

Presioni horizontal që vepron në shufra është më i madh dhe më i vogël kur cos = 1 në përputhje me rrethanat, d.m.th.
![]()
![]()
Presioni i mekanizmit në planin horizontal ka vlerat më të larta dhe më të ulëta kur mëkat në përputhje me rrethanat, d.m.th.
![]()
![]()
Në fakt, problemi i parë i dinamikës është zgjidhur: sipas ekuacioneve të njohura të lëvizjes së qendrës së masës së sistemit (d), forcat e përfshira në lëvizje rikthehen.
Në mungesë të hekurave K Dhe L (Fig. 3.4), mekanizmi mund të fillojë të kërcejë mbi planin horizontal. Kjo do të ndodhë kur, d.m.th. kur , rrjedh se shpejtësia këndore e rrotullimit të manivelit, në të cilën mekanizmi kërcehet, duhet të plotësojë barazinë
 .
.
3. 3. Ligji i ruajtjes së lëvizjes së qendrës së masës
Nëse vektori kryesor i forcave të jashtme që veprojnë në sistem është i barabartë me zero, d.m.th. , pastaj nga(3.6)rrjedh se nxitimi i qendrës së masës është zero, prandaj, shpejtësia e qendrës së masës është konstante në madhësi dhe drejtim. Nëse, në veçanti, në momentin fillestar qendra e masës është në qetësi, atëherë ajo është në qetësi për të gjithë kohën ndërsa vektori kryesor i forcave të jashtme është i barabartë me zero.
Nga kjo teoremë rrjedhin disa përfundime.
· Vetëm forcat e brendshme nuk mund të ndryshojnë natyrën e lëvizjes së qendrës së masës së sistemit.
· Nëse vektori kryesor i forcave të jashtme që veprojnë në sistem është zero, atëherë qendra e masës është në qetësi ose lëviz në mënyrë të njëtrajtshme dhe drejtvizore.
· Nëse projeksioni i vektorit kryesor të forcave të jashtme të sistemit në një bosht të caktuar fiks është i barabartë me zero, atëherë projeksioni i shpejtësisë së qendrës së masës së sistemit në këtë bosht nuk ndryshon.
· Një palë forcash të aplikuara në një trup të ngurtë nuk mund të ndryshojnë lëvizjen e qendrës së masës së tij (mund të bëjë që trupi të rrotullohet rreth qendrës së masës).
Le të shqyrtojmë një shembull që ilustron ligjin e ruajtjes së lëvizjes së qendrës së masës.

Shembulli 3. Dy masa janë të lidhura me një fije të pazgjatur të hedhur përmes një blloku (Fig. 3.5), fiksuar në një pykë me një masë M. Pyka mbështetet në një plan horizontal të lëmuar. Në momentin fillestar sistemi ishte në qetësi. Gjeni zhvendosjen e pykës përgjatë rrafshit kur ngarkesa e parë ulet në një lartësi N. Neglizhoni masën e bllokut dhe fillit.
Zgjidhje. Forcat e jashtme që veprojnë në pykë së bashku me ngarkesat janë graviteti, dhe Mg, si dhe reagimi normal i një sipërfaqeje të lëmuar horizontale N. Për rrjedhojë,
Meqenëse në momentin fillestar sistemi ishte në qetësi, ne kemi .
Le të llogarisim koordinatat e qendrës së masës së sistemit në dhe në moment t 1 kur ngarkesa peshon g do të zbresë në një lartësi H.
Për momentin:
 ,
,
Ku , , X– përkatësisht, koordinatat e qendrës së masës së ngarkesave që peshojnë g, g dhe një pykë që peshon Mg.
Le të supozojmë se pyka në momentin e kohës lëviz në drejtimin pozitiv të boshtit kau nga shuma L, nëse pesha e ngarkesës bie në një lartësi N. Pastaj, për momentin
sepse ngarkesat së bashku me pykën do të lëvizin në L në të djathtë, dhe ngarkesa do të lëvizë lart përgjatë pykës. Që , atëherë pas llogaritjeve marrim
 .
.
3.4. Sasia e lëvizjes së sistemit
3.4.1. Llogaritja e momentit të sistemit
Momenti i një pike materiale është një sasi vektoriale e barabartë me produktin e masës së pikës dhe vektorit të shpejtësisë së saj
Njësia e matjes së momentit -
Momenti i një sistemi mekanik është shuma vektoriale e momentit të pikave individuale të sistemit, d.m.th.
Ku N – numri i pikave të sistemit.
Momenti i një sistemi mekanik mund të shprehet me masën e sistemit M dhe shpejtësinë e qendrës së masës. Vërtet,
ato. Momenti i sistemit është i barabartë me produktin e masës së të gjithë sistemit dhe shpejtësinë e qendrës së tij të masës. Drejtimi është i njëjtë me drejtimin (Fig. 3.6)

Në projeksionet në akset drejtkëndore kemi
ku , , janë projeksionet e shpejtësisë së qendrës së masës së sistemit.
Këtu M– masa e sistemit mekanik; nuk ndryshon kur sistemi lëviz.
Këto rezultate janë veçanërisht të përshtatshme për t'u përdorur kur llogariten sasitë e lëvizjes së trupave të ngurtë.
Nga formula (3.7) është e qartë se nëse një sistem mekanik lëviz në atë mënyrë që qendra e masës së tij të mbetet e palëvizshme, atëherë momenti i sistemit mbetet i barabartë me zero.
3.4.2. Impuls elementar dhe me forcë të plotë
Veprimi i një force në një pikë materiale me kalimin e kohës dt mund të karakterizohet nga një impuls elementar. Impuls total i forcës me kalimin e kohës t, ose impuls i forcës, i përcaktuar nga formula
ose në projeksione mbi koordinatat e boshtit
 (3.8a)
(3.8a)
Njësia e impulsit të forcës është .
3.4.3. Teorema mbi ndryshimin e momentit të një sistemi
Le të zbatohen forcat e jashtme dhe të brendshme në pikat e sistemit. Më pas për çdo pikë të sistemit mund të zbatojmë ligjet diferenciale të lëvizjes (3.3), duke pasur parasysh se ![]() :
:
 .
.
Duke përmbledhur të gjitha pikat e sistemit, marrim
Nga vetia e forcave të brendshme dhe sipas përkufizimit ![]() ne kemi
ne kemi
 (3.9)
(3.9)
Duke shumëzuar të dyja anët e këtij ekuacioni me dt, marrim një teoremë mbi ndryshimin e momentit në formë diferenciale:
![]() , (3.10)
, (3.10)
ato. momenti diferencial i një sistemi mekanik është i barabartë me shumën vektoriale të impulseve elementare të të gjitha forcave të jashtme që veprojnë në pikat e sistemit mekanik.
Llogaritja e integralit të të dy anëve (3.10) me kalimin e kohës nga 0 në t, e marrim teoremën në formë të fundme ose integrale
 (3.11)
(3.11)
Në projeksionet mbi boshtet koordinative do të kemi
Ndryshimi në momentin e një sistemi mekanik me kalimin e kohëst, është e barabartë me shumën vektoriale të të gjitha impulseve të forcave të jashtme që veprojnë në pikat e sistemit mekanik gjatë së njëjtës kohë.
Shembulli 4. Pesha e ngarkesës m zbret në një plan të pjerrët nga prehja nën ndikimin e një force F, proporcionale me kohën: , ku (Fig. 3.7). Çfarë shpejtësie do të fitojë trupi më pas t sekonda pas fillimit të lëvizjes, nëse koeficienti i fërkimit të rrëshqitjes së ngarkesës në planin e pjerrët është i barabartë me f.
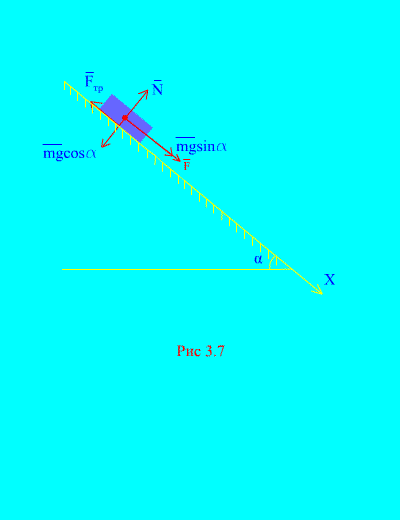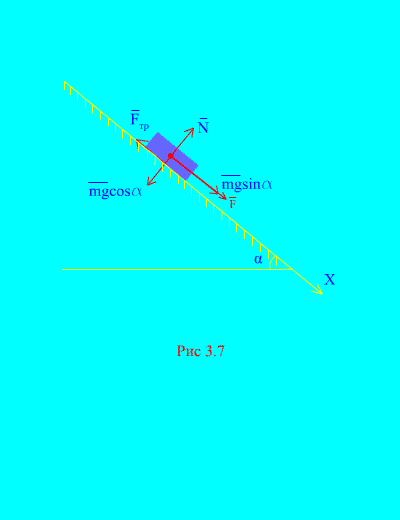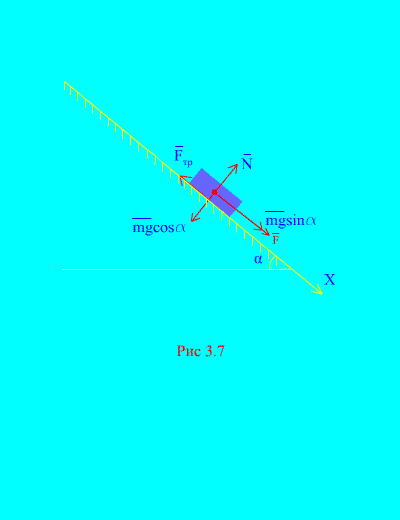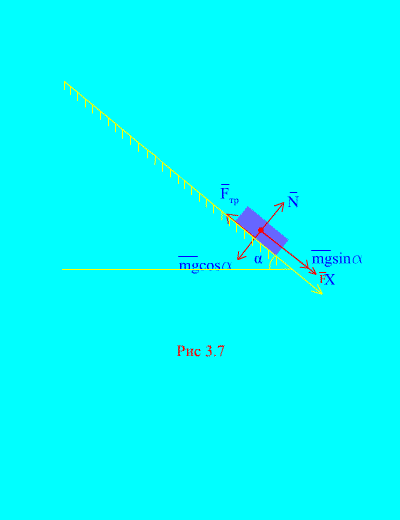
Zgjidhje. Le të përshkruajmë forcat e aplikuara në ngarkesë: mg - forca e gravitetit të ngarkesës, Nështë reaksioni normal i rrafshit, është forca e fërkimit rrëshqitës të ngarkesës në rrafsh dhe . Drejtimi i të gjitha forcave tregohet në (Fig. 3.7).
Le të drejtojmë boshtin X përgjatë rrafshit të pjerrët poshtë. Le të shkruajmë teoremën për ndryshimin e momentit (3.11) në projeksion mbi bosht X:
 (A)
(A)
Sipas kushtit, sepse në momentin fillestar të kohës ngarkesa ishte në qetësi. Shuma e projeksioneve të impulseve të të gjitha forcave në boshtin x është e barabartë me

Prandaj,
 ,
,
 .
.
3.4.4. Ligjet e ruajtjes së momentit
Ligjet e ruajtjes fitohen si raste të veçanta të teoremës për ndryshimin e momentit. Dy raste të veçanta janë të mundshme.
· Nëse shuma vektoriale e të gjitha forcave të jashtme të aplikuara në sistem është e barabartë me zero, d.m.th. , pastaj nga teorema rrjedh (3.9) , Çfarë ,
ato. nëse vektori kryesor i forcave të jashtme të sistemit është zero, atëherë sasia e lëvizjes së sistemit është konstante në madhësi dhe drejtim.
· Nëse projeksioni i vektorit kryesor të forcave të jashtme në çdo bosht koordinativ është i barabartë me zero, për shembull Ox, d.m.th. , atëherë projeksioni i momentit në këtë bosht është një vlerë konstante.
Le të shqyrtojmë një shembull të zbatimit të ligjit të ruajtjes së momentit.

Shembulli 5. Lavjerrësi balistik është një trup me një masë të varur në një fije të gjatë (Fig. 3.8).
Një plumb në masë, që lëviz me shpejtësi V dhe duke goditur një trup të palëvizshëm, ngec në të dhe trupi devijohet. Sa ishte shpejtësia e plumbit nëse trupi ngrihej në një lartësi h ?
Zgjidhje. Lëreni trupin me plumbin e mbërthyer të fitojë shpejtësi. Pastaj, duke përdorur ligjin e ruajtjes së momentit gjatë bashkëveprimit të dy trupave, mund të shkruajmë ![]() .
.
Shpejtësia mund të llogaritet duke përdorur ligjin e ruajtjes së energjisë mekanike  . Pastaj . Si rezultat ne gjejmë
. Pastaj . Si rezultat ne gjejmë
 .
.
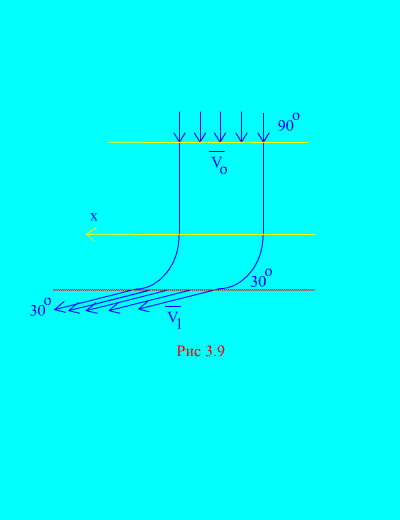
Shembulli 6. Uji hyn në një kanal të palëvizshëm (Fig. 3.9) seksion kryq i ndryshueshëm me shpejtësi në një kënd në horizontale; zona kryq seksionale e kanalit në hyrje; shpejtësia e ujit në dalje nga kanali bën një kënd me horizontin.
Përcaktoni përbërësin horizontal të reaksionit që ka uji në muret e kanalit. Dendësia e ujit  .
.
Zgjidhje. Do të përcaktojmë komponentin horizontal të reaksionit të ushtruar nga muret e kanalit në ujë. Kjo forcë është e barabartë në madhësi dhe e kundërt në shenjë me forcën e dëshiruar. Kemi, sipas (3.11a),
 . (A)
. (A)
Ne llogarisim masën e vëllimit të lëngut që hyn në kanal gjatë kohës t:
Vlera rAV 0 quhet masa e dytë - masa e lëngut që rrjedh nëpër çdo seksion të tubit për njësi të kohës.
E njëjta sasi uji largohet nga kanali në të njëjtën kohë. Shpejtësia fillestare dhe përfundimtare jepen në gjendje.
Le të llogarisim anën e djathtë të barazisë (a), e cila përcakton shumën e projeksioneve në boshtin horizontal të forcave të jashtme të aplikuara në sistem (uji). Forca e vetme horizontale është komponenti horizontal i reaksionit të murit që rezulton R x. Kjo forcë është konstante gjatë lëvizjes së qëndrueshme të ujit. Kjo është arsyeja pse
 . (V)
. (V)
Duke zëvendësuar (b) dhe (c) në (a), marrim
3.5. Momenti kinetik i sistemit
3.5.1. Momenti kryesor i momentit të sistemit

Le të jetë vektori i rrezes së një pike me masën e sistemit në lidhje me një pikë A, të quajtur qendër (Fig. 3.10).
Momenti i momentit (momenti kinetik) i një pike në lidhje me qendrën A quhet vektor , përcaktuar nga formula
![]() . (3.12)
. (3.12)
Në këtë rast, vektori drejtuar pingul me rrafshin që kalon nëpër qendër A dhe vektor .
Momenti i momentit (momenti kinetik) i një pike në raport me boshtin quhet projeksioni mbi këtë bosht i momentit të momentit të një pike në lidhje me çdo qendër të zgjedhur në këtë bosht.
Momenti kryesor i momentit (momenti kinetik) i sistemit në lidhje me qendrën A quhet sasi
 (3.13)
(3.13)
Momenti kryesor i momentit (momenti kinetik) i sistemit në lidhje me boshtin quhet projeksioni në këtë bosht i momentit kryesor të momentit të sistemit në lidhje me çdo të zgjedhur në këtë boshti qendror.
3.5.2. Momenti kinetik i një trupi të ngurtë rrotullues rreth boshtit të rrotullimit
Le të rreshtojmë pikën fikse RRETH trupi i shtrirë në boshtin e rrotullimit RRETHz, me origjinën e sistemit koordinativ Ohooz, boshtet e të cilit do të rrotullohen me trupin (Fig. 3.11). Lë të jetë vektori i rrezes së një pike të trupit në lidhje me origjinën e koordinatave projeksioni i tij në bosht do të shënohet me , , . Ne shënojmë projeksionet e vektorit të shpejtësisë këndore të trupit në të njëjtat boshte si 0, 0, ().
Le të shqyrtojmë lëvizjen e një sistemi të caktuar të objekteve materiale në lidhje me një sistem koordinativ fiks, atëherë ai mund të konsiderohet i lirë nëse i hedhim poshtë lidhjet e imponuara në sistem dhe e zëvendësojmë veprimin e tyre me reaksionet përkatëse.
Le t'i ndajmë të gjitha forcat e aplikuara në sistem në të jashtme dhe të brendshme; të dyja mund të përfshijnë reagime të të hedhura
lidhjet. Le të shënojmë dhe shënojmë vektorin kryesor dhe momentin kryesor të forcave të jashtme në lidhje me pikën A.
1. Teorema mbi ndryshimin e momentit. Nëse është sasia e lëvizjes së sistemit, atëherë (shih)
pra është e vlefshme teorema: derivati kohor i momentit të sistemit është i barabartë me vektorin kryesor të të gjitha forcave të jashtme.
Duke zëvendësuar vektorin përmes shprehjes së tij ku është masa e sistemit, është shpejtësia e qendrës së masës, ekuacionit (4.1) mund t'i jepet një formë tjetër:
Kjo barazi do të thotë që qendra e masës së sistemit lëviz si një pikë materiale masa e së cilës është e barabartë me masën e sistemit dhe ndaj së cilës zbatohet një forcë që gjeometrikisht është e barabartë me vektorin kryesor të të gjitha forcave të jashtme të sistemit. Pohimi i fundit quhet teorema mbi lëvizjen e qendrës së masës (qendrës së inercisë) të sistemit.
Nëse atëherë nga (4.1) del se vektori i momentit është konstant në madhësi dhe drejtim. Duke e projektuar atë në boshtin e koordinatave, marrim tre integrale të para skalare, ekuacione diferenciale të kapakut të dyfishtë të sistemit:
Këto integrale quhen integrale të momentit. Kur shpejtësia e qendrës së masës është konstante, domethënë lëviz në mënyrë të njëtrajtshme dhe drejtvizore.
Nëse projeksioni i vektorit kryesor të forcave të jashtme në çdo bosht, për shembull në një bosht, është i barabartë me zero, atëherë kemi një integral të parë, ose nëse dy projeksione të vektorit kryesor janë të barabarta me zero, atëherë ka dy integrale të momentit.
2. Teorema mbi ndryshimin e momentit këndor. Le të jetë A një pikë arbitrare në hapësirë (lëvizëse ose e palëvizshme), e cila nuk përkon domosdoshmërisht me ndonjë pikë specifike materiale të sistemit gjatë gjithë kohës së lëvizjes. Shpejtësinë e tij në një sistem koordinativ fiks e shënojmë me Teorema mbi ndryshimin e momentit kinetik të një sistemi material në raport me pikën A ka formën
![]()
Nëse pika A është fikse, atëherë barazia (4.3) merr një formë më të thjeshtë:
Kjo barazi shpreh teoremën për ndryshimin e momentit këndor të një sistemi në lidhje me një pikë fikse: derivati kohor i momentit këndor të sistemit, i llogaritur në lidhje me një pikë fikse, është i barabartë me momentin kryesor të të gjitha forcave të jashtme relative. deri në këtë pikë.
Nëse atëherë sipas (4.4) vektori i momentit këndor është konstant në madhësi dhe drejtim. Duke e projektuar atë në boshtet e koordinatave, marrim integralet e para skalare të ekuacioneve diferenciale të sistemit të dyfishtë:
Këto integrale quhen integrale të momentit ose integrale të zonës.
Nëse pika A përkon me qendrën e masës së sistemit, atëherë termi i parë në anën e djathtë të barazisë (4.3) zhduket dhe teorema mbi ndryshimin e momentit këndor ka të njëjtën formë shkrimi (4.4) si në rastin e një pikë fikse A. Vini re (shih. fq. 4 § 3), se në rastin në shqyrtim, momenti këndor absolut i sistemit në anën e majtë të barazisë (4.4) mund të zëvendësohet nga momenti këndor i barabartë i sistemit në lëvizjen e tij në raport me qendrën e masës.
Le të jetë një bosht konstant ose bosht i drejtimit konstant që kalon nëpër qendrën e masës së sistemit dhe le të jetë momenti kinetik i sistemit në lidhje me këtë bosht. Nga (4.4) rrjedh se
ku është momenti i forcave të jashtme në raport me boshtin. Nëse gjatë gjithë lëvizjes kemi integralin e parë
Në veprat e S.A. Chaplygin, u morën disa përgjithësime të teoremës mbi ndryshimin e momentit kinetik, të cilat më pas u aplikuan për të zgjidhur një numër problemesh në topat e rrotullimit. Përgjithësime të mëtejshme të teoremës mbi ndryshimin e momentit mekanik dhe aplikimet e tyre në problemet e dinamikës së trupit të ngurtë janë të përfshira në punime. Rezultatet kryesore të këtyre punimeve janë të lidhura me teoremën mbi ndryshimin e momentit kinetik në raport me një lëvizje, duke kaluar vazhdimisht nëpër një pikë lëvizëse A. Le të jetë një vektor njësi i drejtuar përgjatë këtij boshti. Duke shumëzuar shkallëzues me të dy anët e barazisë (4.3) dhe duke shtuar një term në dy pjesët e tij, marrim
Kur plotësohet kushti kinematik
Ekuacioni (4.5) vjen nga (4.7). Dhe nëse kushti (4.8) plotësohet gjatë gjithë lëvizjes, atëherë ekziston integrali i parë (4.6).
Nëse lidhjet e sistemit janë ideale dhe lejojnë, midis zhvendosjeve virtuale, rrotullimin e sistemit si një trup i ngurtë rreth boshtit dhe, atëherë momenti kryesor i reaksioneve në lidhje me boshtin dhe është i barabartë me zero, dhe më pas vlera në ana e djathtë e ekuacionit (4.5) paraqet momentin kryesor të të gjitha forcave të jashtme aktive në lidhje me boshtin dhe . Barazia me zero e këtij momenti dhe vlefshmëria e relacionit (4.8) do të jenë në rastin në shqyrtim kushte të mjaftueshme për ekzistencën e integralit (4.6).
Nëse drejtimi i boshtit dhe është konstant, atëherë kushti (4.8) do të shkruhet në formë
![]()
Kjo barazi do të thotë se projeksionet e shpejtësisë së qendrës së masës dhe shpejtësisë së pikës A në bosht dhe në një plan pingul me këtë janë paralele. Në veprën e S.A. Chaplygin, në vend të (4.9), kërkohet një kusht më pak i përgjithshëm ku X është një konstante arbitrare.
Vini re se kushti (4.8) nuk varet nga zgjedhja e pikës në . Në të vërtetë, le të jetë P një pikë arbitrare në bosht. Pastaj
dhe për këtë arsye
Si përfundim, vërejmë interpretimin gjeometrik të Rézal-it të ekuacioneve (4.1) dhe (4.4): vektorët e shpejtësisë absolute të skajeve të vektorëve dhe janë të barabartë, përkatësisht, me vektorin kryesor dhe momentin kryesor të të gjitha forcave të jashtme në lidhje me pikën A. .
Përdorimi i sigurimit shëndetësor në zgjidhjen e problemeve shoqërohet me vështirësi të caktuara. Prandaj, zakonisht vendosen marrëdhënie shtesë midis karakteristikave të lëvizjes dhe forcave, të cilat janë më të përshtatshme për aplikim praktik. Marrëdhënie të tilla janë teorema të përgjithshme të dinamikës. Ata, duke qenë pasoja të OMS, vendosin marrëdhënie midis shpejtësisë së ndryshimit të disa masave të lëvizjes të prezantuara posaçërisht dhe karakteristikave të forcave të jashtme.
Teorema mbi ndryshimin e momentit. Le të prezantojmë konceptin e vektorit të momentit (R. Descartes) të një pike materiale (Fig. 3.4):
I i = t V G (3.9)
Oriz. 3.4.
Për sistemin ne prezantojmë konceptin vektori kryesor i momentit të sistemit si shumë gjeometrike:
Q = Y, m "V r
Në përputhje me OZMS: Xu, -^=i) , ose X
R (E) .
Duke marrë parasysh se /w, = const marrim: -Ym,!" = R (E),
ose në formë përfundimtare
dO/di = A (E (3.11)
ato. derivati i parë në lidhje me kohën e vektorit kryesor të momentit të sistemit është i barabartë me vektorin kryesor të forcave të jashtme.
Teorema mbi lëvizjen e qendrës së masës. Qendra e masës së sistemit quhet një pikë gjeometrike, pozicioni i së cilës varet nga T, etj. nga shpërndarja e masave /g/, në sistem dhe përcaktohet nga shprehja për vektorin e rrezes së qendrës së masës (Fig. 3.5):

Ku g s - vektori i rrezes së qendrës së masës.

Oriz. 3.5.
Le të thërrasim = t me masën e sistemit. Pas shumëzimit të shprehjes
duke aplikuar (3.12) në emërues dhe duke dalluar të dyja anët e rezultatit
do të kemi një barazi të vlefshme: g s t s = ^ t.U. = 0, ose 0 = t s U s.
Kështu, vektori kryesor i momentit të sistemit është i barabartë me produktin e masës së sistemit dhe shpejtësisë së qendrës së masës. Duke përdorur teoremën mbi ndryshimin e momentit (3.11), marrim:
t s dU s / dі = A (E) , ose
Formula (3.13) shpreh teoremën mbi lëvizjen e qendrës së masës: qendra e masës së sistemit lëviz si një pikë materiale që ka masën e sistemit, mbi të cilën vepron vektori kryesor i forcave të jashtme.
Teorema mbi ndryshimin e momentit këndor. Le të prezantojmë konceptin e momentit këndor të një pike materiale si produkti vektorial i vektorit të rrezes dhe momentit të saj:
te oh = bl X se, (3.14)
Ku tek OI - momenti këndor i një pike materiale në raport me një pikë fikse RRETH(Fig. 3.6).

Tani ne përcaktojmë momentin këndor të një sistemi mekanik si një shumë gjeometrike:
К() = X ko, = ШУ, ? O-15>
Duke diferencuar (3.15), marrim:
Ґ sek--- X t i U. + g u X t i
Duke marrë parasysh atë = U G U i X t i u i= 0, dhe formulën (3.2), marrim:
сіК а /с1ї - ї 0 .
Bazuar në shprehjen e dytë në (3.6), më në fund do të kemi një teoremë mbi ndryshimin e momentit këndor të sistemit:
Derivati i parë kohor i momentit të momentit të një sistemi mekanik në lidhje me një qendër fikse O është i barabartë me momentin kryesor të forcave të jashtme që veprojnë në këtë sistem në lidhje me të njëjtën qendër.
Gjatë nxjerrjes së relacionit (3.16), supozohej se RRETH- pikë fikse. Megjithatë, mund të tregohet se në një sërë rastesh të tjera forma e relacionit (3.16) nuk do të ndryshojë, veçanërisht nëse në lëvizjen planore pika e momentit zgjidhet në qendër të masës, qendrën e menjëhershme të shpejtësive ose nxitimeve. Përveç kësaj, nëse pika RRETH përkon me një pikë materiale lëvizëse, barazia (3.16) e shkruar për këtë pikë do të kthehet në identitetin 0 = 0.
Teorema mbi ndryshimin e energjisë kinetike. Kur një sistem mekanik lëviz, si energjia "e jashtme" dhe e brendshme e sistemit ndryshon. Nëse karakteristikat e forcave të brendshme, vektori kryesor dhe momenti kryesor, nuk ndikojnë në ndryshimin e vektorit kryesor dhe momentit kryesor të numrit të nxitimeve, atëherë forcat e brendshme mund të përfshihen në vlerësimin e proceseve të gjendjes energjetike të sistemit. Prandaj, kur merren parasysh ndryshimet në energjinë e një sistemi, është e nevojshme të merren parasysh lëvizjet e pikave individuale, në të cilat zbatohen edhe forcat e brendshme.
Energjia kinetike e një pike materiale përcaktohet si sasi
T^tuTsg. (3.17)
Energjia kinetike e një sistemi mekanik është e barabartë me shumën e energjive kinetike të pikave materiale të sistemit:
vini re, se T > 0.
Le të përcaktojmë fuqinë e forcës si produkt skalar i vektorit të forcës dhe vektorit të shpejtësisë:

Shumë shpesh është e mundur të identifikohen tipare të rëndësishme të lëvizjes së një sistemi mekanik pa përdorur integrimin e një sistemi të ekuacioneve diferenciale të lëvizjes. Kjo arrihet duke aplikuar teorema të përgjithshme të dinamikës.
5.1. Konceptet dhe përkufizimet bazë
Forcat e jashtme dhe të brendshme.Çdo forcë që vepron në një pikë të një sistemi mekanik është domosdoshmërisht ose një forcë aktive ose një reagim bashkues. I gjithë grupi i forcave që veprojnë në pikat e sistemit mund të ndahet në dy klasa ndryshe: forcat e jashtme dhe forcat e brendshme (indekset e dhe i - nga fjalët latine externus - e jashtme dhe internus - e brendshme). Forcat e jashtme janë ato që veprojnë në pika të një sistemi nga pika dhe trupa që nuk janë pjesë e sistemit në shqyrtim. Forcat e ndërveprimit ndërmjet pikave dhe trupave të sistemit në shqyrtim quhen të brendshme.
Kjo ndarje varet se cilat pika dhe trupa materiale përfshihen nga studiuesi në sistemin mekanik në shqyrtim. Nëse e zgjerojmë përbërjen e sistemit duke përfshirë pika dhe trupa shtesë, atëherë disa forca që ishin të jashtme për sistemin e mëparshëm mund të bëhen të brendshme për sistemin e zgjeruar.
Vetitë e forcave të brendshme. Meqenëse këto forca janë forca të ndërveprimit midis pjesëve të sistemit, ato hyjnë në sistemin e plotë të forcave të brendshme në "dy", të organizuara në përputhje me aksiomën veprim-reaksion. Secila "dy" e tillë ka pika të forta
vektori kryesor dhe momenti kryesor rreth një qendre arbitrare janë të barabartë me zero. Meqenëse sistemi i plotë i forcave të brendshme përbëhet vetëm nga "dy", atëherë
1) vektori kryesor i sistemit të forcave të brendshme është zero,
2) momenti kryesor i sistemit të forcave të brendshme në lidhje me një pikë arbitrare është i barabartë me zero.
Masa e sistemit është shuma aritmetike e masave mk të të gjitha pikave dhe trupave që formojnë sistemin:
Qendra e masës(qendra e inercisë) e një sistemi mekanik është një pikë gjeometrike C, vektori i rrezes dhe koordinatat e së cilës përcaktohen nga formulat
ku janë vektorët e rrezes dhe koordinatat e pikave që formojnë sistemin.
Për një trup të ngurtë të vendosur në një fushë gravitacionale uniforme, pozicionet e qendrës së masës dhe qendrës së gravitetit përkojnë në raste të tjera, këto janë pika të ndryshme gjeometrike.
Së bashku me sistemin e referencës inerciale, një sistem referimi jo-inercial që lëviz në mënyrë përkthimore shpesh konsiderohet njëkohësisht. Boshtet e tij koordinative (akset König) janë zgjedhur në mënyrë që origjina C të përputhet vazhdimisht me qendrën e masës së sistemit mekanik. Në përputhje me përkufizimin, qendra e masës është e palëvizshme në akset Koenig dhe ndodhet në origjinën e koordinatave.
Momenti i inercisë së sistemit në lidhje me një bosht është një sasi skalare e barabartë me shumën e produkteve të masave mk të të gjitha pikave të sistemit nga katrorët e largësive të tyre me boshtin:
![]()
Nëse sistemi mekanik është një trup i ngurtë, për të gjetur 12 mund të përdorni formulën

ku është dendësia, vëllimi i zënë nga trupi.
Teorema mbi lëvizjen e qendrës së masës. Ekuacionet diferenciale të lëvizjes së një sistemi mekanik. Teorema mbi lëvizjen e qendrës së masës së një sistemi mekanik. Ligji i ruajtjes së lëvizjes së qendrës së masës.
Teorema mbi ndryshimin e momentit. Sasia e lëvizjes së një pike materiale. Impuls elementar i forcës. Forconi impulsin për një periudhë të kufizuar kohore dhe projeksionin e tij në boshtet koordinative. Teorema mbi ndryshimin e momentit të një pike materiale në forma diferenciale dhe të fundme.
Sasia e lëvizjes së një sistemi mekanik; shprehja e tij përmes masës së sistemit dhe shpejtësisë së qendrës së masës së tij. Teorema mbi ndryshimin e momentit të një sistemi mekanik në forma diferenciale dhe të fundme. Ligji i ruajtjes së momentit mekanik
(Koncepti i një trupi dhe një pikë me masë të ndryshueshme. Ekuacioni i Meshchersky. formula e Tsiolkovsky.)
Teorema mbi ndryshimin e momentit këndor. Momenti i momentit të një pike materiale në raport me qendrën dhe në lidhje me boshtin. Teorema mbi ndryshimin e momentit këndor të një pike materiale. Fuqia qendrore. Ruajtja e momentit këndor të një pike materiale në rastin e një force qendrore. (Koncepti i shpejtësisë sektoriale. Ligji i zonave.)
Momenti kryesor i momentit ose momentit kinetik të një sistemi mekanik në lidhje me qendrën dhe në lidhje me boshtin. Momenti kinetik i një trupi të ngurtë rrotullues rreth boshtit të rrotullimit. Teorema mbi ndryshimin e momentit kinetik të një sistemi mekanik. Ligji i ruajtjes së momentit këndor të një sistemi mekanik. (Teorema mbi ndryshimin në momentin këndor të një sistemi mekanik në lëvizje relative në lidhje me qendrën e masës.)
Teorema mbi ndryshimin e energjisë kinetike. Energjia kinetike e një pike materiale. Puna elementare e forcës; shprehje analitike e punës elementare. Puna e bërë nga një forcë në zhvendosjen përfundimtare të pikës së aplikimit të saj. Puna e gravitetit, forcës elastike dhe forcës gravitacionale. Teorema mbi ndryshimin e energjisë kinetike të një pike materiale në forma diferenciale dhe të fundme.
Energjia kinetike e një sistemi mekanik. Formulat për llogaritjen e energjisë kinetike të një trupi të ngurtë gjatë lëvizjes përkthimore, gjatë rrotullimit rreth një boshti fiks dhe në rastin e përgjithshëm të lëvizjes (në veçanti, gjatë lëvizjes plan-paralele). Teorema mbi ndryshimin e energjisë kinetike të një sistemi mekanik në forma diferenciale dhe të fundme. Shuma e punës së bërë nga forcat e brendshme në një trup të ngurtë është e barabartë me zero. Puna dhe fuqia e forcave të aplikuara në një trup të ngurtë që rrotullohet rreth një boshti fiks.
Koncepti i një fushe force. Fusha e forcës potenciale dhe funksioni i forcës. Shprehja e projeksioneve të forcës përmes funksionit të forcës. Sipërfaqe me potencial të barabartë. Puna e një force në zhvendosjen përfundimtare të një pike në një fushë force potenciale. Energji potenciale. Shembuj të fushave të forcës potenciale: fushë uniforme gravitacionale dhe fushë gravitacionale. Ligji i ruajtjes së energjisë mekanike.
Dinamika e ngurtë e trupit. Ekuacionet diferenciale të lëvizjes përkthimore të një trupi të ngurtë. Ekuacioni diferencial për rrotullimin e një trupi të ngurtë rreth një boshti fiks. Lavjerrësi fizik. Ekuacionet diferenciale të lëvizjes planore të një trupi të ngurtë.
Parimi i D'Alembert. Parimi i D'Alembert për një pikë materiale; forcë inerciale. Parimi i D'Alembert për një sistem mekanik. Sjellja e forcave të inercisë së pikave të një trupi të ngurtë në qendër; vektori kryesor dhe momenti kryesor i forcave të inercisë.
(Përcaktimi i reaksioneve dinamike të kushinetave gjatë rrotullimit të një trupi të ngurtë rreth një boshti fiks. Rasti kur boshti i rrotullimit është boshti kryesor qendror i inercisë së trupit.)
Parimi i lëvizjeve të mundshme dhe ekuacioni i përgjithshëm i dinamikës. Lidhjet e vendosura në një sistem mekanik. Lëvizjet e mundshme (ose virtuale) të një pike materiale dhe të një sistemi mekanik. Numri i shkallëve të lirisë së sistemit. Lidhjet ideale. Parimi i lëvizjeve të mundshme. Ekuacioni i përgjithshëm i dinamikës.
Ekuacionet e lëvizjes së një sistemi në koordinata të përgjithësuara (ekuacionet e Lagranzhit). Koordinatat e përgjithësuara të sistemit; shpejtësi të përgjithësuara. Shprehja e punës elementare në koordinata të përgjithësuara. Forcat e përgjithësuara dhe llogaritja e tyre; rasti i forcave me potencial. Kushtet për ekuilibrin e një sistemi në koordinata të përgjithësuara. Ekuacionet diferenciale të lëvizjes së një sistemi në koordinata të përgjithësuara ose ekuacionet e Lagranzhit të llojit të dytë. Ekuacionet e Lagranzhit në rastin e forcave potenciale; Funksioni i Lagranzhit (potenciali kinetik).
Koncepti i stabilitetit të ekuilibrit. Dridhje të vogla të lira të një sistemi mekanik me një shkallë lirie pranë pozicionit të ekuilibrit të qëndrueshëm të sistemit dhe vetive të tyre.
Elementet e teorisë së ndikimit. Dukuria e ndikimit. Forca e goditjes dhe impulsi i goditjes. Veprimi i forcës së goditjes në një pikë materiale. Teorema mbi ndryshimin e momentit të një sistemi mekanik pas goditjes. Ndikimi i drejtpërdrejtë qendror i trupit në një sipërfaqe të palëvizshme; ndikimet elastike dhe joelastike. Koeficienti i rikuperimit të ndikimit dhe përcaktimi eksperimental i tij. Ndikimi i drejtpërdrejtë qendror i dy trupave. Teorema e Carnot.
BIBLIOGRAFI
bazë
Butenin N.V., Lunts Ya-L., Merkin D.R. Kursi i mekanikës teorike. T. 1, 2. M., 1985 dhe botime të mëparshme.
Dobronravov V.V., Nikitin N.N. Kursi i mekanikës teorike. M., 1983.
Starzhinsky V. M. Mekanika teorike. M., 1980.
Targ S. M. Kurs i shkurtër në mekanikën teorike. M., 1986 dhe botime të mëparshme.
Yablonsky A. A., Nikiforova V. M. Kursi i mekanikës teorike. Pjesa 1. M., 1984 dhe botimet e mëparshme.
Yablonsky A. A. Kursi i mekanikës teorike. Pjesa 2. M., 1984 dhe botimet e mëparshme.
Meshchersky I. V. Koleksion problemesh mbi mekanikën teorike. M., 1986 dhe botimet e mëparshme.
Koleksion problemesh mbi mekanikën teorike / Ed. K. S. Kolesnikova. M., 1983.
Shtesë
Bat M. I., Dzhanelidze G. Yu., Kelzon A. S. Mekanika teorike në shembuj dhe problema. Pjesët 1, 2. M., 1984 dhe botimet e mëparshme.
Koleksion problemesh mbi mekanikën teorike/5razhnichen/so N. A., Kan V. L., Mintzberg B. L. dhe të tjerët M., 1987.
Novozhilov I. V., Zatsepin M. F. Llogaritjet tipike të bazuara në kompjuter në mekanikën teorike. M., 1986,
Mbledhja e detyrave për lëndët në mekanikën teorike / Ed. A. A. Yablonsky. M., 1985 dhe botimet e mëparshme (përmban shembuj të zgjidhjes së problemeve).








