Llogaritja e renditjes së një matrice sipas përkufizimit. Përcaktimi i rangut të një matrice

Rreshtat (kolonat). Disa rreshta (kolona) thuhet se janë linearisht të pavarura nëse asnjëra prej tyre nuk mund të shprehet në mënyrë lineare në termat e të tjerëve. Rangu i sistemit të rreshtave është gjithmonë i barabartë me rangun e sistemit të kolonës, dhe ky numër quhet rang i matricës.

Renditja e një matrice është më e larta nga rendet e të gjithë të miturve të mundshëm jo zero të kësaj matrice. Rangu i një matrice zero të çdo madhësie është zero. Nëse të gjithë të miturit e rendit të dytë janë zero, atëherë grada është një, etj.

Rangu i matricës - dimensioni i imazhit dim ⁡ (im ⁡ (A)) (\displaystyle \dim(\emri i operatorit (im) (A))) operator linear të cilit i korrespondon matrica.

Zakonisht rangu i matricës A (\displaystyle A) shënohet me rang ⁡ A (\displaystyle \emri i operatorit (rang) A), r ⁡ A (\displaystyle \emri i operatorit (r) A), rg ⁡ A (\displaystyle \emri i operatorit (rg) A) ose renditja ⁡ A (\displaystyle \emri i operatorit (grada) A). Opsioni i fundit është tipik për gjuhën angleze, ndërsa dy të parat janë për gjermanishten, frëngjishten dhe një sërë gjuhësh të tjera.

YouTube Enciklopedike

1 / 5

Le të jetë një matricë drejtkëndëshe.

Pastaj, sipas përkufizimit, rangu i matricës A (\displaystyle A)është:

Teorema (për korrektësinë e përcaktimit të gradave). Le të gjithë të miturit e matricës A m × n (\shfaqja e stilit A_(m\herë n)) urdhëroj k (\displaystyle k) janë të barabarta me zero ( M k = 0 (\displaystyle M_(k)=0)). Pastaj ∀ M k + 1 = 0 (\displaystyle \përgjithë M_(k+1)=0), nëse ekzistojnë.

Përkufizime të ngjashme

Vetitë

Teorema (për minorin bazë): Le r = rang ⁡ A , M r (\displaystyle r=\emri i operatorit (rang) A,M_(r))- bazë minor i matricës A (\displaystyle A), Pastaj:
Pasojat:
Teorema (për pandryshueshmërinë e rangut nën transformimet elementare): Le të prezantojmë një shënim për matricat e marra nga njëra-tjetra nga transformimet elementare. Atëherë pohimi i mëposhtëm është i vërtetë: Nëse A ∼ B (\displaystyle A\sim B), atëherë gradat e tyre janë të barabarta.
Teorema Kronecker-Capelli: Një sistem ekuacionesh algjebrike lineare është i qëndrueshëm nëse dhe vetëm nëse rangu i matricës së tij kryesore është i barabartë me gradën e matricës së tij të zgjeruar. Veçanërisht:
- Numri i variablave kryesore të sistemit është i barabartë me gradën e sistemit.
- Një sistem konsistent do të përcaktohet (zgjidhja e tij është unike) nëse rangu i sistemit është i barabartë me numrin e të gjitha variablave të tij.
Pabarazia e Silvesterit: Nëse A Dhe B matricat e madhësisë m x n Dhe n x k, Kjo

rang ⁡ A B ≥ rang ⁡ A + rang ⁡ B − n (\displaystyle \operatorname (rang) AB\geq \operatorname (rang) A+\operatorname (rang) B-n)

Ky është një rast i veçantë i pabarazisë së mëposhtme.

Pabarazia e Frobenius: Nëse AB, BC, ABC janë përcaktuar saktë, atëherë

rang ⁡ A B C ≥ rang ⁡ A B + rang ⁡ B C − rang ⁡ B (\displaystyle \operatorname (rang) ABC\geq \operatorname (rang) AB+\operatorname (rang) BC-\operatorname (rang) B)

Transformimi linear dhe rangu i matricës

Le A (\displaystyle A)- matrica e madhësisë m × n (\shfaqja m\herë n) mbi fushë C (\displaystyle C)(ose R (\displaystyle R)). Le T (\displaystyle T)- transformim linear përkatës A (\displaystyle A) mbi baza standarde; do të thotë se T (x) = A x (\displaystyle T(x)=Ax). Rangu i matricës A (\displaystyle A) është dimensioni i diapazonit të transformimit T (\displaystyle T).

Metodat

Ka disa mënyra për të gjetur gradën e një matrice:

Metoda elementare e transformimit

Renditja e një matrice është e barabartë me numrin e rreshtave jo zero në matricë pasi ta reduktoni atë në formë shkalle duke përdorur transformime elementare në rreshtat e matricës.

Metoda e kufirit të të miturve

Lëreni në matricë A (\displaystyle A) Minor jo zero i gjetur k (\displaystyle k)- urdhri M (\displaystyle M). Le të marrim parasysh të gjithë të miturit (k + 1) (\style ekrani (k+1))-të rendit, duke përfshirë (borhe) të vogla M (\displaystyle M); nëse të gjithë janë të barabartë me zero, atëherë rangu i matricës është i barabartë me k (\displaystyle k). Ndryshe, tek të miturit në kufi ka një jozero dhe e gjithë procedura përsëritet.

Ne gjithashtu do të shqyrtojmë një aplikim të rëndësishëm praktik të temës: studimi i një sistemi ekuacionesh lineare për konsistencë.

Cila është rangu i një matrice?

Epigrafi humoristik i artikullit përmban një sasi të madhe të së vërtetës. Ne zakonisht e lidhim fjalën "gradë" me një lloj hierarkie, më shpesh me një shkallë karriere. Sa më shumë njohuri, përvojë, aftësi, lidhje etj. të ketë njeriu. – aq më i lartë është pozicioni i tij dhe diapazoni i mundësive. Në aspektin e të rinjve, grada i referohet shkallës së përgjithshme të "pjerrësisë".

Dhe vëllezërit tanë matematikorë jetojnë me të njëjtat parime. Le të bëjmë një shëtitje disa të rastësishme matricat zero:

Le të mendojmë për këtë, nëse në matricë të gjitha zero, atëherë për çfarë rangu mund të flasim? Të gjithë janë të njohur me shprehjen informale "zero totale". Në shoqërinë e matricave gjithçka është saktësisht e njëjtë:

Renditja e matricës zeroçdo madhësi është e barabartë me zero.

shënim : Matrica zero shënohet me shkronjën greke "theta"

Për të kuptuar më mirë gradën e matricës, në vijim do të përdor materiale për të ndihmuar gjeometria analitike. Konsideroni zero vektoriale hapësira jonë tredimensionale, e cila nuk përcakton një drejtim specifik dhe është e padobishme për ndërtim baza afine. Nga pikëpamja algjebrike, koordinatat e këtij vektori shkruhen në matricë"një nga tre" dhe logjike (në kuptimin gjeometrik të treguar) supozojmë se rangu i kësaj matrice është zero.

Tani le të shohim disa jo zero vektorët e kolonës Dhe vektorët e rreshtave:

Çdo shembull ka të paktën një element jo zero, dhe kjo është diçka!

Rangu i çdo vektori të rreshtit jozero (vektori i kolonës) është i barabartë me një

Dhe në përgjithësi - nëse në matricë madhësi arbitrare ka të paktën një element jo zero, pastaj renditja e tij jo më pak njësi.

Vektorët e rreshtave algjebrikë dhe vektorët e kolonave janë në një masë abstrakte, kështu që le të kthehemi përsëri te shoqërimi gjeometrik. Jo zero vektoriale vendos një drejtim shumë të caktuar në hapësirë dhe është i përshtatshëm për ndërtim bazë, prandaj rangu i matricës do të konsiderohet i barabartë me një.

Informacion teorik : në algjebër lineare, një vektor është një element i një hapësire vektoriale (të përcaktuar me 8 aksioma), i cili, në veçanti, mund të përfaqësojë një rresht (ose kolonë) të renditur të numrave realë me veprimet e mbledhjes dhe shumëzimit me një numër real të përcaktuar. për ata. Informacion më të detajuar rreth vektorëve mund të gjenden në artikull Transformimet lineare.

varur në mënyrë lineare(të shprehura përmes njëri-tjetrit). Nga pikëpamja gjeometrike, rreshti i dytë përmban koordinatat e vektorit kolinear , e cila nuk e avancoi fare çështjen në ndërtim bazë tredimensionale, duke qenë në këtë kuptim i tepërt. Kështu, grada e kësaj matrice është gjithashtu e barabartë me një.

Le të rishkruajmë koordinatat e vektorëve në kolona ( transpozoni matricën):

Çfarë ka ndryshuar për sa i përket gradës? Asgjë. Kolonat janë proporcionale, që do të thotë se grada është e barabartë me një. Nga rruga, vini re se të tre linjat janë gjithashtu proporcionale. Ato mund të identifikohen me koordinatat tre vektorët kolinearë të rrafshit, prej të cilëve vetem nje e dobishme për ndërtimin e një baze "të sheshtë". Dhe kjo është plotësisht në përputhje me ndjenjën tonë gjeometrike të renditjes.

Një deklaratë e rëndësishme rrjedh nga shembulli i mësipërm:

Rangu i matricës në rreshta është i barabartë me gradën e matricës në kolona. Unë tashmë e përmenda këtë pak në mësimin për efektivitetin metodat për llogaritjen e përcaktorit.

shënim : varësia lineare e rreshtave nënkupton varësinë lineare të kolonave (dhe anasjelltas). Por, për të kursyer kohë, dhe jashtë zakonit, pothuajse gjithmonë do të flas për varësinë lineare të vargjeve.

Le të vazhdojmë të trajnojmë kafshën tonë të dashur. Le të shtojmë koordinatat e një vektori tjetër kolinear në matricën në rreshtin e tretë :

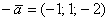A na ndihmoi ai në ndërtimin e një baze tredimensionale? Sigurisht që jo. Të tre vektorët ecin përpara dhe mbrapa përgjatë të njëjtës rrugë, dhe rangu i matricës është i barabartë me një. Ju mund të merrni sa më shumë vektorë kolinearë që të doni, të themi, 100, t'i vendosni koordinatat e tyre në një matricë "njëqind nga tre", dhe renditja e një rrokaqiell të tillë do të mbetet ende një.

Le të njihemi me matricën, rreshtat e së cilës i pavarur në mënyrë lineare. Një çift vektorësh jo-kolinearë është i përshtatshëm për të ndërtuar një bazë tredimensionale. Renditja e kësaj matrice është dy.

Cila është rangu i matricës? Linjat nuk duken të jenë proporcionale... pra, në teori, ato janë tre. Sidoqoftë, rangu i kësaj matrice është gjithashtu dy. Shtova dy rreshtat e parë dhe rezultatin e shkrova në fund, d.m.th. shprehur në mënyrë lineare rreshti i tretë përmes dy të parëve. Gjeometrikisht, rreshtat e matricës korrespondojnë me koordinatat e tre vektorët koplanarë, dhe në mesin e këtyre tre ka një palë shokë jo-kolinearë.

Siç mund ta shihni, varësia lineare në matricën e konsideruar nuk është e qartë, dhe sot do të mësojmë se si ta nxjerrim atë në të hapur.

Unë mendoj se shumë njerëz mund të marrin me mend se cila është shkalla e një matrice!

Konsideroni një matricë rreshtat e së cilës i pavarur në mënyrë lineare. Formohen vektorët baza afine, dhe rangu i kësaj matrice është tre.

Siç e dini, çdo vektor i katërt, i pestë, i dhjetë i hapësirës tre-dimensionale do të shprehet në mënyrë lineare në terma të vektorëve bazë. Prandaj, nëse shtoni ndonjë numër rreshtash në një matricë, atëherë renditja e saj do të jetë ende e barabartë me tre.

Arsyetim i ngjashëm mund të kryhet për matricat me madhësi më të mëdha (natyrisht, pa ndonjë kuptim gjeometrik).

Përkufizimi : Rangu i një matrice është numri maksimal i rreshtave linearisht të pavarur. Ose: Rangu i një matrice është numri maksimal i kolonave lineare të pavarura. Po, numri i tyre është gjithmonë i njëjtë.

Një udhëzim praktik i rëndësishëm rrjedh gjithashtu nga sa më sipër: rangu i matricës nuk e kalon dimensionin e saj minimal. Për shembull, në matricë katër rreshta dhe pesë kolona. Dimensioni minimal është katër, prandaj, renditja e kësaj matrice me siguri nuk do të kalojë 4.

Emërtimet: në teorinë dhe praktikën botërore nuk ka asnjë standard të pranuar përgjithësisht për përcaktimin e gradës së një matrice më të zakonshmet: - siç thonë ata, një anglez shkruan një gjë, një gjerman tjetër; Prandaj, bazuar në shakanë e famshme për ferrin amerikan dhe rus, le të shënojmë gradën e matricës me një fjalë amtare. Për shembull: . Dhe nëse matrica është "pa emër", nga e cila ka shumë, atëherë thjesht mund të shkruani .

Si të gjeni gradën e një matrice duke përdorur të mitur?

Nëse gjyshja ime kishte një kolonë të pestë në matricën e saj, atëherë ajo do të duhej të llogariste një tjetër të vogël të rendit të 4-të ("blu", "mjedër" + kolona e 5-të).

konkluzioni: rendi maksimal i një minoreje jo zero është tre, që do të thotë .

Ndoshta jo të gjithë e kanë kuptuar plotësisht këtë frazë: një minor i rendit të katërt është i barabartë me zero, por në mesin e të miturve të rendit të tretë ka pasur një jozero - prandaj rendi maksimal jo zero e vogël dhe është e barabartë me tre.

Shtrohet pyetja: pse të mos llogarisim menjëherë përcaktorin? Epo, së pari, në shumicën e detyrave matrica nuk është katrore, dhe së dyti, edhe nëse merrni një vlerë jo zero, detyra ka shumë të ngjarë të refuzohet, pasi zakonisht përfshin një zgjidhje standarde "nga poshtë-lart". Dhe në shembullin e konsideruar, përcaktori zero i rendit të 4-të na lejon të deklarojmë se rangu i matricës është vetëm më pak se katër.

Më duhet ta pranoj, problemin që kam analizuar vetë e kam gjetur për të shpjeguar më mirë metodën e kufirit të të miturve. Në praktikën reale, gjithçka është më e thjeshtë:

Shembulli 2

Gjeni rangun e një matrice duke përdorur metodën e minorave të skajeve

Zgjidhja dhe përgjigja janë në fund të mësimit.

Kur funksionon më shpejt algoritmi? Le të kthehemi në të njëjtën matricë katër nga katër. . Natyrisht, zgjidhja do të jetë më e shkurtra në rastin e "mirës" të mitur në qoshe: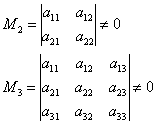

Dhe, nëse , atëherë , përndryshe - .

Mendimi nuk është aspak hipotetik - ka shumë shembuj ku e gjithë çështja kufizohet vetëm tek të miturit këndorë.

Megjithatë, në disa raste, një metodë tjetër është më efektive dhe e preferueshme:

Si të gjeni rangun e një matrice duke përdorur metodën Gaussian?

Paragrafi është i destinuar për lexuesit që tashmë janë njohur me të Metoda Gaussian dhe pak a shumë ia dolën në dorë.

Nga pikëpamja teknike, metoda nuk është e re:

1) duke përdorur transformimet elementare, ne e zvogëlojmë matricën në një formë hap pas hapi;

2) grada e matricës është e barabartë me numrin e rreshtave.

Është absolutisht e qartë se përdorimi i metodës Gaussian nuk e ndryshon rangun e matricës, dhe thelbi këtu është jashtëzakonisht i thjeshtë: sipas algoritmit, gjatë transformimeve elementare, të gjitha rreshtat e panevojshme proporcionale (të varura linearisht) identifikohen dhe hiqen, duke rezultuar në një "mbetje të thatë" - numrin maksimal të rreshtave linearisht të pavarur.

Le të transformojmë matricën e vjetër të njohur me koordinatat e tre vektorëve kolinearë:

(1) Rreshtit të dytë iu shtua rreshti i parë, shumëzuar me –2. Rreshti i parë iu shtua rreshtit të tretë.

(2) Linjat zero janë hequr.

Kështu, ka mbetur një rresht, pra . Eshtë e panevojshme të thuhet se kjo është shumë më e shpejtë se llogaritja e nëntë zero të miturve të rendit të dytë dhe vetëm atëherë nxjerrja e një përfundimi.

Ju kujtoj këtë në vetvete matricë algjebrike asgjë nuk mund të ndryshohet, dhe transformimet bëhen vetëm për qëllimin e përcaktimit të gradës! Meqë ra fjala, le të ndalemi edhe një herë në pyetjen, pse jo? Matrica e burimit 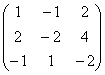mbart informacion që është thelbësisht i ndryshëm nga informacioni i matricës dhe rreshtit. Në disa modele matematikore (pa ekzagjerim), ndryshimi në një numër mund të jetë çështje jete dhe vdekjeje. ...Më kujtuan mësuesit e matematikës të shkollave fillore dhe të mesme që pa mëshirë ulnin notat me 1-2 pikë për pasaktësinë më të vogël apo devijimin nga algoritmi. Dhe ishte tmerrësisht zhgënjyese kur, në vend të një "A" të garantuar në dukje, doli "i mirë" ose edhe më keq. Kuptimi erdhi shumë më vonë - si tjetër t'i besoni satelitëve, kokave bërthamore dhe termocentraleve një personi? Por mos u shqetësoni, unë nuk punoj në këto fusha =)

Le të kalojmë në detyra më kuptimplote, ku ndër të tjera do të njihemi me teknika të rëndësishme llogaritëse Metoda e Gausit:

Shembulli 3

Gjeni gradën e një matrice duke përdorur transformimet elementare

Zgjidhje: jepet një matricë "katër nga pesë", që do të thotë se renditja e saj sigurisht nuk është më shumë se 4.

Në kolonën e parë, nuk ka 1 ose –1, prandaj, kërkohen veprime shtesë për të marrë të paktën një njësi. Gjatë gjithë ekzistencës së sitit, më është bërë vazhdimisht pyetja: "A është e mundur të riorganizoni kolonat gjatë transformimeve elementare?" Këtu - ne riorganizuam kolonën e parë dhe të dytë, dhe gjithçka është në rregull! Në shumicën e detyrave ku përdoret Metoda Gaussian, kolonat me të vërtetë mund të riorganizohen. POR NUK DUHET. Dhe çështja nuk është as në konfuzion të mundshëm me variablat, çështja është se në kursin klasik të matematikës së lartë ky veprim tradicionalisht nuk merret parasysh, kështu që një tundje e tillë do të shikohet SHUMË shtrembër (apo edhe e detyruar të ribëjë gjithçka).

Pika e dytë ka të bëjë me numrat. Ndërsa merrni vendimin tuaj, është e dobishme të përdorni rregullin e përgjithshëm të mëposhtëm: transformimet elementare duhet, nëse është e mundur, të zvogëlojnë numrat e matricës. Në fund të fundit, është shumë më e lehtë të punosh me një, dy, tre sesa, për shembull, me 23, 45 dhe 97. Dhe veprimi i parë synon jo vetëm marrjen e një në kolonën e parë, por edhe eliminimin e numrave 7 dhe 11.

Së pari zgjidhja e plotë, pastaj komentet:

(1) Rreshtit të dytë iu shtua rreshti i parë, shumëzuar me –2. Rreshti i parë iu shtua rreshtit të tretë, shumëzuar me –3. Dhe te grumbulli: rreshti i parë u shtua në rreshtin e 4-të, shumëzuar me –1.

(2) Tre rreshtat e fundit janë proporcionale. Linjat e 3-të dhe të 4-t u hoqën, rreshti i dytë u zhvendos në vendin e parë.

(3) Rreshti i parë iu shtua rreshtit të dytë, shumëzuar me –3.

Matrica e reduktuar në formë shkalle ka dy rreshta.

Përgjigju:

Tani është radha juaj të torturoni matricën katër nga katër:

Shembulli 4

Gjeni gradën e një matrice duke përdorur metodën Gaussian

Ju kujtoj se Metoda Gaussian nuk nënkupton ngurtësi të paqartë, dhe vendimi juaj ka shumë të ngjarë të ndryshojë nga vendimi im. Një shembull i shkurtër i një detyre në fund të mësimit.

Cila metodë duhet të përdor për të gjetur gradën e një matrice?

Në praktikë, shpesh nuk thuhet fare se cila metodë duhet përdorur për të gjetur gradën. Në një situatë të tillë, kushti duhet të analizohet - për disa matrica është më racionale të zgjidhen përmes të miturve, ndërsa për të tjerat është shumë më fitimprurëse të aplikohen transformimet elementare:

Shembulli 5

Gjeni gradën e një matrice

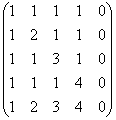
Zgjidhje: metoda e parë disi zhduket menjëherë =)

Pak më lart, unë këshillova të mos prekni kolonat e matricës, por kur ka një kolonë zero, ose kolona proporcionale / përputhëse, atëherë ia vlen të amputohet:

(1) Kolona e pestë është zero, hiqeni atë nga matrica. Kështu, grada e matricës nuk është më shumë se katër. Rreshti i parë është shumëzuar me –1. Kjo është një tjetër veçori e metodës Gauss, e cila e kthen veprimin e mëposhtëm në një shëtitje të këndshme:

(2) Në të gjitha rreshtat, duke filluar nga e dyta, u shtua rreshti i parë.

(3) Rreshti i parë u shumëzua me –1, rreshti i tretë u nda me 2, rreshti i katërt u nda me 3. Rreshti i dytë u shtua në rreshtin e pestë, shumëzuar me –1.

(4) Rreshtit të pestë iu shtua rreshti i tretë, shumëzuar me –2.

(5) Dy rreshtat e fundit janë proporcionalë, i pesti fshihet.

Rezultati është 4 rreshta.

Përgjigju:

Ndërtesa standarde pesëkatëshe për eksplorim të pavarur:

Shembulli 6

Gjeni gradën e një matrice

Një zgjidhje dhe përgjigje e shkurtër në fund të mësimit.

Duhet të theksohet se shprehja "gradë matricë" nuk shihet aq shpesh në praktikë, dhe në shumicën e problemeve mund të bëni pa të fare. Por ka një detyrë ku koncepti në fjalë është personazhi kryesor, dhe ne do ta përfundojmë artikullin me këtë aplikim praktik:

Si të studiojmë një sistem ekuacionesh lineare për konsistencë?

Shpesh, përveç zgjidhjes sistemet e ekuacioneve lineare sipas kushtit, fillimisht kërkohet të ekzaminohet për përputhshmëri, pra të vërtetohet se ekziston fare ndonjë zgjidhje. Një rol kyç në një verifikim të tillë luan Teorema Kronecker-Capelli, të cilin do ta formuloj në formën e nevojshme:

Nëse renditet matricat e sistemit e barabartë me gradën sistemi i matricës së zgjeruar, atëherë sistemi është konsistent dhe nëse ky numër përkon me numrin e të panjohurave, atëherë zgjidhja është unike.

Kështu, për të studiuar sistemin për pajtueshmërinë, është e nevojshme të kontrolloni barazinë , Ku - matrica e sistemit(kujtoni terminologjinë nga mësimi Metoda e Gausit), A - matrica e zgjeruar e sistemit(d.m.th. një matricë me koeficientët e variablave + një kolonë me terma të lirë).

Në secilën matricë, dy rang mund të shoqërohen: një renditje rreshti (grada e sistemit të rreshtave) dhe një renditje e kolonës (grada e sistemit të kolonës).

Teorema

Renditja e rreshtit të një matrice është e barabartë me renditjen e kolonës së saj.

Rangu i matricës

Përkufizimi

Rangu i matricës$A$ është renditja e sistemit të rreshtit ose kolonës.

Shënuar me $\operatorname(rang) A$

Në praktikë, për të gjetur gradën e një matrice, përdoret pohimi i mëposhtëm: grada e një matrice është e barabartë me numrin e rreshtave jo zero pas reduktimit të matricës në formën e echelonit.

Shndërrimet elementare mbi rreshtat (kolonat) e një matrice nuk e ndryshojnë renditjen e saj.

Renditja e një matrice hapi është e barabartë me numrin e rreshtave të saj jo zero.

Shembull

Ushtrimi. Gjeni rangun e matricës $ A=\left(\fille(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & ( 7) \ \ (10) & (18) & (40) & (17) \\ (1) & (7) & (17) & (3)\fund (arrit)\djathtas) $

Zgjidhje. Duke përdorur transformimet elementare në rreshtat e saj, ne e zvogëlojmë matricën $A$ në formën e echelonit. Për ta bërë këtë, së pari zbritni dy të dytat nga rreshti i tretë:

$$ A \sim \left(\fillimi(array)(cccc)(0) & (4) & (10) & (1) \\ (4) & (8) & (18) & (7) \\ (2) & (2) & (4) & (3) \\ (1) & (7) & (17) & (3)\fund (array)\djathtas) $$

Nga rreshti i dytë zbresim rreshtin e katërt, shumëzuar me 4; nga e treta - dy të katërtat:

$$ A \sim \left(\fillim(array)(rrrr)(0) & (4) & (10) & (1) \\ (0) & (-20) & (-50) & (-5 ) \\ (0) & (-12) & (-30) & (-3) \\ (1) & (7) & (17) & (3)\fund (arrit)\djathtas) $$

Pesë të parat i shtojmë në rreshtin e dytë, dhe tre të tretin në të tretën:

$$ A \sim \left(\fille(array)(cccc)(0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\fund (array)\djathtas) $$

Ndërroni rreshtin e parë dhe të dytë:

$$ A \sim \left(\fillimi(array)(cccc)(0) & (0) & (0) & (0) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3)\fund (array)\djathtas) $$

$$ A \sim \left(\fillimi(array)(cccc)(1) & (7) & (17) & (3) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0)\fund (array)\djathtas) \Rightarrow \operatorname(rang) A=2 $$

Përgjigju.$ \operatorname(rang) A=2 $

Metoda e kufirit të të miturve

Një metodë tjetër për të gjetur gradën e një matrice bazohet në këtë teoremë - metodë e vogël e skajeve. Thelbi i kësaj metode është gjetja e të miturve, duke filluar nga urdhrat më të ulët dhe duke kaluar në ato më të larta. Nëse minorja e rendit $n$th nuk është e barabartë me zero, dhe të gjitha minoret e rendit $n+1$th janë të barabarta me zero, atëherë rangu i matricës do të jetë i barabartë me $n$.

Shembull

Ushtrimi. Gjeni rangun e matricës $ A=\left(\fille(array)(rrrr)(1) & (2) & (-1) & (-2) \\ (2) & (4) & (3) & (0 ) \\ (-1) & (-2) & (6) & (6)\end (array)\djathtas) $ duke përdorur metodën e skajeve të vogla.

Zgjidhje. Të miturit e rendit minimal janë minore të rendit të parë, të cilat janë të barabarta me elementët e matricës $A$. Konsideroni, për shembull, minorin $ M_(1)=1 \neq 0 $ . ndodhet në rreshtin e parë dhe në kolonën e parë. E kufizojmë me ndihmën e rreshtit të dytë dhe kolonës së dytë, marrim minorin $ M_(2)^(1)=\left| \begin(array)(ll)(1) & (2) \\ (2) & (4)\end(array)\right|=0 $ ; Le të shqyrtojmë një minor tjetër të rendit të dytë, për këtë e kufizojmë minorin $M_1$ me ndihmën e rreshtit të dytë dhe kolonës së tretë, pastaj kemi minorin $ M_(2)^(2)=\left| \begin(array)(rr)(1) & (-1) \\ (2) & (3)\end(array)\right|=5 \neq 0 $ , domethënë, rangu i matricës është jo më pak se dy. Më pas, ne konsiderojmë të mitur të rendit të tretë që kufizojnë minorin $ M_(2)^(2) $. Ka dy minore të tilla: një kombinim i rreshtit të tretë me kolonën e dytë ose me kolonën e katërt. Le të llogarisim këta të mitur.

Le të jepet një matricë:

Le të zgjedhim në këtë matricë vargjet arbitrare dhe kolona arbitrare
. Pastaj përcaktorja rendi i th, i përbërë nga elementë matricë
, i vendosur në kryqëzimin e rreshtave dhe kolonave të zgjedhura, quhet minor matrica e rendit të th
.

Përkufizimi 1.13. Rangu i matricës
është rendi më i madh i minorit jozero të kësaj matrice.

Për të llogaritur gradën e një matrice, duhet të merren parasysh të gjitha minoret e rendit më të ulët të saj dhe, nëse të paktën njëri prej tyre është i ndryshëm nga zero, duhet të merren parasysh minoret e rendit më të lartë. Kjo qasje për përcaktimin e renditjes së një matrice quhet metoda e kufirit (ose metoda e kufirit të të miturve).

Problemi 1.4. Duke përdorur metodën e kufirit të të miturve, përcaktoni gradën e matricës
.

Konsideroni skajet e rendit të parë, për shembull,
. Pastaj vazhdojmë të shqyrtojmë disa skaje të rendit të dytë.

Për shembull,
.

Së fundi, le të analizojmë kufirin e rendit të tretë.

Pra, rendi më i lartë i një minoreje jo zero është 2, pra
.

Gjatë zgjidhjes së problemit 1.4, mund të vëreni se një numër i të miturve kufitarë të rendit të dytë janë jozero. Në këtë drejtim, zbatohet koncepti i mëposhtëm.

Përkufizimi 1.14. Një minor bazë i një matrice është çdo minor jo zero rendi i të cilit është i barabartë me gradën e matricës.

Teorema 1.2.(Teorema bazë e vogël). Rreshtat bazë (kolonat bazë) janë linearisht të pavarura.

Vini re se rreshtat (kolonat) e një matrice varen në mënyrë lineare nëse dhe vetëm nëse të paktën njëra prej tyre mund të përfaqësohet si një kombinim linear i të tjerëve.

Teorema 1.3. Numri i rreshtave të matricës linearisht të pavarur është i barabartë me numrin e kolonave të matricës linearisht të pavarur dhe është i barabartë me gradën e matricës.

Teorema 1.4.(Kusht i domosdoshëm dhe i mjaftueshëm që përcaktorja të jetë e barabartë me zero). Në mënyrë që përcaktorja - urdhri ishte e barabartë me zero, është e nevojshme dhe e mjaftueshme që rreshtat (kolonat) e saj të jenë të varura në mënyrë lineare.

Llogaritja e renditjes së një matrice bazuar në përkufizimin e saj është shumë e rëndë. Kjo bëhet veçanërisht e rëndësishme për matricat e rendit të lartë. Në këtë drejtim, në praktikë, grada e një matrice llogaritet bazuar në zbatimin e teoremave 10.2 - 10.4, si dhe përdorimin e koncepteve të ekuivalencës së matricës dhe transformimeve elementare.

Përkufizimi 1.15. Dy matrica
Dhe quhen ekuivalente nëse radhët e tyre janë të barabarta, d.m.th.
.

Nëse matricat
Dhe janë ekuivalente, pastaj vini re
 .

Teorema 1.5. Rangu i matricës nuk ndryshon për shkak të transformimeve elementare.

Ne do të quajmë transformime elementare të matricës
ndonjë nga operacionet e mëposhtme në një matricë:

Zëvendësimi i rreshtave me kolona dhe kolonave me rreshtat përkatës;

Rirregullimi i rreshtave të matricës;

Kalimi i një linje elementet e së cilës janë të gjithë zero;

Shumëzimi i një vargu me një numër të ndryshëm nga zero;

Shtimi i elementeve të një rreshti të elementeve përkatës të një rreshti tjetër të shumëzuar me të njëjtin numër
.

Përfundim i Teoremës 1.5. Nëse matrica
të marra nga matrica duke përdorur një numër të kufizuar transformimesh elementare, pastaj matricën
Dhe janë ekuivalente.

Kur llogaritet rangu i një matrice, ajo duhet të reduktohet në një formë trapezoidale duke përdorur një numër të kufizuar transformimesh elementare.

Përkufizimi 1.16. Ne do ta quajmë trapezoidale një formë të paraqitjes së matricës kur në minorën kufitare të rendit më të lartë jo zero, të gjithë elementët poshtë atyre diagonale zhduken. Për shembull:

Këtu
, elementet e matricës
shkoni në zero. Atëherë forma e paraqitjes së një matrice të tillë do të jetë trapezoidale.

Si rregull, matricat reduktohen në një formë trapezoidale duke përdorur algoritmin Gaussian. Ideja e algoritmit të Gausit është që, duke shumëzuar elementët e rreshtit të parë të matricës me faktorët përkatës, arrihet që të gjithë elementët e kolonës së parë të vendosura poshtë elementit.
, do të kthehej në zero. Pastaj, duke shumëzuar elementët e kolonës së dytë me faktorët përkatës, sigurojmë që të gjithë elementët e kolonës së dytë të vendosura poshtë elementit
, do të kthehej në zero. Pastaj vazhdoni në të njëjtën mënyrë.