How to understand the topic of operations with rational numbers. Rational numbers and operations on them

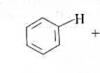
IN this lesson addition and subtraction of rational numbers are considered. The topic is classified as complex. Here it is necessary to use the entire arsenal of previously acquired knowledge.

The rules for adding and subtracting integers also apply to rational numbers. Recall that rational numbers are numbers that can be represented as a fraction, where a – this is the numerator of the fraction, b is the denominator of the fraction. At the same time, b should not be zero.

In this lesson fractions and mixed numbers we will increasingly call them by one general phrase - rational numbers.

Example 1. Find the meaning of the expression:

Let's enclose each rational number in brackets along with its signs. We take into account that the plus given in the expression is a sign of the operation and does not apply to the fraction. This fraction has its own plus sign, which is invisible due to the fact that it is not written down. But we will write it down for clarity:

This is the addition of rational numbers with different signs. To add rational numbers with different signs, you need to subtract the smaller module from the larger module, and before the resulting answer put the sign of the rational number whose module is larger. And in order to understand which modulus is greater and which is smaller, you need to be able to compare the moduli of these fractions before calculating them:

The modulus of a rational number is greater than the modulus of a rational number. Therefore, we subtracted from . We received an answer. Then, reducing this fraction by 2, we got the final answer.

Some primitive actions, such as putting numbers in brackets and adding modules, can be skipped. This example can be written briefly:

Example 2. Find the meaning of the expression:

Let's enclose each rational number in brackets along with its signs. We take into account that the minus standing between rational numbers and is an operation sign and does not refer to a fraction. This fraction has its own plus sign, which is invisible due to the fact that it is not written down. But we will write it down for clarity:

Let's replace subtraction with addition. Let us remind you that to do this you need to add to the minuend the number opposite to the subtrahend:

We obtained the addition of negative rational numbers. To add negative rational numbers, you need to add their modules and put a minus in front of the resulting answer:

Note. It is not necessary to enclose every rational number in parentheses. This is done for convenience, in order to clearly see which signs the rational numbers have.

Example 3. Find the meaning of the expression:

In this expression, the fractions different denominators. To make things easier, let's reduce these fractions to common denominator. We will not dwell in detail on how to do this. If you experience difficulties, be sure to repeat the lesson.

After reducing the fractions to a common denominator, the expression will take the following form:

This is the addition of rational numbers with different signs. We subtract the smaller module from the larger module, and before the resulting answer we put the sign of the rational number whose module is greater:

Let's write down the solution to this example in short:

Example 4. Find the value of an expression

Let's calculate this expression in the following: let's add the rational numbers and then subtract the rational number from the resulting result.

First action:

Second action:

Example 5. Find the meaning of the expression:

Let's represent the integer −1 as a fraction, and convert the mixed number into an improper fraction:

Let's enclose each rational number in brackets along with its signs:

We obtained the addition of rational numbers with different signs. We subtract the smaller module from the larger module, and before the resulting answer we put the sign of the rational number whose module is greater:

We received an answer.

There is a second solution. It consists of putting whole parts together separately.

So, let's go back to the original expression:

Let's enclose each number in parentheses. To do this, the mixed number is temporary:

Let's calculate the integer parts:

(−1) + (+2) = 1

In the main expression, instead of (−1) + (+2), we write the resulting unit:

The resulting expression is . To do this, write the unit and the fraction together:

Let's write the solution this way in a shorter way:

Example 6. Find the value of an expression

Let's convert the mixed number to an improper fraction. We will rewrite the rest of the part without changes:

Let's enclose each rational number in brackets along with its signs:

Let's replace subtraction with addition:

Let's write down the solution to this example in short:

Example 7. Find the value of an expression

Let's represent the integer −5 as a fraction, and convert the mixed number into an improper fraction:

Let's bring these fractions to a common denominator. After bringing them to a common denominator, they will take the following form:

Let's enclose each rational number in brackets along with its signs:

Let's replace subtraction with addition:

We obtained the addition of negative rational numbers. Let’s add the modules of these numbers and put a minus in front of the resulting answer:

Thus, the value of the expression is .

Let's decide this example the second way. Let's return to the original expression:

Let's write the mixed number in expanded form. Let's rewrite the rest without changes:

We enclose each rational number in brackets together with its signs:

Let's calculate the integer parts:

In the main expression, instead of writing the resulting number −7

The expression is an expanded form of writing a mixed number. We write the number −7 and the fraction together to form the final answer:

Let's write this solution briefly:

Example 8. Find the value of an expression

We enclose each rational number in brackets together with its signs:

Let's replace subtraction with addition:

We obtained the addition of negative rational numbers. Let’s add the modules of these numbers and put a minus in front of the resulting answer:

So the value of the expression is

This example can be solved in the second way. It consists of adding whole and fractional parts separately. Let's return to the original expression:

Let's enclose each rational number in brackets along with its signs:

Let's replace subtraction with addition:

We obtained the addition of negative rational numbers. Let's add the modules of these numbers and put a minus in front of the resulting answer. But this time we will add the whole parts (−1 and −2), both fractional and

Let's write this solution briefly:

Example 9. Find expression expressions

Let's convert mixed numbers to improper fractions:

Let's enclose a rational number in brackets together with its sign. There is no need to put a rational number in parentheses, since it is already in parentheses:

We obtained the addition of negative rational numbers. Let’s add the modules of these numbers and put a minus in front of the resulting answer:

So the value of the expression is

Now let's try to solve the same example in the second way, namely by adding integer and fractional parts separately.

This time, in order to obtain short solution, let's try to skip some steps, such as: writing a mixed number in expanded form and replacing subtraction with addition:

Please note that fractional parts have been reduced to a common denominator.

Example 10. Find the value of an expression

Let's replace subtraction with addition:

The resulting expression does not contain negative numbers, which are the main reason for errors. And since there are no negative numbers, we can remove the plus in front of the subtrahend and also remove the parentheses:

The result is a simple expression that is easy to calculate. Let's calculate it in any way convenient for us:

Example 11. Find the value of an expression

This is the addition of rational numbers with different signs. Let us subtract the smaller module from the larger module, and before the resulting answer we put the sign of the rational number whose module is greater:

Example 12. Find the value of an expression

The expression consists of several rational numbers. According to, first of all it is necessary to perform the actions in brackets.

First, we calculate the expression, then we add the obtained results.

First action:

Second action:

Third action:

Answer: expression value equals

Example 13. Find the value of an expression

Let's convert mixed numbers to improper fractions:

Let's put the rational number in brackets along with its sign. There is no need to put the rational number in parentheses, since it is already in parentheses:

Let's bring these fractions to a common denominator. After bringing them to a common denominator, they will take the following form:

Let's replace subtraction with addition:

We obtained the addition of rational numbers with different signs. Let us subtract the smaller module from the larger module, and before the resulting answer we put the sign of the rational number whose module is greater:

Thus, the meaning of the expression equals

Let's look at adding and subtracting decimals, which are also rational numbers and can be either positive or negative.

Example 14. Find the value of the expression −3.2 + 4.3

Let's enclose each rational number in brackets along with its signs. We take into account that the plus given in the expression is an operation sign and does not apply to the decimal fraction 4.3. This decimal fraction has its own plus sign, which is invisible due to the fact that it is not written down. But we will write it down for clarity:

(−3,2) + (+4,3)

This is the addition of rational numbers with different signs. To add rational numbers with different signs, you need to subtract the smaller module from the larger module, and before the resulting answer put the rational number whose module is larger. And in order to understand which module is larger and which is smaller, you need to be able to compare the modules of these decimal fractions before calculating them:

(−3,2) + (+4,3) = |+4,3| − |−3,2| = 1,1

The modulus of the number 4.3 is greater than the modulus of the number −3.2, so we subtracted 3.2 from 4.3. We received the answer 1.1. The answer is positive, since the answer must be preceded by the sign of the rational number whose modulus is greater. And the modulus of the number 4.3 is greater than the modulus of the number −3.2

Thus, the value of the expression −3.2 + (+4.3) is 1.1

−3,2 + (+4,3) = 1,1

Example 15. Find the value of the expression 3.5 + (−8.3)

This is the addition of rational numbers with different signs. As in the previous example, we subtract the smaller one from the larger module and before the answer we put the sign of the rational number whose module is greater:

3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8

Thus, the value of the expression 3.5 + (−8.3) is −4.8

This example can be written briefly:

3,5 + (−8,3) = −4,8

Example 16. Find the value of the expression −7.2 + (−3.11)

This is the addition of negative rational numbers. To add negative rational numbers, you need to add their modules and put a minus in front of the resulting answer.

You can skip the entry with modules so as not to clutter the expression:

−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31

Thus, the value of the expression −7.2 + (−3.11) is −10.31

This example can be written briefly:

−7,2 + (−3,11) = −10,31

Example 17. Find the value of the expression −0.48 + (−2.7)

This is the addition of negative rational numbers. Let's add their modules and put a minus in front of the resulting answer. You can skip the entry with modules so as not to clutter the expression:

−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18

Example 18. Find the value of the expression −4.9 − 5.9

Let's enclose each rational number in brackets along with its signs. We take into account that the minus, which is located between the rational numbers −4.9 and 5.9, is an operation sign and does not belong to the number 5.9. This rational number has its own plus sign, which is invisible due to the fact that it is not written down. But we will write it down for clarity:

(−4,9) − (+5,9)

Let's replace subtraction with addition:

(−4,9) + (−5,9)

We obtained the addition of negative rational numbers. Let’s add their modules and put a minus in front of the resulting answer:

(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8

Thus, the value of the expression −4.9 − 5.9 is −10.8

−4,9 − 5,9 = −10,8

Example 19. Find the value of the expression 7 − 9.3

Let's put each number in brackets along with its signs.

(+7) − (+9,3)

Replace subtraction with addition

(+7) + (−9,3)

(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3

Thus, the value of the expression 7 − 9.3 is −2.3

Let's write down the solution to this example in short:

7 − 9,3 = −2,3

Example 20. Find the value of the expression −0.25 − (−1.2)

Let's replace subtraction with addition:

−0,25 + (+1,2)

We obtained the addition of rational numbers with different signs. Let us subtract the smaller module from the larger module, and before the answer we put the sign of the number whose module is greater:

−0,25 + (+1,2) = 1,2 − 0,25 = 0,95

Let's write down the solution to this example in short:

−0,25 − (−1,2) = 0,95

Example 21. Find the value of the expression −3.5 + (4.1 − 7.1)

Let's perform the actions in brackets, then add the resulting answer with the number −3.5

First action:

4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0

Second action:

−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5

Answer: the value of the expression −3.5 + (4.1 − 7.1) is −6.5.

Example 22. Find the value of the expression (3.5 − 2.9) − (3.7 − 9.1)

Let's do the steps in parentheses. Then, from the number that was obtained as a result of executing the first brackets, subtract the number that was obtained as a result of executing the second brackets:

First action:

3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6

Second action:

3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4

Third act

0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6

Answer: the value of the expression (3.5 − 2.9) − (3.7 − 9.1) is 6.

Example 23. Find the value of an expression −3,8 + 17,15 − 6,2 − 6,15

Let us enclose each rational number in brackets along with its signs

(−3,8) + (+17,15) − (+6,2) − (+6,15)

Let's replace subtraction with addition where possible:

(−3,8) + (+17,15) + (−6,2) + (−6,15)

The expression consists of several terms. According to the combinatory law of addition, if an expression consists of several terms, then the sum will not depend on the order of actions. This means that the terms can be added in any order.

Let's not reinvent the wheel, but add all the terms from left to right in the order they appear:

First action:

(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35

Second action:

13,35 + (−6,2) = 13,35 − −6,20 = 7,15

Third action:

7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1

Answer: the value of the expression −3.8 + 17.15 − 6.2 − 6.15 is 1.

Example 24. Find the value of an expression

Let's convert the decimal fraction −1.8 to a mixed number. Let's rewrite the rest without changing:

Then a + b = b + a, a+(b + c) = (a + b) + c.

Adding zero does not change the number, but the sum of opposite numbers is zero.

This means that for any rational number we have: a + 0 = a, a + (- a) = 0.

Multiplication of rational numbers also has commutative and associative properties. In other words, if a, b and c are any rational numbers, then ab - ba, a(bc) - (ab)c.

Multiplication by 1 does not change a rational number, but the product of a number and its inverse is equal to 1.

This means that for any rational number a we have:

a) x + 8 - x - 22; c) a-m + 7-8+m;
b) -x-a + 12+a -12; d) 6.1 -k + 2.8 + p - 8.8 + k - p.

1190. Having chosen a convenient calculation order, find the value of the expression:

1191. Formulate in words the commutative property of multiplication ab = ba and check it when:

1192. Formulate in words associative property multiply a(bc)=(ab)c and check it with:

1193. Choosing a convenient calculation order, find the value of the expression:

1194. What number will you get (positive or negative) if you multiply:

a) one negative number and two positive numbers;
b) two negative and one positive number;
c) 7 negative and several positive numbers;
d) 20 negative and several positive? Draw a conclusion.

1195. Determine the sign of the product:

a) - 2 (- 3) (- 9) (-1.3) 14 (- 2.7) (- 2.9);
b) 4 (-11) (-12) (-13) (-15) (-17) 80 90.

a) Vitya, Kolya, Petya, Seryozha and Maxim gathered in the gym (Fig. 91, a). It turned out that each of the boys knew only two others. Who knows whom? (The edge of the graph means “we know each other.”)

b) Brothers and sisters of one family are walking in the yard. Which of these children are boys and which are girls (Fig. 91, b)? (The dotted edges of the graph mean “I am a sister,” and the solid ones mean “I am a brother.”)

1205. Calculate:

1206. Compare:

a) 2 3 and 3 2; b) (-2) 3 and (-3) 2; c) 1 3 and 1 2; d) (-1) 3 and (-1) 2.

1207. Round 5.2853 to thousandths; to hundredths; up to tenths; up to units.

1208. Solve the problem:

1) A motorcyclist catches up with a cyclist. Now there are 23.4 km between them. The speed of a motorcyclist is 3.6 times the speed of a cyclist. Find the speeds of the cyclist and the motorcyclist if it is known that the motorcyclist will catch up with the cyclist in an hour.
2) A car is catching up with a bus. Now there are 18 km between them. The speed of the bus is the same as that of a passenger car. Find the speeds of the bus and the car if it is known that the car will catch up with the bus in an hour.

1209. Find the meaning of the expression:

1) (0,7245:0,23 - 2,45) 0,18 + 0,07 4;
2) (0,8925:0,17 - 4,65) 0,17+0,098;
3) (-2,8 + 3,7 -4,8) 1,5:0,9;
4) (5,7-6,6-1,9) 2,1:(-0,49).

Check your calculations with micro calculator.
1210. Having chosen a convenient calculation procedure, find the value of the expression:

1211. Simplify the expression:

1212. Find the meaning of the expression:

1213. Follow these steps:

1214. The students were given the task of collecting 2.5 tons of scrap metal. They collected 3.2 tons of scrap metal. By what percentage did the students complete the task and by what percentage did they exceed the task?

1215. The car traveled 240 km. Of these, 180 km she walked along a country road, and the rest of the way along the highway. Gasoline consumption per 10 km country road was 1.6 liters, and on the highway - 25% less. How many liters of gasoline were consumed on average for every 10 km of travel?

1216. Leaving the village, the cyclist noticed a pedestrian on the bridge walking in the same direction and caught up with him 12 minutes later. Find the speed of a pedestrian if the speed of a cyclist is 15 km/h and the distance from the village to the bridge is 1 km 800 m?

1217. Follow these steps:

a) - 4.8 3.7 - 2.9 8.7 - 2.6 5.3 + 6.2 1.9;
b) -14.31:5.3 - 27.81:2.7 + 2.565:3.42+4.1 0.8;
c) 3.5 0.23 - 3.5 (- 0.64) + 0.87 (- 2.5).

People, as you know, became acquainted with rational numbers gradually. At first, when counting objects, natural numbers arose. At first there were few of them. Thus, until recently, among the natives of the islands in the Torres Strait (separating New Guinea from Australia) there were only two numbers in the language: “urapun” (one) and “okaz” (two). The islanders counted as follows: “Okaza-urapun” (three), “Okaza-Okaza” (four), etc. The natives called all numbers, starting from seven, with a word meaning “many.”

Scientists believe that the word for hundreds appeared more than 7,000 years ago, for thousands - 6,000 years ago, and 5,000 years ago in Ancient Egypt and in Ancient Babylon names appear for huge numbers - up to a million. But for a long time the natural series of numbers was considered finite: people thought that there was a largest number.

The greatest ancient Greek mathematician and physicist Archimedes (287-212 BC) came up with a way to describe huge numbers. The largest number that Archimedes could name was so large that to digitally record it would require a tape two thousand times longer than the distance from the Earth to the Sun.

But they had not yet been able to write down such huge numbers. This became possible only after Indian mathematicians in the 6th century. the number zero was invented and it began to denote the absence of units in the digits decimal notation numbers.

When dividing the spoils and later when measuring values, and in other similar cases, people encountered the need to introduce “broken numbers” - common fractions. Operations with fractions were considered the most difficult area of ​​mathematics back in the Middle Ages. To this day, the Germans say about a person who finds himself in a difficult situation that he “fell into fractions.”

To make it easier to work with fractions, decimals were invented fractions. In Europe they were introduced in X585 by the Dutch mathematician and engineer Simon Stevin.

Negative numbers appeared later than fractions. For a long time such numbers were considered “non-existent”, “false” primarily due to the fact that the accepted interpretation for positive and negative numbers “property - debt” led to confusion: you can add or subtract “property” or “debts”, but how to understand the product or private “property” and “debt”?

However, despite such doubts and perplexities, rules for multiplying and dividing positive and negative numbers were proposed in the 3rd century. the Greek mathematician Diophantus (in the form: “What is subtracted, multiplied by what is added, gives the subtrahend; what is subtracted by the subtrahend gives what is added,” etc.), and later the Indian mathematician Bhaskar (XII century) expressed the same rules in the concepts of “property”, “debt” (“The product of two property or two debts is property; the product of property and debt is debt.” The same rule applies to division).

It was found that the properties of actions over negative numbers the same as over positive ones (for example, addition and multiplication have the commutative property). And finally, since the beginning of the last century, negative numbers have become equal to positive numbers.

Later, new numbers appeared in mathematics - irrational, complex and others. You learn about them in high school.

N.Ya.Vilenkin, A.S. Chesnokov, S.I. Shvartsburd, V.I. Zhokhov, Mathematics for grade 6, Textbook for high school

Books and textbooks according to the calendar plan for 6th grade mathematics download, help for schoolchildren online

Open lesson on mathematics in 6th grade.

Subject: Operations with rational numbers. (One number lesson)

Target: consolidate skills in operations with positive and negative numbers. Preparing for test work.

Tasks:

• Review the concepts of positive and negative numbers; consolidate skills in performing actions with positive and negative numbers.

• To promote interest in the subject through unconventional shape conducting a lesson.
• Develop logical ingenuity and creative thinking.

Lesson type: lesson of repetition and consolidation of students' knowledge using IT.

Forms of organization educational activities: collective, individual, pair, brainstorming.

Equipment: computer, projector, PowerPoint presentation (attached), set of individual cards.

Lesson progress

1. Organizational moment.

We write down the topic of the lesson and the date in a notebook. Why is the topic written so unusually? (Actions with diet al numbers.)

Warm-up: it’s dark outside, it seems like night, but it’s time to wake up and get ready for school. So that it doesn’t turn out like the saying: They raised you up, but forgot to wake you up. I decided to wake you up just in case...

Charger: Good morning: I ask a question to a student, if he answers, he’s sitting, no, he can forward it to someone else, someone who isn’t sitting yet. Answered correctly, names whom next question. (Brainstorm)

1) smallest natural number (1)

2) the result of multiplication (Product)

3) The number opposite to 4?

4) A segment connecting a point on a circle with its center (Radius)

5) One hundredth of a number (Percentage)

6) tool for measuring angles (Protractor)

7) Is it possible to get 0 when dividing numbers (yes)

8) what do plants and equations have? (Root)

9) what is 10² equal to? (100)

10) numbers that are used when counting objects?

12) what is heavier than 1 kg of cotton wool or 1 kg of iron?

13) distance from the origin to the number on the coordinate line (modulus)

14) the sum of two opposite numbers (0)

15) 2³ (8)

16) is it possible to divide by zero?

17) module – 9 (9)

18) result of division (quotient)

19) What number is obtained by multiplying two negative numbers (positive)

20) product of mutual reciprocal numbers (1)

21) Numbers with a “-” sign are called (negative)

22) result of addition (sum)

23) A number showing the position of a point on a coordinate line (coordinate)

24) Numbers with a “+” sign are called (positive)

25) Natural numbers, their opposites and zero are (integers)

26) Which number is neither positive nor negative. (zero)

Today in class we will repeat, summarize and systematize the knowledge you gained in previous classes. Let's prepare for the test.

And one thing will help us with this very much interesting number. Try to guess which one?

Tips:

That's right - this is the number 30.

• Why do you think this number is? (Our class is 30 people)

I think that in the life of each of you some event is connected with the number 30. For example, this is my wedding date. What about you? (students' answers)

1. Oral work.

• Let's answer a few questions.

1. Please tell me what we know about the number 30?

(positive, integer, even, composite)

1. Where is this number located on the coordinate line?

(This number on the coordinate line is located to the left of zero)

1. Name two integers adjacent to the given number.

(29 and 31)

1. What number will be the opposite of this?

(Number -30)

1. Why modulus is equal given number?

(The modulus of this number is 30)

1. The reciprocal of this?

{ }

1. A number symmetrical to the number 30 relative to 0?

{ }

In addition, in mathematics there are several other interesting facts associated with the number 30:

Well, we will continue

1. Tasks to review the material covered.

Let's draw a figure on coordinate plane:

1. (-5;3); (-4;4); (-2;4);(-1;3);(-1;1);(-3;0)(-1;-1);(-1;-4);(-2;-5);(-4;-5);(-5;-4)
2. (1;3);(2;4);(4;4);(5;3);(5;-4);(4;-5);(2;-5);(1;-4);(1;3).

What does this number mean in the world of numbers or spiritual numerology:

The number 30 is made up of two digits 3 and 0. Therefore, to truly understand the meaning of the number 30 you need to know main meaning these numbers. The main meaning of the troika is Love in all its manifestations, starting from the most “base”, physiological, and ending with the most “high”, spiritual and intuitive.

The meaning of zero in spiritual numerology is peace, tranquility, tranquility. Therefore, thirty is translated from the language of numbers as “tranquility in love” or “tranquility in love”, or “love that has exhausted itself.” The choice of wording depends on a number of subjective and objective factors in the life of an individual.

meaning of number 30

The number 30 indirectly creates the preconditions for success in everything. The number 30 is not directly related to making a profit, material prosperity and career. But (!) indirectly this number can contribute to profit, career, and EVERYTHING!

Still, the main thing that the number 30 promotes is love. Number 30 does not like sudden movements, hot words and loud vows. The number 30 simply fills everyone who comes into contact with it with LOVE or PEACE!

As a date, the number 30 ends a significant portion of the months of the year.

The 30th of the calendar is ideal for summing up results. Even if in as a last resort, commercial results, if in principle you are not going to summarize any others. The main thing is not to start anything on the 30th!

People born on the 30th are peaceful but very strong. They are calm and thorough. They need a specific outcome. The result of everything: the result of love, commerce or, say, a performance.

Number 30 people do not like vague phrases. They need a clear and concise yes or no.

1. Practical tasks. (physical training + practical application)

• Everyone has a number on the table. Your task: find a pair in the class so that the sum of your numbers is equal to 30.

(Numbers: -30 and 60; -5 and 35; -2.72 and 32.72; 2 and 27; -0.25 and 30 ; and 29.5; -6 and 36; I-2.5I and 27.5; I- I and 21; - and 30.5; 5 and 24.25; 38.6 and -8; -120 and 150.)

As soon as each pair has found each other, they take a task from the board (with the lowest number) and complete it: (chain of calculations). The chain is projected onto the screen. The pair that finishes early and correctly gets a “5”.

1. Interesting facts about the number 30:

• In the Bible

1. The age at which Jesus was baptized.
2. Judas received 30 pieces of silver for betraying Jesus

• In literature

1. In fairy tales: in the thirtieth kingdom, in the thirtieth state...
2. In Pushkin's fairy tale “About the Golden Fish” the old man and the old woman lived for 30 years and 3 years.
3. In Dostoevsky's novel "Crime and Punishment"The number 30 is dedicated to the story about the various financial problems of the heroes. Sonya brings 30 rubles, promises to send 30 rubles to Raskolnikov’s mother, Svidrigailov is ransomed for 30 thousand.
4. On October 19, 1811, Pushkin was admitted to the number 30 pupils Tsarskoye Selo Lyceum.

• In natural science

1. In the periodic table, number 30 is a brittle metal - zinc.
2. Number of days inApril , June , September , November
3. At temperatures below thirty degrees, classes for grades 1-9 are canceled.
4. February 30 . Three times in history, some countries have had 30 days in February.

The rest are working with a table of numbers at this time.

• Connection of numbers: blue and red. Using the options, find the action sign (one) due to which the calculation result is 30. The first option is blue, the second is red. (blue numbers product equals 30; red numbers sum equals 30).

Arrange the numbers in ascending order.

• Now let's check what you got.

(Blue: -2/3; -1/3; 0.25; 5/7;21;36

Reds: )

Let's summarize.

Test

1. Which numerical interval belongs to the number 30.

A) C) (25.7;30)

2. What is the abscissa of a point, if the sum of the coordinates of the point is 30,

And the ordinate is 5 times larger than the abscissa.

1. 5 B) 6 C) 4

1. Find the value of the expression: 2.7: (-0.3)+(-7.63+9.24) – 11.305*2

1. – 30 B) 30 C) 0.3

1. 20 B) 75 C) 12

Test key: BACAC. (Scores for correctly solving the test). Slide 2

Goals and objectives of the lesson: consolidate skills in operations with positive and negative numbers. Practice constructing points using their coordinates. Preparation for the test. Strengthening meta-subject connections.

NUMBER RIDDLE What is half an hour? What is 2/3 of a lesson equal to? How many days are there in September?

What do we know about the number 30? What can you say about the number 30? positive, integer, even, composite And where is this number located on the coordinate line? to the right of zero Name two integers adjacent to the given number. 29 and 31 And what number will be the opposite of this? -30 What is the modulus of this number? 30 What is the reciprocal of this? 1/30 A number symmetrical to the number 30, relative to 0? -30

Math facts 10 30 is called a nonillion. 2 30 = 1 073 741 824, binary prefix: gibi (Gi). The number of edges of the icosahedron and dodecahedron. Sum of squares of the first four numbers. (1²+2²+3²+4²). The minimum number that is product of three various prime numbers. (2*3*5) Three consecutive identical numbers in the Roman number system (XXX).

Coordinate plane Draw a figure on the coordinate plane: (-5;3); (-4;4); (-2;4); (- 1;3);(-1;1);(-3;0) (- 1;-1);(-1;-4);(-2;-5);(-4;-5 );(-5;-4) (1;3);(2;4);(4;4);(5;3);(5;-4);(4;-5);(2; -5);(1;-4);(1;3).

The meaning of the number 30 (spiritual numerology) The number 30 consists of two numbers 3 and 0. The main meaning of 3 is Love. 0 is peace, tranquility, tranquility. 30 - translated as “tranquility in love” or “tranquility in love”, or “love that has exhausted itself.” The number 30 indirectly creates the preconditions for success in everything. . The number 30 fills everyone who comes into contact with it with LOVE or PEACE! The 30th of the calendar is ideal for summing up results. People born on the 30th are peaceful but very strong.

Find the pair -30 and 60; - 5 and 35; - 2.72 and 32.72; 2 and 27; - 0.25 and 30; and 29.5; -6 and 36; I - I and 21; - and 30.5; 5 and 24.25; 38.6 and -8; - 120 and 150. I -2.5 I and 27.5;

Chain of calculations -27.5 +(-7.24)= –(-35.96)= *2.3= +(- 3.906)= : = *(-5) = : (-0.25) = + 58.4 = * 3 = : 8 = *(- 8.6)= –(- 8.56)= + 11.12 =

Interesting facts about the number 30: In literature In fairy tales: in the thirtieth kingdom, in the thirtieth state... In Pushkin’s fairy tale “About the Goldfish” the old man and the old woman lived 30 years and 3 years. In Dostoevsky's novel Crime and Punishment, the number 30 is associated with the story about the various financial problems of the heroes. Sonya brings 30 rubles, promises to send 30 rubles to Raskolnikov’s mother, Svidrigailov is ransomed for 30 thousand. On October 19, 1811, Pushkin was accepted as one of the 30 students at the Tsarskoye Selo Lyceum. In the Bible the age at which Jesus was baptized. Judas received 30 pieces of silver for betraying Jesus In natural science In the periodic table, number 30 is zinc. Number of days in April, June, September, November When the temperature is below thirty degrees, classes for grades 1-9 are canceled. February 30. Three times in history, some countries have had 30 days in February.

Number connection - 2.5 0.1 9.6 21 0.25 36 8.9 - 2.5 0.1 9.6 21 0.25 36 8.9 Blue: -2/3; -1/3; 0.25; 5/7;21;36 Red:

Test 1. Which numerical interval does the number 30 belong to? A) C) (25.7;30) 2. What is the abscissa of a point equal to if the sum of the coordinates of the point is 30, and the ordinate is 5 times greater than the abscissa. A) 5 B) 6 C) 4 3. By what number should we divide (-2 so that the quotient is equal to 30. A) 13 B) - 66 C) – 13.5 4. Find the value of the expression: 2.7: (- 0.3)+(-7.63+9.24) – 11.305*2 A)– 30 B) 30 C) 0.3 5. How many times is contained in 30. A) 20 B) 75 C) 12

In this lesson we will recall the basic properties of operations with numbers. We will not only review the basic properties, but also learn how to apply them to rational numbers. We will consolidate all the knowledge gained by solving examples.

Basic properties of operations with numbers:

The first two properties are properties of addition, the next two are properties of multiplication. The fifth property applies to both operations.

There is nothing new in these properties. They were valid for both natural and integer numbers. They are also true for rational numbers and will be true for the numbers we will study next (for example, irrational numbers).

Permutation properties:

Rearranging the terms or factors does not change the result.

Combination properties:, .

Adding or multiplying multiple numbers can be done in any order.

Distribution property:.

The property connects both operations - addition and multiplication. Also, if you read it from left to right, then it is called the rule for opening parentheses, and if in reverse side- rule of adjudication common multiplier out of brackets.

The following two properties describe neutral elements for addition and multiplication: adding zero and multiplying by one does not change the original number.

Two more properties that describe symmetrical elements for addition and multiplication, the sum of opposite numbers is zero; the product of reciprocal numbers is equal to one.

Next property: . If a number is multiplied by zero, the result will always be zero.

The last property we'll look at is: .

Multiplying the number by , we get opposite number. This property has a special feature. All other properties considered could not be proven using the others. The same property can be proven using the previous ones.

Multiplying by

Let us prove that if we multiply a number by , we get the opposite number. For this we use the distribution property: .

This is true for any numbers. Let's substitute and instead of the number:

On the left in parentheses is the sum of mutually opposite numbers. Their sum is zero (we have such a property). On the left now. On the right, we get: .

Now we have zero on the left, and the sum of two numbers on the right. But if the sum of two numbers is zero, then these numbers are mutually opposite. But the number has only one opposite number: . So, this is what it is: .

The property has been proven.

Such a property, which can be proven using previous properties, is called theorem

Why are there no subtraction and division properties here? For example, one could write the distributive property for subtraction: .

But since:

• Subtracting any number can be equivalently written as addition by replacing the number with its opposite:

• Division can be written as multiplication by its reciprocal:

This means that the properties of addition and multiplication can be applied to subtraction and division. As a result, the list of properties that need to be remembered is shorter.

All the properties we have considered are not exclusively properties of rational numbers. Other numbers, for example, irrational ones, also obey all these rules. For example, the sum of its opposite number is zero: .

Now we will move on to the practical part, solving several examples.

Rational numbers in life

Those properties of objects that we can describe quantitatively, designate with some number, are called values: length, weight, temperature, quantity.

The same quantity can be denoted by both an integer and a fractional number, positive or negative.

For example, your height is m - fractional number. But we can say that it is equal to cm - this is already an integer (Fig. 1).

Rice. 1. Illustration for example

Another example. A negative temperature on the Celsius scale will be positive on the Kelvin scale (Fig. 2).

Rice. 2. Illustration for example

When building the wall of a house, one person can measure the width and height in meters. He produces fractional quantities. He will carry out all further calculations with fractional (rational) numbers. Another person can measure everything in the number of bricks in width and height. Having received only integer values, he will carry out calculations with integers.

The quantities themselves are neither integer nor fractional, neither negative nor positive. But the number with which we describe the value of a quantity is already quite specific (for example, negative and fractional). It depends on the measurement scale. And when we move from real values ​​to mathematical model, then we work with a specific type of numbers

Let's start with addition. The terms can be rearranged in any way that is convenient for us, and the actions can be performed in any order. If terms of different signs end in the same digit, then it is convenient to perform operations with them first. To do this, let's swap the terms. For example:

Common fractions with same denominators easy to fold.

Opposite numbers add up to zero. Numbers with the same decimal tails are easy to subtract. Using these properties, as well as the commutative law of addition, you can make it easier to calculate the value of, for example, the following expression:

Numbers with complementary decimal tails are easy to add. With whole and in fractional parts It is convenient to work with mixed numbers separately. We use these properties when calculating the value of the following expression:

Let's move on to multiplication. There are pairs of numbers that are easy to multiply. Using the commutative property, you can rearrange the factors so that they are adjacent. The number of minuses in a product can be counted immediately and a conclusion can be drawn about the sign of the result.

Consider this example:

If from the factors equal to zero, then the product is equal to zero, for example: .

The product of reciprocal numbers is equal to one, and multiplication by one does not change the value of the product. Consider this example:

Let's look at an example using distributive property. If you open the parentheses, then each multiplication is easy.

Operations with decimal fractions.
 Adding and subtracting decimals.
1. Equalize the number of digits after the decimal point.
2. Add or subtract decimals comma under comma by digits.
 Multiplying decimals.
1. Multiply without paying attention to commas.
2. In the product of a comma, separate as many digits from the right as there are in all factors
together after the decimal point.
 Dividing decimals.
1. In the dividend and divisor, move the commas to the right by as many digits as there are after the decimal point
in the divider.
2. Divide the whole part and put a comma in the quotient. (If whole part less than divisor, That
the quotient starts from zero integers)
3. Continue dividing.
Actions with positive and negative numbers.
Adding and subtracting positive and negative numbers.
a – (– c) = a + c
All other cases are considered as addition of numbers.
 Addition of two negative numbers:
1. write the result with a “–” sign;
2. We add the modules.
 Addition of numbers with different signs:
1. put the sign of the greater module;
2. subtract the smaller one from the larger module.
 Multiplying and dividing positive and negative numbers.
1. When multiplying and dividing numbers with different signs, the result is written with a sign
minus.
2. When multiplying and dividing numbers with identical signs the result is written with a sign
plus.
Operations with ordinary fractions.
Addition and subtraction.
1. Reduce fractions to a common denominator.
2. Add or subtract the numerators, but leave the denominator unchanged.
Multiply the numerator by the numerator, and the denominator by the denominator (reduce if possible).
“Flip” the divisor (second fraction) and perform the multiplication.
Division.
Multiplication.
Isolating the whole part from an improper fraction.
38
5 = 38: 5 = 7(remaining 3) = 7
3
5
Converting a mixed number to an improper fraction.
2
7 + =
4
4·7+2
7
30
7
=

1
.
+
Reducing a fraction.
Reduce a fraction - divide the numerator and denominator by the same number.
6
7
6
7. In short:
30:5
35:5 =
30
35 =
For example:
30
35 =
.
1.
Break down the denominators of fractions into prime ones
multipliers.
Reducing fractions to a common denominator.
5 4
7
16 +

36
80 =
71
80
2. Cross out identical factors.
3. Remaining factors from the denominator of the first
multiply fractions and write as
an additional factor for the second fraction, and
from the second fraction to the first fraction.
2∙2∙2∙2 2∙2∙5
4. Multiply the numerator and denominator of each fraction
by its additional multiplier.
9
20 =
35
80 +
Addition and subtraction of mixed numbers.
Add or subtract separately whole parts and fractional parts separately.
"Special" cases:
"Convert" 1 into a fraction whose numerator and

2
2
5
6
3
5 =
3
5 = 2
1
1
Take 1 and “turn” it into a fraction whose numerator and
denominators are equal to the denominator of the given fraction.
Take 1 and add the denominator to the numerator.
3
5 =
3
5 = 2
5
5 ‒
5
5 ‒
‒
1
‒
3
2
5
1 ‒
3
3
5 = 2
5
5 1 ‒
3
5 = 1
2
5
1
5
1 ‒
3
5 = 2
6
5 1‒
3
3
5 = 1
3
5
Convert mixed numbers to improper fractions and perform multiplication or division.
Multiplication and division of mixed numbers.

2
7 + ∙ 2
4
4
5 + =
30
7 ∙
14
5 =
30·14
7·5
6·2
1 1 =
12
1 = 12
=
∙ ∙
6
7