Lecture 14 Random processes Canonical expansion of random processes. Spectral decomposition stationary random process. SluLecture 14
Random processes
Canonical expansion of random processes.
Spectral decomposition of stationary random
process. Random processes with independent
sections. Markov processes and Markov chains.
Normal random processes. Periodically
non-stationary random processes
(Akhmetov S.K.)
Canonical expansion of random processes
Any SP X(t) m.b. presented inthe form of its decomposition, i.e. as a sum
elementary processes:
Vk – random variables
φk(t) – non-random functions (sinusoids, exponentials, power
functions, etc.)
A special case of such decomposition is Canonical
decomposition
SP X(t), which has the form
mx(t) = M – mathematical expectation of SP X(t)
V1, V2…Vk – uncorrelated and centered SVs
D1, D2…Dk- SW dispersions V1, V2…Vk
φk(t) – non-random functions of the argument t
Random variables V1, V2…Vk are called coefficients of the canonical
decomposition,
and non-random functions φ1(t), φ2(t) φk(t) - coordinate functions
canonical expansion
Main characteristics of the SP defined by the canonical decomposition
M – mathematical expectation of SP X(t)Kx(t,t’) – correlation function SP X(t)
Expression
- canonical decomposition correlation
functions
If t=t’, then in accordance with the first
property of the correlation function
Expression
Dk(t) –
dispersion
canonical expansion of the variance of the SP X(t)
Spectral decomposition of a stationary SP
Stationary joint venture m.b. represented by the canonical decompositionVk and Uk – uncorrelated and centered SVs with dispersions
D = D = Dk
ω – non-random value (frequency)
In this case, the canonical expansion of the correlation function
is determined by the expression
Submitted
canonical
decomposition
JV
X(t)
called
spectral decomposition of SP and
expressed as
Θk - phase harmonic vibration elementary stationary SP,
being a SW uniformly distributed in the interval (0, 2π);
Zk – SV, which is the amplitude of the harmonic oscillation
elementary stationary SP
Spectral decomposition of stationary SP (2)
The random variables Θk and Zk are dependent and the following holds true for them:Vk = Zk cos Θk
Uk = Zk sin Θk
Stationary joint venture m.b. presented as a sum of harmonics
oscillations with random amplitudes Zk and random phases Θk on
various non-random frequencies ωk
The correlation function of the stationary SP X(t) is even
function of its argument, i.e. kx(τ) = kx(-τ). Therefore, on the interval (-T,
T) can be expanded into a Fourier series in even (cosine) harmonics:
The variance of the stationary SP X(t) is equal to
amount
variances
everyone
harmonics
his
spectral decomposition
The dependence Dk = f(wk) is called the discrete dispersion spectrum or
discrete spectrum of a stationary SP.
Spectral decomposition of stationary SP (3)
At ∆ω→ 0 there will be a transition to a continuous spectrum
Sx(ω) - spectral density
Thus, the correlation function and spectral density
connected by cosine – Fourier transform. Therefore, the spectral
density of stationary joint venture m.b. expressed through correlation
function by formula
Random processes with independent cross sections
In hydrology, it is believed that the series corresponds to a random modelvalues, if there is no significant correlation between members of this series
for any shift τ.
A random process with independent cross sections is a stochastic process for which
at values t and t’
mx(t) = mx
Dx(t) = Dx
Kx(t,t’) = kx(τ) = (Dx for τ = 0 and 0 for τ ≠ 0)
Such a process is stationary and has ergodic
property
For such processes, the characteristics of the one-dimensional distribution law
can be assessed both for any section and for any (enough
long-term) implementation
Such processes have no correlation between members within any
implementation
Accepting such a model, it is assumed that a number of hydrological quantities
represents one implementation of the joint venture
A random process with independent cross sections is sometimes called
"white noise" by analogy with white light
Markov processes and Markov chains
Random processis called Markovian if for any
at time t the probability of each state of the system in the future
(at t > t0) depends only on its state in the present (at t = t0) and not
depends on its state in the past (at t< t0)
Markov chain or simple Markov chain called
Markov process with discrete state and discrete time
Markov SP is completely described by a two-dimensional law
distributions. If Markov process is stationary and
ergodic, then its characteristics can be estimated based on one
implementation.
The circuit in which conditional probabilities states in the future depend
from its state in several previous steps is called complex
Markov chain.
Normal (Gaussian) random processes
A normal (Gaussian) random process X(t) is calledSP, in which in all sections the SP X(ti) has a normal
distribution
Periodically non-stationary joint ventures
When studying annual, monthly, daily, etc. processes are usually
observed intra-annually, etc. fluctuations. In this case, as
mathematical model, you can use the model periodically
non-stationary random process (NSRP)
A random process is called periodically nonstationary if
his probabilistic characteristics invariants under shifts by
positive number T. For example, with a discrete step of one month
invariance should be preserved for shifts of 12, 24, 36, etc.
I. V. Yakovlev | Mathematics materials | MathUs.ru
Problem C6 on the Unified State Exam in mathematics
1 Necessary theory | ||
Number sets. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
Divisibility. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
Parity. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
Division with remainder. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
Canonical expansion. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||
1.6 Coprime numbers. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.7 Sequences. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.8 Arithmetic progression. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
It is known that on the Unified State Exam in mathematics, many schoolchildren do not start problem C6 and do not even read it (why? I still can’t solve it, they say). And in vain!
As a rule, task C6 consists of two or three points, some of which are quite simple. For the entire task, 4 primary points are given, 1-2 points for each point. Therefore, having completed at least part of the task (say, simply presenting the right example in one of the points), you can get additional primary points. And they will give an increase in the final result on a hundred-point scale!
To solve problem C6 you need minimum stock knowledge. This is 6th grade arithmetic (everything related to divisibility) and information on progressions from 9th grade algebra. Nothing else.
Why is problem C6 considered (and, in general, is) the most difficult on the Unified State Exam in mathematics? She is unconventional. It requires the so-called mathematical culture, the ability to reason competently. And the vast majority of schoolchildren completely lack this skill because, unfortunately, at school, things usually don’t come to the point of developing a mathematical culture.
Learning to reason culturally is possible and absolutely necessary. Problem C6 provides an excellent opportunity for this. It won’t start happening right away, so you should start preparing for C6 long before the Unified State Exam. There is only one recipe: decide, decide, decide.
This manual was written to help schoolchildren learn to solve non-standard tasks type C6. It contains everything you need theoretical material and tasks, most of which were offered on the Unified State Exam and diagnostic works of MIOO recently.
Solutions are provided for all problems. At the same time, the goal was not to make the solution concise and as technically perfect as possible (at the expense of the presentation of ideas). After all, learning mathematics means grasping ideas; The main emphasis is placed on clarifying the ideas underlying the solution of each problem.
1 Necessary theory
1.1 Number sets
IN this section we will determine number sets, necessary for task C6. You need to know the introduced terminology firmly!
Natural numbers are the numbers 1; 2; 3; : : : We use natural numbers for counting, and counting starts from one. Therefore, attention: zero is not a natural number! (After all, it would hardly occur to us to say: “There are zero cups on the table.”)
The set of natural numbers is denoted by N.
Integers are the numbers 0; 1; 2; 3; : : : Thus, the integers are zero and ¾plus minus natural numbers¿. Natural numbers are positive integers.
The set of integers is denoted by Z. (This is the notation we constantly use in trigonometric equations to record answers.)
Rational numbers are all kinds of fractions m = n with integers m and n (in this case, of course, n 6 = 0; to avoid this reservation, they also say that m is an integer and n is a natural number).
Any integer is at the same time rational (for example, 3 = 6 = 2). However, 1/2 is not an integer.
A bunch of rational numbers denoted by Q.
1.2 Divisibility
The concept of divisibility applies to whole numbers (in particular, natural numbers). From this point on, all numbers are considered integers. If in any case this turns out not to be the case, we will make a special reservation.
We denote integers by a; b; c; : : : ; k; l; m; n; : : : ; x; y; z, that is, we use everything lower case Latin alphabet.
You know very well that the number 12 is divisible by 4, but not divisible by 5. What is formal definition divisibility? Here it is.
Definition. The number a is divided by the number b 6= 0 if there is a number c such that a = bc.
If a is divisible by b, then b is called a divisor of a. For example, the number 12 has six divisors: 1, 2, 3, 4, 6 and 12.
Exercise. Prove that if the numbers a and b are divisible by c, then a + b is also divisible by c.
Let us formulate the most important signs divisibility.
a is divisible by 2, last digit a is 0, 2, 4, 6 or 8;
a is divisible by 5, the last digit of a is 0 or 5;
a is divisible by 10, the last digit of a is 0;
a is divisible by 3, the sum of the digits of a is divisible by 3;
a is divisible by 9, the sum of the digits of a is divisible by 9.
1.3 Parity
Considerations related to evenness and oddness often appear in C6 problems. Therefore, it makes sense to especially note the necessary facts.
Definition. A number is called even if it is divisible by 2. A number is called odd if it is not divisible by 2.
Here are all the even numbers: 0; 2; 4; 6; : : : If a is even, then it has the form a = 2n. But all odd numbers: 1; 3; 5; : : : It is clear that if a is odd, then it has the form a = 2n + 1.
The following statements are very obvious, and you can use them to solve Problem C6 (no one will ask you to prove them). But you can prove them as an exercise.
The sum of any number of even terms is even.
The sum of an even number of odd terms is even. The sum of an odd number of odd terms is odd.
Let there be a product of several factors. If all factors are odd, then the product is odd. If at least one factor is even, then the product is even.
1.4 Division with remainder
The number 13 is not divisible by 5. Largest number which is divisible by 5 and does not exceed 13 is 10 = 5 2. Thus, 13 = 5 2+3, and we say that dividing 13 by 5 gives the quotient of 2 and the remainder of 3.
It turns out that any number a can be divided with a remainder by any number b 6 = 0. Namely, there are two numbers q and r such that a = bq + r, and the inequality 0 6 r will be satisfied< jbj. Число q назвается частным, а число r остатком от деления a на b.
If r = 0, that is, a = bq, then a is divisible by b.
Exercise. Find the quotient and remainder of division: a) 7 by 2; b) 15 by 4; c) 2012 at 5; d) 1001 by 13; e) 9 by 8; e) 8 by 9.
Remainder when dividing any odd number by 2 equal to one. That's why everything odd number can be written as 2n + 1.
Leftovers prove useful in many situations. Let's say that while solving a problem you need to prove that the equality n2 = 3k + 2 cannot be true for any integers n and k. We reason as follows.
The number n when divided by 3 can give remainders of 0, 1 or 2. In other words, three cases are possible: n = 3m, n = 3m + 1 or n = 3m + 2. What remainders will the number n2 have when divided by 3? Let's see what happens in each of the three cases.
(3m)2 = 9m2 (remainder 0);
(3m + 1)2 = 9m2 + 6m + 1 (remainder 1);
(3m + 2)2 = 9m2 + 12m + 4 = (9m2 + 12m + 3) + 1 (remainder 1):
Thus, the square of an integer when divided by 3 cannot leave a remainder of 2. Therefore, the equality n2 = 3k + 2 is indeed impossible for any n and k.
Exercise. Prove that the number 100: : : 004 (there are any number of zeros between 1 and 4) is not a square of an integer.
Exercise. Prove that the square of an integer when divided by 4 can give only two remainders: 0 and 1.
Exercise. Prove that n3 + 2n is divisible by 3.
1.5 Canonical expansion
Every number is divisible by 1 and itself. If natural number p is not equal to 1 and has no others natural divisors, except 1 and p, then such a number p is called prime.
Here are the first few prime numbers: 2, 3, 5, 7, 11, 13, 17, 19. The number 2 is the only even prime number.
A number that is not equal to 1 and is not prime is called composite. For example, 15 is a composite number (it is divisible by 3). The number 1036 is also a composite number (it is even). The unit is neither prime number, nor composite.
Exercise. The number 315 1 is composite. Why?
It turns out that every number can be decomposed into prime factors. For example:
30 = 2 3 5; 504 = 2 2 2 3 3 7 = 23 32 7:
Such an expansion is unique up to the order of the factors and is called the canonical expansion. The statement about the existence and uniqueness of the canonical decomposition is called the fundamental theorem of arithmetic.
The canonical expansion gives full picture divisors of a given number (and, in particular, allows you to find their number). Namely, let a = pn 1 1 pn 2 2 : : : pn s s be the canonical expansion of the number a. Then the canonical expansion of any divisor of a number consists of prime factors included in the set fp1 ; p2 ; : : : ; ps g, the exponents of which do not exceed the numbers n1, respectively; n2 ; : : : ; ns. For example, any divisor of the number 504 = 23 32 7 has the form 2a 3b 7c, where a 2 f0; 1; 2; 3g, b 2 f0; 1; 2g and c 2 f0; 1g.
Exercise. Let p be a prime number. How many divisors does the number have: a) p2 ; b) p3; c) pn?
Exercise. Let p and q be prime numbers. How many divisors does the number have: a) pq; b) p2 q3 ; c) pm qn?
Exercise. Having generalized the reasoning of point c) of the previous exercise, show that the number of divisors of the number a = pn 1 1 pn 2 2 : : : pn s s is equal to (n1 + 1)(n2 + 1) : : : (ns + 1). Find how many divisors the number 504 has.
Exercise. Find the canonical expansions of the numbers 540 and 252. Using the resulting expansions, find the gcd (540; 252) of the largest common divisor these numbers.
1.6 Coprime numbers
Numbers are called coprime if they have no common divisors other than 1. In other words, numbers a and b are coprime if gcd (a; b) = 1. You can also say this: numbers a and b are coprime if and only if when the fraction a=b is irreducible.
For example, the numbers 8 and 15 are coprime. The numbers 9 and 15 are not relatively prime; they have a common divisor of 3.
Numbers are relatively prime if and only if their canonical expansions consist of disjoint sets of prime numbers. For example, the numbers 23 5 132 and 32 73 11 are relatively prime.
Properties of coprime numbers. Let the numbers a and b be coprime. Then the following statements are true.
1. If a number is divisible by a and b, then it is also divisible by their product ab.
2. If an is divisible by b, then n is divisible by b.
(You can easily understand why this happens if you imagine the “disjoint” canonical expansions of the numbers a and b and, in addition, remember that the canonical expansion of the divisor serves as a “part” of the canonical expansion of the dividend.)
According to Statement 1, for example, if a certain number is divisible by 8 and 15, then it is divisible by 8 15 = 120. The fact that the numbers are relatively prime, important condition. So, 12 is divisible by 4 and 6, but not divisible by 4 6 = 24.
Exercise. What numbers can be inserted instead of asterisks in the entries 35 4 so that the resulting five digit number divisible by 45?
Statement 2 usually works in situations like the following. Let, for example, 5n = 9m. Since 5n is divisible by 9 and the numbers 5 and 9 are coprime, then n is divisible by 9. For the same reason, m is divisible by 5.
1.7 Sequences
What is a sequence? Imagine a device that produces one number after another at certain intervals. For example: 2, 3, 15, 28, 6, 0, 3, . . . The set of numbers at the output of this device will be a sequence.
More strictly, a sequence of numbers, or number sequence is a set of numbers in which each number can be assigned a certain number, and each number corresponds singular of this set. A number is a natural number; numbering starts from one.
So, in the above sequence, the first number is 2 (this is the first member of the sequence), and number five is the number 6 (this is the fifth member of the sequence).
Number with number n (that is nth term sequences) is denoted by an (or bn, cn, . . .). It is very convenient when the nth term of the sequence can be specified by some formula. For example, the formula an = 2n 3 specifies the sequence: 1; 1; 3; 5; 7; : : : Formula an = (1)n
sets the sequence: 1; 1; 1; 1; : : :
Exercise. Come up with a formula for the nth term for the following sequences: a) 1; 3; 5; 7; : : : ; b) 5; 8; eleven; 14; : : : ; in 1; 4; 9; 16; : : : ; d) 1; 2; 3; 4; : : :
All the sequences we have considered are infinite, that is, containing infinite set numbers. But there are also finite sequences. Actually, any finite set of numbers is a finite sequence. For example, final sequence 1; 2; 3; 4; 5 is made up of five numbers.
Problem C6 requires two special types sequences: arithmetic and geometric progressions.
1.8 Arithmetic progression
An arithmetic progression is a sequence in which each term (starting from the second) equal to the sum the previous term and some fixed number:
an+1 = an + d (n = 1; 2; : : :):
The fixed number d is called the difference of an arithmetic progression.
For example, sequence 2; 5; 8; eleven; : : : is arithmetic progression with the first term 2 and the difference 3.
In this article you will find all necessary information answering the question how to factor a number into prime factors. First given general idea about the decomposition of a number into prime factors, examples of decompositions are given. The following shows the canonical form of decomposing a number into prime factors. After this, the decomposition algorithm is given arbitrary numbers into prime factors and examples of decomposition of numbers using this algorithm are given. Alternative methods are also considered that allow you to quickly factor small integers into prime factors using divisibility tests and multiplication tables.
Page navigation.
What does it mean to factor a number into prime factors?
First, let's look at what prime factors are.
It is clear that since the word “factors” is present in this phrase, then there is a product of some numbers, and the qualifying word “simple” means that each factor is a prime number. For example, in a product of the form 2·7·7·23 there are four prime factors: 2, 7, 7 and 23.
What does it mean to factor a number into prime factors?
It means that given number must be represented as a product of prime factors, and the value of this product must be equal to the original number. As an example, consider the product of three prime numbers 2, 3 and 5, it is equal to 30, thus the decomposition of the number 30 into prime factors is 2·3·5. Usually the decomposition of a number into prime factors is written as an equality; in our example it will be like this: 30=2·3·5. We emphasize separately that prime factors in the expansion can be repeated. This clearly illustrates next example: 144=2·2·2·2·3·3 . But a representation of the form 45=3·15 is not a decomposition into prime factors, since the number 15 is a composite number.
Arises next question: “What numbers can be factorized into prime factors?”
In search of an answer to it, we present the following reasoning. Prime numbers, by definition, are among those greater than one. Taking into account this fact and , it can be argued that the product of several prime factors is an integer positive number, exceeding one. Therefore, factorization takes place only for positive integers that are greater than 1.
But can all integers greater than one be factored into prime factors?
It is clear that it is not possible to factor simple integers into prime factors. This is explained by the fact that prime numbers have only two positive divisors - one and itself, so they cannot be represented as a product of two or more prime numbers. If the integer z could be represented as the product of prime numbers a and b, then the concept of divisibility would allow us to conclude that z is divisible by both a and b, which is impossible due to the simplicity of the number z. However, they believe that any prime number is itself a decomposition.
What about composite numbers? Are composite numbers decomposed into prime factors, and are all composite numbers subject to such decomposition? The fundamental theorem of arithmetic gives an affirmative answer to a number of these questions. The basic theorem of arithmetic states that any integer a that is greater than 1 can be decomposed into the product of prime factors p 1, p 2, ..., p n, and the decomposition has the form a = p 1 p 2 ... p n, and this the expansion is unique, if you do not take into account the order of the factors
Canonical factorization of a number into prime factors
In the expansion of a number, prime factors can be repeated. Repeating prime factors can be written more compactly using . Let in the decomposition of a number the prime factor p 1 occur s 1 times, the prime factor p 2 – s 2 times, and so on, p n – s n times. Then the prime factorization of the number a can be written as a=p 1 s 1 ·p 2 s 2 ·…·p n s n. This form of recording is the so-called canonical factorization of a number into prime factors.
Let us give an example of the canonical decomposition of a number into prime factors. Let us know the decomposition 609 840=2 2 2 2 3 3 5 7 11 11, its canonical notation has the form 609 840=2 4 3 2 5 7 11 2.
The canonical factorization of a number into prime factors allows you to find all the divisors of the number and the number of divisors of the number.
Algorithm for factoring a number into prime factors
To successfully cope with the task of decomposing a number into prime factors, you need to have a very good knowledge of the information in the article prime and composite numbers.
The essence of the process of decomposing a positive integer number a that exceeds one is clear from the proof of the fundamental theorem of arithmetic. The point is sequential finding the smallest prime divisors p 1 , p 2 , …, p n of the numbers a, a 1 , a 2 , …, a n-1 , which allows us to obtain a series of equalities a = p 1 · a 1 , where a 1 = a: p 1 , a=p 1 ·a 1 =p 1 ·p 2 ·a 2 , where a 2 =a 1:p 2 , …, a=p 1 ·p 2 ·…·p n ·a n , where a n =a n-1 :p n . When it turns out a n =1, then the equality a=p 1 ·p 2 ·…·p n will give us the desired decomposition of the number a into prime factors. It should also be noted here that p 1 ≤p 2 ≤p 3 ≤…≤p n.
It remains to figure out how to find the smallest prime factors at each step, and we will have an algorithm for decomposing a number into prime factors. A table of prime numbers will help us find prime factors. Let us show how to use it to obtain the smallest prime divisor of the number z.
We sequentially take prime numbers from the table of prime numbers (2, 3, 5, 7, 11, and so on) and divide the given number z by them. The first prime number by which z is evenly divided will be its smallest prime divisor. If the number z is prime, then its smallest prime divisor will be the number z itself. It should be recalled here that if z is not a prime number, then its smallest prime divisor does not exceed the number , where is from z. Thus, if among the prime numbers not exceeding , there was not a single divisor of the number z, then we can conclude that z is a prime number (more about this is written in the theory section under the heading This number is prime or composite).
As an example, we will show how to find the smallest prime divisor of the number 87. Let's take the number 2. Divide 87 by 2, we get 87:2=43 (remaining 1) (if necessary, see article). That is, when dividing 87 by 2, the remainder is 1, so 2 is not a divisor of the number 87. We take the next prime number from the prime numbers table, this is the number 3. Divide 87 by 3, we get 87:3=29. Thus, 87 is divisible by 3, therefore, the number 3 is the smallest prime divisor of the number 87.
Note that in general case To factor the number a into prime factors, we need a table of prime numbers up to a number not less than . We will have to refer to this table at every step, so we need to have it at hand. For example, to factorize the number 95 into prime factors, we will only need a table of prime numbers up to 10 (since 10 is greater than ). And to decompose the number 846,653, you will already need a table of prime numbers up to 1,000 (since 1,000 is greater than ).
We now have enough information to write down algorithm for factoring a number into prime factors. The algorithm for decomposing the number a is as follows:
- Sequentially sorting through the numbers from the table of prime numbers, we find the smallest prime divisor p 1 of the number a, after which we calculate a 1 =a:p 1. If a 1 =1, then the number a is prime, and it itself is its decomposition into prime factors. If a 1 is not equal to 1, then we have a=p 1 ·a 1 and move on to the next step.
- We find the smallest prime divisor p 2 of the number a 1 , to do this we sequentially sort through the numbers from the table of prime numbers, starting with p 1 , and then calculate a 2 =a 1:p 2 . If a 2 =1, then the required decomposition of the number a into prime factors has the form a=p 1 ·p 2. If a 2 is not equal to 1, then we have a=p 1 ·p 2 ·a 2 and move on to the next step.
- Going through the numbers from the table of prime numbers, starting with p 2, we find the smallest prime divisor p 3 of the number a 2, after which we calculate a 3 =a 2:p 3. If a 3 =1, then the required decomposition of the number a into prime factors has the form a=p 1 ·p 2 ·p 3. If a 3 is not equal to 1, then we have a=p 1 ·p 2 ·p 3 ·a 3 and move on to the next step.
- We find the smallest prime divisor p n of the number a n-1 by sorting through the prime numbers, starting with p n-1, as well as a n =a n-1:p n, and a n is equal to 1. This step is the last step of the algorithm; here we obtain the desired decomposition of the number a into prime factors: a=p 1 ·p 2 ·…·p n.
For clarity, all the results obtained at each step of the algorithm for decomposing a number into prime factors are presented in the form of the following table, in which the numbers a, a 1, a 2, ..., a n are written sequentially in a column to the left of the vertical line, and to the right of the line - the corresponding smallest prime divisors p 1, p 2, ..., p n.
All that remains is to consider a few examples of the application of the resulting algorithm for decomposing numbers into prime factors.
Examples of prime factorization
Now we will look in detail examples of factoring numbers into prime factors. When decomposing, we will use the algorithm from the previous paragraph. Let's start with simple cases, and we will gradually complicate them in order to encounter all the possible nuances that arise when decomposing numbers into simple factors.
Example.
Factor the number 78 into its prime factors.
Solution.
We start searching for the first smallest prime divisor p 1 numbers a=78 . To do this, we begin to sequentially sort through prime numbers from the table of prime numbers. We take the number 2 and divide 78 by it, we get 78:2=39. The number 78 is divided by 2 without a remainder, so p 1 =2 is the first found prime divisor of the number 78. In this case, a 1 =a:p 1 =78:2=39. So we come to the equality a=p 1 ·a 1 having the form 78=2·39. Obviously, a 1 =39 is different from 1, so we move on to the second step of the algorithm.
Now we are looking for the smallest prime divisor p 2 of the number a 1 =39. We begin enumerating numbers from the table of prime numbers, starting with p 1 =2. Divide 39 by 2, we get 39:2=19 (remaining 1). Since 39 is not evenly divisible by 2, then 2 is not a divisor. Then we take the next number from the table of prime numbers (number 3) and divide 39 by it, we get 39:3=13. Therefore, p 2 =3 is the smallest prime divisor of the number 39, while a 2 =a 1:p 2 =39:3=13. We have the equality a=p 1 ·p 2 ·a 2 in the form 78=2·3·13. Since a 2 =13 is different from 1, we move on to the next step of the algorithm.
Here we need to find the smallest prime divisor of the number a 2 =13. In search of the smallest prime divisor p 3 of the number 13, we will sequentially sort through the numbers from the table of prime numbers, starting with p 2 =3. The number 13 is not divisible by 3, since 13:3=4 (rest. 1), also 13 is not divisible by 5, 7 and 11, since 13:5=2 (rest. 3), 13:7=1 (rest. 6) and 13:11=1 (rest. 2). The next prime number is 13, and 13 is divisible by it without a remainder, therefore, the smallest prime divisor p 3 of 13 is the number 13 itself, and a 3 =a 2:p 3 =13:13=1. Since a 3 =1, this step of the algorithm is the last, and the desired decomposition of the number 78 into prime factors has the form 78=2·3·13 (a=p 1 ·p 2 ·p 3 ).
Answer:
78=2·3·13.
Example.
Express the number 83,006 as a product of prime factors.
Solution.
At the first step of the algorithm for decomposing a number into prime factors, we find p 1 =2 and a 1 =a:p 1 =83,006:2=41,503, from which 83,006=2·41,503.
At the second step, we find out that 2, 3 and 5 are not prime divisors of the number a 1 =41,503, but the number 7 is, since 41,503:7=5,929. We have p 2 =7, a 2 =a 1:p 2 =41,503:7=5,929. Thus, 83,006=2 7 5 929.
The smallest prime divisor of the number a 2 =5 929 is the number 7, since 5 929:7 = 847. Thus, p 3 =7, a 3 =a 2:p 3 =5 929:7 = 847, from which 83 006 = 2·7·7·847.
Next we find that the smallest prime divisor p 4 of the number a 3 =847 is equal to 7. Then a 4 =a 3:p 4 =847:7=121, so 83 006=2·7·7·7·121.
Now we find the smallest prime divisor of the number a 4 =121, it is the number p 5 =11 (since 121 is divisible by 11 and not divisible by 7). Then a 5 =a 4:p 5 =121:11=11, and 83 006=2·7·7·7·11·11.
Finally, the smallest prime divisor of the number a 5 =11 is the number p 6 =11. Then a 6 =a 5:p 6 =11:11=1. Since a 6 =1, this step of the algorithm for decomposing a number into prime factors is the last, and the desired decomposition has the form 83 006 = 2·7·7·7·11·11.
The result obtained can be written as the canonical decomposition of the number into prime factors 83 006 = 2·7 3 ·11 2.
Answer:
83 006=2 7 7 7 11 11=2 7 3 11 2 991 is a prime number. Indeed, it does not have a single prime divisor not exceeding ( can be roughly estimated as , since it is obvious that 991<40 2
), то есть, наименьшим делителем числа 991
является оно само. Тогда p 3 =991
и a 3 =a 2:p 3 =991:991=1
. Следовательно, искомое разложение числа 897 924 289
на простые множители имеет вид 897 924 289=937·967·991
.
Answer:
897 924 289 = 937 967 991 .
Using divisibility tests for prime factorization
In simple cases, you can decompose a number into prime factors without using the decomposition algorithm from the first paragraph of this article. If the numbers are not large, then to decompose them into prime factors it is often enough to know the signs of divisibility. Let's give examples for clarification.
For example, we need to factor the number 10 into prime factors. From the multiplication table we know that 2·5=10, and the numbers 2 and 5 are obviously prime, so the prime factorization of the number 10 looks like 10=2·5.
Another example. Using the multiplication table, we will factor the number 48 into prime factors. We know that six is eight - forty-eight, that is, 48 = 6·8. However, neither 6 nor 8 are prime numbers. But we know that twice three is six, and twice four is eight, that is, 6=2·3 and 8=2·4. Then 48=6·8=2·3·2·4. It remains to remember that two times two is four, then we get the desired decomposition into prime factors 48 = 2·3·2·2·2. Let's write this expansion in canonical form: 48=2 4 ·3.
But when factoring the number 3,400 into prime factors, you can use the divisibility criteria. The signs of divisibility by 10, 100 allow us to state that 3,400 is divisible by 100, with 3,400=34·100, and 100 is divisible by 10, with 100=10·10, therefore, 3,400=34·10·10. And based on the test of divisibility by 2, we can say that each of the factors 34, 10 and 10 is divisible by 2, we get 3 400=34 10 10=2 17 2 5 2 5. All factors in the resulting expansion are simple, so this expansion is the desired one. All that remains is to rearrange the factors so that they go in ascending order: 3 400 = 2·2·2·5·5·17. Let us also write down the canonical decomposition of this number into prime factors: 3 400 = 2 3 ·5 2 ·17.
When decomposing a given number into prime factors, you can use in turn both the signs of divisibility and the multiplication table. Let's imagine the number 75 as a product of prime factors. The test of divisibility by 5 allows us to state that 75 is divisible by 5, and we obtain that 75 = 5·15. And from the multiplication table we know that 15=3·5, therefore, 75=5·3·5. This is the required decomposition of the number 75 into prime factors.
Bibliography.
- Vilenkin N.Ya. and others. Mathematics. 6th grade: textbook for general education institutions.
- Vinogradov I.M. Fundamentals of number theory.
- Mikhelovich Sh.H. Number theory.
- Kulikov L.Ya. and others. Collection of problems in algebra and number theory: Textbook for students of physics and mathematics. specialties of pedagogical institutes.
Formulation. Given a natural number n (n > 1). Obtain its canonical decomposition into simple factors, that is, present it as a product of simple factors. In this case, it is permissible to indicate a factor of 1 in the expansion. For example, 264 = 2 * 2 * 2 * 3 * 11 (the program can produce the answer 264 = 1 * 2 * 2 * 2 * 3 * 11).
Solution. This task has a pretty nice solution.
From fundamental theorem of arithmetic it is known that for any natural number greater than 1 there is a canonical decomposition into prime factors, and this decomposition is unique up to the order of the factors. That is, for example, 12 = 2 * 2 * 2 and 12 = 3 * 2 * 2 are the same expansions.
Let's consider canonical form any number for specific example. For example, 264 = 2 * 2 * 2 * 3 * 11. How can this structure be identified? To answer this question, let us recall those stated in any school course algebra rules for dividing monomials, imagining that the numbers in the canonical expansion are variables. As you know, if you divide an expression into a variable to some degree contained in this expression to the same degree, it is crossed out in its notation.
That is, if we divide 264 by 2, then in its canonical expansion there will be one two. Then we can check whether the resulting quotient is again divisible by 2. The answer will be yes, but the third time the division will give a remainder. Then you need to take the next natural number 3 for consideration - the quotient will be divided by it once. As a result, passing the number line in the positive direction, we will reach the number 11, and after dividing by 11 n will become equal to 1, which will indicate the need to complete the procedure.
Why, with such “crossing out” of the found factors, do we not get divisibility into composite numbers? In fact, everything is simple here - any composite number is the product of prime factors smaller than it. As a result, it turns out that we will cross out n all factors of any composite number, until we reach it itself in the chain of divisions. For example, with such an exhaustive search n will never be divided by 4, since “on the way” to this number we will delete from n all factors are twos.
Algorithm in natural language:
1) Input n;
2) Assignment to a variable p numbers 2;
3) Output the number n, equal sign and unit to formalize the expansion;
4) Starting a loop with a precondition n< > 1 . In a loop:
- If mmodp = 0, then display the multiplication sign and the variable p, then divide n on p, otherwise increase the value i by 1;
- program PrimeFactors;
- n, p: word;
- begin
- p:= 2;
- readln(n);
- write(n, ‘ = 1’);
- while n<>1 do begin
- if (n mod p) = 0 then begin
- write(‘ * ‘, p);
- n:= n div p
- else begin
- inc(p)
The random variable V is called centered , if its mathematical expectation is equal to 0. An elementary centered random process is the product of a centered random variable V and a non-random function φ(t):X(t)=Vφ(t). An elementary centered random process has the following characteristics:
Expression of the form  , where φ
k
(
t
),
k
=1;2;…-non-random functions;
, where φ
k
(
t
),
k
=1;2;…-non-random functions;  ,
k
=1;2;…-uncorrelated centered random variables, called the canonical expansion of the random processX
(
t
), while the random variables
,
k
=1;2;…-uncorrelated centered random variables, called the canonical expansion of the random processX
(
t
), while the random variables  are called the coefficients of the canonical expansion; and non-random functions φ
k
(
t
) - coordinate functions of the canonical expansion.
are called the coefficients of the canonical expansion; and non-random functions φ
k
(
t
) - coordinate functions of the canonical expansion.
Let's consider the characteristics of a random process



Since by condition  That
That


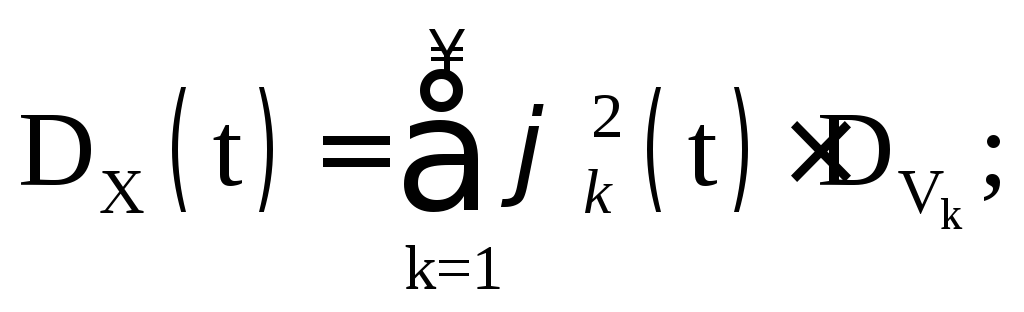

Obviously, the same random process has different kinds canonical expansion depending on the choice of coordinate functions. Moreover, even with the selection of coordinate functions, there is arbitrariness in the distribution of random variables V k. In practice, based on the results of experiments, estimates are obtained for the mathematical expectation and the correlation function:  . After decomposition
. After decomposition  into a double Fourier series in coordinate functions φ to (t):
into a double Fourier series in coordinate functions φ to (t):

get variance values  random variables V k .
random variables V k .
4.2. The concept of a generalized function. Dirac delta function. Integral canonical representation of random processes.
Generalized function is called the limit of a sequence of a one-parameter family of continuous functions.
Dirac delta function  -
this is a generalized function resulting from passing to the limit at
-
this is a generalized function resulting from passing to the limit at  in a family of functions
in a family of functions 

Among the properties  -functions we note the following:
-functions we note the following:
2.

3. If f(t)- continuous function, That


Random process X( t ), the correlation function of which has the form called non-stationary “white noise”. If W ( t 1 )= W - const , then X( t )-stationary “white noise”.
As follows from the definition, no two, even however close, sections “ white noise» are not correlated. The expression W(t) is called intensity of "white noise".
Integral canonical representation of the random process X(
t
) is called an expression of the form  Where
Where  - random centered function;
- random centered function;  - non-random function of continuous arguments
- non-random function of continuous arguments 
The correlation function of such a random process has the form:
It can be shown that there is a non-random function G(λ) such that
where G(λ 1) is the dispersion density; δ(x) is the Dirac delta function. We get 
Therefore, the variance of the random process X(t):
 .
.
4.3. Linear and nonlinear transformations of random processes
The following problem is considered: an “input signal” having the character of a random process X(t) is supplied to the input of the system (device, converter) S. The system converts it into an “output signal” Y(t):
 .
.
Formally, the transformation of a random process X(t) into Y(t) can be described using the so-called system operator A t:
Y(t)=A t (X(t)).
The index t indicates that this operator performs a time conversion. The following formulations of the problem of transforming a random process are possible.
The laws of distribution are known or General characteristics random process X(t) at the input to the system S, the operator A t of the system S is given, it is necessary to determine the distribution law or general characteristics of the random process Y(t) at the output of the system S.
The laws of distribution (general characteristics) of the random process X(t) and the requirements for the random process Y(t) are known; it is necessary to determine the type of operator A t of the system S that best satisfies the given requirements kY(t).
The distribution laws (general characteristics) of the random process Y(t) are known and the operator A t of the system S is given; it is required to determine the distribution laws or general characteristics of the random process X(t).
P  The following classification of operators A t of the system S is accepted:
The following classification of operators A t of the system S is accepted:
System Operators
Linear LNonlinearN
Linear homogeneous L 0 Linear inhomogeneous L n

Let us consider the impact of a linear inhomogeneous system
L n (...)=L 0 (...)+φ(t)
to a random process X(t) having the following canonical expansion:
 .
.
We get:

let us introduce the notation



then the canonical expansion of Y(t) takes the form:
 .
.
Mathematical expectation of the random process Y(t):
correlation function of the random process Y(t):

hence,
On the other side

Variance of the random process Y(t):
In conclusion of this paragraph, we note that the operators of differentiation and integration of random processes are linear homogeneous.
2. The quadratic transformation is considered:
Y(t)=(X(t)) 2 , 
V k -centered random variables having a distribution symmetric about zero; any four of them are jointly independent. Then


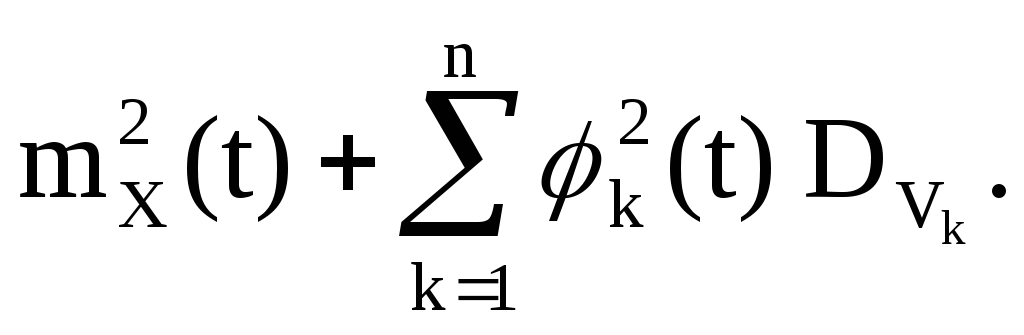
Let's introduce non-random functions
and random variables
then the random process Y(t) takes the form
A canonical expansion of the random process Y(t) is obtained. Correlation functionY(t):









