Commençons par expliquer ce qu'est l'espace à quatre dimensions.
Il s’agit d’un espace unidimensionnel, c’est-à-dire simplement l’axe OX. Tout point sur celui-ci est caractérisé par une coordonnée.

Dessinons maintenant l'axe OY perpendiculaire à l'axe OX. Nous obtenons donc un espace bidimensionnel, c'est-à-dire le plan XOY. Tout point sur celui-ci est caractérisé par deux coordonnées - l'abscisse et l'ordonnée.

Traçons l'axe OZ perpendiculairement aux axes OX et OY. Le résultat est un espace tridimensionnel dans lequel tout point a une abscisse, une ordonnée et une applicative.

Il est logique que le quatrième axe, OQ, soit perpendiculaire aux axes OX, OY et OZ en même temps. Mais nous ne pouvons pas construire avec précision un tel axe et nous ne pouvons donc qu’essayer de l’imaginer. Chaque point dans l'espace à quatre dimensions a quatre coordonnées : x, y, z et q.
Voyons maintenant comment est apparu le cube à quatre dimensions.

L'image montre une figure dans un espace unidimensionnel - une ligne.

Si vous effectuez une translation parallèle de cette ligne le long de l'axe OY, puis connectez les extrémités correspondantes des deux lignes résultantes, vous obtiendrez un carré.

De même, si vous effectuez une translation parallèle du carré le long de l'axe OZ et connectez les sommets correspondants, vous obtiendrez un cube.

Et si nous effectuons une translation parallèle du cube le long de l'axe OQ et connectons les sommets de ces deux cubes, alors nous obtiendrons un cube à quatre dimensions. D'ailleurs, ça s'appelle tesseract.
Pour dessiner un cube sur un avion, il vous en faut projet. Visuellement, cela ressemble à ceci : 
Imaginons qu'il soit suspendu dans les airs au-dessus de la surface modèle filaire cube, c'est-à-dire comme s'il était « fait de fil », et au-dessus se trouve une ampoule. Si vous allumez l'ampoule, tracez l'ombre du cube avec un crayon, puis éteignez l'ampoule, une projection du cube sera représentée sur la surface.
Passons à quelque chose d'un peu plus complexe. Regardez à nouveau le dessin avec l'ampoule : comme vous pouvez le voir, tous les rayons convergent en un point. On l'appelle Point de fuite et est utilisé pour construire projection en perspective(et cela arrive aussi parallèlement, lorsque tous les rayons sont parallèles entre eux. Il en résulte que la sensation de volume ne se crée pas, mais elle est plus légère, et de plus, si le point de fuite est assez éloigné de l'objet projeté, alors la différence entre ces deux projections est peu perceptible). Pour projeter un point donné sur un plan donné à l'aide d'un point de fuite, vous devez tracer une ligne droite passant par le point de fuite et le point donné, puis trouver le point d'intersection de la ligne droite résultante et du plan. Et pour projeter une figure plus complexe, par exemple un cube, vous devez projeter chacun de ses sommets, puis connecter les points correspondants. Il convient de noter que algorithme de projection de l'espace sur le sous-espace peut être généralisé au cas de la 4D->3D, et pas seulement de la 3D->2D.
Comme je l'ai dit, nous ne pouvons pas imaginer exactement à quoi ressemble l'axe OQ, tout comme le tesseract. Mais on peut s'en faire une idée limitée si on le projette sur un volume puis en le dessinant sur un écran d'ordinateur !
Parlons maintenant de la projection tesseract.

A gauche se trouve la projection du cube sur le plan, et à droite le tesseract sur le volume. Ils sont assez similaires : la projection d'un cube ressemble à deux carrés, petit et grand, l'un dans l'autre, et dont les sommets correspondants sont reliés par des lignes. Et la projection du tesseract ressemble à deux cubes, petit et grand, l'un dans l'autre, et dont les sommets correspondants sont reliés. Mais nous avons tous vu le cube, et nous pouvons affirmer avec certitude que le petit carré et le grand carré, ainsi que les quatre trapèzes au-dessus, en dessous, à droite et à gauche du petit carré, sont en réalité des carrés, et ils sont égaux. . Et le tesseract a la même chose. Et un grand cube, et un petit cube, et six pyramides tronquées sur les côtés d'un petit cube - ce sont tous des cubes, et ils sont égaux.
Mon programme peut non seulement dessiner la projection d'un tesseract sur un volume, mais aussi le faire pivoter. Voyons comment cela se fait.
Tout d'abord, je vais vous dire ce que c'est rotation parallèle au plan.
Imaginez que le cube tourne autour de l'axe OZ. Ensuite chacun de ses sommets décrit un cercle autour de l’axe OZ. 
Un cercle est une figure plate. Et les plans de chacun de ces cercles sont parallèles entre eux, et en l'occurrence parallèles au plan XOY. Autrement dit, nous pouvons parler non seulement de rotation autour de l'axe OZ, mais également de rotation parallèle au plan XOY. Comme nous le voyons, pour les points qui tournent parallèlement à l'axe XOY, seules l'abscisse et l'ordonnée changent, tandis que l'appliquée reste. inchangé. Et, en fait, nous ne pouvons parler de rotation autour d’une ligne droite que lorsqu’il s’agit d’un espace tridimensionnel. Dans l'espace à deux dimensions tout tourne autour d'un point, dans l'espace à quatre dimensions tout tourne autour d'un plan, dans l'espace à cinq dimensions on parle de rotation autour d'un volume. Et si nous pouvons imaginer une rotation autour d’un point, alors la rotation autour d’un plan et d’un volume est quelque chose d’impensable. Et si nous parlons de rotation parallèle au plan, alors dans n'importe quel espace à n dimensions, un point peut tourner parallèlement au plan.
Beaucoup d’entre vous ont probablement entendu parler de la matrice de rotation. En multipliant le point par celui-ci, nous obtenons un point tourné parallèlement au plan d'un angle phi. Pour un espace à deux dimensions, cela ressemble à ceci : 
Comment multiplier : x d'un point tourné d'un angle phi = cosinus de l'angle phi*ix du point d'origine moins sinus de l'angle phi*ig du point d'origine ;
ig d'un point tourné d'un angle phi = sinus de l'angle phi * ix du point d'origine plus cosinus de l'angle phi * ig du point d'origine.
Xa`=cosф*Xa - sinф*Ya
Ya`=sinф*Xa + cosф*Ya
, où Xa et Ya sont l'abscisse et l'ordonnée du point à faire pivoter, Xa` et Ya` sont l'abscisse et l'ordonnée du point déjà pivoté
Pour l'espace tridimensionnel, cette matrice se généralise comme suit : 
Rotation parallèle au plan XOY. Comme vous pouvez le voir, la coordonnée Z ne change pas, mais seuls X et Y changent
Xa`=cosф*Xa - sinф*Ya + Za*0
Ya`=sinф*Xa +cosф*Ya + Za*0
Za`=Xa*0 + Ya*0 + Za*1 (essentiellement, Za`=Za)

Rotation parallèle au plan XOZ. Rien de nouveau,
Xa`=cosф*Xa + Ya*0 - sinф*Za
Ya`=Xa*0 + Ya*1 + Za*0 (essentiellement, Ya`=Ya)
Za`=sinф*Xa + Ya*0 + cosф*Za

Et la troisième matrice.
Xa`=Xa*1 + Ya*0 + Za*0 (essentiellement, Xa`=Xa)
Ya`=Xa*0 + cosф*Ya - sinф*Za
Za`=Xa*0 + sinф*Ya + cosф*Za
Et pour la quatrième dimension, ils ressemblent à ceci : 
Je pense que vous savez déjà par quoi multiplier, je n'entrerai donc pas dans les détails. Mais je remarque qu'elle fait la même chose qu'une matrice de rotation parallèle à un plan dans un espace tridimensionnel ! Les deux ne changent que l'ordonnée et l'appliquée, et ne touchent pas les autres coordonnées, elles peuvent donc être utilisées dans le cas tridimensionnel, sans simplement prêter attention à la quatrième coordonnée.
Mais avec la formule de projection, tout n'est pas si simple. Peu importe le nombre de forums que j’ai lus, aucune des méthodes de projection n’a fonctionné pour moi. La projection parallèle ne me convenait pas, car la projection n'aurait pas l'air tridimensionnelle. Dans certaines formules de projection, pour trouver un point il faut résoudre un système d'équations (et je ne sais pas comment apprendre à un ordinateur à les résoudre), d'autres je n'ai tout simplement pas compris... En général, j'ai décidé de trouver ma propre voie. Pour cela, considérons la projection 2D->1D.

pov signifie "Point de vue", ptp signifie "Point vers le projet" (le point à projeter), et ptp` est le point souhaité sur l'axe OX.
Les angles povptpB et ptpptp`A sont égaux comme correspondant (la ligne pointillée est parallèle à l'axe OX, la droite povptp est une sécante).
Le x du point ptp` est égal au x du point ptp moins la longueur du segment ptp`A. Ce segment peut être trouvé à partir du triangle ptpptp`A : ptp`A = ptpA/tangente de l'angle ptpptp`A. On peut retrouver cette tangente à partir du triangle povptpB : tangente ptpptp`A = (Ypov-Yptp)(Xpov-Xptp).
Réponse : Xptp`=Xptp-Yptp/tangente de l'angle ptpptp`A.
Je n'ai pas décrit cet algorithme en détail ici, car il existe de nombreux cas particuliers où la formule change quelque peu. Si quelqu'un est intéressé, regardez le code source du programme, tout y est décrit dans les commentaires.
Afin de projeter un point de l'espace tridimensionnel sur un plan, nous considérons simplement deux plans - XOZ et YOZ, et résolvons ce problème pour chacun d'eux. Dans le cas d'un espace à quatre dimensions, il faut considérer trois plans : XOQ, YOQ et ZOQ.
Et enfin, à propos du programme. Cela fonctionne comme ceci : initialiser seize sommets du tesseract -> en fonction des commandes saisies par l'utilisateur, le faire pivoter -> le projeter sur le volume -> en fonction des commandes saisies par l'utilisateur, faire pivoter sa projection -> le projeter sur l'avion -> dessiner.
J'ai écrit moi-même les projections et les rotations. Ils fonctionnent selon les formules que je viens de décrire. La bibliothèque OpenGL dessine des lignes et gère également le mélange des couleurs. Et les coordonnées des sommets du tesseract sont calculées de cette manière :
Coordonnées des sommets d'une ligne centrée à l'origine et de longueur 2 - (1) et (-1) ;
- " - " - carré - " - " - et avec une arête de longueur 2 :
(1 ; 1), (-1 ; 1), (1 ; -1) et (-1 ; -1) ;
- " - " - cube - " - " -:
(1; 1; 1), (-1; 1; 1), (1; -1; 1), (-1; -1; 1), (1; 1; -1), (-1; 1; -1), (1; -1; -1), (-1; -1; -1);
Comme vous pouvez le voir, un carré est une ligne au-dessus de l'axe OY et une ligne en dessous de l'axe OY ; un cube est un carré devant le plan XOY et un derrière ; Le tesseract est un cube de l'autre côté du volume XOYZ et un de ce côté. Mais il est beaucoup plus facile de percevoir cette alternance de uns et de moins s'ils sont écrits dans une colonne.
1; 1; 1
-1; 1; 1
1; -1; 1
-1; -1; 1
1; 1; -1
-1; 1; -1
1; -1; -1
-1; -1; -1
Dans la première colonne, un et moins un alternent. Dans la deuxième colonne, il y a d’abord deux plus, puis deux moins. Dans le troisième - quatre plus un, puis quatre moins un. C'étaient les sommets du cube. Le tesseract en possède deux fois plus, et il a donc fallu écrire une boucle pour les déclarer, sinon il est très facile de se tromper.
Mon programme peut également dessiner des anaglyphes. Les heureux propriétaires de lunettes 3D peuvent observer une image stéréoscopique. Il n'y a rien de compliqué à dessiner une image ; il suffit de dessiner deux projections sur l'avion, pour les yeux droit et gauche. Mais le programme devient beaucoup plus visuel et intéressant, et surtout, il donne une meilleure idée du monde en quatre dimensions.
Des fonctions moins importantes sont l'éclairage de l'un des bords en rouge afin que les virages soient mieux vus, ainsi que des commodités mineures - régulation des coordonnées des points « œil », augmentation et diminution de la vitesse de rotation.
Archivez avec le programme, le code source et le mode d'emploi.
Bakalyar Maria
Les méthodes d'introduction du concept de cube à quatre dimensions (tesseract), sa structure et certaines propriétés sont étudiées. La question de savoir quels objets tridimensionnels sont obtenus lorsqu'un cube à quatre dimensions est coupé par des hyperplans parallèles à ses faces tridimensionnelles. , ainsi que les hyperplans perpendiculaires à sa diagonale principale sont abordés. L'appareil de géométrie analytique multidimensionnelle utilisé pour la recherche est considéré.
Télécharger:
Aperçu:
Introduction………………………………………………………………………………….2
Partie principale……………………………………………………………..4
Conclusions………….. ………………………………………………………..12
Références………………………………………………………..13
Introduction
L'espace à quatre dimensions a longtemps attiré l'attention des mathématiciens professionnels et des personnes éloignées de l'étude de cette science. L'intérêt pour la quatrième dimension peut être dû à l'hypothèse selon laquelle notre monde tridimensionnel est « immergé » dans un espace à quatre dimensions, tout comme un plan est « immergé » dans un espace tridimensionnel, une ligne droite est « immergée » dans un espace tridimensionnel. plan, et un point est sur une ligne droite. En outre, l'espace à quatre dimensions joue un rôle important dans la théorie moderne de la relativité (appelée espace-temps ou espace de Minkowski) et peut également être considéré comme un cas particulier.espace euclidien dimensionnel (avec).
Un cube à quatre dimensions (tesseract) est un objet dans un espace à quatre dimensions qui a la dimension maximale possible (tout comme un cube ordinaire est un objet dans un espace à trois dimensions). A noter qu'il présente également un intérêt direct, à savoir qu'il peut apparaître dans des problèmes d'optimisation de programmation linéaire (comme domaine dans lequel se trouve le minimum ou le maximum d'une fonction linéaire à quatre variables), et est également utilisé en microélectronique numérique (lorsque programmation du fonctionnement d'un affichage de montre électronique). De plus, le processus même d'étude d'un cube à quatre dimensions contribue au développement de la pensée spatiale et de l'imagination.
Par conséquent, l’étude de la structure et des propriétés spécifiques d’un cube à quatre dimensions est tout à fait pertinente. Il convient de noter qu'en termes de structure, le cube à quatre dimensions a été assez bien étudié. La nature de ses sections par divers hyperplans est bien plus intéressante. Ainsi, l'objectif principal de ce travail est d'étudier la structure du tesseract, ainsi que de clarifier la question de savoir quels objets tridimensionnels seront obtenus si un cube à quatre dimensions est disséqué par des hyperplans parallèles à l'un de ses éléments tridimensionnels. faces dimensionnelles, ou par des hyperplans perpendiculaires à sa diagonale principale. Un hyperplan dans un espace à quatre dimensions sera appelé un sous-espace à trois dimensions. On peut dire qu'une droite sur un plan est un hyperplan unidimensionnel, un plan dans un espace tridimensionnel est un hyperplan bidimensionnel.
Le but a déterminé les objectifs de l'étude :
1) Étudier les faits de base de la géométrie analytique multidimensionnelle ;
2) Étudier les caractéristiques de la construction de cubes de dimensions de 0 à 3 ;
3) Étudier la structure d'un cube à quatre dimensions ;
4) Décrire analytiquement et géométriquement un cube à quatre dimensions ;
5) Réaliser des modèles d'évolutions et de projections centrales de cubes tridimensionnels et quadridimensionnels.
6) À l'aide de l'appareil de géométrie analytique multidimensionnelle, décrire des objets tridimensionnels résultant de l'intersection d'un cube à quatre dimensions avec des hyperplans parallèles à l'une de ses faces tridimensionnelles, ou des hyperplans perpendiculaires à sa diagonale principale.
Les informations ainsi obtenues nous permettront de mieux comprendre la structure du tesseract, ainsi que d'identifier des analogies profondes dans la structure et les propriétés des cubes de différentes dimensions.
Partie principale
Tout d’abord, nous décrivons l’appareil mathématique que nous utiliserons au cours de cette étude.
1) Coordonnées vectorielles : si, Que
2) Équation d'un hyperplan avec un vecteur normal on dirait ici
3) Avions et sont parallèles si et seulement si
4) La distance entre deux points est déterminée comme suit : si, Que
5) Condition d'orthogonalité des vecteurs :
Tout d’abord, découvrons comment décrire un cube à quatre dimensions. Cela peut être fait de deux manières : géométrique et analytique.
Si nous parlons de la méthode géométrique de spécification, il est alors conseillé de retracer le processus de construction des cubes, en partant de la dimension zéro. Un cube de dimension nulle est un point (notons d'ailleurs qu'un point peut aussi jouer le rôle d'une boule de dimension nulle). Ensuite, nous introduisons la première dimension (l'axe des x) et sur l'axe correspondant nous marquons deux points (deux cubes de dimension zéro) situés à une distance de 1 l'un de l'autre. Le résultat est un segment - un cube unidimensionnel. Notons immédiatement un trait caractéristique : la limite (extrémités) d'un cube (segment) à une dimension est constituée de deux cubes à dimension zéro (deux points). Ensuite, nous introduisons la deuxième dimension (axe des ordonnées) et sur le planConstruisons deux cubes unidimensionnels (deux segments) dont les extrémités sont à une distance de 1 l'une de l'autre (en fait, l'un des segments est une projection orthogonale de l'autre). En reliant les extrémités correspondantes des segments, nous obtenons un carré - un cube à deux dimensions. Encore une fois, notez que la limite d'un cube bidimensionnel (carré) est constituée de quatre cubes unidimensionnels (quatre segments). Enfin, nous introduisons la troisième dimension (axe applicable) et construisons dans l'espacedeux carrés de telle sorte que l'un d'eux soit une projection orthogonale de l'autre (les sommets correspondants des carrés sont à une distance de 1 l'un de l'autre). Relions les sommets correspondants avec des segments - nous obtenons un cube tridimensionnel. Nous voyons que la limite d’un cube tridimensionnel est constituée de six cubes bidimensionnels (six carrés). Les constructions décrites permettent d'identifier le schéma suivant : à chaque étapele cube dimensionnel « bouge en laissant une trace » danse mesure à une distance de 1, alors que la direction du mouvement est perpendiculaire au cube. C'est la suite formelle de ce processus qui permet d'arriver au concept de cube à quatre dimensions. A savoir, nous forcerons le cube tridimensionnel à se déplacer dans la direction de la quatrième dimension (perpendiculaire au cube) d'une distance de 1. En agissant de la même manière que le précédent, c'est-à-dire en reliant les sommets correspondants des cubes, nous obtiendrons un cube à quatre dimensions. Il convient de noter que géométriquement une telle construction dans notre espace est impossible (puisqu'il est tridimensionnel), mais nous ne rencontrons ici aucune contradiction d'un point de vue logique. Passons maintenant à la description analytique d'un cube à quatre dimensions. Elle s’obtient également formellement, par analogie. Ainsi, la spécification analytique d'un cube unitaire de dimension zéro a la forme :
La tâche analytique d'un cube unitaire unidimensionnel a la forme :
La tâche analytique d'un cube unitaire bidimensionnel a la forme :
La tâche analytique d'un cube unitaire tridimensionnel a la forme :
Or il est très simple de donner une représentation analytique d’un cube à quatre dimensions, à savoir :
Comme nous pouvons le voir, les méthodes géométriques et analytiques de définition d'un cube à quatre dimensions utilisaient la méthode des analogies.
Maintenant, en utilisant l'appareil de géométrie analytique, nous allons découvrir quelle est la structure d'un cube à quatre dimensions. Voyons d’abord quels éléments il comprend. Là encore on peut recourir à une analogie (pour émettre une hypothèse). Les limites d'un cube unidimensionnel sont des points (cubes zéro dimension), d'un cube bidimensionnel - des segments (cubes unidimensionnels), d'un cube tridimensionnel - des carrés (faces bidimensionnelles). On peut supposer que les limites du tesseract sont des cubes tridimensionnels. Pour le prouver, clarifions ce que l’on entend par sommets, arêtes et faces. Les sommets d'un cube sont ses sommets. Autrement dit, les coordonnées des sommets peuvent être des zéros ou des uns. Ainsi, un lien se révèle entre la dimension du cube et le nombre de ses sommets. Appliquons la règle du produit combinatoire - puisque le sommetle cube mesuré a exactementcoordonnées dont chacune est égale à zéro ou un (indépendant de tous les autres), alors au total il y apics Ainsi, pour tout sommet, toutes les coordonnées sont fixes et peuvent être égales à ou . Si l'on fixe toutes les coordonnées (en mettant chacune d'elles égale ou , quelles que soient les autres), sauf une, on obtient des droites contenant les arêtes du cube. Semblable au précédent, vous pouvez compter qu'il y a exactementdes choses. Et si maintenant nous fixons toutes les coordonnées (en mettant chacune d'elles égale ou , indépendamment des autres), à l'exception de deux, on obtient des plans contenant des faces bidimensionnelles du cube. En utilisant la règle combinatoire, on trouve qu’il y a exactementdes choses. Ensuite, de la même manière - fixer toutes les coordonnées (en mettant chacune d'elles égale ou , quels que soient les autres), à l'exception de trois, on obtient des hyperplans contenant des faces tridimensionnelles du cube. En utilisant la même règle, nous calculons leur nombre - exactementetc. Cela suffira pour nos recherches. Appliquons les résultats obtenus à la structure d'un cube à quatre dimensions, c'est-à-dire dans toutes les formules dérivées que nous mettons. Par conséquent, un cube à quatre dimensions a : 16 sommets, 32 arêtes, 24 faces bidimensionnelles et 8 faces tridimensionnelles. Pour plus de clarté, définissons analytiquement tous ses éléments.
Sommets d'un cube à quatre dimensions :
Arêtes d'un cube à quatre dimensions ():
Faces bidimensionnelles d'un cube à quatre dimensions (restrictions similaires) :
Faces tridimensionnelles d'un cube à quatre dimensions (restrictions similaires) :
Maintenant que la structure d'un cube à quatre dimensions et les méthodes pour le définir ont été décrites de manière suffisamment détaillée, passons à la mise en œuvre de l'objectif principal - clarifier la nature des différentes sections du cube. Commençons par le cas élémentaire où les sections d'un cube sont parallèles à l'une de ses faces tridimensionnelles. Par exemple, considérons ses sections avec des hyperplans parallèles au visageDe la géométrie analytique, on sait que toute section de ce type sera donnée par l'équationDéfinissons analytiquement les sections correspondantes :
Comme nous pouvons le voir, nous avons obtenu une spécification analytique pour un cube unitaire tridimensionnel situé dans un hyperplan
Pour établir une analogie, écrivons la section d'un cube tridimensionnel par un plan On a:
C'est un carré situé dans un plan. L'analogie est évidente.
Sections d'un cube à quatre dimensions par hyperplansdonnent des résultats complètement similaires. Il s'agira également de cubes tridimensionnels uniques situés dans des hyperplans respectivement.
Considérons maintenant les sections d'un cube à quatre dimensions avec des hyperplans perpendiculaires à sa diagonale principale. Tout d’abord, résolvons ce problème pour un cube tridimensionnel. En utilisant la méthode décrite ci-dessus pour définir un cube tridimensionnel unitaire, il conclut que comme diagonale principale, on peut prendre, par exemple, un segment avec des extrémités Et . Cela signifie que le vecteur de la diagonale principale aura pour coordonnées. Par conséquent, l’équation de tout plan perpendiculaire à la diagonale principale sera :
Déterminons les limites du changement de paramètre. Parce que , puis en additionnant ces inégalités terme par terme, on obtient :
Ou .
Si donc (en raison de restrictions). De même - si, Que . Alors, quand et quand le plan coupant et le cube ont exactement un point commun ( Et respectivement). Notons maintenant ce qui suit. Si(encore une fois en raison de limitations variables). Les plans correspondants coupent trois faces à la fois, car sinon le plan de coupe serait parallèle à l'une d'elles, ce qui n'est pas le cas selon la condition. Si, alors le plan coupe toutes les faces du cube. Si, alors le plan coupe les faces. Présentons les calculs correspondants.
Laisser Puis l'avionfranchit la ligne en ligne droite, et . Le bord, en plus. Bord le plan se coupe en ligne droite, et
Laisser Puis l'avionfranchit la ligne :
bord en ligne droite, et .
bord en ligne droite, et .
bord en ligne droite, et .
bord en ligne droite, et .
bord en ligne droite, et .
bord en ligne droite, et .
Cette fois, nous obtenons six segments qui ont des extrémités communes séquentiellement :
Laisser Puis l'avionfranchit la ligne en ligne droite, et . Bord le plan se coupe en ligne droite, et . Bord le plan se coupe en ligne droite, et . Autrement dit, nous obtenons trois segments qui ont des extrémités communes par paire :Ainsi, pour les valeurs de paramètres spécifiéesle plan coupe le cube le long d'un triangle régulier avec des sommets
Voici donc une description complète des figures planes obtenues lorsqu'un cube est coupé par un plan perpendiculaire à sa diagonale principale. L'idée principale était la suivante. Il est nécessaire de comprendre quelles faces le plan coupe, le long de quels ensembles il les coupe et comment ces ensembles sont liés les uns aux autres. Par exemple, s'il s'avère que le plan coupe exactement trois faces le long de segments qui ont des extrémités communes par paires, alors la section est un triangle équilatéral (ce qui est prouvé en comptant directement les longueurs des segments), dont les sommets sont ces extrémités des segments.
En utilisant le même dispositif et la même idée d'étude des sections, on peut déduire de manière tout à fait analogue les faits suivants :
1) Le vecteur d'une des diagonales principales d'un cube unitaire à quatre dimensions a pour coordonnées
2) Tout hyperplan perpendiculaire à la diagonale principale d'un cube à quatre dimensions peut s'écrire sous la forme.
3) Dans l'équation d'un hyperplan sécant, le paramètrepeut varier de 0 à 4 ;
4) Quand et un hyperplan sécant et un cube à quatre dimensions ont un point commun ( Et respectivement);
5) Quand la section efficace produira un tétraèdre régulier ;
6) Quand en coupe transversale, le résultat sera un octaèdre ;
7) Quand la section efficace produira un tétraèdre régulier.
En conséquence, ici l'hyperplan coupe le tesseract le long d'un plan sur lequel, en raison des limitations des variables, une région triangulaire est attribuée (une analogie - le plan a coupé le cube le long d'une ligne droite, sur laquelle, en raison des contraintes du variables, un segment a été attribué). Dans le cas 5), l'hyperplan coupe exactement quatre faces tridimensionnelles du tesseract, c'est-à-dire que l'on obtient quatre triangles qui ont des côtés communs par paire, en d'autres termes, formant un tétraèdre (la façon dont cela peut être calculé est correcte). Dans le cas 6), l'hyperplan coupe exactement huit faces tridimensionnelles du tesseract, c'est-à-dire que l'on obtient huit triangles qui ont des côtés séquentiellement communs, en d'autres termes, formant un octaèdre. Le cas 7) est complètement similaire au cas 5).
Illustrons cela avec un exemple précis. A savoir, nous étudions la section d'un cube à quatre dimensions par un hyperplanEn raison de restrictions variables, cet hyperplan coupe les faces tridimensionnelles suivantes : Bord se croise le long d'un planEn raison des limitations des variables, nous avons :On obtient une zone triangulaire avec des sommetsPlus loin,on obtient un triangleQuand un hyperplan coupe une faceon obtient un triangleQuand un hyperplan coupe une faceon obtient un triangleAinsi, les sommets du tétraèdre ont les coordonnées suivantes. Comme il est facile de le calculer, ce tétraèdre est bien régulier.
conclusions
Ainsi, au cours de cette recherche, les faits fondamentaux de la géométrie analytique multidimensionnelle ont été étudiés, les caractéristiques de la construction de cubes de dimensions de 0 à 3 ont été étudiées, la structure d'un cube à quatre dimensions a été étudiée, un cube à quatre dimensions a été décrits analytiquement et géométriquement, des modèles d'évolutions et de projections centrales de cubes tridimensionnels et quadridimensionnels ont été réalisés, les cubes tridimensionnels étaient des objets décrits analytiquement résultant de l'intersection d'un cube quadridimensionnel avec des hyperplans parallèles à l'un de ses éléments tridimensionnels. faces dimensionnelles, ou avec des hyperplans perpendiculaires à sa diagonale principale.
Les recherches menées ont permis d'identifier des analogies profondes dans la structure et les propriétés de cubes de différentes dimensions. La technique d'analogie utilisée peut être appliquée à la recherche, par exemple,sphère dimensionnelle ousimplexe dimensionnel. À savoir,une sphère dimensionnelle peut être définie comme un ensemble de pointsespace dimensionnel équidistant d'un point donné, appelé centre de la sphère. Plus loin,un simplexe dimensionnel peut être défini comme une partieespace dimensionnel limité par le nombre minimumhyperplans dimensionnels. Par exemple, un simplexe à une dimension est un segment (une partie d'un espace à une dimension, limitée par deux points), un simplexe à deux dimensions est un triangle (une partie d'un espace à deux dimensions, limitée par trois lignes droites), un simplexe tridimensionnel est un tétraèdre (une partie d'un espace tridimensionnel, limitée par quatre plans). Enfin,nous définissons le simplexe dimensionnel comme la partieespace dimensionnel, limitéhyperplan de dimension.
A noter que, malgré les nombreuses applications du tesseract dans certains domaines scientifiques, cette recherche reste encore en grande partie une étude mathématique.
Bibliographie
1) Bugrov Ya.S., Nikolsky S.M.Mathématiques supérieures, vol. 1 – M. : Outarde, 2005 – 284 p.
2) Quantique. Cube à quatre dimensions / Duzhin S., Rubtsov V., n° 6, 1986.
3) Quantique. Comment dessiner cube dimensionnel / Demidovich N.B., n° 8, 1974.
En géométrie hypercube- Ce n-analogie dimensionnelle d'un carré ( n= 2) et le cube ( n= 3). Il s'agit d'une figure convexe fermée constituée de groupes de lignes parallèles situées sur les bords opposés de la figure et reliées les unes aux autres à angle droit.
Ce chiffre est également connu sous le nom tesseract(tesseract). Le tesseract est au cube ce que le cube est au carré. Plus formellement, un tesseract peut être décrit comme un polytope quadridimensionnel convexe régulier (polyèdre) dont la limite est constituée de huit cellules cubiques.
Selon l'Oxford English Dictionary, le mot « tesseract » a été inventé en 1888 par Charles Howard Hinton et utilisé dans son livre « A New Era of Thought ». Le mot est dérivé du grec « τεσσερες ακτινες » (« quatre rayons »), sous la forme de quatre axes de coordonnées. De plus, dans certaines sources, le même chiffre était appelé tétracube(tétracube).
n-l'hypercube dimensionnel est également appelé n-cube.
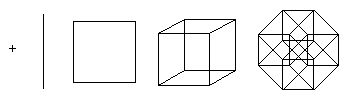
Un point est un hypercube de dimension 0. Si vous déplacez le point d'une unité de longueur, vous obtenez un segment d'unité de longueur - un hypercube de dimension 1. De plus, si vous déplacez le segment d'une unité de longueur dans une direction perpendiculaire dans la direction du segment, vous obtenez un cube - un hypercube de dimension 2. En décalant le carré d'une unité de longueur dans la direction perpendiculaire au plan du carré, vous obtenez un cube - un hypercube de dimension 3. Ce processus peut être généralisé à un nombre quelconque de dimensions. Par exemple, si vous déplacez un cube d’une unité de longueur dans la quatrième dimension, vous obtenez un tesseract.
La famille des hypercubes est l'un des rares polyèdres réguliers pouvant être représenté dans n'importe quelle dimension.
Éléments d'un hypercube
Hypercube dimensionnel n a 2 n"côtés" (une ligne unidimensionnelle a 2 points ; un carré bidimensionnel - 4 côtés ; un cube tridimensionnel - 6 faces ; un tesseract quadridimensionnel - 8 cellules). Le nombre de sommets (points) d'un hypercube est 2 n(par exemple, pour un cube - 2 3 sommets).
Quantité m hypercubes dimensionnels sur la frontière n-cube est égal
Par exemple, aux limites d’un hypercube, il y a 8 cubes, 24 carrés, 32 arêtes et 16 sommets.
| n-cube | Nom | Sommet (0-visage) |
Bord (1 face) |
Bord (2 faces) |
Cellule (3 faces) |
(4 faces) | (5 faces) | (6 faces) | (7 faces) | (8 faces) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-cube | Point | 1 | ||||||||
| 1 cube | Segment de ligne | 2 | 1 | |||||||
| 2 cubes | Carré | 4 | 4 | 1 | ||||||
| 3 cubes | cube | 8 | 12 | 6 | 1 | |||||
| 4 cubes | Tesseract | 16 | 32 | 24 | 8 | 1 | ||||
| 5 cubes | Pentecôtre | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6 cubes | Hexérat | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7 cubes | Heptact | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8 cubes | Octérat | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9 cubes | Eneneract | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Projection sur un avion
La formation d’un hypercube peut être représentée de la manière suivante :
- Deux points A et B peuvent être connectés pour former un segment de droite AB.
- Deux segments parallèles AB et CD peuvent être connectés pour former un carré ABCD.
- Deux carrés parallèles ABCD et EFGH peuvent être connectés pour former un cube ABCDEFGH.
- Deux cubes parallèles ABCDEFGH et IJKLMNOP peuvent être connectés pour former l'hypercube ABCDEFGHIJKLMNOP.
Cette dernière structure n'est pas facile à visualiser, mais il est possible de représenter sa projection dans un espace bidimensionnel ou tridimensionnel. De plus, les projections sur un plan bidimensionnel peuvent être plus utiles en permettant de réorganiser les positions des sommets projetés. Dans ce cas, il est possible d'obtenir des images qui ne reflètent plus les relations spatiales des éléments au sein du tesseract, mais illustrent la structure des connexions des sommets, comme dans les exemples ci-dessous.

La première illustration montre comment, en principe, un tesseract est formé en joignant deux cubes. Ce schéma est similaire au schéma permettant de créer un cube à partir de deux carrés. Le deuxième diagramme montre que tous les bords du tesseract ont la même longueur. Ce schéma vous oblige également à rechercher des cubes connectés les uns aux autres. Dans le troisième diagramme, les sommets du tesseract sont situés en fonction des distances le long des faces par rapport au point bas. Ce schéma est intéressant car il est utilisé comme schéma de base pour la topologie de réseau des processeurs connectés lors de l'organisation du calcul parallèle : la distance entre deux nœuds quelconques ne dépasse pas 4 longueurs de bord et il existe de nombreux chemins différents pour équilibrer la charge.
L'hypercube dans l'art
L'hypercube est apparu dans la littérature de science-fiction depuis 1940, lorsque Robert Heinlein, dans l'histoire « Et il a construit une maison tordue », a décrit une maison construite sous la forme d'un scan tesseract. Dans l'histoire de ce Suivant, cette maison s'effondre, se transformant en un tesseract à quatre dimensions. Après cela, l’hypercube apparaît dans de nombreux livres et nouvelles.
Le film Cube 2 : Hypercube raconte l'histoire de huit personnes piégées dans un réseau d'hypercubes.
Le tableau de Salvador Dali "Crucifixion (Corpus Hypercubus)", 1954, représente Jésus crucifié sur un scan tesseract. Ce tableau est visible au Metropolitan Museum of Art de New York.
Conclusion
Un hypercube est l'un des objets à quatre dimensions les plus simples, sur l'exemple duquel on peut voir toute la complexité et l'insolite de la quatrième dimension. Et ce qui semble impossible en trois dimensions est possible en quatre, par exemple des figures impossibles. Ainsi, par exemple, les barres d'un triangle impossible à quatre dimensions seront reliées à angle droit. Et cette figure ressemblera à ceci sous tous les points de vue, et ne sera pas déformée, contrairement aux implémentations d'un triangle impossible dans un espace tridimensionnel (voir.
Lorsque j’étais étudiant en première année, j’ai eu une vive dispute avec un de mes camarades de classe. Il a dit qu'un cube à quatre dimensions ne peut être représenté sous aucune forme, mais j'ai assuré qu'il peut être représenté assez clairement. Ensuite, j'ai même réalisé une projection d'un hypercube sur notre espace tridimensionnel à partir de trombones... Mais parlons de tout dans l'ordre.
Qu'est-ce qu'un hypercube et un espace à quatre dimensions
Notre espace habituel a trois dimensions. D'un point de vue géométrique, cela signifie que trois lignes mutuellement perpendiculaires peuvent y être indiquées. Autrement dit, pour n’importe quelle droite, vous pouvez trouver une deuxième droite perpendiculaire à la première, et pour une paire, vous pouvez trouver une troisième droite perpendiculaire aux deux premières. Il ne sera plus possible de trouver une quatrième ligne perpendiculaire aux trois existantes.
Espace à quatre dimensions ne diffère du nôtre qu'en ce qu'il a une direction supplémentaire. Si vous avez déjà trois lignes perpendiculaires entre elles, vous pouvez en trouver une quatrième, de telle sorte qu’elle soit perpendiculaire aux trois.
Hypercube c'est juste un cube dans un espace à quatre dimensions.
Est-il possible d’imaginer un espace à quatre dimensions et un hypercube ?
Cette question s'apparente à la question : « est-il possible d'imaginer la Cène en regardant le tableau du même nom (1495-1498) de Léonard de Vinci (1452-1519) ?
D'une part, bien sûr, vous n'imaginerez pas ce que Jésus a vu (il est assis face au spectateur), d'autant plus que vous ne sentirez pas le jardin par la fenêtre et ne goûterez pas la nourriture sur la table, vous n'entendrez pas les oiseaux chanter... Vous n'aurez pas une image complète de ce qui s'est passé à cette heure-là le soir, mais on ne peut pas dire que vous n'apprendrez rien de nouveau et que l'image n'a aucun intérêt.
La situation est similaire avec la question de l’hypercube. Il est impossible de l’imaginer pleinement, mais vous pouvez mieux comprendre à quoi cela ressemble.
Construction d'un hypercube
cube à 0 dimension
Commençons par le début – avec un cube à 0 dimension. Ce cube contient 0 faces mutuellement perpendiculaires, c’est-à-dire qu’il ne s’agit que d’un point.
Cube à 1 dimension
Dans un espace unidimensionnel, nous n’avons qu’une seule direction. Nous déplaçons le point dans cette direction et obtenons un segment.
Il s'agit d'un cube unidimensionnel.
cube en 2 dimensions
Nous avons une deuxième dimension, nous déplaçons notre cube (segment) unidimensionnel dans le sens de la deuxième dimension et nous obtenons un carré.
C'est un cube dans un espace à deux dimensions.
cube en 3 dimensions
Avec l'avènement de la troisième dimension, on fait de même : on déplace le carré et on obtient un cube régulier en trois dimensions.

Cube à 4 dimensions (hypercube)
Nous avons maintenant une quatrième dimension. C'est-à-dire que nous avons à notre disposition une direction perpendiculaire aux trois précédentes. Utilisons-le exactement de la même manière. Un cube à quatre dimensions ressemblera à ceci.

Naturellement, les cubes tridimensionnels et quadridimensionnels ne peuvent pas être représentés sur un plan d'écran bidimensionnel. Ce que j'ai dessiné, ce sont des projections. Nous parlerons de projections un peu plus tard, mais pour l'instant quelques faits et chiffres.
Nombre de sommets, arêtes, faces
Veuillez noter que la face d'un hypercube est notre cube tridimensionnel ordinaire. Si vous regardez attentivement le dessin d’un hypercube, vous pouvez en réalité trouver huit cubes.
Projections et vision d'un habitant d'un espace à quatre dimensions
Quelques mots sur la vision
Nous vivons dans un monde tridimensionnel, mais nous le considérons comme bidimensionnel. Cela est dû au fait que la rétine de nos yeux est située dans un plan qui n'a que deux dimensions. C'est pourquoi nous sommes capables de percevoir des images bidimensionnelles et de les trouver similaires à la réalité.
(Bien sûr, grâce à l’accommodation, l’œil peut estimer la distance jusqu’à un objet, mais il s’agit d’un effet secondaire associé à l’optique intégrée à nos yeux.)
Les yeux d'un habitant d'un espace à quatre dimensions doivent avoir une rétine à trois dimensions. Une telle créature peut voir immédiatement la totalité de la figure tridimensionnelle : tous ses visages et ses intérieurs. (De la même manière, nous pouvons voir une figure en deux dimensions, toutes ses faces et ses intérieurs.)
Ainsi, avec l’aide de nos organes de vision, nous ne sommes pas capables de percevoir un cube à quatre dimensions de la même manière que le percevrait un habitant d’un espace à quatre dimensions. Hélas. Il ne vous reste plus qu'à vous fier à votre esprit et à votre imagination, qui, heureusement, n'ont aucune limite physique.
Cependant, lorsque je représente un hypercube sur un plan, je suis simplement obligé de le projeter sur un espace bidimensionnel. Tenez compte de ce fait lors de l’étude des dessins.
Intersections de bords
Naturellement, les bords de l’hypercube ne se croisent pas. Les intersections apparaissent uniquement dans les dessins. Cependant, cela ne devrait pas surprendre, car les bords d’un cube ordinaire sur les images se croisent également.
Longueurs de bord
Il convient de noter que toutes les faces et arêtes d’un cube à quatre dimensions sont égales. Sur la figure, ils ne sont pas égaux uniquement parce qu’ils sont situés à des angles différents par rapport à la direction de vue. Cependant, il est possible de faire pivoter un hypercube pour que toutes les projections aient la même longueur.
À propos, sur cette figure, huit cubes, qui sont les faces d'un hypercube, sont clairement visibles.
L'hypercube est vide à l'intérieur
C’est difficile à croire, mais entre les cubes qui délimitent l’hypercube, il y a de l’espace (un fragment d’espace à quatre dimensions).
Pour mieux comprendre cela, regardons une projection bidimensionnelle d'un cube tridimensionnel ordinaire (je l'ai délibérément rendue quelque peu schématique).

Pouvez-vous en deviner qu’il y a de l’espace à l’intérieur du cube ? Oui, mais seulement en utilisant votre imagination. L'œil ne voit pas cet espace.
Cela se produit parce que les bords situés dans la troisième dimension (qui ne peuvent pas être représentés dans un dessin à plat) se sont désormais transformés en segments situés dans le plan du dessin. Ils ne fournissent plus de volume.
Les carrés entourant l'espace du cube se chevauchaient. Mais on peut imaginer que dans la figure originale (un cube tridimensionnel) ces carrés étaient situés dans des plans différents, et non les uns sur les autres dans le même plan, comme c'est le cas sur la figure.
La situation est exactement la même avec un hypercube. Les faces des cubes d'un hypercube ne se chevauchent pas réellement, comme cela nous semble sur la projection, mais sont situées dans un espace à quatre dimensions.
Balayages
Ainsi, un résident d’un espace à quatre dimensions peut voir un objet en trois dimensions simultanément de tous les côtés. Pouvons-nous voir un cube tridimensionnel de tous les côtés en même temps ? Avec l'œil - non. Mais les gens ont trouvé un moyen de représenter simultanément toutes les faces d'un cube tridimensionnel sur un dessin plat. Une telle image s’appelle un scan.
Développement d'un cube tridimensionnel
Tout le monde sait probablement comment se forme le développement d’un cube tridimensionnel. Ce processus est montré dans l'animation.

Pour plus de clarté, les bords des faces du cube sont translucides.
Il convient de noter que nous ne pouvons percevoir cette image bidimensionnelle que grâce à notre imagination. Si l’on considère les phases qui se déroulent d’un point de vue purement bidimensionnel, le processus semblera étrange et pas du tout clair.

Cela ressemble à l'apparition progressive des contours d'abord de carrés déformés, puis à leur mise en place tout en prenant simultanément la forme souhaitée.
Si vous regardez le cube qui se déroule dans la direction d'une de ses faces (de ce point de vue, le cube ressemble à un carré), alors le processus de formation du dépliage est encore moins clair. Tout ressemble à des carrés sortant du carré initial (pas au cube déplié).
Mais pas visuel scanner uniquement pour œil.
Comment comprendre l’espace à 4 dimensions ?
C’est grâce à votre imagination que vous pourrez en tirer de nombreuses informations.
Développement d'un cube à quatre dimensions
Il est tout simplement impossible de rendre le processus animé de déploiement d'un hypercube au moins quelque peu visuel. Mais ce processus peut être imaginé. (Pour ce faire, vous devez le regarder à travers les yeux d’un être à quatre dimensions.)
L'analyse ressemble à ceci.

Les huit cubes délimitant l'hypercube sont visibles ici.
Les bords qui doivent s'aligner une fois pliés sont peints avec les mêmes couleurs. Les visages pour lesquels les paires ne sont pas visibles sont laissés en gris. Après le pliage, la face supérieure du cube supérieur doit être alignée avec le bord inférieur du cube inférieur. (Le déroulement d’un cube tridimensionnel est réduit de la même manière.)
A noter qu'après convolution, toutes les faces des huit cubes entreront en contact, fermant l'hypercube. Et enfin, lorsque vous imaginez le processus de pliage, n'oubliez pas que lors du pliage, ce n'est pas le chevauchement des cubes qui se produit, mais leur enroulement autour d'une certaine zone quadridimensionnelle (hypercubique).
Salvador Dali (1904-1989) a représenté la crucifixion à plusieurs reprises et des croix apparaissent dans plusieurs de ses tableaux. Le tableau « La Crucifixion » (1954) utilise un scan hypercube.
Espace-temps et espace euclidien à quatre dimensions
J'espère que vous avez pu imaginer l'hypercube. Mais avez-vous réussi à mieux comprendre comment fonctionne l’espace-temps à quatre dimensions dans lequel nous vivons ? Hélas, pas tout à fait.
Nous avons parlé ici de l’espace euclidien à quatre dimensions, mais l’espace-temps a des propriétés complètement différentes. En particulier, lors d'éventuelles rotations, les segments restent toujours inclinés par rapport à l'axe du temps, soit d'un angle inférieur à 45 degrés, soit d'un angle supérieur à 45 degrés.
J'ai consacré une série de notes aux propriétés de l'espace-temps.
Tridimensionnalité de l'image
Le monde est tridimensionnel. Son image est bidimensionnelle. Une tâche importante de la peinture et, désormais, de la photographie est de transmettre la tridimensionnalité de l’espace. Les Romains maîtrisaient déjà certaines techniques, puis elles furent oubliées et commencèrent à revenir à la peinture classique avec la Renaissance.
 La principale technique pour créer un espace tridimensionnel en peinture est la perspective. Les rails du chemin de fer, s'éloignant du spectateur, sont visuellement étroits. En peinture, les rails peuvent être physiquement rétrécis. En photographie, la perspective se produit automatiquement : l'appareil photo photographiera les rails aussi rétrécis que l'œil les voit. Cependant, ne le laissez pas se fermer presque : il ne ressemblera plus à une perspective, mais à une figure étrange ; Il doit y avoir un écart notable entre les rails, les côtés de la rue et les berges de la rivière.
La principale technique pour créer un espace tridimensionnel en peinture est la perspective. Les rails du chemin de fer, s'éloignant du spectateur, sont visuellement étroits. En peinture, les rails peuvent être physiquement rétrécis. En photographie, la perspective se produit automatiquement : l'appareil photo photographiera les rails aussi rétrécis que l'œil les voit. Cependant, ne le laissez pas se fermer presque : il ne ressemblera plus à une perspective, mais à une figure étrange ; Il doit y avoir un écart notable entre les rails, les côtés de la rue et les berges de la rivière.
Il est important de comprendre que la perspective linéaire est la manière la plus primitive et la plus réaliste de transmettre le monde.
Navigation des articles
Ce n'est pas un hasard si son apparition est associée à un décor théâtral (Florensky, « Perspective inversée »). Le caractère conventionnel et la simplicité de la transmission d'une scène théâtrale de faible profondeur conviennent très bien à la photographie, qui n'a pas la variété des techniques disponibles en peinture.
Il existe des perspectives bien plus intéressantes que la perspective linéaire. Dans les œuvres des maîtres chinois, il existe une perspective flottante, lorsque les objets sont représentés simultanément d'en bas, d'en haut et de face. Il ne s'agit pas d'une erreur technique commise par des artistes incompétents : l'auteur légendaire de cette technique, Guo Xi, a écrit qu'un tel affichage permet de se rendre compte du monde dans sa totalité. La technique de la peinture d’icônes russe est similaire, dans laquelle le spectateur peut voir le visage et le dos du personnage en même temps. Une technique intéressante de peinture d'icônes, également trouvée chez les artistes d'Europe occidentale, était la perspective inversée, dans laquelle les objets éloignés, au contraire, sont plus grands que les objets proches, soulignant ainsi leur importance. Ce n'est que de nos jours qu'il a été établi qu'une telle perspective est correcte : contrairement aux objets éloignés, le gros plan est en réalité perçu en perspective inversée (Rauschenbach). À l'aide de Photoshop, vous pouvez obtenir une perspective inversée en agrandissant les objets d'arrière-plan. Pour un spectateur habitué aux lois de la photographie, une telle image paraîtra étrange.
Introduire dans le cadre l’angle d’un bâtiment à partir duquel les murs divergent dans les deux sens crée un semblant de perspective isométrique. Le cerveau comprend que les murs sont à angle droit et organise le reste de l’image en conséquence. Cette perspective est plus dynamique que la perspective frontale et plus naturelle pour le gros plan. Introduisez simplement les angles d'extrémité des objets et des bâtiments voisins dans le cadre.
Du fait de l'agrandissement, la perspective isométrique est majeure, ce qui convient rarement à un portrait classique. La perspective linéaire, en raison du rétrécissement, transmet mieux les émotions mineures.
Au stade de la prise de vue, le photographe dispose de nombreux outils pour mettre en valeur la perspective. Des objets d'égale largeur s'étendant au loin (pistes, rues, colonnes, sillons) par leur rétrécissement et même simplement en s'éloignant indiquent au spectateur la tridimensionnalité de l'espace. L'effet est plus fort si vous photographiez sous un angle faible pour augmenter la distorsion de la perspective. C'est suffisant pour la photographie de paysage, mais avec une faible profondeur d'image pour la photographie d'intérieur, l'effet est à peine perceptible. Il peut être un peu amélioré en post-traitement en rétrécissant le haut de l'image (Transformer Perspective). Cependant, même dans un paysage, une perspective exagérée peut paraître intéressante.
La profondeur peut être évidente dans le sens de l'image : les bâtiments sont séparés par une rue ou une rivière. La diagonale met l'accent sur la tridimensionnalité ; par exemple, un pont sur une rivière.
Les objets d'une taille connue du spectateur en arrière-plan déterminent l'échelle et, par conséquent, forment la perspective. En photographie de paysage, cet objet pourrait être une voiture, mais en photographie de portrait, essayez de plier votre jambe (loin de l'appareil photo) sous la chaise pour qu'elle paraisse plus petite tout en restant visible. Vous pouvez même rendre cette jambe un peu plus petite en post-traitement.
L'ornement transmet la perspective en réduisant visuellement les éléments. Un exemple serait de grands carreaux sur le sol, marquant des lignes sur la route.
Il existe une technique appelée premier plan hypertrophié. De taille disproportionnée, il crée de la profondeur dans l’image. En comparant l'échelle du premier plan et celle du modèle, l'œil arrive à la conclusion que le modèle est bien plus éloigné qu'il n'y paraît. L’exagération doit rester subtile pour que l’image ne soit pas perçue comme une erreur. Cette technique fonctionne non seulement pour le post-traitement, mais aussi pour la prise de vue : déformer les proportions en photographiant avec un objectif 35 ou 50 mm. La prise de vue avec un objectif grand angle étire l’espace, renforçant sa tridimensionnalité en brisant les proportions. L'effet est plus fort si l'on photographie le modèle à bout portant, mais attention aux proportions grotesques : seuls les auteurs d'images religieuses peuvent représenter un personnage plus grand qu'un édifice.
L'intersection fonctionne très bien. Si la pomme recouvre partiellement la poire, alors le cerveau ne s'y trompera pas : la pomme est devant la poire. Le modèle recouvre partiellement les meubles, créant ainsi de la profondeur à l'intérieur.
L'alternance de taches claires et sombres donne également de la profondeur à l'image. Le cerveau sait par expérience que les objets proches sont éclairés à peu près de la même manière, il interprète donc les objets éclairés différemment comme étant situés à des distances différentes. Pour cet effet, les points alternent dans la direction de l'axe de perspective - en profondeur dans l'image et non à travers celle-ci. Par exemple, lorsque vous photographiez un modèle allongé loin de la caméra dans un cadre sombre, placez les reflets près des fesses et près des jambes. Vous pouvez éclaircir/assombrir les zones en post-traitement.
La séquence d'objets de plus en plus sombres est perçue comme diminuant. En ombrant progressivement les objets le long de la ligne active, vous pouvez obtenir une subtile impression de perspective. De même, la profondeur s'exprime en atténuant la lumière : projetez une bande de lumière sur les meubles ou sur le sol.
Une image tridimensionnelle peut être obtenue grâce non seulement à la lumière, mais également au contraste des couleurs. Cette technique était connue des peintres flamands, qui plaçaient des taches de couleurs vives sur leurs natures mortes. Une grenade rouge et un citron jaune côte à côte auront un aspect tridimensionnel même sous un éclairage frontal plat. Ils se démarqueront particulièrement bien sur fond de raisins violets : une couleur chaude sur fond froid. Les surfaces aux couleurs vives ressortent bien de l'obscurité, même avec une lumière faible, typique des natures mortes. Le contraste des couleurs fonctionne mieux avec les couleurs primaires : rouge, jaune, bleu plutôt qu'avec les nuances.
Sur fond noir, le jaune apparaît, le bleu se cache. Sur fond blanc, c’est l’inverse. La saturation des couleurs renforce cet effet. Pourquoi cela arrive-t-il? La couleur jaune n’est jamais sombre, c’est pourquoi le cerveau refuse de croire qu’un objet jaune puisse être immergé dans un fond sombre et non éclairé. Le bleu, au contraire, est sombre.
Améliorer la perspective en post-traitement revient à simuler la perception atmosphérique : les objets distants apparaissent plus clairs, plus flous, avec un contraste réduit en termes de luminosité, de saturation et de tonalité.
Outre les longues distances, les effets atmosphériques semblent naturels dans la brume matinale, le brouillard ou dans un bar enfumé. Tenez compte de la météo : par temps nuageux ou au crépuscule, il se peut qu'il n'y ait pas de différence significative entre le premier plan et l'arrière-plan.
Le facteur le plus important est le contraste de luminosité. Dans les réglages, c'est le contraste habituel. Réduisez le contraste des objets distants, augmentez le contraste du premier plan - et l'image deviendra convexe. Nous ne parlons pas du contraste entre le premier plan et l'arrière-plan, mais du contraste de l'arrière-plan, qui doit être inférieur au contraste du premier plan. Cette méthode convient non seulement à la photographie de paysage et de genre, mais également aux portraits en studio : augmentez le contraste du devant du visage, réduisez le contraste sur les cheveux, les pommettes et les vêtements. Les filtres de portrait font quelque chose de similaire, brouillant la peau du modèle et laissant les yeux et les lèvres durs.
Le réglage du contraste est le moyen le plus simple d’effectuer le post-traitement d’une image 3D. Contrairement à d'autres processus, le spectateur ne remarquera pratiquement aucun changement, ce qui permettra de conserver un maximum de naturel.
Le flou est similaire à la réduction du contraste, mais ce sont des processus différents. L'image peut être peu contrastée tout en restant nette. En raison de la profondeur de champ limitée, le flou des objets distants reste le moyen le plus populaire de transmettre la tridimensionnalité en photographie et peut facilement être amélioré en floutant les sujets distants en post-production. Par conséquent, moins de détails doivent être placés à l’arrière-plan – le cerveau ne s’attend pas à ce que des objets distinguables soient visibles au loin. Pendant ce temps, la réduction du contraste correspond mieux à la perception naturelle : les montagnes lointaines sont visibles avec un faible contraste, et non floues, car lors du balayage du paysage, l'œil est constamment recentré et le problème de la profondeur de champ lui est étranger. En rendant l'arrière-plan flou, vous pouvez en même temps rendre le premier plan plus net. De plus, au premier plan, vous pouvez améliorer les lignes de l'image (Filtre passe-haut ou Clarté). C'est la grande netteté du premier plan qui explique la bosse caractéristique de l'image des objectifs de haute qualité. Attention : dans un souci d'augmentation légère de la tridimensionnalité, vous risquez de rendre l'image trop rigide.
Les objets plus légers apparaissent plus loin. Cela est dû au fait que dans la nature, nous voyons des objets lointains à travers l’épaisseur de l’air diffusant la lumière ; les montagnes lointaines semblent légères. En photographie de paysage, il faut donc faire attention au placement des objets lumineux au premier plan.
Illuminez les objets éloignés. Plus ils sont éloignés, plus ils se fondent dans la luminosité et la tonalité du ciel. Veuillez noter que les objets horizontaux (sol, mer) sont mieux éclairés que les objets verticaux (murs, arbres), alors n'en faites pas trop en éclaircissant ces derniers. Dans tous les cas, les objets doivent rester sensiblement plus légers que le ciel.
 Eh bien, si vous remarquez que l'esquive est un autre moyen de réduire le contraste de la luminosité de l'arrière-plan. Assombrir légèrement le premier plan pour améliorer l'effet de relief.
Eh bien, si vous remarquez que l'esquive est un autre moyen de réduire le contraste de la luminosité de l'arrière-plan. Assombrir légèrement le premier plan pour améliorer l'effet de relief.
Il semblerait qu'à l'intérieur, tout soit inversé. Si, dans la rue, l'œil est habitué au fait que la distance est claire, alors dans la pièce, la lumière est souvent concentrée sur la personne et l'intérieur est plongé dans l'obscurité ; le cerveau est habitué à l’éclairage de premier plan et non à l’éclairage de fond.
Dans les images d’intérieur avec une faible profondeur de scène, contrairement aux images de paysage, le modèle éclairé dépasse d’un fond sombre. Mais il y a aussi un facteur inverse : pendant 99 % de son évolution, l'homme a observé la perspective dans des espaces ouverts, et avec l'avènement des pièces, le cerveau n'a pas encore eu le temps de se restructurer. Vermeer préférait un fond clair pour ses portraits, et ses portraits sont vraiment proéminents. L'éclairage d'un fond vertical, recommandé en photographie, non seulement en sépare le modèle, mais aussi, en éclaircissant le fond, donne à l'image une légère tridimensionnalité. Nous sommes ici confrontés au fait que le cerveau analyse la localisation des objets en fonction de plusieurs facteurs, et ceux-ci peuvent être contradictoires.
L'éclairage du studio semble intéressant, dans lequel des points lumineux se trouvent sur des zones du modèle éloignées de la caméra. Par exemple, le sein le plus éloigné de la caméra est mis en évidence.
Réduire la saturation des couleurs sur les objets distants : en raison de l'épaisseur de l'air qui nous sépare, les montagnes lointaines sont désaturées presque au niveau du monochrome et recouvertes d'une brume bleue. La saturation du premier plan peut être augmentée.
Puisque le jaune est clair et que le bleu et le rouge sont foncés, le contraste des couleurs est également un contraste de luminosité.
Lorsque vous désaturez un arrière-plan éloigné, ne le laissez pas disparaître de la vue. Souvent, au contraire, il faut augmenter la saturation du fond pour le révéler. C’est plus important que la tridimensionnalité.
De nombreux conseils en photographie 3D se concentrent sur le contraste de température. En fait, cet effet est très faible et est facilement interrompu par le contraste de luminosité. De plus, le contraste de température est gênant et perceptible.
Les objets très éloignés semblent de couleur plus froide car l’air absorbe la lumière orange chaude. Lorsque vous photographiez un modèle sur la plage avec des navires à l'horizon en arrière-plan, diminuez la température de couleur de la mer lointaine et des navires en post-traitement. Un mannequin en maillot de bain rouge émerge de la mer bleue, et un mannequin à la lumière jaune d'un réverbère émerge du crépuscule bleuté.
C'est l'essence même de la tonification séparée : nous rendons le modèle plus chaud, l'arrière-plan plus froid. Le cerveau comprend qu'il n'y a pas de températures de couleur différentes dans un même plan et perçoit une telle image tridimensionnelle dans laquelle le modèle dépasse de l'arrière-plan. La tonalité divisée ajoute de la profondeur aux paysages : rendez le premier plan plus chaud et l'arrière-plan plus froid.
Une exception importante à la tonalité séparée : au lever et au coucher du soleil, l'arrière-plan lointain n'est pas du tout froid, mais chaud, avec des tons jaunes et rouge-orange. La solution évidente – utiliser un mannequin blanc dans un maillot de bain violet – ne fonctionne pas car la lumière du coucher du soleil projette également une teinte chaude sur le corps du mannequin.
Résumons : pour donner à une photo une tridimensionnalité basée sur des effets atmosphériques, il faut contraster le premier plan et l'arrière-plan. Le contraste principal est basé sur le contraste habituel : le premier plan est très contrasté, l'arrière-plan est peu contrasté. Le deuxième contraste est au niveau de la netteté : le premier plan est net, l'arrière-plan est flou. Le troisième contraste est en termes de luminosité : le premier plan est sombre, l'arrière-plan est clair. Le quatrième contraste est en termes de saturation : les couleurs du premier plan sont saturées, les couleurs du fond sont désaturées. Le cinquième contraste est celui de la température : le premier plan est chaud, l'arrière-plan est froid.
Les facteurs répertoriés sont souvent multidirectionnels. Le jaune est plus brillant que le bleu et les objets clairs apparaissent plus éloignés des objets sombres. Il serait naturel de s’attendre à ce que le jaune recule et que le bleu se rapproche du spectateur. En fait, c'est l'inverse : une couleur chaude émerge d'un fond froid. Autrement dit, la couleur s’avère être un facteur plus important que la luminosité. Ce qui, à la réflexion, n’est pas surprenant : le jaune et le rouge ne se distinguent clairement que de près, et le spectateur ne s’attend pas à les voir de loin.
Conclusion : gardez l'arrière-plan à faible contraste, délavé, clair, désaturé, bleuâtre. Et préparez-vous au fait que le spectateur, habitué à la 3D hypertrophiée des films, trouvera la tridimensionnalité que vous avez créée à peine perceptible ou absente.
En photographie de portrait, il est préférable de s'appuyer sur l'effet clair-obscur éprouvé - le jeu d'ombre et de lumière sur le visage du modèle, qui rendra l'image assez convexe. Dans la photographie de genre, la perspective donne l’effet tridimensionnel le plus visible. Dans une nature morte, le facteur principal sera l'intersection (chevauchement) d'objets.
Ne vous laissez pas emporter par cette perspective ; ce n'est qu'un arrière-plan pour le plan frontal sur lequel flotte votre image. Dans la peinture moderne, qui est loin du réalisme, la perspective n’est pas très appréciée.
Téléchargez le livre en entier : pdfepubazw3mobifb2litContents
Points (±1, ±1, ±1, ±1). En d’autres termes, il peut être représenté par l’ensemble suivant :
Le tesseract est limité par huit hyperplans dont l'intersection avec le tesseract lui-même définit ses faces tridimensionnelles (qui sont des cubes ordinaires). Chaque paire de faces 3D non parallèles se croise pour former des faces 2D (carrés), et ainsi de suite. Enfin, le tesseract possède 8 faces 3D, 24 faces 2D, 32 arêtes et 16 sommets.
Description populaire
Essayons d'imaginer à quoi ressemblera un hypercube sans quitter l'espace tridimensionnel.
Dans un « espace » unidimensionnel - sur une ligne - nous sélectionnons un segment AB de longueur L. Sur un plan bidimensionnel à une distance L de AB, nous dessinons un segment DC parallèle à celui-ci et connectons leurs extrémités. Le résultat est un CDBA carré. En répétant cette opération avec le plan, on obtient un cube tridimensionnel CDBAGHFE. Et en décalant le cube dans la quatrième dimension (perpendiculaire aux trois premières) d'une distance L, on obtient l'hypercube CDBAGHFEKLJIOPNM.
Construction d'un tesseract sur un avion
Le segment unidimensionnel AB sert de côté du carré bidimensionnel CDBA, le carré - de côté du cube CDBAGHFE, qui, à son tour, sera le côté de l'hypercube à quatre dimensions. Un segment de droite a deux points limites, un carré a quatre sommets et un cube en a huit. Dans un hypercube à quatre dimensions, il y aura donc 16 sommets : 8 sommets du cube original et 8 de celui décalé dans la quatrième dimension. Il a 32 arêtes - 12 donnent chacune les positions initiale et finale du cube d'origine, et 8 autres arêtes "dessinent" ses huit sommets, qui se sont déplacés vers la quatrième dimension. Le même raisonnement peut être fait pour les faces d’un hypercube. Dans l'espace à deux dimensions, il n'y en a qu'un (le carré lui-même), un cube en a 6 (deux faces du carré déplacé et quatre autres qui décrivent ses côtés). Un hypercube à quatre dimensions possède 24 faces carrées : 12 carrés du cube d'origine dans deux positions et 12 carrés de ses douze arêtes.
Tout comme les côtés d'un carré sont 4 segments à une dimension et les côtés (faces) d'un cube sont 6 carrés à deux dimensions, de même pour un « cube à quatre dimensions » (tesseract), les côtés sont 8 cubes à trois dimensions. . Les espaces de paires opposées de cubes tesseract (c'est-à-dire les espaces tridimensionnels auxquels appartiennent ces cubes) sont parallèles. Sur la figure ce sont les cubes : CDBAGHFE et KLJIOPNM, CDBAKLJI et GHFEOPNM, EFBAMNJI et GHDCOPLK, CKIAGOME et DLJBHPNF.
De la même manière, nous pouvons poursuivre notre raisonnement pour les hypercubes d'un plus grand nombre de dimensions, mais il est beaucoup plus intéressant de voir à quoi ressemblera un hypercube à quatre dimensions pour nous, résidents d'un espace tridimensionnel. Pour cela, nous utiliserons la méthode déjà familière des analogies.
Prenons le cube métallique ABCDHEFG et regardons-le d'un œil du côté du bord. Nous verrons et pourrons dessiner deux carrés sur le plan (ses bords proches et éloignés), reliés par quatre lignes - bords latéraux. De même, un hypercube à quatre dimensions dans un espace tridimensionnel ressemblera à deux « boîtes » cubiques insérées l’une dans l’autre et reliées par huit arêtes. Dans ce cas, les « boîtes » elles-mêmes - des faces tridimensionnelles - seront projetées sur « notre » espace, et les lignes qui les relient s'étireront en direction du quatrième axe. Vous pouvez également essayer d'imaginer le cube non pas en projection, mais dans une image spatiale.
Tout comme un cube tridimensionnel est formé d’un carré décalé de la longueur de sa face, un cube décalé dans la quatrième dimension formera un hypercube. Il est limité par huit cubes qui, en perspective, ressembleront à une figure plutôt complexe. L’hypercube à quatre dimensions lui-même est constitué d’un nombre infini de cubes, tout comme un cube à trois dimensions peut être « découpé » en un nombre infini de carrés plats.
En découpant les six faces d'un cube tridimensionnel, vous pouvez le décomposer en une figure plate - un développement. Il y aura un carré de chaque côté de la face d'origine plus un autre - la face opposée. Et le développement tridimensionnel d'un hypercube à quatre dimensions comprendra le cube original, six cubes « grandissant » à partir de celui-ci, plus un autre - l'« hyperface » finale.
Les propriétés d'un tesseract représentent une continuation des propriétés des figures géométriques de dimension inférieure dans un espace à quatre dimensions.
Projections
Vers un espace à deux dimensions
Cette structure est difficile à imaginer, mais il est possible de projeter un tesseract dans des espaces à deux ou trois dimensions. De plus, la projection sur un plan permet de comprendre facilement l'emplacement des sommets de l'hypercube. De cette manière, il est possible d'obtenir des images qui ne reflètent plus les relations spatiales au sein du tesseract, mais qui illustrent la structure de connexion des sommets, comme dans les exemples suivants :

La troisième image montre le tesseract en isométrie, par rapport au point de construction. Cette représentation est intéressante lors de l'utilisation d'un tesseract comme base d'un réseau topologique pour relier plusieurs processeurs dans un calcul parallèle.
Vers l'espace tridimensionnel
L'une des projections d'un tesseract sur un espace tridimensionnel représente deux cubes tridimensionnels imbriqués dont les sommets correspondants sont reliés par des segments. Les cubes intérieurs et extérieurs ont des tailles différentes dans l’espace tridimensionnel, mais dans l’espace quadridimensionnel, ce sont des cubes égaux. Pour comprendre l'égalité de tous les cubes tesseract, un modèle tesseract rotatif a été créé.
|
|
- Les six pyramides tronquées le long des bords du tesseract sont des images de six cubes égaux. Cependant, ces cubes sont à un tesseract comme les carrés (faces) le sont à un cube. Mais en fait, le tesseract peut être divisé en un nombre infini de cubes, tout comme un cube peut être divisé en un nombre infini de carrés, ou un carré en un nombre infini de segments.
Une autre projection intéressante du tesseract sur un espace tridimensionnel est un dodécaèdre rhombique avec ses quatre diagonales reliant des paires de sommets opposés aux grands angles des losanges. Dans ce cas, 14 des 16 sommets du tesseract sont projetés dans 14 sommets du dodécaèdre rhombique, et les projections des 2 restants coïncident en son centre. Dans une telle projection sur un espace tridimensionnel, l'égalité et le parallélisme de tous les côtés unidimensionnels, bidimensionnels et tridimensionnels sont préservés.
Paire stéréo
Une paire stéréo de tesseract est représentée comme deux projections sur un espace tridimensionnel. Cette image du tesseract a été conçue pour représenter la profondeur comme quatrième dimension. La paire stéréo est visualisée de telle sorte que chaque œil ne voit qu'une seule de ces images, une image stéréoscopique apparaît qui reproduit la profondeur du tesseract.
Déballage du Tesseract
La surface d'un tesseract peut être dépliée en huit cubes (de la même manière que la surface d'un cube peut être dépliée en six carrés). Il existe 261 modèles de tesseract différents. Le déroulement d'un tesseract peut être calculé en traçant les angles connectés sur un graphique.
Tesseract dans l'art
- Dans "New Abbott Plain" d'Edwina A., l'hypercube fait office de narrateur.
- Dans un épisode des Aventures de Jimmy Neutron, le « garçon génie » Jimmy invente un hypercube tridimensionnel identique à la boîte pliante du roman Glory Road (1963) de Robert Heinlein.
- Robert E. Heinlein a mentionné les hypercubes dans au moins trois histoires de science-fiction. Dans "La Maison aux Quatre Dimensions" ("La Maison que Sarcelle a construite"), il a décrit une maison construite comme un tesseract non emballé, puis, en raison d'un tremblement de terre, "pliée" dans la quatrième dimension et devenue un "vrai" tesseract. .
- Le roman Glory Road de Heinlein décrit une boîte hyper-taille qui était plus grande à l'intérieur qu'à l'extérieur.
- L'histoire d'Henry Kuttner « Tous les Tenali sont des Borogov » décrit un jouet éducatif pour les enfants d'un futur lointain, de structure similaire à un tesseract.
- Dans le roman d'Alex Garland (), le terme « tesseract » est utilisé pour désigner le déploiement tridimensionnel d'un hypercube à quatre dimensions, plutôt que l'hypercube lui-même. Il s’agit d’une métaphore conçue pour montrer que le système cognitif doit être plus large que le connaissable.
- L'intrigue de Cube 2 : Hypercube est centrée sur huit inconnus piégés dans un « hypercube », ou un réseau de cubes connectés.
- La série télévisée Andromeda utilise des générateurs de tesseract comme dispositif d'intrigue. Ils sont principalement conçus pour manipuler l’espace et le temps.
- Peinture « La Crucifixion » (Corpus Hypercubus) de Salvador Dali ().
- La bande dessinée Nextwave représente un véhicule qui comprend 5 zones tesseract.
- Dans l'album Voivod Nothingface, l'une des compositions s'appelle « In my hypercube ».
- Dans le roman Route Cube d'Anthony Pearce, l'une des lunes en orbite de l'Association internationale de développement est appelée un tesseract qui a été compressé en 3 dimensions.
- Dans la troisième saison de la série « Black Hole School », il y a un épisode « Tesseract ». Lucas appuie sur un bouton secret et l'école commence à « prendre forme comme un tesseract mathématique ».
- Le terme « tesseract » et son terme dérivé « tesserate » se retrouvent dans le récit « Une ride dans le temps » de Madeleine L’Engle.
- TesseracT est le nom d'un groupe de djent britannique.
- Dans la série de films Marvel Cinematic Universe, le Tesseract est un élément clé de l'intrigue, un artefact cosmique en forme d'hypercube.
- Dans l'histoire de Robert Sheckley « Miss Souris et la Quatrième Dimension », un écrivain ésotérique, une connaissance de l'auteur, tente de voir le tesseract en fixant pendant des heures l'appareil qu'il a conçu : une balle sur une jambe avec des tiges plantées dedans, sur quels cubes sont montés, recouverts de toutes sortes de symboles ésotériques. L'histoire mentionne le travail de Hinton.
- Dans les films The First Avenger, The Avengers. Tesseract - l'énergie de l'univers entier
Autres noms
- Hexadécachore Hexadécachore)
- Octochoron (anglais) Octachoron)
- Tétracube
- 4 cubes
- Hypercube (si le nombre de dimensions n'est pas précisé)
Remarques
Littérature
- Charles H. Hinton. Quatrième Dimension, 1904. ISBN 0-405-07953-2
- Martin Gardner, Carnaval mathématique, 1977. ISBN 0-394-72349-X
- Ian Stewart, Concepts de mathématiques modernes, 1995. ISBN 0-486-28424-7
Liens
En russe- Programme Transformator4D. Formation de modèles de projections tridimensionnelles d'objets quadridimensionnels (dont l'Hypercube).
- Un programme qui implémente la construction d'un tesseract et toutes ses transformations affines, avec un code source en C++.
En anglais
- Mushware Limited - programme de sortie tesseract ( Entraîneur Tesseract, licence compatible GPLv2) et un jeu de tir à la première personne dans un espace à quatre dimensions ( Adanaxis; les graphiques sont principalement en trois dimensions ; Il existe une version GPL dans les référentiels du système d'exploitation).
| Polyèdres | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Correct (Solides platoniciens) |
|||||||||
| Dodécaèdre étoilé Icosidodécaèdre étoilé Icosaèdre étoilé Polyèdre étoilé Octaèdre étoilé | |||||||||
| Convexe |
|
||||||||
| Formules, théorèmes, théories |
|||||||||
| Autre | |||||||||
Fondation Wikimédia.









