L'étude d'une fonction de continuité en un point s'effectue selon un schéma de routine déjà établi, qui consiste à vérifier trois conditions de continuité :

Exemple 1

Examinez la fonction pour la continuité. Déterminer la nature des discontinuités de fonction, si elles existent. Exécutez le dessin.

Solution:

1) Le seul point dans le champ d'application est celui où la fonction n'est pas définie.

Les limites unilatérales sont finies et égales.

Ainsi, à ce moment-là, la fonction souffre d'une discontinuité amovible.

A quoi ressemble le graphique de cette fonction ?

je voudrais simplifier , et il semble qu'une parabole ordinaire soit obtenue. MAIS la fonction d'origine n'est pas définie au point , donc la clause suivante est requise :

Faisons le dessin :

Répondre: la fonction est continue sur toute la droite numérique sauf le point où elle subit une discontinuité amovible.

La fonction peut être définie plus en détail d'une manière bonne ou moins bonne, mais selon la condition, cela n'est pas requis.

Vous dites que c'est un exemple tiré par les cheveux ? Pas du tout. Cela s'est produit des dizaines de fois dans la pratique. La quasi-totalité des tâches du site proviennent de véritables travaux et tests indépendants.

Débarrassons-nous de nos modules préférés :

Exemple 2

Fonction Explorer pour la continuité. Déterminer la nature des discontinuités de fonction, si elles existent. Exécutez le dessin.

Solution: Pour une raison quelconque, les étudiants ont peur et n'aiment pas les fonctions avec un module, même si elles n'ont rien de compliqué. Nous avons déjà abordé un peu ces choses dans la leçon. Transformations géométriques des graphiques. Le module étant non négatif, il est développé comme suit : , où « alpha » est une expression. Dans ce cas, notre fonction doit être écrite par morceaux :

Mais les fractions des deux morceaux doivent être réduites de . La réduction, comme dans l’exemple précédent, ne se fera pas sans conséquences. La fonction d'origine n'est pas définie au point puisque le dénominateur tend vers zéro. Par conséquent, le système doit en outre spécifier la condition et rendre la première inégalité stricte :

Parlons maintenant d'une technique de décision TRÈS UTILE: avant de finaliser la tâche sur un brouillon, il est avantageux de faire un dessin (peu importe si les conditions l'exigent ou non). Cela aidera, d'une part, à voir immédiatement les points de continuité et les points de discontinuité, et, d'autre part, cela vous protégera à 100 % des erreurs lors de la recherche de limites unilatérales.

Faisons le dessin. Conformément à nos calculs, à gauche du point il faut dessiner un fragment de parabole (couleur bleue), et à droite - un morceau de parabole (couleur rouge), alors que la fonction n'est pas définie au point lui-même :

En cas de doute, prenez quelques valeurs x et branchez-les dans la fonction (en vous rappelant que le module détruit l'éventuel signe moins) et vérifiez le graphique.

Examinons analytiquement la fonction de continuité :

1) La fonction n'est pas définie au point, on peut donc immédiatement dire qu'elle n'y est pas continue.

2) Établissons la nature de la discontinuité ; pour ce faire, nous calculons des limites unilatérales :

Les limites unilatérales sont finies et différentes, ce qui fait que la fonction subit une discontinuité de 1ère espèce avec un saut au point . Notez que peu importe que la fonction au point d'arrêt soit définie ou non.

Il ne reste plus qu'à transférer le dessin du brouillon (il a été réalisé comme avec l'aide de la recherche ;-)) et à terminer la tâche :

Répondre: la fonction est continue sur toute la droite numérique sauf au point où elle subit une discontinuité de première espèce avec un saut.

Parfois, ils nécessitent une indication supplémentaire du saut de discontinuité. Il est calculé simplement - de la limite droite, vous devez soustraire la limite gauche : , c'est-à-dire qu'au point d'arrêt, notre fonction a sauté de 2 unités (comme nous l'indique le signe moins).

Exemple 3

Fonction Explorer pour la continuité. Déterminer la nature des discontinuités de fonction, si elles existent. Faites un dessin.

Ceci est un exemple à résoudre par vous-même, un exemple de solution à la fin de la leçon.

Passons à la version la plus populaire et la plus répandue de la tâche, lorsque la fonction se compose de trois parties :

Exemple 4

Examiner la continuité d'une fonction et tracer un graphique de la fonction

Solution: il est évident que les trois parties de la fonction sont continues sur les intervalles correspondants, il ne reste donc plus qu'à vérifier deux points de « jonction » entre les pièces. Commençons par faire un brouillon de dessin ; j'ai commenté la technique de construction de manière suffisamment détaillée dans la première partie de l'article. La seule chose est qu'il faut suivre attentivement nos points singuliers : en raison de l'inégalité, la valeur appartient à la droite (point vert), et en raison de l'inégalité, la valeur appartient à la parabole (point rouge) :

Bon, en principe, tout est clair =) Il ne reste plus qu'à formaliser la décision. Pour chacun des deux points « joints », nous vérifions classiquement 3 conditions de continuité :

JE)

Les limites unilatérales sont finies et différentes, ce qui fait que la fonction subit une discontinuité de 1ère espèce avec un saut au point .

Calculons le saut de discontinuité comme la différence entre les limites droite et gauche :
, c'est-à-dire que le graphique a augmenté d'une unité.

II) Nous examinons le point de continuité

1) - la fonction est définie en un point donné.

2) Trouvez des limites unilatérales :

- les limites unilatérales sont finies et égales, ce qui signifie qu'il existe une limite générale.

Au stade final, nous transférons le dessin vers la version finale, après quoi nous mettons l'accord final :

Répondre: la fonction est continue sur toute la droite numérique, à l'exception du point où elle subit une discontinuité de première espèce avec un saut.

Exemple 5

Examiner une fonction pour la continuité et construire son graphique .

Ceci est un exemple de solution indépendante, une solution courte et un échantillon approximatif du problème à la fin de la leçon.

On peut avoir l’impression qu’à un moment donné la fonction doit être continue et à un autre il doit y avoir une discontinuité. En pratique, ce n’est pas toujours le cas. Essayez de ne pas négliger les exemples restants - il y aura plusieurs fonctionnalités intéressantes et importantes :

Exemple 6

Étant donné une fonction . Étudiez la fonction pour la continuité à certains points. Construisez un graphique.

Solution: et encore une fois, exécutez immédiatement le dessin sur le brouillon :

La particularité de ce graphique est que la fonction par morceaux est donnée par l'équation de l'axe des abscisses. Ici cette zone est dessinée en vert, mais dans un cahier elle est généralement mise en évidence en gras avec un simple crayon. Et bien sûr, n’oubliez pas nos béliers : la valeur appartient à la branche tangente (point rouge), et la valeur appartient à la droite.

Tout est clair sur le dessin - la fonction est continue sur toute la droite numérique, il ne reste plus qu'à formaliser la solution, qui est amenée à une automatisation complète littéralement après 3-4 exemples similaires :

JE) Nous examinons le point de continuité

2) Calculons les limites unilatérales :

, ce qui signifie qu'il existe une limite générale.

Une petite chose amusante s'est produite ici. Le fait est que j'ai créé beaucoup de matériaux sur les limites d'une fonction, et plusieurs fois je l'ai voulu, mais plusieurs fois j'ai oublié une question simple. Et ainsi, avec un effort de volonté incroyable, je me suis forcé à ne pas perdre la pensée =) Très probablement, certains lecteurs « nuls » doutent : quelle est la limite de la constante ? La limite d’une constante est égale à la constante elle-même. Dans ce cas, la limite de zéro est égale à zéro lui-même (limite à gauche).

3) - la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Ainsi, une fonction est continue en un point par la définition de continuité d'une fonction en un point.

II) Nous examinons le point de continuité

1) - la fonction est définie en un point donné.

2) Trouvez des limites unilatérales :

Et ici, dans la limite de droite, la limite de l'unité est égale à l'unité elle-même.

- il existe une limite générale.

3) - la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Ainsi, une fonction est continue en un point par la définition de continuité d'une fonction en un point.

Comme d'habitude, après recherche nous transférons notre dessin vers la version finale.

Répondre: la fonction est continue aux points.

Veuillez noter que dans la condition, on ne nous a rien demandé sur l'étude de la continuité de la fonction entière, et il est considéré comme une bonne forme mathématique de formuler précis et clair la réponse à la question posée. À propos, si les conditions ne vous obligent pas à construire un graphique, vous avez parfaitement le droit de ne pas le construire (bien que plus tard, l'enseignant puisse vous forcer à le faire).

Un petit « virelangue » mathématique pour le résoudre vous-même :

Exemple 7

Étant donné une fonction .

Étudiez la fonction pour la continuité à certains points. Classez les points d’arrêt, le cas échéant. Exécutez le dessin.

Essayez de "prononcer" tous les "mots" correctement =) Et dessinez le graphique plus précisément, avec précision, ce ne sera pas superflu partout ;-)

Comme vous vous en souvenez, j'ai recommandé de terminer immédiatement le dessin sous forme de brouillon, mais de temps en temps, vous rencontrez des exemples où vous ne pouvez pas comprendre immédiatement à quoi ressemble le graphique. Par conséquent, dans certains cas, il est avantageux de trouver d’abord les limites unilatérales et ensuite seulement, sur la base de l’étude, de représenter les branches. Dans les deux derniers exemples, nous apprendrons également une technique pour calculer certaines limites unilatérales :

Exemple 8

Examinez la continuité de la fonction et construisez son graphique schématique.

Solution: les mauvais points sont évidents : (réduit le dénominateur de l'exposant à zéro) et (réduit le dénominateur de la fraction entière à zéro). On ne sait pas exactement à quoi ressemble le graphique de cette fonction, ce qui signifie qu'il est préférable de faire quelques recherches d'abord :

JE) Nous examinons le point de continuité

2) Trouvez des limites unilatérales :

Veuillez noter méthode typique pour calculer une limite unilatérale: au lieu de « x » nous remplaçons . Il n'y a pas de crime au dénominateur : « l'addition » « moins zéro » ne joue aucun rôle, et le résultat est « quatre ». Mais au numérateur, il y a un petit thriller : nous tuons d'abord -1 et 1 au dénominateur de l'indicateur, ce qui donne . Unité divisée par , est égal à « moins l’infini », donc : . Et enfin, le « deux » dans degré négatif infiniment grandégal à zéro : . Ou, pour être encore plus précis : .

Calculons la limite de droite :

Et ici, au lieu de « X », nous remplaçons . Au dénominateur, l'« additif » ne joue pas non plus de rôle : . Au numérateur, des actions similaires à la limite précédente sont réalisées : on détruit les nombres opposés et on divise un par :

La limite de droite est infinie, ce qui signifie que la fonction subit une discontinuité de 2ème espèce au point .

II) Nous examinons le point de continuité

1) La fonction n'est pas définie à ce stade.

2) Calculons la limite du côté gauche :

La méthode est la même : on remplace « X » dans la fonction. Il n'y a rien d'intéressant dans le numérateur - il s'avère que c'est un nombre fini positif. Et au dénominateur on ouvre les parenthèses, on supprime les « trois », et « l'additif » joue un rôle décisif.

En conséquence, le nombre positif final divisé par nombre positif infinitésimal, donne « plus l'infini » : .

La limite de droite est comme un frère jumeau, à la seule exception qu'elle apparaît au dénominateur nombre négatif infinitésimal:

Les limites unilatérales sont infinies, ce qui signifie que la fonction subit une discontinuité de 2ème espèce au point .

Nous avons donc deux points de rupture et, évidemment, trois branches du graphique. Pour chaque branche, il convient de réaliser une construction point par point, c'est à dire prenez plusieurs valeurs « x » et remplacez-les par . Veuillez noter que la condition permet la construction d'un dessin schématique et qu'une telle relaxation est naturelle pour le travail manuel. Je construis des graphiques à l'aide d'un programme, donc je n'ai pas de telles difficultés, voici une image assez précise :

Les directs sont asymptotes verticales pour le graphique de cette fonction.

Répondre: la fonction est continue sur toute la droite numérique sauf pour les points où elle subit des discontinuités de 2ème espèce.

Une fonction plus simple à résoudre par vous-même :

Exemple 9

Examinez la continuité de la fonction et réalisez un dessin schématique.

Un exemple approximatif d'une solution à la fin qui est passée inaperçue.

À bientôt!

Solutions et réponses :

Exemple 3 :Solution : transformer la fonction : . Considérant la règle de divulgation du module et le fait que , nous réécrivons la fonction sous forme par morceaux :

Examinons la fonction pour la continuité.

1) La fonction n'est pas définie au point .

Les limites unilatérales sont finies et différentes, ce qui fait que la fonction subit une discontinuité de 1ère espèce avec un saut au point . Faisons le dessin :

Répondre: la fonction est continue sur toute la droite numérique sauf le point , dans lequel il subit une discontinuité du premier type avec un saut. Espace de saut : (deux unités plus haut).

Exemple 5 :Solution : Chacune des trois parties de la fonction est continue sur son propre intervalle.
JE)
1)

2) Calculons les limites unilatérales :

, ce qui signifie qu'il existe une limite générale.
3) - la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.
Donc la fonction continu en un point en définissant la continuité d'une fonction en un point.
II) Nous examinons le point de continuité

1) - la fonction est définie en un point donné. la fonction souffre d'une discontinuité de 2ème espèce au point

Comment trouver le domaine d'une fonction ?

Exemples de solutions

S’il manque quelque chose quelque part, c’est qu’il y a quelque chose quelque part

Nous continuons notre étude de la section « Fonctions et graphiques », et la prochaine étape de notre voyage est Domaine de fonction. Une discussion active sur ce concept a commencé dès la première leçon à propos des graphiques de fonctions, où j'ai étudié les fonctions élémentaires et, en particulier, leurs domaines de définition. Par conséquent, je recommande aux nuls de commencer par les bases du sujet, puisque je ne m'attarderai pas encore sur certains points fondamentaux.

Il est supposé que le lecteur connaît les domaines de définition des fonctions de base : fonctions linéaires, quadratiques, cubiques, polynômes, exponentielle, logarithme, sinus, cosinus. Ils sont définis le . Pour les tangentes, les arcs sinus, qu'il en soit ainsi, je vous pardonne =) Les graphiques plus rares ne sont pas immédiatement mémorisés.

La portée de la définition semble être une chose simple, et une question logique se pose : de quoi portera l’article ? Dans cette leçon, j'examinerai les problèmes courants liés à la recherche du domaine d'une fonction. Nous répéterons d’ailleurs inégalités à une variable, dont les compétences en résolution seront également requises dans d'autres problèmes de mathématiques supérieures. Soit dit en passant, le matériel est entièrement du matériel scolaire, il sera donc utile non seulement aux étudiants, mais aussi aux étudiants. L'information, bien sûr, n'a pas la prétention d'être encyclopédique, mais il ne s'agit pas ici d'exemples « morts » farfelus, mais de marrons grillés, tirés de véritables travaux pratiques.

Commençons par une introduction rapide au sujet. En bref sur l'essentiel : nous parlons d'une fonction d'une variable. Son domaine de définition est plusieurs significations de "x", pour lequel exister significations du terme « joueurs ». Regardons un exemple hypothétique :

Le domaine de définition de cette fonction est une union d'intervalles :
(pour ceux qui ont oublié : - icône d'unification). En d'autres termes, si vous prenez une valeur de « x » à partir de l'intervalle , ou de , ou de , alors pour chacun de ces « x », il y aura une valeur « y ».

En gros, là où se trouve le domaine de définition, il existe un graphique de la fonction. Mais le demi-intervalle et le point « tse » ne sont pas inclus dans la zone de définition, il n'y a donc pas de graphique là-bas.

Oui, d'ailleurs, si quelque chose n'est pas clair dans la terminologie et/ou le contenu des premiers paragraphes, il vaut mieux revenir à l'article Graphiques et propriétés des fonctions élémentaires.

Une sélection de calculatrices en ligne pour une étude complète de la fonction et tracer un graphique.

Rechercher un domaine de fonction

Calculer la fonction de parité

Calcul des points d'intersection du graphe avec l'axe (fonction zéros)

Trouver les extrema de la fonction

Points d'inflexion, intervalles de convexité et de concavité

Représenter graphiquement la fonction

Ce calculateur est conçu pour trouver les points de discontinuité des fonctions en ligne.

Les points de discontinuité de fonction sont des points auxquels la fonction présente une discontinuité et la fonction en ces points n'est pas continue.

Il existe une certaine classification des points de discontinuité fonctionnelle. Les points de discontinuité fonctionnelle sont divisés en points de discontinuité du premier type et en points de discontinuité du deuxième type.

Des points de discontinuité du premier type en x=a se produisent s'il existe des limites à gauche et à droite : lim(x→a-0)⁡f(x) et lim(x→a+0)⁡f(x) . Ces limites doivent être finies. Si au moins une des limites unilatérales est égale à zéro ou à l'infini, alors dans ce cas la fonction présente des points de discontinuité du deuxième type.

Afin de rechercher des points d'arrêt de fonction en ligne, vous devez spécifier la fonction et la valeur de l'argument.

Pour obtenir la progression complète de la solution, cliquez sur Étape par étape dans la réponse.

Explorez la fonction, créez un graphique

Plan Recherche de fonctions et représentation graphique.

La réponse signifie ce qui suit : pair - la fonction est paire, impaire - la fonction est impaire, ni paire ni impaire - la fonction n'est ni paire ni impaire.

3. Points d'intersection du graphe de fonctions avec les axes de coordonnées ;

4. Continuité de fonction, points de rupture ;

5. Asymptotes du graphe d'une fonction ;

6. Intervalles de monotonie et points critiques ;

7. Intervalles de convexité et points d'inflexion ;

8. Dessiner un graphique basé sur les recherches menées.

Services éducatifs en ligne : théorie et pratique

Solutions à des problèmes typiques - Analyse mathématique

Examinez la fonction pour la continuité, déterminez la nature de la discontinuité.

Exemple 1 .

La fonction n'est pas définie aux points, la première condition de continuité a déjà été violée, donc en ces points la fonction connaît une discontinuité.

Pour clarifier la nature de la discontinuité, il est nécessaire de calculer des limites unilatérales en certains points.

Puisque la limite gauche en un point est égale à l’infini, alors elle présente une discontinuité du deuxième type.

Puisque la limite droite en un point est égale à l’infini, il existe alors une discontinuité du deuxième type.

Exemple 2 La fonction est définie sur toute la droite numérique, mais elle n'est pas continue, puisque, c'est-à-dire les limites droite et gauche à zéro ne sont pas égales entre elles et ne sont pas égales à la valeur de la fonction à zéro, les 2ème et 3ème conditions de continuité sont violées. Puisque les limites droite et gauche à zéro existent et sont finies, il s’agit d’une discontinuité de première espèce.

Exemple 3 La fonction n'est pas définie à zéro, c'est donc un point de discontinuité.

Puisque et est une discontinuité amovible, la fonction peut être définie davantage à zéro « par continuité » en la mettant égale à un.

Exemple 4

La fonction est élémentaire, elle est donc continue dans le domaine de sa définition. Le domaine de définition n'inclut pas les points ; ce sont donc des points d'arrêt de cette fonction.

Déterminons le type de points d'arrêt.

Depuis, le point est un point

discontinuité du deuxième type de fonction.

Les limites unilatérales de la fonction en un point sont égales, mais la fonction en n'est pas définie, il s'agit donc d'un point de discontinuité amovible du premier type.

Puisque la fonction donnée est une fonction paire, il est évident que

Et c’est le point d’arrêt du deuxième type de fonction.

Pour construire une esquisse du graphique de la fonction, nous examinons le comportement de la fonction lorsque

Et. Puisque la fonction est paire, alors

Dessinons un croquis du graphique de la fonction.

Nous proposons les meilleurs manuels, à notre avis, pour l'auto-apprentissage des mathématiques et de l'économie

Documents de référence compacts, formules pour diverses sections de mathématiques supérieures et de statistiques économiques.

Certains problèmes peuvent être résolus en ligne en saisissant des valeurs numériques, avec des solutions détaillées.

Construisons (examinons) un graphique de la fonction y=f(x), pour ce faire, définissons la fonction f(x)

Important: un devrait être moins b, sinon le graphique ne pourra pas être construit. Gardez un œil sur l'échelle - s'il n'y a pas de graphique sur l'image, vous devez alors varier les valeurs. un Et b

Utilisation du diplôme

(carré et cube) et fractions

Utiliser le sinus et le cosinus

Sinus et cosinus hyperboliques

Tangente hyperbolique et cotangente

Arc sinus et arc cosinus hyperboliques

Arctangente hyberbolique et arccotangente

Pour les fonctions périodiques, le graphique de la fonction est étudié uniquement sur l'intervalle de période

Notre calculatrice vous permet d'examiner le graphique d'une fonction. Mais jusqu’à présent, il n’existe aucun moyen de trouver le domaine d’une fonction

Ce que cette calculatrice peut trouver :

Règles de saisie des expressions et des fonctions

Les expressions peuvent être constituées de fonctions (les notations sont données par ordre alphabétique) :

absolu(x) Valeur absolue x

(module x ou |x|) arccos(x) Fonction - arc cosinus de x arccosh(x) Arc cosinus hyperbolique de x arc sinus (x) Arc sinus de x arcsinh(x) Arcsinus hyperbolique de x arctan(x) Fonction - arctangente de x arctgh(x) Arctangente hyperbolique de x e e un nombre qui est approximativement égal à 2,7 exp(x) Fonction - exposant de x(ce qui est e^x) journal(x) ou ln(x) Logarithme népérien de x

(Obtenir journal7(x), vous devez saisir log(x)/log(7) (ou, par exemple, pour log10(x)=log(x)/log(10)) pi Le nombre est "Pi", qui est approximativement égal à 3,14 péché(x) Fonction - Sinus de x cos(x) Fonction - Cosinus de x sinh(x) Fonction - Sinus hyperbolique de x cosh(x) Fonction - Cosinus hyperbolique de x carré(x) Fonction - racine carrée de x carré(x) ou x^2 Fonction - Carré x bronzage(x) Fonction - Tangente de x tgh(x) Fonction - Tangente hyperbolique de x cbrt(x) Fonction - racine cubique de x étage(x) Fonction - arrondi x vers le bas (exemple floor(4.5)==4.0) signe(x) Fonction - Signe x erf(x) Fonction d'erreur (Laplace ou intégrale de probabilité)

Les opérations suivantes peuvent être utilisées dans les expressions :

Chiffres réels entrez comme 7.5 , Pas 7,5 2*x- multiplications 3/x- division x^3- exponentiation x+7- ajout x-6- soustraction

Test RU - calculateurs en ligne

Définition points d'arrêt de fonction et leurs types s'inscrivent dans la continuité du thème de la continuité de la fonction. Une explication visuelle (graphique) de la signification des points de rupture d'une fonction est également donnée en contraste avec le concept de continuité. Apprenons à trouver les points d'arrêt d'une fonction et à déterminer leurs types. Et nos amis fidèles nous y aideront - les limites gauche et droite, généralement appelées limites unilatérales. Si quelqu’un craint des limites unilatérales, nous le dissiperons bientôt.

Les points d'un graphique qui ne sont pas connectés les uns aux autres sont appelés points d'arrêt de fonction . Le graphique d'une telle fonction, qui subit une discontinuité au point x=2 - - dans la figure ci-dessous.

Une généralisation de ce qui précède est la définition suivante. Si une fonction n'est pas continue en un point, alors elle a une discontinuité en ce point et le point lui-même est appelé point d'arrêt . Les perturbations sont du premier type et du deuxième type .

Afin de déterminer types (caractère) de points d'arrêt les fonctions doivent être trouvées en toute confiance limites, c'est donc une bonne idée d'ouvrir la leçon correspondante dans une nouvelle fenêtre. Mais en ce qui concerne les points d'arrêt, nous avons quelque chose de nouveau et d'important : des limites unilatérales (gauche et droite). En général ils s'écrivent (limite droite) et (limite gauche). Comme dans le cas d'une limite en général, pour trouver la limite d'une fonction, il faut substituer X dans l'expression de la fonction à ce vers quoi X tend. Mais, peut-être, demandez-vous, en quoi les limites droite et gauche différeront-elles, si dans le cas de celle de droite quelque chose est ajouté à X, mais que ce quelque chose est nul, et dans le cas de celle de gauche, quelque chose est soustrait de X, mais ce quelque chose - zéro aussi ? Et vous aurez raison. Dans la plupart des cas.

Mais dans la pratique de recherche des points de discontinuité d'une fonction et de détermination de leur type, il existe deux cas typiques où les limites droite et gauche ne sont pas égales :

une fonction a deux expressions ou plus en fonction de la partie de la droite numérique à laquelle x appartient (ces expressions sont généralement écrites entre accolades après f(x)= );
en substituant ce vers quoi X tend, nous obtenons une fraction dont le dénominateur reste soit plus zéro (+0) soit moins zéro (-0) et donc une telle fraction signifie soit plus l'infini, soit moins l'infini, et ce sont des choses complètement différentes.

Points de discontinuité de premier type

Point de rupture du premier type : une fonction a à la fois une limite gauche finie (c'est-à-dire non égale à l'infini) et une limite droite finie, mais la fonction n'est pas définie en un point ou les limites gauche et droite sont différentes (non égales).

Point de discontinuité amovible du premier genre. Les limites gauche et droite sont égales. Dans ce cas, il est possible de définir davantage la fonction en un point. Définir une fonction en un point, en termes simples, signifie fournir une connexion de points entre lesquels se trouve un point auquel les limites gauche et droite se trouvent égales l'une à l'autre. Dans ce cas, la connexion ne doit représenter qu’un seul point où la valeur de la fonction doit être trouvée.

Exemple 1. Déterminez le point d'arrêt de la fonction et le type (caractère) du point d'arrêt.

Points de discontinuité du deuxième type

Point de rupture du deuxième type : le point auquel au moins une des limites (gauche ou droite) est infinie (égale à l'infini).

Exemple 3.

Solution. De l'expression du pouvoir à e il est clair que la fonction n'est pas définie sur le point. Trouvons les limites gauche et droite de la fonction à ce stade :

L'une des limites est égale à l'infini, le point est donc un point de discontinuité de seconde espèce. Le graphique d'une fonction avec un point d'arrêt se trouve en dessous de l'exemple.

La recherche de points d'arrêt d'une fonction peut être soit une tâche indépendante, soit une partie de Recherche et graphiques complets .

Exemple 4. Déterminer le point d'arrêt de la fonction et le type (caractère) du point d'arrêt de la fonction

Solution. D’après l’expression de la puissance en 2, il ressort clairement que la fonction n’est pas définie au point. Trouvons à ce stade les limites gauche et droite de la fonction.

Continuité de fonction. Points de rupture.

Le taureau marche, se balance, soupire en marchant :
- Oh, la planche s'épuise, maintenant je vais tomber !

Dans cette leçon, nous examinerons le concept de continuité d'une fonction, la classification des points de discontinuité et un problème pratique courant études de continuité des fonctions. D'après le nom même du sujet, de nombreuses personnes devinent intuitivement ce qui sera discuté et pensent que le matériel est assez simple. C'est vrai. Mais ce sont les tâches simples qui sont le plus souvent punies pour négligence et approche superficielle de leur résolution. Par conséquent, je vous recommande d'étudier l'article très attentivement et d'en saisir toutes les subtilités et techniques.

Que faut-il savoir et pouvoir faire ? Pas grand-chose. Pour bien apprendre la leçon, il faut comprendre de quoi il s'agit limite d'une fonction. Pour les lecteurs ayant un faible niveau de préparation, il suffit de comprendre l'article Limites de fonction. Exemples de solutions et regardez la signification géométrique de la limite dans le manuel Graphiques et propriétés des fonctions élémentaires. Il est également conseillé de se familiariser avec transformations géométriques de graphiques, puisque la pratique consiste dans la plupart des cas à construire un dessin. Les perspectives sont optimistes pour tout le monde, et même une bouilloire pleine sera capable de faire face seule à la tâche dans une heure ou deux !

Continuité de fonction. Points d'arrêt et leur classification

Notion de continuité de fonction

Considérons une fonction continue sur toute la droite numérique :

Ou, pour le dire plus succinctement, notre fonction est continue sur (l'ensemble des nombres réels).

Quel est le critère « philistin » de continuité ? Évidemment, le graphique d’une fonction continue peut être tracé sans retirer le crayon du papier.

Dans ce cas, deux notions simples doivent être clairement distinguées : domaine d'une fonction Et continuité de fonction. En général ce n'est pas la même chose. Par exemple:

Cette fonction est définie sur toute la droite numérique, c'est-à-dire pour tout le monde La signification de « x » a sa propre signification de « y ». En particulier, si , alors . A noter que l'autre point est ponctué, car par la définition d'une fonction, la valeur de l'argument doit correspondre à la seule chose valeur de la fonction. Ainsi, domaine de définition notre fonction : .

Cependant cette fonction n'est pas activée en continu ! Il est bien évident qu'au moment où elle souffre écart. Le terme est également tout à fait intelligible et visuel ; en effet, ici il faudra de toute façon arracher le crayon du papier. Un peu plus tard, nous examinerons la classification des points d'arrêt.

Continuité d'une fonction en un point et sur un intervalle

Dans un problème mathématique particulier, on peut parler de continuité d'une fonction en un point, de continuité d'une fonction sur un intervalle, un demi-intervalle, ou encore de continuité d'une fonction sur un segment. C'est, il n’y a pas de « simple continuité »– la fonction peut être continue QUELQUE PART. Et la « pierre angulaire » fondamentale de tout le reste est continuité de fonction au point .

La théorie de l'analyse mathématique donne une définition de la continuité d'une fonction en un point en utilisant les voisinages « delta » et « epsilon », mais en pratique il existe une définition différente en usage, à laquelle nous porterons une attention particulière.

Rappelons-nous d'abord limites unilatérales qui a fait irruption dans nos vies dès la première leçon à propos des graphiques de fonctions. Considérons une situation quotidienne :

Si l'on s'approche de l'axe jusqu'au point gauche(flèche rouge), puis les valeurs correspondantes des « jeux » iront le long de l'axe jusqu'au point (flèche cramoisie). Mathématiquement, ce fait est corrigé en utilisant limite à gauche:

Faites attention à l'entrée (lit "x tend vers ka à gauche"). L'« additif » « moins zéro » symbolise , cela signifie essentiellement que nous approchons du nombre du côté gauche.

De même, si vous approchez du point « ka » droite(flèche bleue), alors les « jeux » auront la même valeur, mais le long de la flèche verte, et limite à droite sera formaté comme suit :

"Additif" symbolise , et l'entrée se lit comme suit : "x tend vers ka à droite."

Si les limites unilatérales sont finies et égales(comme dans notre cas) : , alors nous dirons qu'il existe une limite GÉNÉRALE. C'est simple, la limite générale est notre « habituelle » limite d'une fonction, égal à un nombre fini.

Notez que si la fonction n'est pas définie en (faites ressortir le point noir sur la branche du graphique), alors les calculs ci-dessus restent valides. Comme cela a déjà été souligné à plusieurs reprises, notamment dans l'article sur les fonctions infinitésimales, les expressions signifient que "x" infiniment proche aborde le sujet, tandis que N'IMPORTE PAS, que la fonction elle-même soit définie à un moment donné ou non. Un bon exemple sera trouvé dans le paragraphe suivant, lorsque la fonction sera analysée.

Définition: une fonction est continue en un point si la limite de la fonction en un point donné est égale à la valeur de la fonction en ce point : .

La définition est détaillée dans les termes suivants :

1) La fonction doit être définie au point, c'est-à-dire que la valeur doit exister.

2) Il doit y avoir une limite générale de la fonction. Comme indiqué ci-dessus, cela implique l'existence et l'égalité de limites unilatérales : .

3) La limite de la fonction en un point donné doit être égale à la valeur de la fonction en ce point : .

En cas de violation au moins un des trois conditions, alors la fonction perd la propriété de continuité au point .

Continuité d'une fonction sur un intervalle est formulée ingénieusement et très simplement : une fonction est continue sur l'intervalle si elle est continue en tout point de l'intervalle donné.

En particulier, de nombreuses fonctions sont continues sur un intervalle infini, c'est-à-dire sur l'ensemble des nombres réels. Il s'agit d'une fonction linéaire, polynômes, exponentielle, sinus, cosinus, etc. Et en général, tout fonction élémentaire continu sur son domaine de définition, par exemple, une fonction logarithmique est continue sur l'intervalle . J'espère que vous avez maintenant une assez bonne idée de ce à quoi ressemblent les graphiques des fonctions de base. Des informations plus détaillées sur leur continuité peuvent être obtenues auprès d'un homme aimable nommé Fichtenholtz.

Avec la continuité d'une fonction sur un segment et des demi-intervalles, tout n'est pas non plus difficile, mais il est plus approprié d'en parler en classe sur la recherche des valeurs minimales et maximales d'une fonction sur un segment, mais pour l’instant ne nous en inquiétons pas.

Classement des points de rupture

La vie passionnante des fonctions est riche de toutes sortes de particularités, et les points d'arrêt ne sont qu'une des pages de leur biographie.

Note : au cas où, je m'attarderai sur un point élémentaire : le point de rupture est toujours point unique– il n’y a pas de « plusieurs points de rupture d’affilée », c’est-à-dire qu’il n’existe pas d’« intervalle de pause ».

Ces points, à leur tour, sont divisés en deux grands groupes : ruptures du premier type Et ruptures du deuxième type. Chaque type d'écart a ses propres caractéristiques, que nous allons examiner tout de suite :

Point de discontinuité du premier type

Si la condition de continuité est violée en un point et limites unilatérales fini , alors on l'appelle point de discontinuité du premier type.

Commençons par le cas le plus optimiste. Selon l'idée originale de la leçon, je voulais raconter la théorie « en termes généraux », mais afin de démontrer la réalité de la matière, j'ai opté pour l'option avec des personnages spécifiques.

C'est triste, comme une photo de jeunes mariés sur fond de Flamme éternelle, mais le plan suivant est généralement accepté. Représentons le graphique de la fonction dans le dessin :

Cette fonction est continue sur toute la droite numérique, à l’exception du point. Et en fait, le dénominateur ne peut pas être égal à zéro. Cependant, conformément au sens de la limite, on peut infiniment proche approchez-vous de « zéro » à la fois par la gauche et par la droite, c'est-à-dire que des limites unilatérales existent et coïncident évidemment :
(La condition n°2 de continuité est satisfaite).

Mais la fonction n'est pas définie à ce point, par conséquent, la condition n° 1 de continuité est violée et la fonction souffre d'une discontinuité à ce point.

Une rupture de ce type (avec l'existant limite générale) sont appelés espace réparable. Pourquoi amovible ? Parce que la fonction peut redéfinir au point de rupture :

Est-ce que ça a l'air étrange ? Peut être. Mais une telle notation de fonction ne contredit rien ! Maintenant, l'écart est comblé et tout le monde est content :

Effectuons un contrôle formel :

2) – il existe une limite générale ;
3)

Ainsi, les trois conditions sont satisfaites et la fonction est continue en un point par la définition de continuité d'une fonction en un point.

Cependant, les détracteurs du matan peuvent mal définir la fonction, par exemple :

Il est intéressant de noter que les deux premières conditions de continuité sont ici satisfaites :
1) – la fonction est définie en un point donné ;
2) – il existe une limite générale.

Mais la troisième frontière n'a pas été franchie : , c'est-à-dire la limite de la fonction au point pas égal la valeur d'une fonction donnée en un point donné.

Ainsi, à un moment donné, la fonction subit une discontinuité.

Le deuxième cas, plus triste, s'appelle rupture du premier type avec un saut. Et la tristesse est évoquée par des limites unilatérales qui fini et différent. Un exemple est montré dans le deuxième dessin de la leçon. Un tel écart se produit généralement dans fonctions définies par morceaux, qui ont déjà été mentionnés dans l'article à propos des transformations graphiques.

Considérons la fonction par morceaux et nous terminerons son dessin. Comment construire un graphique ? Très simple. Sur un demi-intervalle, nous dessinons un fragment de parabole (vert), sur un intervalle - un segment de droite (rouge) et sur un demi-intervalle - une ligne droite (bleue).

De plus, en raison de l'inégalité, la valeur est déterminée pour la fonction quadratique (point vert), et en raison de l'inégalité, la valeur est déterminée pour la fonction linéaire (point bleu) :

Dans le cas le plus difficile, il faudra recourir à une construction point par point de chaque élément du graphique (voir le premier leçon sur les graphiques de fonctions).

Maintenant, nous ne nous intéresserons qu'au point. Examinons-le pour la continuité :

2) Calculons les limites unilatérales.

Sur la gauche, nous avons un segment de ligne rouge, donc la limite du côté gauche est :

A droite se trouve la droite bleue, et la limite de droite :

En conséquence, nous avons reçu nombres finis, et ils pas égal. Depuis les limites unilatérales fini et différent: , alors notre fonction tolère discontinuité du premier type avec saut.

Il est logique que l'écart ne puisse pas être éliminé - la fonction ne peut vraiment pas être définie davantage et « collée ensemble », comme dans l'exemple précédent.

Points de discontinuité du deuxième type

Habituellement, tous les autres cas de rupture sont judicieusement classés dans cette catégorie. Je ne vais pas tout énumérer, car en pratique, dans 99% des problèmes que vous rencontrerez écart sans fin– qu’on soit gaucher ou droitier, et le plus souvent, les deux limites sont infinies.

Et bien sûr, l’image la plus évidente est l’hyperbole au point zéro. Ici, les deux limites unilatérales sont infinies : , la fonction subit donc une discontinuité du deuxième type au point .

J'essaie de remplir mes articles avec un contenu le plus diversifié possible, regardons donc le graphique d'une fonction qui n'a pas encore été rencontrée :

selon le schéma standard :

1) La fonction n'est pas définie à ce stade car le dénominateur tend vers zéro.

Bien sûr, on peut immédiatement conclure que la fonction subit une discontinuité au point , mais il serait bon de classifier la nature de la discontinuité, ce qui est souvent requis par la condition. Pour ce faire :

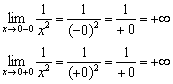
Permettez-moi de vous rappeler que par enregistrement, nous entendons nombre négatif infinitésimal, et sous l'entrée - nombre positif infinitésimal.

Les limites unilatérales sont infinies, ce qui signifie que la fonction subit une discontinuité de 2ème espèce au point . L'axe y est asymptote verticale pour le graphique.

Il n'est pas rare que les deux limites unilatérales existent, mais une seule d'entre elles est infinie, par exemple :

C'est le graphique de la fonction.

Nous examinons le point de continuité :

1) La fonction n'est pas définie à ce stade.

2) Calculons les limites unilatérales :

Nous parlerons de la méthode de calcul de ces limites unilatérales dans les deux derniers exemples de la conférence, bien que de nombreux lecteurs aient déjà tout vu et tout deviné.

La limite de gauche est finie et égale à zéro (on ne « va » pas au point lui-même), mais la limite de droite est infinie et la branche orange du graphe se rapproche de l’infini de son asymptote verticale, donné par l'équation (ligne pointillée noire).

La fonction en souffre donc discontinuité de deuxième type au point.

Comme pour une discontinuité de 1ère espèce, la fonction peut être définie au point de discontinuité lui-même. Par exemple, pour une fonction par morceaux N'hésitez pas à mettre un point noir gras à l'origine des coordonnées. A droite se trouve une branche d'une hyperbole et la limite de droite est infinie. Je pense que presque tout le monde a une idée de ce à quoi ressemble ce graphique.

Ce que tout le monde attendait avec impatience :

Comment examiner la continuité d’une fonction ?

L'étude d'une fonction de continuité en un point s'effectue selon un schéma de routine déjà établi, qui consiste à vérifier trois conditions de continuité :

Exemple 1

Fonction Explorer

Solution:

1) Le seul point dans le champ d'application est celui où la fonction n'est pas définie.

2) Calculons les limites unilatérales :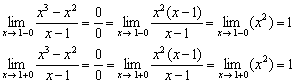

Les limites unilatérales sont finies et égales.

Ainsi, à ce moment-là, la fonction souffre d'une discontinuité amovible.

A quoi ressemble le graphique de cette fonction ?

je voudrais simplifier , et il semble qu'une parabole ordinaire soit obtenue. MAIS la fonction d'origine n'est pas définie au point , donc la clause suivante est requise :

Faisons le dessin :

Répondre: la fonction est continue sur toute la droite numérique sauf le point où elle subit une discontinuité amovible.

La fonction peut être définie plus en détail d'une manière bonne ou moins bonne, mais selon la condition, cela n'est pas requis.

Débarrassons-nous de nos modules préférés :

Exemple 2

Fonction Explorer pour la continuité. Déterminer la nature des discontinuités de fonction, si elles existent. Exécutez le dessin.

Examinons analytiquement la fonction de continuité :

1) La fonction n'est pas définie au point, on peut donc immédiatement dire qu'elle n'y est pas continue.

2) Établissons la nature de la discontinuité ; pour ce faire, nous calculons des limites unilatérales :

Les limites unilatérales sont finies et différentes, ce qui fait que la fonction subit une discontinuité de 1ère espèce avec un saut au point . Notez encore une fois que lors de la recherche de limites, peu importe que la fonction au point d'arrêt soit définie ou non.

Il ne reste plus qu'à transférer le dessin du brouillon (il a été réalisé comme avec l'aide de la recherche ;-)) et à terminer la tâche :

Répondre: la fonction est continue sur toute la droite numérique sauf au point où elle subit une discontinuité de première espèce avec un saut.

Exemple 3

Fonction Explorer pour la continuité. Déterminer la nature des discontinuités de fonction, si elles existent. Faites un dessin.

Ceci est un exemple à résoudre par vous-même, un exemple de solution à la fin de la leçon.

Passons à la version la plus populaire et la plus répandue de la tâche, lorsque la fonction se compose de trois parties :

Exemple 4

Examiner la continuité d'une fonction et tracer un graphique de la fonction .

JE) Nous examinons le point de continuité

Les limites unilatérales sont finies et différentes, ce qui fait que la fonction subit une discontinuité de 1ère espèce avec un saut au point .

Calculons le saut de discontinuité comme la différence entre les limites droite et gauche :
, c'est-à-dire que le graphique a augmenté d'une unité.

II) Nous examinons le point de continuité

1) – la fonction est définie en un point donné.

2) Trouvez des limites unilatérales :

– les limites unilatérales sont finies et égales, ce qui signifie qu’il existe une limite générale.

3) – la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Au stade final, nous transférons le dessin vers la version finale, après quoi nous mettons l'accord final :

Répondre: la fonction est continue sur toute la droite numérique, à l'exception du point où elle subit une discontinuité de première espèce avec un saut.

Exemple 5

Examiner une fonction pour la continuité et construire son graphique .

Ceci est un exemple de solution indépendante, une solution courte et un échantillon approximatif du problème à la fin de la leçon.

Exemple 6

Étant donné une fonction . Étudiez la fonction pour la continuité à certains points. Construisez un graphique.

Solution: et encore une fois, exécutez immédiatement le dessin sur le brouillon :

JE) Nous examinons le point de continuité

1) – la fonction est définie en un point donné.

2) Calculons les limites unilatérales :

, ce qui signifie qu'il existe une limite générale.

Au cas où, permettez-moi de vous rappeler un fait trivial : la limite d'une constante est égale à la constante elle-même. Dans ce cas, la limite de zéro est égale à zéro lui-même (limite à gauche).

3) – la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Ainsi, une fonction est continue en un point par la définition de continuité d'une fonction en un point.

II) Nous examinons le point de continuité

1) – la fonction est définie en un point donné.

2) Trouvez des limites unilatérales :

Et ici – la limite d’un est égale à l’unité elle-même.

– il existe une limite générale.

3) – la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Ainsi, une fonction est continue en un point par la définition de continuité d'une fonction en un point.

Comme d'habitude, après recherche nous transférons notre dessin vers la version finale.

Répondre: la fonction est continue aux points.

Un petit « virelangue » mathématique pour le résoudre vous-même :

Exemple 7

Étant donné une fonction . Étudiez la fonction pour la continuité à certains points. Classez les points d’arrêt, le cas échéant. Exécutez le dessin.

Essayez de "prononcer" tous les "mots" correctement =) Et dessinez le graphique plus précisément, avec précision, ce ne sera pas superflu partout ;-)

Exemple 8

Examinez la continuité de la fonction et construisez son graphique schématique.

Établissement d'enseignement "État biélorusse

Académie agricole"

Département de mathématiques supérieures

Lignes directrices

pour étudier le thème « Continuité des fonctions d'une variable »

étudiants de la faculté de comptabilité par correspondance

éducation (NISPO)

Gorki, 2013

Continuité des fonctions d'une variable

Limites unilatérales

Laissez la fonction
défini sur le plateau
. Introduisons le concept de limites unilatérales d'une fonction à
. Nous considérerons les valeurs suivantes X, Quoi
. Cela signifie que
, restant tout le temps à gauche de
à
alors ça s'appelle limite gauche cette fonction au point (ou quand
) et est noté

Laisse-le maintenant
, restant tout le temps à droite de , c'est-à-dire rester plus longtemps . S'il y a une limite à la fonction
, alors on l'appelle limite droite cette fonction au point et est désigné

Les limites gauche et droite sont appelées limites à sens unique fonctionne en un point.

S'il y a des limites unilatérales d'une fonction en un point et qu'elles sont égales les unes aux autres, alors la fonction a la même limite en ce point:

Si les limites unilatérales d'une fonction en un point existent, mais ne sont pas égaux, alors la limite de la fonction à ce stade n'existe pas .

Continuité d'une fonction en un point

Laissez la fonction
défini sur un ensemble D. Soit la variable indépendante X part d'une de ses valeurs (initiales)
à une autre valeur (finale) . La différence entre les valeurs finales et initiales s'appelle incrément quantités X et est désigné
. L'incrément peut être positif ou négatif. Dans le premier cas, la valeur X en déménageant de À X augmente et dans le second cas - diminue.

Si la variable indépendante X obtient un incrément
, alors la fonction
obtient un incrément
. Parce que
, Que.

Incrément de fonction
au point s'appelle la différence, où
– incrément de la variable indépendante.

Plusieurs définitions de la continuité d'une fonction en un point peuvent être données.

La fonction s'appelle continu dans l'intervalle , s'il est continu en tout point de cet intervalle. Continuité géométrique d'une fonction
dans un intervalle fermé signifie que le graphique de la fonction est une ligne continue sans coupures.

Les fonctions continues sur un intervalle ont des propriétés importantes qui sont exprimées par les instructions suivantes.

Si la fonction
est continue sur l'intervalle [ un, b], alors il est limité sur ce segment.

Si la fonction
est continue sur l'intervalle [ un, b], il atteint alors ses valeurs minimales et maximales sur ce segment.

Si la fonction
est continue sur l'intervalle [ un, b] Et
, alors quel que soit le nombre AVEC, entouré de chiffres UN Et DANS, il y a un point
, Quoi
.

De cette affirmation il résulte que si la fonction
est continu sur [ un, b] et aux extrémités de ce segment prend des valeurs de signes différents, alors il y a au moins un point sur ce segment c, dans lequel la fonction disparaît.

La déclaration suivante est vraie : si des opérations arithmétiques sont effectuées sur des fonctions continues, le résultat est une fonction continueJE.

Exemple 1 .

au point
.

Solution . Valeur de fonction à
Il y a
. Calculons les limites unilatérales de la fonction au point
:

Puisque les limites unilatérales à
sont égaux entre eux et égaux à la valeur de la fonction en ce point, alors cette fonction est continue en ce point
.

3. Continuité des fonctions élémentaires

Considérez la fonction
. Cette fonction constante est continue en tout point , parce que
.

Fonction
est également continu en tout point
, parce que
. Parce que
, puis basé sur la déclaration ci-dessus sur les opérations arithmétiques sur les fonctions continues
sera continu. Les fonctions seront également continues
.

De même, nous pouvons montrer la continuité des fonctions élémentaires restantes.

Ainsi, toute fonction élémentaire est continue dans son domaine de définition, c'est-à-dire Le domaine de définition d'une fonction élémentaire coïncide avec le domaine de sa continuité.

Continuité des fonctions complexes et inverses

Laissez la fonction
continu en un point , et la fonction
continu en un point
. Alors la fonction complexe
continu en un point . Cela signifie que si une fonction complexe est composée de fonctions continues, alors elle sera également continue, c'est-à-dire une fonction continue à partir d'une fonction continue est une fonction continue . Cette définition s'étend à un nombre fini de fonctions continues.

De cette définition il résulte que sous le signe d'une fonction continue on peut aller à la limite :

Cela signifie que si la fonction est continue, alors le signe de la limite et le signe de la fonction peuvent être intervertis.

Laissez la fonction
défini, strictement monotone et continu sur l'intervalle [ un, b]. Alors sa fonction inverse
défini, strictement monotone et continu sur l'intervalle [ UN, B], Où
.

Points d'arrêt et leur classification je

Comme on le sait déjà, si la fonction
défini sur le plateau D et au point
la condition est remplie
, alors la fonction est continue à ce stade. Si cette condition de continuité n'est pas satisfaite, alors au point X La fonction 0 a un écart.

Point appelé point de discontinuité du premier type fonctions
, si à ce stade la fonction a des limites finies unilatérales qui ne sont pas égales les unes aux autres, c'est-à-dire . Dans ce cas, la valeur

appelé brusquement fonctions
au point .

Point appelé point de rupture amovible fonctions
, si les limites unilatérales de la fonction en ce point sont égales les unes aux autres et ne sont pas égales à la valeur de la fonction en ce point, c'est-à-dire Dans ce cas, pour éliminer l'écart au point il faut mettre

Point X 0 est appelé point de discontinuité du deuxième type fonctions
si au moins une des limites unilatérales
ou
à ce stade, soit n'existe pas, soit est égal à l'infini.

Exemple 2 . Examiner la continuité d'une fonction

Solution . La fonction est définie et continue sur toute la droite numérique, à l'exception du point
. À ce stade, la fonction présente une discontinuité. Trouvons les limites unilatérales de la fonction au point
:

Puisqu'au moment
les limites unilatérales sont égales les unes aux autres et la fonction à ce stade n'est pas définie, alors le point
est un point de rupture amovible. Pour éliminer l'écart à ce stade, il est nécessaire de définir davantage la fonction en mettant
.

Exemple 3 . Examiner la continuité d'une fonction

Solution . La fonction est définie et continue sur l'ensemble des nombres réels sauf
. À ce stade, la fonction présente une discontinuité. Trouvons les limites unilatérales de la fonction à
:

Puisque cette fonction au point
a des limites finies unilatérales qui ne sont pas égales entre elles, alors ce point est un point de discontinuité de première espèce. Saut d'une fonction en un point
égal.